Gaussian Processes for Vegetation Parameter Estimation from Hyperspectral Data with Limited Ground Truth
Abstract
1. Introduction
2. Background
2.1. Gaussian Processes for Regression
2.2. Covariance Functions
2.2.1. Stationary Covariance Functions
2.2.2. Non-Stationary Covariance Functions
Spectral covariance functions:
2.3. Multitask Learning
3. Datasets
3.1. Algae Dataset
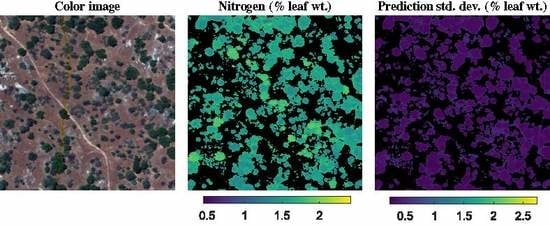
3.2. NEON Dataset
3.3. SPARC Dataset
3.4. Synthetic Dataset
4. Experimental Results
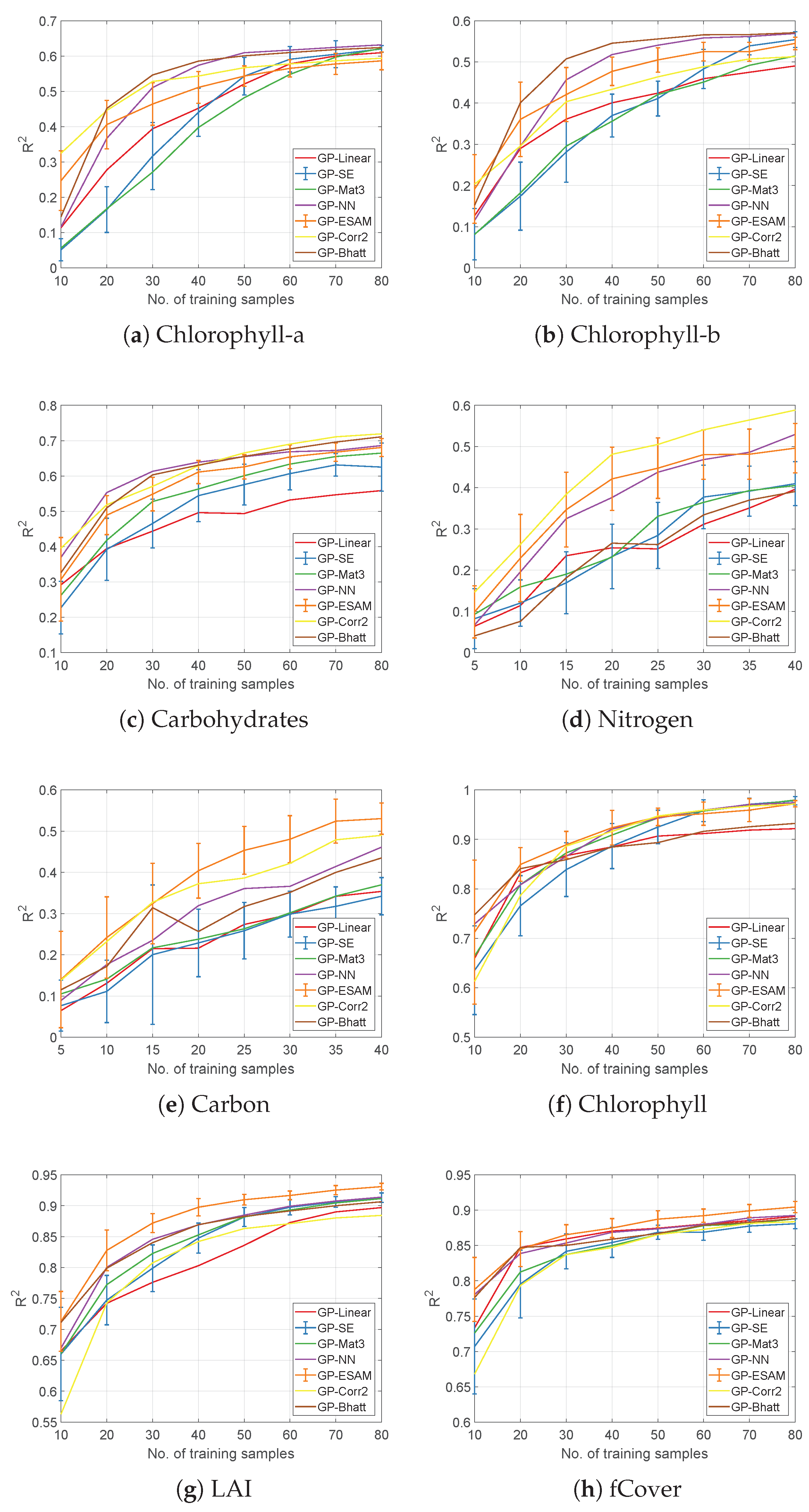
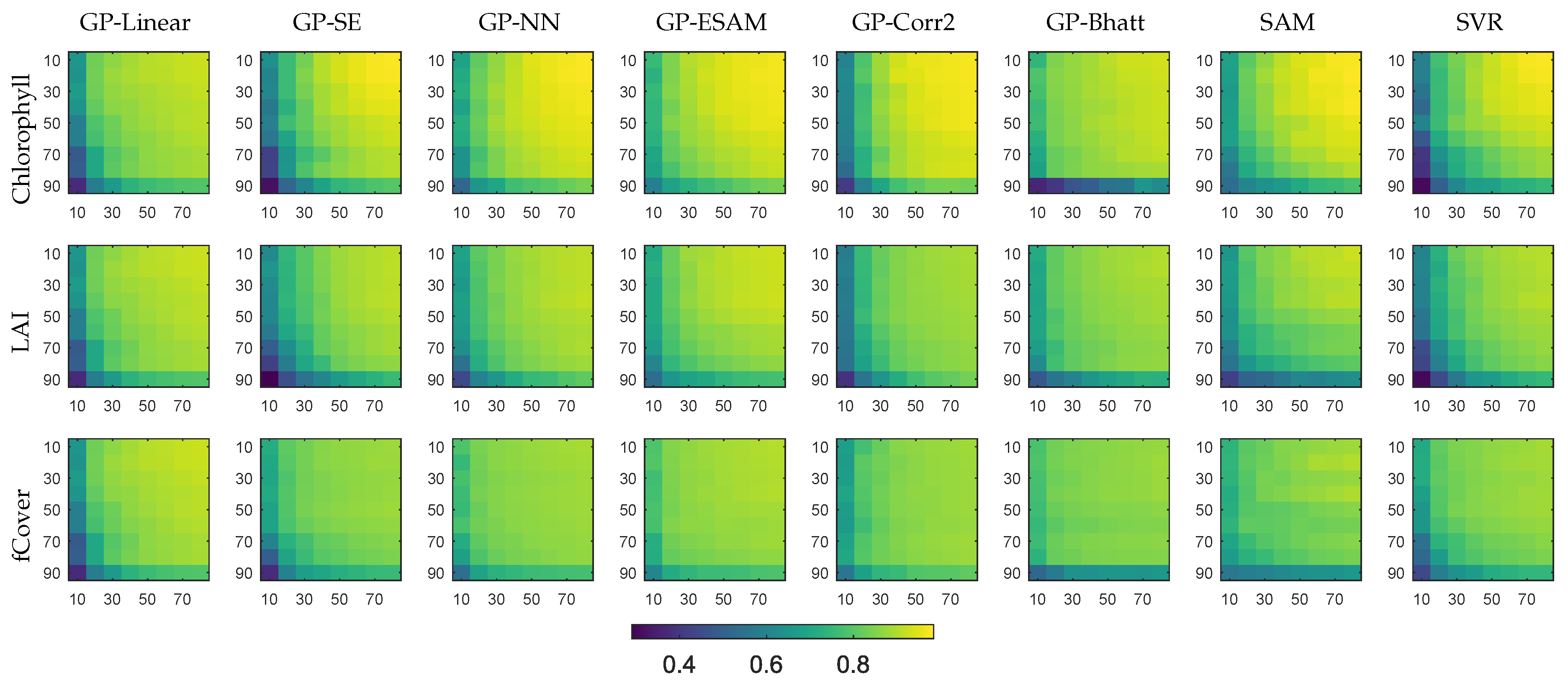
4.1. Evaluation of Covariance Functions
4.2. Evaluation of Multitask Gaussian Processes
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Verrelst, J.; Malenovskỳ, Z.; Van der Tol, C.; Camps-Valls, G.; Gastellu-Etchegorry, J.P.; Lewis, P.; North, P.; Moreno, J. Quantifying Vegetation Biophysical Variables from Imaging Spectroscopy Data: A Review on Retrieval Methods. Surv. Geophys. 2019, 40, 589–629. [Google Scholar] [CrossRef]
- Eismann, M.T. Hyperspectral Remote Sensing; SPIE Press: Bellingham, WA, USA, 2012. [Google Scholar]
- Ramoelo, A.; Skidmore, A.; Cho, M.; Mathieu, R.; Heitkönig, I.; Dudeni-Tlhone, N.; Schlerf, M.; Prins, H. Non-linear partial least square regression increases the estimation accuracy of grass nitrogen and phosphorus using in situ hyperspectral and environmental data. ISPRS J. Photogramm. Remote Sens. 2013, 82, 27–40. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C.; Corsi, F.; Cho, M. LAI and chlorophyll estimation for a heterogeneous grassland using hyperspectral measurements. ISPRS J. Photogramm. Remote Sens. 2008, 63, 409–426. [Google Scholar] [CrossRef]
- Verrelst, J.; Muñoz-Marí, J.; Alonso, L.; Delegido, J.; Rivera, J.P.; Camps-Valls, G.; Moreno, J. Machine learning regression algorithms for biophysical parameter retrieval: Opportunities for Sentinel-2 and -3. Remote Sens. Environ. 2012, 118, 127–139. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Muñoz-Marí, J.; Gómez-Chova, L.; Richter, K.; Calpe-Maravilla, J. Biophysical parameter estimation with a semisupervised support vector machine. IEEE Geosci. Remote Sens. Lett. 2009, 6, 248–252. [Google Scholar] [CrossRef]
- Verrelst, J.; Alonso, L.; Caicedo, J.P.R.; Moreno, J.; Camps-Valls, G. Gaussian process retrieval of chlorophyll content from imaging spectroscopy data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 867–874. [Google Scholar] [CrossRef]
- Verrelst, J.; Alonso, L.; Camps-Valls, G.; Delegido, J.; Moreno, J. Retrieval of Vegetation Biophysical Parameters Using Gaussian Process Techniques. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1832–1843. [Google Scholar] [CrossRef]
- Pasolli, E.; Melgani, F.; Alajlan, N.; Bazi, Y. Active learning methods for biophysical parameter estimation. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4071–4084. [Google Scholar] [CrossRef]
- Bannari, A.; Morin, D.; Bonn, F.; Huete, A. A review of vegetation indices. Remote Sens. Rev. 1995, 13, 95–120. [Google Scholar] [CrossRef]
- Pasqualotto, N.; Delegido, J.; Van Wittenberghe, S.; Verrelst, J.; Rivera, J.P.; Moreno, J. Retrieval of canopy water content of different crop types with two new hyperspectral indices: Water Absorption Area Index and Depth Water Index. Int. J. Appl. Earth Obs. Geoinf. 2018, 67, 69–78. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT+ SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Gewali, U.B.; Monteiro, S.T.; Saber, E. Machine learning based hyperspectral image analysis: A survey. arXiv 2018, arXiv:1802.08701. [Google Scholar]
- Camps-Valls, G.; Verrelst, J.; Muñoz-Marí, J.; Laparra, V.; Mateo-Jimenez, F.; Gomez-Dans, J. A Survey on Gaussian Processes for Earth-Observation Data Analysis: A Comprehensive Investigation. IEEE Geosci. Remote Sens. Mag. 2016, 4, 58–78. [Google Scholar] [CrossRef]
- Pasolli, L.; Melgani, F.; Blanzieri, E. Gaussian process regression for estimating chlorophyll concentration in subsurface waters from remote sensing data. IEEE Geosci. Remote Sens. Lett. 2010, 7, 464–468. [Google Scholar] [CrossRef]
- Lázaro-Gredilla, M.; Titsias, M.K.; Verrelst, J.; Camps-Valls, G. Retrieval of biophysical parameters with heteroscedastic Gaussian processes. IEEE Geosci. Remote Sens. Lett. 2014, 11, 838–842. [Google Scholar] [CrossRef]
- Bazi, Y.; Melgani, F. Semisupervised Gaussian process regression for biophysical parameter estimation. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 July 2010; pp. 4248–4251. [Google Scholar] [CrossRef]
- Muñoz-Marí, J.; Verrelst, J.; Lázaro-Gredilla, M.; Camps-Vails, G. Biophysical parameter retrieval with warped Gaussian processes. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 13–16. [Google Scholar]
- Svendsen, D.H.; Martino, L.; Campos-Taberner, M.; García-Haro, F.J.; Camps-Valls, G. Joint Gaussian processes for biophysical parameter retrieval. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1718–1727. [Google Scholar] [CrossRef]
- Ni, C.; Wang, D.; Tao, Y. Variable weighted convolutional neural network for the nitrogen content quantization of Masson pine seedling leaves with near-infrared spectroscopy. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2019, 209, 32–39. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, T.; Xu, J.; Luo, X.; Ying, Y. DeepSpectra: An end-to-end deep learning approach for quantitative spectral analysis. Anal. Chim. Acta 2019, 1058, 48–57. [Google Scholar] [CrossRef] [PubMed]
- Rasmussen, C.E.; Williams, C. Gaussian Processes for Machine Learning; The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Cho, Y.; Saul, L.K. Kernel methods for deep learning. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2009; pp. 342–350. Available online: https://papers.nips.cc/paper/3628-kernel-methods-for-deep-learning (accessed on 8 May 2019).
- Paciorek, C.J.; Schervish, M.J. Nonstationary covariance functions for Gaussian process regression. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2004; pp. 273–280. Available online: https://papers.nips.cc/paper/2350-nonstationary-covariance-functions-for-gaussian-process-regression (accessed on 8 May 2019).
- Remes, S.; Heinonen, M.; Kaski, S. Non-stationary spectral kernels. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2017; pp. 4642–4651. Available online: https://papers.nips.cc/paper/7050-non-stationary-spectral-kernels (accessed on 8 May 2019).
- Zorzi, M.; Chiuso, A. The harmonic analysis of kernel functions. Automatica 2018, 94, 125–137. [Google Scholar] [CrossRef]
- Paciorek, C.J.; Schervish, M.J. Spatial modelling using a new class of nonstationary covariance functions. Environmetrics 2006, 17, 483–506. [Google Scholar] [CrossRef]
- Lang, T.; Plagemann, C.; Burgard, W. Adaptive Non-Stationary Kernel Regression for Terrain Modeling. In Robotics: Science and Systems; MIT Press: Cambridge, MA, USA, 2007; Volume 6. [Google Scholar]
- Zorzi, M.; Chiuso, A. Sparse plus low rank network identification: A nonparametric approach. Automatica 2017, 76, 355–366. [Google Scholar] [CrossRef]
- Van der Meer, F. The effectiveness of spectral similarity measures for the analysis of hyperspectral imagery. Int. J. Appl. Earth Obs. Geoinf. 2006, 8, 3–17. [Google Scholar] [CrossRef]
- Melkumyan, A.; Nettleton, E. An Observation Angle Dependent Nonstationary Covariance Function for Gaussian Process Regression. In Neural Information Processing; Lecture Notes in Computer Science; Springer: Berlin, Germany, 2009; pp. 331–339. [Google Scholar]
- Schneider, S.; Murphy, R.J.; Melkumyan, A. Evaluating the performance of a new classifier–the GP-OAD: A comparison with existing methods for classifying rock type and mineralogy from hyperspectral imagery. ISPRS J. Photogramm. Remote Sens. 2014, 98, 145–156. [Google Scholar] [CrossRef]
- Gewali, U.B.; Monteiro, S.T. A novel covariance function for predicting vegetation biochemistry from hyperspectral imagery with Gaussian processes. In Proceedings of the International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 2216–2220. [Google Scholar] [CrossRef]
- Jiang, H.; Ching, W.K. Correlation kernels for support vector machines classification with applications in cancer data. Comput. Math. Methods Med. 2012, 2012, 205025. [Google Scholar] [CrossRef] [PubMed]
- Moreno, P.J.; Ho, P.P.; Vasconcelos, N. A Kullback-Leibler divergence based kernel for SVM classification in multimedia applications. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Vancouver, BC, Canada, 13–18 December 2004; pp. 1385–1392. [Google Scholar]
- Chan, A.B.; Vasconcelos, N.; Moreno, P.J. A Family of Probabilistic Kernels Based on Information Divergence; Technical Report SVCL-TR-2004-1; University of California: San Diego, CA, USA, 2004. [Google Scholar]
- Maji, S.; Berg, A.C.; Malik, J. Efficient classification for additive kernel SVMs. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 66–77. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Bonilla, E.V.; Chai, K.M.; Williams, C. Multi-task Gaussian process prediction. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2008; pp. 153–160. Available online: https://papers.nips.cc/paper/3189-multi-task-gaussian-process-prediction (accessed on 8 May 2019).
- Rakitsch, B.; Lippert, C.; Borgwardt, K.; Stegle, O. It is all in the noise: Efficient multi-task Gaussian process inference with structured residuals. In Advances in Neural Information Processing Systems (NIPS); The MIT Press: Cambridge, MA, USA, 2013; pp. 1466–1474. Available online: https://papers.nips.cc/paper/5089-it-is-all-in-the-noise-efficient-multi-task-gaussian-process-inference-with-structured-residuals (accessed on 8 May 2019).
- Nguyen, T.V.; Bonilla, E.V. Collaborative Multi-output Gaussian Processes. In Proceedings of the Uncertainty in Artificial Intelligence (UAI), Quebec City, QC, Canada, 23–27 July 2014; pp. 643–652. [Google Scholar]
- Melkumyan, A.; Ramos, F. Multi-kernel Gaussian processes. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), Barcelona, Spain, 16–22 July 2011. [Google Scholar]
- Álvarez, M.A.; Lawrence, N.D. Computationally efficient convolved multiple output Gaussian processes. J. Mach. Learn. Res. 2011, 12, 1459–1500. [Google Scholar]
- Parra, G.; Tobar, F. Spectral mixture kernels for multi-output Gaussian processes. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 6681–6690. [Google Scholar]
- Leen, G.; Peltonen, J.; Kaski, S. Focused multi-task learning in a Gaussian process framework. Mach. Learn. 2012, 89, 157–182. [Google Scholar] [CrossRef]
- Liu, H.; Cai, J.; Ong, Y.S. Remarks on multi-output Gaussian process regression. Knowl.-Based Syst. 2018, 144, 102–121. [Google Scholar] [CrossRef]
- Murphy, R.J.; Tolhurst, T.J.; Chapman, M.G.; Underwood, A.J. Estimation of surface chlorophyll-a on an emersed mudflat using field spectrometry: accuracy of ratios and derivative-based approaches. Int. J. Remote Sens. 2005, 26, 1835–1859. [Google Scholar] [CrossRef]
- National Ecological Observatory Network (NEON). 2013. Available online: http://data.neonscience.org (accessed on 8 August 2016).
- Kampe, T.; Leisso, N.; Musinsky, J.; Petroy, S.; Karpowiez, B.; Krause, K.; Crocker, R.I.; DeVoe, M.; Penniman, E.; Guadagno, T.; et al. The NEON 2013 airborne campaign at domain 17 terrestrial and aquatic sites in California. In NEON Technical Memorandum Series, TM-005; National Ecological Observatory Network (NEON): Boulder, CO, USA, 2013. [Google Scholar]
- Moreno, J.; Alonso, L.; Fernández, G.; Fortea, J.; Gandía, S.; Guanter, L.; García, J.; Martí, J.; Melia, J.; De Coca, F.; et al. The SPECTRA Barrax Campaign (SPARC): Overview and First Results from CHRIS Data. In Proceedings of the 2nd CHRIS/Proba Workshop, Frascati, Italy, 28–30 April 2004; Available online: http://earth.esa.int/workshops/chris_proba_04/book.pdf (accessed on 8 May 2019).
- Teillet, P. Image correction for radiometric effects in remote sensing. Int. J. Remote Sens. 1986, 7, 1637–1651. [Google Scholar] [CrossRef]
- Vermote, E.F.; Tanré, D.; Deuze, J.L.; Herman, M.; Morcette, J.J. Second simulation of the satellite signal in the solar spectrum, 6S: An overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Smith, G.M.; Milton, E.J. The use of the empirical line method to calibrate remotely sensed data to reflectance. Int. J. Remote Sens. 1999, 20, 2653–2662. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Gómez-Chova, L.; Muñoz-Marí, J.; Lázaro-Gredilla, M.; Verrelst, J. simpleR: A Simple Educational Matlab Toolbox for Statistical Regression, V2.1. 2013. Available online: http://www.uv.es/gcamps/code/simpleR.html (accessed on 20 January 2019).
- Caicedo, J.P.R.; Verrelst, J.; Muñoz-Marí, J.; Moreno, J.; Camps-Valls, G. Toward a semiautomatic machine learning retrieval of biophysical parameters. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1249–1259. [Google Scholar] [CrossRef]
- Verrelst, J.; Dethier, S.; Rivera, J.P.; Muñoz-Marí, J.; Camps-Valls, G.; Moreno, J. Active learning methods for efficient hybrid biophysical variable retrieval. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1012–1016. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Gitelson, A.; Delegido, J.; Moreno, J.; Camps-Valls, G. Spectral band selection for vegetation properties retrieval using Gaussian processes regression. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 554–567. [Google Scholar] [CrossRef]
- Rivera-Caicedo, J.P.; Verrelst, J.; Muñoz-Marí, J.; Camps-Valls, G.; Moreno, J. Hyperspectral dimensionality reduction for biophysical variable statistical retrieval. ISPRS J. Photogramm. Remote Sens. 2017, 132, 88–101. [Google Scholar] [CrossRef]
- Mateo-Sanchis, A.; Muñoz-Marí, J.; Pérez-Suay, A.; Camps-Valls, G. Warped Gaussian Processes in Remote Sensing Parameter Estimation and Causal Inference. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1647–1651. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Nickisch, H. Gaussian processes for machine learning (GPML) toolbox. J. Mach. Learn. Res. 2010, 11, 3011–3015. [Google Scholar]
- Izquierdo-Verdiguier, E.; Gómez-Chova, L.; Camps-Valls, G.; Muñoz-Marí, J. simFeat 2.2: MATLAB Feature Extraction Toolbox. Available online: https://github.com/IPL-UV/simFeat (accessed on 2 April 2019).
- Bishop, C.M. Pattern Recognition and Machine Learning (Information Science and Statistics); Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Verhoef, W.; Jia, L.; Xiao, Q.; Su, Z. Unified optical-thermal four-stream radiative transfer theory for homogeneous vegetation canopies. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1808–1822. [Google Scholar] [CrossRef]
- Major, D.J.; McGinn, S.M.; Gillespie, T.J.; Baret, F. A technique for determination of single leaf reflectance and transmittance in field studies. Remote Sens. Environ. 1993, 43, 209–215. [Google Scholar] [CrossRef]
- Kallel, A.; Le Hégarat-Mascle, S.; Ottlé, C.; Hubert-Moy, L. Determination of vegetation cover fraction by inversion of a four-parameter model based on isoline parametrization. Remote Sens. Environ. 2007, 111, 553–566. [Google Scholar] [CrossRef]
- Snelson, E.; Ghahramani, Z. Sparse Gaussian processes using pseudo-inputs. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2006; pp. 1257–1264. Available online: https://papers.nips.cc/paper/2857-sparse-gaussian-processes-using-pseudo-inputs (accessed on 8 May 2019).
- Dezfouli, A.; Bonilla, E.V. Scalable Inference for Gaussian Process Models with Black-Box Likelihoods. In Advances in Neural Information Processing Systems (NIPS); The MIT Press: Cambridge, MA, USA, 2015; pp. 1414–1422. Available online: https://papers.nips.cc/paper/5665-scalable-inference-for-gaussian-process-models-with-black-box-likelihoods (accessed on 8 May 2019).
- Titsias, M. Variational learning of inducing variables in sparse Gaussian processes. In Proceedings of the Artificial Intelligence and Statistics, Clearwater Beach, FL, USA, 16–18 April 2009; pp. 567–574. [Google Scholar]
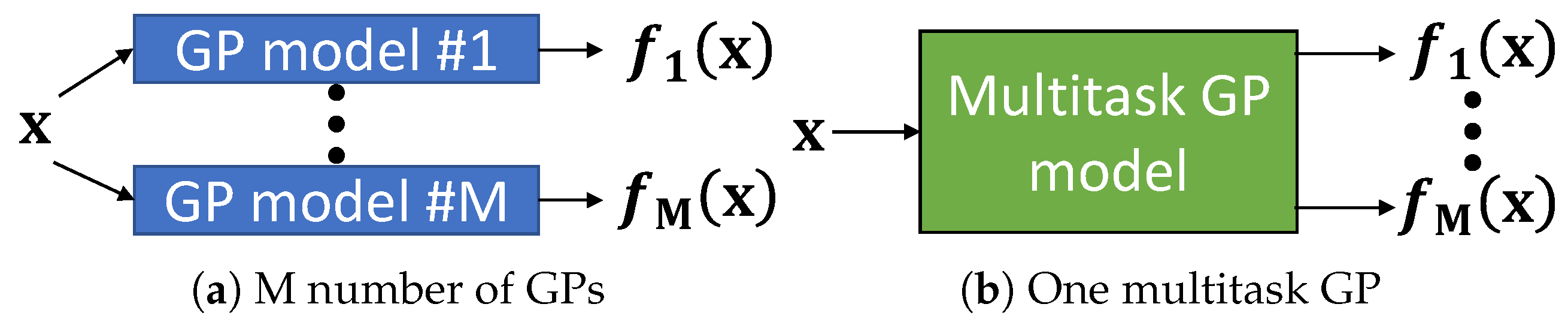


| Covariance Functions | |
|---|---|
| Squared exponential (SE) | |
| Exponential (Exp) | |
| Matern 3/2 (Mat3) | |
| Matern 5/2 (Mat5) |
| Covariance Functions | |
|---|---|
| Linear | |
| Polynomial (Poly) | |
| Neural network (NN) | |
| Spectral Functions | |
| Exponential SAM (ESAM) | |
| Observation angle dependent (OAD) | |
| Correlation-1 (Corr-1) | |
| Correlation-2 (Corr-2) | |
| Spectral information divergence (SID) | |
| Bhattacharya (Bhatt) | |
| Chi-squared (Chi2) |
| Method | Algae Dataset | NEON Dataset | SPARC Dataset | |||||
|---|---|---|---|---|---|---|---|---|
| Chlorophyll-a | Chlorophyll-b | Carbohydrates | Nitrogen | Carbon | Chlorophyll | LAI | fCover | |
| GP-SE | 0.623 ± 0.011 | 0.562 ± 0.008 | 0.660 ± 0.022 | 0.463 ± 0.039 | 0.392 ± 0.035 | 0.986 ± 0.001 | 0.925 ± 0.003 | 0.888 ± 0.006 |
| GP-Exp | 0.496 ± 0.031 | 0.470 ± 0.016 | 0.688 ± 0.016 | 0.401 ± 0.037 | 0.447 ± 0.038 | 0.980 ± 0.014 | 0.929 ± 0.004 | 0.891 ± 0.007 |
| GP-Mat3 | 0.627 ± 0.011 | 0.543 ± 0.016 | 0.684 ± 0.016 | 0.441 ± 0.042 | 0.401 ± 0.034 | 0.987 ± 0.001 | 0.919 ± 0.004 | 0.899 ± 0.004 |
| GP-Mat5 | 0.627 ± 0.010 | 0.560 ± 0.015 | 0.668 ± 0.017 | 0.448 ± 0.041 | 0.381 ± 0.036 | 0.987 ± 0.001 | 0.921 ± 0.005 | 0.897 ± 0.006 |
| GP-Linear | 0.619 ± 0.009 | 0.506 ± 0.013 | 0.562 ± 0.012 | 0.446 ± 0.043 | 0.392 ± 0.033 | 0.929 ± 0.005 | 0.908 ± 0.003 | 0.900 ± 0.005 |
| GP-Poly2 | 0.621 ± 0.012 | 0.561 ± 0.009 | 0.614 ± 0.018 | 0.515 ± 0.046 | 0.388 ± 0.034 | 0.964 ± 0.004 | 0.920 ± 0.003 | 0.897 ± 0.005 |
| GP-Poly3 | 0.623 ± 0.010 | 0.557 ± 0.009 | 0.632 ± 0.016 | 0.509 ± 0.048 | 0.387 ± 0.034 | 0.965 ± 0.004 | 0.920 ± 0.003 | 0.890 ± 0.005 |
| GP-NN | 0.634 ± 0.011 | 0.575 ± 0.009 | 0.695 ± 0.011 | 0.548 ± 0.043 | 0.541 ± 0.045 | 0.983 ± 0.001 | 0.927 ± 0.003 | 0.908 ± 0.005 |
| GP-ESAM | 0.598 ± 0.021 | 0.549 ± 0.014 | 0.690 ± 0.017 | 0.528 ± 0.037 | 0.550 ± 0.035 | 0.981 ± 0.002 | 0.938 ± 0.004 | 0.912 ± 0.005 |
| GP-OAD | 0.599 ± 0.020 | 0.550 ± 0.014 | 0.691 ± 0.016 | 0.530 ± 0.037 | 0.550 ± 0.035 | 0.981 ± 0.002 | 0.938 ± 0.004 | 0.912 ± 0.005 |
| GP-Corr1 | 0.596 ± 0.011 | 0.520 ± 0.012 | 0.723 ± 0.011 | 0.624 ± 0.029 | 0.500 ± 0.026 | 0.944 ± 0.004 | 0.898 ± 0.004 | 0.889 ± 0.003 |
| GP-Corr2 | 0.599 ± 0.014 | 0.526 ± 0.017 | 0.724 ± 0.011 | 0.617 ± 0.023 | 0.525 ± 0.045 | 0.975 ± 0.003 | 0.896 ± 0.003 | 0.897 ± 0.005 |
| GP-SID | 0.607 ± 0.029 | 0.570 ± 0.008 | 0.584 ± 0.092 | 0.563 ± 0.076 | 0.182 ± 0.098 | 0.285 ± 0.115 | 0.325 ± 0.128 | 0.707 ± 0.132 |
| GP-Bhatt | 0.623 ± 0.012 | 0.573 ± 0.008 | 0.727 ± 0.011 | 0.441 ± 0.037 | 0.465 ± 0.032 | 0.938 ± 0.004 | 0.916 ± 0.004 | 0.899 ± 0.005 |
| GP-Chi2 | 0.617 ± 0.012 | 0.568 ± 0.008 | 0.731 ± 0.010 | 0.553 ± 0.041 | 0.442 ± 0.038 | 0.982 ± 0.002 | 0.926 ± 0.005 | 0.911 ± 0.007 |
| PLS | 0.622 ± 0.011 | 0.538 ± 0.011 | 0.640 ± 0.022 | 0.606 ± 0.058 | 0.501 ± 0.058 | 0.915 ± 0.007 | 0.901 ± 0.008 | 0.881 ± 0.008 |
| RF | 0.471 ± 0.036 | 0.415 ± 0.025 | 0.610 ± 0.019 | 0.460 ± 0.037 | 0.406 ± 0.039 | 0.910 ± 0.018 | 0.915 ± 0.006 | 0.880 ± 0.010 |
| SAM | 0.412 ± 0.041 | 0.370 ± 0.027 | 0.566 ± 0.027 | 0.295 ± 0.048 | 0.371 ± 0.039 | 0.992 ± 0.003 | 0.921 ± 0.005 | 0.896 ± 0.013 |
| SVR | 0.606 ± 0.022 | 0.556 ± 0.022 | 0.660 ± 0.031 | 0.441 ± 0.062 | 0.347 ± 0.051 | 0.987 ± 0.001 | 0.927 ± 0.006 | 0.906 ± 0.009 |
| KRR | 0.594 ± 0.049 | 0.544 ± 0.029 | 0.633 ± 0.086 | 0.461 ± 0.099 | 0.355 ± 0.083 | 0.982 ± 0.003 | 0.923 ± 0.006 | 0.896 ± 0.009 |
| VHGPR | 0.585 ± 0.033 | 0.526 ± 0.023 | 0.627 ± 0.029 | 0.208 ± 0.068 | 0.472 ± 0.055 | 0.983 ± 0.004 | 0.934 ± 0.006 | 0.872 ± 0.014 |
| GP-BAT | 0.605 ± 0.018 | 0.555 ± 0.013 | 0.653 ± 0.023 | 0.333 ± 0.096 | 0.313 ± 0.086 | 0.986 ± 0.002 | 0.926 ± 0.007 | 0.861 ± 0.015 |
| PLS-GPR | 0.611 ± 0.020 | 0.550 ± 0.018 | 0.684 ± 0.023 | 0.388 ± 0.077 | 0.441 ± 0.063 | 0.986 ± 0.002 | 0.899 ± 0.008 | 0.834 ± 0.016 |
| WGP | 0.636 ± 0.012 | 0.563 ± 0.012 | 0.688 ± 0.052 | 0.427 ± 0.109 | 0.481 ± 0.078 | 0.982 ± 0.010 | 0.926 ± 0.004 | 0.887 ± 0.008 |
| Method | Algae Dataset | NEON Dataset | SPARC Dataset | |||||
|---|---|---|---|---|---|---|---|---|
| Chlorophyll-a | Chlorophyll-b | Carbohydrates | Nitrogen | Carbon | Chlorophyll | LAI | fCover | |
| GP-SE | 9.716 ± 0.138 | 0.323 ± 0.003 | 8.701 ± 0.278 | 0.275 ± 0.012 | 1.712 ± 0.057 | 2.134 ± 0.106 | 0.457 ± 0.008 | 0.115 ± 0.003 |
| GP-Exp | 11.284 ± 0.330 | 0.355 ± 0.005 | 8.343 ± 0.218 | 0.290 ± 0.011 | 1.632 ± 0.062 | 2.486 ± 0.564 | 0.443 ± 0.011 | 0.113 ± 0.003 |
| GP-Mat3 | 9.667 ± 0.135 | 0.330 ± 0.006 | 8.397 ± 0.202 | 0.281 ± 0.013 | 1.700 ± 0.054 | 2.072 ± 0.079 | 0.475 ± 0.012 | 0.109 ± 0.002 |
| GP-Mat5 | 9.662 ± 0.136 | 0.323 ± 0.005 | 8.604 ± 0.216 | 0.279 ± 0.013 | 1.730 ± 0.059 | 2.059 ± 0.075 | 0.467 ± 0.014 | 0.110 ± 0.003 |
| GP-Linear | 9.766 ± 0.123 | 0.343 ± 0.005 | 9.896 ± 0.139 | 0.278 ± 0.012 | 1.711 ± 0.052 | 4.764 ± 0.176 | 0.504 ± 0.009 | 0.108 ± 0.003 |
| GP-Poly2 | 9.736 ± 0.152 | 0.323 ± 0.003 | 9.286 ± 0.218 | 0.261 ± 0.014 | 1.717 ± 0.053 | 3.367 ± 0.167 | 0.472 ± 0.008 | 0.110 ± 0.003 |
| GP-Poly3 | 9.717 ± 0.135 | 0.325 ± 0.003 | 9.060 ± 0.201 | 0.263 ± 0.015 | 1.718 ± 0.053 | 3.361 ± 0.165 | 0.469 ± 0.009 | 0.113 ± 0.002 |
| GP-NN | 9.575 ± 0.139 | 0.318 ± 0.003 | 8.238 ± 0.144 | 0.251 ± 0.014 | 1.517 ± 0.094 | 2.326 ± 0.069 | 0.450 ± 0.009 | 0.104 ± 0.003 |
| GP-ESAM | 10.035 ± 0.256 | 0.327 ± 0.005 | 8.311 ± 0.223 | 0.256 ± 0.011 | 1.478 ± 0.066 | 2.509 ± 0.143 | 0.416 ± 0.012 | 0.101 ± 0.003 |
| GP-OAD | 10.017 ± 0.248 | 0.327 ± 0.005 | 8.302 ± 0.220 | 0.255 ± 0.011 | 1.478 ± 0.066 | 2.505 ± 0.143 | 0.416 ± 0.012 | 0.102 ± 0.003 |
| GP-Corr1 | 10.062 ± 0.138 | 0.338 ± 0.004 | 7.850 ± 0.150 | 0.229 ± 0.009 | 1.554 ± 0.045 | 4.221 ± 0.133 | 0.530 ± 0.010 | 0.114 ± 0.002 |
| GP-Corr2 | 10.017 ± 0.179 | 0.336 ± 0.006 | 7.835 ± 0.159 | 0.234 ± 0.008 | 1.543 ± 0.106 | 2.817 ± 0.148 | 0.537 ± 0.008 | 0.110 ± 0.003 |
| GP-SID | 9.918 ± 0.365 | 0.320 ± 0.003 | 9.668 ± 1.031 | 0.248 ± 0.021 | 2.079 ± 0.152 | 15.069 ± 1.236 | 1.362 ± 0.134 | 0.181 ± 0.042 |
| GP-Bhatt | 9.711 ± 0.151 | 0.318 ± 0.003 | 7.800 ± 0.160 | 0.278 ± 0.012 | 1.605 ± 0.053 | 4.429 ± 0.134 | 0.483 ± 0.012 | 0.109 ± 0.003 |
| GP-Chi2 | 9.792 ± 0.158 | 0.320 ± 0.003 | 7.745 ± 0.147 | 0.253 ± 0.014 | 1.690 ± 0.088 | 2.399 ± 0.135 | 0.454 ± 0.015 | 0.102 ± 0.004 |
| PLS | 9.773 ± 0.163 | 0.335 ± 0.005 | 9.191 ± 0.364 | 0.247 ± 0.026 | 1.683 ± 0.139 | 5.213 ± 0.224 | 0.525 ± 0.023 | 0.120 ± 0.005 |
| RF | 11.514 ± 0.391 | 0.373 ± 0.008 | 9.320 ± 0.219 | 0.272 ± 0.009 | 1.686 ± 0.056 | 5.342 ± 0.516 | 0.485 ± 0.017 | 0.119 ± 0.005 |
| SAM | 13.270 ± 0.603 | 0.421 ± 0.012 | 10.372 ± 0.327 | 0.360 ± 0.018 | 2.111 ± 0.102 | 1.608 ± 0.257 | 0.473 ± 0.017 | 0.112 ± 0.007 |
| SVR | 10.007 ± 0.278 | 0.326 ± 0.008 | 8.714 ± 0.407 | 0.289 ± 0.023 | 1.820 ± 0.095 | 2.078 ± 0.110 | 0.451 ± 0.020 | 0.105 ± 0.005 |
| KRR | 10.119 ± 0.607 | 0.330 ± 0.011 | 9.236 ± 1.393 | 0.287 ± 0.040 | 1.896 ± 0.208 | 2.370 ± 0.210 | 0.464 ± 0.020 | 0.110 ± 0.005 |
| VHGPR | 10.241 ± 0.415 | 0.336 ± 0.009 | 9.125 ± 0.347 | 0.337 ± 0.018 | 1.595 ± 0.084 | 2.343 ± 0.288 | 0.429 ± 0.019 | 0.123 ± 0.007 |
| GP-BAT | 9.954 ± 0.245 | 0.325 ± 0.005 | 8.833 ± 0.312 | 0.324 ± 0.041 | 2.087 ± 0.375 | 2.096 ± 0.138 | 0.406 ± 0.019 | 0.113 ± 0.006 |
| PLS-GPR | 9.878 ± 0.260 | 0.327 ± 0.007 | 8.416 ± 0.325 | 0.312 ± 0.029 | 1.726 ± 0.161 | 2.129 ± 0.142 | 0.473 ± 0.018 | 0.123 ± 0.006 |
| WGP | 9.659 ± 0.132 | 0.326 ± 0.004 | 8.380 ± 0.700 | 0.297 ± 0.054 | 1.736 ± 0.259 | 2.368 ± 0.505 | 0.453 ± 0.013 | 0.115 ± 0.004 |
| Algae Dataset | ||||
| No. Samples | 10 | 30 | 50 | 70 |
| Primary: Chlorophyll-a, Secondary: Chlorophyll-b | ||||
| GP | 0.246 ± 0.082 | 0.475 ± 0.055 | 0.538 ± 0.044 | 0.583 ± 0.028 |
| MTGP1 | 0.438 ± 0.031 | 0.546 ± 0.024 | 0.555 ± 0.031 | 0.574 ± 0.039 |
| MTGP2 | 0.412 ± 0.039 | 0.518 ± 0.043 | 0.564 ± 0.024 | 0.583 ± 0.024 |
| Primary: Chlorophyll-b, Secondary: Chlorophyll-a | ||||
| GP | 0.192 ± 0.071 | 0.435 ± 0.071 | 0.492 ± 0.043 | 0.528 ± 0.024 |
| MTGP1 | 0.444 ± 0.039 | 0.493 ± 0.039 | 0.519 ± 0.028 | 0.528 ± 0.025 |
| MTGP2 | 0.428 ± 0.039 | 0.499 ± 0.034 | 0.530 ± 0.028 | 0.539 ± 0.020 |
| NEON Dataset | ||||
| No. Samples | 5 | 15 | 25 | 35 |
| Primary: Nitrogen, Secondary: Carbon | ||||
| GP | 0.115 ± 0.074 | 0.330 ± 0.103 | 0.475 ± 0.072 | 0.505 ± 0.055 |
| MTGP1 | 0.094 ± 0.086 | 0.462 ± 0.077 | 0.493 ± 0.051 | 0.514 ± 0.050 |
| MTGP2 | 0.029 ± 0.033 | 0.412 ± 0.087 | 0.499 ± 0.068 | 0.517 ± 0.047 |
| Primary: Carbon, Secondary: Nitrogen | ||||
| GP | 0.139 ± 0.102 | 0.341 ± 0.109 | 0.469 ± 0.057 | 0.513 ± 0.053 |
| MTGP1 | 0.364 ± 0.116 | 0.465 ± 0.052 | 0.503 ± 0.055 | 0.530 ± 0.044 |
| MTGP2 | 0.326 ± 0.129 | 0.495 ± 0.060 | 0.518 ± 0.050 | 0.522 ± 0.040 |
| SPARC Dataset | ||||
| No. Samples | 5 | 10 | 15 | 20 |
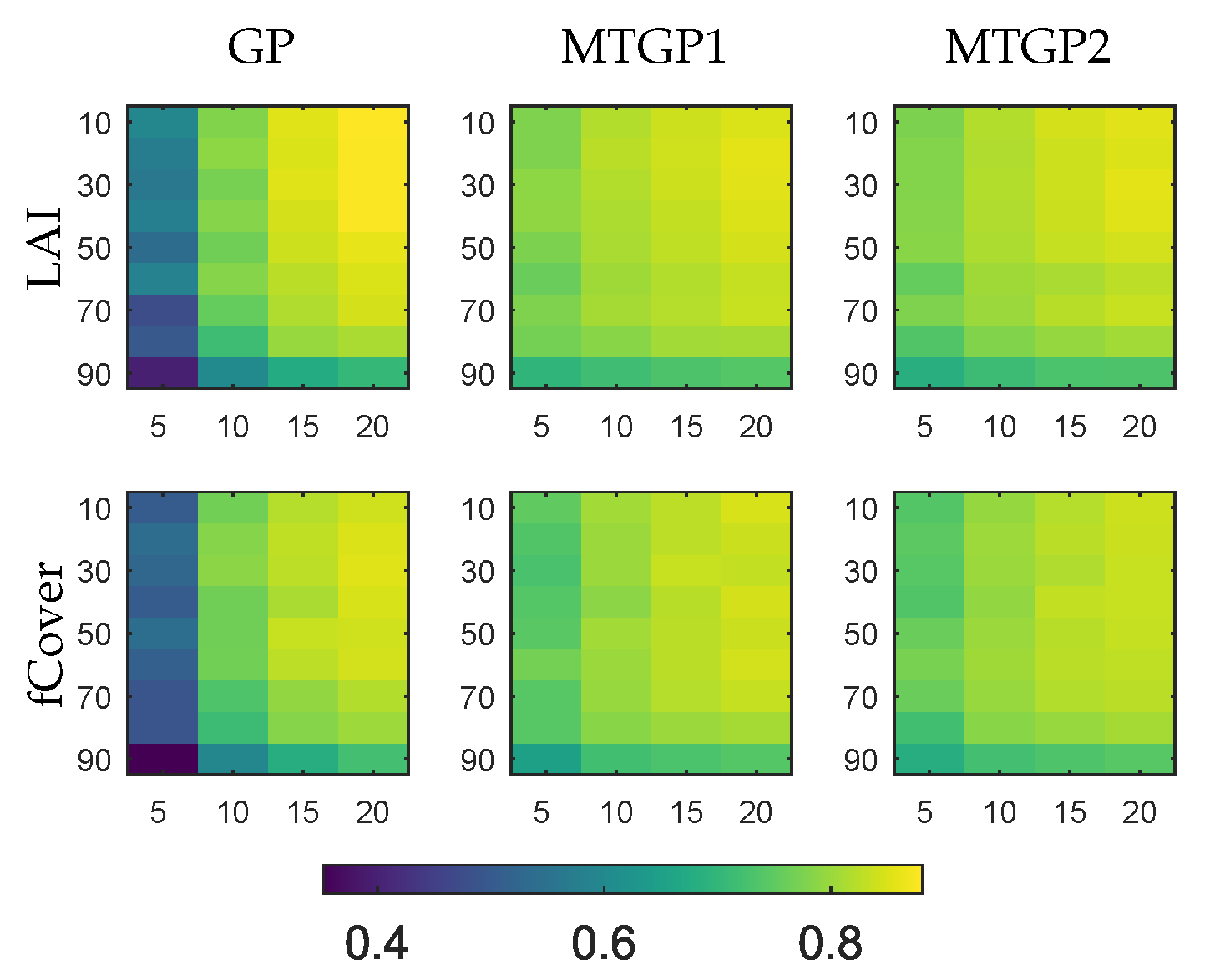
| Primary: LAI, Secondary: fCover | ||||
| GP | 0.615 ± 0.099 | 0.784 ± 0.045 | 0.851 ± 0.023 | 0.870 ± 0.023 |
| MTGP1 | 0.768 ± 0.048 | 0.806 ± 0.033 | 0.814 ± 0.076 | 0.836 ± 0.020 |
| MTGP2 | 0.771 ± 0.047 | 0.811 ± 0.016 | 0.827 ± 0.014 | 0.847 ± 0.014 |
| Primary: fCover, Secondary: LAI | ||||
| GP | 0.569 ± 0.110 | 0.762 ± 0.062 | 0.822 ± 0.047 | 0.852 ± 0.015 |
| MTGP1 | 0.738 ± 0.058 | 0.809 ± 0.022 | 0.825 ± 0.018 | 0.845 ± 0.014 |
| MTGP2 | 0.745 ± 0.050 | 0.799 ± 0.025 | 0.828 ± 0.018 | 0.838 ± 0.017 |
| Algae Dataset | ||||
| No. Samples | 10 | 30 | 50 | 70 |
| Primary: Chlorophyll-a, Secondary: Carbohydrates | ||||
| GP | 0.222 ± 0.075 | 0.471 ± 0.054 | 0.535 ± 0.032 | 0.576 ± 0.025 |
| MTGP1 | 0.230 ± 0.043 | 0.383 ± 0.072 | 0.498 ± 0.050 | 0.566 ± 0.027 |
| MTGP2 | 0.229 ± 0.045 | 0.364 ± 0.055 | 0.515 ± 0.052 | 0.569 ± 0.030 |
| Primary: Chlorophyll-b, Secondary: Carbohydrates | ||||
| GP | 0.168 ± 0.093 | 0.412 ± 0.069 | 0.497 ± 0.039 | 0.532 ± 0.026 |
| MTGP1 | 0.298 ± 0.074 | 0.410 ± 0.046 | 0.471 ± 0.037 | 0.513 ± 0.033 |
| MTGP2 | 0.333 ± 0.049 | 0.385 ± 0.043 | 0.462 ± 0.041 | 0.509 ± 0.023 |
| Primary: Carbohydrates, Secondary: Chlorophyll-a | ||||
| GP | 0.319 ± 0.101 | 0.553 ± 0.056 | 0.634 ± 0.027 | 0.670 ± 0.024 |
| MTGP1 | 0.283 ± 0.079 | 0.534 ± 0.049 | 0.620 ± 0.044 | 0.660 ± 0.027 |
| MTGP2 | 0.295 ± 0.058 | 0.521 ± 0.044 | 0.623 ± 0.036 | 0.664 ± 0.018 |
| Primary: Carbohydrates, Secondary: Chlorophyll-b | ||||
| GP | 0.297 ± 0.085 | 0.532 ± 0.053 | 0.625 ± 0.038 | 0.665 ± 0.031 |
| MTGP1 | 0.415 ± 0.061 | 0.536 ± 0.036 | 0.601 ± 0.051 | 0.651 ± 0.026 |
| MTGP2 | 0.426 ± 0.060 | 0.528 ± 0.036 | 0.601 ± 0.040 | 0.654 ± 0.026 |
| SPARC Dataset | ||||
| No. Samples | 5 | 10 | 15 | 20 |
| Primary: Chlorophyll, Secondary: LAI | ||||
| GP | 0.541 ± 0.130 | 0.758 ± 0.061 | 0.819 ± 0.038 | 0.852 ± 0.042 |
| MTGP1 | 0.284 ± 0.108 | 0.552 ± 0.135 | 0.718 ± 0.078 | 0.761 ± 0.086 |
| MTGP2 | 0.270 ± 0.108 | 0.659 ± 0.082 | 0.800 ± 0.047 | 0.842 ± 0.041 |
| Primary: Chlorophyll, Secondary: fCover | ||||
| GP | 0.452 ± 0.129 | 0.733 ± 0.095 | 0.837 ± 0.040 | 0.867 ± 0.027 |
| MTGP1 | 0.370 ± 0.128 | 0.584 ± 0.172 | 0.757 ± 0.112 | 0.763 ± 0.127 |
| MTGP2 | 0.360 ± 0.133 | 0.612 ± 0.129 | 0.811 ± 0.038 | 0.861 ± 0.040 |
| Primary: LAI, Secondary: Chlorophyll | ||||
| GP | 0.459 ± 0.118 | 0.700 ± 0.056 | 0.789 ± 0.039 | 0.828 ± 0.027 |
| MTGP1 | 0.243 ± 0.160 | 0.586 ± 0.113 | 0.705 ± 0.128 | 0.785 ± 0.068 |
| MTGP2 | 0.246 ± 0.147 | 0.493 ± 0.105 | 0.704 ± 0.062 | 0.789 ± 0.049 |
| Primary: fCover, Secondary: Chlorophyll | ||||
| GP | 0.539 ± 0.137 | 0.746 ± 0.094 | 0.833 ± 0.029 | 0.841 ± 0.033 |
| MTGP1 | 0.234 ± 0.179 | 0.534 ± 0.230 | 0.602 ± 0.251 | 0.727 ± 0.188 |
| MTGP2 | 0.274 ± 0.136 | 0.600 ± 0.082 | 0.766 ± 0.055 | 0.809 ± 0.048 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gewali, U.B.; Monteiro, S.T.; Saber, E. Gaussian Processes for Vegetation Parameter Estimation from Hyperspectral Data with Limited Ground Truth. Remote Sens. 2019, 11, 1614. https://doi.org/10.3390/rs11131614
Gewali UB, Monteiro ST, Saber E. Gaussian Processes for Vegetation Parameter Estimation from Hyperspectral Data with Limited Ground Truth. Remote Sensing. 2019; 11(13):1614. https://doi.org/10.3390/rs11131614
Chicago/Turabian StyleGewali, Utsav B., Sildomar T. Monteiro, and Eli Saber. 2019. "Gaussian Processes for Vegetation Parameter Estimation from Hyperspectral Data with Limited Ground Truth" Remote Sensing 11, no. 13: 1614. https://doi.org/10.3390/rs11131614
APA StyleGewali, U. B., Monteiro, S. T., & Saber, E. (2019). Gaussian Processes for Vegetation Parameter Estimation from Hyperspectral Data with Limited Ground Truth. Remote Sensing, 11(13), 1614. https://doi.org/10.3390/rs11131614