Crack Propagation and Fracture Process Zone (FPZ) of Wood in the Longitudinal Direction Determined Using Digital Image Correlation (DIC) Technique
Abstract
1. Introduction
2. Methods
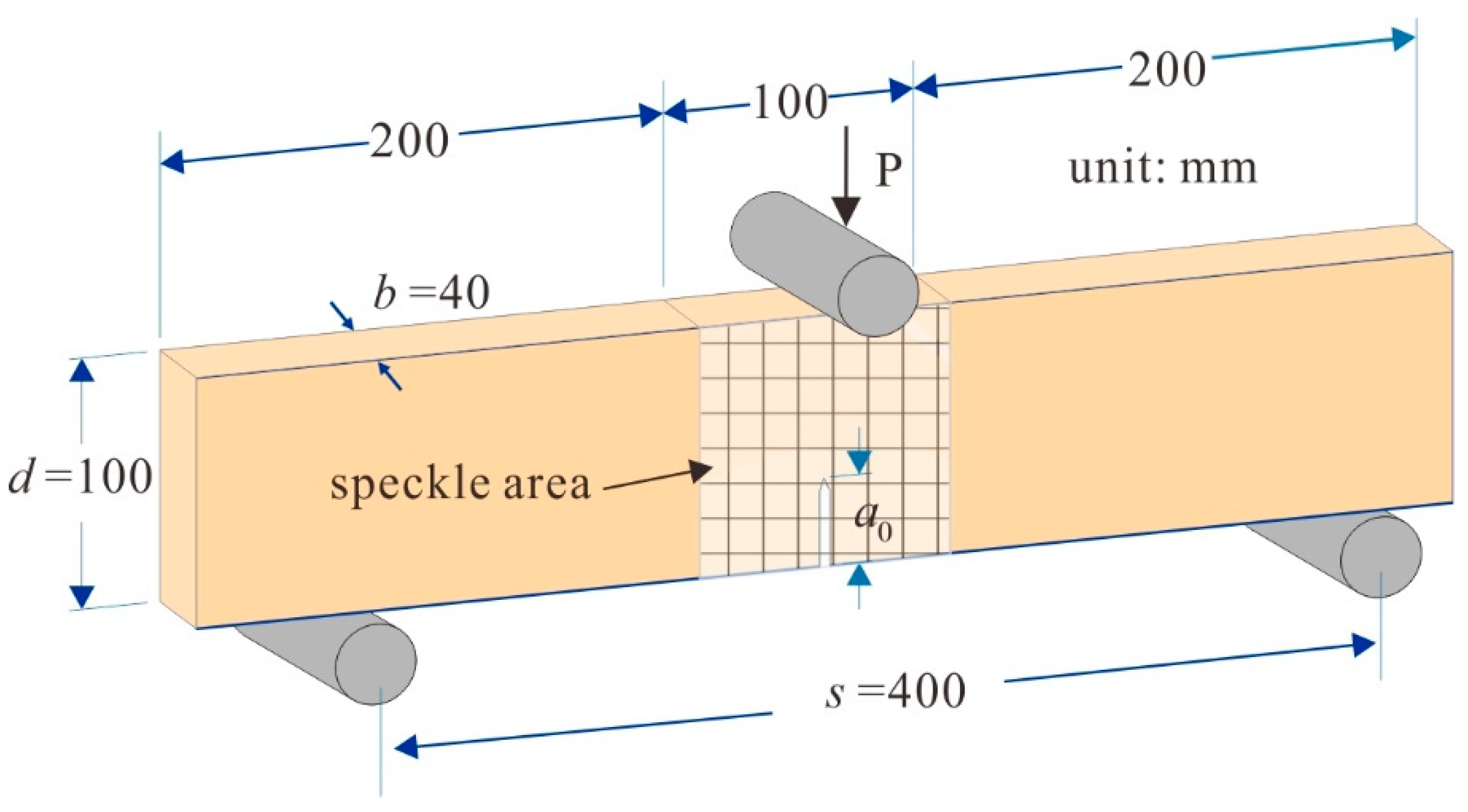
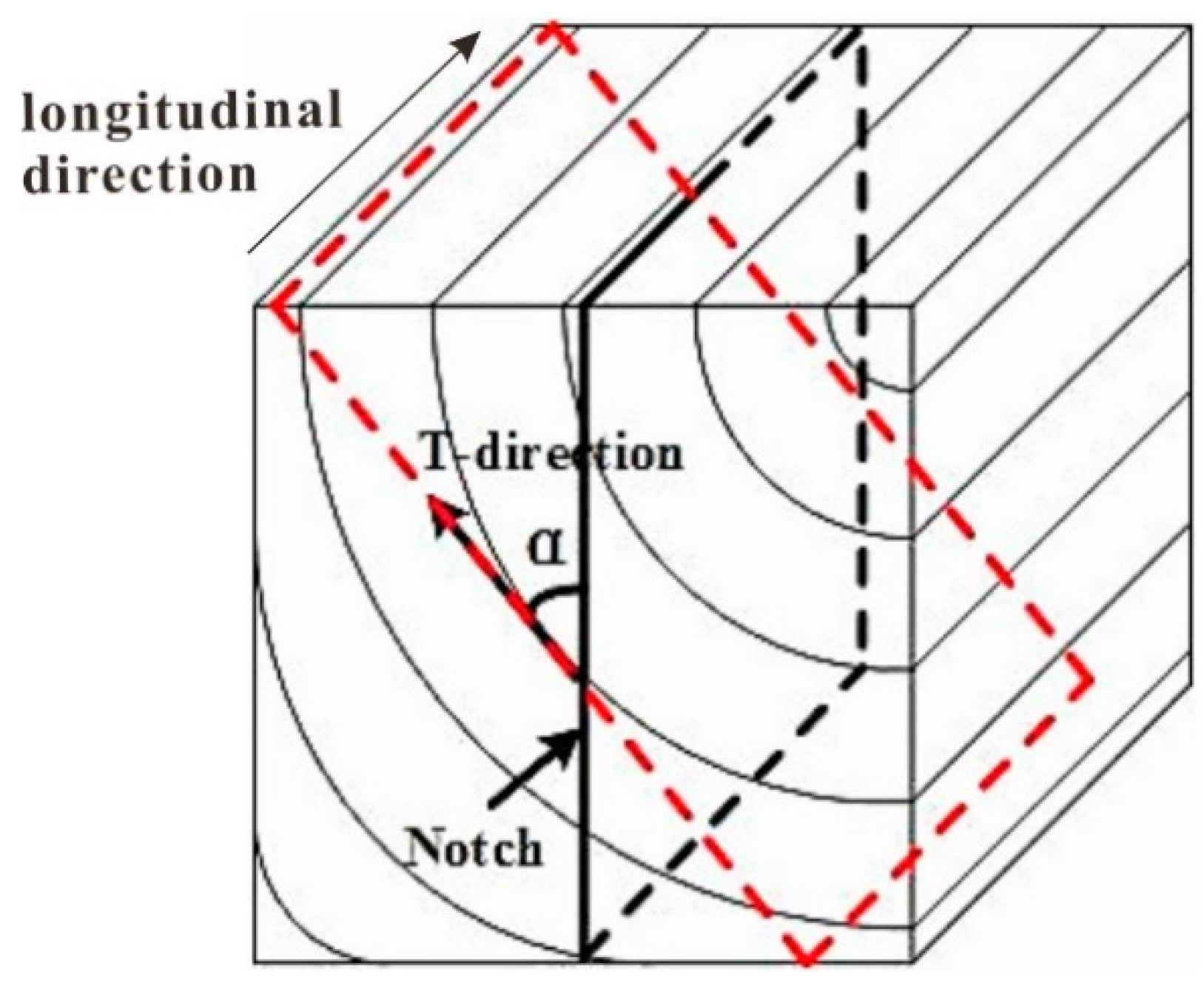
2.1. 3-p-b Fracture and DIC Test
2.2. Test Set-Up
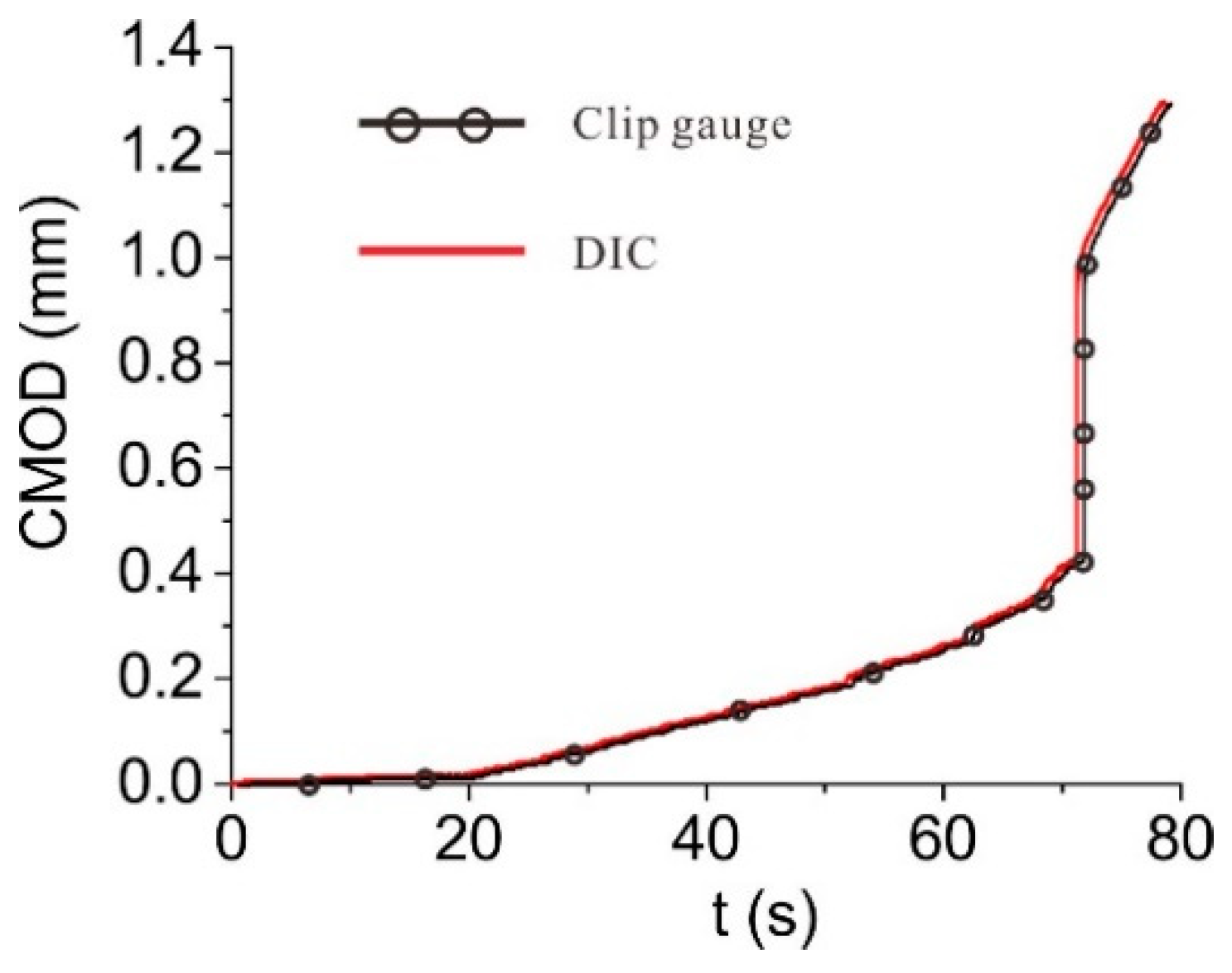
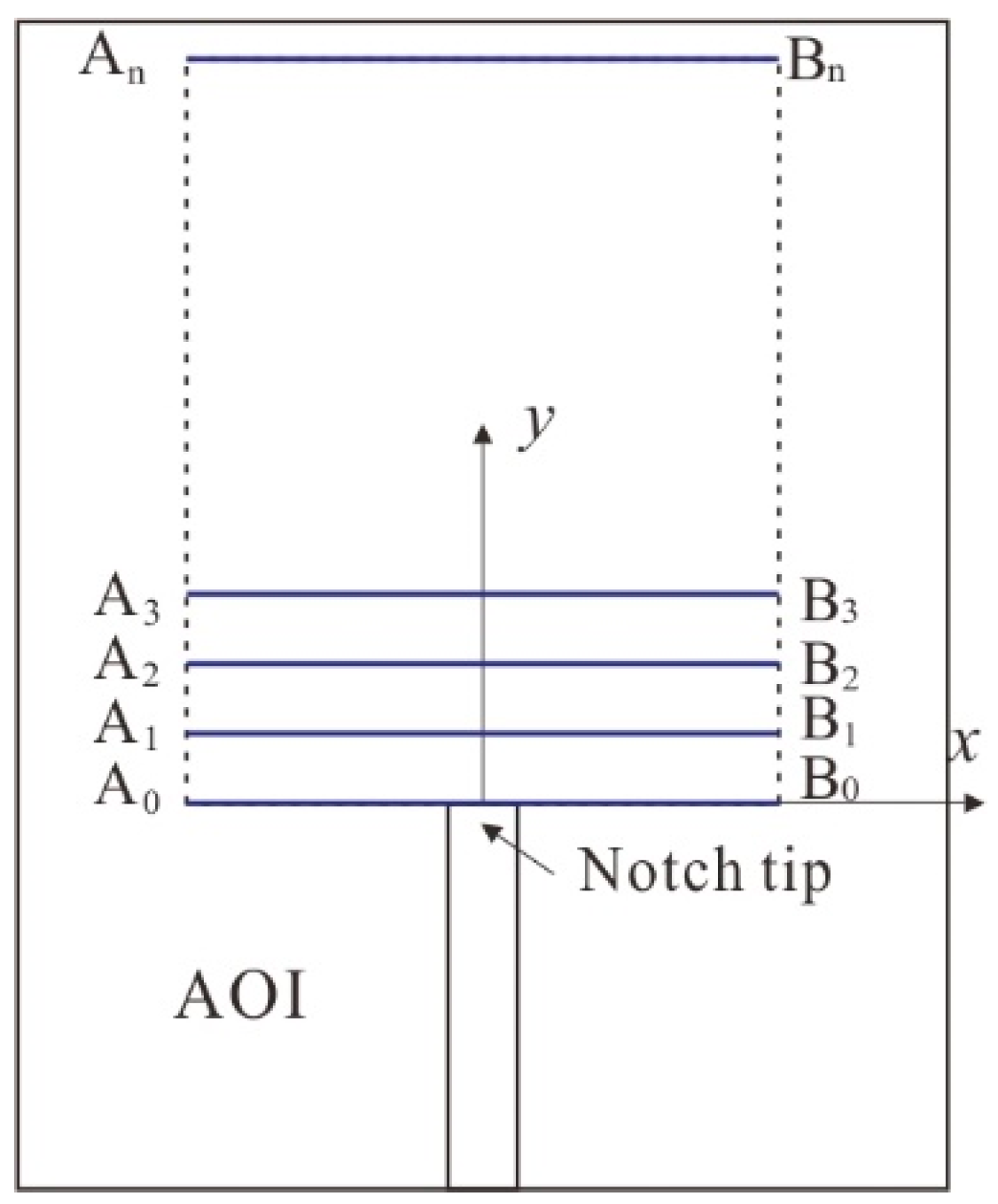
2.3. Verification of DIC Results
3. Results
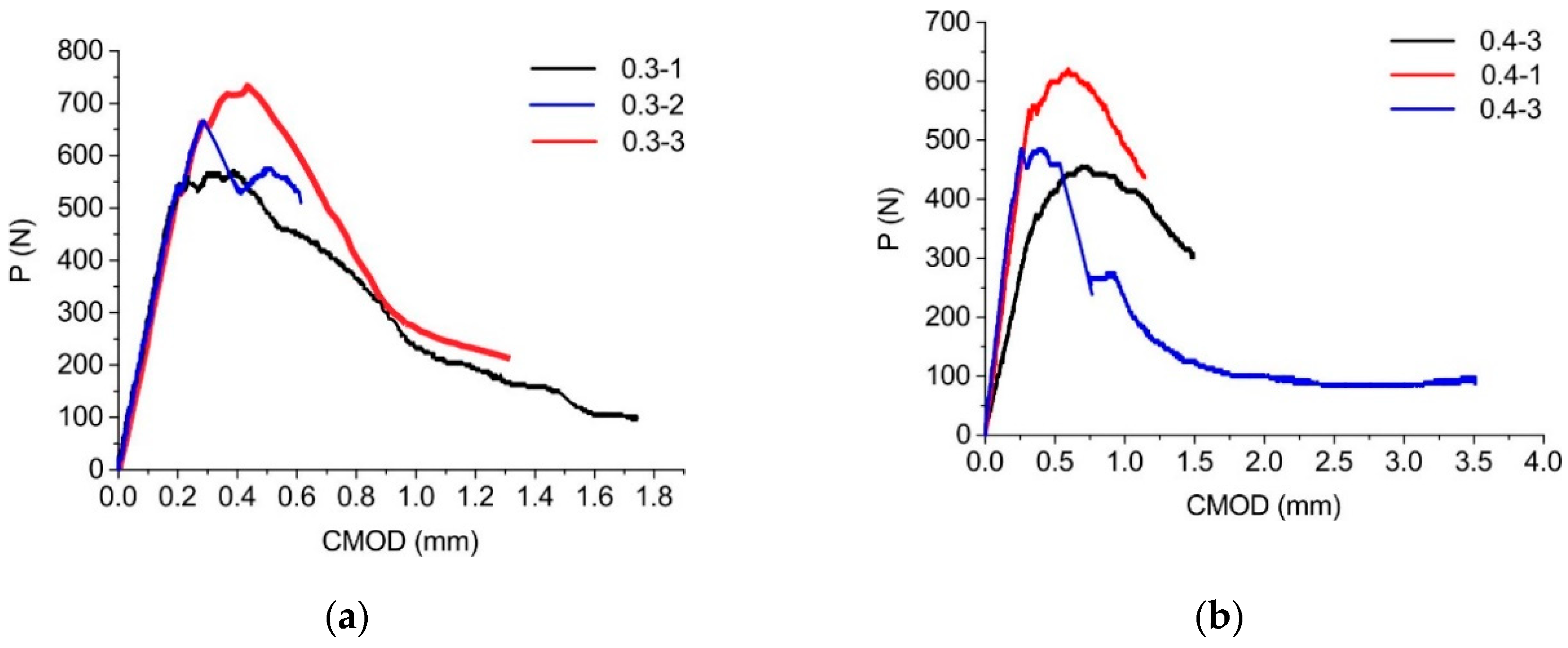
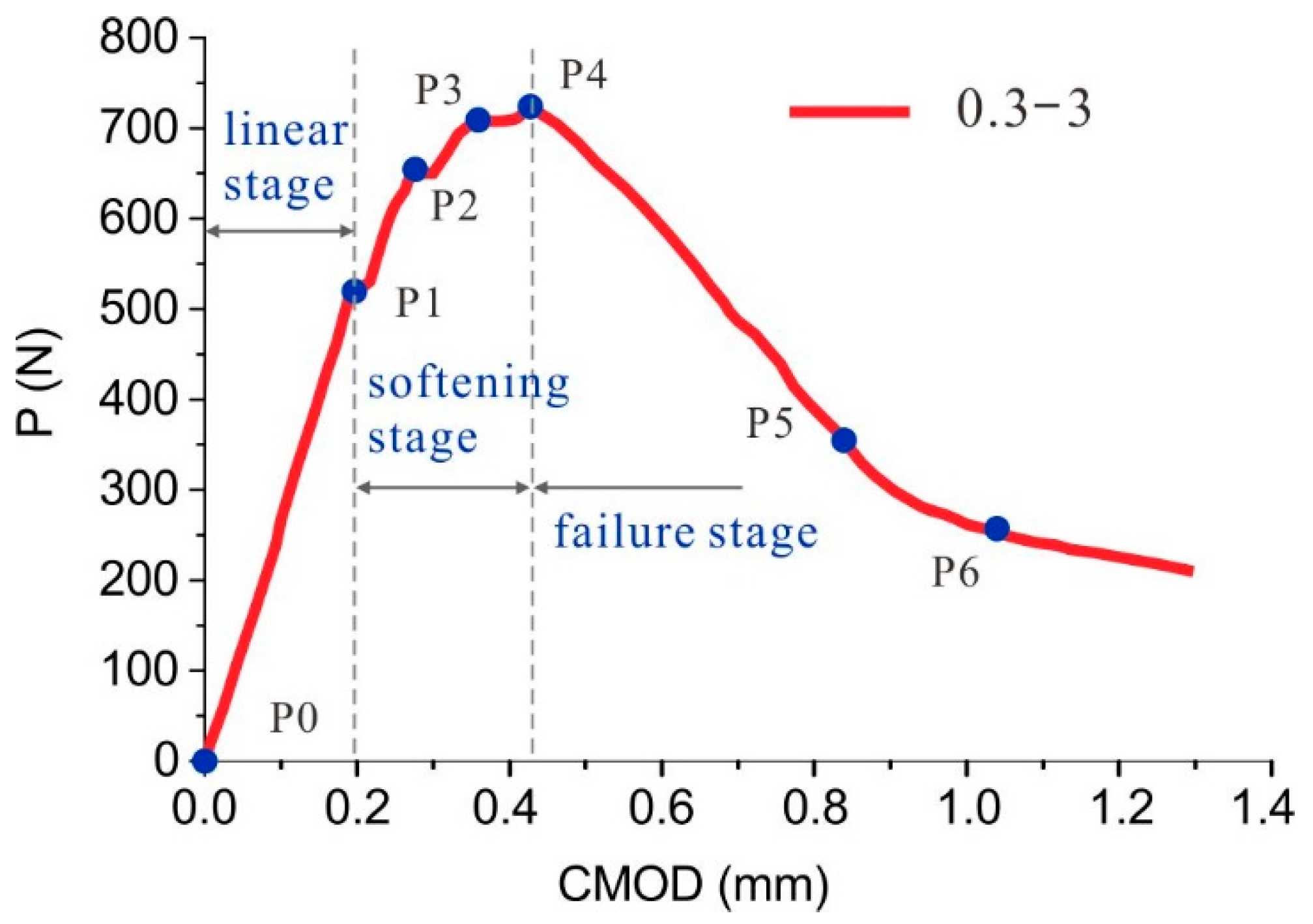
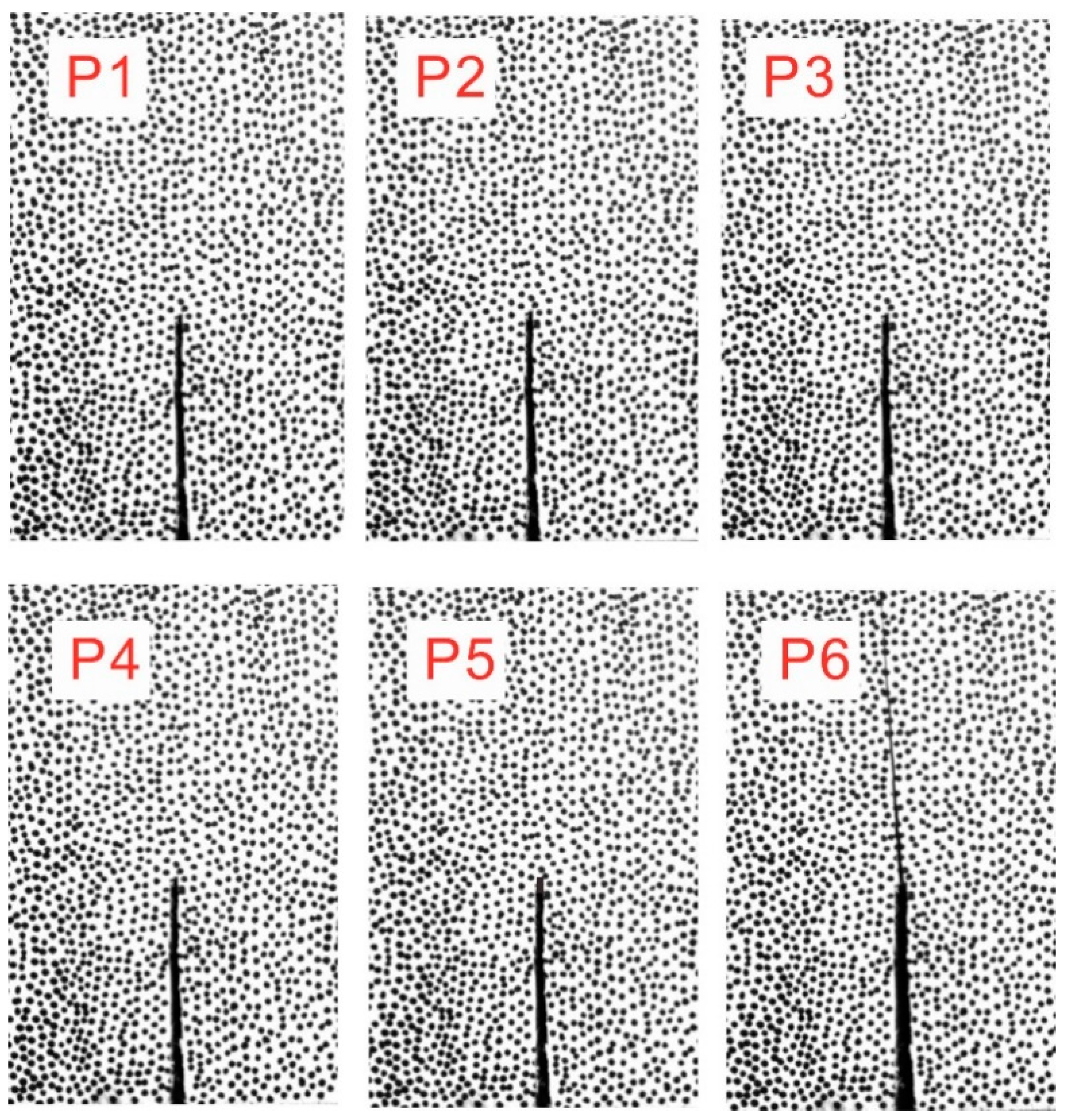
3.1. Quasi-Brittle Fracture Process of the Wood in the Longitudinal Direction
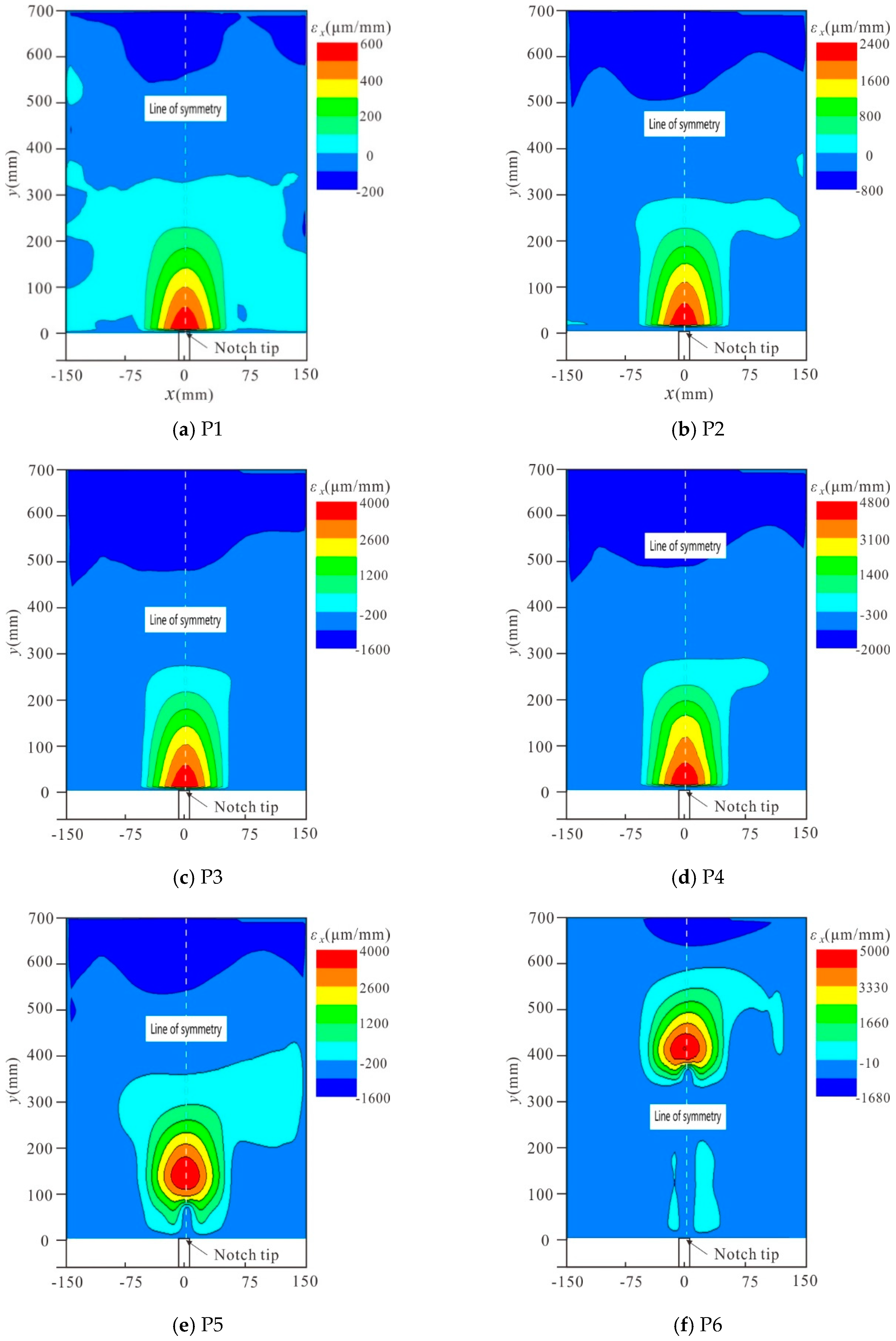
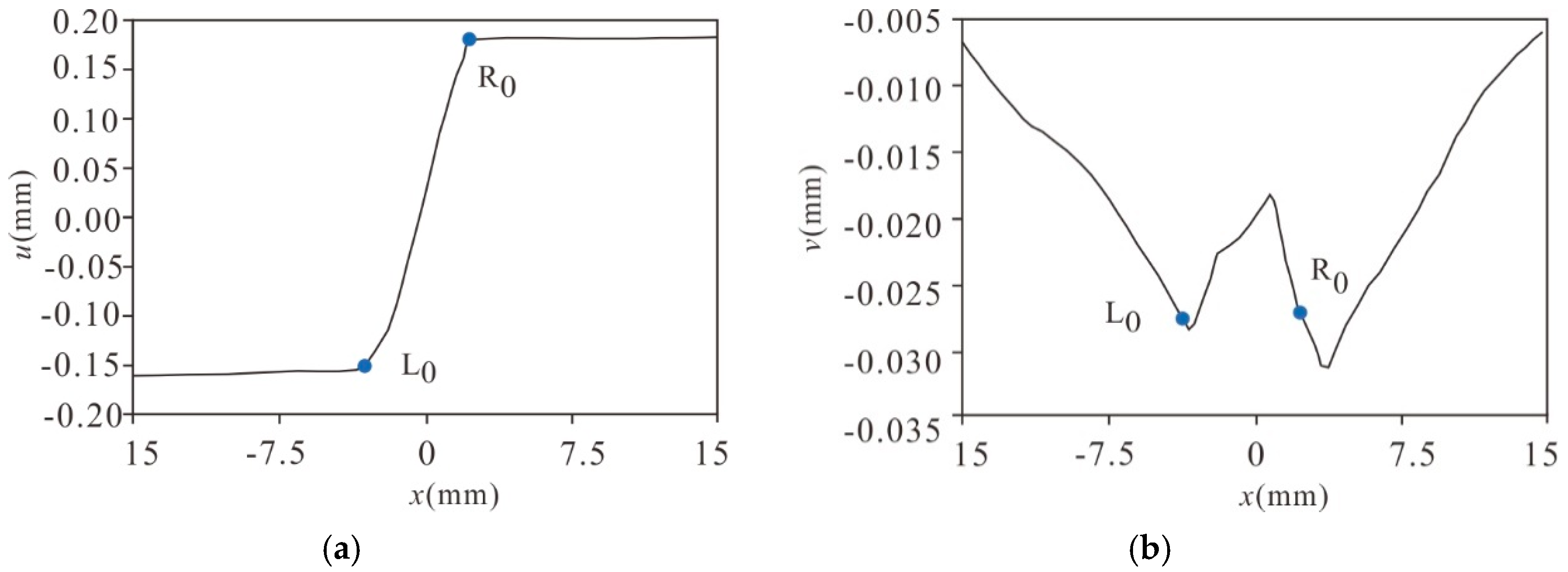
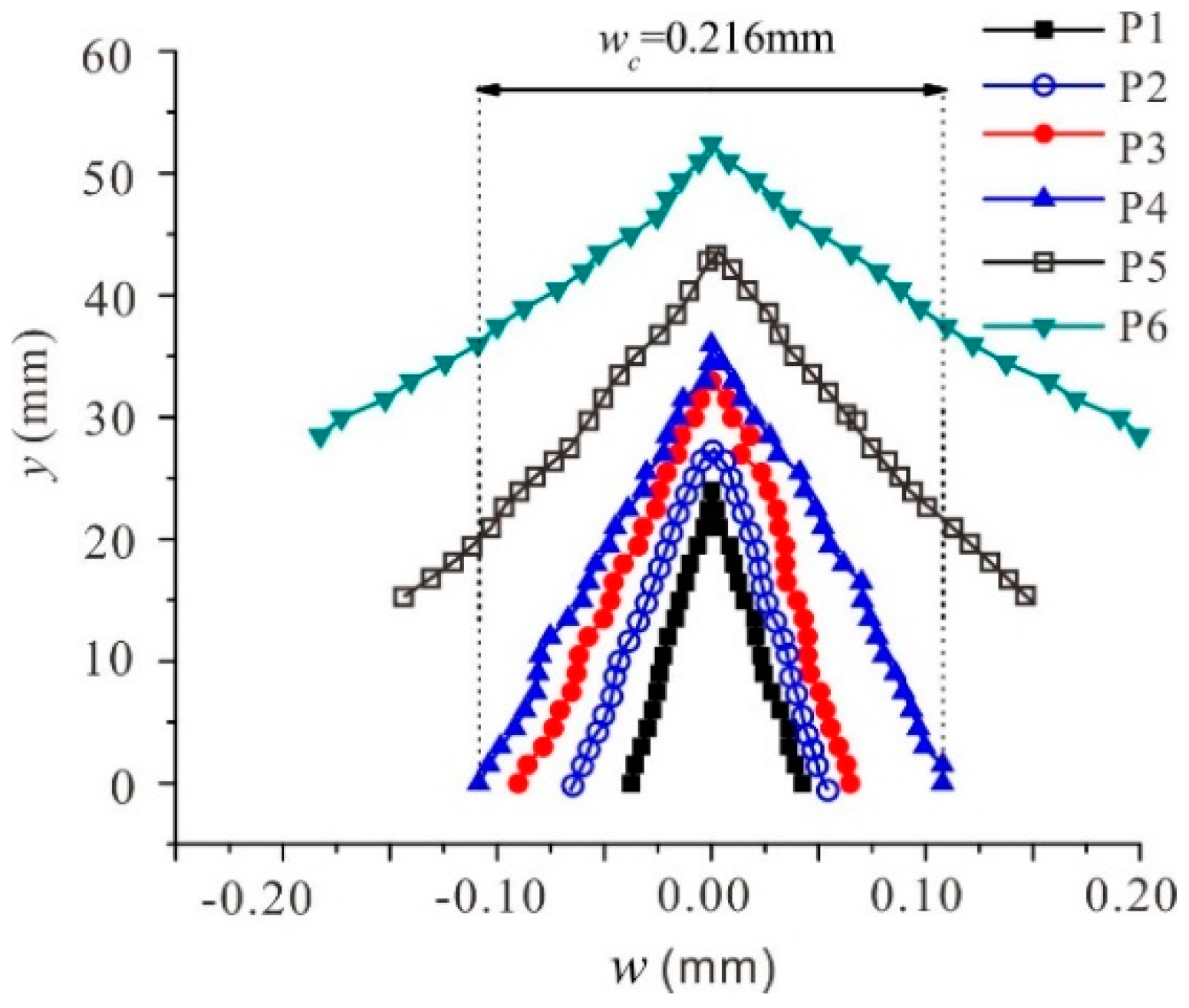
3.2. FPZ Evaluation by DIC Technique
4. Discussion
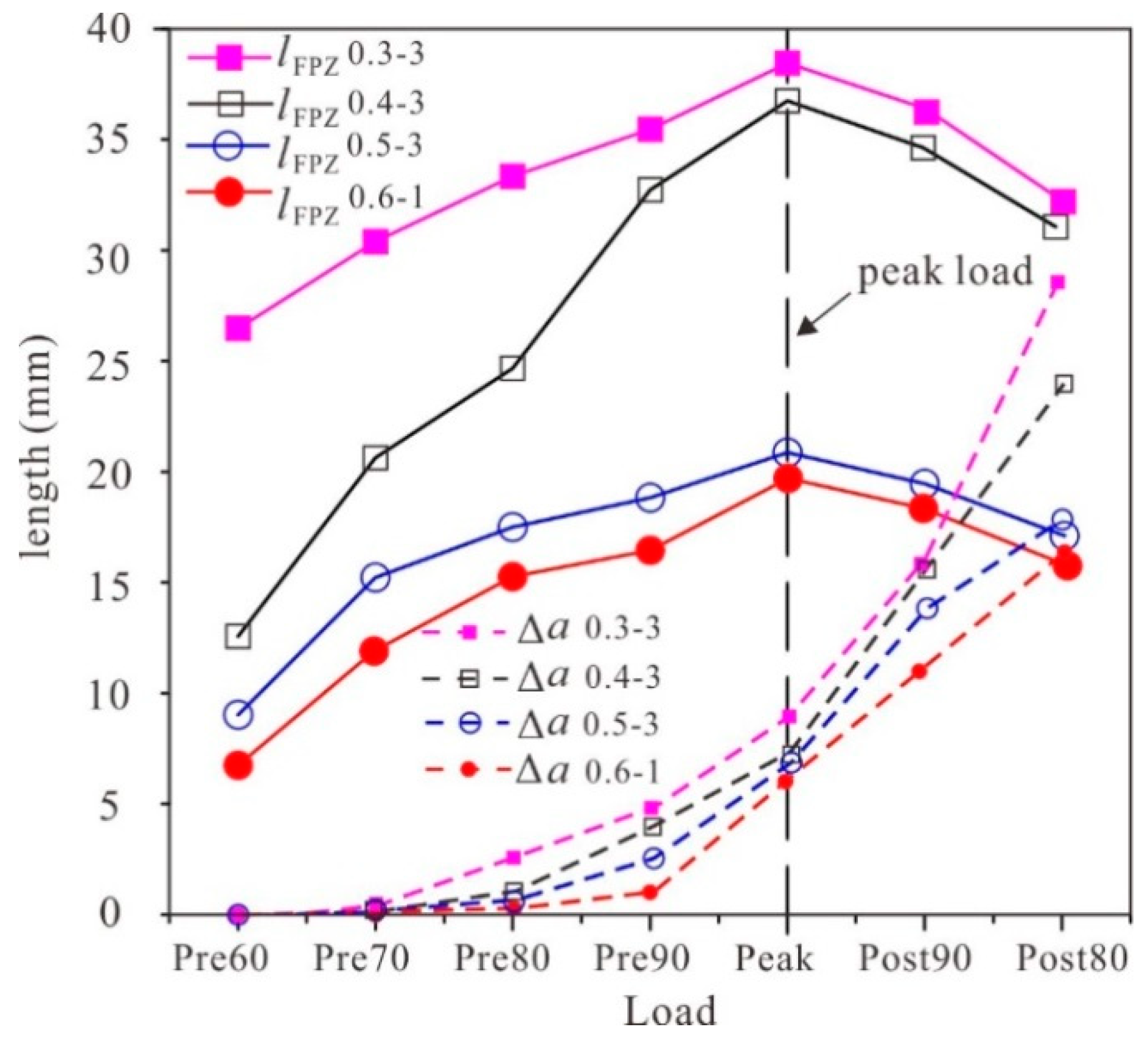
4.1. FPZ Development during the Fracture Process
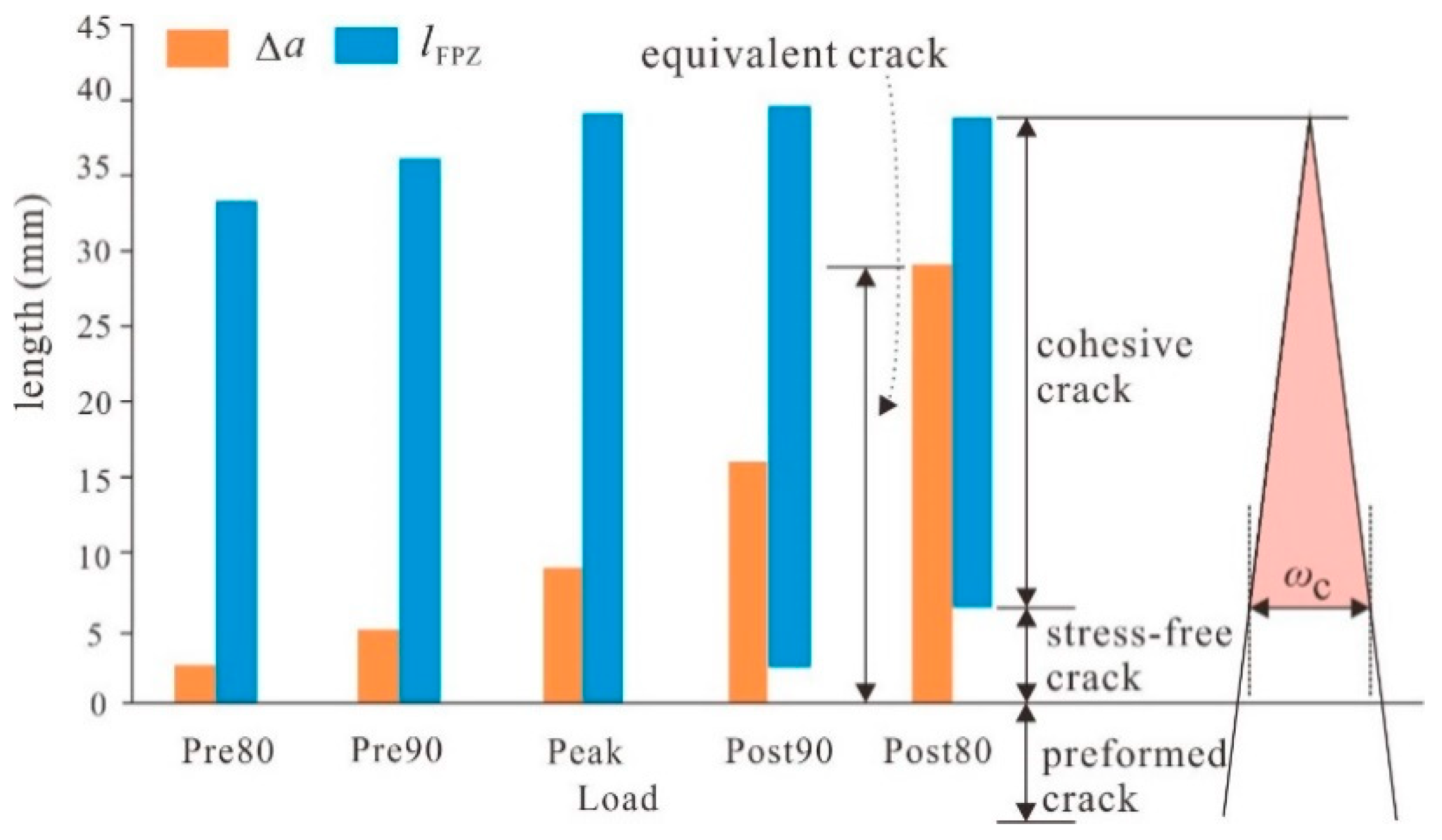
4.2. Comparison between the Equivalent Elastic Crack and FPZ
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Smith, I.; Landies, E.; Gong, M. Fracture and Fatigue in Wood; John Wiley & Sons, Ltd.: New Jersey, NJ, USA, 2003. [Google Scholar]
- Stanzl-Tschegg, S.E.; Tan, D.M.; Tschegg, E.K. New splitting method for wood fracture characterization. Wood Sci. Technol. 1995, 29, 31–50. [Google Scholar] [CrossRef]
- De Moura, M.F.S.F.; Dourado, N. Wood Fracture Characterization; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Hillerborg, A.; Modéer, M.; Petersson, P.E. Analysis of crack formation and crackgrowth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–781. [Google Scholar] [CrossRef]
- Morel, S.; Lespine, C.; Coureau, J.-L.; Planas, J.; Dourado, N. Bilinear softening parameters and equivalent LEFM R-curve in quasibrittle failure. Int. J. Solids Struct. 2010, 47, 837–850. [Google Scholar] [CrossRef]
- Yoshihara, H.; Satoh, A. Shear and crack tip deformation correction for the double cantilever beam and three-point-end-notched flexure specimens for mode I and mode II fracture toughness measurement of wood. Eng. Fract. Mech. 2009, 76, 335–346. [Google Scholar] [CrossRef]
- De Moura, M.F.S.F.; Morais, J.J.L.; Dourado, N. A new data reduction scheme for mode I wood fracture characterization using the double cantilever beam test. Eng. Fract. Mech. 2008, 75, 3852–3865. [Google Scholar] [CrossRef]
- Hu, X.; Duan, K. Size effect: Influence of proximity of fracture process zone to specimen boundary. Eng. Fract. Mech. 2007, 74, 1093. [Google Scholar] [CrossRef]
- Dai, Y.; Gruber, D.; Harmuth, H. Observation and quantification of the fracture process zone for two magnesia refractories with different brittleness. J. Eur. Ceram. Soc. 2017, 37, 2521–2529. [Google Scholar] [CrossRef]
- Watanabe, K.; Shida, S.; Ohta, M. Evaluation of end-check propagation based on mode I fracture toughness of sugi (Crytomeria japonica). J. Wood Sci. 2011, 57, 371–376. [Google Scholar] [CrossRef]
- Reiterer, A.; Sinn, G.; Stanzl-Tschegg, S.E. Fracture characteristics of different wood species under mode I loading perpendicular to the grain. Mat. Sci. Eng. A Struct. 2002, 332, 29–36. [Google Scholar] [CrossRef]
- Alam, S.Y.; Saliba, J.; Loukili, A. Fracture examination in concrete through combined digital image correlation and acoustic emission techniques. Constr. Build. Mater. 2014, 69, 232–242. [Google Scholar] [CrossRef]
- Cai, M.F.; Liu, D.M. Study of failure mechanisms of rock under compressive–shear loading using real-time laser holography. Int. J. Rock Mech. Min. Sci. 2009, 46, 59–68. [Google Scholar] [CrossRef]
- Lin, Q.; Fakhimi, A.; Haggerty, M.; Labuz, J.F. Initiation of tensile and mixed-mode fracture in sandstone. Int. J. Rock Mech. Min. Sci. 2009, 46, 489–497. [Google Scholar] [CrossRef]
- Sciammarella, C.; Sciammarella, A.; Federico, M. Experimental Mechanics of Solids; John Wiley & Sons, Ltd.: Chichester, UK, 2012; pp. 607–629. [Google Scholar]
- Gencturk, B.; Hossain, K.; Kapadia, A.; Labib, E.; Mo, Y.L. Use of digital image correlation technique in full-scale testing of prestressed concrete structures. Measurement 2014, 47, 505–515. [Google Scholar] [CrossRef]
- Yates, J.R.; Zanganeh, M.; Tai, Y.H. Quantifying crack tip displacement fields with DIC. Eng. Fract. Mech. 2010, 77, 2063–2076. [Google Scholar] [CrossRef]
- Lin, Q.; Labuz, J.F. Fracture of sandstone characterized by digital image correlation. Int. J. Rock Mech. Min. Sci. 2013, 60, 235–245. [Google Scholar] [CrossRef]
- Dong, W.; Wu, Z.M.; Zhou, X.M.; Dong, L.H.; Kastiukas, G. An experimental study on crack propagation at rock-concrete interface using digital image correlation technique. Eng. Fract. Mech. 2017, 171, 50–63. [Google Scholar] [CrossRef]
- Morel, S.; Mourot, G.; Schmittbuhl, J. Influence of the specimen geometry on R-curve behavior and roughening of fracture surfaces. Int. J. Fract. 2003, 121, 23–42. [Google Scholar] [CrossRef]
- Coureau, J.L.; Morel, S.; Dourado, N. Cohesive zone model and quasibrittle failure of wood: A new light on the adapted specimen geometries for fracture tests. Eng. Fract. Mech. 2013, 109, 328–340. [Google Scholar] [CrossRef]
- Correlated Solutions. VIC-2D Reference Manual; Correlated Solutions, Inc.: Columbia, SC, USA, 2014. [Google Scholar]
- Lamberti, L.; Lin, M.T.; Furlong, C.; Sciammarella, C.; Phillip, L.R.; Michael, A.S. Advancement of Optical Methods & Digital Image Correlation in Experimental Mechanics; Springer: New York, NY, USA, 2018; Volume 3. [Google Scholar]
- Patel, J.; Peralta, P. Mechanisms for Kink Band Evolution in Polymer Matrix Composites: A Digital Image Correlation and Finite Element Study. In Mechanics of Solids, Structures and Fluids; NDE, Diagnosis, and Prognosis, Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Phoenix, AZ, USA, 11–17 November 2016; ASME: New York, NY, USA, 2016; Volume 9. [Google Scholar] [CrossRef]
- Nizolek, T.J.; Begley, M.R.; McCabe, R.J.; Avallone, J.T.; Mara, N.A.; Beyerlein, I.J.; Pollock, T.M. Strain fields induced by kink band propagation in Cu-Nb nanolaminate composites. Acta Mater. 2017, 133, 303–315. [Google Scholar] [CrossRef]
- Ye, X.W.; Dong, C.Z.; Liu, T. Image-based structural dynamic displacement measurement using different multi-object tracking algorithms. Smart Struct. Syst. 2016, 17, 935–956. [Google Scholar] [CrossRef]
- Ye, X.W.; Yi, T.H.; Dong, C.Z.; Liu, T. Vision-based structural displacement measurement: System performance evaluation and influence factor analysis. Measurement 2016, 88, 372–384. [Google Scholar] [CrossRef]
- Correlated Solutions. Vic-2D Manual; Correlated Solutions, Inc.: Columbia, SC, USA, 2010; Available online: www.correlatedsolutions.com (accessed on May 31 2010).
- John, T.W. Relating Cohesive Zone Models to Linear Elastic Fracture Mechanics; NASA Langley Research Center: Hampton, VA, USA, 2010.
- Barris, C.; Torres, L.; Vilanova, I.; Miàs, C.; Llorens, M. Experimental study on crack width and crack spacing for Glass-FRP reinforced concrete beams. Eng. Struct. 2017, 2013, 231–242. [Google Scholar] [CrossRef]
- Petersson, P.E. Crack Growth and Development of Fracture Zones in Plain Concrete and Similar Materials. Doctoral Dissertation; Lund Institute of Technology: Lund, Sweden, 1981. [Google Scholar]
- Xu, S.L.; Reinhardt, H.W. Determination of double-K criterion for crack propagation in quasi-brittle fracture, Part I: Experimental investigation of crack propagation. Int. J. Fract. 1999, 98, 111–149. [Google Scholar] [CrossRef]
- Xu, S.L.; Reinhardt, H.W. Determination of double-K criterion for crack propagation in quasi-brittle fracture, Part II: Analytical evaluating and practical measuring methods for three-point bending notched beams. Int. J. Fract. 1999, 98, 151–177. [Google Scholar] [CrossRef]
- Tada, H.; Paris, P.C.; Irwin, G.R. The Stress Analysis of Cracks Handbook; ASME Press: New York, NY, USA, 2000. [Google Scholar]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Zeng, W.; Liu, W.; Zhang, H.; Wang, X. Crack Propagation and Fracture Process Zone (FPZ) of Wood in the Longitudinal Direction Determined Using Digital Image Correlation (DIC) Technique. Remote Sens. 2019, 11, 1562. https://doi.org/10.3390/rs11131562
Yu Y, Zeng W, Liu W, Zhang H, Wang X. Crack Propagation and Fracture Process Zone (FPZ) of Wood in the Longitudinal Direction Determined Using Digital Image Correlation (DIC) Technique. Remote Sensing. 2019; 11(13):1562. https://doi.org/10.3390/rs11131562
Chicago/Turabian StyleYu, Ying, Weihang Zeng, Wen Liu, He Zhang, and Xiaohong Wang. 2019. "Crack Propagation and Fracture Process Zone (FPZ) of Wood in the Longitudinal Direction Determined Using Digital Image Correlation (DIC) Technique" Remote Sensing 11, no. 13: 1562. https://doi.org/10.3390/rs11131562
APA StyleYu, Y., Zeng, W., Liu, W., Zhang, H., & Wang, X. (2019). Crack Propagation and Fracture Process Zone (FPZ) of Wood in the Longitudinal Direction Determined Using Digital Image Correlation (DIC) Technique. Remote Sensing, 11(13), 1562. https://doi.org/10.3390/rs11131562






