Inland Waters Suspended Solids Concentration Retrieval Based on PSO-LSSVM for UAV-Borne Hyperspectral Remote Sensing Imagery
Abstract
:1. Introduction
2. Materials and Methods
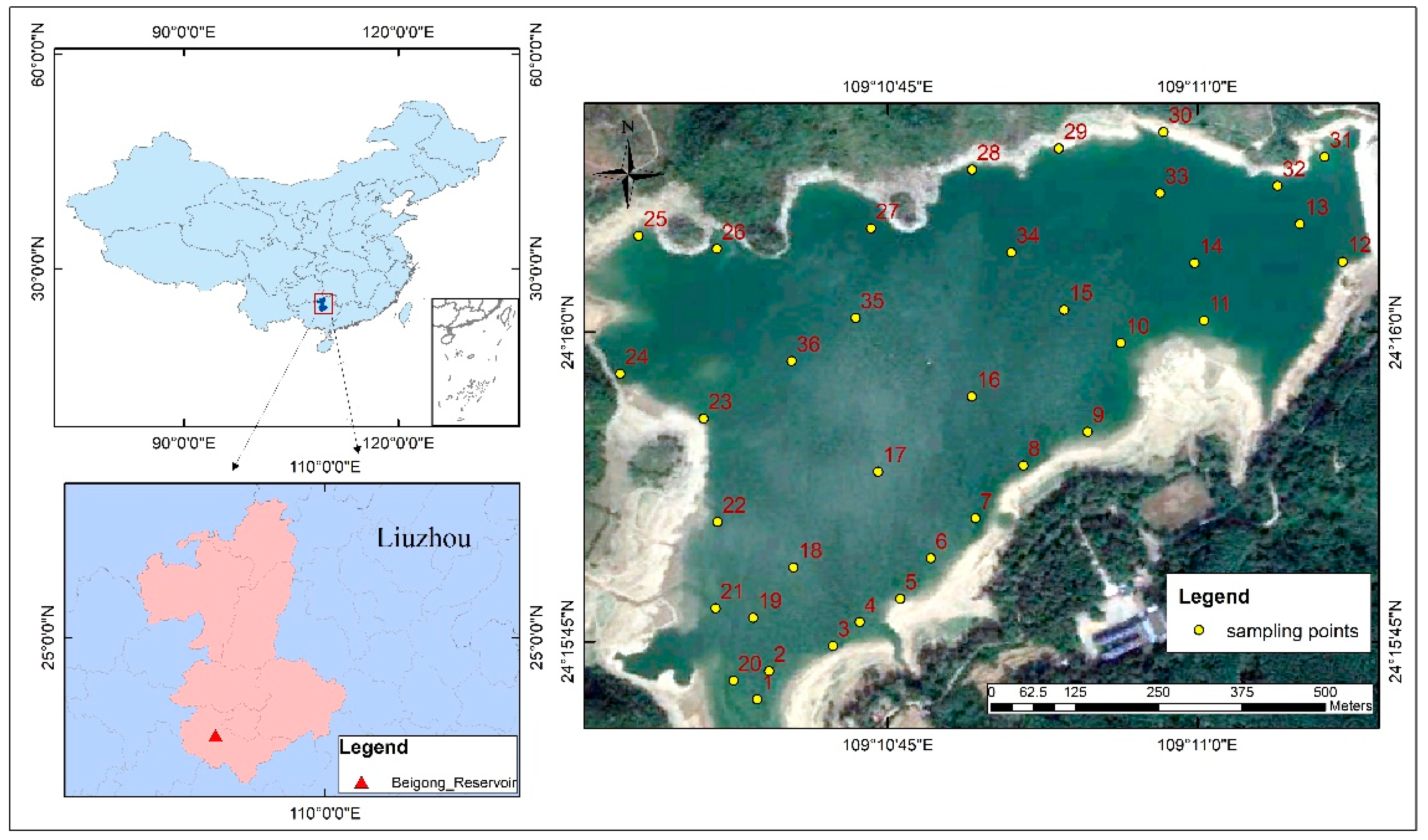
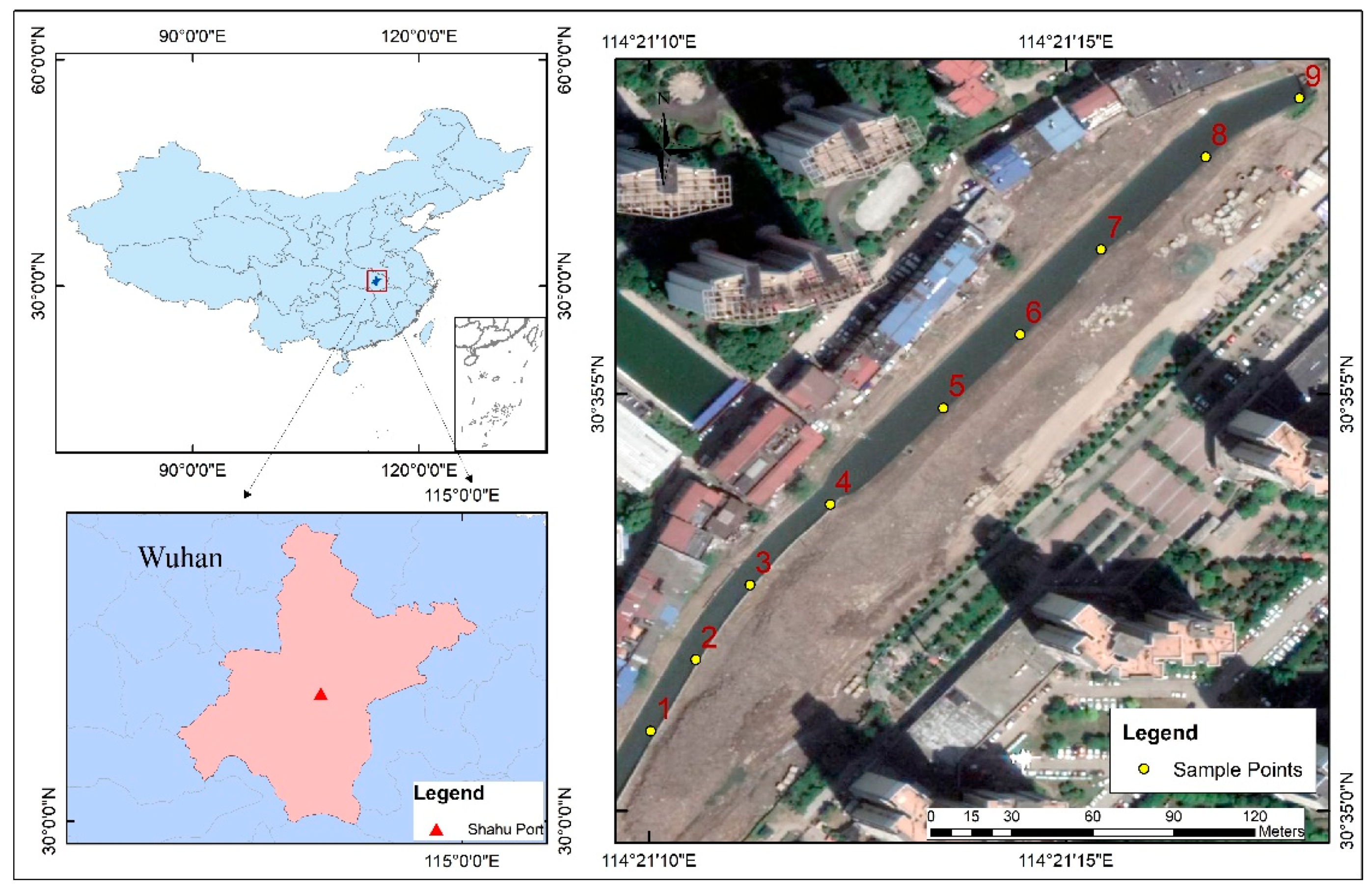
2.1. Study Area
2.2. Data Collection
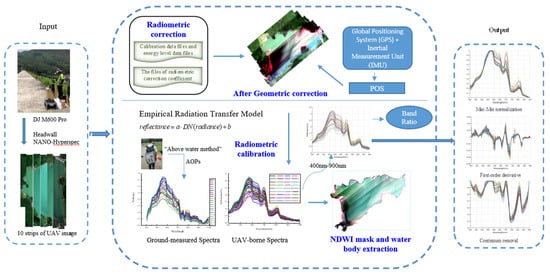
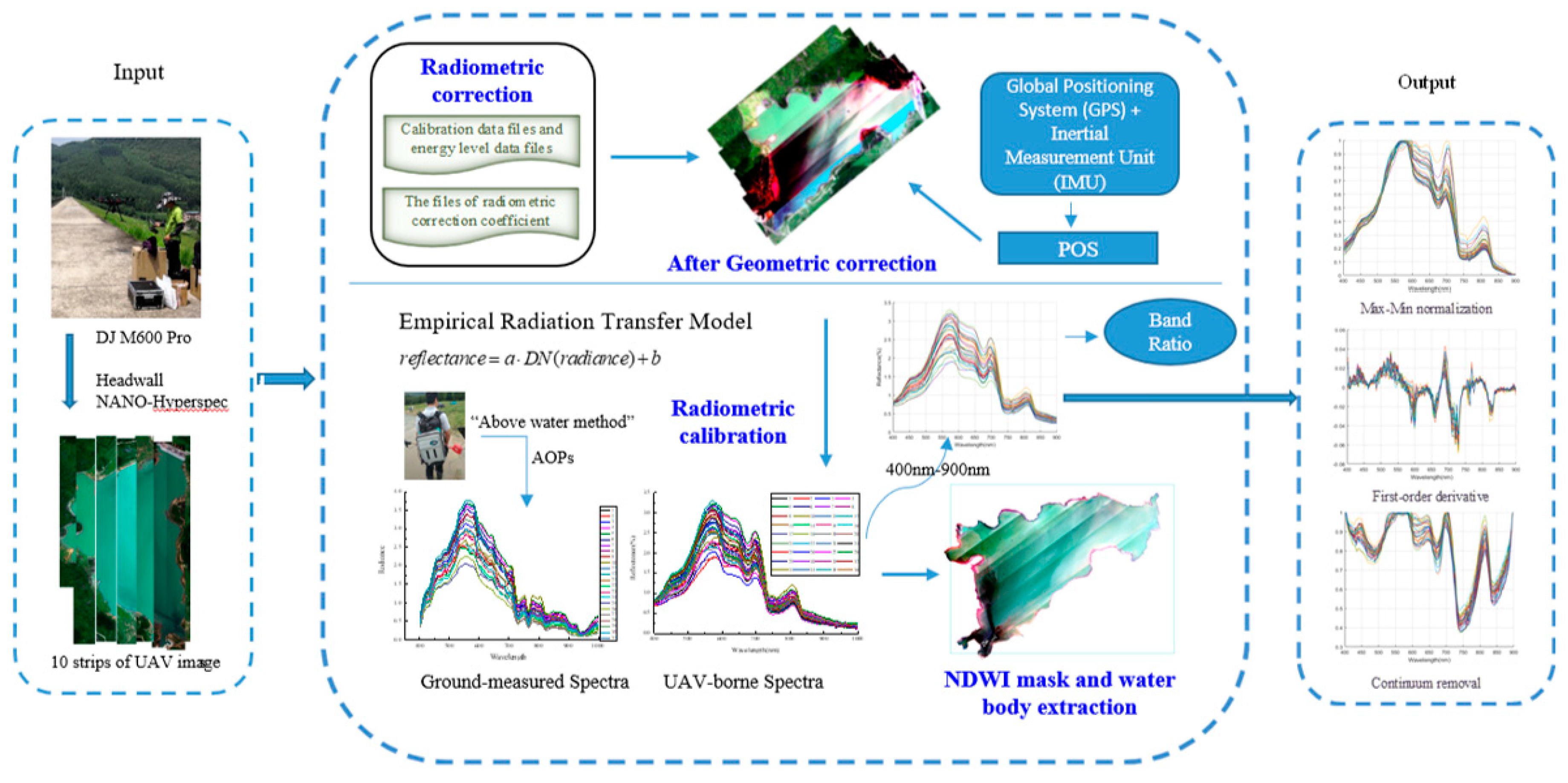
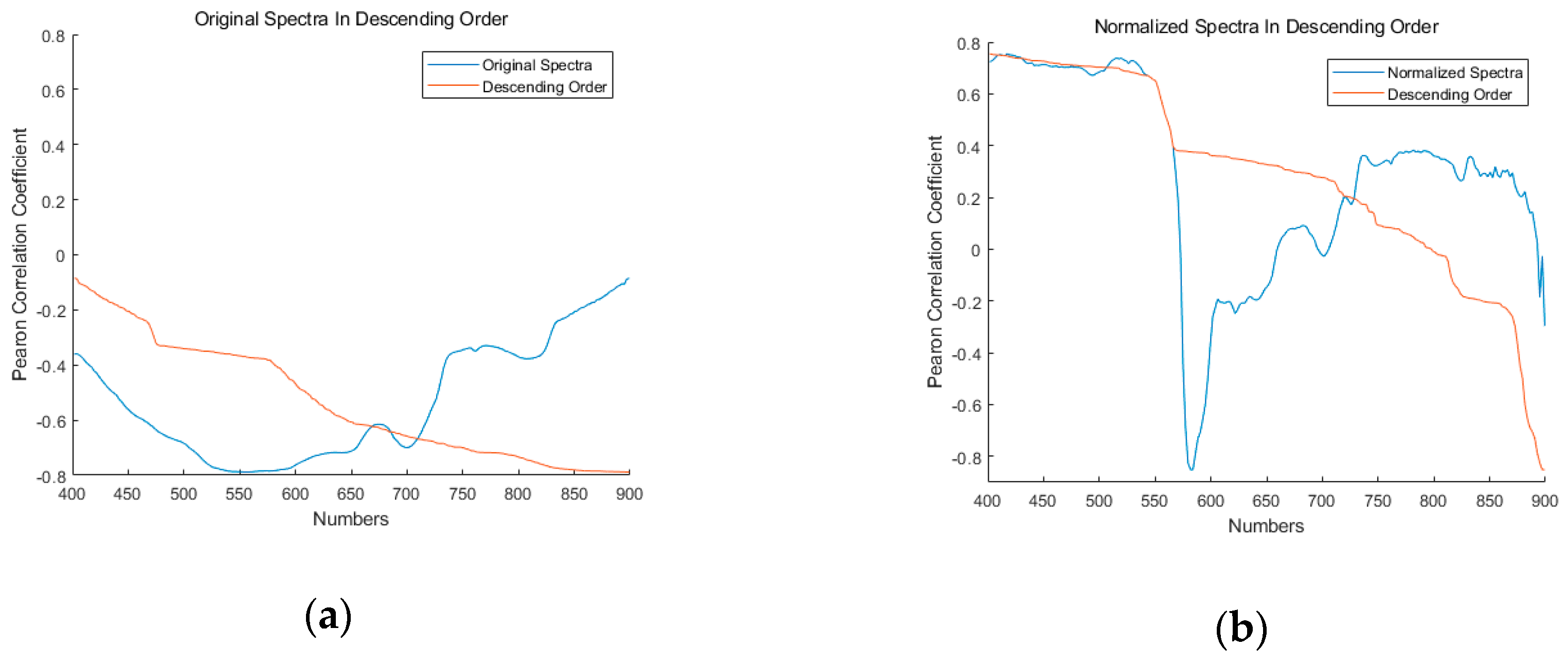
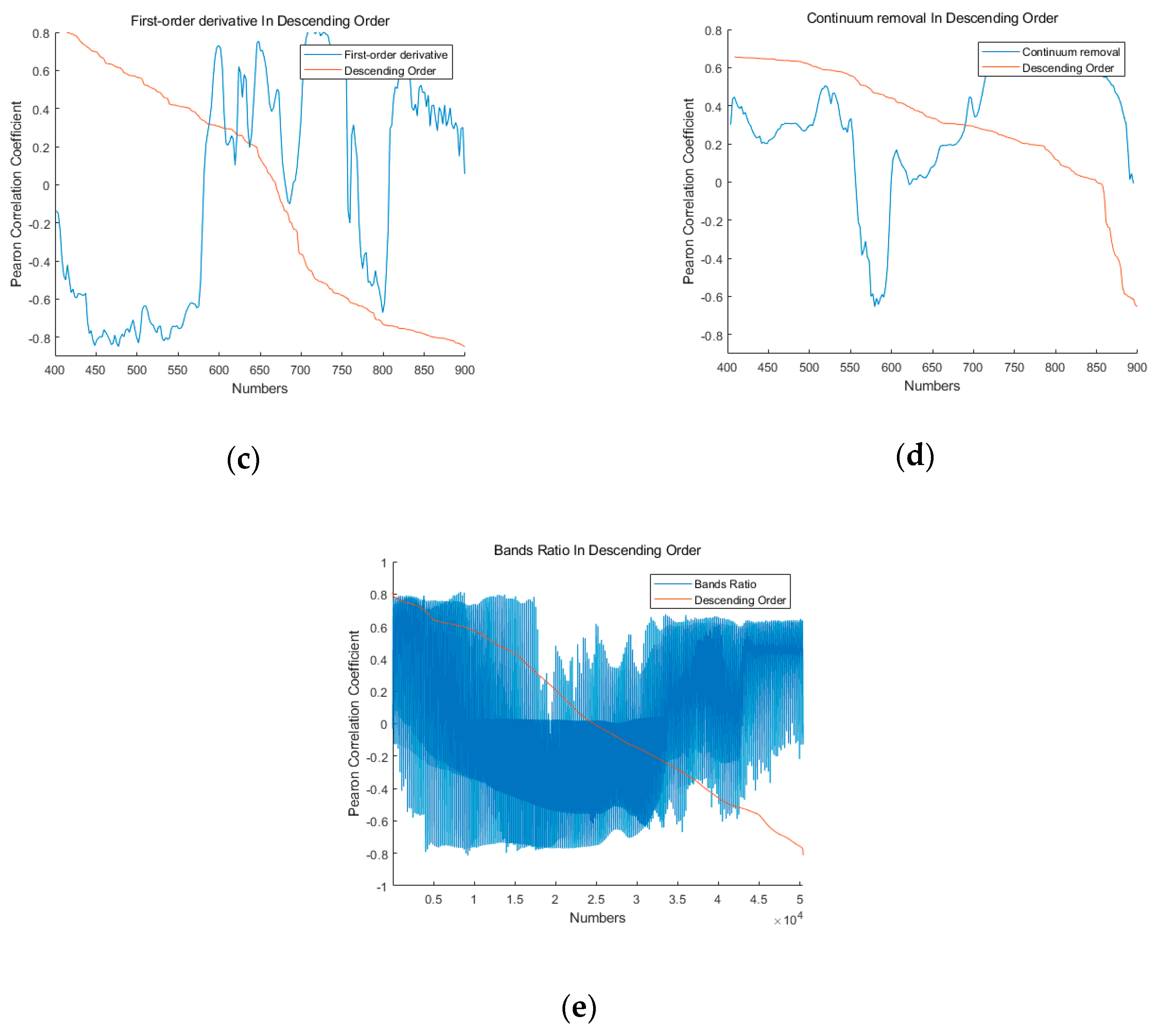
2.3. Preprocessing of the UAV Images and Spectra
2.4. Methods
2.4.1. Support Vector Machine and Least Squares Support Vector Machine
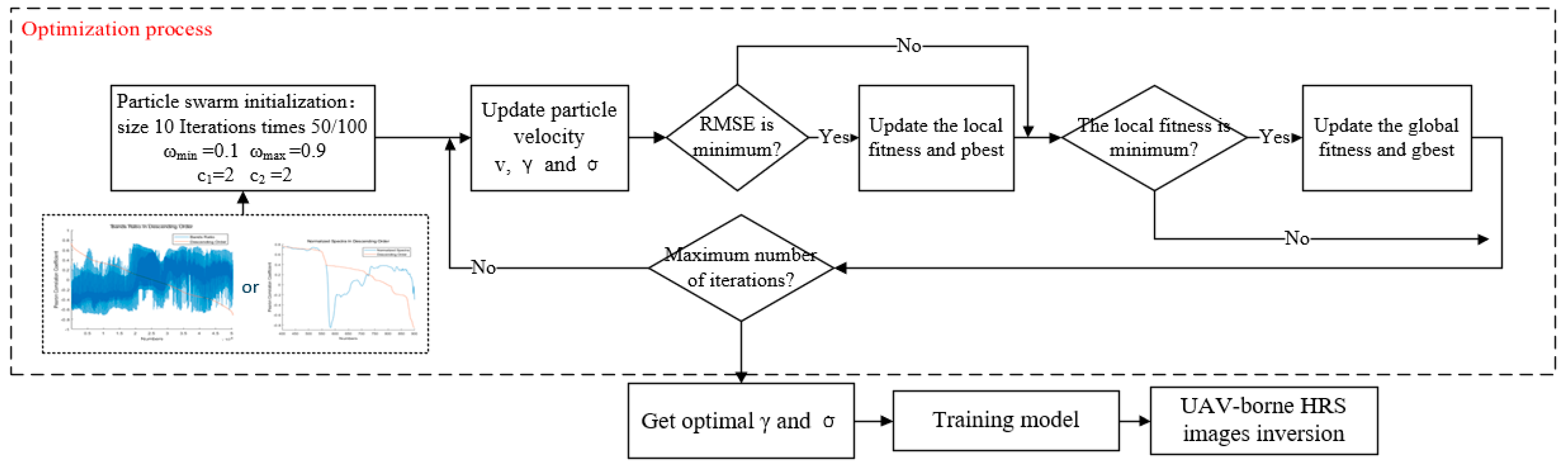
2.4.2. Particle Swarm Optimization Algorithm
2.4.3. Statistical Analysis
3. Experiments and Analysis
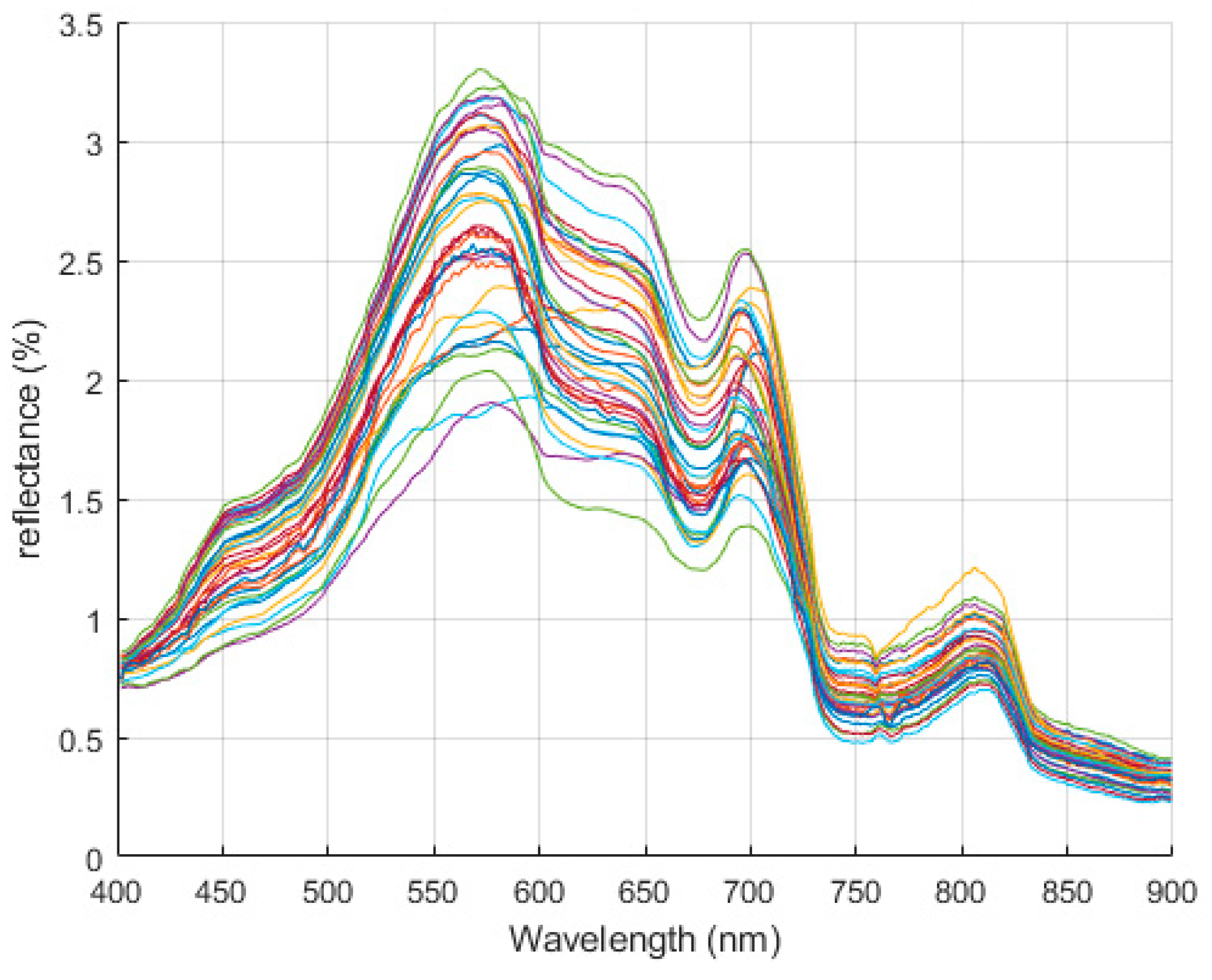
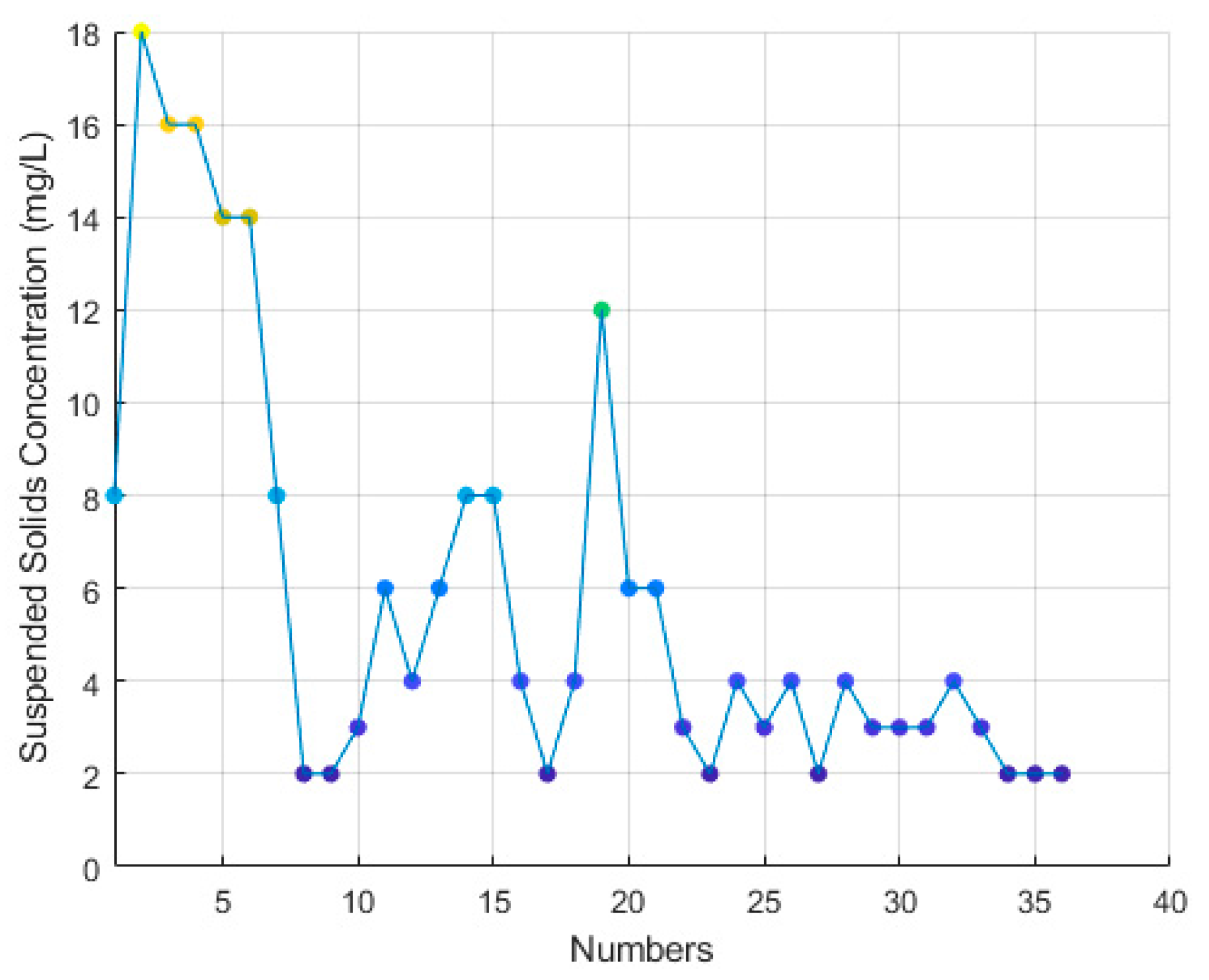
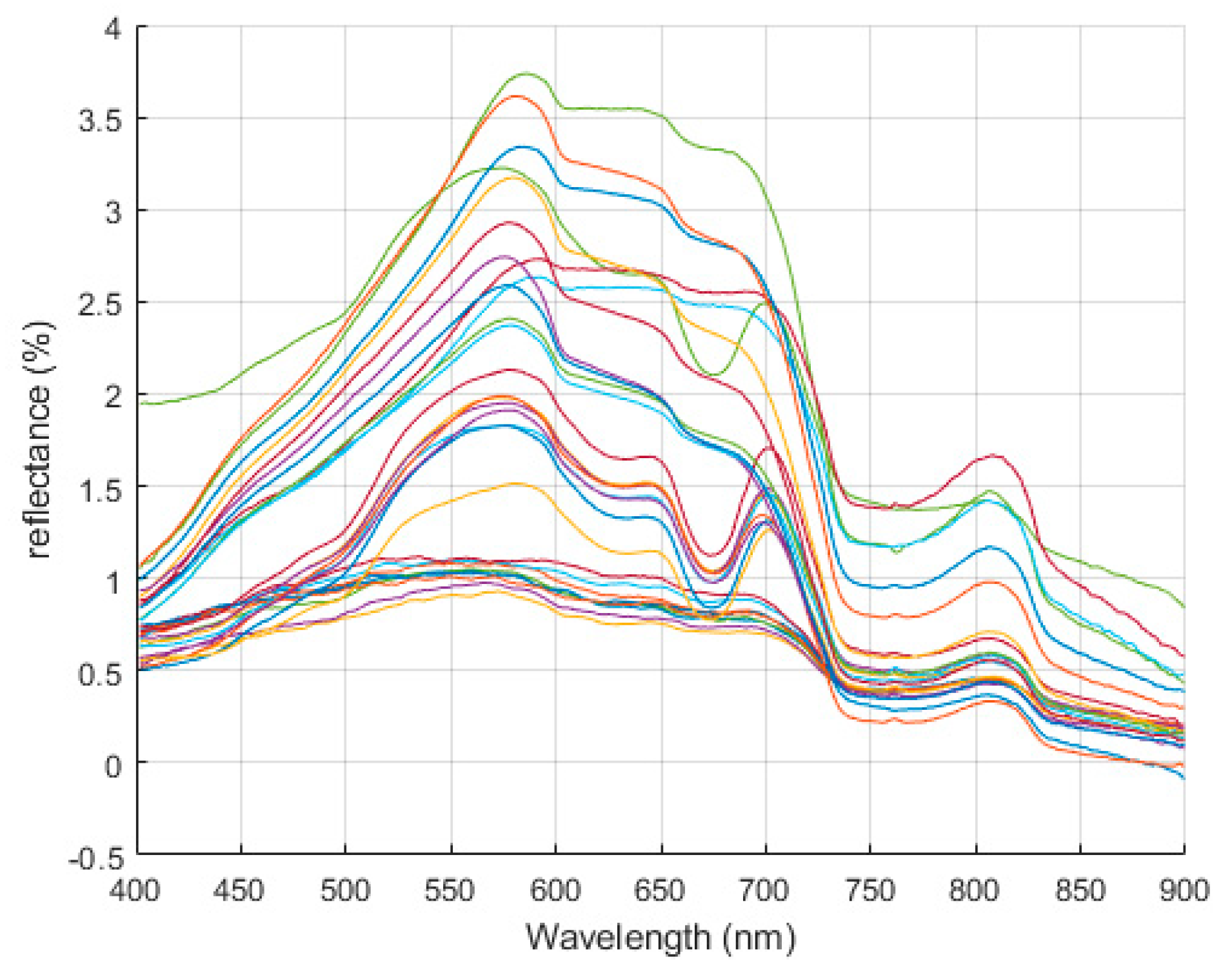
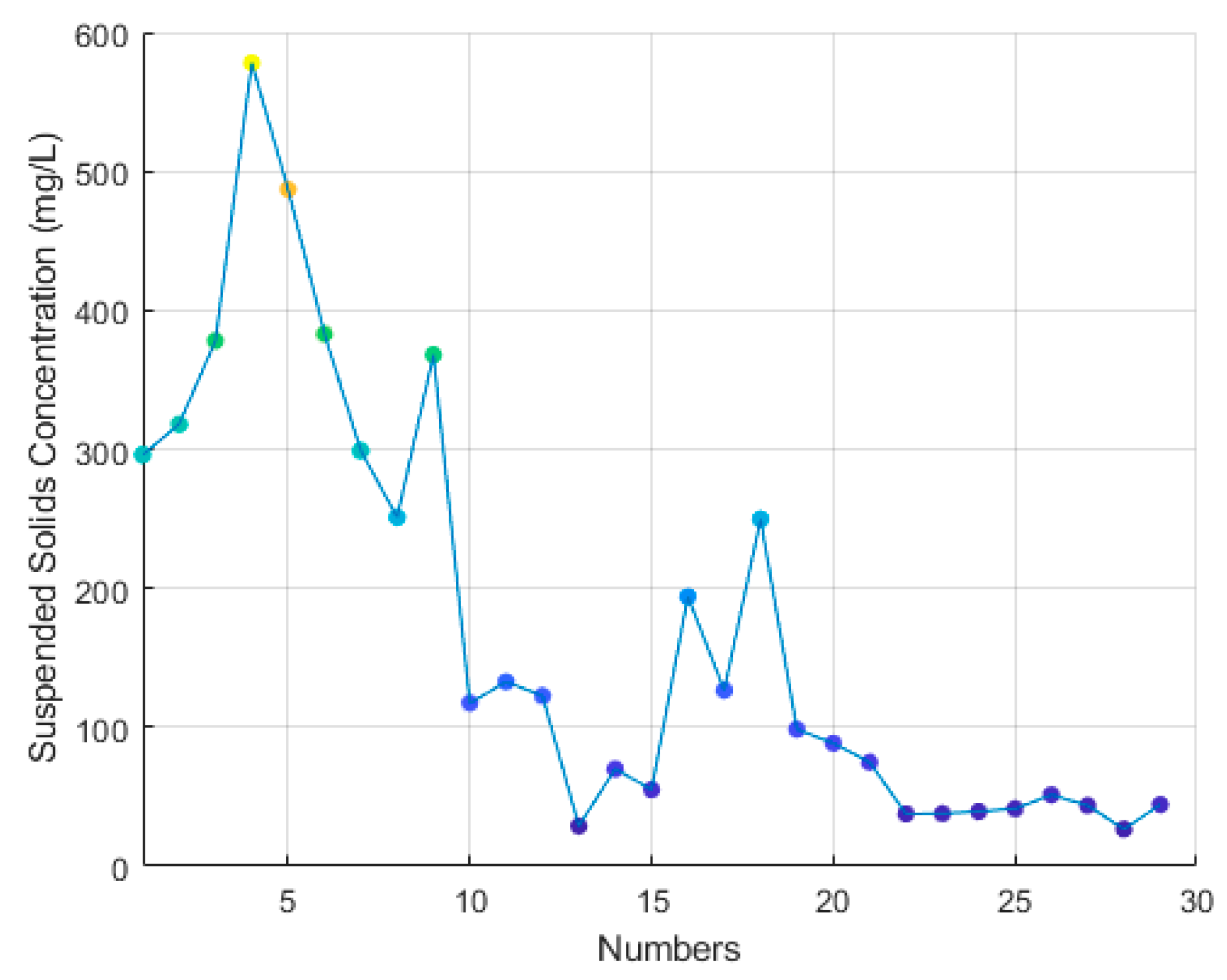
3.1. Data Analysis of Beigong Reservoir Samples
3.2. Data Analysis of Shahu Port Samples
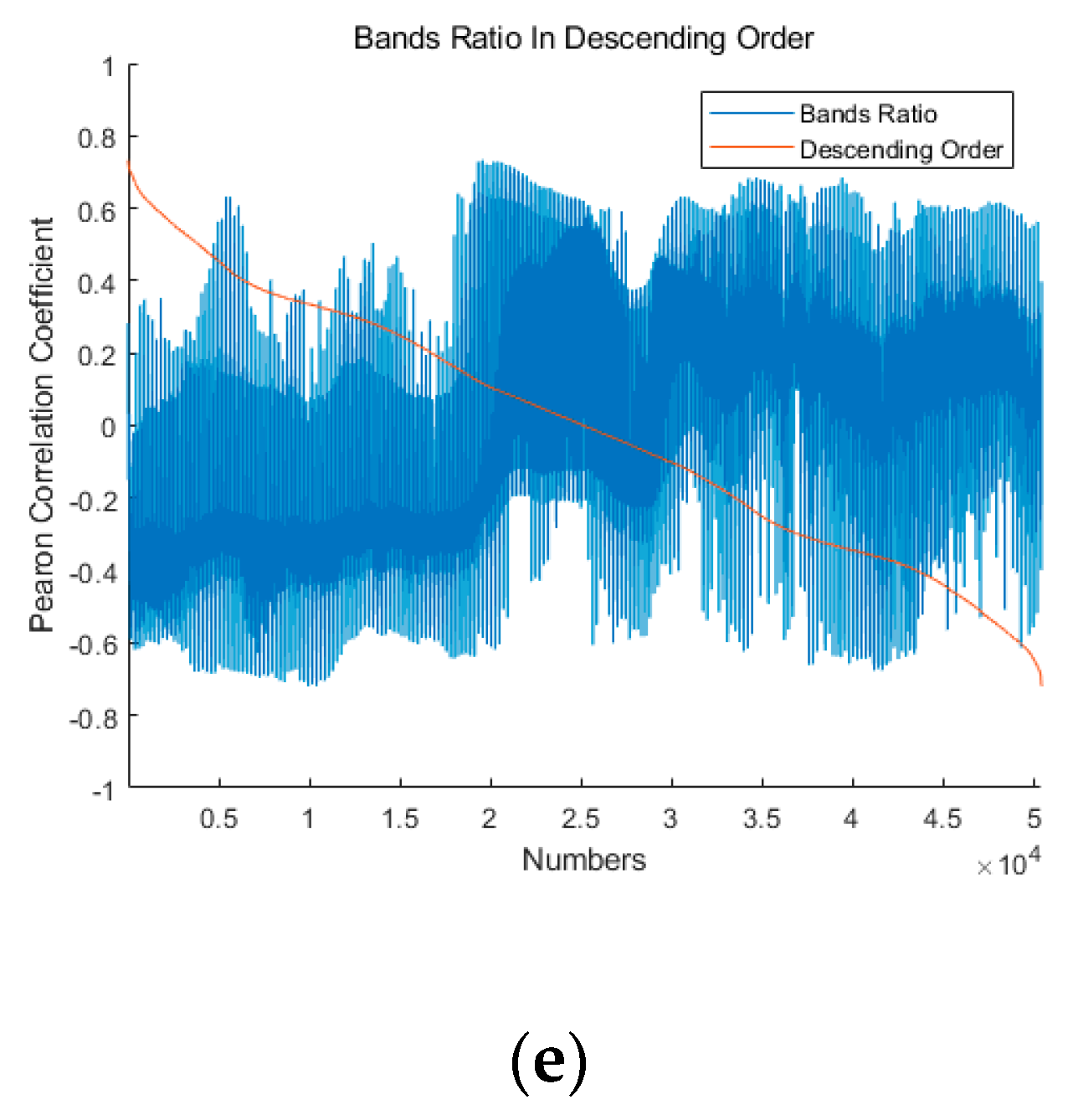
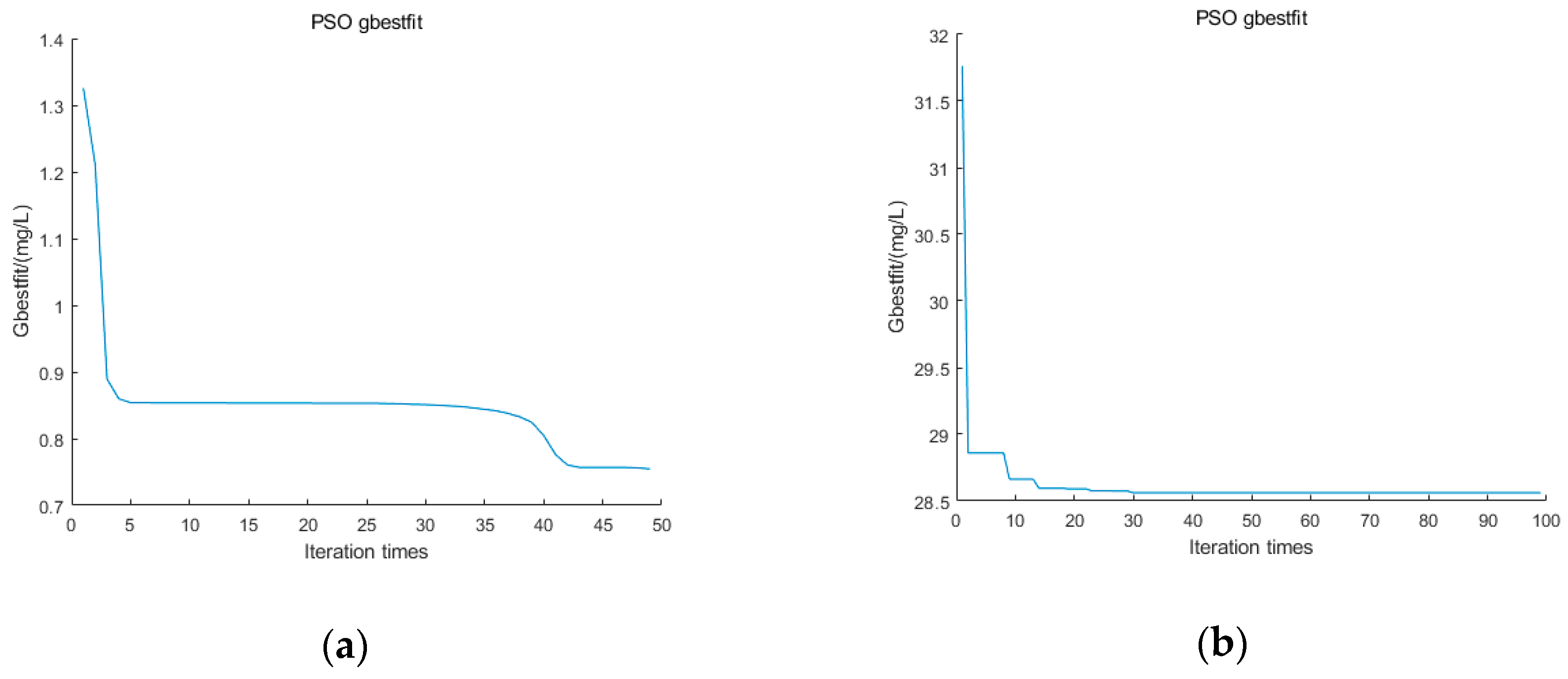
3.3. Particle Swarm Optimization-based Least Squares Support Vector Machine Modeling
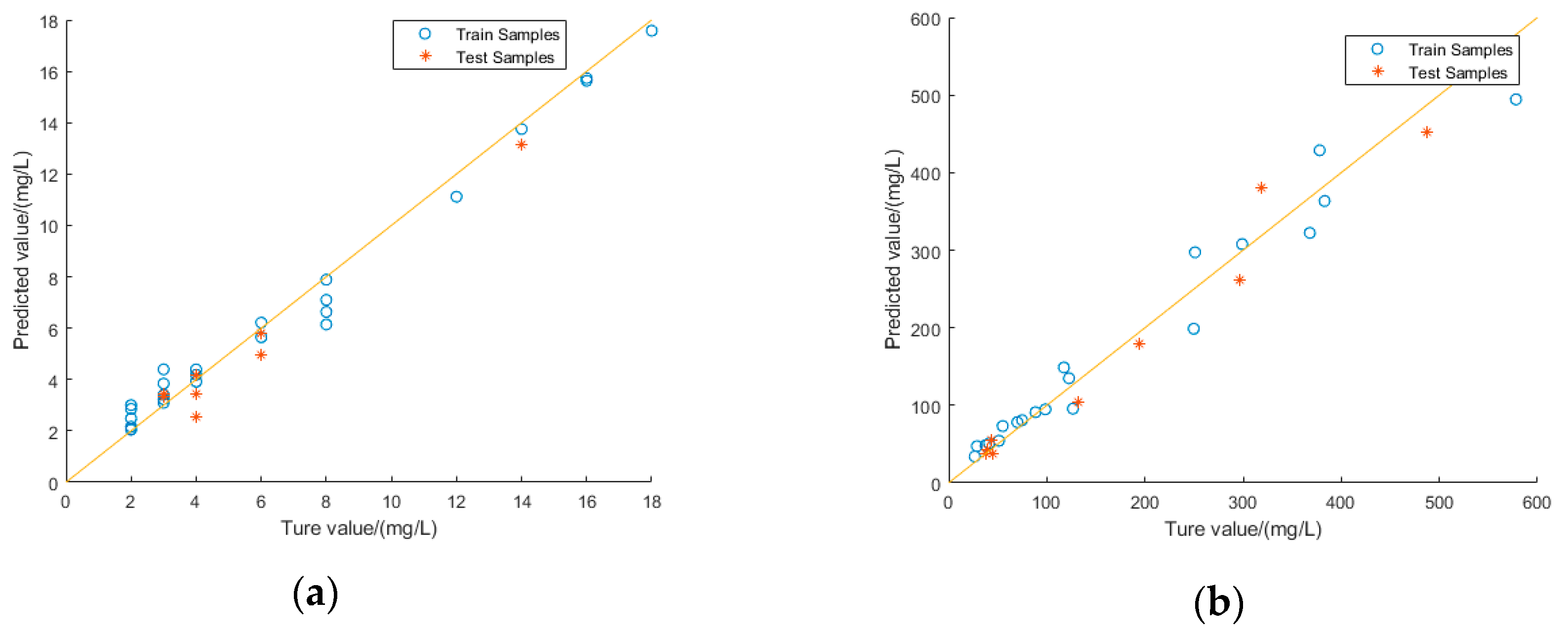
3.4. Accuracy Evaluation of the PSO-LSSVM and Other Models
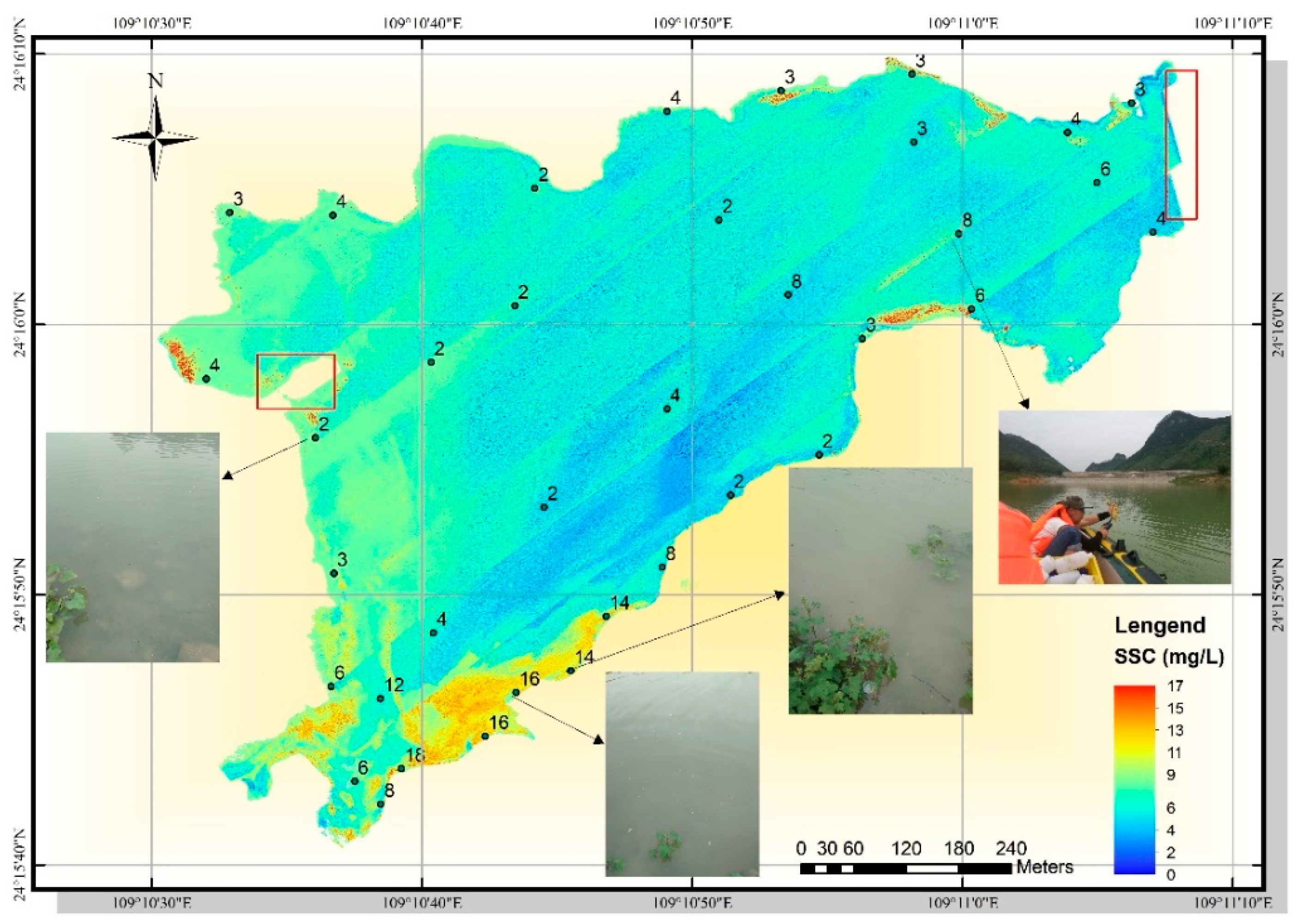
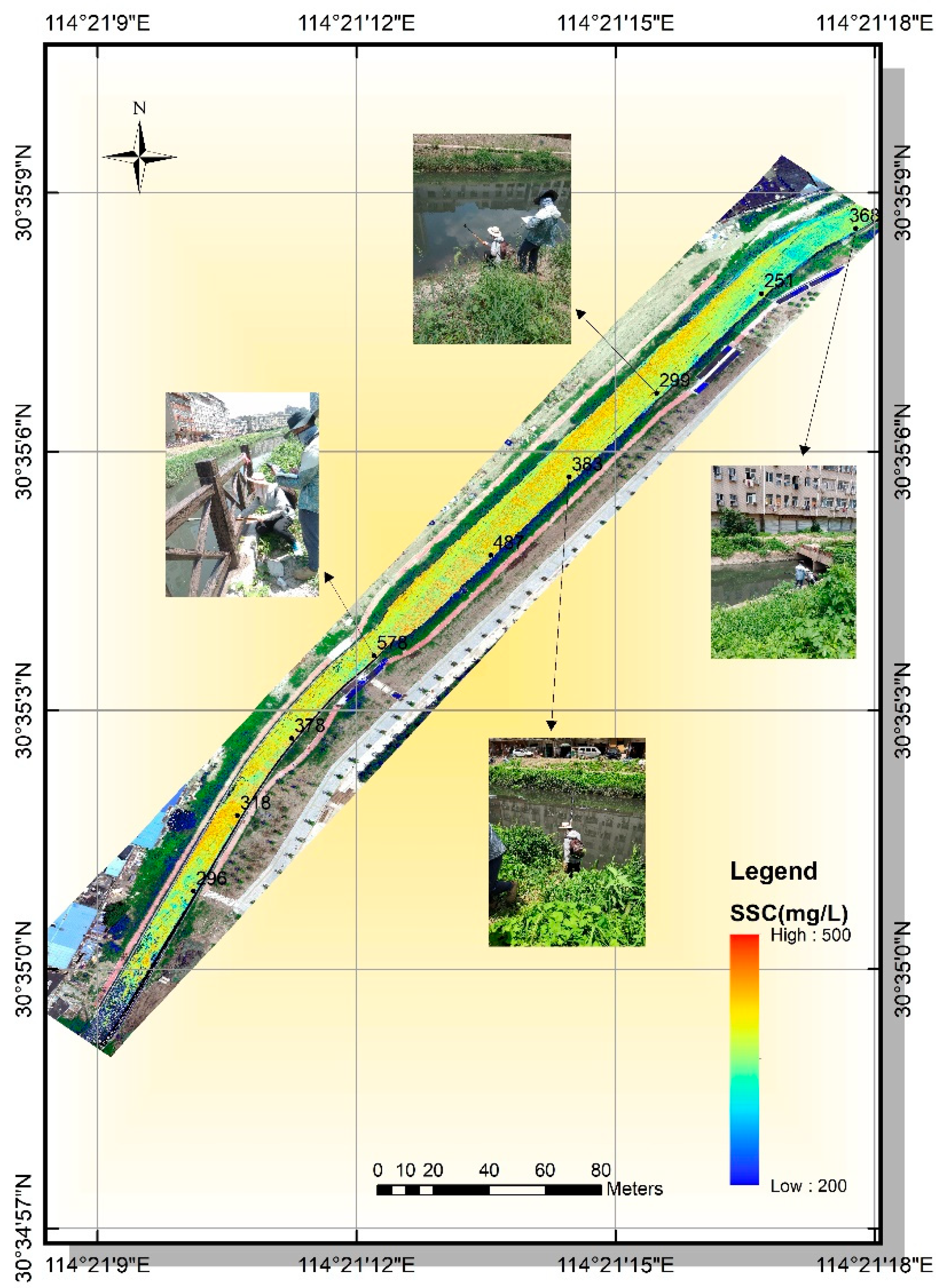
3.5. UAV Image Inversion Based on PSO-LSSVM
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- AL-Fahdawi, A.A.H.; Rabee, A.M.; Al-Hirmizy, S.M. Water quality monitoring of Al-Habbaniyah Lake using remote sensing and in situ measurements. Environ. Monit. Assess. 2015, 187, 367. [Google Scholar] [CrossRef] [PubMed]
- Lei, G.; Zhang, Y.; Pan, D.; Wang, D.; Fu, D. Parameter selection and model research on remote sensing evaluation for nearshore water quality. Acta Oceanol. Sin. 2016, 35, 114–117. [Google Scholar] [CrossRef]
- Doxaran, D.; Lamquin, N.; Park, Y.-J.; Mazeran, C.; Ryu, J.-H.; Wang, M.; Poteau, A. Retrieval of the seawater reflectance for suspended solids monitoring in the East China Sea using MODIS, MERIS and GOCI satellite data. Remote Sens. Environ. 2014, 146, 36–48. [Google Scholar] [CrossRef]
- Volpe, V.; Silvestri, S.; Marani, M. Remote sensing retrieval of suspended sediment concentration in shallow waters. Remote Sens. Environ. 2011, 115, 44–54. [Google Scholar] [CrossRef]
- Giardino, C.; Oggioni, A.; Bresciani, M.; Yan, H. Remote Sensing of Suspended Particulate Matter in Himalayan Lakes: A Case Study of Alpine Lakes in the Mount Everest Region. Mt. Res. Dev. 2010, 30, 157–168. [Google Scholar] [CrossRef]
- Li, D.; Li, M. Research Advance and Application Prospect of Unmanned Aerial Vehicle Remote Sensing System. Geomat. Inf. Sci. Wuhan Univ. 2014, 39, 505–513. [Google Scholar]
- Zhong, Y.; Wang, X.; Xu, Y.; Wang, S.; Zhang, L. Mini-UAV-Borne Hyperspectral Remote Sensing: From Observation and Processing to Applications. IEEE Geosci. Remote Sens. Mag. 2018, 6, 46–62. [Google Scholar] [CrossRef]
- Ma, R.; Duan, H.; Tang, J.; Chen, Z. Remote Sensing of Lake Water Environment, 1st ed.; Science Press: Beijing, China, 2010; ISBN 978-7-03-028776-2. [Google Scholar]
- Giardino, C.; Brando, V.E.; Dekker, A.G.; Strömbeck, N.; Candiani, G. Assessment of water quality in Lake Garda (Italy) using Hyperion. Remote Sens. Environ. 2007, 109, 183–195. [Google Scholar] [CrossRef]
- Härmä, P.; Vepsäläinen, J.; Hannonen, T.; Pyhälahti, T.; Kämäri, J.; Kallio, K.; Eloheimo, K.; Koponen, S. Detection of water quality using simulated satellite data and semi-empirical algorithms in Finland. Sci. Total Environ. 2001, 268, 107–121. [Google Scholar] [CrossRef]
- Ahn, Y.H.; Moon, J.E.; Gallegos, S. Development of Suspended Particulate Matter Algorithms for Ocean Color Remote Sensing. Korean J. Remote Sens. 2001, 17, 285–295. [Google Scholar]
- Gitelson, A.; Garbuzov, G.; Szilagyi, F.; Mittenzwey, K.H.; Karnieli, A.; Kaiser, A. Quantitative remote sensing methods for real-time monitoring of inland waters quality. Int. J. Remote Sens. 1993, 14, 1269–1295. [Google Scholar] [CrossRef]
- Wang, Z.; Kawamura, K.; Sakuno, Y.; Fan, X.; Gong, Z.; Lim, J. Retrieval of Chlorophyll-a and Total Suspended Solids Using Iterative Stepwise Elimination Partial Least Squares (ISE-PLS) Regression Based on Field Hyperspectral Measurements in Irrigation Ponds in Higashihiroshima, Japan. Remote Sens. 2017, 9, 264. [Google Scholar] [CrossRef]
- Hafeez, S.; Wong, M.; Ho, H.; Nazeer, M.; Nichol, J.; Abbas, S.; Tang, D.; Lee, K.; Pun, L. Comparison of Machine Learning Algorithms for Retrieval of Water Quality Indicators in Case-II Waters: A Case Study of Hong Kong. Remote Sens. 2019, 11, 617. [Google Scholar] [CrossRef]
- Singh, K.P.; Basant, N.; Gupta, S. Support vector machines in water quality management. Anal. Chim. Acta 2012, 703, 152–162. [Google Scholar] [CrossRef] [PubMed]
- Mueller, J.L.; Fargion, G.S.; McClain, C.R.; Mueller, J.L.; Morel, A.; Frouin, R.; Davis, C.; Arnone, R.; Carder, K.; Steward, R.G.; et al. Ocean Optics Protocols for Satellite Ocean Color Sensor Validation, 4th ed.; Radiometric Measurements and Data Analysis Protocols; Goddard Space Flight Space Center: Greenbelt, MD, USA, 2003; Volume III.
- Watanabe, F.; Alcântara, E.; Rodrigues, T.; Imai, N.; Barbosa, C.; Rotta, L. Estimation of Chlorophyll-a Concentration and the Trophic State of the Barra Bonita Hydroelectric Reservoir Using OLI/Landsat-8 Images. Int. J. Environ. Res. Public Health 2015, 12, 10391–10417. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Han, L.; Chen, X.; Li, D.; Sun, L.; Li, Y. Estimating wide range Total Suspended Solids concentrations from MODIS 250-m imageries: An improved method. ISPRS J. Photogramm. Remote Sens. 2015, 99, 58–69. [Google Scholar] [CrossRef]
- Gong, C.L.; Yin, Q.; Kuang, D.B. Correlations Between Water Quality Indexes and Reflectance Spectra of Huangpujiang River. J. Remote Sens. 2006, 10, 910–916. [Google Scholar]
- Rinnan, Å.; Berg, F.V.D.; Engelsen, S.B. Review of the most common pre-processing techniques for near-infrared spectra. Trends Anal. Chem. 2009, 28, 1201–1222. [Google Scholar] [CrossRef]
- Rundquist, D.C.; Han, L.; Schalles, J.F.; Peake, J.S. Remote Measurement of Algal Chlorophyll in Surface Waters: The Case for the First Derivative of Reflectance Near 690 nm. Photogramm. Eng. Remote Sens. 1996, 62, 195–200. [Google Scholar]
- Zhang, M. Spectral indices for estimating ecological indicators of karst rocky desertification. Int. J. Remote Sens. 2010, 31, 2115–2122. [Google Scholar]
- Pulliainen, J.; Kallio, K.; Eloheimo, K.; Koponen, S.; Servomaa, H.; Hannonen, T.; Tauriainen, S.; Hallikainen, M. A semi-operative approach to lake water quality retrieval from remote sensing data. Sci. Total Environ. 2001, 268, 79–93. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Suykens, J.; Vandewalle, J. Least Squares Support Vector Machine Classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Ismail, S.; Shabri, A.; Samsudin, R. A hybrid model of self-organizing maps (SOM) and least square support vector machine (LSSVM) for time-series forecasting. Expert Syst. Appl. 2011, 38, 10574–10578. [Google Scholar] [CrossRef]
- Yan, Z.G. The PSO-LSSVM model for predicting the failure depth of coal seam floor. In Proceedings of the Intelligent Control & Automation, Beijing, China, 6 July 2012. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. Proc. IEEE Int. Conf. Neural. Netw. Piscataway. IEEE Serv. Cent. 1995, 12, 1941–1948. [Google Scholar]
- Eberhart, R.C.; Shi, Y. Particle swarm optimization: Developments, applications and resources. In Proceedings of the Congress on Evolutionary Computation, Wellington, New Zealand, 10 June 2002. [Google Scholar]
- Eberhart, R.C.; Shi, Y. Comparison between genetic algorithms and particle swarm optimization. In Proceedings of the International Conference on Evolutionary Programming, Berlin, Germany, 1998. [Google Scholar]
- Zhu, X.L.; Xiong, W.L.; Xu, B.G. A Particle Swarm Optimization Algorithm Based on Dynamic Intertia Weight. Comput. Simul. 2007, 24, 154–157. [Google Scholar]
- Kumar, D.N.; Janga Reddy, M. Multipurpose Reservoir Operation Using Particle Swarm Optimization. J. Water Resour. Plan. Manag. 2007, 133, 192–201. [Google Scholar]
- Sedki, A.; Ouazar, D. Hybrid particle swarm optimization and differential evolution for optimal design of water distribution systems. Adv. Eng. Inform. 2012, 26, 582–591. [Google Scholar] [CrossRef]
- Kallio, K.; Koponen, S.; Ylöstalo, P.; Kervinen, M.; Pyhälahti, T.; Attila, J. Validation of MERIS spectral inversion processors using reflectance, IOP and water quality measurements in boreal lakes. Remote Sens. Environ. 2015, 157, 147–157. [Google Scholar] [CrossRef]
- Han, L.; Rundquist, D.C. The response of both surface reflectance and the underwater light field to various levels of suspended sediments: Preliminary results. Photogramm. Eng. Remote Sens. 1994, 60, 1463–1471. [Google Scholar]
- Berthon, J.F.; Zibordi, G. Optically black waters in the northern Baltic Sea. Geophys. Res. Lett. 2010, 37, 232–256. [Google Scholar] [CrossRef]
- Duan, H.; Ma, R.; Loiselle, S.A.; Shen, Q.; Yin, H.; Zhang, Y. Optical characterization of black water blooms in eutrophic waters. Sci. Total Environ. 2014, 482–483, 174–183. [Google Scholar] [CrossRef] [PubMed]
- Doxaran, D.; Froidefond, J.M.; Lavender, S.; Castaing, P. Spectral signature of highly turbid waters: Application with SPOT data to quantify suspended particulate matter concentrations. Remote Sens. Environ. 2002, 81, 149–161. [Google Scholar] [CrossRef]

| Class | Parameter | Class | Parameter | ||||
|---|---|---|---|---|---|---|---|
| Wavelength range | 400–1000 nm | Field of view | 33 | 22 | 16 | ||
| Number of spectral channels | 270 | IFOV single pixel spatial resolution | 0.9 | 0.61 | 0.43 | ||
| Number of spatial channels | 640 | Instrument power consumption | <13 W | ||||
| Spectral sampling interval | 2.2 nm/pixel | Bit depth | 12 bit | ||||
| Spectral resolution | 6 nm @ 20 µm | Storage | 480 GB | ||||
| Secondary sequence filter | Yes | Cell size | 7.4 µm | ||||
| Numerical aperture | F/2.5 | Camera type | COMS | ||||
| Light path design | Coaxial reflection imaging spectrometer | Maximum frame rate | 300 fps | ||||
| Slit width | 20 µm | Weight | <0.6 kg (no lens) | ||||
| Lens focal length | 8 mm | 12 mm | 17 mm | Operating temperature | 0–50 °C | ||
| n | Max | Min | Mean | SD | CV |
|---|---|---|---|---|---|
| 36 | 18.00 | 2.00 | 5.86 | 4.61 | 0.79 |
| n | Max | Min | Mean | SD | CV |
|---|---|---|---|---|---|
| 36 | 578.00 | 26.64 | 173.74 | 154.64 | 0.89 |
| Modeling Method | Independent Variables | Mathematical Model | Training Data | Test Data | ||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAPE | R2 | RMSE | MAPE | |||
| PSO-LSSVM | 135(number) | — | 0.980 | 0.68 | 12.66% | 0.950 | 0.75 | 13.38% |
| Cars-PLS | 135(number) | — | 0.522 | 3.33 | 58.93% | 0.580 | 2.19 | 47.44% |
| RF | 135(number) | — | 0.799 | 2.16 | 43.16% | 0.888 | 1.13 | 17.56% |
| EF | 0.586 | 3.10 | 52.38% | 0.791 | 1.55 | 31.94% | ||
| LogF | 0.508 | 3.38 | 61.85% | 0.650 | 2.01 | 44.68% | ||
| QP | 0.596 | 3.06 | 53.77% | 0.804 | 1.50 | 27.50% | ||
| LinF | 0.517 | 3.35 | 60.66% | 0.665 | 1.96 | 43.90% | ||
| PF | 0.586 | 3.10 | 51.51% | 0.780 | 1.59 | 33.31% | ||
| Modeling Method | Independent Variables | Mathematical Model | Training Data | Test Data | ||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAPE | R2 | RMSE | MAPE | |||
| PSO-LSSVM | 225(number) | — | 0.957 | 31.63 | 17.96% | 0.964 | 28.56 | 13.12% |
| Cars-PLS | 225 (number) | — | 0.557 | 101.31 | 87.06% | 0.609 | 94.63 | 101.2% |
| RF | 225 (number) | — | 0.810 | 66.38 | 41.87% | 0.740 | 77.21 | 47.30% |
| EF | 0.640 | 91.36 | 98.48% | 0.489 | 108.16 | 99.30% | ||
| LogF | 0.743 | 77.22 | 59.71% | 0.661 | 88.08 | 45.96% | ||
| QP | 0.748 | 76.48 | 59.32% | 0.709 | 81.67 | 38.98% | ||
| LinF | 0.743 | 77.10 | 59.61% | 0.666 | 87.51 | 45.14% | ||
| PF | 0.655 | 89.35 | 81.70% | 0.489 | 108.13 | 84.57% | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, L.; Huang, C.; Zhong, Y.; Wang, Z.; Hu, X.; Lin, L. Inland Waters Suspended Solids Concentration Retrieval Based on PSO-LSSVM for UAV-Borne Hyperspectral Remote Sensing Imagery. Remote Sens. 2019, 11, 1455. https://doi.org/10.3390/rs11121455
Wei L, Huang C, Zhong Y, Wang Z, Hu X, Lin L. Inland Waters Suspended Solids Concentration Retrieval Based on PSO-LSSVM for UAV-Borne Hyperspectral Remote Sensing Imagery. Remote Sensing. 2019; 11(12):1455. https://doi.org/10.3390/rs11121455
Chicago/Turabian StyleWei, Lifei, Can Huang, Yanfei Zhong, Zhou Wang, Xin Hu, and Liqun Lin. 2019. "Inland Waters Suspended Solids Concentration Retrieval Based on PSO-LSSVM for UAV-Borne Hyperspectral Remote Sensing Imagery" Remote Sensing 11, no. 12: 1455. https://doi.org/10.3390/rs11121455
APA StyleWei, L., Huang, C., Zhong, Y., Wang, Z., Hu, X., & Lin, L. (2019). Inland Waters Suspended Solids Concentration Retrieval Based on PSO-LSSVM for UAV-Borne Hyperspectral Remote Sensing Imagery. Remote Sensing, 11(12), 1455. https://doi.org/10.3390/rs11121455