An Automated Python Language-Based Tool for Creating Absence Samples in Groundwater Potential Mapping
Abstract
1. Introduction
2. Development of the SAS Tool
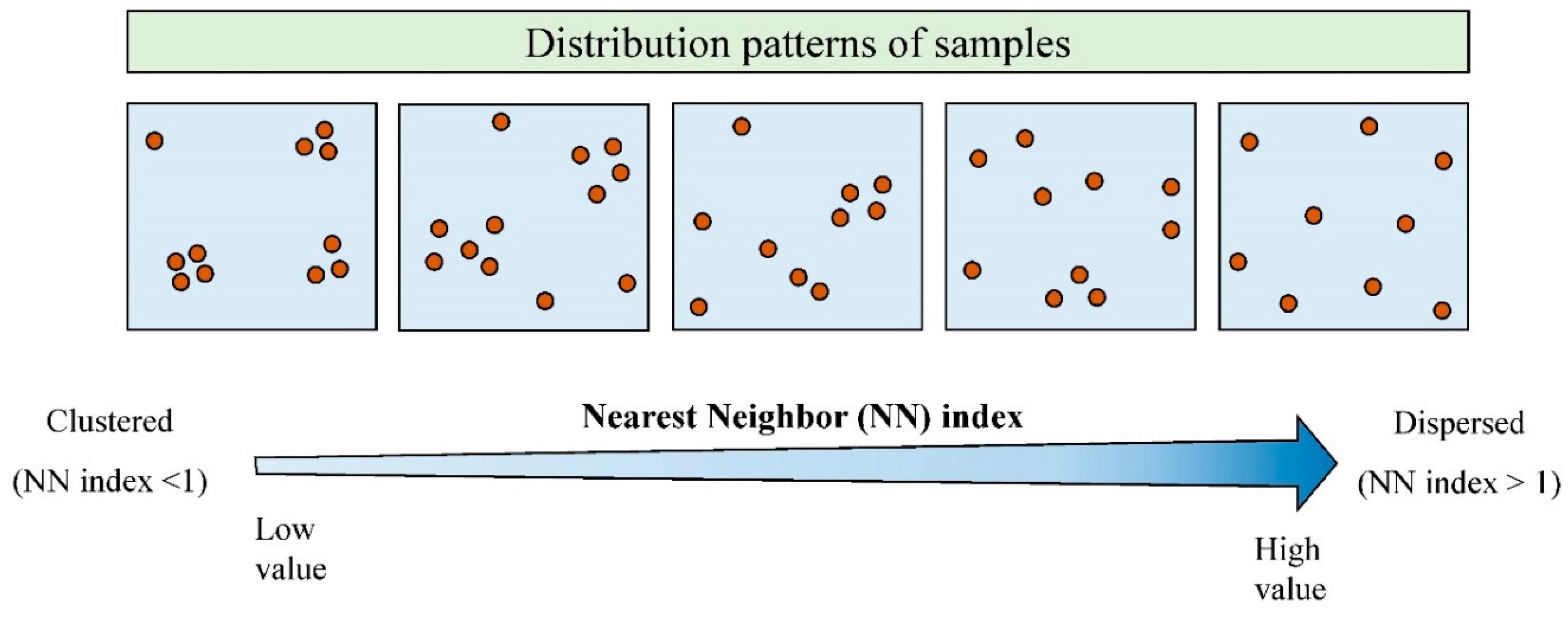
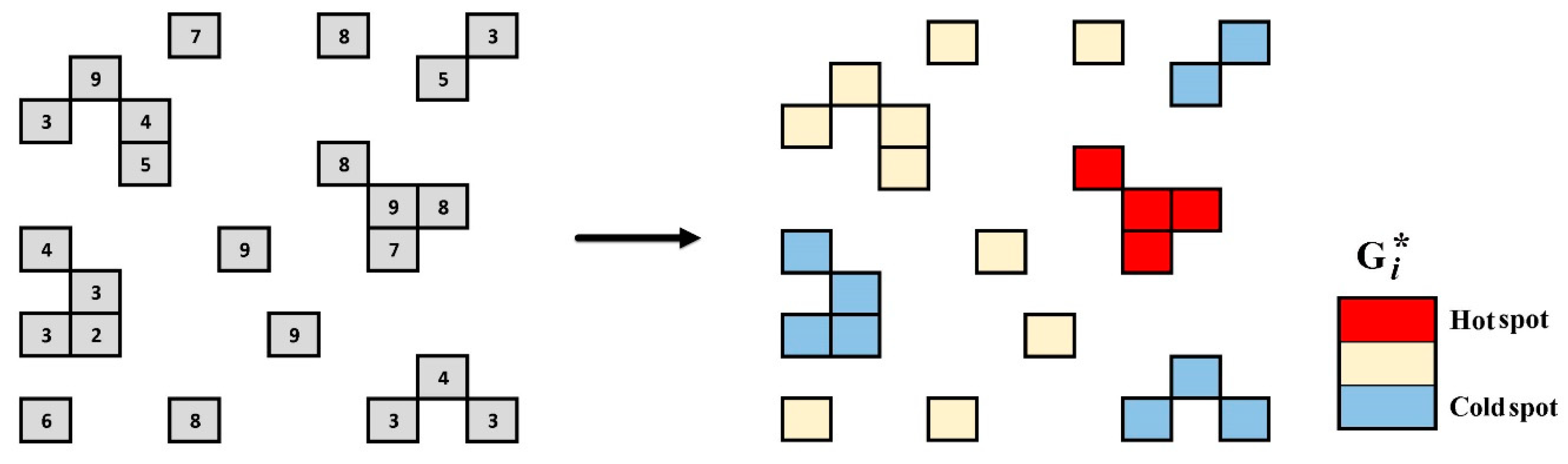
2.1. Technical Background
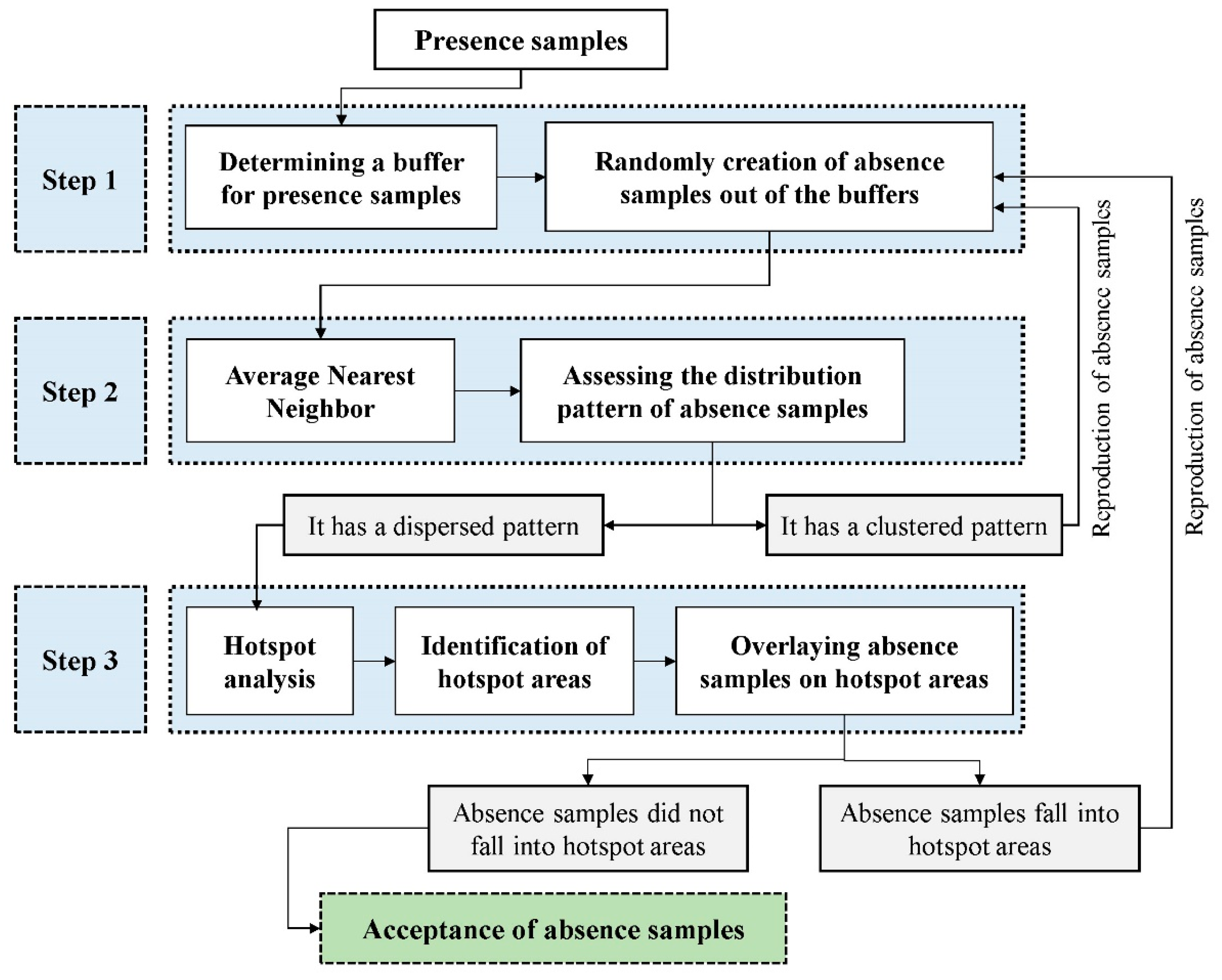
2.2. Designing the SAS Tool
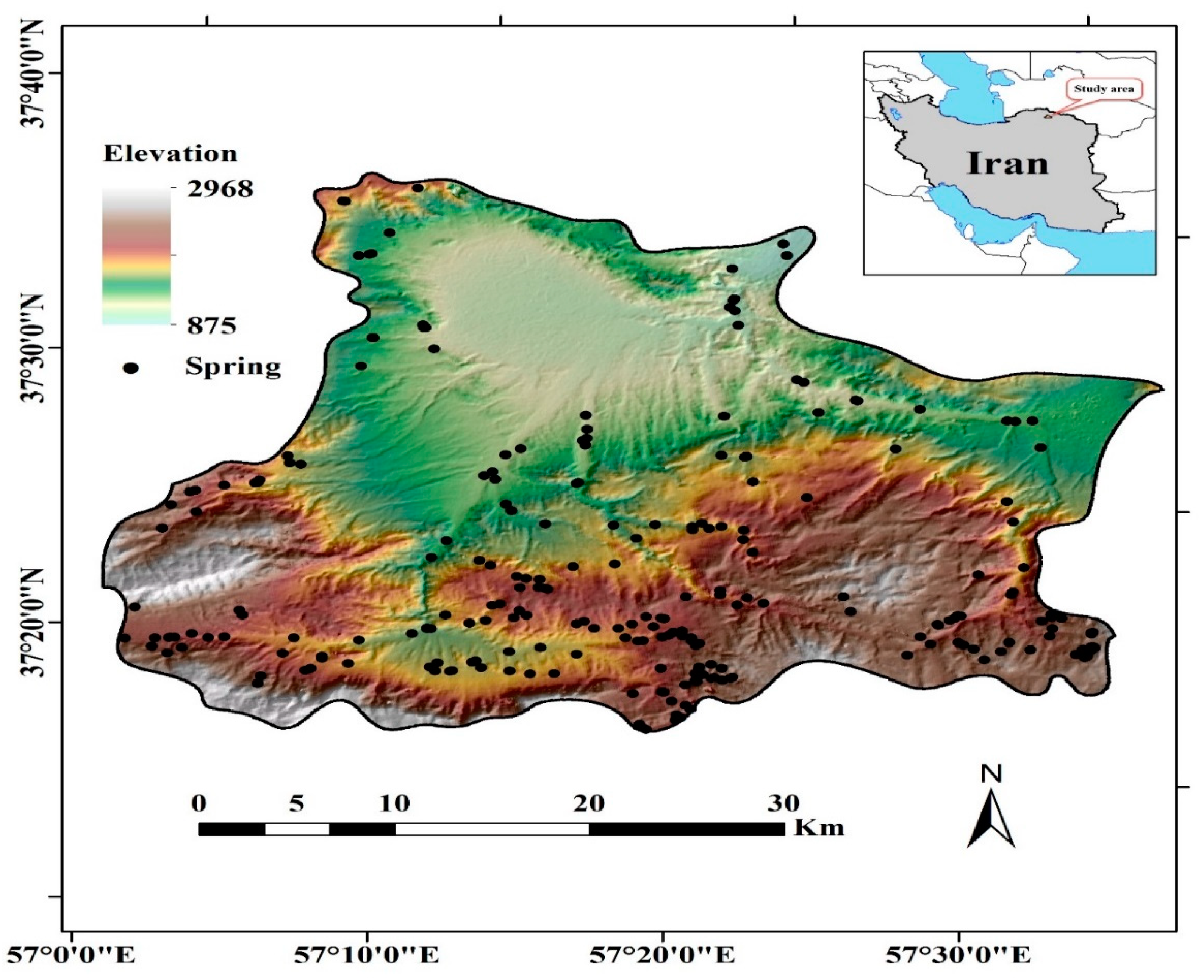
3. Case Study
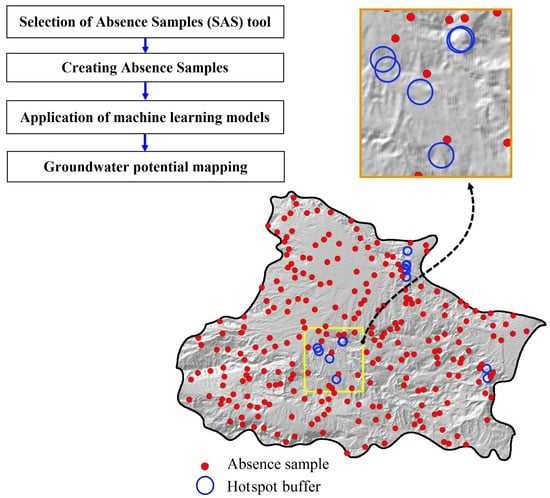
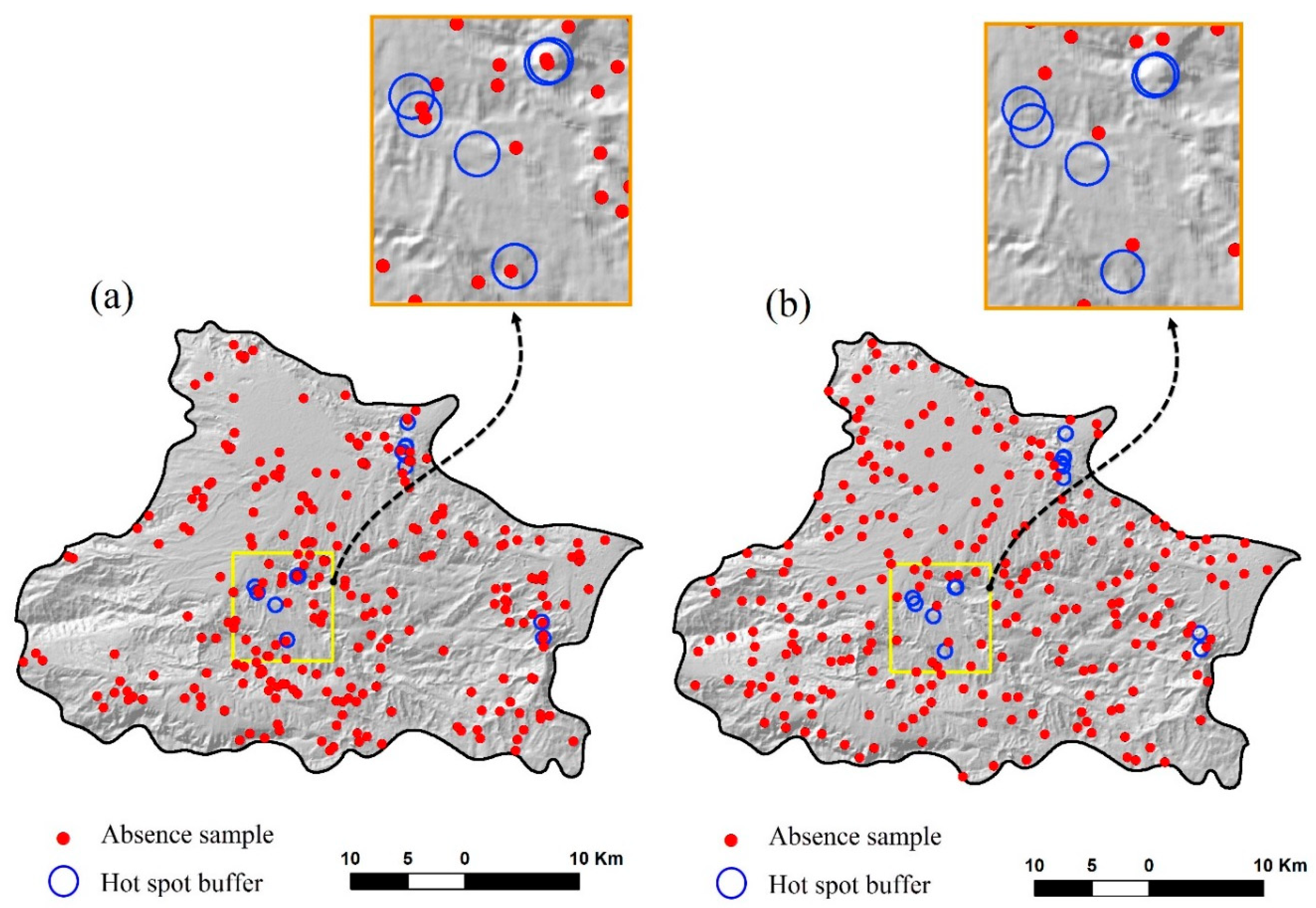
3.1. Application of the SAS Tool
3.2. Groundwater-Affecting Factors
3.3. Groundwater Potential Modeling
3.3.1. Random Forest (RF)
- it is relatively robust to noise and outliers;
- it provides an internal unbiased estimate of the generalization error through out-of-bag (OOB) error;
- it estimates the importance of variables in the modeling process (i.e., contribution of variables);
- it can handle numerous input variables (i.e., predictive factors) without variable deletion;
- it efficiently handles large databases; and
- it reduces the computational burden and is computationally lighter than other tree-based models.
3.3.2. Multivariate Adaptive Regression Splines (MARS)
3.4. Accuracy Assessment
4. Results and Discussion
4.1. Selection of Absence Samples and Accuracy Assessment
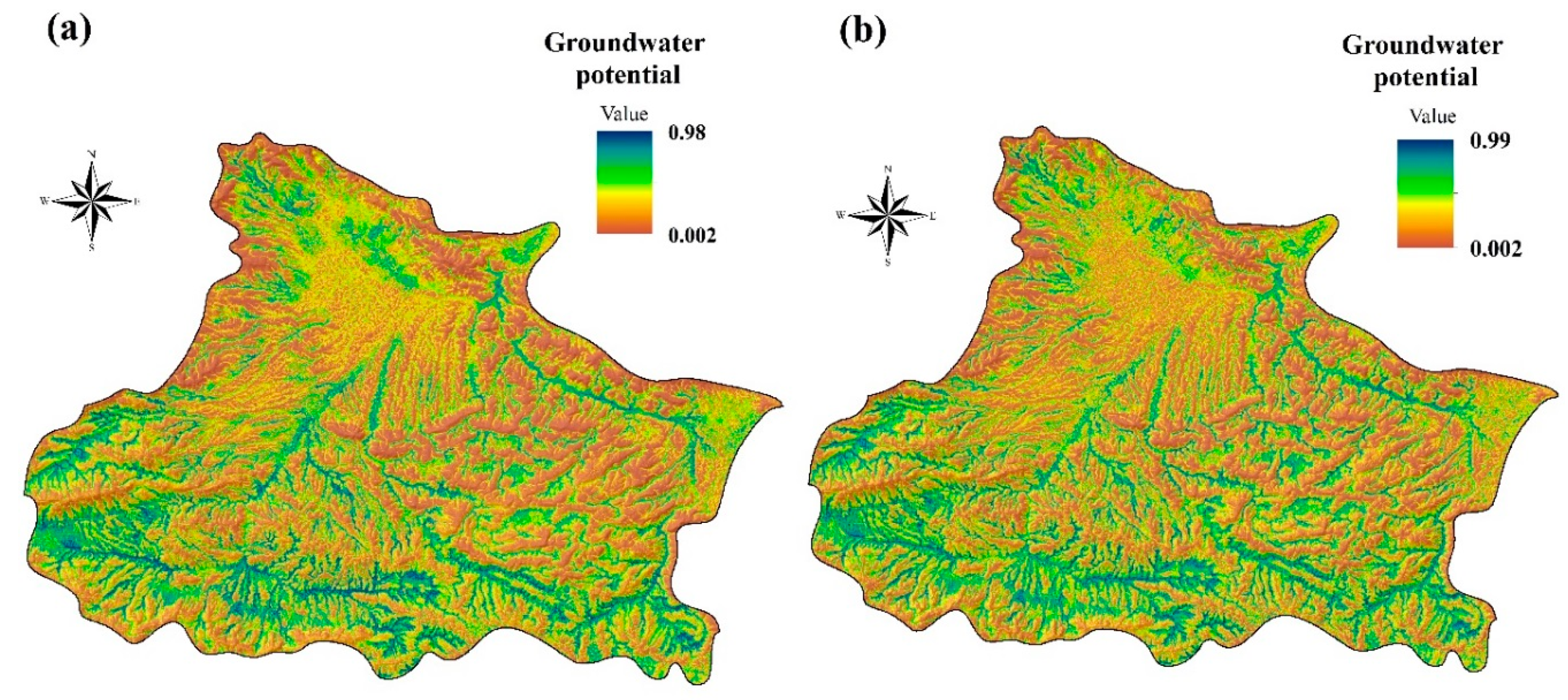
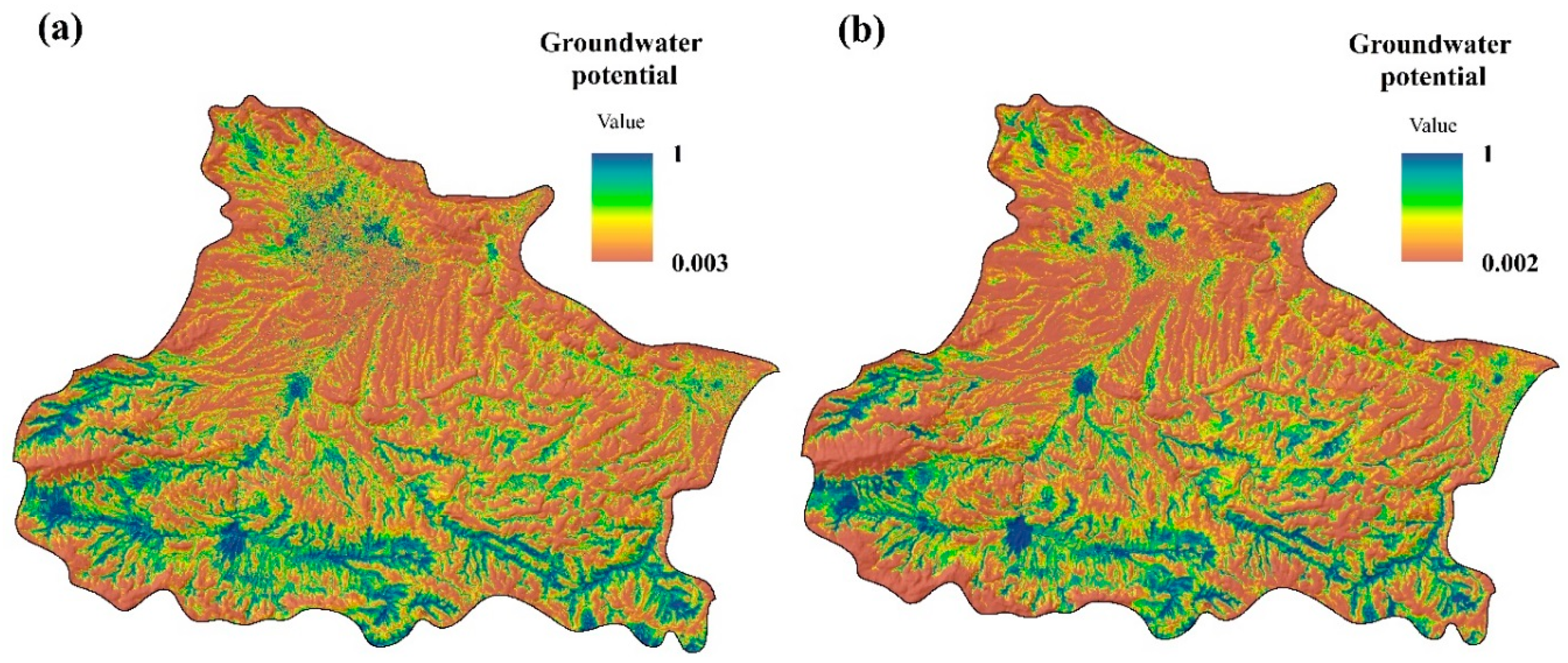
4.2. Groundwater Potential Mapping
5. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hong, H.; Pradhan, B.; Sameen, M.I.; Kalantar, B.; Zhu, A.; Chen, W. Improving the accuracy of landslide susceptibility model using a novel region-partitioning approach. Landslides 2018, 15, 753–772. [Google Scholar] [CrossRef]
- Van Westen, C.J.; Castellanos, E.; Kuriakose, S.L. Spatial data for landslide susceptibility, hazard, and vulnerability assessment: An overview. Eng. Geol. 2008, 102, 112–131. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Pourghasemi, H.R. A comparative assessment between three machine learning models and their performance comparison by bivariate and multivariate statistical methods in groundwater potential mapping. Water Resour. Manag. 2015, 29, 5217–5236. [Google Scholar] [CrossRef]
- Nefeslioglu, H.A.; Gokceoglu, C.; Sonmez, H. An assessment on the use of logistic regression and artificial neural networks with different sampling strategies for the preparation of landslide susceptibility maps. Eng. Geol. 2008, 97, 171–191. [Google Scholar] [CrossRef]
- Corsini, A.; Cervi, F.; Ronchetti, F. Weight of evidence and artificial neural networks for potential groundwater spring mapping: An application to the Mt. Modino area (Northern Apennines, Italy). Geomorphology 2009, 111, 79–87. [Google Scholar] [CrossRef]
- Pradhan, B. A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using GIS. Comput. Geosci. 2013, 51, 350–365. [Google Scholar] [CrossRef]
- Conoscenti, C.; Rotigliano, E.; Cama, M.; Caraballo-Arias, N.A.; Lombardo, L.; Agnesi, V. Exploring the effect of absence selection on landslide susceptibility models: A case study in Sicily, Italy. Geomorphology 2016, 261, 222–235. [Google Scholar] [CrossRef]
- Gorsevski, P.V.; Gessler, P.E.; Foltz, R.B.; Elliot, W.J. Spatial prediction of landslide hazard using logistic regression and ROC analysis. Trans. GIS 2006, 10, 395–415. [Google Scholar] [CrossRef]
- Formetta, G.; Capparelli, G.; Versace, P. Evaluating performance of simplified physically based models for shallow landslide susceptibility. Hydrol. Earth Syst. Sci. 2016, 20, 4585–4603. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Pourghasemi, H.R.; Dixon, B. GIS-based groundwater potential mapping using boosted regression tree, classification and regression tree, and random forest machine learning models in Iran. Environ. Monit. Assess. 2016, 188, 44. [Google Scholar] [CrossRef]
- Wilson, J.P. Digital terrain modeling. Geomorphology 2012, 137, 107–121. [Google Scholar] [CrossRef]
- Tien Bui, D.; Pradhan, B.; Lofman, O.; Revhaug, I.; Dick, O.B. Landslide susceptibility mapping at Hoa Binh province (Vietnam) using an adaptive neuro-fuzzy inference system and GIS. Comput. Geosci. 2012, 45, 199–211. [Google Scholar] [CrossRef]
- Chen, T.-C.; Soo, V.-W. Feature Selection in Learning Common Sense Associations Using Matrix Factorization. Int. J. Fuzzy Syst. 2017, 19, 1217–1226. [Google Scholar] [CrossRef]
- Choubin, B.; Rahmati, O.; Soleimani, F.; Alilou, H.; Moradi, E.; Alamdari, N. Regional Groundwater Potential Analysis Using Classification and Regression Trees. In Spatial Modeling in GIS and R for Earth and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2019; pp. 485–498. [Google Scholar]
- Golkarian, A.; Naghibi, S.A.; Kalantar, B.; Pradhan, B. Groundwater potential mapping using C5.0, random forest, and multivariate adaptive regression spline models in GIS. Environ. Monit. Assess. 2018, 190, 149. [Google Scholar] [CrossRef] [PubMed]
- Lee, S. Current and Future Status of GIS-based Landslide Susceptibility Mapping: A Literature Review. Korean J. Remote Sens. 2019, 35, 179–193. [Google Scholar]
- Ahlmer, A.-K.; Cavalli, M.; Hansson, K.; Koutsouris, A.J.; Crema, S.; Kalantari, Z. Soil moisture remote-sensing applications for identification of flood-prone areas along transport infrastructure. Environ. Earth Sci. 2018, 77, 533. [Google Scholar] [CrossRef]
- Falah, F.; Rahmati, O.; Rostami, M.; Ahmadisharaf, E.; Daliakopoulos, I.N.; Pourghasemi, H.R. Artificial Neural Networks for Flood Susceptibility Mapping in Data-Scarce Urban Areas. In Spatial Modeling in GIS and R for Earth and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2019; pp. 323–336. [Google Scholar]
- Pham, B.T.; Prakash, I.; Singh, S.K.; Shirzadi, A.; Shahabi, H.; Bui, D.T. Landslide susceptibility modeling using Reduced Error Pruning Trees and different ensemble techniques: Hybrid machine learning approaches. Catena 2019, 175, 203–218. [Google Scholar] [CrossRef]
- Plug, C.; Xia, J.C.; Caulfield, C. Spatial and temporal visualisation techniques for crash analysis. Accid. Anal. Prev. 2011, 43, 1937–1946. [Google Scholar] [CrossRef] [PubMed]
- Pourghasemi, H.R.; Rahmati, O. Prediction of the landslide susceptibility: Which algorithm, which precision? Catena 2018, 162, 177–192. [Google Scholar] [CrossRef]
- Conoscenti, C.; Angileri, S.; Cappadonia, C.; Rotigliano, E.; Agnesi, V.; Märker, M. Gully erosion susceptibility assessment by means of GIS-based logistic regression: A case of Sicily (Italy). Geomorphology 2014, 204, 399–411. [Google Scholar] [CrossRef]
- Gayen, A.; Pourghasemi, H.R.; Saha, S.; Keesstra, S.; Bai, S. Gully erosion susceptibility assessment and management of hazard-prone areas in India using different machine learning algorithms. Sci. Total Environ. 2019, 668, 124–138. [Google Scholar] [CrossRef] [PubMed]
- Pourghasemi, H.R.; Yousefi, S.; Kornejady, A.; Cerdà, A. Performance assessment of individual and ensemble data-mining techniques for gully erosion modeling. Sci. Total Environ. 2017, 609, 764–775. [Google Scholar] [CrossRef] [PubMed]
- Rahmati, O.; Tahmasebipour, N.; Haghizadeh, A.; Pourghasemi, H.R.; Feizizadeh, B. Evaluation of different machine learning models for predicting and mapping the susceptibility of gully erosion. Geomorphology 2017, 298, 118–137. [Google Scholar] [CrossRef]
- Lee, S.; Lee, C.-W. Application of decision-tree model to groundwater productivity-potential mapping. Sustainability 2015, 7, 13416–13432. [Google Scholar] [CrossRef]
- Lee, S.; Park, I.; Choi, J.-K. Spatial prediction of ground subsidence susceptibility using an artificial neural network. Environ. Manag. 2012, 49, 347–358. [Google Scholar] [CrossRef] [PubMed]
- Park, I.; Choi, J.; Lee, M.J.; Lee, S. Application of an adaptive neuro-fuzzy inference system to ground subsidence hazard mapping. Comput. Geosci. 2012, 48, 228–238. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Saravi, M.M. Land-Subsidence Spatial Modeling Using the Random Forest Data-Mining Technique. In Spatial Modeling in GIS and R for Earth and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2019; pp. 147–159. [Google Scholar]
- Rahmati, O.; Golkarian, A.; Biggs, T.; Keesstra, S.; Mohammadi, F.; Daliakopoulos, I.N. Land subsidence hazard modeling: Machine learning to identify predictors and the role of human activities. J. Environ. Manag. 2019, 236, 466–480. [Google Scholar] [CrossRef]
- Bui, D.T.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar]
- Chapi, K.; Singh, V.P.; Shirzadi, A.; Shahabi, H.; Bui, D.T.; Pham, B.T.; Khosravi, K. A novel hybrid artificial intelligence approach for flood susceptibility assessment. Environ. Modell. Softw. 2017, 95, 229–245. [Google Scholar] [CrossRef]
- Kalantari, Z.; Ferreira, C.S.S.; Koutsouris, A.J.; Ahmer, A.-K.; Cerdà, A.; Destouni, G. Assessing flood probability for transportation infrastructure based on catchment characteristics, sediment connectivity and remotely sensed soil moisture. Sci. Total Environ. 2019, 661, 393–406. [Google Scholar] [CrossRef]
- Rutherford, G.; Guisan, A.; Zimmermann, N. Evaluating sampling strategies and logistic regression methods for modelling complex land cover changes. J. Appl. Ecol. 2007, 44, 414–424. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Pradhan, B.; Jebur, M.N. Flood susceptibility mapping using a novel ensemble weights-of-evidence and support vector machine models in GIS. J. Hydrol. 2014, 512, 332–343. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Pradhan, B.; Mansor, S.; Ahmad, N. Flood susceptibility assessment using GIS-based support vector machine model with different kernel types. Catena 2015, 125, 91–101. [Google Scholar] [CrossRef]
- Termeh, S.V.R.; Kornejady, A.; Pourghasemi, H.R.; Keesstra, S. Flood susceptibility mapping using novel ensembles of adaptive neuro fuzzy inference system and metaheuristic algorithms. Sci. Total Environ. 2018, 615, 438–451. [Google Scholar] [CrossRef] [PubMed]
- Perry, G.L.; Dickson, M.E. Using Machine Learning to Predict Geomorphic Disturbance: The Effects of Sample Size, Sample Prevalence, and Sampling Strategy. J. Geophys. Res.-Earth 2018, 123, 2954–2970. [Google Scholar] [CrossRef]
- Xu, C.; He, H.S.; Hu, Y.; Chang, Y.; Li, X.; Bu, R. Latin hypercube sampling and geostatistical modeling of spatial uncertainty in a spatially explicit forest landscape model simulation. Ecol. Model. 2005, 185, 255–269. [Google Scholar] [CrossRef]
- Sameen, M.I.; Pradhan, B.; Lee, S. Self-learning random forests model for mapping groundwater yield in data-scarce areas. Nat. Resour. Res. 2018, 28, 757–775. [Google Scholar] [CrossRef]
- Zabihi, M.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Behzadfar, M. GIS-based multivariate adaptive regression spline and random forest models for groundwater potential mapping in Iran. Environ. Earth Sci. 2016, 75, 665. [Google Scholar] [CrossRef]
- Ichnowski, J.; Alterovitz, R. Fast nearest neighbor search in SE (3) for sampling-based motion planning. In Algorithmic Foundations of Robotics XI; Springer: Berlin/Heidelberg, Germany, 2015; pp. 197–214. [Google Scholar]
- Vadrevu, K.P.; Badarinath, K.; Anuradha, E. Spatial patterns in vegetation fires in the Indian region. Environ. Monit. Assess. 2008, 147, 1. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Li, H.; Hou, E.; Wang, S.; Wang, G.; Panahi, M.; Li, T.; Peng, T.; Guo, C.; Niu, C. GIS-based groundwater potential analysis using novel ensemble weights-of-evidence with logistic regression and functional tree models. Sci. Total Environ. 2018, 634, 853–867. [Google Scholar] [CrossRef]
- Chen, Y.; Ge, Y. Spatial point pattern analysis on the villages in China’s poverty-stricken areas. Procedia Environ. Sci. 2015, 27, 98–105. [Google Scholar] [CrossRef]
- Bajat, B.; Blagojević, D.; Kilibarda, M.; Luković, J.; Tošić, I. Spatial analysis of the temperature trends in Serbia during the period 1961–2010. Theor. Appl. Climatol. 2015, 121, 289–301. [Google Scholar] [CrossRef]
- Koch, S.L.; Shriver, M.D.; Jablonski, N.G. Variation in human hair ultrastructure among three biogeographic populations. J. Struct. Biol. 2019, 205, 60–66. [Google Scholar] [CrossRef] [PubMed]
- Prasannakumar, V.; Vijith, H.; Charutha, R.; Geetha, N. Spatio-temporal clustering of road accidents: GIS based analysis and assessment. Proc. Soc. Behv. 2011, 21, 317–325. [Google Scholar] [CrossRef]
- Zou, G.; Wu, H.-I. Nearest-neighbor distribution of interacting biological entities. J. Theor. Biol. 1995, 172, 347–353. [Google Scholar] [CrossRef] [PubMed]
- Bishop, M.A. Nearest neighbor analysis of mega-barchanoid dunes, Ar Rub’al Khali, sand sea: The application of geographical indices to the understanding of dune field self-organization, maturity and environmental change. Geomorphology 2010, 120, 186–194. [Google Scholar] [CrossRef]
- Chainey, S. Advanced Hotspot Analysis: Spatial Significance Mapping Using Gi*; UCL Jill Dando Institute of Crime Science, University College London: London, UK, 2010. [Google Scholar]
- McMillan, H.; Jackson, B.; Clark, M.; Kavetski, D.; Woods, R. Rainfall uncertainty in hydrological modelling: An evaluation of multiplicative error models. J. Hydrol. 2011, 400, 83–94. [Google Scholar] [CrossRef]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Kiss, R. Determination of drainage network in digital elevation models, utilities and limitations. J. Hung. Geomath. 2004, 2, 16–29. [Google Scholar]
- San, B.T. An evaluation of SVM using polygon-based random sampling in landslide susceptibility mapping: The Candir catchment area (western Antalya, Turkey). Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 399–412. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology/Un modèle à base physique de zone d’appel variable de l’hydrologie du bassin versant. Hydrol. Sci. J. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Wang, Z.; Lai, C.; Chen, X.; Yang, B.; Zhao, S.; Bai, X. Flood hazard risk assessment model based on random forest. J. Hydrol. 2015, 527, 1130–1141. [Google Scholar] [CrossRef]
- Qi, Y. Random forest for bioinformatics. In Ensemble Machine Learning; Springer: Berlin/Heidelberg, Germany, 2012; pp. 307–323. [Google Scholar]
- Archer, K.J.; Kimes, R.V. Empirical characterization of random forest variable importance measures. Comput. Stat. Data Anal. 2008, 52, 2249–2260. [Google Scholar] [CrossRef]
- Devetyarov, D.; Nouretdinov, I. Prediction with confidence based on a random forest classifier. In Proceedings of the IFIP International Conference on Artificial Intelligence Applications and Innovations, Larnaca, Cyprus, 6–7 October 2010; pp. 37–44. [Google Scholar]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Gutiérrez, Á.G.; Schnabel, S.; Contador, J.F.L. Using and comparing two nonparametric methods (CART and MARS) to model the potential distribution of gullies. Ecol. Model. 2009, 220, 3630–3637. [Google Scholar] [CrossRef]
- Leathwick, J.; Elith, J.; Hastie, T. Comparative performance of generalized additive models and multivariate adaptive regression splines for statistical modelling of species distributions. Ecol. Model. 2006, 199, 188–196. [Google Scholar] [CrossRef]
- Leathwick, J.; Rowe, D.; Richardson, J.; Elith, J.; Hastie, T. Using multivariate adaptive regression splines to predict the distributions of New Zealand’s freshwater diadromous fish. Freshw. Biol. 2005, 50, 2034–2052. [Google Scholar] [CrossRef]
- Lee, T.S.; Chiu, C.-C.; Chou, Y.-C.; Lu, C.-J. Mining the customer credit using classification and regression tree and multivariate adaptive regression splines. Comput. Stat. Data Anal. 2006, 50, 1113–1130. [Google Scholar] [CrossRef]
- Lacoste, M.; Lemercier, B.; Walter, C. Regional mapping of soil parent material by machine learning based on point data. Geomorphology 2011, 133, 90–99. [Google Scholar] [CrossRef]
- Lee, S.; Hong, S.M.; Jung, H.S. GIS-based groundwater potential mapping using artificial neural network and support vector machine models: The case of Boryeong city in Korea. Geocarto Int. 2018, 33, 847–861. [Google Scholar] [CrossRef]
- Lee, S.; Park, I. Application of decision tree model for the ground subsidence hazard mapping near abandoned underground coal mines. J. Environ. Manag. 2013, 127, 166–176. [Google Scholar] [CrossRef] [PubMed]
- Allouche, O.; Tsoar, A.; Kadmon, R. Assessing the accuracy of species distribution models: Prevalence, kappa and the true skill statistic (TSS). J. Appl. Ecol. 2006, 43, 1223–1232. [Google Scholar] [CrossRef]
- Peres, D.; Cancelliere, A. Derivation and evaluation of landslide-triggering thresholds by a Monte Carlo approach. Hydrol. Earth Syst. Sci. 2014, 18, 4913–4931. [Google Scholar] [CrossRef]
- Pradhan, B.; Lee, S.; Buchroithner, M.F. A GIS-based back-propagation neural network model and its cross-application and validation for landslide susceptibility analyses. Comput. Environ. Urban 2010, 34, 216–235. [Google Scholar] [CrossRef]
- Rahmati, O.; Naghibi, S.A.; Shahabi, H.; Bui, D.T.; Pradhan, B.; Azareh, A.; Rafiei-Sardooi, E.; Samani, A.N.; Melesse, A.M. Groundwater spring potential modelling: Comprising the capability and robustness of three different modeling approaches. J. Hydrol. 2018, 565, 248–261. [Google Scholar] [CrossRef]
- Frattini, P.; Crosta, G.; Carrara, A. Techniques for evaluating the performance of landslide susceptibility models. Eng. Geol. 2010, 111, 62–72. [Google Scholar] [CrossRef]
- Greiner, M.; Pfeiffer, D.; Smith, R. Principles and practical application of the receiver-operating characteristic analysis for diagnostic tests. Prev. Vet. Med. 2000, 45, 23–41. [Google Scholar] [CrossRef]
- Hussin, H.Y.; Zumpano, V.; Reichenbach, P.; Sterlacchini, S.; Micu, M.; van Westen, C.; Bălteanu, D. Different landslide sampling strategies in a grid-based bi-variate statistical susceptibility model. Geomorphology 2016, 253, 508–523. [Google Scholar] [CrossRef]
- Rahmati, O.; Kornejady, A.; Samadi, M.; Deo, R.C.; Conoscenti, C.; Lombardo, L.; Dayal, K.; Taghizadeh-Mehrjardi, R.; Pourghasemi, H.R.; Kumar, S. PMT: New analytical framework for automated evaluation of geo-environmental modelling approaches. Sci. Total Environ. 2019, 664, 296–311. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.-J.; Sawada, K.; Moriguchi, S. Landslide susceptibility analysis with logistic regression model based on FCM sampling strategy. Comput. Geosci. 2013, 57, 81–92. [Google Scholar] [CrossRef]
- Zhou, L. Performance of corporate bankruptcy prediction models on imbalanced dataset: The effect of sampling methods. Knowl.-Based Syst. 2013, 41, 16–25. [Google Scholar] [CrossRef]
- Kordestani, M.D.; Naghibi, S.A.; Hashemi, H.; Ahmadi, K.; Kalantar, B.; Pradhan, B. Groundwater potential mapping using a novel data-mining ensemble model. Hydrogeol. J. 2019, 27, 211–224. [Google Scholar] [CrossRef]
- Sharma, G. Pros and cons of different sampling techniques. Int. J. Appl. Res. 2017, 3, 749–752. [Google Scholar]
- Ye, Y.; Wu, Q.; Huang, J.Z.; Ng, M.K.; Li, X. Stratified sampling for feature subspace selection in random forests for high dimensional data. Pattern Recogn. 2013, 46, 769–787. [Google Scholar] [CrossRef]
- Cardini, A.; Elton, S. Sample size and sampling error in geometric morphometric studies of size and shape. Zoomorphology 2007, 126, 121–134. [Google Scholar] [CrossRef]
- Jha, M.K.; Chowdary, V.; Chowdhury, A. Groundwater assessment in Salboni Block, West Bengal (India) using remote sensing, geographical information system and multi-criteria decision analysis techniques. Hydrogeol. J. 2010, 18, 1713–1728. [Google Scholar] [CrossRef]
- Saha, D.; Ray, R.K. Groundwater resources of India: Potential, challenges and management. In Groundwater Development and Management; Springer: Berlin/Heidelberg, Germany, 2019; pp. 19–42. [Google Scholar]
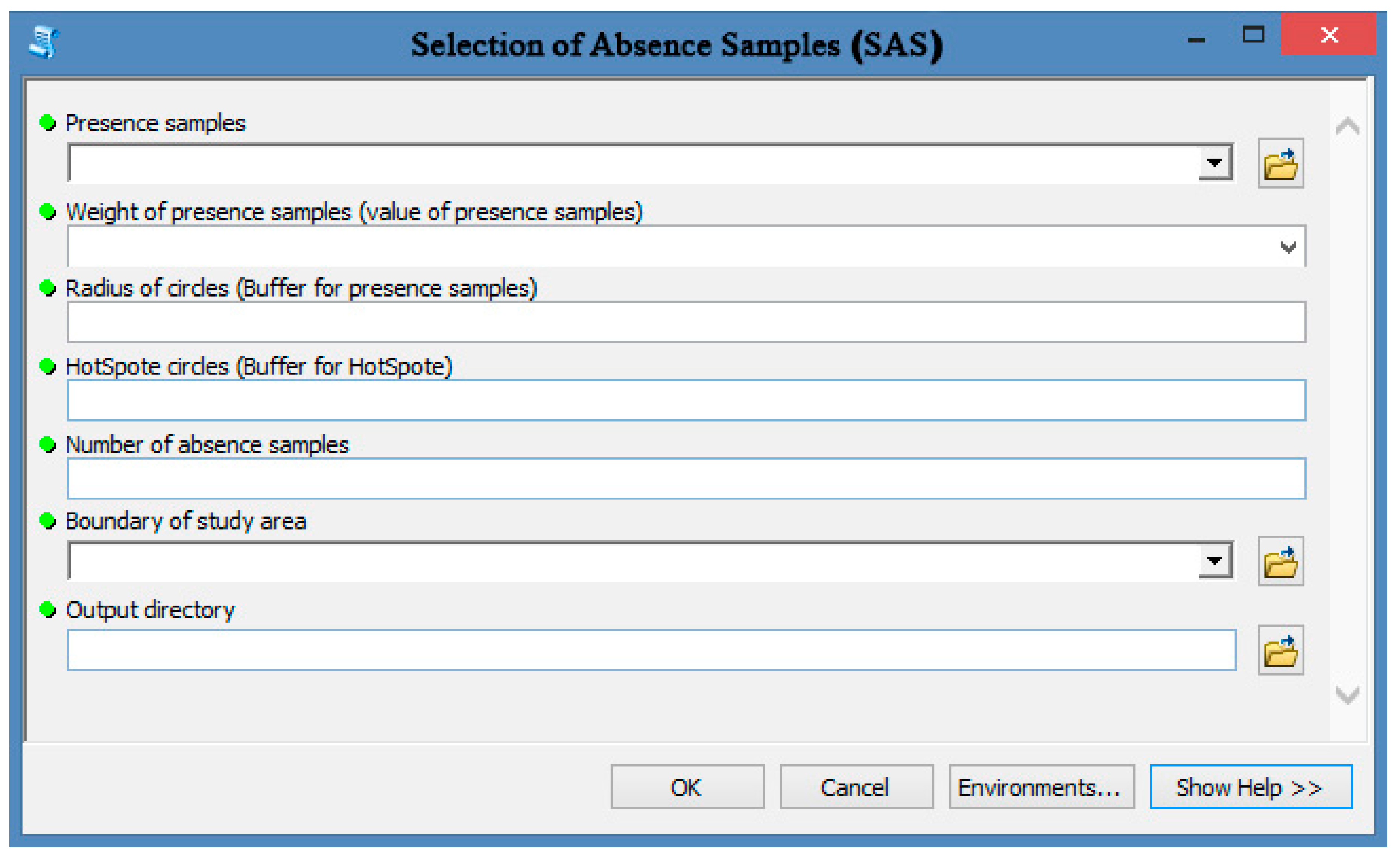
| ID | Setting | Description |
|---|---|---|
| 1 | Input a layer of presence samples | The layer of presence samples (positive points) showing the location of occurrences for a given phenomenon should be input in this field. For example, a spring file (include locations and groundwater discharge) should be introduced here. |
| 2 | Weight of presence samples | Each presence sample has a value or weight. For example, springs have groundwater discharge. |
| 3 | Radius of circles (Buffer for presence samples) | Buffer for presence samples should be determined. These buffer/circles do not allow random absence samples to be placed inside them. Therefore, absence samples are placed in an area that is free of the given phenomenon (e.g., landslide-free area, spring-free area). |
| 4 | Hotspot circles (buffer for hotspots) | After determining hotspot locations, users should determine a buffer for them that does not allow absence samples to be placed there. |
| 5 | Number of absence samples | In general, the number of absence samples is equal to the number of presence samples. The number of absence samples usually influences the model output. |
| 6 | Boundary of the study area | The SAS tool needs a specific area such as a study area to determine the permitted sites for producing absence samples. Users can introduce the study area file for this field. |
| ID | Setting | Description |
|---|---|---|
| 1 | Absence samples layer | This file is the main output of the SAS tool, and explains the location of absence samples in the study area. These absence samples are produced based on average nearest neighbor and hotspot analyses. This approach for producing absence samples is better than the simple random method. |
| 2 | Hotspot and coldspot layer | This file shows the result of hotspot analysis. It classifies presence samples into three groups: coldspot, medium, and hotspot. This type of classification is based on the value of presence samples (e.g., groundwater discharge) and their distance from each other. |
| 3 | Significant hotspot samples | This layer explains which presence samples are significant hotspots in comparison with other presence samples. The selection of hotspot samples depends on both z-score and p-value in hotspot analysis based on the Gi* metric. |
| Era | Period | Lithology |
|---|---|---|
| Cenozoic | Quaternary (Q) | Low level piedmont fan and valley terrace deposits |
| Cenozoic | Neogene (N) | Red marl, gypsiferous marl, sandstone, and conglomerate |
| Mesozoic | Cretaceous (C) | Olive green glauconitic sandstone and shale |
| Mesozoic | Early Cretaceous (EC) | Ammonite bearing shale with orbitolin limestone |
| Mesozoic | Jurassic-Cretaceous (JC) | Pale red argillaceous limestone, sandstone, and conglomerate |
| Mesozoic | Triassic–Jurassic (TJ) | Subordinate sandy limestone, dark grey shale, and sandstone |
| Observed | Predicted | |
|---|---|---|
| Non-Occurrence | Occurrence | |
| Non-occurrence | True negative (TN) | False positive (FP) |
| Occurrence | False negative (FN) | True positive (TP) |
| Sampling Strategies | Evaluation Criteria | Models | |
|---|---|---|---|
| RF | MARS | ||
| Selection of Absence Samples (SAS) method | AUC-ROC 1 | 0.944 | 0.925 |
| TSS 2 | 0.891 | 0.852 | |
| Efficiency (E) | 0.946 | 0.926 | |
| True positive rate (TPR) | 0.938 | 0.921 | |
| False positive rate (FPR) | 0.046 | 0.069 | |
| True negative rate (TNR) | 0.953 | 0.931 | |
| False negative rate (FNR) | 0.061 | 0.078 | |
| Simple random method | AUC-ROC 1 | 0.926 | 0.898 |
| TSS 2 | 0.852 | 0.789 | |
| Efficiency (E) | 0.926 | 0.894 | |
| True positive rate (TPR) | 0.921 | 0.892 | |
| False positive rate (FPR) | 0.069 | 0.102 | |
| True negative rate (TNR) | 0.931 | 0.897 | |
| False negative rate (FNR) | 0.078 | 0.107 | |
| Sampling Strategy | Evaluation Criteria | Models | |
|---|---|---|---|
| RF | MARS | ||
| Selection of Absence Samples (SAS) method | AUC-ROC 1 | 0.913 | 0.889 |
| TSS 2 | 0.72 | 0.705 | |
| Efficiency (E) | 0.926 | 0.90 | |
| True positive rate (TPR) | 0.921 | 0.905 | |
| False positive rate (FPR) | 0.067 | 0.105 | |
| True negative rate (TNR) | 0.932 | 0.894 | |
| False negative rate (FNR) | 0.078 | 0.094 | |
| Simple random method | AUC-ROC 1 | 0.872 | 0.833 |
| TSS 2 | 0.681 | 0.67 | |
| Efficiency (E) | 0.906 | 0.86 | |
| True positive rate (TPR) | 0.896 | 0.855 | |
| False positive rate (FPR) | 0.082 | 0.135 | |
| True negative rate (TNR) | 0.917 | 0.864 | |
| False negative rate (FNR) | 0.103 | 0.144 | |
| Model | Simple Random Method | SAS Method | ||||||
|---|---|---|---|---|---|---|---|---|
| Minimum | Maximum | Mean | SD | Minimum | Maximum | Mean | SD | |
| RF | 0.002 | 0.989 | 0.339 | 0.228 | 0.003 | 0.994 | 0.351 | 0.232 |
| MARS | 0.010 | 1.000 | 0.309 | 0.307 | 0.010 | 1.000 | 0.287 | 0.300 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahmati, O.; Moghaddam, D.D.; Moosavi, V.; Kalantari, Z.; Samadi, M.; Lee, S.; Tien Bui, D. An Automated Python Language-Based Tool for Creating Absence Samples in Groundwater Potential Mapping. Remote Sens. 2019, 11, 1375. https://doi.org/10.3390/rs11111375
Rahmati O, Moghaddam DD, Moosavi V, Kalantari Z, Samadi M, Lee S, Tien Bui D. An Automated Python Language-Based Tool for Creating Absence Samples in Groundwater Potential Mapping. Remote Sensing. 2019; 11(11):1375. https://doi.org/10.3390/rs11111375
Chicago/Turabian StyleRahmati, Omid, Davoud Davoudi Moghaddam, Vahid Moosavi, Zahra Kalantari, Mahmood Samadi, Saro Lee, and Dieu Tien Bui. 2019. "An Automated Python Language-Based Tool for Creating Absence Samples in Groundwater Potential Mapping" Remote Sensing 11, no. 11: 1375. https://doi.org/10.3390/rs11111375
APA StyleRahmati, O., Moghaddam, D. D., Moosavi, V., Kalantari, Z., Samadi, M., Lee, S., & Tien Bui, D. (2019). An Automated Python Language-Based Tool for Creating Absence Samples in Groundwater Potential Mapping. Remote Sensing, 11(11), 1375. https://doi.org/10.3390/rs11111375