Comparison of Three Algorithms for the Evaluation of TanDEM-X Data for Gully Detection in Krumhuk Farm (Namibia)
Abstract
1. Introduction
2. Study Site and Materials
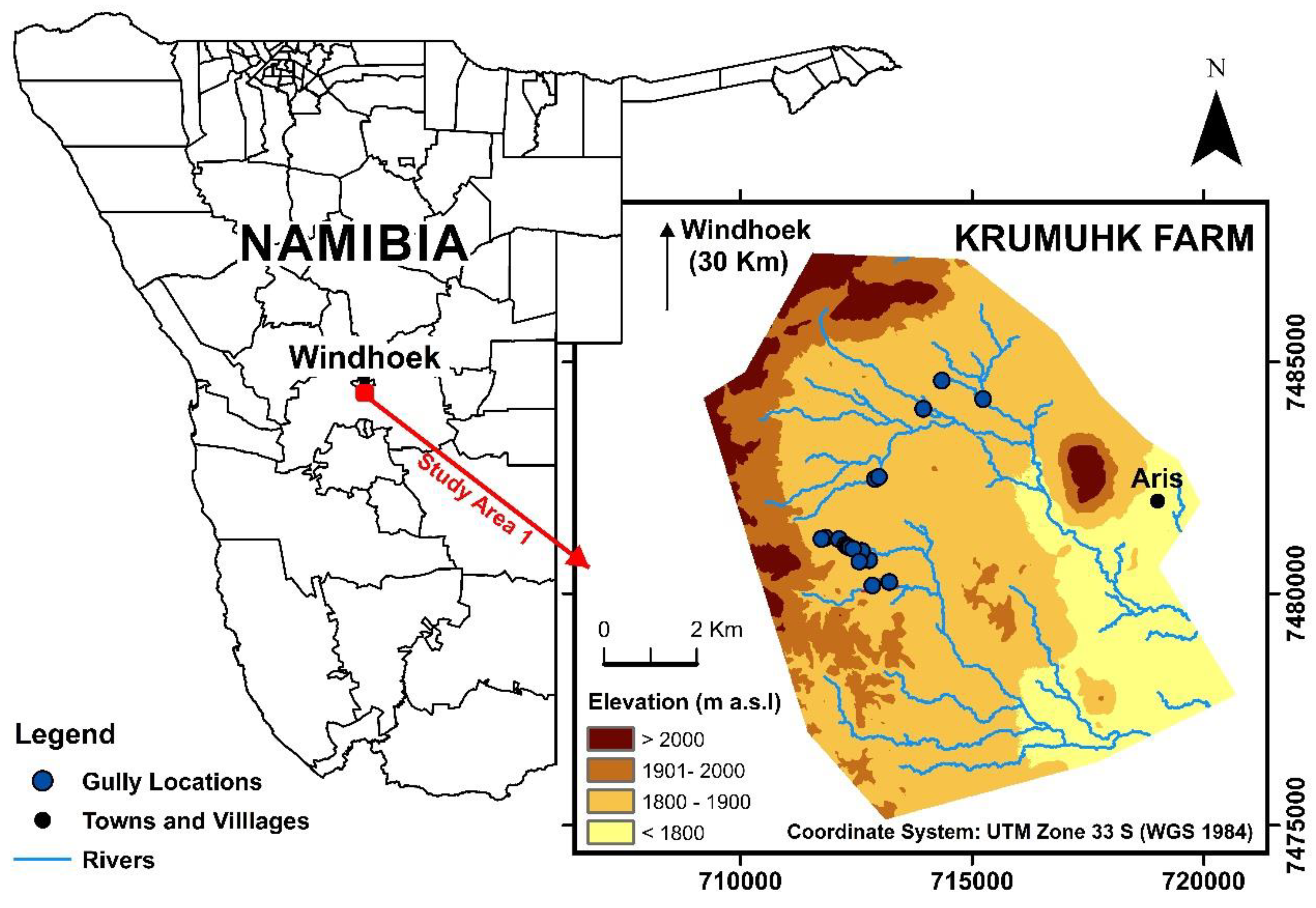
2.1. Study Site
2.2. TanDEM-X Data
3. Methods for Gully Detection
3.1. Algorithms
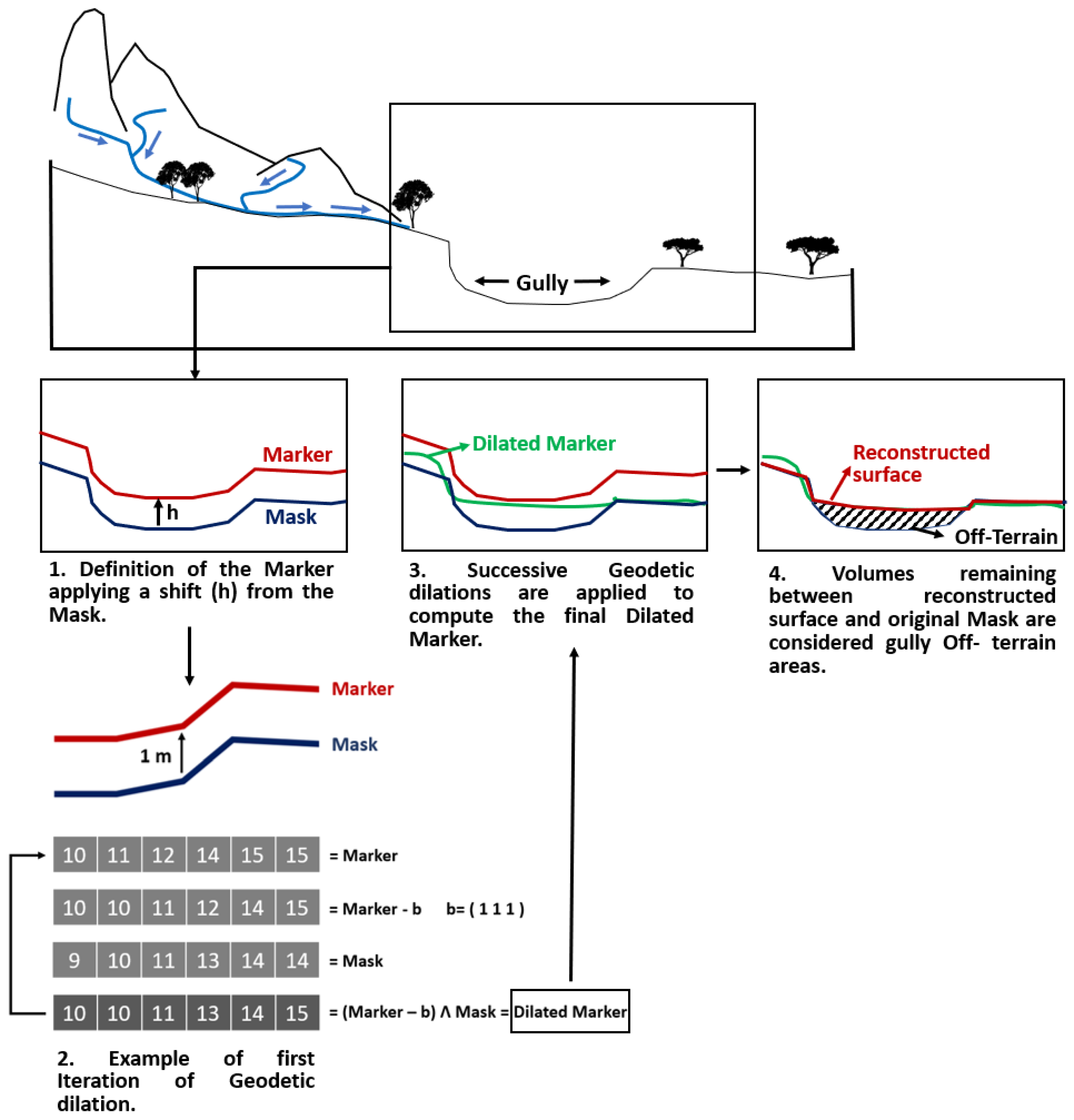
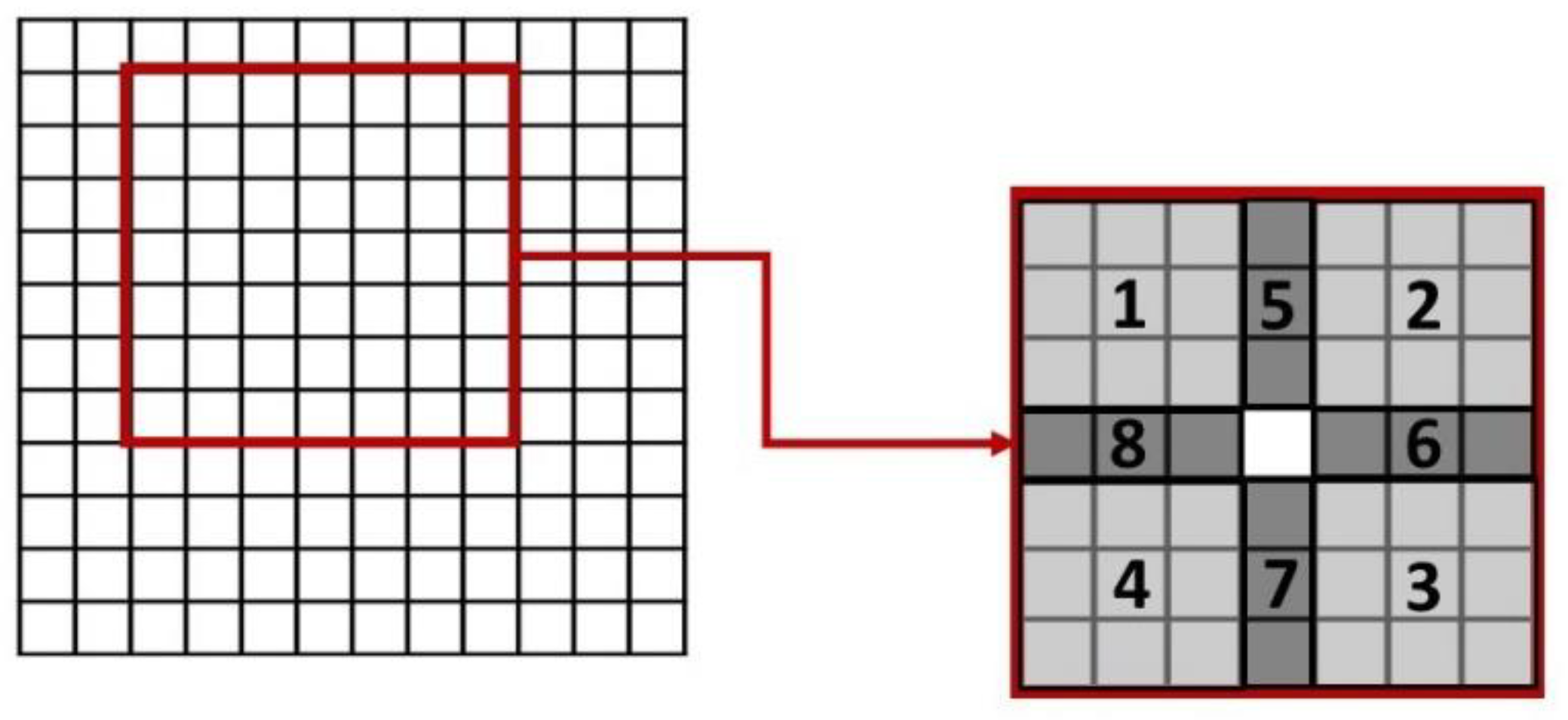
3.1.1. Inverted Morphological Reconstruction (IMR)
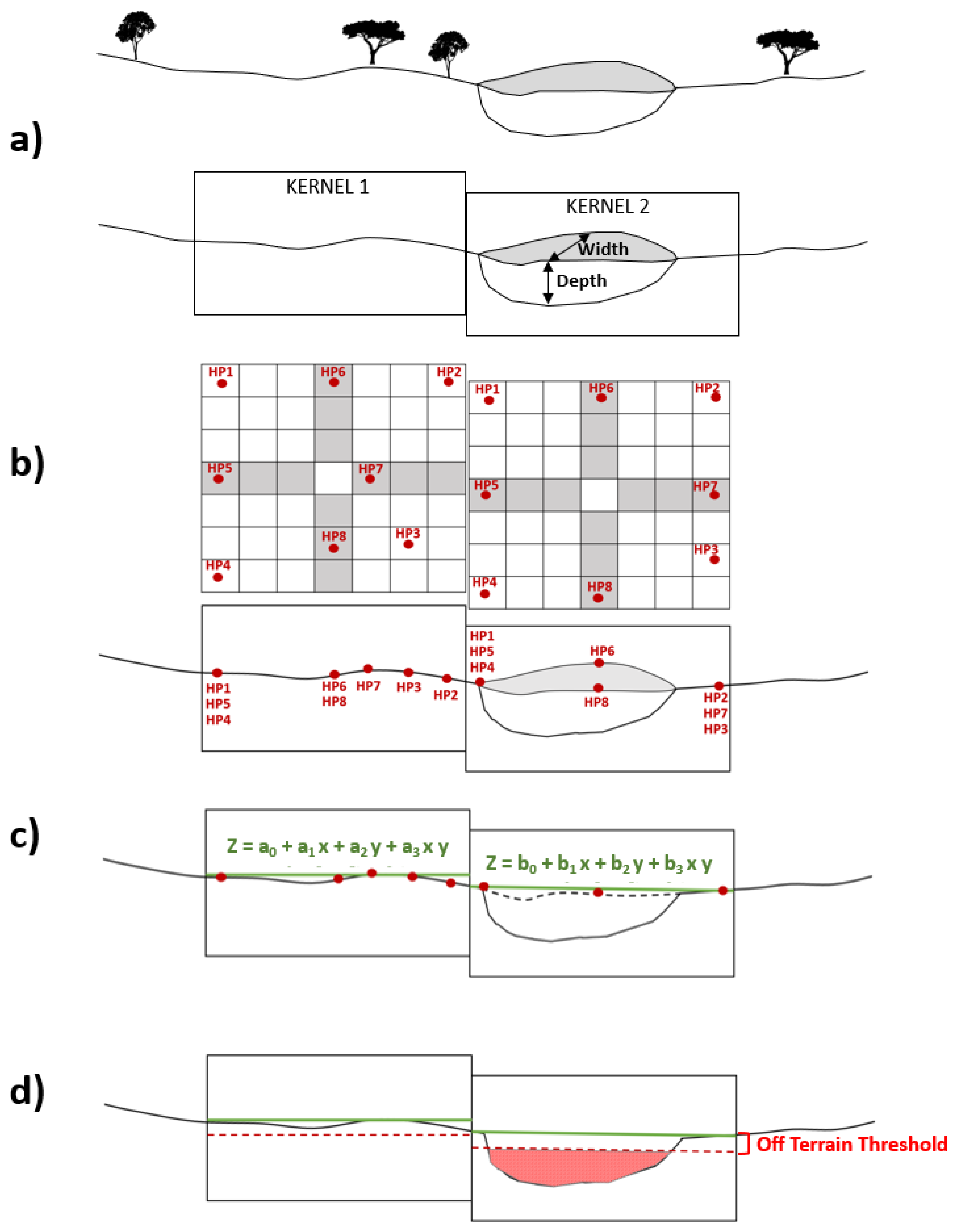
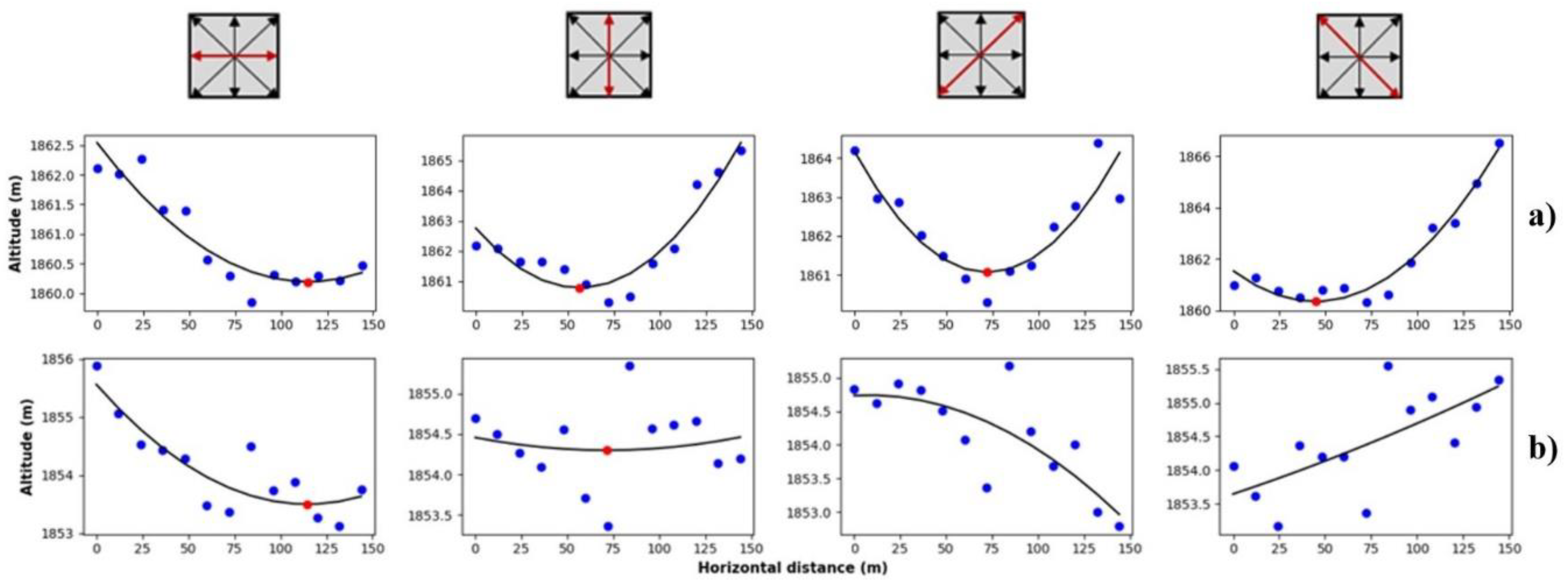
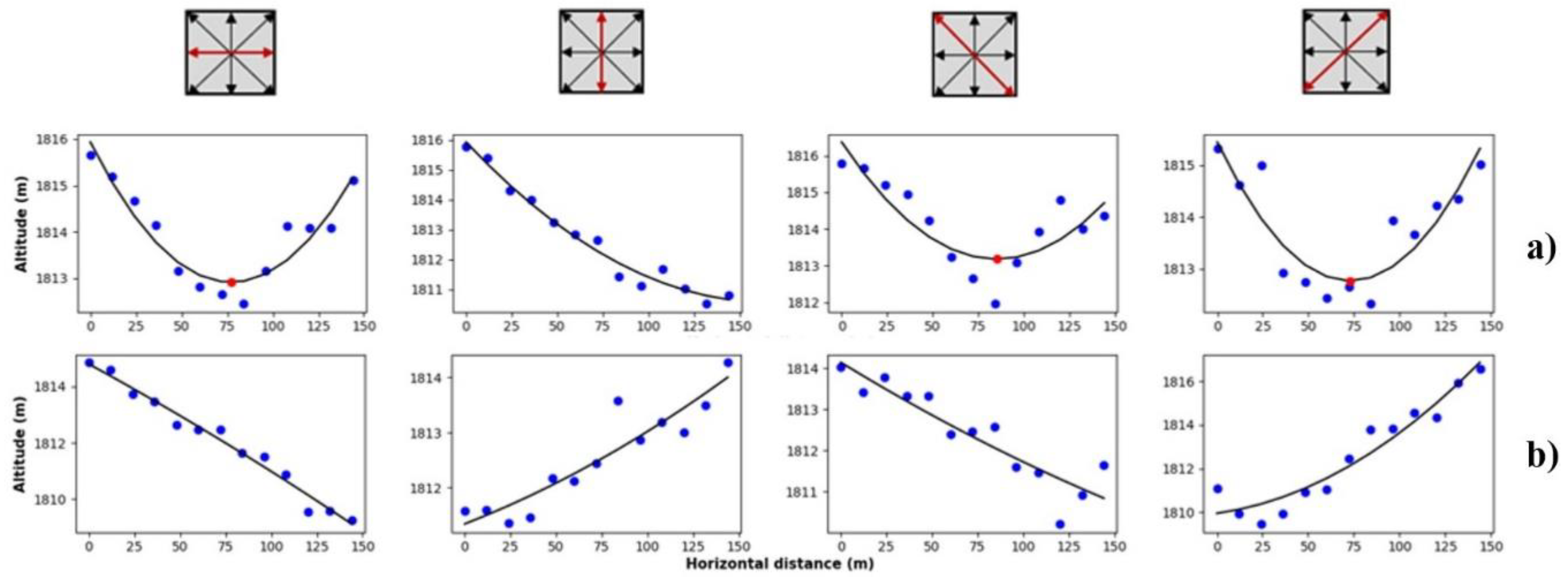
3.1.2. Smoothing Moving Polynomial Fitting (SMPF)
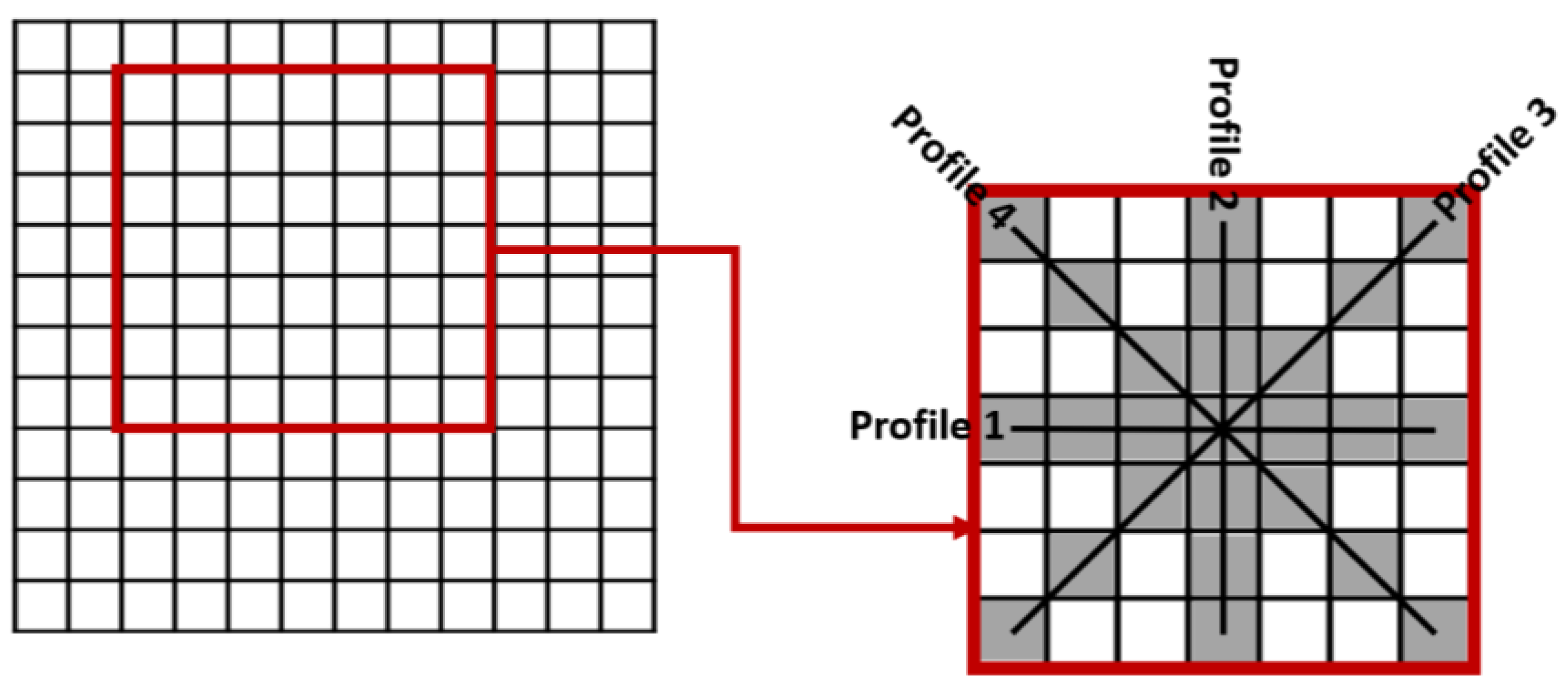
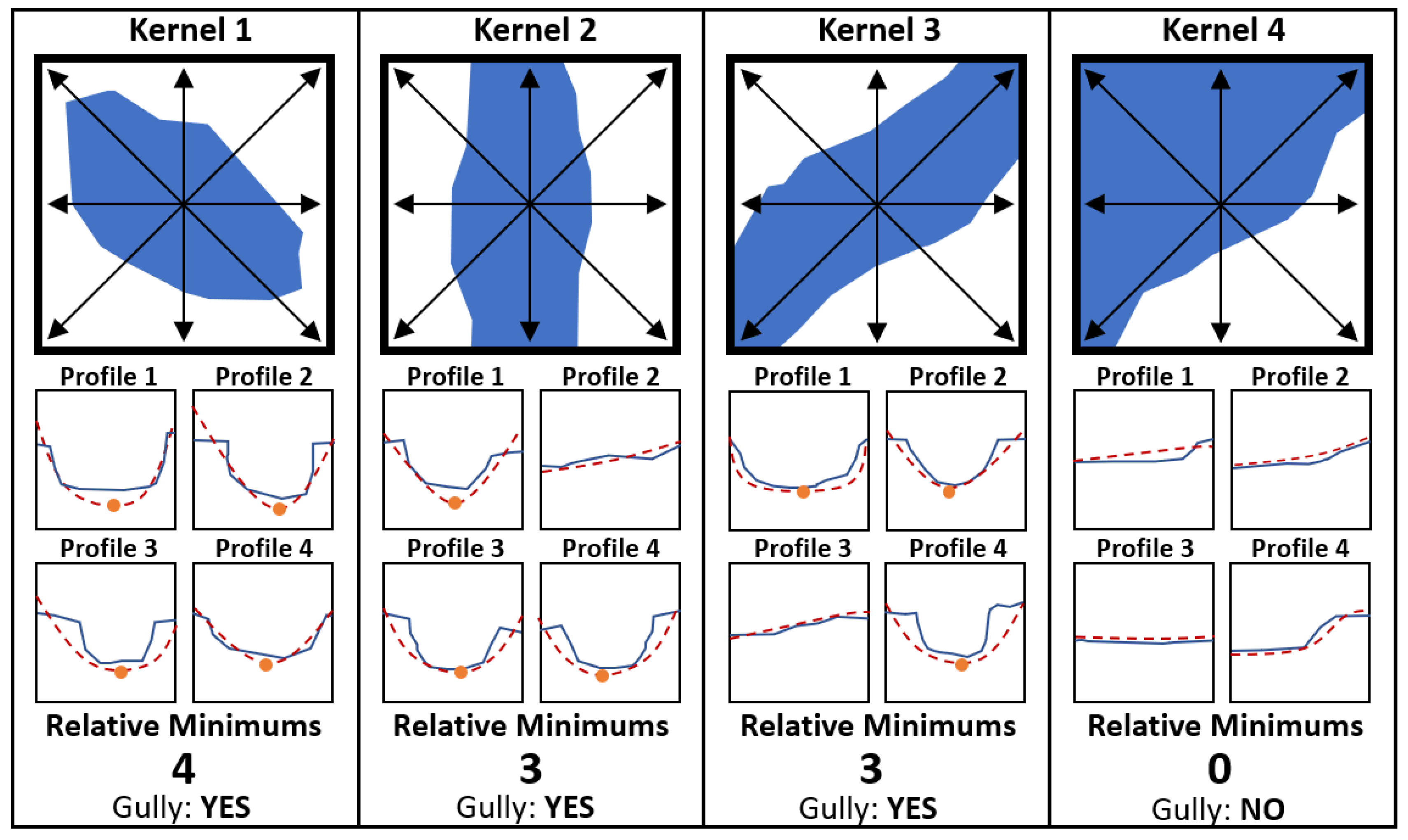
3.1.3. Multi-Profile Curvature Analysis (MPCA)
3.2. Field Gully Characterization
3.3. Algorithm Settings
4. Results
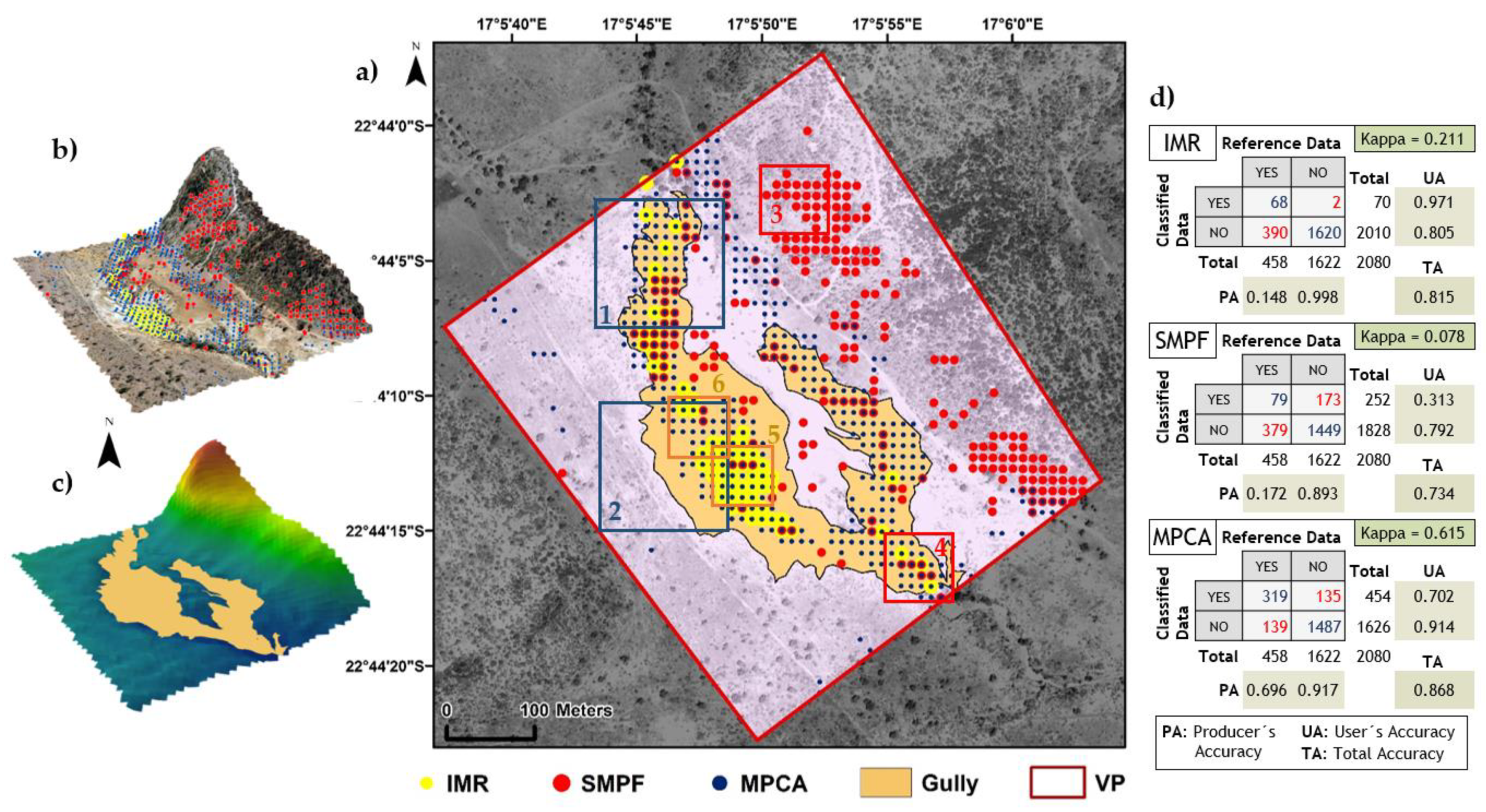
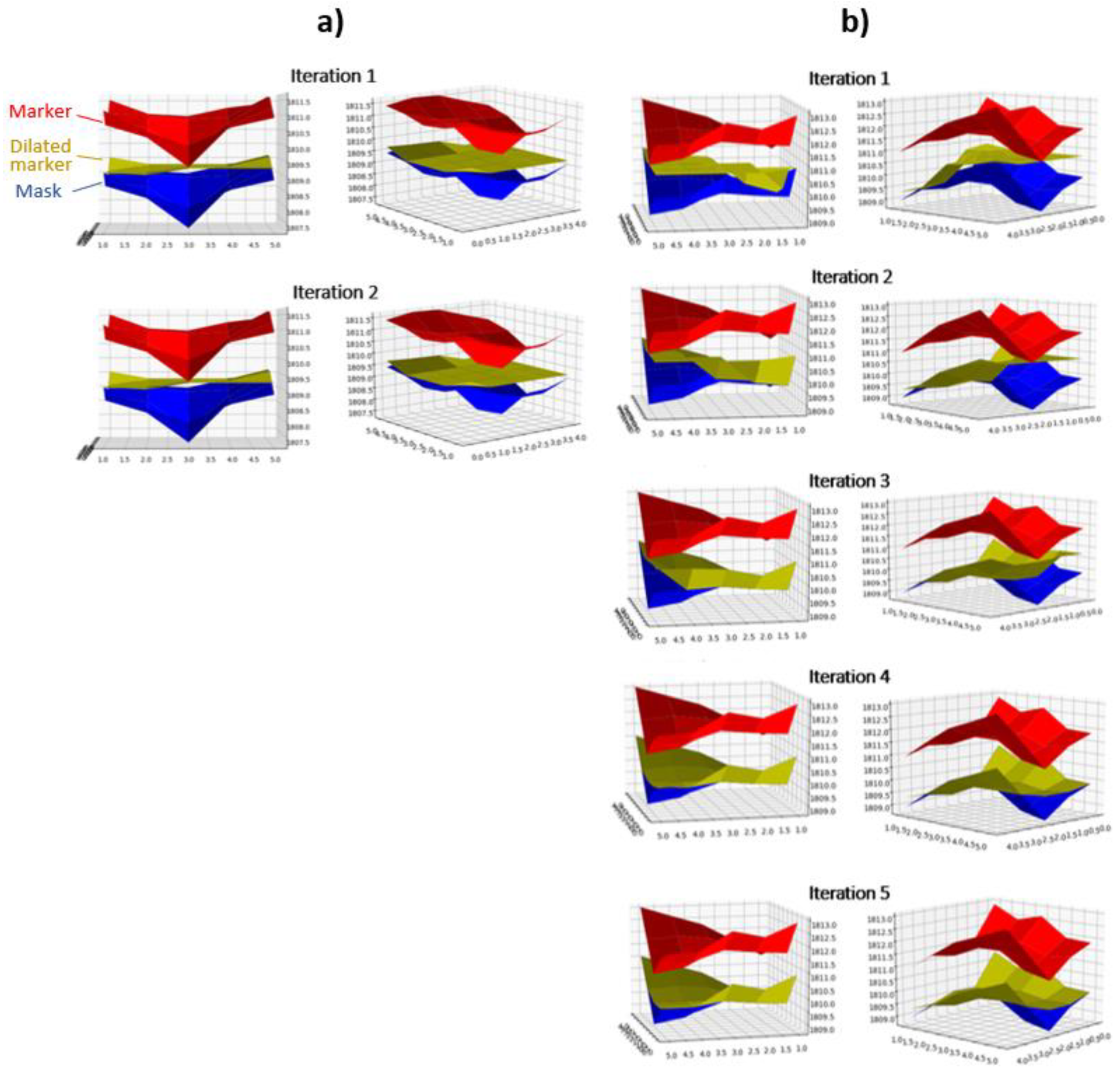
4.1. Visual Interpretation of Results
4.2. Validation and Analysis of Results
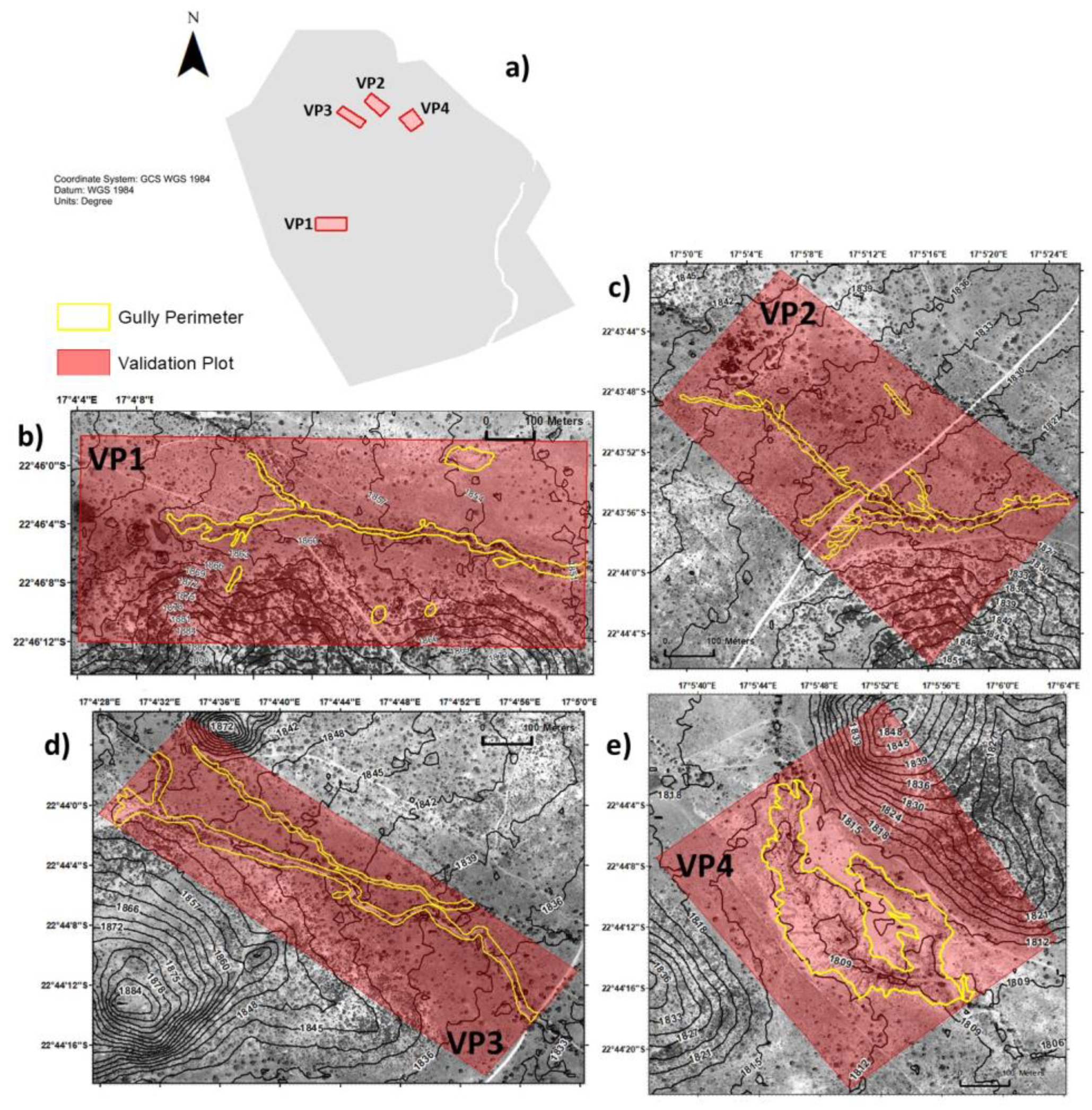
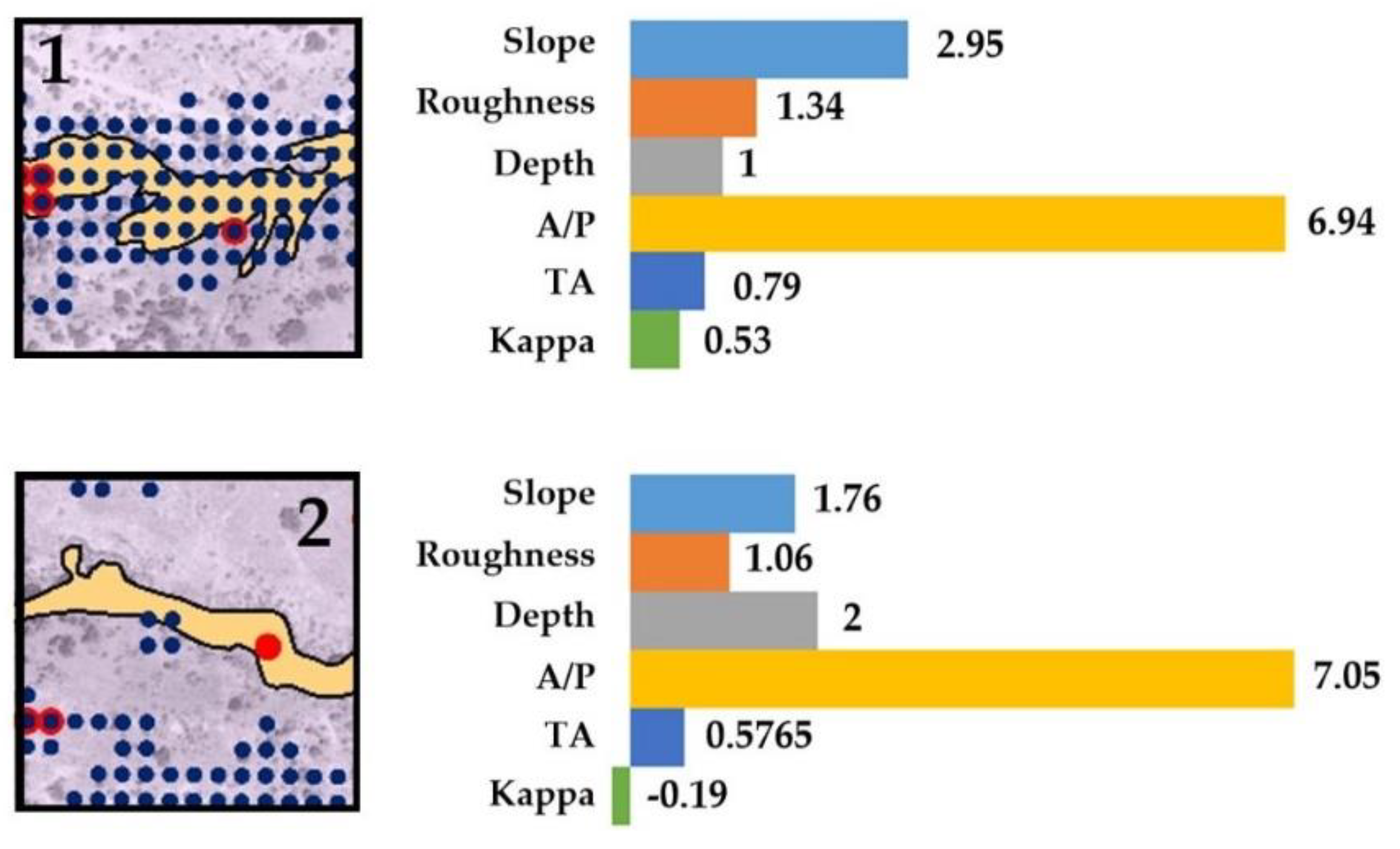
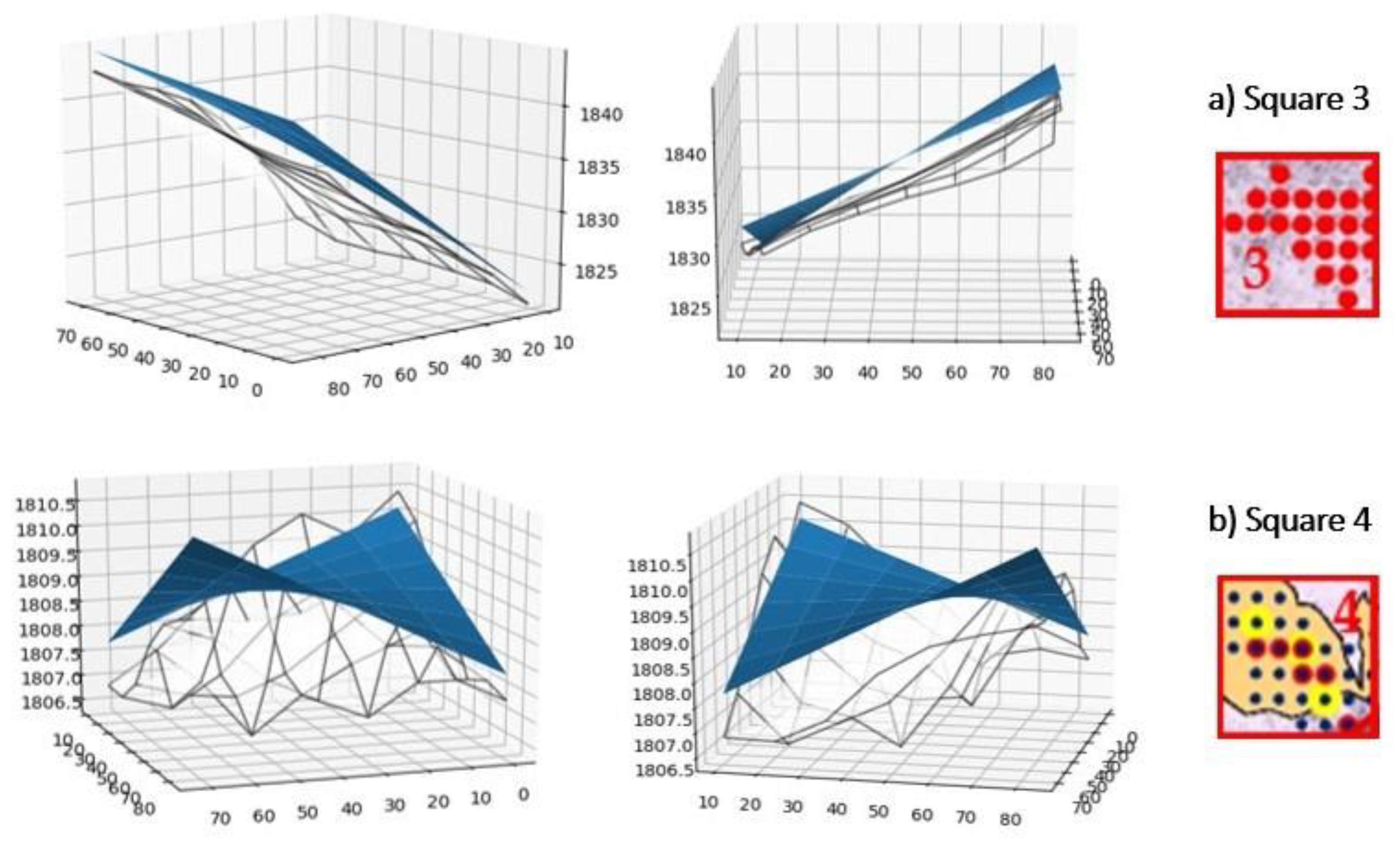
4.2.1. Validation Plot 1 (VP1)
4.2.2. Validation Plot 4 (VP4)
5. Discussion
6. Conclusions
- (1)
- improve MPCA according to the suggestions provided in the discussion to achieve at least 0.50 in gully class both of UA and PA.
- (2)
- derive geomorphological and geomorphometric features from the pixel-based classification, such as gully outline and depth, in order to estimate gully volumes.
- (3)
- explore the fusion of TanDEM-X data with multispectral (i.e., Sentinel 2) and RADAR (i.e., Sentinel 1), to perform time series analysis and monitor gully evolution and its erosion activity. This can generate valuable knowledge of gully dynamics for geomorphologists and agronomists working on land degradation in Namibia. In this way, gully categorization can also be implemented as part of the automatic gully identification method; for example, in classifying their activity as low, medium, or high and estimating the economic damage for commercial and communal farmers.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Valentin, C.; Poesen, J.; Li, Y. Gully erosion: Impacts, factors and control. Catena 2005, 63, 132–153. [Google Scholar] [CrossRef]
- Fao Soils Portal: Soil Degradation. Available online: http://www.fao.org/soils-portal/soil-degradation-restoration/en/ (accessed on 29 September 2018).
- Republic of Namibia, Ministry of Environment and Tourism. Third National Action Programme for Namibia To Implement the United Nations Convention to Combat Desertification 2014–2024; Republic of Namibia, Ministry of Environment and Tourism: Windhoek, Namibia, 2014; p. 80.
- Wasson, R.J.; Caitcheon, G.; Murray, A.S.; McCulloch, M.; Quade, J. Sourcing sediment using multiple tracers in the catchment of Lake Argyle, Northwestern Australia. Environ. Manag. 2002, 29, 634–646. [Google Scholar] [CrossRef]
- Krause, J.S.; Franks, A.K.; Kalma, S.W.; Loughran, J.D.; Rowan, R.J. Multi parameter fingerprinting of sediment deposition in a small gullied catchment in SE Australia. Catena 2003, 53, 327–348. [Google Scholar] [CrossRef]
- Huon, S.; Bellanger, B.; Bonté, P.; Sogon, S.; Podwojewski, P.; Girardin, C.; Valentin, C.; de Rouw, A.; Velasquez, F.; Bricquet, J.-P.; et al. Monitoring soil organic carbon erosion with isotopic tracers: Two case studies on cultivated tropical catchments with steep slopes (Laos, Venezuela). In Soil Erosion and Carbon Dynamics, 1st ed.; Roose, E.J., Lal, R., Feller, C., Barthés, B., Stewart, B., Eds.; Taylor & Francis: Boca Raton, FL, USA, 2006; pp. 301–328. [Google Scholar]
- Pringle, H.; Zimmermann, I.; Tinley, K. Accelerating landscape incision and the downward spiralling rain use efficiency of Namibian rangelands. Agricola 2011, 21, 43–52. [Google Scholar]
- Poesen, J.; Vandaele, K.; van Wesemael, B. Gully erosion: Importance and model implications. In Modelling Soil Erosion by Water; Springer: Berlin/Heidelberg, Germany, 1998; Volume 55, pp. 285–311. [Google Scholar] [CrossRef]
- Poesen, J. Soil erosion in the Anthropocene: Research needs. Earth Surf. Process. Landf. 2018, 43, 64–84. [Google Scholar] [CrossRef]
- Sean, B.J.; Wells, R.R. Gully erosion processes, disciplinary fragmentation, and technological innovation. Earth Surf. Process. Landf. 2019, 44, 46–53. [Google Scholar] [CrossRef]
- Castillo, C.; Perez, R. Comparing the Accuracy of Several Field Methods for Measuring Gully Erosion. Soil Sci. Soc. Am. J. 2012, 76, 1319–1332. [Google Scholar] [CrossRef]
- SASSCAL Research Portfolio: Task 041: Landscape Literacy. Available online: http://sasscal.org/wp-content/uploads/external-assets/tasksheets/task_041_na_ag.pdf (accessed on 15 July 2017).
- Burkard, M.B.; Kostaschuk, R.A. Initiation and evolution of gullies along the shoreline of Lake Huron. Geomorphology 1995, 14, 211–219. [Google Scholar] [CrossRef]
- Betts, H.D.; DeRose, R.C. Digital elevation models as a tool for monitoring and measuring gully erosion. Int. J. Appl. Earth Obs. Geoinf. 1999, 1, 91–101. [Google Scholar] [CrossRef]
- Martínez-Casasnovas, J.A.; Ramos, M.C.; Poesen, J. Assessment of sidewall erosion in large gullies using multi-temporal DEMs and logistic regression analysis. Geomorphology 2004, 58, 305–321. [Google Scholar] [CrossRef]
- Ionita, I. Gully development in the Moldavian Plateau of Romania. Catena 2006, 68, 133–140. [Google Scholar] [CrossRef]
- James, L.A.; Watson, D.G.; Hansen, W.F. Using LiDAR data to map gullies and headwater streams under forest canopy: South Carolina, USA. Catena 2007, 71, 132–144. [Google Scholar] [CrossRef]
- Collins, B.D.; Brown, K.M.; Fairley, H.C. Evaluation of Terrestrial LIDAR for Monitoring Geomorphic Change at Archeological Sites in Grand Canyon National Park; USGS Publications Warehouse: Reston, VA, USA, 2008. [CrossRef]
- Evans, M.; Lindsay, J. High resolution quantification of gully erosion in upland peatlands at the landscape scale. Earth Surf. Process. Landf. 2010, 35, 876–886. [Google Scholar] [CrossRef]
- Stöcker, C.; Eltner, A.; Karrasch, P. Measuring gullies by synergetic application of UAV and close range photogrammetry—A case study from Andalusia, Spain. Catena 2015, 132, 1–11. [Google Scholar] [CrossRef]
- Höfle, B.; Griesbaum, L.; Forbriger, M. GIS-Based detection of gullies in terrestrial lidar data of the cerro llamoca peatland (Peru). Remote Sens. 2013, 5, 5851–5870. [Google Scholar] [CrossRef]
- Gómez-gutiérrez, A.; Schnabel, S.; Berenguer-sempere, F.; Lavado-contador, F.; Rubio-delgado, J. Using 3D photo-reconstruction methods to estimate gully headcut erosion. Catena 2014, 120, 91–101. [Google Scholar] [CrossRef]
- Castillo, C.; Marin-Moreno, V.J.; Pérez, R.; Munoz-Salinas, R.; Taguas, E.V. Accurate automated assessment of gully cross-section geometry using the photogrammetric interface FreeXSapp. Earth Surf. Process. Landf. 2018, 43, 1726–1736. [Google Scholar] [CrossRef]
- Morgan, R.P.C. Soil Erosion and Conservation, 3rd ed.; Blackwell Science Ltd.: Malden, MA, USA, 2013; pp. 65–66. [Google Scholar]
- Billi, P.; Dramis, F. Geomorphological Investigation on Gully Erosion in the Rift Valley and the Northern Highlands of Ethiopia. Catena 2003, 50, 353–368. [Google Scholar] [CrossRef]
- Vandekerckhove, L.J.; Poesen, J.; Govers, G. MidTerm Gully Headcut Retreat Rates in Southeast Spain Determined from Aerial Photographs and Ground Measurements. Catena 2003, 50, 329–352. [Google Scholar] [CrossRef]
- Marzolff, I.; Poesen, J. The potential of 3D gully monitoring with GIS using high-resolution aerial photography and a digital photogrammetry system. Geomorphology 2009, 111, 48–60. [Google Scholar] [CrossRef]
- Herfort, B.; Höfle, B.; Klonner, C. 3D micro-mapping: Towards assessing the quality of crowdsourcing to support 3D point cloud analysis. ISPRS J. Photogramm. Remote Sens. 2018, 137, 73–83. [Google Scholar] [CrossRef]
- Fritz, S.; See, L. The Role of Citizen Science in Earth Observation. Remote Sens. 2017, 9, 357. [Google Scholar] [CrossRef]
- Igboekwe, J.; Akinyede, J.; Dang, B.; Alaga, T.; Ono, M.; Nnudu, V.; Anike, L. Mapping and monitoring of the impact of gully erosion in SE Nigeria with satellite remote sensing and Geographic Information System. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 865–872. [Google Scholar]
- Brolly, M.; Iro, S. Using the Landsat Archive to Monitor Gully Erosion Development, in SE Nigeria, as a Response to Land-use Classification and Environmental Variability; American Geophysical Union: Washington, DC, USA, 2016. [Google Scholar]
- Mararakanye, N.; Nethengwe, N.S. Gully Erosion Mapping Using Remote Sensing Techniques in the Capricorn District, Limpopo. S. Afr. J. Geomat. 2012, 1, 109–118. [Google Scholar]
- Brooks, A.; Spencer, J.; Knight, J. Alluvial gully erosion in Australia’ s tropical rivers: A conceptual model as a basis for a remote sensing mapping procedure. In Proceedings of the 5th Australian Stream Management Conference. Australian Rivers: Making a Difference, Albury, Australia, 21–25 May 2007. [Google Scholar]
- D’Oleire-Oltmanns, S.; Marzolff, I.; Tiede, D.; Blaschke, T. Detection of gully-affected areas by applying object-based image analysis (OBIA) in the region of Taroudannt, Morocco. Remote Sens. 2014, 6, 8287–8309. [Google Scholar] [CrossRef]
- Chaplot, V.; Coadou Le Brozec, E.; Silvera, N.; Valentin, C. Spatial and temporal assessment of linear erosion in catchments under sloping lands of northern Laos. Catena 2005, 63, 167–184. [Google Scholar] [CrossRef]
- Pringle, H.; Zimmermann, I.; Shamathe, K.; Nott, C.; Tinley, K. Landscape incision processes favour bush encroachment over open grasslands in the two extremes of soil moisture balance in arid zones across southern africa and australia. Agricola 2013, 2013, 7–13. [Google Scholar]
- Mwazi, F.N.; Shamathe, G.N. Assessment of the status of soil macro-elements along a gully at Farm Krumhuk, Khomas Region, Namibia (2007). Agricola 2007, 17, 38–41. [Google Scholar]
- Jones, A.; Breuning-Madsen, H.; Brossard, M.; Dampha, A.; Deckers, J.; Dewitte, O.; Gallali, T.; Hallett, S.; Jones, R.; Kilasara, M.; et al. Soil Atlas of Africa; Publications Office of the European Union: Luxembourg, 2013; pp. 117–124. [Google Scholar]
- ISRIC-World Soil Information. 2016. Available online: https://soilgrids.org/#!/?layer=ORCDRC_M_sl2_250m&vector=1 (accessed on 27 September 2018).
- Krieger, G.; Moreira, A.; Fiedler, H.; Hajnsek, I.; Zink, M.; Werner, M. TanDEM-X: Mission Concept, Product Definition and Performance Prediction. In Proceedings of the European Conference on Synthetic Aperture Radar (EUSAR), Dresden, Germany, 16–18 May 2006. [Google Scholar]
- Wessel, B.; Huber, M.; Wohlfart, C.; Marschalk, U.; Kosmann, D.; Roth, A. Accuracy assessment of the global TanDEM-X Digital Elevation Model with GPS data. ISPRS J. Photogramm. Remote Sens. 2018, 13, 171–182. [Google Scholar] [CrossRef]
- Serra, J.; Vincent, L. An overview of morphological filtering. Circuits Syst. Signal Process. 1992, 11, 47–108. [Google Scholar] [CrossRef]
- Arefi, H.; Hahn, M. A morphological reconstruction algorithm for separating off-terrain points from terrain points in laser scanning data. ISPRS 2005, 3, 120–125. [Google Scholar]
- Kim, K.H.; Shan, J. Adaptive morphological filtering for DEM generation. Int. Geosci. Remote Sens. Symp. 2011. [Google Scholar] [CrossRef]
- Arefi, H.; D’Angelo, P.; Mayer, H.; Reinartz, P. Iterative approach for efficient digital terrain model production from CARTOSAT-1 stereo images. J. Appl. Remote Sens. 2011, 5, 1–21. [Google Scholar] [CrossRef][Green Version]
- Jóźków, G. Moving polynomial surface model for generation dtm and dsm from aiborne laser scanning data. 2007; Unpublished work. [Google Scholar]
- Fleishman, S.; Cohen-or, D.; Silva, T. Robust Moving Least-squares Fitting with Sharp Features. ACM Trans. Graph. (TOG) 2000, 24, 544–552. [Google Scholar] [CrossRef]
- Berry, J.K. Characterizing Micro-Terrain Features. In Map Analysis: Understanding Spatial Patterns and Relationships; GeoTec Media: Denver, CO, USA, 2007; Volume 11. [Google Scholar]
- Schillaci, C.; Braun, A. Terrain analysis and landform recognition. In Geomorphological Techniques, 1st ed.; Lucy Clarke, L., Nield, J., Eds.; British Society for Geomorphology: London, UK, 2015; Chapter 2.4.2. [Google Scholar] [CrossRef]
- Dey, A.K.; Tsujimoto, T.; Kitamura, T. Perturbations effects along and on gully formation. Hydraul. Coast. Environ. Eng. JSCE 2001, 677, 205–213. [Google Scholar] [CrossRef]
- Casalí, J.; Giménez, R.; Campo-Bescós, M.A. Gully geometry: What are we measuring? Soil 2015, 1, 509–513. [Google Scholar] [CrossRef]
- Adediji, A.; Ibitoye, M.O.; Ekanade, O. Accelerated Erosion: Generation of Digital Elevation Models (DEMS) for Gullies in Irele Local Government Area of Ondo-State, Nigeria. Afr. J. Environ. Sci. Technol. 2009, 3, 1–11. [Google Scholar]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Castillo, C.; Gómez, J.A. A century of gully erosion research: Urgency, complexity and study approaches. Earth-Sci. Rev. 2016, 160, 300–319. [Google Scholar] [CrossRef]



| Requirement | Definition | HRTI-3 |
|---|---|---|
| Relative Vertical Accuracy | 90% linear point-to-point error | 2 m (slope < 20%) |
| Absolute Vertical Accuracy | 90% linear error | 10 m |
| Horizontal Accuracy | 90% circular error | 10 m |
| Spatial Resolution | Independent pixels | 12 m |
| VP | VP Area (ha) | Gully Area (ha) | Gully Perimeter (km) | Gully Maximum Depth (m) | Gully Maximum Width (m) | Description |
|---|---|---|---|---|---|---|
| VP1 | 28.9 | 2.33 | 3.11 | 2 | 40 | Main Gully #1 Secondary Gullies #4 |
| VP2 | 42.4 | 1.92 | 3.77 | 4 | 30 | Main Gully #1 Secondary Gullies #1 |
| VP3 | 24.0 | 3.91 | 2.88 | 3 | 45 | Main Gully #1 Secondary Gullies #1 |
| VP4 | 29.9 | 6.60 | 2.66 | 6 | 150 | Main Gully #1 Secondary Gullies #0 |
| IMR | |||||||
| KS (m) | OT (m) | PA (Gully) | PA (Non-Gully) | UA (Gully) | UA (Non-Gully) | KAPPA | TA |
| 36 | 1 | 0.439 | 0.672 | 0.142 | 0.906 | 0.058 | 0.646 |
| 60 | 1 | 0.035 | 0.999 | 0.895 | 0.893 | 0.060 | 0.893 |
| 84 | 1 | 0.022 | 1.000 | 1.000 | 0.892 | 0.038 | 0.892 |
| 108 | 1 | 0.009 | 1.000 | 1.000 | 0.890 | 0.017 | 0.891 |
| 36 | 2 | 0.661 | 0.596 | 0.169 | 0.934 | 0.113 | 0.603 |
| 60 | 2 | 0.071 | 0.999 | 0.944 | 0.896 | 0.118 | 0.897 |
| 84 | 2 | 0.028 | 1.000 | 1.000 | 0.892 | 0.049 | 0.893 |
| 108 | 2 | 0.009 | 1.000 | 1.000 | 0.890 | 0.017 | 0.891 |
| 36 | 4 | 0.837 | 0.505 | 0.173 | 0.961 | 0.128 | 0.541 |
| 60 | 4 | 0.071 | 0.999 | 0.944 | 0.896 | 0.118 | 0.897 |
| 84 | 4 | 0.028 | 1.000 | 1.000 | 0.892 | 0.049 | 0.893 |
| 108 | 4 | 0.009 | 1.000 | 1.000 | 0.890 | 0.017 | 0.891 |
| SMPF | |||||||
| KS (m) | MS (m) | PA (Gully) | PA (Non-Gully) | UA (Gully) | UA (Non-Gully) | KAPPA | TA |
| 60 | 1 | 0.255 | 0.843 | 0.168 | 0.901 | 0.081 | 0.778 |
| 84 | 1 | 0.323 | 0.830 | 0.191 | 0.908 | 0.119 | 0.775 |
| 108 | 1 | 0.332 | 0.747 | 0.140 | 0.900 | 0.050 | 0.701 |
| 132 | 1 | 0.333 | 0.659 | 0.108 | 0.888 | −0.004 | 0.623 |
| 84 | 1.5 | 0.134 | 0.948 | 0.242 | 0.898 | 0.102 | 0.858 |
| 60 | 2 | 0.019 | 0.986 | 0.142 | 0.890 | 0.008 | 0.879 |
| 84 | 2 | 0.041 | 0.981 | 0.218 | 0.892 | 0.035 | 0.878 |
| 108 | 2 | 0.068 | 0.952 | 0.149 | 0.892 | 0.026 | 0.854 |
| 132 | 2 | 0.078 | 0.903 | 0.091 | 0.888 | −0.020 | 0.812 |
| 60 | 3 | 0.000 | 0.997 | 0.000 | 0.889 | −0.005 | 0.887 |
| 84 | 3 | 0.002 | 0.996 | 0.056 | 0.889 | −0.004 | 0.886 |
| 108 | 3 | 0.010 | 0.988 | 0.101 | 0.889 | −0.002 | 0.880 |
| 132 | 3 | 0.022 | 0.959 | 0.062 | 0.888 | −0.026 | 0.856 |
| MPCA | |||||||
| KS (m) | PA (Gully) | PA (Non-Gully) | UA (Gully) | UA (Non-Gully) | KAPPA | TA | |
| 36 | 0.337 | 0.751 | 0.144 | 0.901 | 0.055 | 0.705 | |
| 60 | 0.400 | 0.819 | 0.215 | 0.917 | 0.158 | 0.773 | |
| 84 | 0.452 | 0.851 | 0.273 | 0.926 | 0.235 | 0.807 | |
| 108 | 0.506 | 0.865 | 0.317 | 0.934 | 0.294 | 0.825 | |
| 132 | 0.554 | 0.866 | 0.338 | 0.940 | 0.328 | 0.831 | |
| 156 | 0.581 | 0.861 | 0.341 | 0.943 | 0.338 | 0.830 | |
| 180 | 0.000 | 1.000 | 0.000 | 0.890 | 0.000 | 0.890 | |
| IMR | SMPF | MPCA | |
|---|---|---|---|
| Kernel Size | 60 × 60 m | 84 × 84 m | 156 × 156 m |
| Mask Shift | 2 m | - | - |
| Off-Terrain Threshold | - | 1.5 m | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vallejo Orti, M.; Negussie, K.; Corral-Pazos-de-Provens, E.; Höfle, B.; Bubenzer, O. Comparison of Three Algorithms for the Evaluation of TanDEM-X Data for Gully Detection in Krumhuk Farm (Namibia). Remote Sens. 2019, 11, 1327. https://doi.org/10.3390/rs11111327
Vallejo Orti M, Negussie K, Corral-Pazos-de-Provens E, Höfle B, Bubenzer O. Comparison of Three Algorithms for the Evaluation of TanDEM-X Data for Gully Detection in Krumhuk Farm (Namibia). Remote Sensing. 2019; 11(11):1327. https://doi.org/10.3390/rs11111327
Chicago/Turabian StyleVallejo Orti, Miguel, Kaleb Negussie, Eva Corral-Pazos-de-Provens, Bernhard Höfle, and Olaf Bubenzer. 2019. "Comparison of Three Algorithms for the Evaluation of TanDEM-X Data for Gully Detection in Krumhuk Farm (Namibia)" Remote Sensing 11, no. 11: 1327. https://doi.org/10.3390/rs11111327
APA StyleVallejo Orti, M., Negussie, K., Corral-Pazos-de-Provens, E., Höfle, B., & Bubenzer, O. (2019). Comparison of Three Algorithms for the Evaluation of TanDEM-X Data for Gully Detection in Krumhuk Farm (Namibia). Remote Sensing, 11(11), 1327. https://doi.org/10.3390/rs11111327






