1. Introduction
High-resolution remote sensing imagery captured by satellite or unmanned aerial vehicle (UAV) contains rich information and is significant in many applications, including land-use analysis, environment protection and urban planning [
1]. Due to the rapid development of remote sensing technology, especially the improvement of imaging sensors, a massive number of high-quality images are available to be utilized [
2]. With the support of sufficient data, dense semantic labeling, also known as semantic segmentation in computer vision, is now an essential aspect in research and is playing an increasingly critical role in many applications [
3].
To better understand the scene, dense semantic labeling aims at segmenting the objects of given categories from the background of the images at the pixel-level, such as buildings, trees and cars [
4]. In the past decades, a vast number of algorithms have been proposed. These algorithms can be divided into two major parts, that is, traditional machine learning methods and convolutional neural network (CNN) methods [
5].
Traditional machine learning methods usually adopt a two-stage architecture consisting of a feature extractor and a classifier [
6]. The feature extractor aims at extracting spatial and textural features from local portions of the image, encoding the spatial arrangements of pixels into a high-dimensional representation [
7]. Many powerful feature extractors have been presented before, such as Histogram of oriented gradients (HOG) [
8], Scale invariant Feature Transform (SIFT) [
9] and Speeded up robust features (SURF) [
10]. Meanwhile, the classifier makes the prediction of every pixel in the image based on the extracted features. Support vector machines [
11], Random forests [
12] and K-means [
13] are usually employed. However, these traditional machine learning methods cannot achieve a satisfactory result, due to massive changes in illumination in the images and the strong similarity of shape and color with different categories of objects. It is challenging to have a robust prediction [
14].
In recent years, convolutional neural networks have achieved extreme success in many domains of computer vision tasks, including dense semantic labeling [
15,
16]. CNNs learn the network parameters directly from data using backpropagation and have more hidden layers which means a more powerful nonlinear fitting ability [
17]. In the early stage, CNNs focused on classification tasks, significantly outperformed the traditional machine learning methods on ImageNet large scale visual recognition competition (ILSVRC) [
18]. Afterwards, many excellent networks were proposed, such as VGG [
19], Deep residual network (ResNet) [
20] and DenseNet [
21]. However, dense semantic labeling is a pixel-level classification task [
22]. To retain the spatial structure, fully convolutional networks (FCN) [
23] replace the fully connected layers with upsampling layers. Through the upsampling operations, the downsampled feature maps can be restored to the original resolution of the input image. The FCN model is the first end-to-end, pixels-to-pixels network and most further networks are based on it [
24].
Nowadays, the classification accuracy of FCN-based models is relatively high. The primary objective in dense semantic labeling tasks is to obtain a more accurate boundary of objects and deal with the misclassification problem of small objects. The challenge comes from two aspects. First, the pooling layers or convolution striding used between convolution layers can augment the receptive field; meanwhile, they can also downsample the resolution of feature maps which cause the loss of spatial information. Second, objects of the same category exist in multiple scales of shape and small objects are hard to classify correctly [
25]. Therefore, simply employing upsampling operations such as deconvolution or bilinear interpolation after the feature extractor parts of a network cannot guarantee a fine prediction result. Many network structures have been proposed to handle these problems; among them, atrous spatial pyramid pooling (DeepLab) [
26] and encoder-decoder (U-net) [
27] are the state-of-art structures.
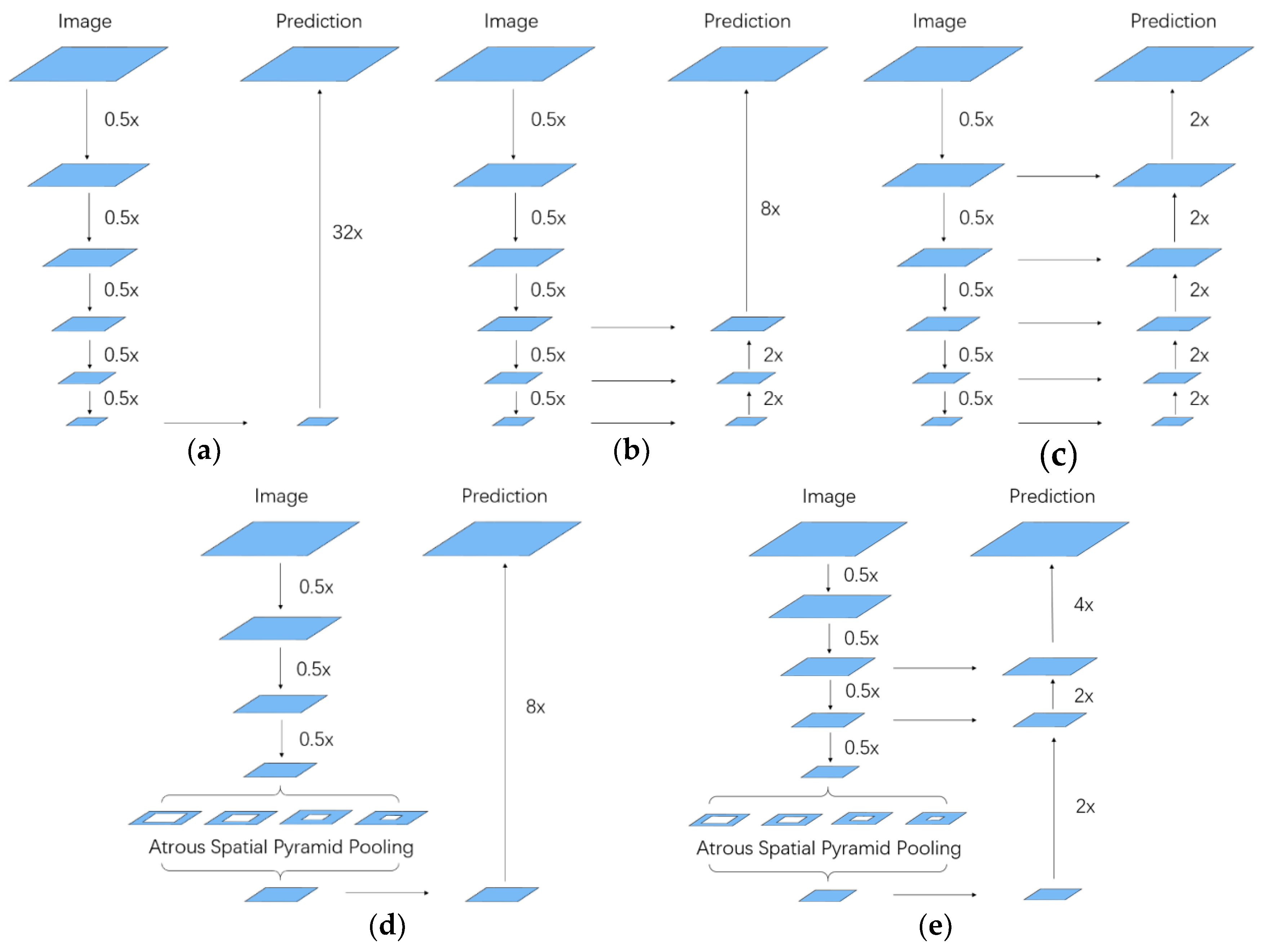
The atrous spatial pyramid pooling (ASPP) network structure from the DeepLab model has been well-known for achieving robust and efficient dense semantic labeling performance and it aims at handling the problem of segmenting objects at multiple scales [
28]. The network structure consists of several branches of atrous convolution operations and each branch has a different rate of the convolution kernels to probe an incoming feature map at specific effective field-of-view. Therefore, ASPP shows better performance on detecting objects at different scales of shape, especially the small objects. But DeepLab model only utilized a simple bilinear interpolation after ASPP to restore the resolution of feature maps that lead to a bad impact on getting fine boundary of the objects.
The encoder-decoder structure from U-net has been widely used in the dense semantic labeling tasks of remote sensing imageries [
14,
29]. It adopts several skip connections between top layers and bottom layers at the upsampling stage. Due to the combination of contextual information at scales of 1,
,
,
of the input resolution, spatial information damaged by the pooling operations can be better restored, so objects in the final prediction have a sharper boundary after the decoder. However, U-net has no consideration for the extraction of multiple scales of features.
These two powerful network structures only focus on the two problems in dense semantic labeling respectively and no works have taken them into account simultaneously before. Therefore, a model employing both of them could further improve the performance.
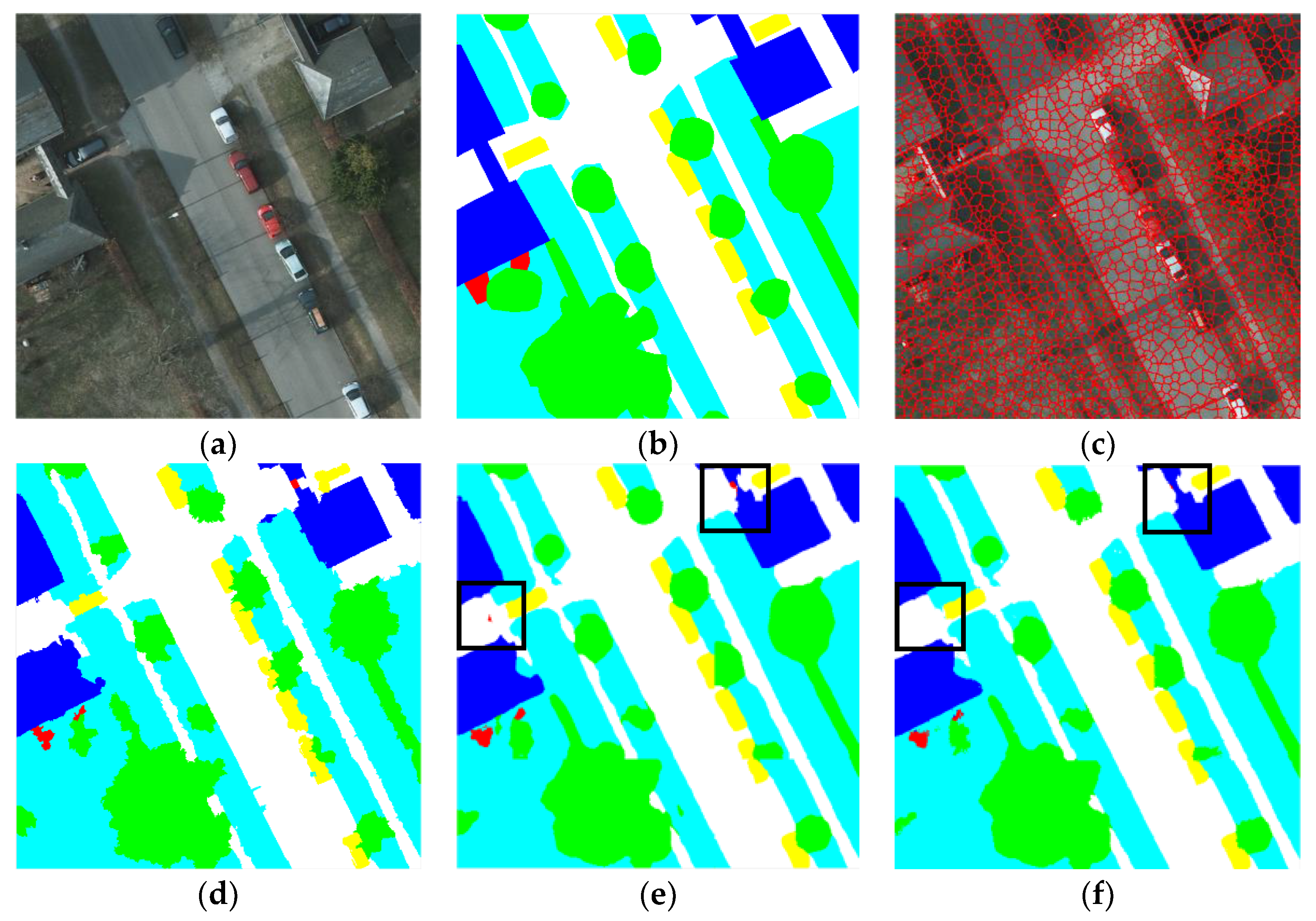
Figure 1 shows details of alternative network structures of dense semantic labeling.
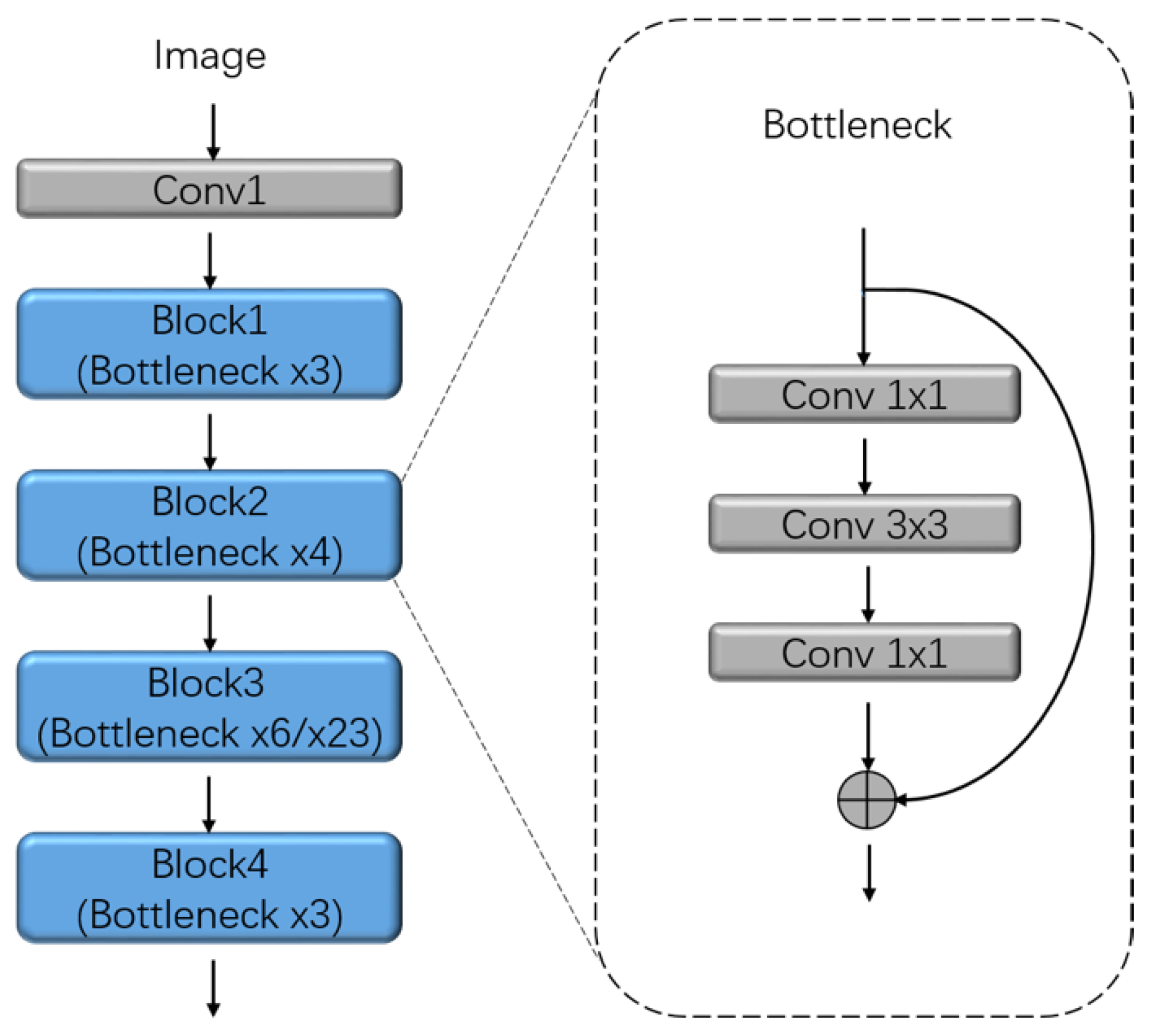
Inspired by the analysis above, we propose a novel architecture of the fully convolutional network that aims at not only detecting objects of different shapes but also restoring sharper object boundaries simultaneously. Our model adopts the deep residual network (ResNet) as the backbone, followed by atrous spatial pyramid pooling (ASPP) structure to extract multi-scale contextual information; these two parts constitute the encoder. Then we design the decoder structures by fusing two scales of low-level feature maps from ResNet with the corresponding predictions to restore the spatial information. To make this two structure fusion effective, we append a multi-scale softmax cross-entropy loss function with corresponding weights at the end of networks. Different from the loss function in Reference [
29], our proposed loss function guides every scale of prediction during the training procedure which helps better optimize the parameters in the intermediate layers. After the networks, we improve the dense conditional random field (DenseCRF) using a superpixel algorithm in post-processing that gives an additional boost to performance. Experiments on the Potsdam and Vaihingen datasets demonstrate that our model outperformed other state-of-art networks and achieved 88.4% and 87.0% overall accuracy respectively with the calculation of the boundary pixels of objects. The main contributions of our study are listed as follows:
We propose a novel convolutional neural network that combines the advantages of ASPP and encoder-decoder structures.
We enhance the learning procedure by employing a multi-scale loss function.
We improve the dense conditional random field with a superpixel algorithm to optimize the prediction further.
The remainder of this paper is organized as follows:
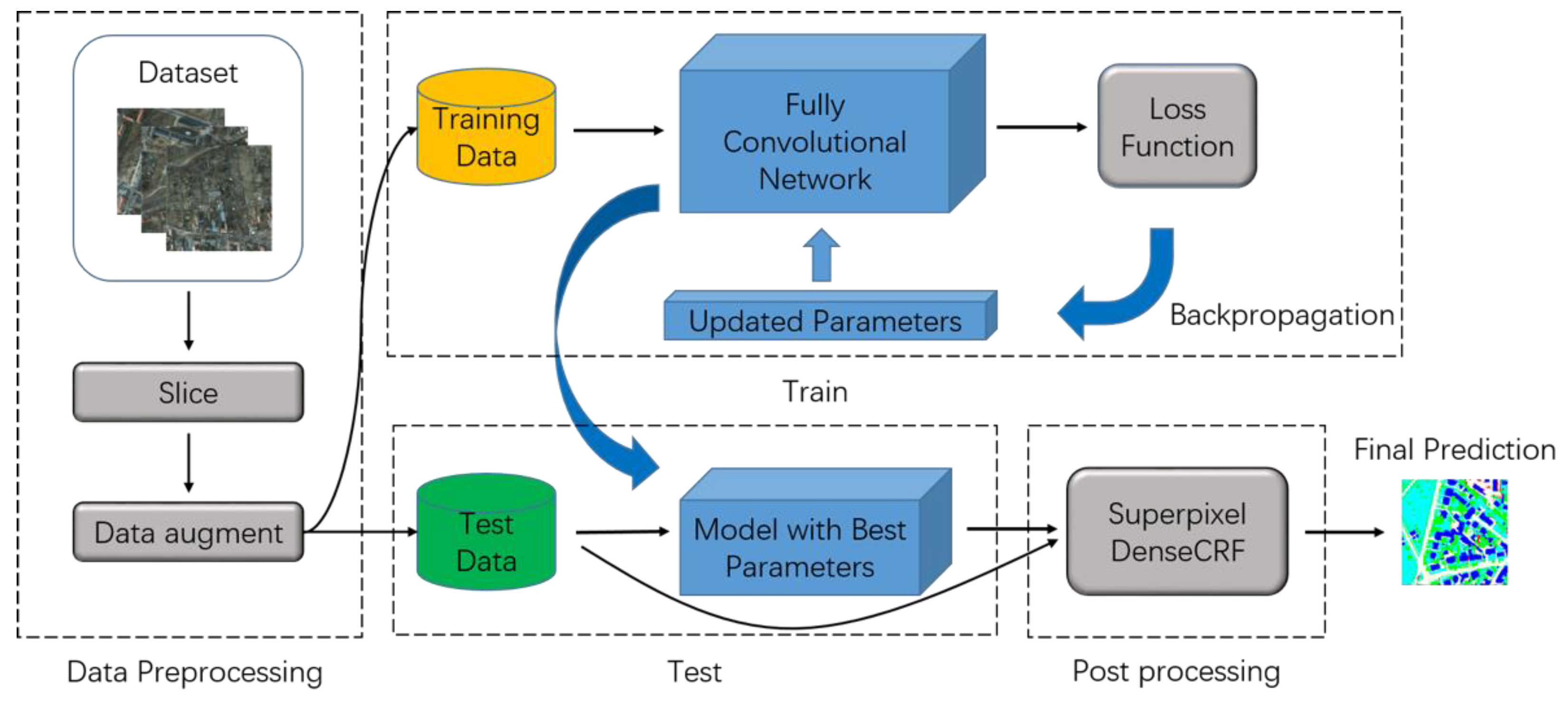
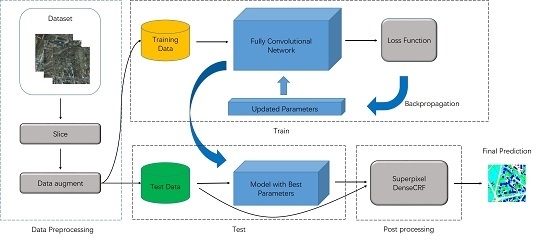
Section 2 describes our dense semantic labeling system which includes the proposed model and the superpixel-based DenseCRF.
Section 3 presents the datasets, preprocessing methods, training protocol and results.
Section 4 is the discussion of our method and
Section 5 concludes the whole study.
5. Conclusions
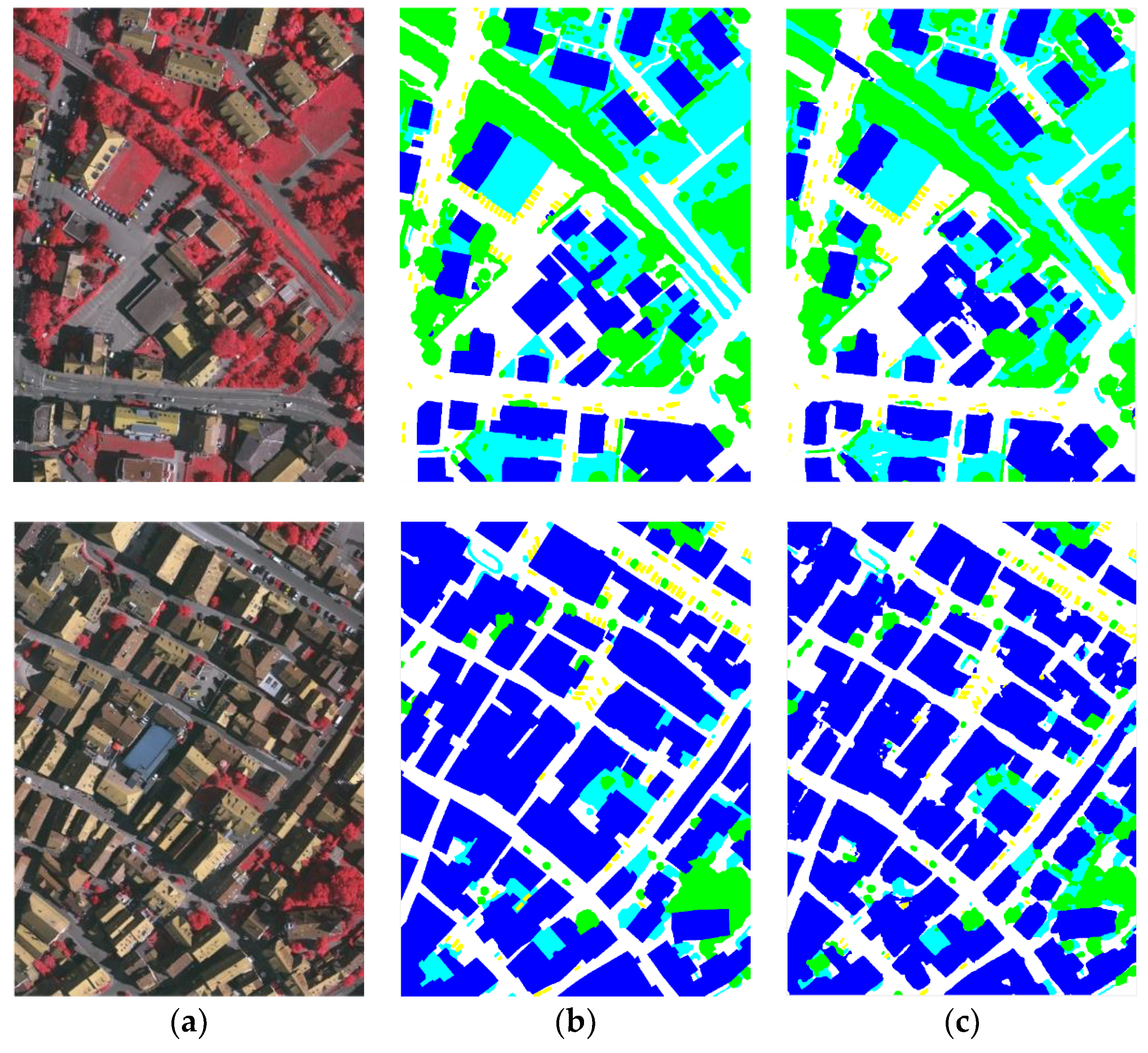
In this paper, a novel fully convolutional network to perform dense semantic labeling on high-resolution remote sensing imageries is proposed. The main contribution of this work consists of analyzing the advantage of existing FCN-based models, pointing out the encoder-decoder and ASPP as two powerful structures and fusing them in one model with an additional multi-scale loss function to take effect. Moreover, we employ several data augment methods before our model and a superpixel-based CRF as the postprocessing method. The objective of our work is to further improve the performance of fully convolutional network on dense semantic labeling tasks. Experiments were implemented on ISPRS 2D challenge which includes two high-resolution remote sensing imagery datasets of Potsdam and Vaihingen. Every object of the given categories was extracted successfully by our proposed method with fewer classification errors and sharper boundary. The comparison was taken between U-net, DeepLab_v3, DeepLab_v3+ and even some methods from the leaderboard including the recently published one. The results indicate that our methods outperformed other methods and achieved significant improvement.
Nowadays, remote sensing technology develops at a high-speed, especially the popularization of unmanned aerial vehicles and high-resolution sensors. More and more remote sensing imageries are available to be utilized. Meanwhile, deep learning based methods have achieved an acceptable result for practical applications. However, the groundtruth of remote sensing imageries are manually annotated and so will take too much labor. Therefore, semi-supervised or weak supervision methods should be taken into account in the future works.