Development of Shoreline Extraction Method Based on Spatial Pattern Analysis of Satellite SAR Images
Abstract
1. Introduction
2. Materials and Methods
2.1. Input Data
2.2. Methods
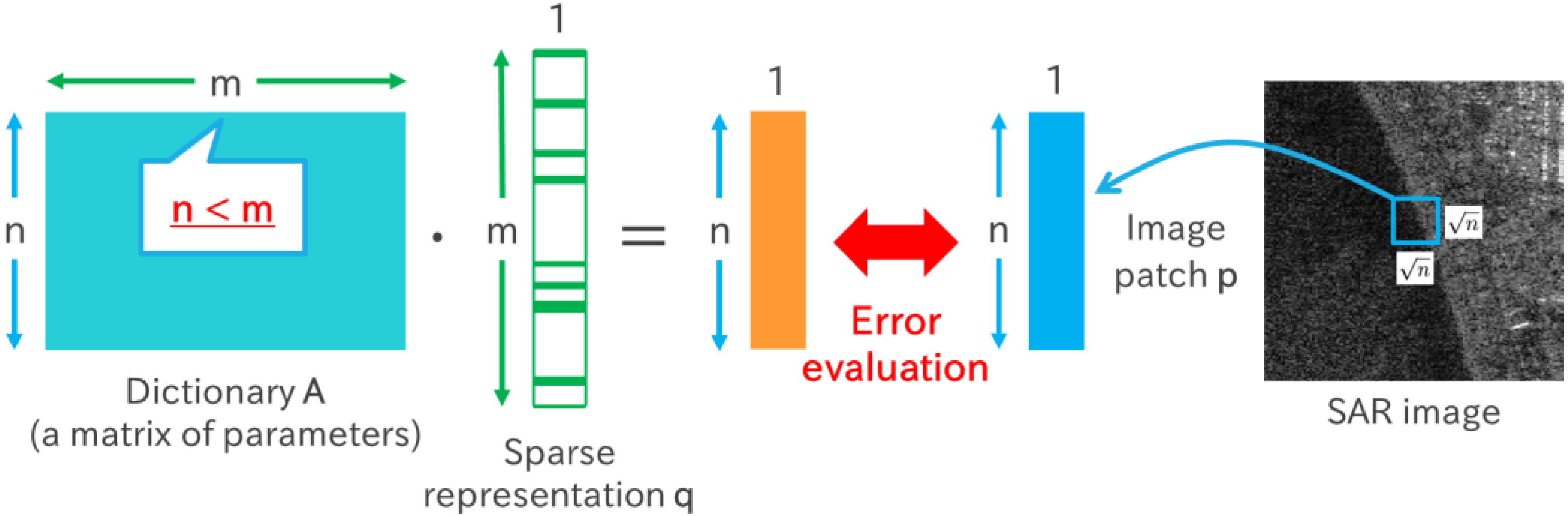
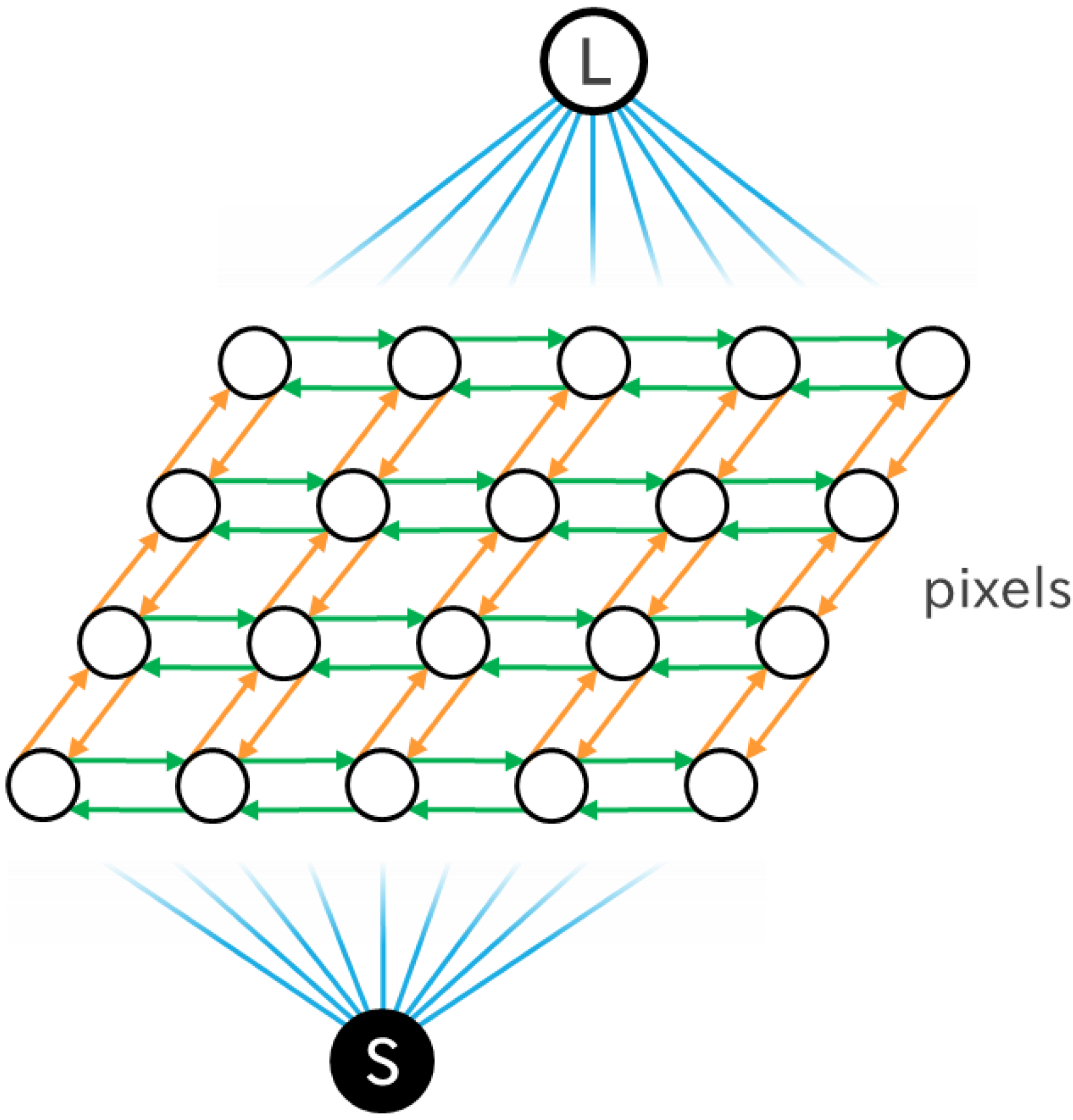
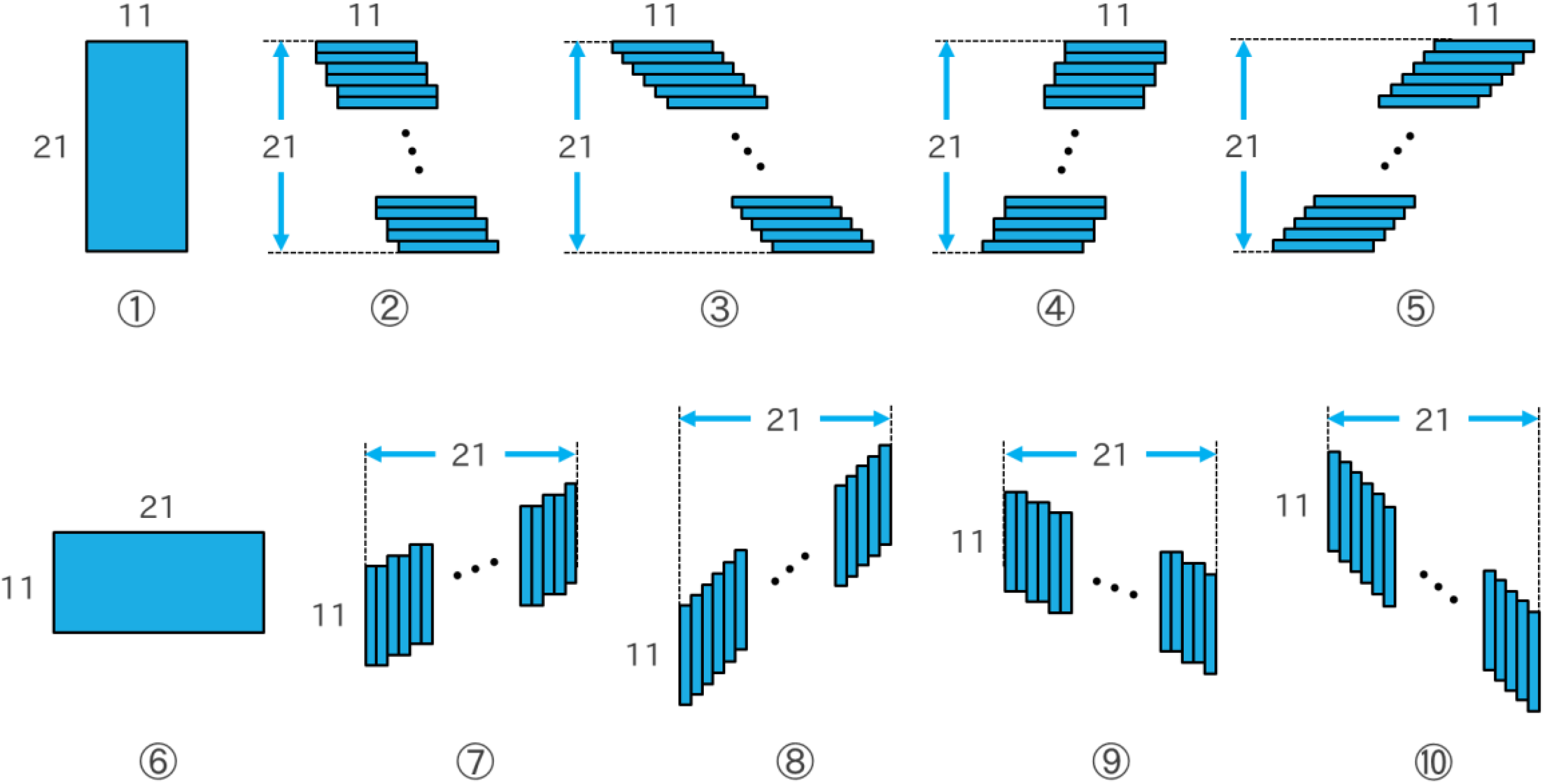
2.2.1. Image Decomposition Based on Spatial Patterns
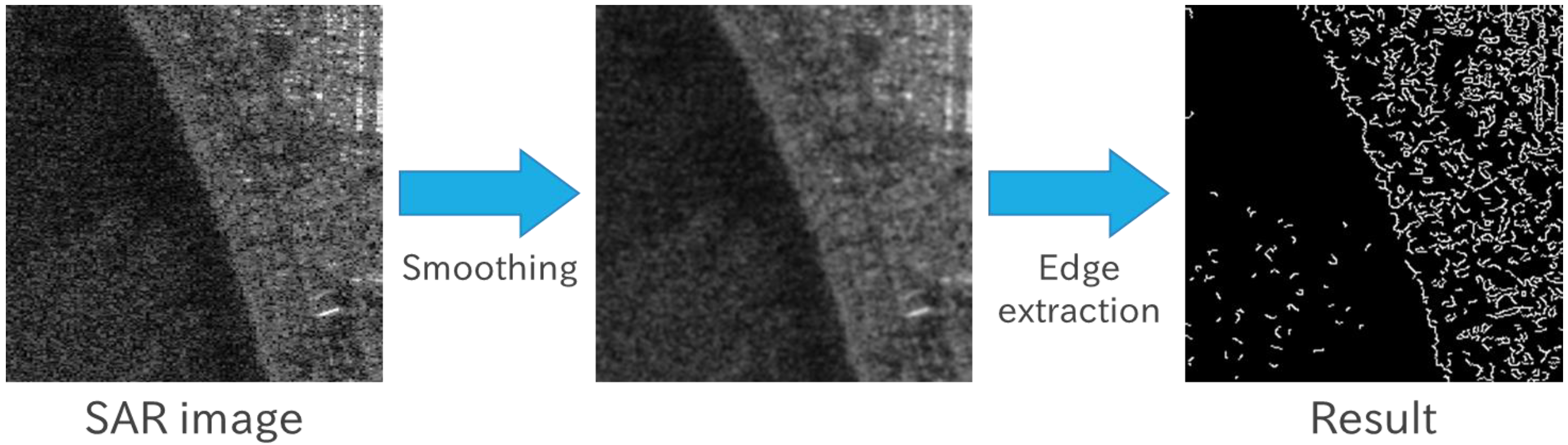
2.2.2. Smoothing
2.2.3. Sea–Land Binarization
2.2.4. Refinement of the Extracted Shoreline
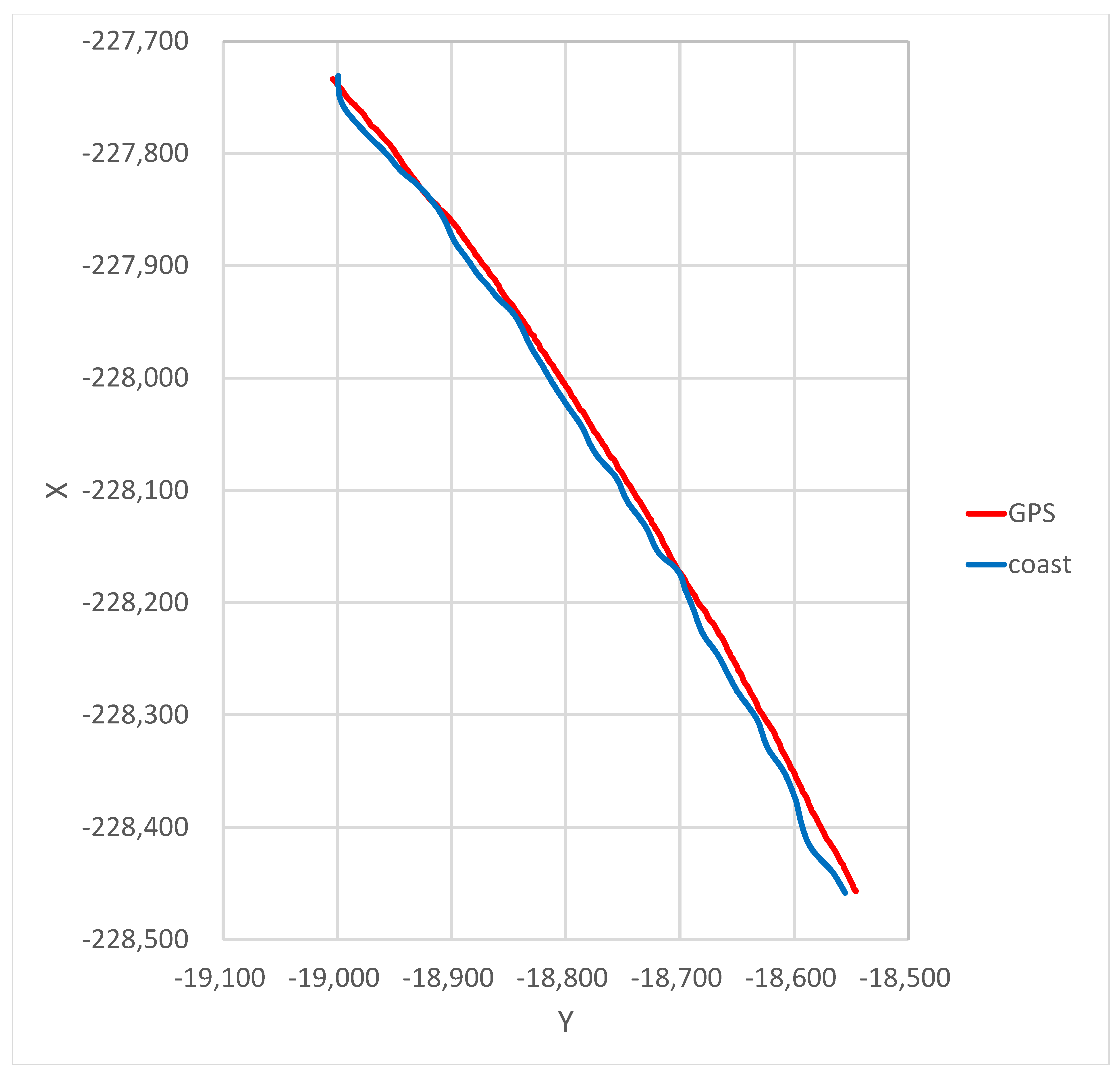
2.2.5. Method for Accuracy Verification
3. Results and Discussion
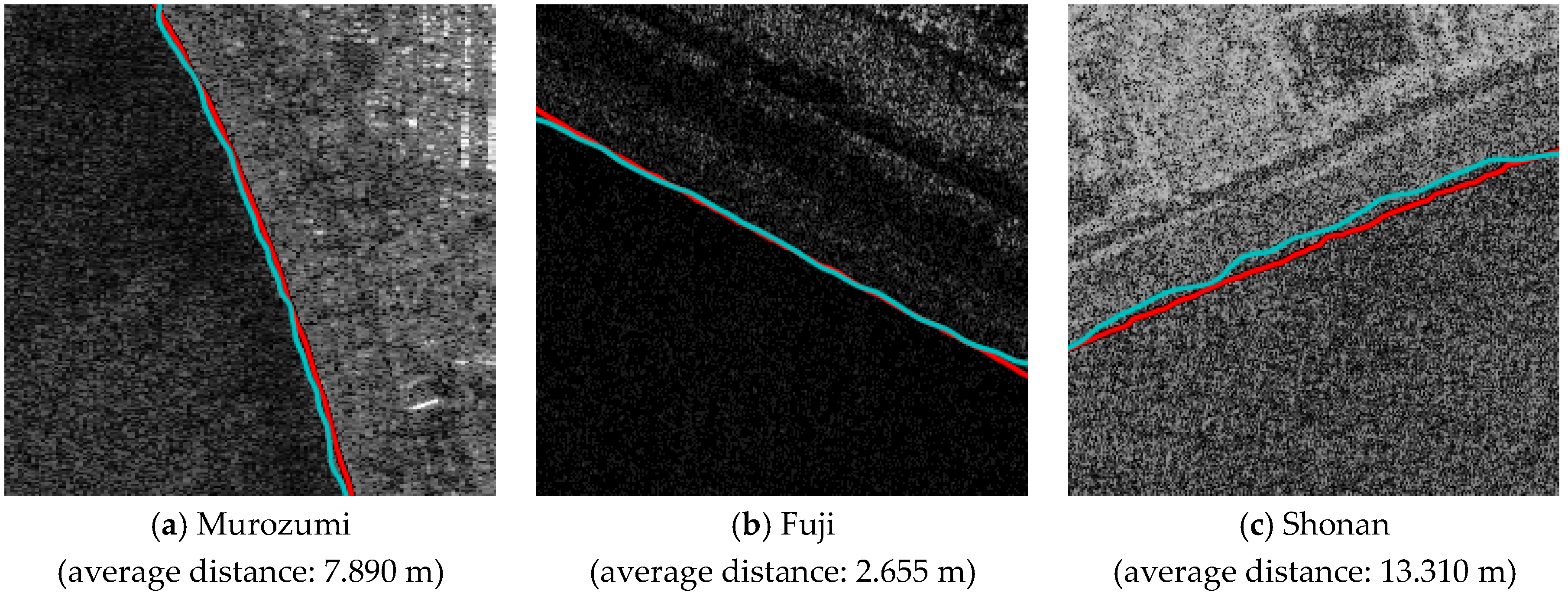
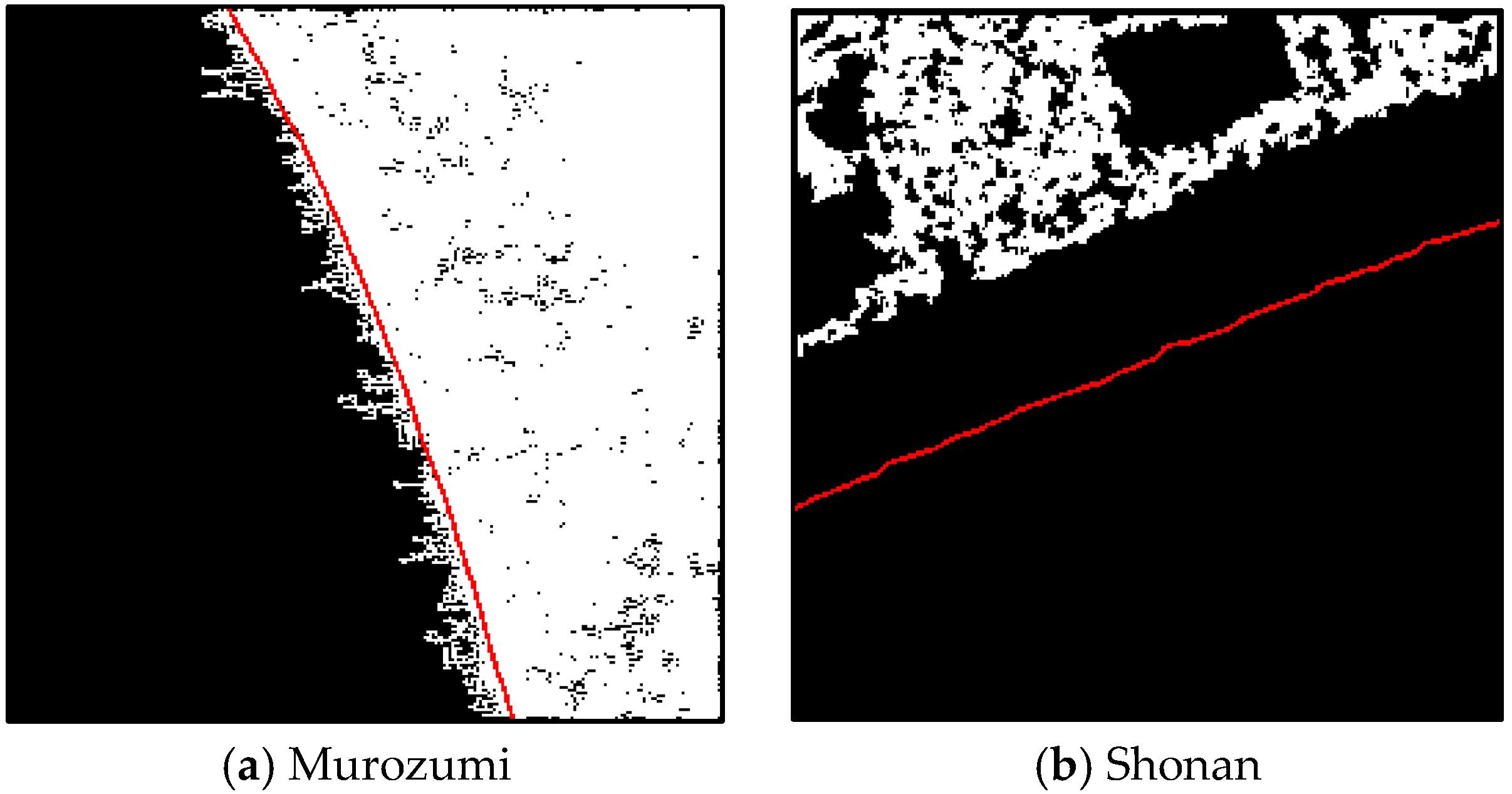
3.1. Accuracy Verification of the Shoreline Extraction Method
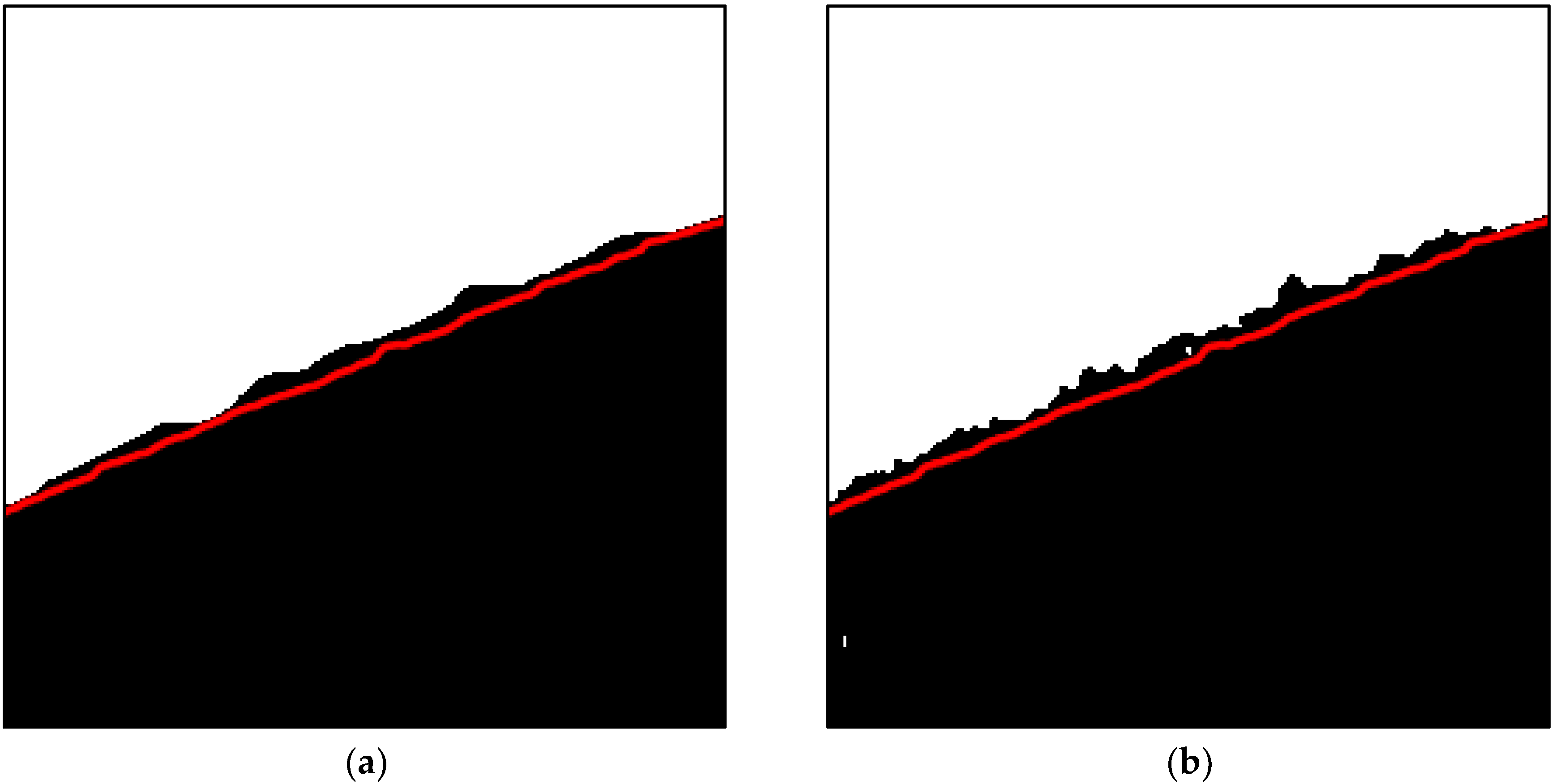
3.2. Validation Using SAR Images with Breakwaters
3.3. Validation Using SAR Image with Wave Crest Lines
3.4. Verification on Dictionary Sharing
- Type 1: Use a dictionary learned from another part of the same SAR scene,
- Type 2: Use a dictionary learned from a SAR image of another coast.
4. Conclusions
Supplementary Materials
Supplementary File 1Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lee, J.S.; Jurkevich, I. Coastline detection and tracing in SAR images. IEEE Trans. Geosci. Remote Sens. 1990, 28, 662–668. [Google Scholar]
- Mason, D.C.; Davenport, I.J. Accurate and efficient determination of the shoreline in ERS-1 SAR images. IEEE Trans. Geosci. Remote Sens. 1996, 34, 1243–1253. [Google Scholar] [CrossRef]
- Liu, H.; Jezek, K.C. Automated extraction of coastline from satellite imagery by integrating Canny edge detection and locally adaptive thresholding methods. Int. J. Remote Sens. 2004, 25, 937–958. [Google Scholar] [CrossRef]
- Wang, Y.; Allen, T.R. Estuarine shoreline change detection using Japanese ALOS PALSAR HH and JERS-1 L-HH SAR data in the Albemarle-Pamlico Sounds, North Carolina, USA. Int. J. Remote Sens. 2008, 29, 4429–4442. [Google Scholar] [CrossRef]
- Asaka, T.; Yamamoto, Y.; Aoyama, S.; Iwashita, K.; Kudou, K. Automated method for tracing shorelines in L-band SAR images. In Proceedings of the 2013 Asia-Pacific Conference on Synthetic Aperture Radar, Tsukuba, Japan, 23–27 September 2013; pp. 325–328. [Google Scholar]
- Zhang, D.; Gool, L.V.; Oosterlinck, A. Coastline detection from SAR images. IEEE Geosci. Remote Sens. Symp. 1994, 4, 2134–2136. [Google Scholar]
- Nunziata, F.; Buono, A.; Migliaccio, M.; Benassai, G. Dual-polarimetric C- and X-band SAR data for coastline extraction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4921–4928. [Google Scholar] [CrossRef]
- Vandebroek, E.; Lindenbergh, R.; van Leijen, R.; de Schipper, M.; de Vries, S.; Hanssen, R. Semi-automated monitoring of a mega-scale beach nourishment using high-resolution TerraSAR-X satellite data. Remote Sens. 2017, 9, 653. [Google Scholar] [CrossRef]
- Touzi, R.; Lopes, A.; Bousquet, P. A statistical and geometrical edge detector for SAR images. IEEE Trans. Geosci. Remote Sens. 1988, 26, 764–773. [Google Scholar] [CrossRef]
- Kass, M.; Witkin, A.; Terzopoulos, D. Snakes: Active contour models. Int. J. Comput. Vis. 1988, 1, 321–331. [Google Scholar] [CrossRef]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 6, 679–698. [Google Scholar] [CrossRef]
- GSI Maps. Available online: https://maps.gsi.go.jp/ (accessed on 16 March 2018).
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar]
- Zhu, S.C.; Shi, K.; Si, Z. Learning explicit and implicit visual manifolds by information projection. Pattern Recognit. Lett. 2010, 31, 667–685. [Google Scholar] [CrossRef]
- Starck, J.L.; Elad, M.; Donoho, D.L. Image decomposition via the combination of sparse representations and a variational approach. IEEE Trans. Image Process. 2005, 14, 1570–1582. [Google Scholar] [CrossRef] [PubMed]
- Elad, M.; Starck, J.L.; Querre, P.; Donoho, D.L. Simultaneous cartoon and texture image inpainting using morphological component analysis (MCA). Appl. Comput. Harmon. Anal. 2005, 19, 340–358. [Google Scholar] [CrossRef]
- Bobin, J.; Moudden, Y.; Starck, J.L.; Elad, M. Morphological diversity and source separation. IEEE Trans. Signal Process. 2006, 13, 409–412. [Google Scholar] [CrossRef]
- Candés, E.J.; Recht, B. Exact matrix completion via convex optimization. Found. Comput. Math. 2009, 9, 717–772. [Google Scholar] [CrossRef]
- Elad, M.; Aharon, M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans. Image Process. 2006, 15, 3736–3745. [Google Scholar] [CrossRef] [PubMed]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via Orthogonal Matching Pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Penna, P.A.A.; Mascarenhas, N.D.A. Non-homomorphic approaches to denoise intensity SAR images with non-local means and stochastic distance. Comput. Geosci. 2018, 111, 127–138. [Google Scholar] [CrossRef]
- Deledalle, L.; Denis, L.; Poggi, G.; Tupin, F.; Verdoliva, L. Exploiting patch similarity for SAR image processing: The nonlocal paradigm. IEEE Signal Process. Mag. 2014, 31, 69–78. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J.M. A non-local algorithm for image denoising. IEEE Comput. Vis. Pattern Recognit. 2005, 2, 60–65. [Google Scholar]
- Boykov, Y.Y.; Jolly, M.P. Interactive graph cuts for optimal boundary & region segmentation of objects in N-D images. In Proceedings of the Eighth IEEE International Conference on Computer Vision (ICCV), Vancouver, BC, Canada, 7–14 July 2001; pp. 105–112. [Google Scholar]
- Busacker, R.G.; Saaty, T.L. Finite Graphs and Networks: An Introduction with Applications; McGraw-Hill Inc.: New York, NY, USA, 1965. [Google Scholar]
- Schmidt, F.R.; Toppe, E.; Cremers, D. Efficient planar graph cuts with applications in computer vision. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami Beach, FL, USA, 20–25 June 2009. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
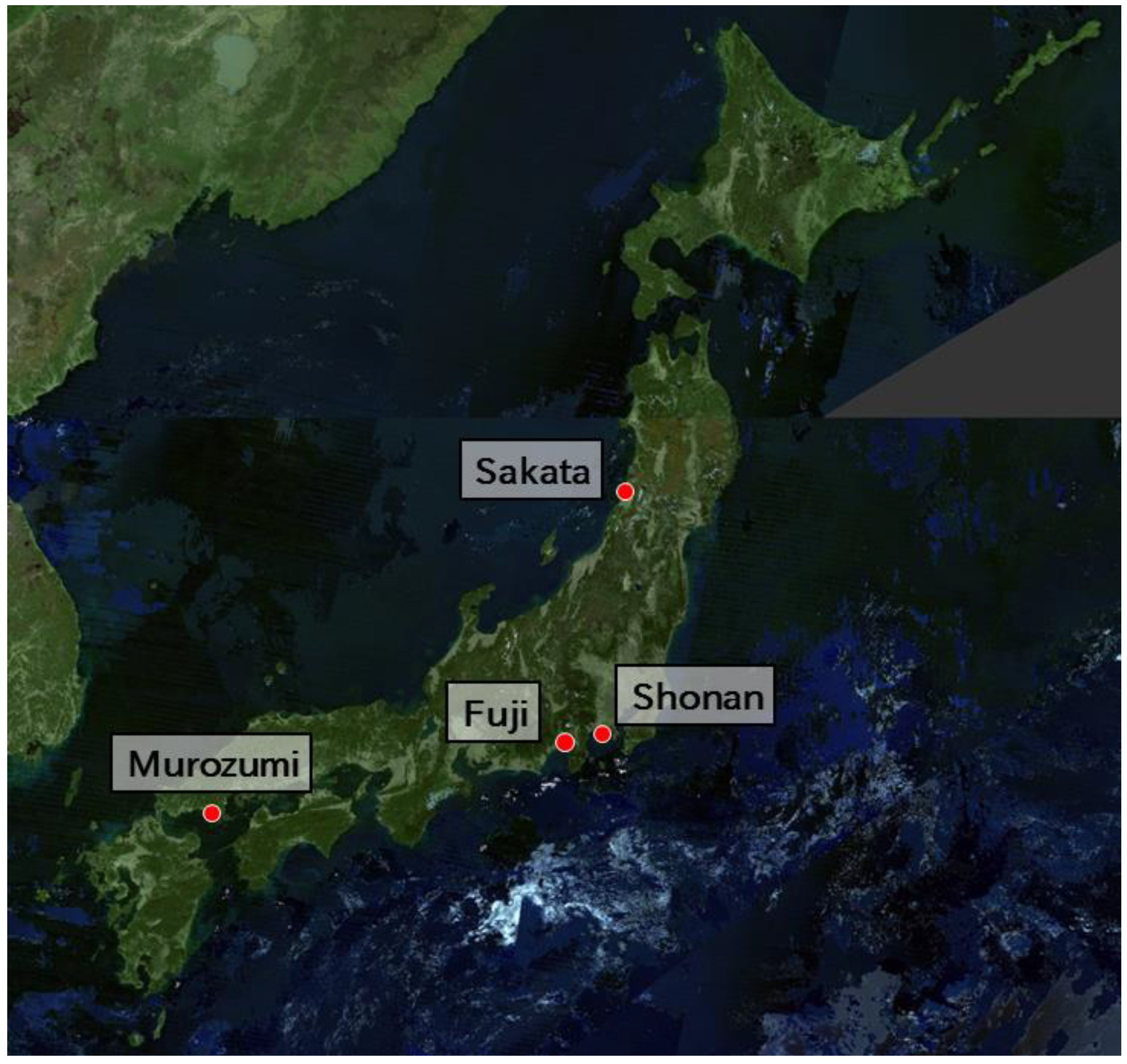






| Coast Name | Processing Level | On-Site Observation Date | ALOS-2 Observation Date | Ascending (A)/Descending (D) | Off-Nadir Angle (ONA) [deg] |
|---|---|---|---|---|---|
| Murozumi | 1.5 | 26/08/2016 | 20/08/2016 | A | 28.4 |
| Shonan | 1.1 | 30/11/2016 | 01/12/2016 | D | 35.8 |
| Fuji | 1.1 | 03/12/2016 | 09/12/2016 | A | 38.7 |
| Sakata | 1.1 | 15/12/2016 | 18/12/2016 | A | 38.7 |
| Patch Size | Dictionary Size | Average Distance (m) | ||
|---|---|---|---|---|
| 2 | 8 × 8 | 8.469 | ||
| 4 | 7.890 | |||
| 6 | 7.556 | |||
| 8 | 7.310 | |||
| 10 | 7.679 | |||
| 4 | 8 × 8 | 8.054 | ||
| 7.890 | ||||
| 7.627 | ||||
| 4 | 6 × 6 | 7.593 | ||
| 8 × 8 | 7.890 | |||
| 10 × 10 | 7.822 | |||
| 12 × 12 | 7.723 | |||
| 4 | 8 × 8 | 7.609 | ||
| 7.890 | ||||
| 7.528 |
| Coast Name | Learning from the Input Image | Learning from Another Part of The Same Scene | Using Murozumi’s Dictionary | Using Shonan’s Dictionary | Using Fuji’s Dictionary |
|---|---|---|---|---|---|
| Murozumi | 7.890 | 7.422 | ---- | 7.426 | 7.270 |
| Shonan | 13.310 | 13.037 | 13.027 | ---- | 16.506 |
| Fuji | 2.655 | 2.638 | 2.035 | 2.572 | ---- |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fuse, T.; Ohkura, T. Development of Shoreline Extraction Method Based on Spatial Pattern Analysis of Satellite SAR Images. Remote Sens. 2018, 10, 1361. https://doi.org/10.3390/rs10091361
Fuse T, Ohkura T. Development of Shoreline Extraction Method Based on Spatial Pattern Analysis of Satellite SAR Images. Remote Sensing. 2018; 10(9):1361. https://doi.org/10.3390/rs10091361
Chicago/Turabian StyleFuse, Takashi, and Takashi Ohkura. 2018. "Development of Shoreline Extraction Method Based on Spatial Pattern Analysis of Satellite SAR Images" Remote Sensing 10, no. 9: 1361. https://doi.org/10.3390/rs10091361
APA StyleFuse, T., & Ohkura, T. (2018). Development of Shoreline Extraction Method Based on Spatial Pattern Analysis of Satellite SAR Images. Remote Sensing, 10(9), 1361. https://doi.org/10.3390/rs10091361





