A Novel Approach of Slope Detection Combined with Lv’s Distribution for Airborne SAR Imagery of Fast Moving Targets
Abstract
:1. Introduction
2. Airborne SAR Echo Signal Model and Analysis
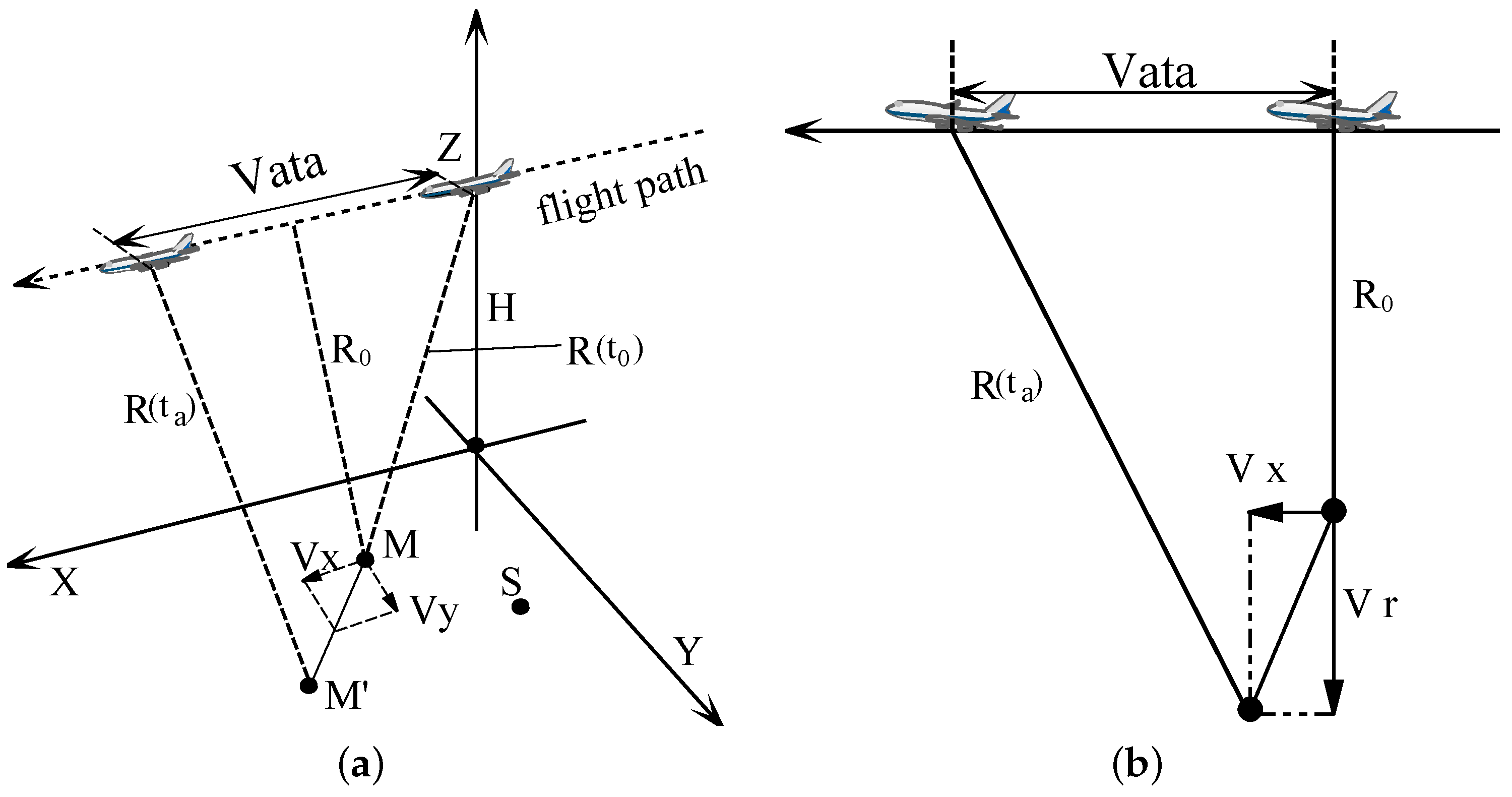
2.1. SAR Geometry of Fast Moving Target
2.2. Motion Parameters Analysis
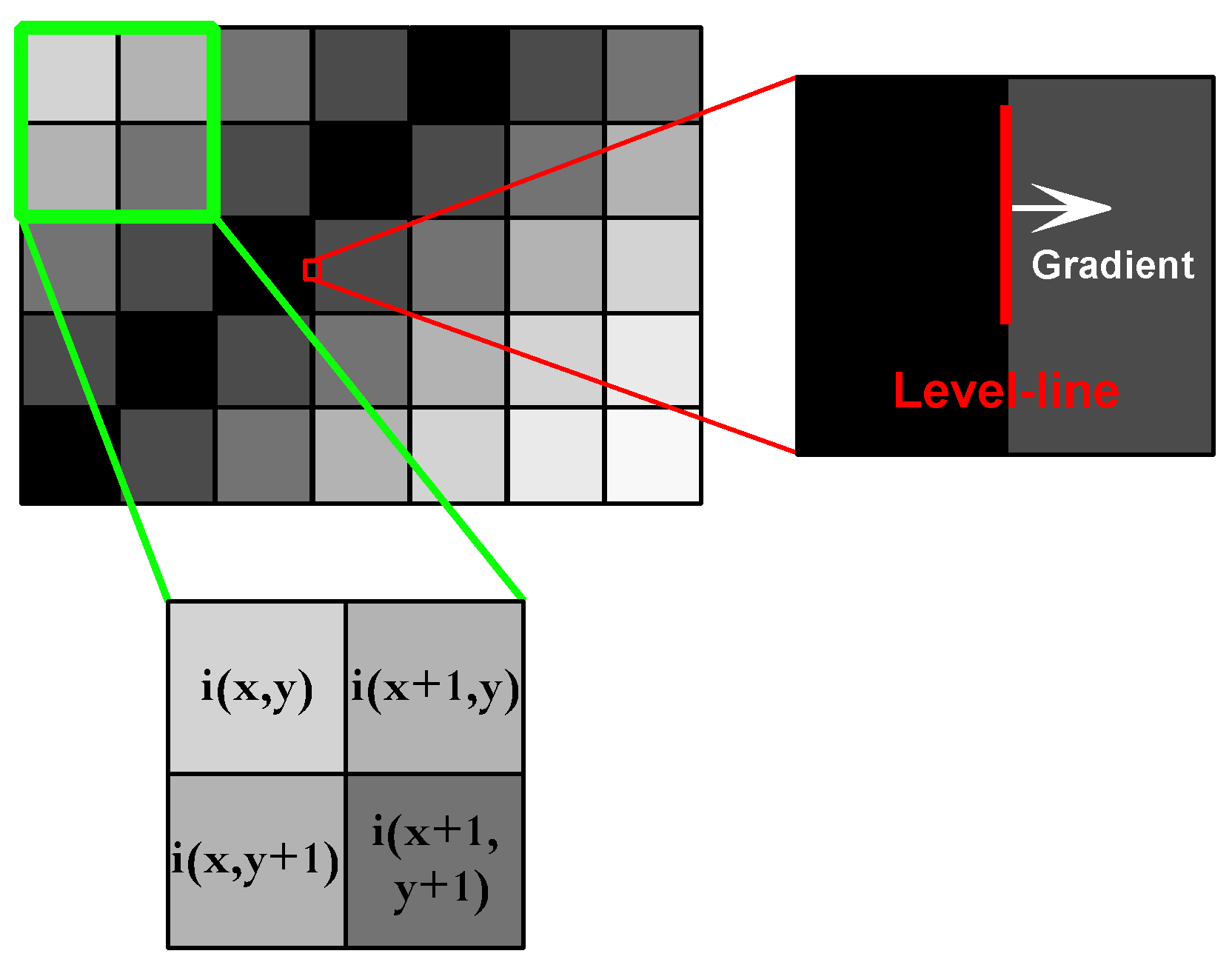
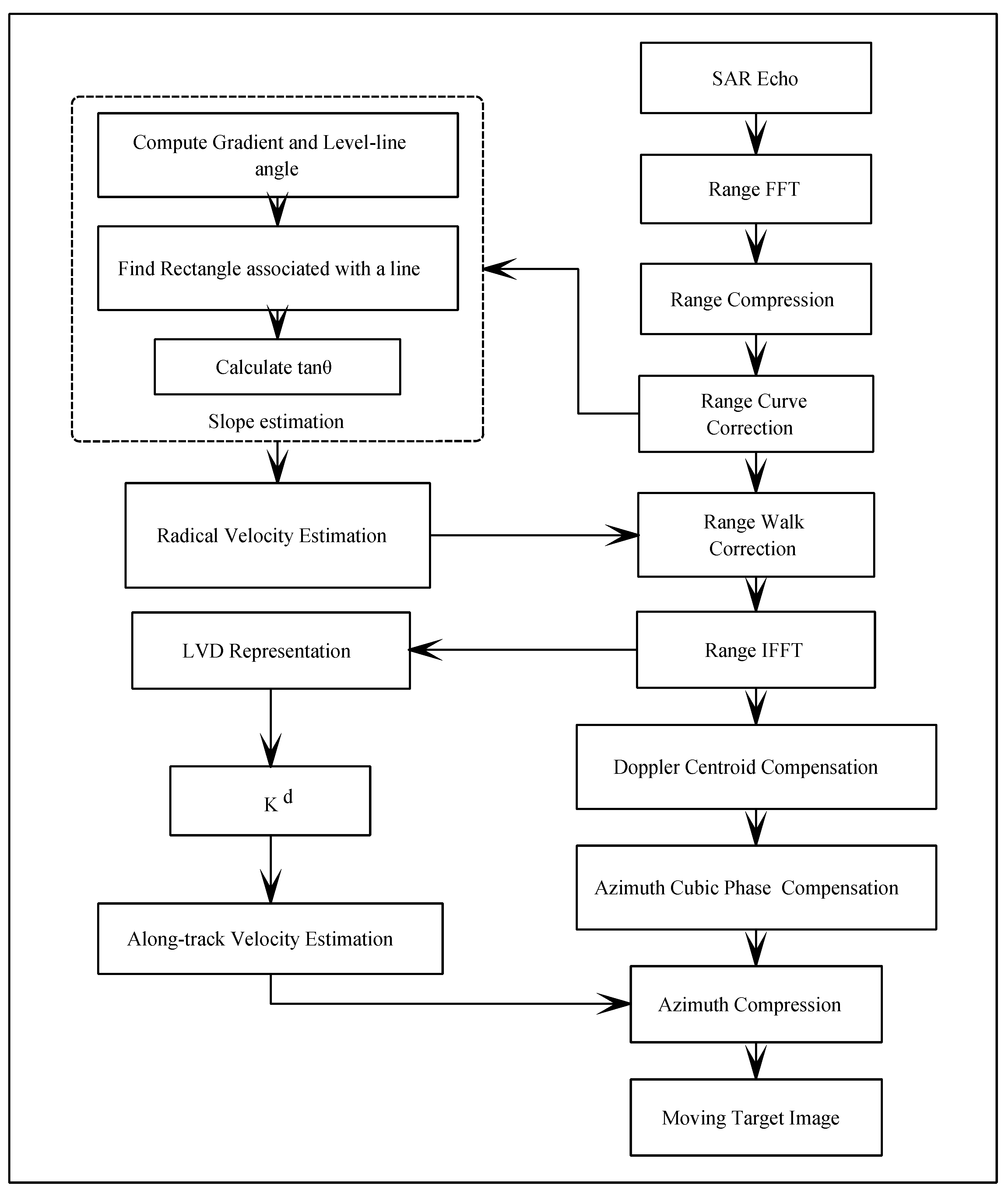
3. Algorithm Description
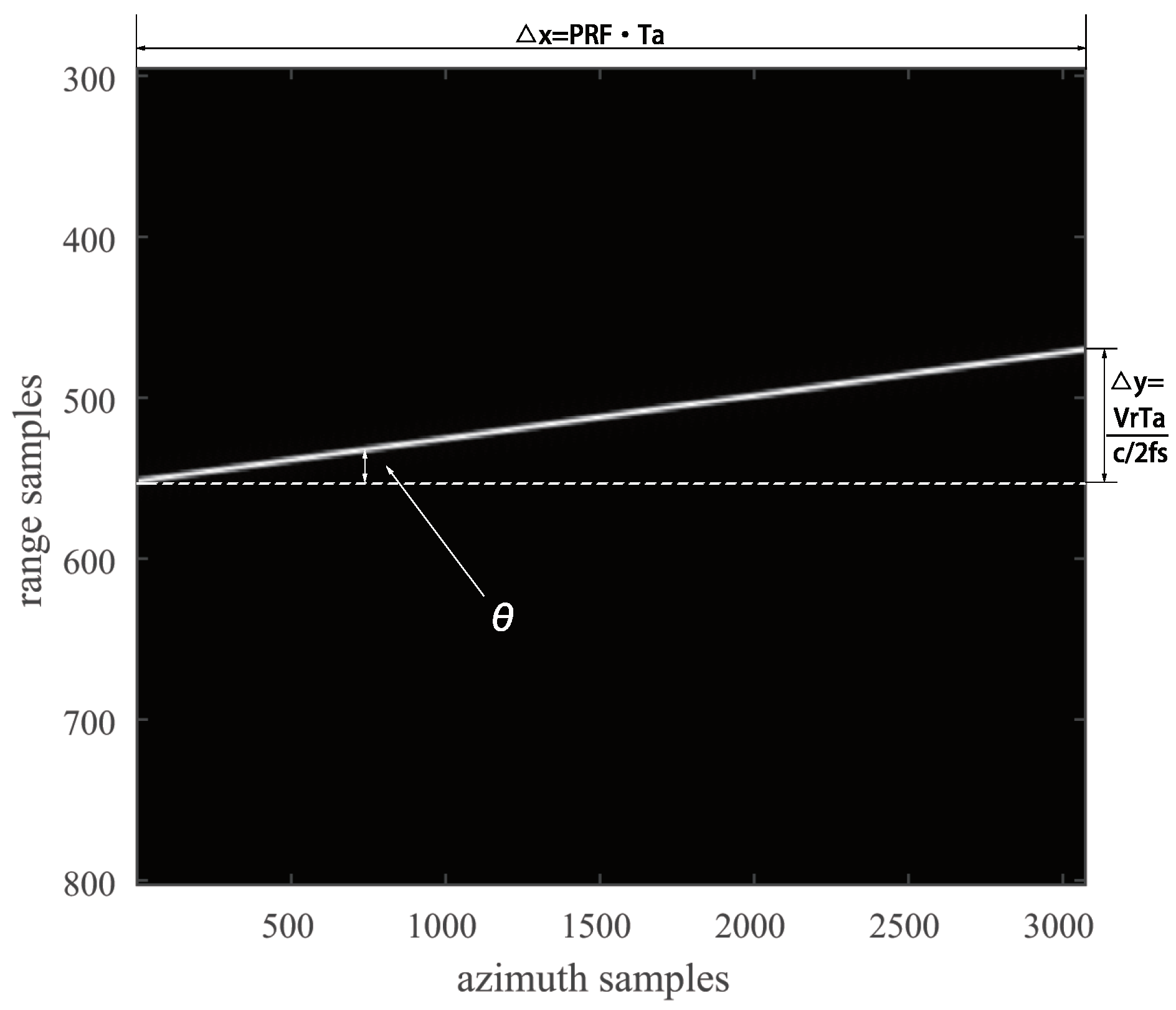
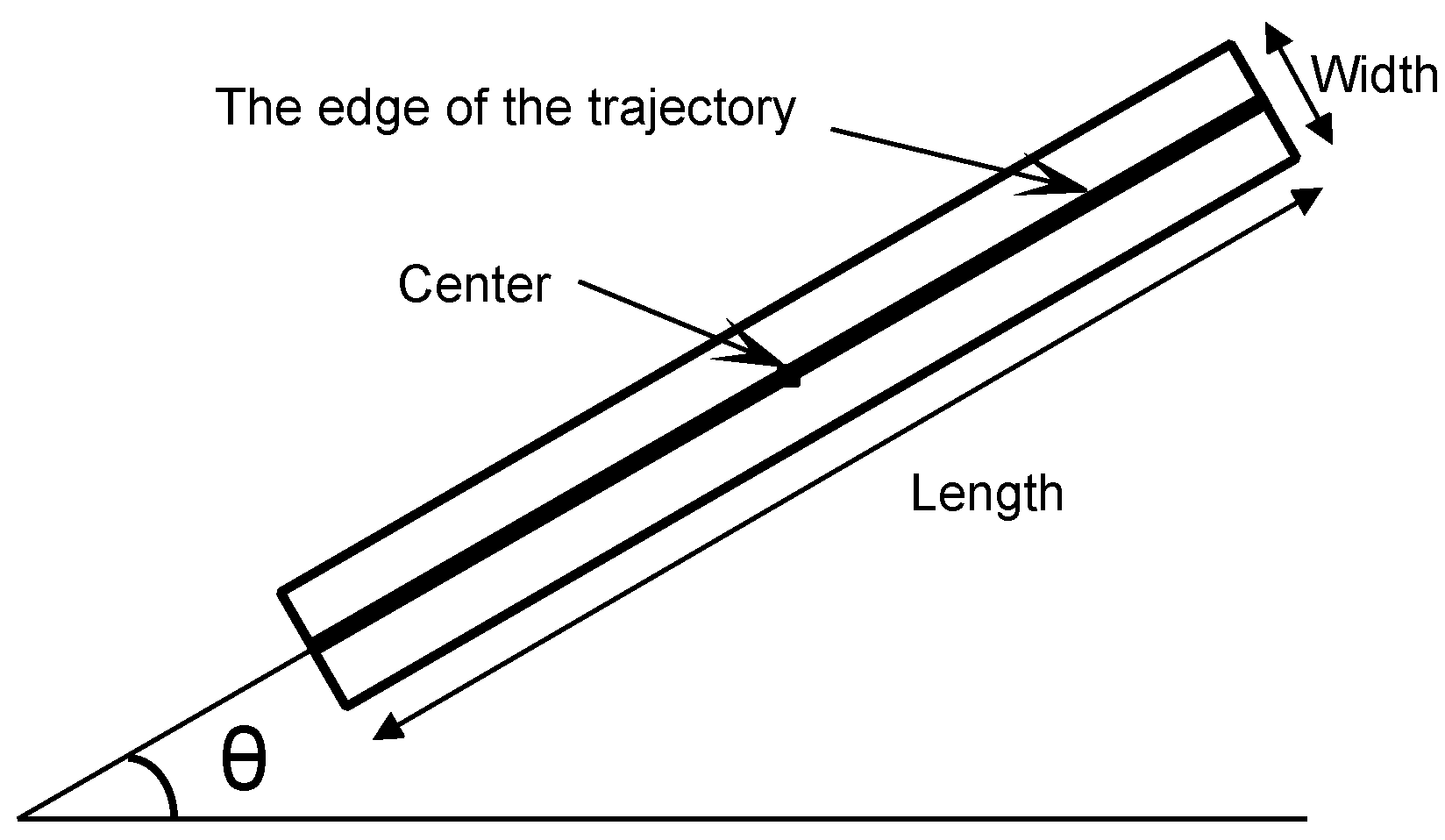
3.1. RCMC and Radial Velocity Estimation
3.2. Along-Track Velocity Estimation
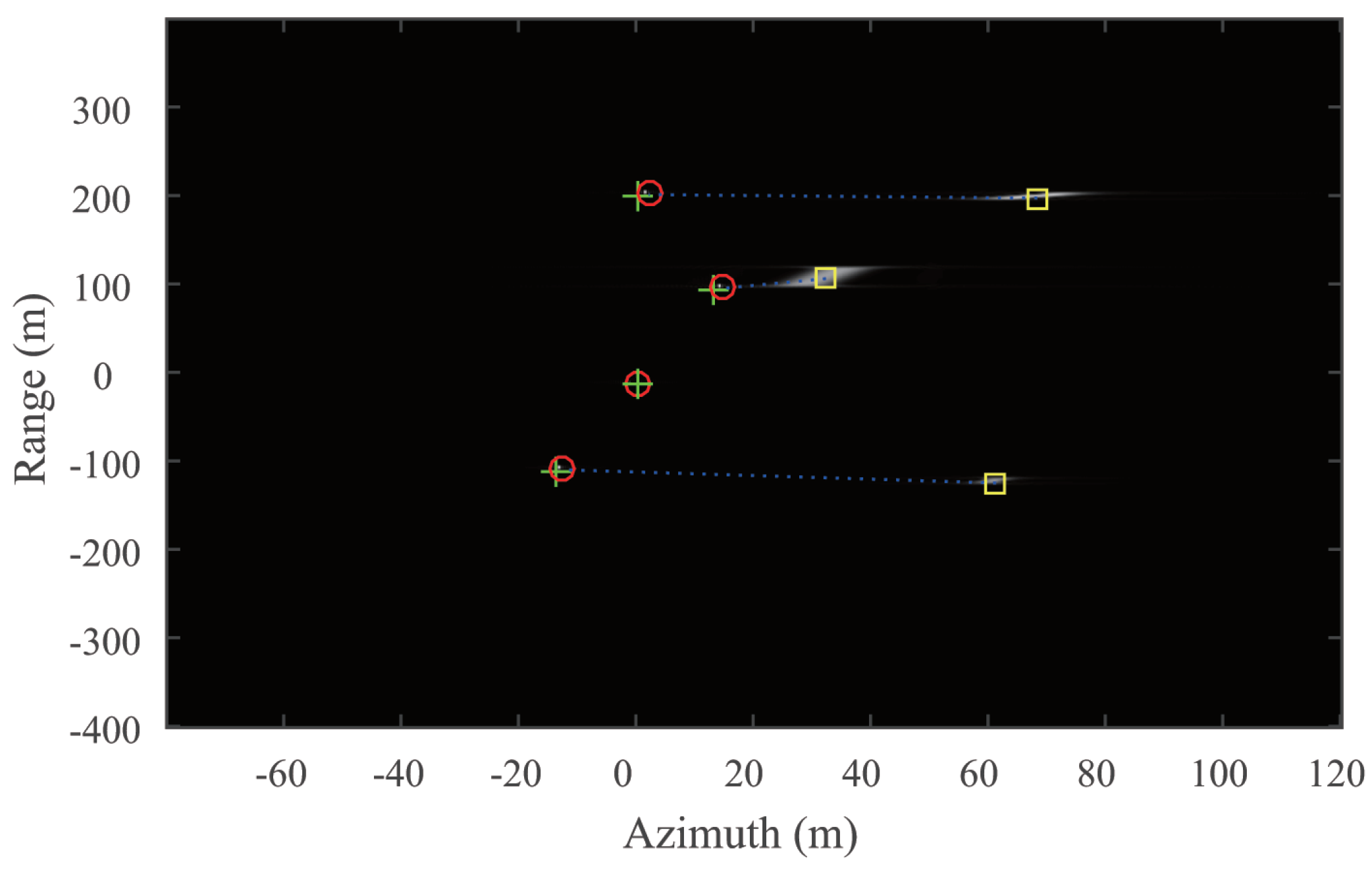
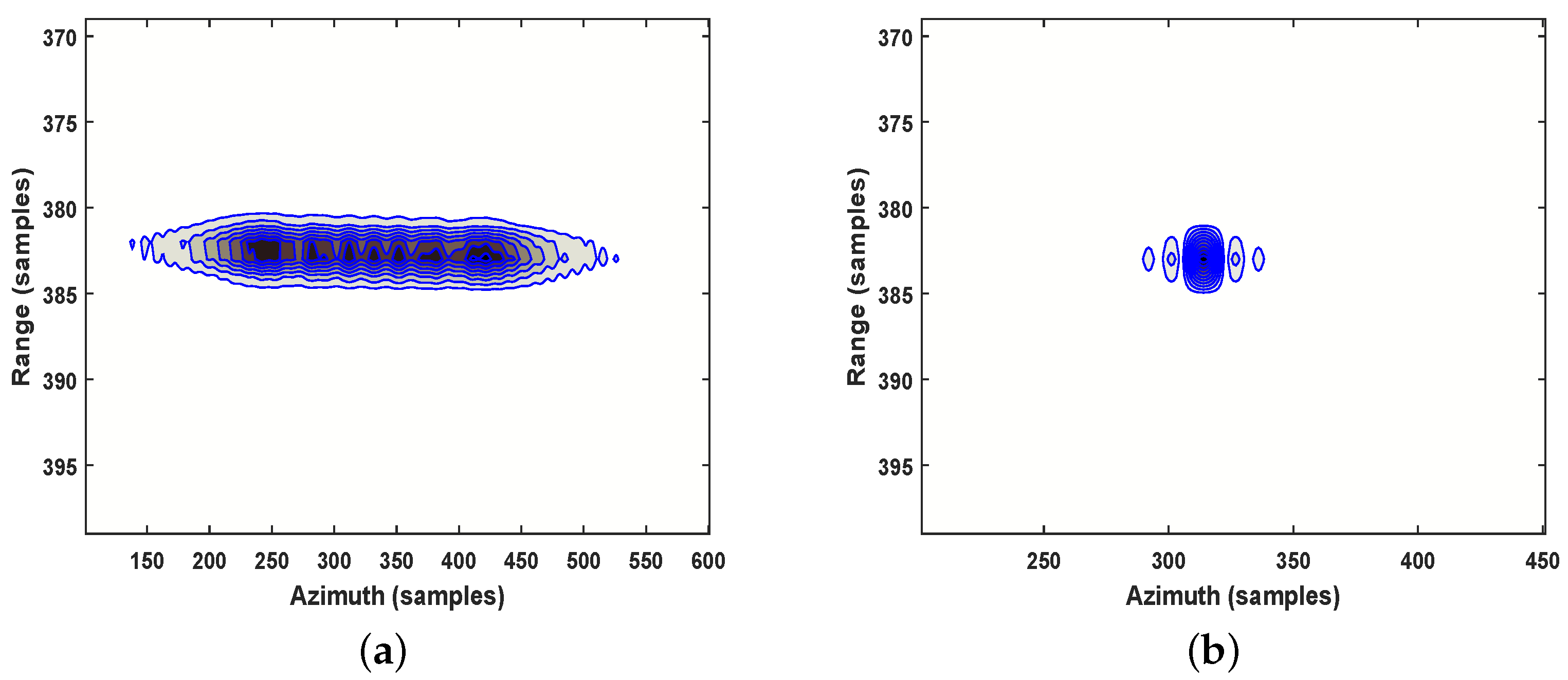
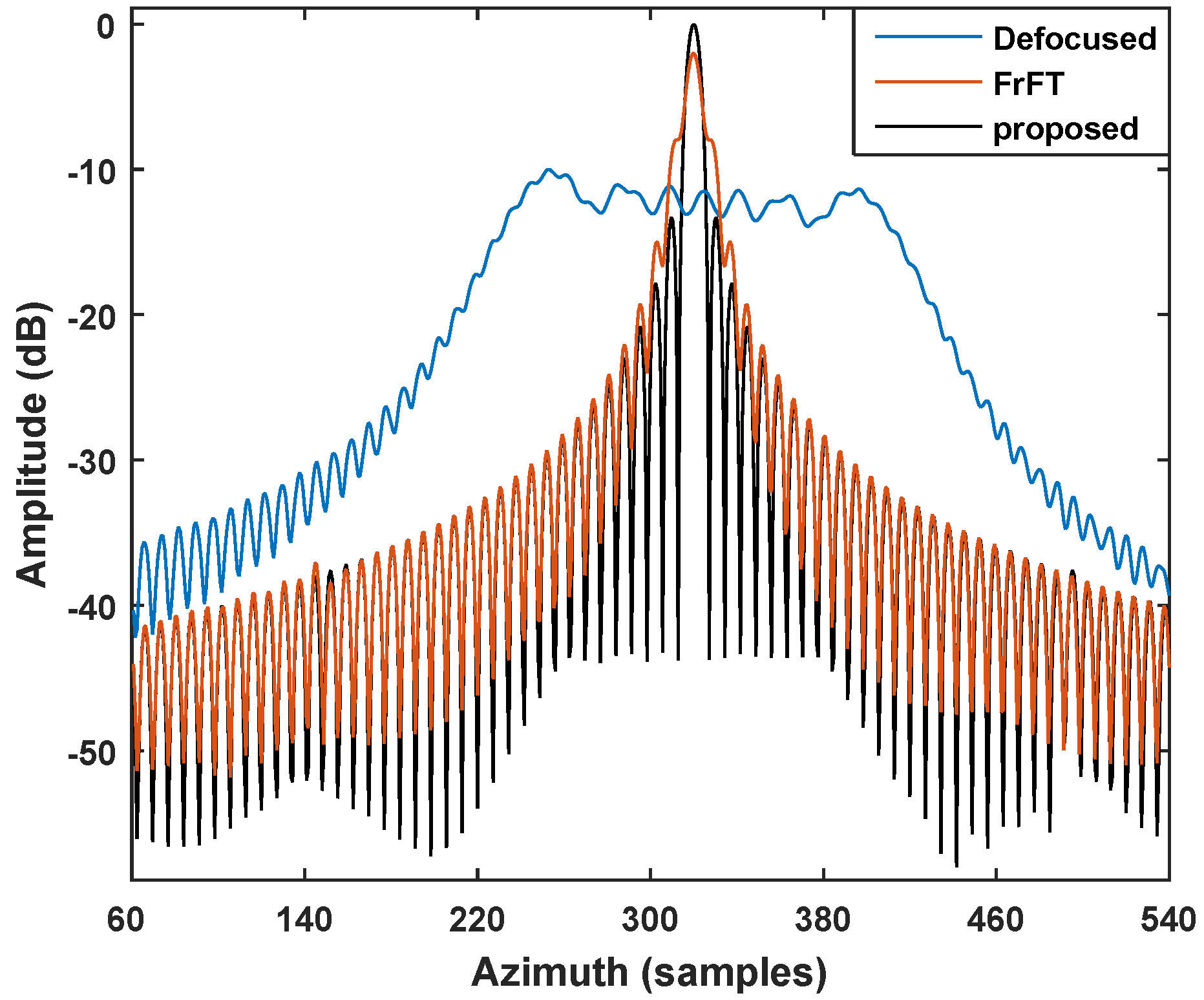
4. Experiments
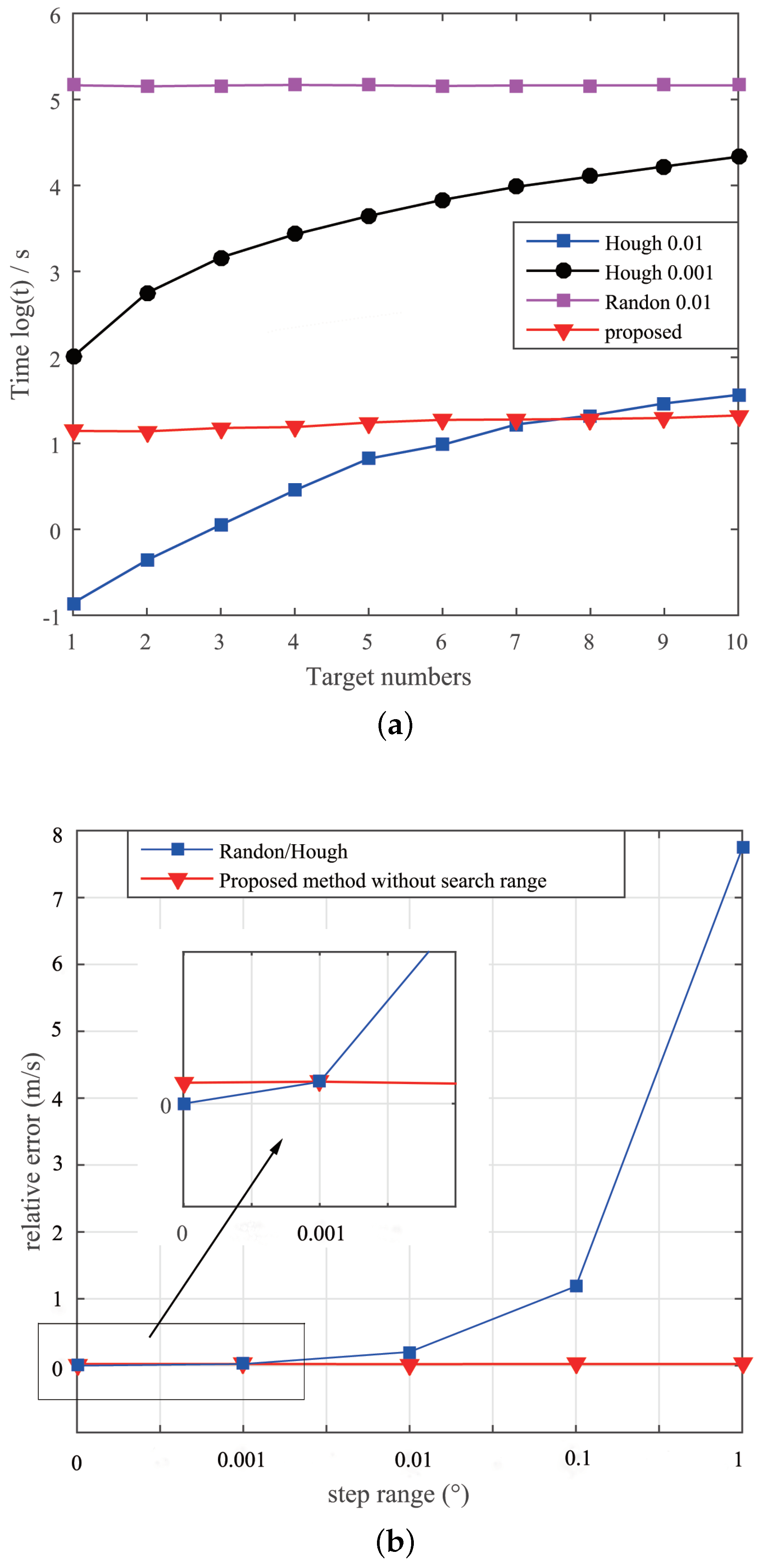
4.1. The Analysis of Parameters Error
4.2. Performance Comparison
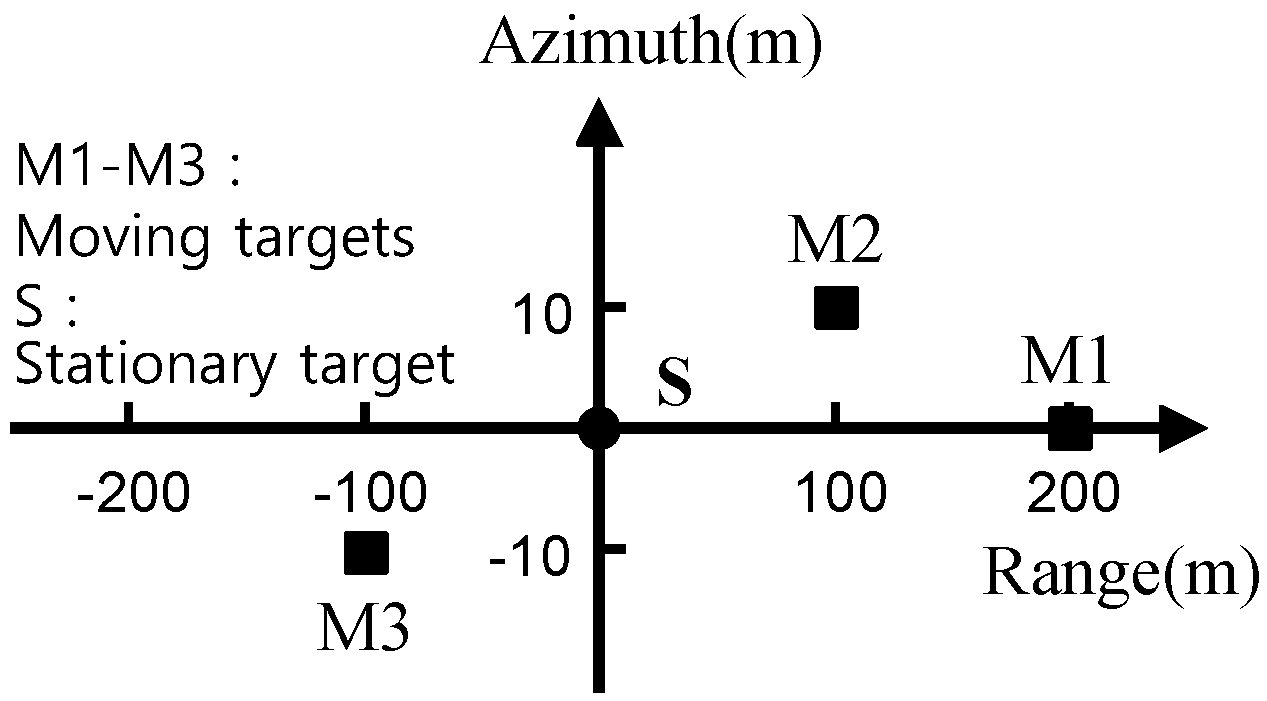
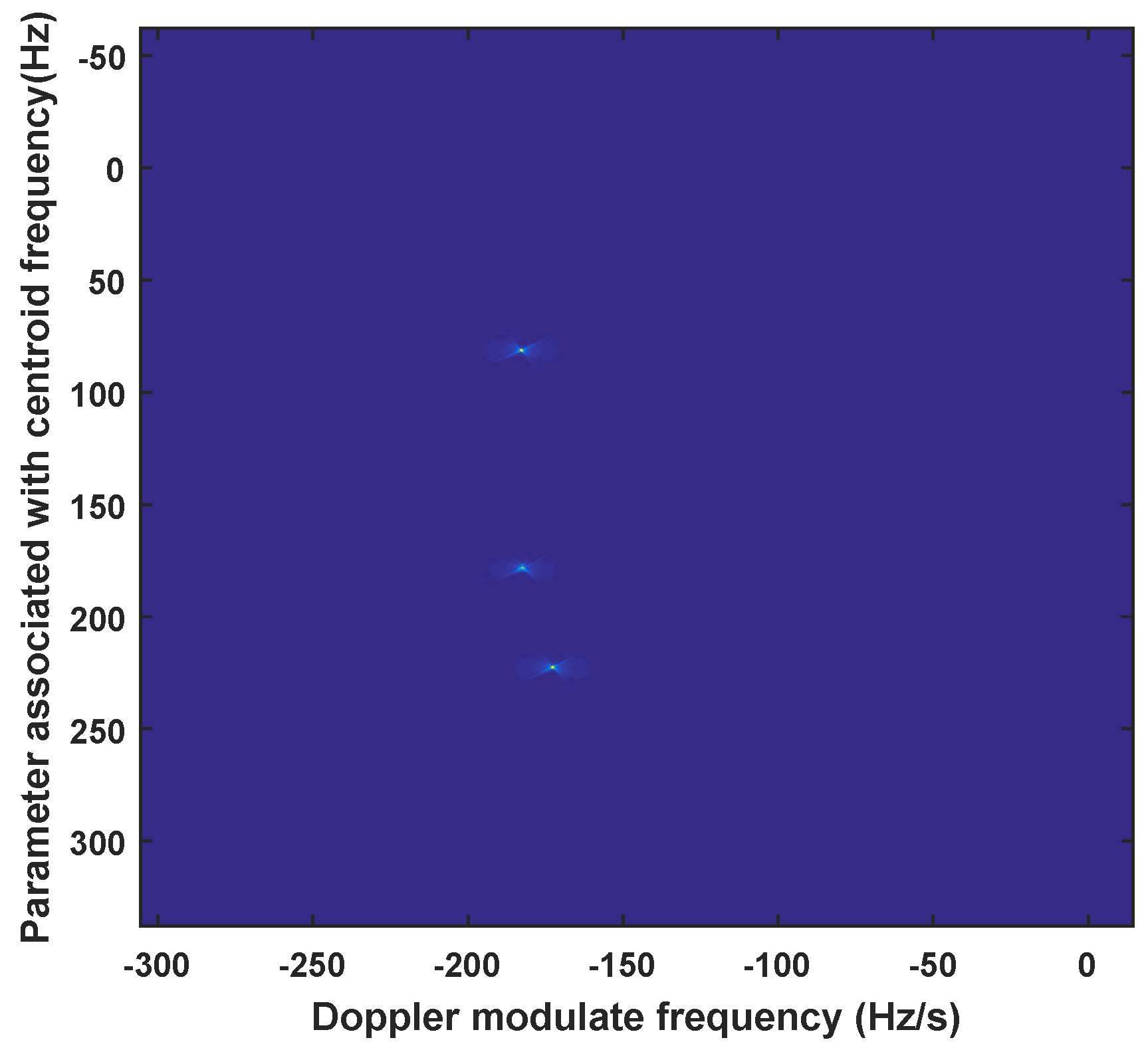
4.3. Simulated Data Processing
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Yang, J.; Liu, C.; Wang, Y. Imaging and Parameter Estimation of Fast-Moving Targets With Single-Antenna SAR. IEEE Geosci. Remote Sens. Lett. 2013, 11, 529–533. [Google Scholar] [CrossRef]
- Jin, T.; Qiu, X.; Hu, D.; Ding, C. An ml-based radial velocity estimation algorithm for moving targets in spaceborne high-resolution and wide-swath sar systems. Remote Sens. 2017, 9, 404. [Google Scholar] [CrossRef]
- Zhu, S.; Liao, G.; Qu, Y.; Zhou, Z.; Liu, X. Ground Moving Targets Imaging Algorithm for Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 2010, 49, 462–477. [Google Scholar] [CrossRef]
- Gao, G.; Shi, G. The CFAR Detection of Ground Moving Targets Based on a Joint Metric of SAR Interferogram’s Magnitude and Phase. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3618–3624. [Google Scholar] [CrossRef]
- Gao, G.; Shi, G.; Yang, L.; Zhou, S. Moving target detection based on the spreading characteristics of SAR interferograms in the magnitude-phase plane. IEEE Trans. Remote Sens. 2015, 7, 1836–1854. [Google Scholar] [CrossRef]
- Sun, G.; Xing, M.; Xia, X.G.; Wu, Y.; Bao, Z. Robust Ground Moving-Target Imaging Using Deramp-Keystone Processing. IEEE Trans. Geosci. Remote Sens. 2013, 51, 966–982. [Google Scholar] [CrossRef]
- Hansen, R.E.; Sabo, T.O.; Synnes, S.A.; Lorentzen, O.E. Synthetic aperture sonar interferometry for detailed seabed mapping: Performance considerations. J. Acoust. Soc. Am. 2017, 141, 4004. [Google Scholar] [CrossRef]
- Hooper, A. A multi-temporal InSAR method incorporating both persistent scatterer and small baseline approaches. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Plank, S.; Martinis, S.; Twele, A. Rapid Landslide Mapping by Means of Post-Event Polarimetric SAR Imagery. In Proceedings of the Conference on Living Planet Symposium, Prague, Czech Republic, 9–13 May 2016; Volume 740, p. 307. [Google Scholar]
- Yang, L.; Bi, G.; Xing, M.; Zhang, L. Airborne sar moving target signatures and imagery based on LVD. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5958–5971. [Google Scholar] [CrossRef]
- Dragosevic, M.V.; Burwash, W.; Shen, C. Detection and estimation with radarsat-2 moving-object detection experiment modes. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3527–3543. [Google Scholar] [CrossRef]
- Sikaneta, I.C.; Chouinard, J.Y. Eigendecomposition of the multi-channel covariance matrix with applications to SAR-GMTI. Signal Process. 2004, 84, 1501–1535. [Google Scholar] [CrossRef]
- Baumgartner, S.V.; Krieger, G. Experimental Verification of High-Resolution Wide-Swath Moving Target Indication. In Proceedings of the 9th European Conference on Synthetic Aperture Radar (EUSAR), Nuremberg, Germany, 23–26 April 2008; pp. 437–440. [Google Scholar]
- Yang, T.L.; Wang, Y. A novel algorithm to estimate moving target velocity for a spaceborne HRWS SAR/GMTI system. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3242–3245. [Google Scholar]
- Wang, X.Y.; Wang, R.; Li, N.; Zhou, C. A velocity estimation method of moving target for HRWS SAR. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 6819–6822. [Google Scholar]
- Zhang, S.X.; Xing, M.D.; Xia, X.G.; Guo, R.; Liu, Y.Y.; Bao, Z. Robust clutter suppression and moving target imaging approach for multichannel in azimuth high-resolution and wide-swath synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 2014, 53, 687–709. [Google Scholar] [CrossRef]
- Wu, Q.; Xing, M.; Qiu, C.; Liu, B.; Bao, Z.; Yeo, T.S. Motion parameter estimation in the sar system with low prf sampling. IEEE Geosci. Remote Sens. Lett. 2010, 7, 450–454. [Google Scholar] [CrossRef]
- Zhang, S.X.; Xing, M.D.; Xia, X.G.; Guo, R.; Liu, Y.Y.; Bao, Z. A novel moving target imaging algorithm for hrws sar based on local maximum-likelihood minimum entropy. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5333–5348. [Google Scholar] [CrossRef]
- Wang, L.B.; Wang, D.W.; Li, J.J.; Xu, J.; Xie, C.; Wang, L. Ground moving target detection and imaging using a virtual multichannel scheme in hrws mode. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5028–5043. [Google Scholar] [CrossRef]
- Jao, J.K. Theory of synthetic aperture radar imaging of a moving target. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1984–1992. [Google Scholar]
- Arii, M. Efficient motion compensation of a moving object on sar imagery based on velocity correlation function. IEEE Trans. Geosci. Remote Sens. 2014, 52, 936–946. [Google Scholar] [CrossRef]
- Budillon, A.; Pascazio, V.; Schirinzi, G. Moving targets detection and velocity estimation via multi-channel along-track interferometry. In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Seoul, Korea, 25–29 July 2005; pp. 2672–2675. [Google Scholar]
- Wang, H.S.C. Mainlobe clutter cancellation by DPCA for space-based radars. In Proceedings of the IEEE Aerospace Applications Conference, Crested Butte, CO, USA, 3–8 February 1991. [Google Scholar]
- Hou, Y.; Wang, J.; Liu, X.; Wang, K.; Gao, Y. An automatic SAR-GMTI algorithm based on DPCA. In Proceedings of the 2014 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 13–18 July 2014; pp. 592–595. [Google Scholar]
- Vu, V.T.; Sjogren, T.K.; Pettersson, M.I. Space time adaptive processing for moving target detection and imaging in bistatic SAR. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Sendai, Japan, 31 July–5 August 2014; pp. 592–595. [Google Scholar]
- Cerutti-Maori, D.; Sikaneta, I. Optimum GMTI processing for space-based SAR/GMTI systems-theoretical derivation. In Proceedings of the EUSAR, Aachen, Germany, 7–10 June 2010; pp. 1–4. [Google Scholar]
- Raney, R.K. Synthetic aperture imaging radar and moving targets. IEEE Trans. Aerosp. Electron. Syst. 1971, 7, 499–505. [Google Scholar] [CrossRef]
- Guo, B.; Vu, D.; Xu, L.; Xue, M.; Li, J. Ground moving target indication via multichannel airborne SAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3753–3764. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, X.; Li, H.; Wang, Z.; Zhuang, Y. Detection and imaging of moving objects with multichannel SAR system. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 2417–2420. [Google Scholar]
- Wang, G.; Xia, X.G.; Chen, V.C.; Fielder, R.L. Detection, location, and imaging of fast moving targets using multifrequency antenna array SAR. SPIE Proc. 2004, 40, 345–355. [Google Scholar]
- Tan, K.; Li, W. Imaging and parameter estimating for fast moving targets in airborne SAR. IEEE Trans. Comput. Imaging 2017, 3, 126–140. [Google Scholar] [CrossRef]
- Perry, R.P.; Dipietro, R.C.; Fante, R.L. SAR imaging of moving targets. IEEE Trans. Aerosp. Electr. Syst. 1999, 35, 188–200. [Google Scholar] [CrossRef]
- Zhou, F.; Wu, R.; Xing, M.; Bao, Z. Approach for single channel sar ground moving target imaging and motion parameter estimation. IET Radar Sonar Navig. 2007, 1, 59–66. [Google Scholar] [CrossRef]
- Li, G.; Xia, X.G.; Peng, Y.N. Doppler keystone transform: An approach suitable for parallel implementation of sar moving target imaging. IEEE Geosci. Remote Sens. Lett. 2008, 5, 573–577. [Google Scholar] [CrossRef]
- Yang, J.; Huang, X.; Tian, J.; Thompson, J.; Zhou, Z. New approach for sar imaging of ground moving targets based on a keystone transform. IEEE Geosci. Remote Sens. Lett. 2011, 8, 829–833. [Google Scholar]
- Zhu, D.; Li, Y.; Zhu, Z. A keystone transform without interpolation for sar ground moving-target imaging. IEEE Geosci. Remote Sens. Lett. 2007, 4, 18–22. [Google Scholar] [CrossRef]
- Kong, Y.K.; Cho, B.L.; Kim, Y.S. Ambiguity-free doppler centroid estimation technique for airborne sar using the radon transform. IEEE Trans. Geosci. Remote Sens. 2005, 43, 715–721. [Google Scholar] [CrossRef]
- Xu, R.; Zhang, D.; Hu, D.; Qiu, X.; Ding, C. A novel motion parameter estimation algorithm of fast moving targets via single-antenna airborne SAR system. IEEE Geosci. Remote Sens. Lett. 2012, 9, 920–924. [Google Scholar]
- Zhu, S.; Liao, G.; Qu, Y.; Liu, X.; Zhou, Z. A new slant-range velocity ambiguity resolving approach of fast moving targets for SAR system. IEEE Trans. Geosci. Remote Sens. 2009, 48, 432–451. [Google Scholar]
- Cumming, I.G.; Li, S. Improved slope estimation for sar doppler ambiguity resolution. IEEE Trans. Geosci. Remote Sens. 2006, 44, 707–718. [Google Scholar] [CrossRef]
- Yang, J.; Liu, C.; Wang, Y. Detection and imaging of ground moving targets with real SAR data. IEEE Trans. Geosci. Remote Sens. 2015, 53, 920–932. [Google Scholar] [CrossRef]
- Hou, L.; Song, H.; Zheng, M.; Wang, W. Fast moving target imaging and motion parameters estimation based on radon transform and bi-directional approach. IET Radar Sonar Navig. 2016, 10, 1013–1023. [Google Scholar] [CrossRef]
- Li, W.; Yang, J.; Huang, Y. Improved doppler parameter estimation of squint SAR based on slope detection. Int. J. Remote Sens. 2014, 35, 1417–1431. [Google Scholar] [CrossRef]
- Xia, X.G.; Chen, V.C. A quantitative snr analysis for the pseudo Wigner-Ville distribution. IEEE Trans. Signal Process. 1999, 47, 2891–2894. [Google Scholar]
- Almeida, L.B. The fractional fourier transform and time-frequency representations. IEEE Trans. Signal Process. 1994, 42, 3084–3091. [Google Scholar] [CrossRef]
- Lv, X.; Bi, G.; Wan, C.; Xing, M. Lv’s distribution: Principle, implementation, properties, and performance. IEEE Trans. Signal Process. 2011, 59, 3576–3591. [Google Scholar] [CrossRef]
- Gioi, R.G.V.; Jakubowicz, J.; Morel, J.M.; Randall, G. On straight line segment detection. J. Math. Imaging Vis. 2008, 59, 3576–3591. [Google Scholar]
- Yu, W.; Su, W.; Gu, H. Fast method for radar maneuvering target detection and motion parameter estimation. Multidimens. Syst. Signal Process. 2017, 4, 1–15. [Google Scholar] [CrossRef]
- Yang, L.; Zhao, L.; Bi, G.; Zhang, L. Sar ground moving target imaging algorithm based on parametric and dynamic sparse bayesian learning. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2254–2267. [Google Scholar] [CrossRef]
- Yu, W.; Su, W.; Gu, H. Ground moving target motion parameter estimation using radon modified lv’s distribution. Digit. Signal Process. 2017, 69, 212–223. [Google Scholar] [CrossRef]
- Yu, W.; Su, W.; Gu, H. Ground maneuvering target detection based on discrete polynomial-phase transform and Lv’s distribution. Signal Process. 2018, 144, 364–372. [Google Scholar] [CrossRef]
- Gioi, R.G.V.; Jakubowicz, J.; Morel, J.M.; Randall, G. Lsd: A line segment detector. Image Process. Line 2012, 2, 35–55. [Google Scholar] [CrossRef]

| Vreal | Vestimate | |||
|---|---|---|---|---|
| 25 m/s | searching ranges | |||
| 1° | 0.1° | 0.01° | 0.001° | |
| 32.7382214 m/s | 26.18674612 m/s | 25.20426081 m/s | 25.02414457 m/s | |
| Parameter Name | Value |
|---|---|
| carrier Frequency | 9.6 GHz |
| pulse time width | 4 µs |
| pulse bandwidth | 80 MHz |
| nearest slant range | 7500 m |
| pulse repetition frequency | 1000 Hz |
| platform velocity | 150 m/s |
| Vr (m/s) | Vx (m/s) | (m/s) | (m/s) | |
|---|---|---|---|---|
| M1 | 10 | 10 | 9.9975 | 10.0123 |
| M2 | 25 | 5 | 24.9964 | 5.0215 |
| M3 | 10 | 3 | 9.9973 | 3.0118 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Han, S.; Yang, J.; Zhang, L.; Xu, H.; Wang, J. A Novel Approach of Slope Detection Combined with Lv’s Distribution for Airborne SAR Imagery of Fast Moving Targets. Remote Sens. 2018, 10, 764. https://doi.org/10.3390/rs10050764
Zhao Y, Han S, Yang J, Zhang L, Xu H, Wang J. A Novel Approach of Slope Detection Combined with Lv’s Distribution for Airborne SAR Imagery of Fast Moving Targets. Remote Sensing. 2018; 10(5):764. https://doi.org/10.3390/rs10050764
Chicago/Turabian StyleZhao, Yuefeng, Shengliang Han, Jimin Yang, Liren Zhang, Huaqiang Xu, and Jingjing Wang. 2018. "A Novel Approach of Slope Detection Combined with Lv’s Distribution for Airborne SAR Imagery of Fast Moving Targets" Remote Sensing 10, no. 5: 764. https://doi.org/10.3390/rs10050764
APA StyleZhao, Y., Han, S., Yang, J., Zhang, L., Xu, H., & Wang, J. (2018). A Novel Approach of Slope Detection Combined with Lv’s Distribution for Airborne SAR Imagery of Fast Moving Targets. Remote Sensing, 10(5), 764. https://doi.org/10.3390/rs10050764





