Detecting Trends in Wetland Extent from MODIS Derived Soil Moisture Estimates
Abstract
1. Introduction
1.1. Background and Objective
1.2. Optical Soil Moisture Detection
1.3. Validation of Satellite Derived Soil Moisture Products
1.4. Trend Detection
2. Materials and Methods
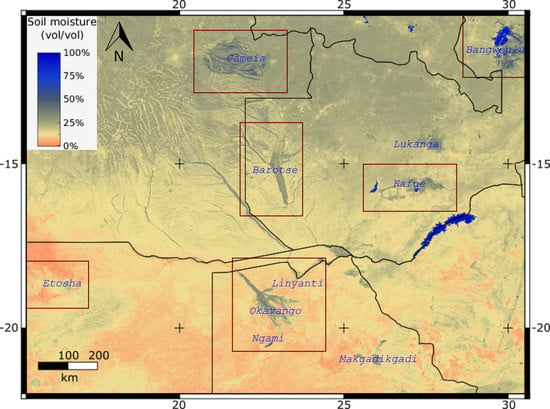
2.1. Datasets
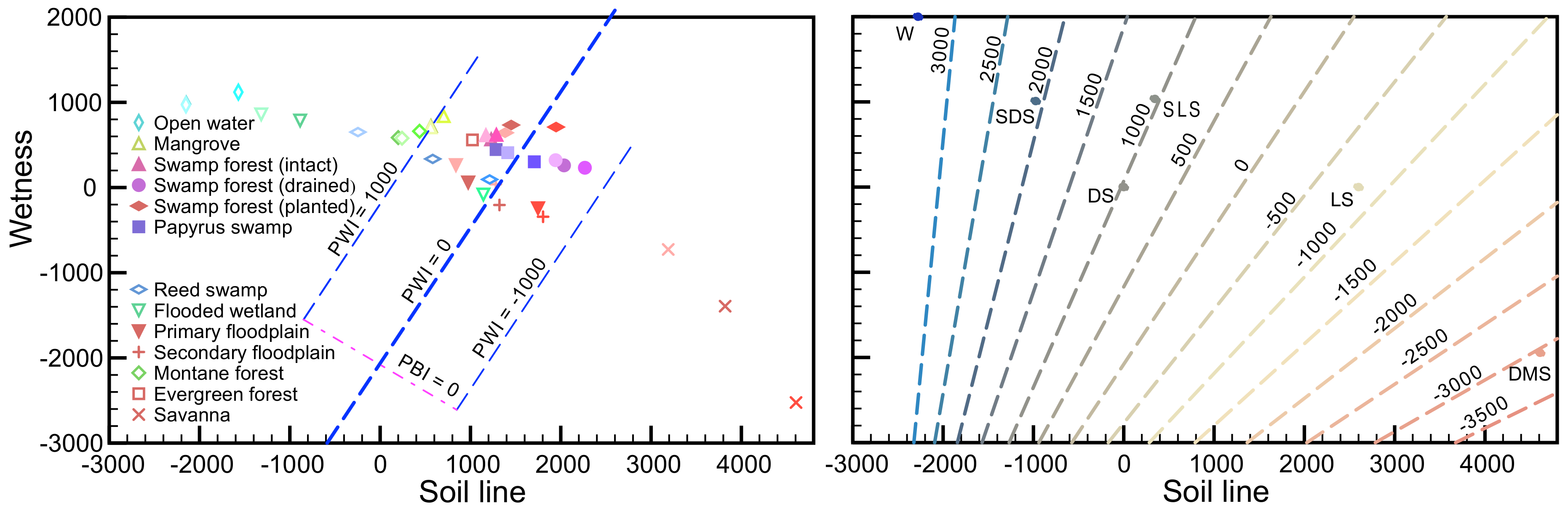
2.2. Defining the Transformed Wetness Index (TWI)
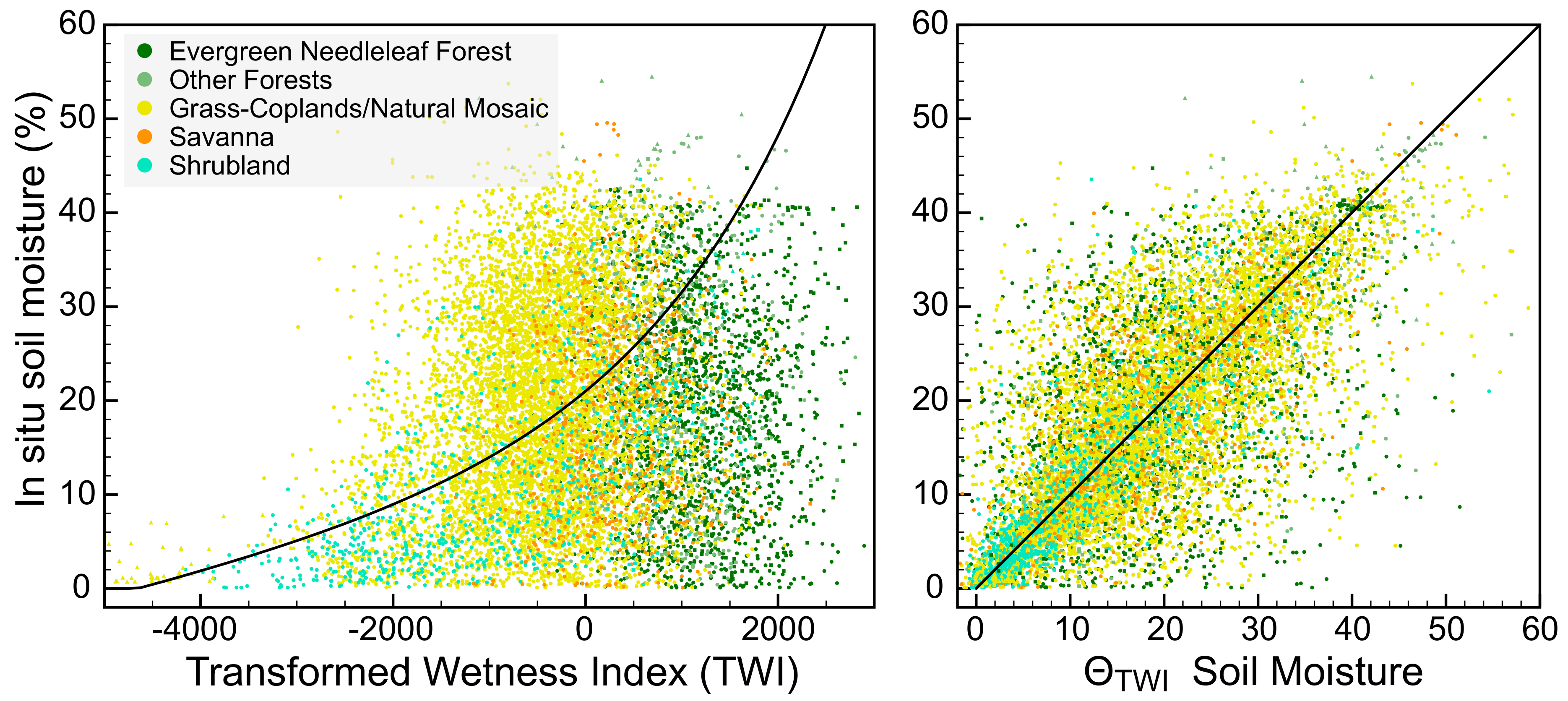
2.3. TWI Performance Validation
2.4. TWI Compared to Microwave Soil-Moisture Products
2.5. Trend Detection
3. Results
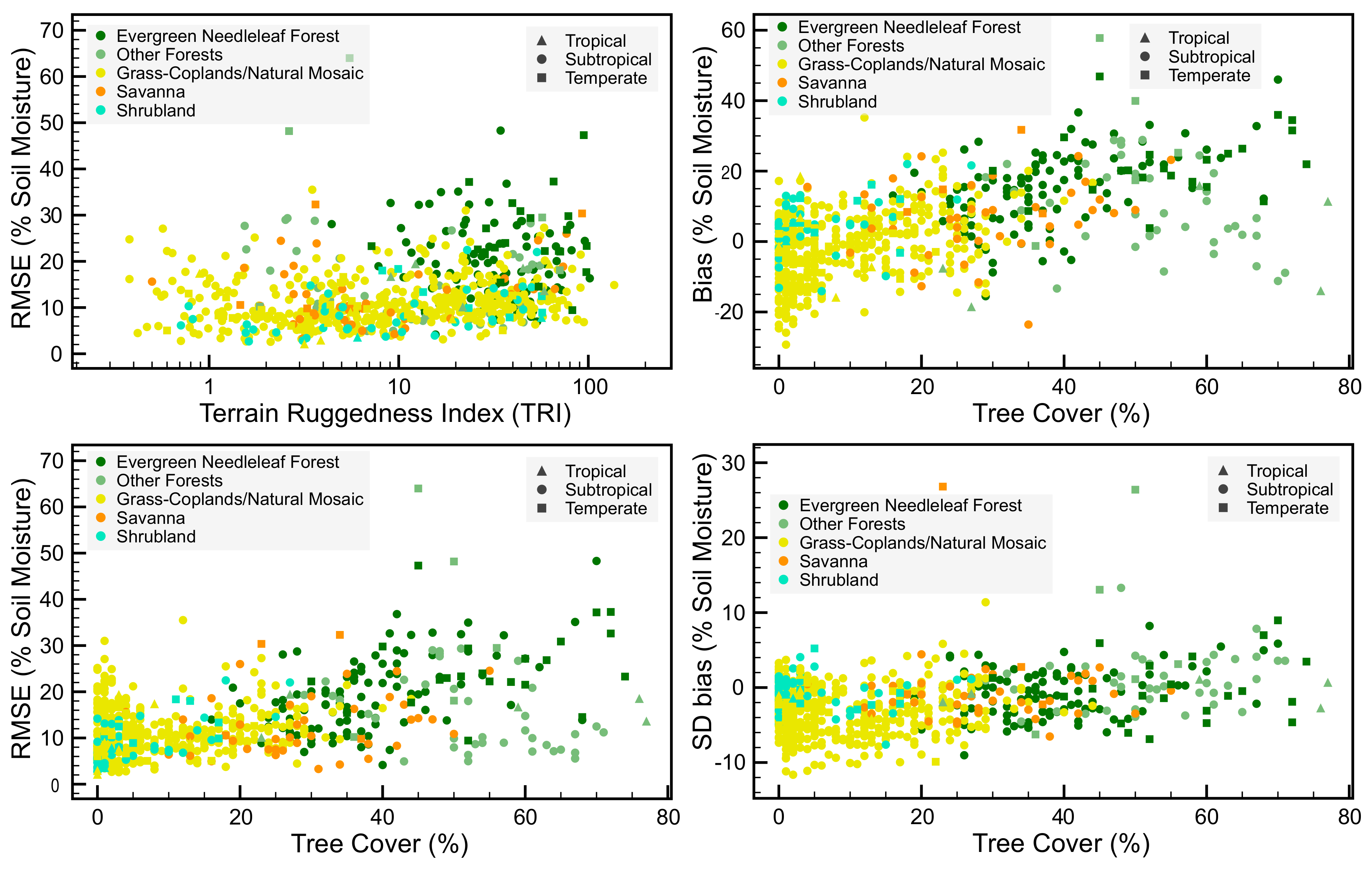
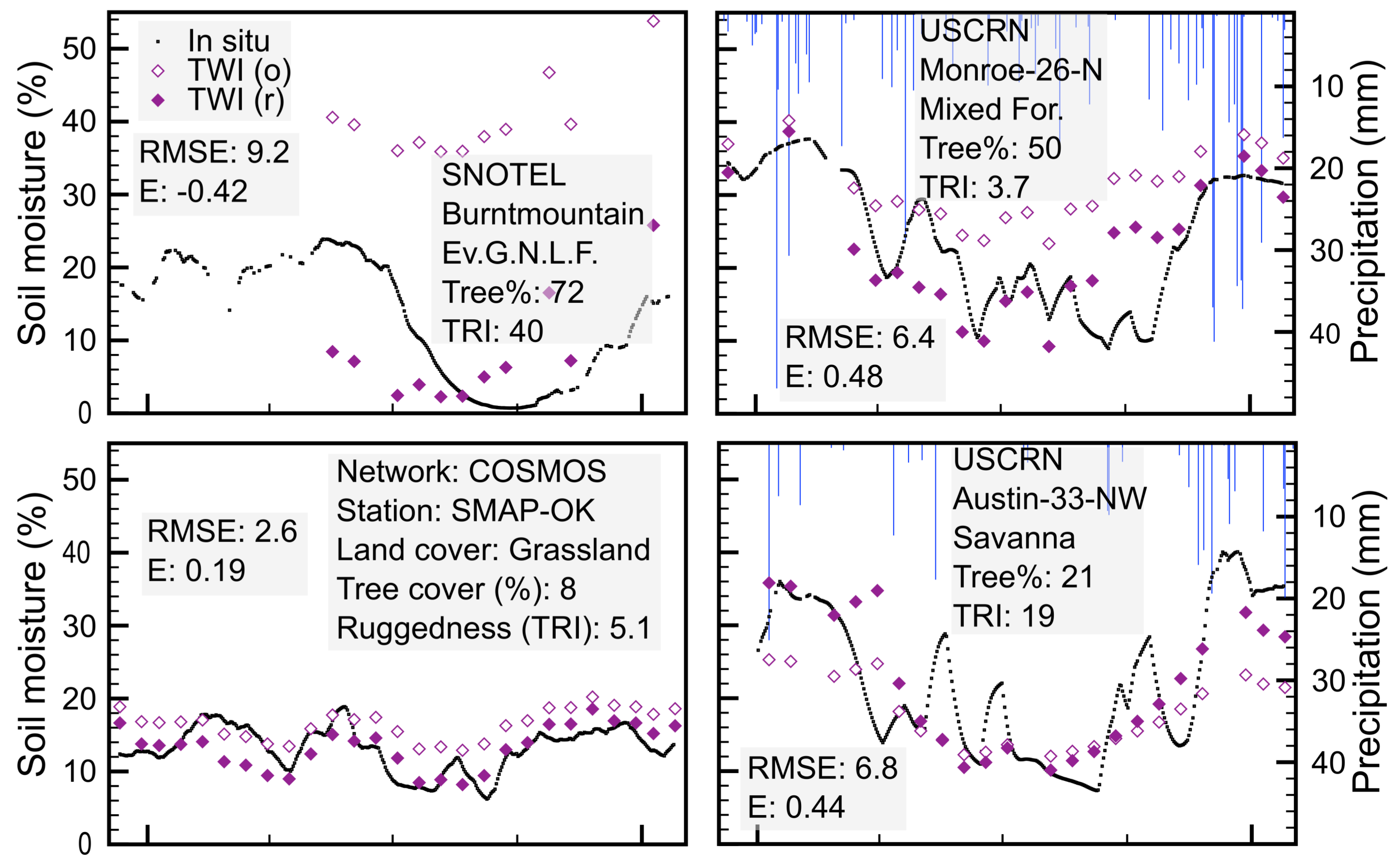
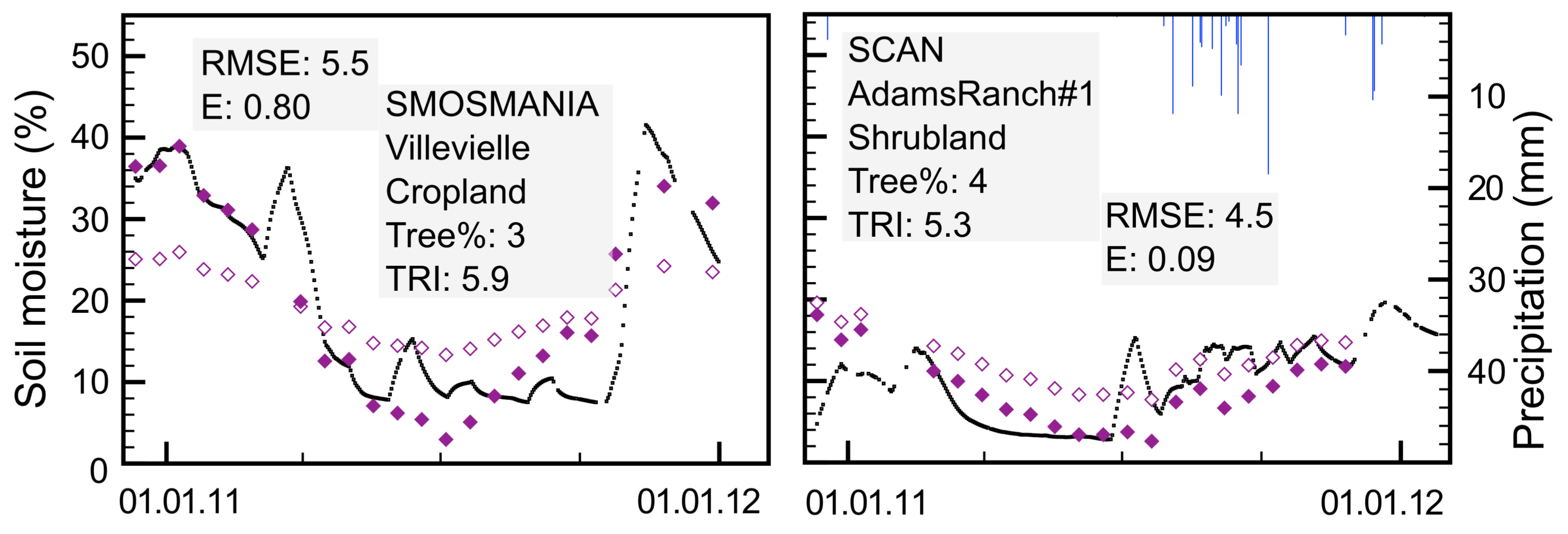
3.1. Model Performance
3.2. Comparison with Microwave Soil Moisture Products
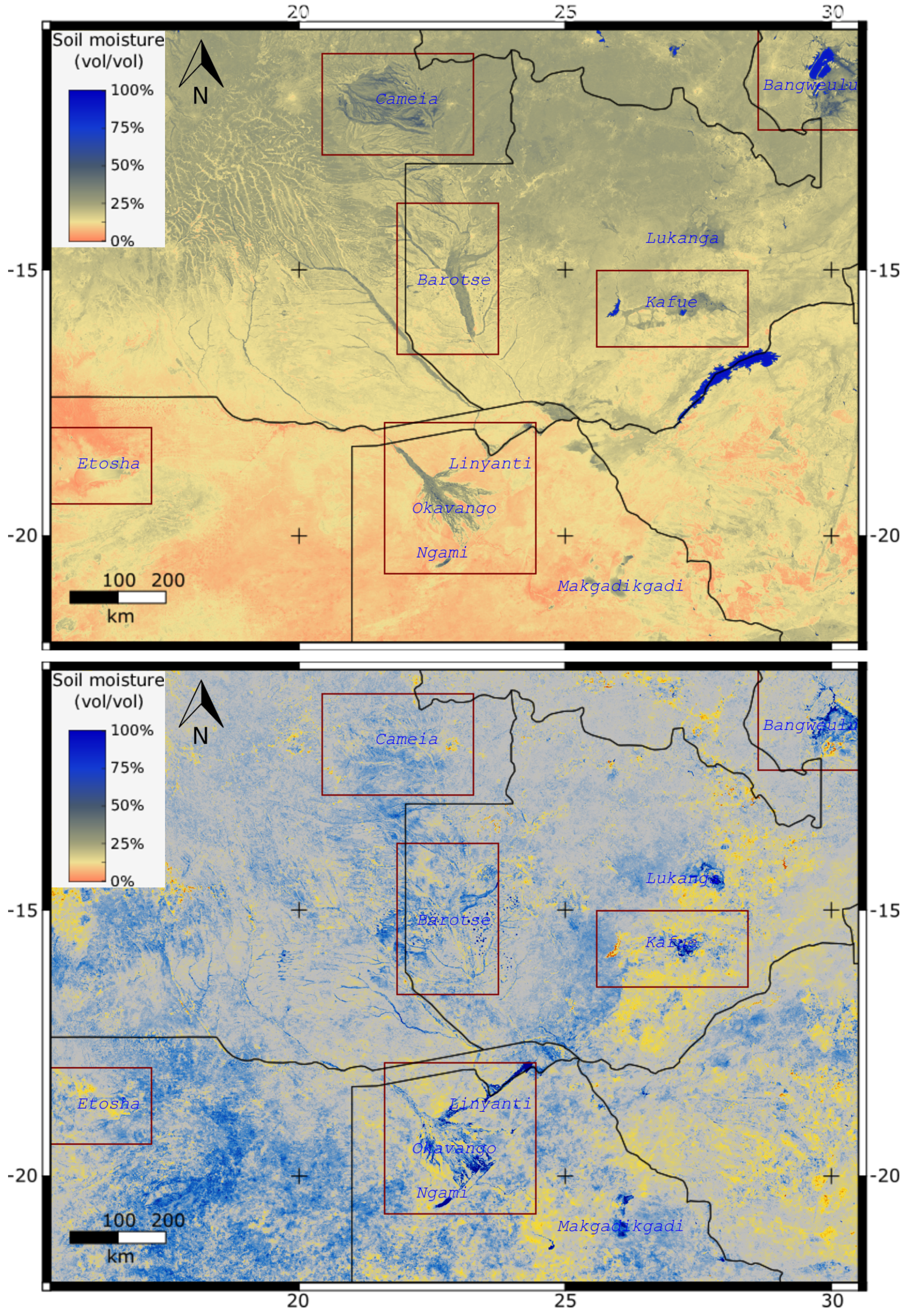
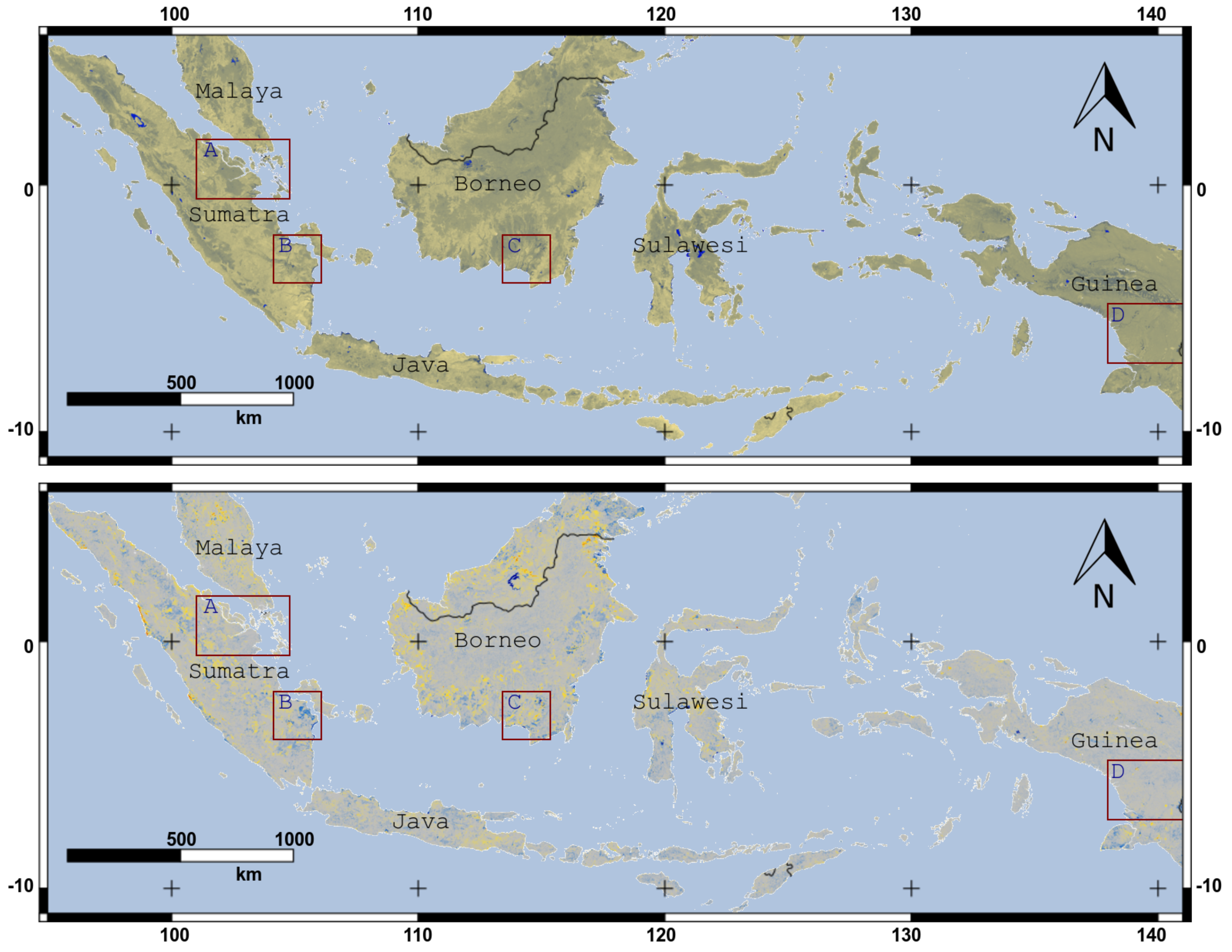
3.3. Soil Moisture Trends
4. Discussion
4.1. Model Performance
4.2. Comparison with Microwave Soil Moisture Products
4.3. Soil Moisture Trends
4.4. Further Development
5. Conclusions
Supplementary Materials
Acknowledgments
Conflicts of Interest
References
- He, L.; Chen, J.M.; Liu, J.; Bélair, S.; Luo, X. Assessment of SMAP soil moisture for global simulation of gross primary production. J. Geophys. Res. Biogeosci. 2017, 122, 1549–1563. [Google Scholar] [CrossRef]
- Prigent, C.; Matthews, E.; Aires, F.; Rossow, W.B. Remote sensing of global wetland dynamics with multiple satellite data sets. Geophys. Res. Lett. 2001, 28, 4631–4634. [Google Scholar] [CrossRef]
- Papa, F.; Prigent, C.; Aires, F.; Jimenez, C.; Rossow, W.B.; Matthews, E. Interannual variability of surface water extent at the global scale, 1993–2004. J. Geophys. Res. 2010, 115, D12111. [Google Scholar] [CrossRef]
- Rodell, M. Satellite Gravimetry Applied to Drought Monitoring. In Remote Sensing of Drought; Wardlow, B.D., Anderson, M.C., Verdin, J.P., Eds.; CRC Press, Taylor & Francis: Boca Raton, FL, USA, 2012; Chapter 11; pp. 261–277. [Google Scholar]
- Moran, S.M.; Peters-Lidard, C.D.; Watts, J.M.; McElroy, S. Estimating soil moisture at the watershed scale with satellite-based radar and land surface models. Can. J. Remote Sens. 2004, 30, 805–826. [Google Scholar] [CrossRef]
- Wagner, W.; Blöschl, G.; Pampaloni, P.; Calvet, J.C.; Bizzarri, B.; Wigneron, J.P.; Kerr, Y. Operational readiness of microwave remote sensing of soil moisture for hydrologic applications. Nord. Hydrol. 2007, 38, 1. [Google Scholar] [CrossRef]
- Nghiem, S.V.; Wardlow, B.D.; Allured, D.; Svoboda, M.D.; LeComte, D.; Rosencrans, M.; Chan, S.K.; Neumann, G. Microwave Remote Sensing of Soil Moisture, Science and applications. In Remote Sensing of Drought; Wardlow, B.D., Anderson, M.C., Verdin, J.P., Eds.; CRC Press; Taylor & Franciss: Boca Raton, FL, USA, 2012; Chapter 9; pp. 197–226. [Google Scholar]
- He, L.; Chen, J.M.; Chen, K.S. Simulation and SMAP Observation of Sun-Glint Over the Land Surface at the L-Band. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2589–2604. [Google Scholar] [CrossRef]
- Kerr, Y.; Waldteufel, P.; Wigneron, J.P.; Martinuzzi, J.; Font, J.; Berger, M. Soil moisture retrieval from space: The Soil Moisture and Ocean Salinity (SMOS) mission. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1729–1735. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS Mission: New Tool for Monitoring Key Elements of the Global Water Cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Njoku, E.; Jackson, T.; Lakshmi, V.; Chan, T.; Nghiem, S. Soil moisture retrieval from AMSR-E. IEEE Trans. Geosci. Remote Sens. 2003, 41, 215–229. [Google Scholar] [CrossRef]
- Merzouki, A.; McNairn, H.; Pacheco, A. Mapping Soil Moisture Using RADARSAT-2 Data and Local Autocorrelation Statistics. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 128–137. [Google Scholar] [CrossRef]
- Chan, S.; Bindlish, R.; O’Neill, P.; Jackson, T.; Njoku, E.; Dunbar, S.; Chaubell, J.; Piepmeier, J.; Yueh, S.; Entekhabi, D.; et al. Development and assessment of the SMAP enhanced passive soil moisture product. Remote Sens. Environ. 2018, 204, 931–941. [Google Scholar] [CrossRef]
- Cui, C.; Xu, J.; Zeng, J.; Chen, K.S.; Bai, X.; Lu, H.; Chen, Q.; Zhao, T. Soil Moisture Mapping from Satellites: An Intercomparison of SMAP, SMOS, FY3B, AMSR2, and ESA CCI over Two Dense Network Regions at Different Spatial Scales. Remote Sens. 2017, 10, 33. [Google Scholar] [CrossRef]
- Gallant, A. The Challenges of Remote Monitoring of Wetlands. Remote Sens. 2015, 7, 10938–10950. [Google Scholar] [CrossRef]
- Lang, M.; Bourgeau-Chavez, L.; Tiner, R.; Klemas, V. Advances in remotely sensed data and techniques for wetland mapping and monitoring. In Remote Sensing of Wetlands: Applications And Advances; Tiner, R., Lang, M., Klemas, V., Eds.; CRC Press: Boca Raton, FL, USA, 2015; Chapter 5; pp. 79–117. [Google Scholar]
- Gumbricht, T. Hybrid Mapping of Pantropical Wetlands from Optical Satellite Images, Hydrology, and Geomorphology. In Remote Sensing of Wetlands: Applications and Advances; Tiner, R.W., Lang, M.W., Klemas, V.V., Eds.; CRC Press: Boca Raton, FL, USA, 2015; Chapter 20; pp. 433–452. [Google Scholar]
- Gumbricht, T.; Roman-Cuesta, R.M.; Verchot, L.; Herold, M.; Wittmann, F.; Householder, E.; Herold, N.; Murdiyarso, D. An expert system model for mapping tropical wetlands and peatlands reveals South America as the largest contributor. Glob. Chang. Biol. 2017, 23, 3581–3599. [Google Scholar] [CrossRef] [PubMed]
- Ordoyne, C.; Friedl, M.A. Using MODIS data to characterize seasonal inundation patterns in the Florida Everglades. Remote Sens. Environ. 2008, 112, 4107–4119. [Google Scholar] [CrossRef]
- Landmann, T.; Schramm, M.; Colditz, R.R.; Dietz, A.; Dech, S. Wide Area Wetland Mapping in Semi-Arid Africa Using 250-Meter MODIS Metrics and Topographic Variables. Remote Sens. 2010, 2, 1751–1766. [Google Scholar] [CrossRef]
- Aires, F.; Papa, F.; Prigent, C.; Crétaux, J.F.; Berge-Nguyen, M. Characterization and space/time downscaling of the inundation extent over the Inner Niger Delta using GIEMS and MODIS data. J. Hydrometeorol. 2013, 15, 171–192. [Google Scholar] [CrossRef]
- Aires, F.; Prigent, C.; Papa, F. Downscaling of inundation extents. In Proceedings of the EGU General Assembly, Vienna, Austria, 27 April–2 May 2014; Volume 16, p. 11668. [Google Scholar]
- Aires, F.; Miolane, L.; Prigent, C.; Pham, B.; Fluet-Chouinard, E.; Lehner, B.; Papa, F. A Global Dynamic Long-Term Inundation Extent Dataset at High Spatial Resolution Derived through Downscaling of Satellite Observations. J. Hydrometeorol. 2017, 18, 1305–1325. [Google Scholar] [CrossRef]
- Merlin, O.; Al Bitar, A.; Walker, J.P.; Kerr, Y. An improved algorithm for disaggregating microwave-derived soil moisture based on red, near-infrared and thermal-infrared data. Remote Sens. Environ. 2010, 114, 2305–2316. [Google Scholar] [CrossRef]
- Merlin, O.; Rudiger, C.; Al Bitar, A.; Richaume, P.; Walker, J.P.; Kerr, Y.H. Disaggregation of SMOS Soil Moisture in Southeastern Australia. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1556–1571. [Google Scholar] [CrossRef]
- Piles, M.; Camps, A.; Vall-llossera, M.; Corbella, I.; Panciera, R.; Rüdiger, C.; Kerr, Y.H.; Walker, J. Downscaling SMOS-Derived Soil Moisture Using MODIS Visible/Infrared Data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3156–3166. [Google Scholar] [CrossRef]
- Gillies, R.R.; Carlson, T.N. Thermal Remote Sensing of Surface Soil Water Content with Partial Vegetation Cover for Incorporation into Climate Models. J. Appl. Meteorol. 1995, 34, 745–756. [Google Scholar] [CrossRef]
- Petropoulos, G.; Carlson, T.; Wooster, M.; Islam, S. A review of Ts/VI remote sensing based methods for the retrieval of land surface energy fluxes and soil surface moisture. Prog. Phys. Geogr. 2009, 33, 224–250. [Google Scholar] [CrossRef]
- Yang, Y.; Guan, H.; Long, D.; Liu, B.; Qin, G.; Qin, J.; Batelaan, O. Estimation of Surface Soil Moisture from Thermal Infrared Remote Sensing Using an Improved Trapezoid Method. Remote Sens. 2015, 7, 8250–8270. [Google Scholar] [CrossRef]
- Gumbricht, T. Soil Moisture Dynamics Estimated from MODIS Time Series Images. In Multitemporal Remote Sensing: Methods and Applications; Ban, Y., Ed.; Springer: Berlin, Germany, 2016; pp. 233–253. [Google Scholar]
- Muller, E.; Décamps, H. Modeling soil moisture-reflectance. Remote Sens. Environ. 2000, 76, 173–180. [Google Scholar] [CrossRef]
- Lobell, D.B.; Asner, G.P. Moisture Effects on Soil Reflectance. Soil Sci. Soc. Am. J. 2002, 66, 722–727. [Google Scholar] [CrossRef]
- Kaleita, A.L.; Tian, L.F.; Hirschi, M.C. Relationship Between Soil Moisture Content and Soil Surface Reflectance. Trans. ASAE 2005, 48, 1979–1986. [Google Scholar] [CrossRef]
- Gao, Z.; Xu, X.; Wang, J.; Yang, H.; Huang, W.; Feng, H. A method of estimating soil moisture based on the linear decomposition of mixture pixels. Math. Comput. Model. 2013, 58, 606–613. [Google Scholar] [CrossRef]
- Zhang, D.; Zhou, G. Estimation of Soil Moisture from Optical and Thermal Remote Sensing: A Review. Sensors 2016, 16, 1308. [Google Scholar] [CrossRef] [PubMed]
- Anne, N.J.; Abd-Elrahman, A.H.; Lewis, D.B.; Hewitt, N.A. Modeling soil parameters using hyperspectral image reflectance in subtropical coastal wetlands. Int. J. Appl. Earth Obs. Geoinf. 2014, 33, 47–56. [Google Scholar] [CrossRef]
- Ji, L.; Zhang, L.; Wylie, B. Analysis of Dynamic Thresholds for the Normalized Difference Water Index. Photogramm. Eng. Remote Sens. 2009, 75, 1307–1317. [Google Scholar] [CrossRef]
- Gao, B.C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Ceccato, P.; Gobron, N.; Flasse, S.; Pinty, B.; Tarantola, S. Designing a spectral index to estimate vegetation water content from remote sensing data: Part 1: Theoretical approach. Remote Sens. Environ. 2002, 82, 188–197. [Google Scholar] [CrossRef]
- Ceccato, P.; Flasse, S.; Grégoire, J.M. Designing a spectral index to estimate vegetation water content from remote sensing data: Part 2 Validation and application. Remote Sens. Environ. 2002, 82, 198–207. [Google Scholar] [CrossRef]
- Weidong, L.; Baret, F.; Xingfa, G.; Qingxi, T.; Lanfen, Z.; Bing, Z. Relating soil surface moisture to reflectance. Remote Sens. Environ. 2002, 81, 238–246. [Google Scholar] [CrossRef]
- Jackson, T.J.; Cosh, M.H.; Bindlish, R.; Starks, P.J.; Bosch, D.D.; Seyfried, M.; Goodrich, D.C.; Moran, M.S.; Du, J. Validation of Advanced Microwave Scanning Radiometer Soil Moisture Products. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4256–4272. [Google Scholar] [CrossRef]
- Reichle, R.H.; Koster, R.D. Bias reduction in short records of satellite soil moisture. Geophys. Res. Lett. 2004, 31, L19501. [Google Scholar] [CrossRef]
- Reichle, R.H.; Koster, R.D.; Liu, P.; Mahanama, S.P.P.; Njoku, E.G.; Owe, M. Comparison and assimilation of global soil moisture retrievals from the Advanced Microwave Scanning Radiometer for the Earth Observing System (AMSR-E) and the Scanning Multichannel Microwave Radiometer (SMMR). J. Geophys. Res. Atmos. 2007, 112, D09108. [Google Scholar] [CrossRef]
- Wagner, W.; Naeimi, V.; Scipal, K.; Jeu, R.; Martínez-Fernández, J. Soil moisture from operational meteorological satellites. Hydrogeol. J. 2007, 15, 121–131. [Google Scholar] [CrossRef]
- Draper, C.S.; Walker, J.P.; Steinle, P.J.; de Jeu, R.A.M.; Holmes, T.R.H. An evaluation of AMSR–E derived soil moisture over Australia. Remote Sens. Environ. 2009, 113, 703–710. [Google Scholar] [CrossRef]
- Dall’Amico, J.T.; Schlenz, F.; Loew, A.; Mauser, W. First Results of SMOS Soil Moisture Validation in the Upper Danube Catchment. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1507–1516. [Google Scholar] [CrossRef]
- Draper, C.; Reichle, R.; de Jeu, R.; Naeimi, V.; Parinussa, R.; Wagner, W. Estimating root mean square errors in remotely sensed soil moisture over continental scale domains. Remote Sens. Environ. 2013, 137, 288–298. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Pearson, K. Notes on regression and inheritance in the case of two parents. Proc. R. Soc. Lond. 1895, 58, 240–242. [Google Scholar] [CrossRef]
- Zreda, M.; Desilets, D.; Ferré, T.P.A.; Scott, R.L. Measuring soil moisture content non-invasively at intermediate spatial scale using cosmic-ray neutrons. Geophys. Res. Lett. 2008, 35, L21402. [Google Scholar] [CrossRef]
- Jha, M.K.; Singh, A.K. Trend analysis of extreme runoff events in major river basins of Peninsular Malaysia. Int. J. Water 2013, 7, 142. [Google Scholar] [CrossRef]
- Martinez, C.J.; Maleski, J.J.; Miller, M.F. Trends in precipitation and temperature in Florida, USA. J. Hydrol. 2012, 452-453, 259–281. [Google Scholar] [CrossRef]
- Modarres, R.; Sarhadi, A. Rainfall trends analysis of Iran in the last half of the twentieth century. J. Geophys. Res. 2009, 114, D03101. [Google Scholar] [CrossRef]
- Sonali, P.; Nagesh Kumar, D. Review of trend detection methods and their application to detect temperature changes in India. J. Hydrol. 2013, 476, 212–227. [Google Scholar] [CrossRef]
- Hu, Z.; Zhou, Q.; Chen, X.; Qian, C.; Wang, S.; Li, J. Variations and changes of annual precipitation in Central Asia over the last century. Int. J. Climatol. 2017, 37, 157–170. [Google Scholar] [CrossRef]
- Zhao, W.; Du, H.; Wang, L.; He, H.S.; Wu, Z.; Liu, K.; Guo, X.; Yang, Y. A comparison of recent trends in precipitation and temperature over Western and Eastern Eurasia. Q. J. R. Meteorol. Soc. 2018, 144, 604–613. [Google Scholar] [CrossRef]
- Sayemuzzaman, M.; Jha, M.K. Seasonal and annual precipitation time series trend analysis in North Carolina, United States. Atmos. Res. 2014, 137, 183–194. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245. [Google Scholar] [CrossRef]
- Muhlbauer, A.; Spichtinger, P.; Lohmann, U. Application and Comparison of Robust Linear Regression Methods for Trend Estimation. J. Appl. Meteorol. Climatol. 2009, 48, 1961–1970. [Google Scholar] [CrossRef]
- Theil, H. A Rank-Invariant Method of Linear and Polynomial Regression Analysis. Proc. R. Neth. Acad. Sci. 1950, 53, 386–392. [Google Scholar]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Ochsner, T.E.; Cosh, M.H.; Cuenca, R.H.; Dorigo, W.A.; Draper, C.S.; Hagimoto, Y.; Kerr, Y.H.; Njoku, E.G.; Small, E.E.; Zreda, M. State of the Art in Large-Scale Soil Moisture Monitoring. Soil Sci. Soc. Am. J. 2013, 77, 1888. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Wagner, W.; Hohensinn, R.; Hahn, S.; Paulik, C.; Xaver, A.; Gruber, A.; Drusch, M.; Mecklenburg, S.; van Oevelen, P.; et al. The International Soil Moisture Network: A data hosting facility for global in situ soil moisture measurements. Hydrol. Earth Syst. Sci. 2011, 15, 1675–1698. [Google Scholar] [CrossRef]
- Danielson, J.; Gesch, D. Global Multi-resolution Terrain Elevation Data 2010 (GMTED2010)—Open-File Report 2011–1073; Technical Report 2011–1073; USGS: Reston, VA, USA, 2011.
- Wilson, M.F.J.; O’Connell, B.; Brown, C.; Guinan, J.C.; Grehan, A.J. Multiscale Terrain Analysis of Multibeam Bathymetry Data for Habitat Mapping on the Continental Slope. Mar. Geod. 2007, 30, 3–35. [Google Scholar] [CrossRef]
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- Njoku, E. AMSR-E/Aqua Daily L3 Surface Soil Moisture, Interpretive Parameters, & QC EASE-Grids. version 2; AMSR_E_L3_DailyLand_V07. 2004. Available online: http://nsidc.org/data/ae_land3 (accessed on 15 April 2018).
- Kauth, R.J.; Thomas, G.S. The Tasseled Cap—A graphic description of the spectral-temporal development of agricultural crops as seen by Landsat. In Proceedings of the Symposium on Machine Processing of Remotely Sensed Data, West Lafayette, Indiana, 29 June–1 July 1976; pp. 4B41–4B51. [Google Scholar]
- Crist, E.P.; Cicone, R.C. A physically-based transformation of thematic mapper data—The TM tasseled cap. IEEE Trans. Geosci. Remote Sens. 1984, GE-22, 256–263. [Google Scholar] [CrossRef]
- Yarbrough, L.D.; Easson, G.; Kuszmaul, J.S. Quickbird 2 Tasseled Cap Transform Coefficients: A Comparison of Derivation Methods. In Proceedings of the Pecora 16 Global Priorities in Land Remote Sensing, Sioux Falls, SD, USA, 23–27 October 2005. [Google Scholar]
- Lobser, S.E.; Cohen, W. MODIS tasselled cap: Land cover characteristics expressed through transformed MODIS data. Int. J. Remote Sens. 2007, 28, 5079–5101. [Google Scholar] [CrossRef]
- Small, C.; Milesi, C. Multi-scale standardized spectral mixture models. Remote Sens. Environ. 2013, 136, 442–454. [Google Scholar] [CrossRef]
- Baret, F.; Jacquemoud, S.; Hanocq, J.F. The soil line concept in remote sensing. Remote Sens. Rev. 1993, 7, 65–82. [Google Scholar] [CrossRef]
- Richardson, A.J.; Wiegand, C.L. Distinguishing vegetation from soil background information. Photogramm. Eng. Remote Sens. 1977, 43, 1541–1552. [Google Scholar]
- Fox, G.A.; Sabbagh, G.J.; Searcy, S.W.; Yang, C. An Automated Soil Line Identification Routine for Remotely Sensed Images. Soil Sci. Soc. Am. J. 2004, 68, 1326–1331. [Google Scholar] [CrossRef]
- Paris, J.F. FAQs by Jack E: Grand Unified Vegetation Index Images. 2005. Available online: http://www.microimages.com/sml/ParisScripts/FAQsbyJackE.pdf (accessed on 15 April 2018).
- Baldridge, A.; Hook, S.; Grove, C.; Rivera, G. The ASTER spectral library version 2.0. Remote Sens. Environ. 2009, 113, 711–715. [Google Scholar] [CrossRef]
- Mladenova, I.; Jackson, T.; Njoku, E.; Bindlish, R.; Chan, S.; Cosh, M.; Holmes, T.; de Jeu, R.; Jones, L.; Kimball, J.; et al. Remote monitoring of soil moisture using passive microwave-based techniques—Theoretical basis and overview of selected algorithms for AMSR-E. Remote Sens. Environ. 2014, 144, 197–213. [Google Scholar] [CrossRef]
- Ali, I.; Greifeneder, F.; Stamenkovic, J.; Neumann, M.; Notarnicola, C. Review of Machine Learning Approaches for Biomass and Soil Moisture Retrievals from Remote Sensing Data. Remote Sens. 2015, 7, 16398–16421. [Google Scholar] [CrossRef]
- Santi, E.; Pettinato, S.; Paloscia, S.; Pampaloni, P.; Macelloni, G.; Brogioni, M. An algorithm for generating soil moisture and snow depth maps from microwave spaceborne radiometers: HydroAlgo. Hydrol. Earth Syst. Sci. 2012, 16, 3659–3676. [Google Scholar] [CrossRef]
| Material | Red | NIR | Blue | Green | SWIRa | SWIRb | SWIRc |
|---|---|---|---|---|---|---|---|
| 610 | 985 | 518 | 631 | 1310 | 1249 | 869 | |
| (208) | (397) | (220) | (269) | (676) | (739) | (556) | |
| 1279 | 1674 | 809 | 1099 | 2102 | 2213 | 1816 | |
| (292) | (430) | (226) | (220) | (746) | (909) | (797) | |
| 493 | 4431 | 296 | 790 | 4040 | 2421 | 1013 | |
| (130) | (425) | (78) | (124) | (298) | (209) | (226) | |
| 290 | 202 | 386 | 402 | 198 | 200 | 135 | |
| (326) | (158) | (141) | (283) | (124) | (105) | (82) |
| Material | Red | NIR | Blue | Green | SWIRa | SWIRb | SWIRc |
|---|---|---|---|---|---|---|---|
| 563 | 1008 | 147 | 507 | 1531 | 1836 | 1699 | |
| 0.314812 | 0.320970 | 0.359456 | 0.336364 | 0.249772 | 0.657334 | 0.247078 | |
| −0.193666 | 0.798701 | −0.140345 | −0.094762 | 0.390175 | −0.199024 | −0.322562 | |
| 0.482520 | 0.134057 | −0.025535 | 0.347607 | 0.071952 | −0.653813 | 0.441669 | |
| 0.188177 | 0.038364 | 0.493917 | 0.350060 | −0.358132 | −0.173122 | −0.662112 |
| 2∗Region/Network | Pearson Corr. > 0 % of n Stations | Pearson Corr. > 0 and p < 0.05 % of n Stations | Stations n |
|---|---|---|---|
| Global | 74 | 40 | 459 |
| Tropical | 80 | 40 | 15 |
| Sub-tropical | 74 | 41 | 417 |
| Temperate | 62 | 29 | 27 |
| COSMOS | 78 | 31 | 32 |
| Model | RMSE | E | n stn | n | |||
|---|---|---|---|---|---|---|---|
| Global region | |||||||
| 21.9 a | 9.6 b | 14.0 | 0.02 | −0.56 | 745 | 12,294 | |
| 19.4 | 11.2 | 8.5 | – | – | 745 | 12,294 | |
| Tropical region | |||||||
| 19.0 b,d | 11.4 b,c | 13.4 | 0.26 | 0.16 | 19 | 372 | |
| 22.0 c | 14.7 c | 6.3 d | – | – | 19 | 372 | |
| Sub-tropical region | |||||||
| 21.4 a,d | 8.8 b,d | 13.5 d | 0.02 | −0.48 | 657 | 11,036 | |
| 19.1 d | 11.1 d | 8.5 d | – | – | 657 | 11,036 | |
| Temperate region | |||||||
| 29.6 a,c | 14.1 a,c | 19.4 c | 0.0 | −2.2 | 69 | 886 | |
| 21.6 c | 10.8 d | 10.2 c | – | – | 69 | 886 | |
| COSMOS network (cosmic-ray probes across all regions) | |||||||
| 24.0 a,c | 11.0 b | 14.3 | 0.07 | −0.50 | 52 | 771 | |
| 20.3 c | 11.7 c | 5.3 d | – | – | 52 | 771 | |
| non Forested sites across all regions | |||||||
| 18.7 b,d | 6.8 b,d | 11.6 d | 0.05 | −0.09 | 574 | 9679 | |
| 19.1 d | 11.1 | 8.0 d | – | – | 574 | 9679 | |
| Sensor | RMSE | E | n stn | n | |||
|---|---|---|---|---|---|---|---|
| Global | a | b | c | ||||
| MODIS (o) | 19.2 | 8.1 | 12.2 | 0.07 | −0.13 | 516 | 6886 |
| MODIS (r) | 19.6 | 7.6 | 11.5 | 0.11 | 0.0 | 468 | 6560 |
| AMSR-E | 12.8 | 3.3 | 12.0 | 0.15 | −0.11 | 497 | 56,153 |
| SMOS | 12.2 | 9.0 | 12.4 | 0.24 | −0.21 | 517 | 52,457 |
| Unbiased | d | ||||||
| MODIS (o) | 18.8 | 11.4 | 7.1 | – | – | 516 | 6886 |
| MODIS (r) | 18.9 | 11.4 | 6.8 | – | – | 468 | 6560 |
| AMSR-E | 18.5 | 11.4 | 6.3 | – | – | 497 | 56,153 |
| SMOS | 18.9 | 11.3 | 5.6 | – | – | 517 | 52,457 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gumbricht, T. Detecting Trends in Wetland Extent from MODIS Derived Soil Moisture Estimates. Remote Sens. 2018, 10, 611. https://doi.org/10.3390/rs10040611
Gumbricht T. Detecting Trends in Wetland Extent from MODIS Derived Soil Moisture Estimates. Remote Sensing. 2018; 10(4):611. https://doi.org/10.3390/rs10040611
Chicago/Turabian StyleGumbricht, Thomas. 2018. "Detecting Trends in Wetland Extent from MODIS Derived Soil Moisture Estimates" Remote Sensing 10, no. 4: 611. https://doi.org/10.3390/rs10040611
APA StyleGumbricht, T. (2018). Detecting Trends in Wetland Extent from MODIS Derived Soil Moisture Estimates. Remote Sensing, 10(4), 611. https://doi.org/10.3390/rs10040611