Elevation Change Derived from SARAL/ALtiKa Altimetric Mission: Quality Assessment and Performance of the Ka-Band
Abstract
1. Introduction
2. Data and Method
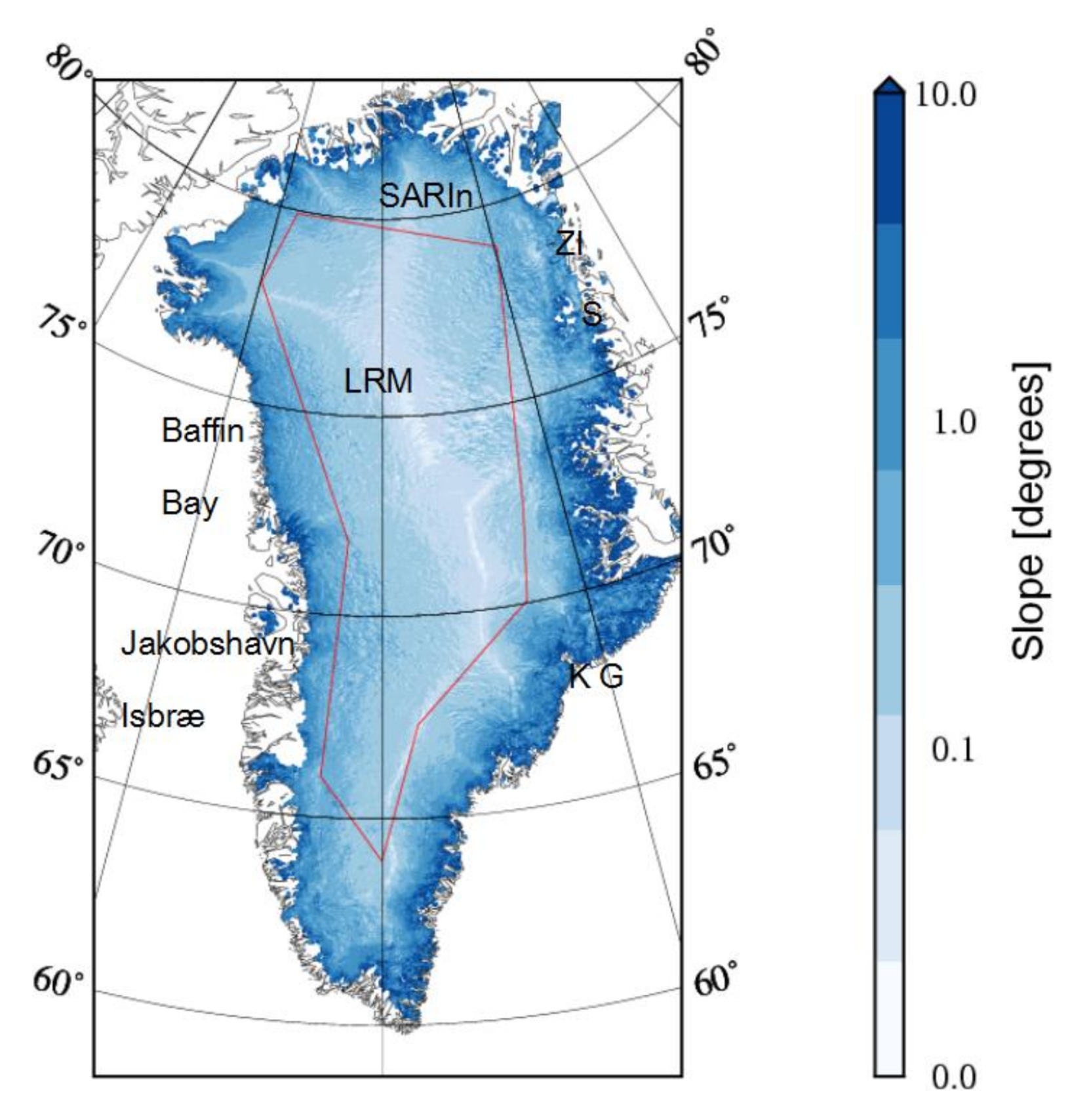
2.1. SARAL Data
2.2. Operation ICEBridge Surface Elevation Change Data
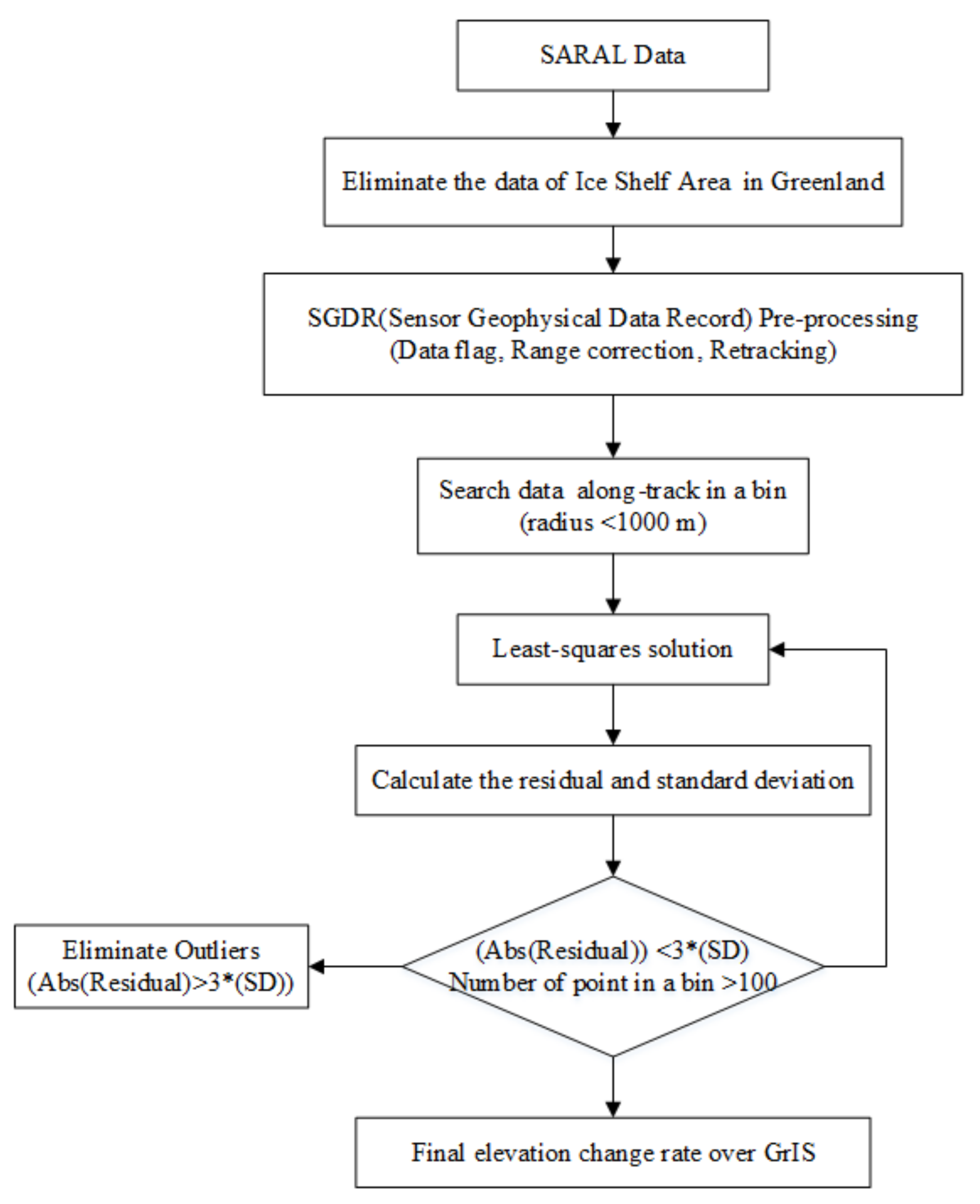
2.3. Algorithm for the Elevation Change Estimation from the SARAL Data
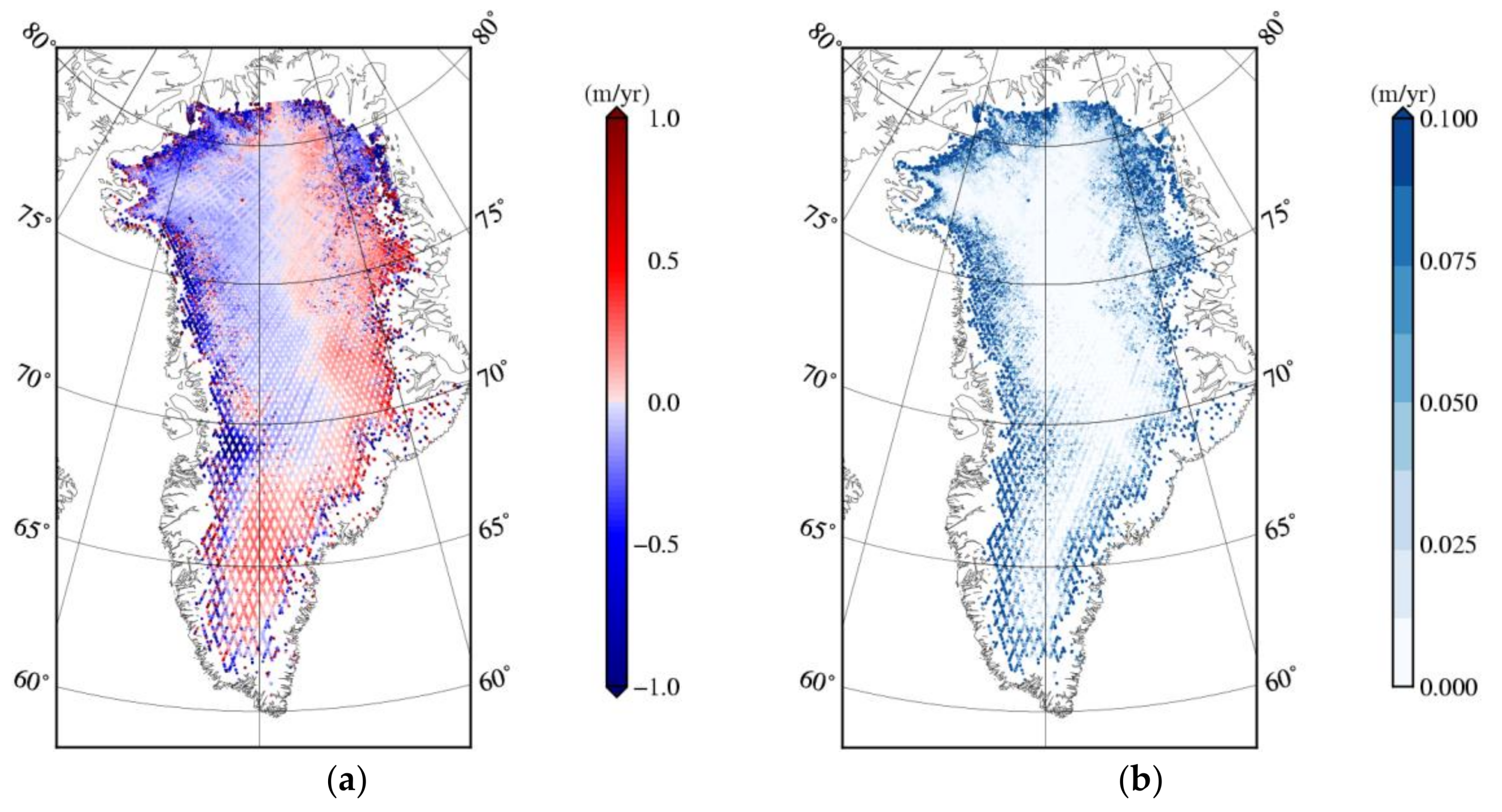
3. Results
3.1. Crossover Analysis of SARAL
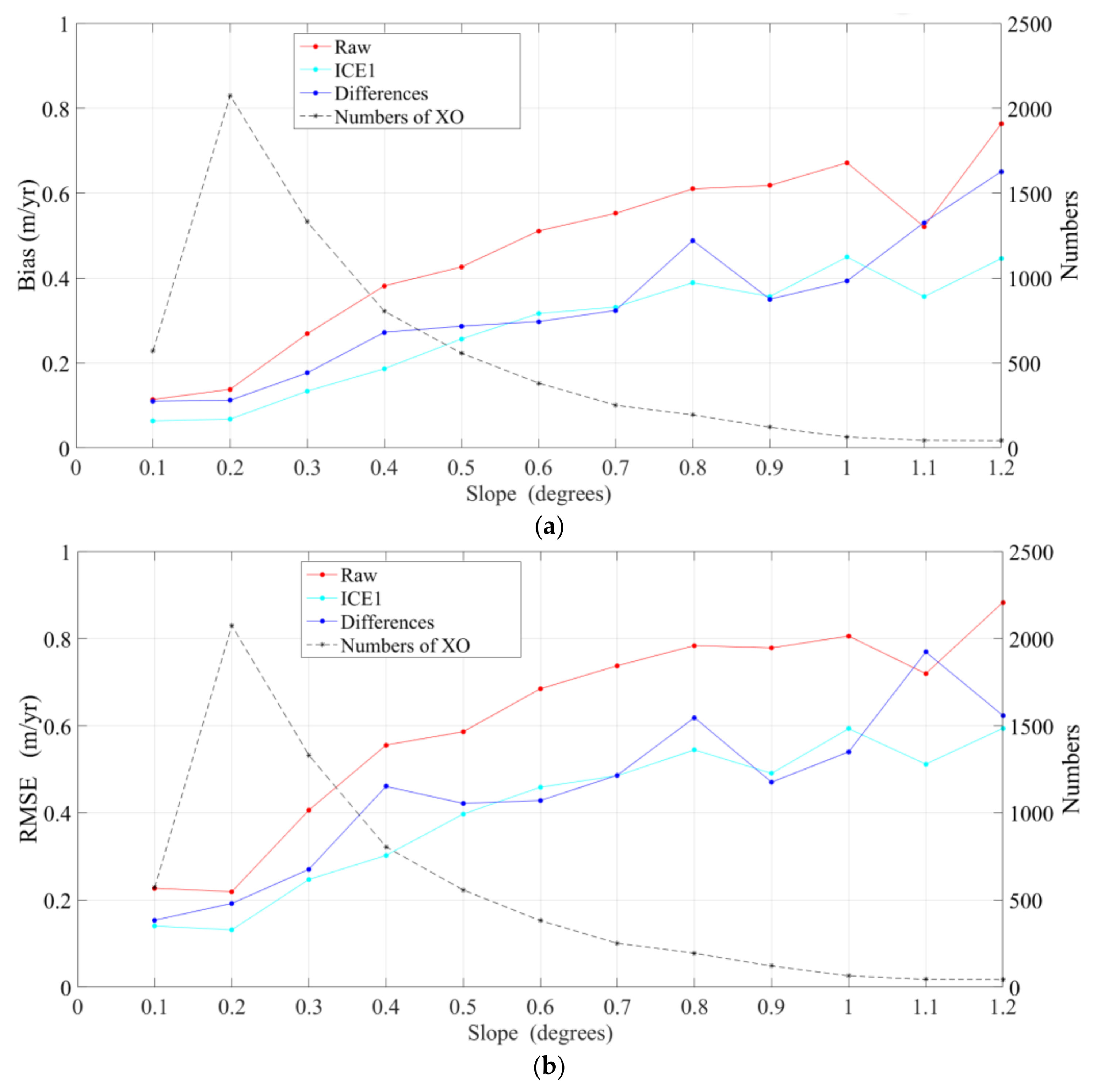
3.2. Accuracy Analysis of Elevation Change Derived from SARAL with Different Waveform Retrackers
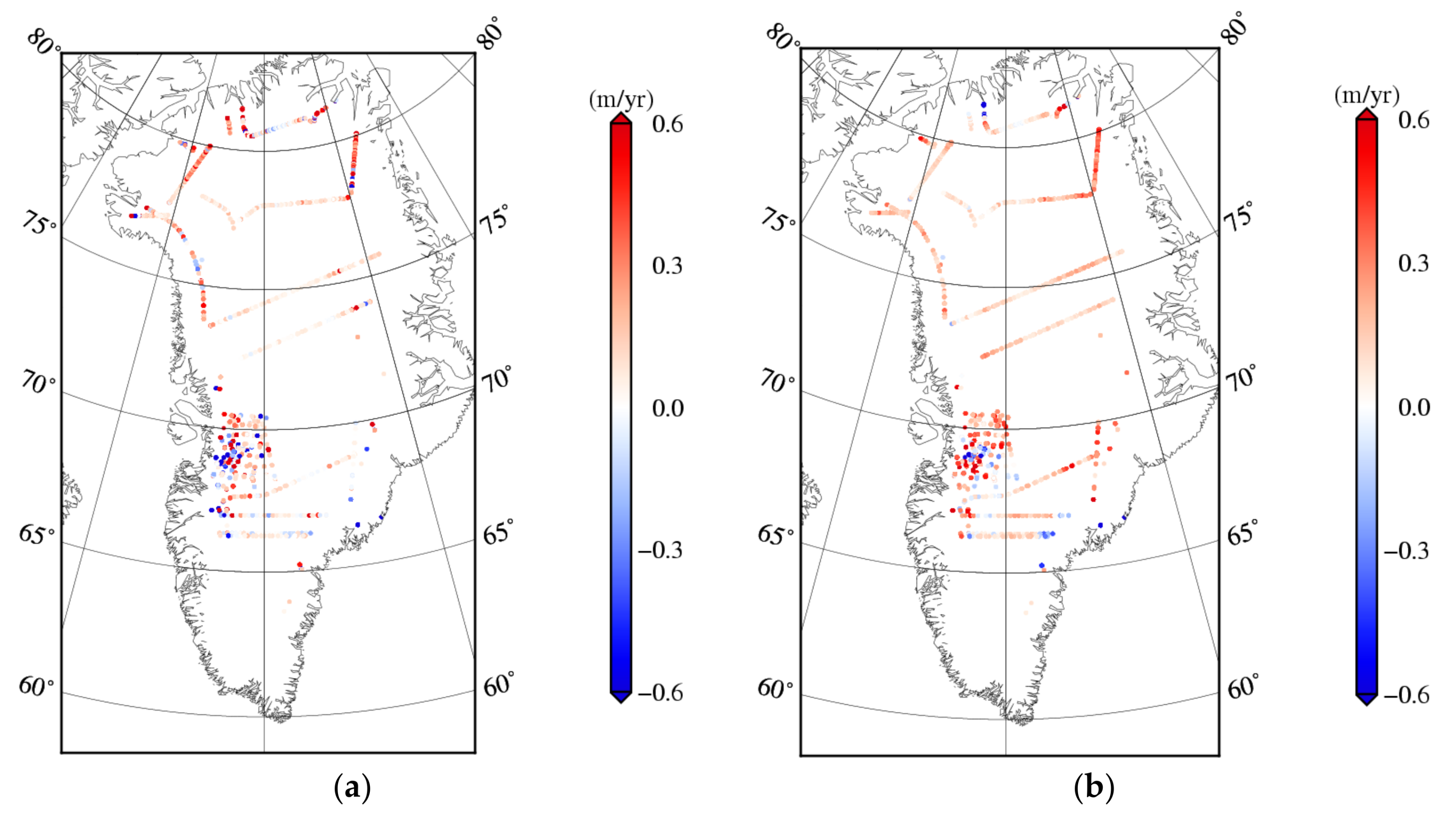
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Church, J.A.; Clark, P.U.; Cazenave, A.; Gregory, J.M.; Jevrejeva, S.; Levermann, A.; Merrifield, M.A.; Milne, G.A.; Nerem, R.S.; Nunn, P.D.; et al. Sea-level rise by 2100. Science 2013, 342, 1445. [Google Scholar] [CrossRef] [PubMed]
- Dowdeswell, J.A. The Greenland ice sheet and global sea-level rise. Science 2006, 311, 963–964. [Google Scholar] [CrossRef] [PubMed]
- Broeke, M.V.D.; Bamber, J.; Ettema, J.; Rignot, E.; Schrama, E.; Berg, W.J.V.D.; Meijgaard, E.V.; Velicogna, I.; Wouters, B. Partitioning recent Greenland mass loss. Science 2009, 326, 984–986. [Google Scholar] [CrossRef] [PubMed]
- Rignot, E.; Kanagaratnam, P. Changes in the velocity structure of the Greenland ice sheet. Science 2006, 311, 986–990. [Google Scholar] [CrossRef] [PubMed]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Krabill, W.B. ICEBridge ATM L4 Surface Elevation Rate of Change; IDHDT4_2014-2010_atm_dhdt_greenland; Technical Report; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2014.
- Sasgen, I.; Dobslaw, H.; Martinec, Z.; Thomas, M. Antarctic snow accumulation variability related to ENSO from GRACE. In Proceedings of the 2010 EGU General Assembly Conference, Vienna, Austria, 2–7 May 2010; p. 1723. [Google Scholar]
- Velicogna, I. Increasing rates of ice mass loss from the Greenland and Antarctic ice sheets revealed by GRACE. Geophys. Res. Lett. 2009, 36, 158–168. [Google Scholar] [CrossRef]
- Jin, S.; Zou, F. Re-estimation of glacier mass loss in Greenland from GRACE with correction of land–ocean leakage effects. Glob. Planet. Chang. 2015, 135, 170–178. [Google Scholar] [CrossRef]
- Ewert, H.; Groh, A.; Dietrich, R. Volume and mass changes of the Greenland ice sheet inferred from ICESat and GRACE. J. Geodyn. 2012, 59–60, 111–123. [Google Scholar] [CrossRef]
- Nilsson, J.; Vallelonga, P.; Simonsen, S.B.; Sørensen, L.S.; Forsberg, R.; Dahl-Jensen, D.; Hirabayashi, M.; Goto-Azuma, K.; Hvidberg, C.S.; Kjær, H.A.; et al. Greenland 2012 melt event effects on cryosat-2 radar altimetry. Geophys. Res. Lett. 2015, 42, 3919–3926. [Google Scholar] [CrossRef]
- Pritchard, H.D.; Arthern, R.J.; Vaughan, D.G.; Edwards, L.A. Extensive dynamic thinning on the margins of the Greenland and Antarctic ice sheets. Nature 2009, 461, 971–975. [Google Scholar] [CrossRef] [PubMed]
- Smith, B.E.; Fricker, H.A.; Joughin, I.R.; Tulaczyk, S. An inventory of active subglacial lakes in Antarctica detected by ICESat (2003–2008). J. Glaciol. 2009, 55, 573–595. [Google Scholar] [CrossRef]
- Sørensen, L.S.; Simonsen, S.B.; Nielsen, K.; Lucaspicher, P.; Spada, G.; Adalgeirsdottir, G.; Forsberg, R.; Hvidberg, C.S. Mass balance of the Greenland ice sheet (2003–2008) from ICESat data—The impact of interpolation, sampling and firn density. Cryosphere 2011, 5, 173–186. [Google Scholar] [CrossRef]
- Smith, B.E.; Bentley, C.R.; Raymond, C.F. Recent elevation changes on the ice streams and ridges of the Ross Embayment from ICESat crossovers. Geophys. Res. Lett. 2005, 32, 205–213. [Google Scholar] [CrossRef]
- Frappart, F.; Legrésy, B.; Niño, F.; Blarel, F.; Fuller, N.; Fleury, S.; Birol, F.; Calmant, S. An ERS-2 altimetry reprocessing compatible with ENVISAT for long-term land and ice sheets studies. Remote Sens. Environ. 2016, 184, 558–581. [Google Scholar] [CrossRef]
- Hwang, C.; Yang, Y.; Kao, R.; Han, J.; Shum, C.K.; Galloway, D.L.; Sneed, M.; Hung, W.C.; Cheng, Y.S.; Fei, L. Time-varying land subsidence detected by radar altimetry: California, Taiwan and North China. Sci. Rep. 2016, 6, 28160. [Google Scholar] [CrossRef] [PubMed]
- Sørensen, L.S.; Simonsen, S.B.; Meister, R.; Forsberg, R.; Levinsen, J.F.; Flament, T. Envisat-derived elevation changes of the Greenland ice sheet, and a comparison with ICESat results in the accumulation area. Remote Sens. Environ. 2015, 160, 56–62. [Google Scholar] [CrossRef]
- Bonnefond, P.; Verron, J.; Aublanc, J.; Babu, K.N.; Bergé-Nguyen, M.; Cancet, M.; Chaudhary, A.; Crétaux, J.F.; Frappart, F.; Haines, B.J.; et al. The benefits of the Ka-band as evidenced from the SARAL/Altika altimetric mission: Quality assessment and unique characteristics of Altika data. Remote Sens. 2018, 10, 83. [Google Scholar] [CrossRef]
- Armitage, T.W.K.; Ridout, A.L. Arctic sea ice freeboard from Altika and comparison with CryoSat-2 and Operation ICEBridge. Geophys. Res. Lett. 2015, 42, 6724–6731. [Google Scholar] [CrossRef]
- Bronner, E.; Gulliot, A.; Picot, N.; Noubel, J. Saral/Altika Products Handbook; No. CNES:SALP-MU-M-OP-15984-CN; CENS: Paris, France, 2013.
- Studinger. ICEBridge ATM L4 Surface Elevation Rate of Change; version 1; Indicate Subset Used; Updated 2017; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2014. [CrossRef]
- Simonsen, S.B.; Sørensen, L.S. Implications of changing scattering properties on Greenland ice sheet volume change from Cryosat-2 altimetry. Remote Sens. Environ. 2017, 190, 207–216. [Google Scholar] [CrossRef]
- Martin, C.F.; Krabill, W.B.; Manizade, S.S.; Russell, R.L.; Sonntag, J.G.; Swift, R.N.; Yungel, J.K. Airborne Topographic Mapper Calibration Procedures and Accuracy Assessment; NASA: Washington, DC, USA, 2012.
- Flament, T.; Rémy, F. Dynamic thinning of Antarctic glaciers from along-track repeat radar altimetry. J. Glaciol. 2012, 58, 830–840. [Google Scholar] [CrossRef]
- Legrésy, B.; Rémy, F.; Blarel, F. Along track repeat altimetry for ice sheets and continental surface studies. In Proceedings of the Symposium on 15 Years of Progress in Radar Altimetry; European Space Agency, Venice, Italy, 13–18 March 2006. [Google Scholar]
- Malcolm, M.; Amber, L.; Shepherd, A.; Briggs, K.; Armitage, T.W.; Hogg, A.; Kuipers Munneke, P.; Broeke, M.; Noel, B.; Berg, W.J.; et al. A high-resolution record of Greenland mass balance. Geophys. Res. Lett. 2016, 43, 7002–7010. [Google Scholar]
- Mcmillan, M.; Shepherd, A.; Sundal, A.; Briggs, K.; Muir, A.; Ridout, A.; Hogg, A.; Wingham, D. Increased ice losses from Antarctica detected by CryoSat-2. Geophys. Res. Lett. 2014, 41, 3899–3905. [Google Scholar] [CrossRef]
- Gunter, B.C.; Didova, O.; Riva, R.E.M.; Ligtenberg, S.R.M.; Lenaerts, J.T.M.; King, M.A.; Van den Broeke, M.R.; Urban, T. Empirical estimation of present-day Antarctic glacial isostatic adjustment and ice mass change. Cryosphere 2014, 8, 743–760. [Google Scholar] [CrossRef]
- Zhou, X.; Miao, H.; Wang, Y.; Fan, C.; Cui, T. Study on the determination of crossovers by piecewise fitting of satellite ground track. Acta Geod. Cartogr. Sin. 2012, 41, 811–815. [Google Scholar]
- Zwally, H.J.; DiMarzio, J.P.; Brenner, A.C. Glas/Icesat Antarctic and Greenland Grids; Digital Media; NASA: Washington, DC, USA, 2012.
- Brenner, A.C.; Dimarzio, J.P.; Zwally, H.J. Precision and accuracy of satellite radar and laser altimeter data over the continental ice sheets. IEEE Trans. Geosci. Remote Sens. 2007, 45, 321–331. [Google Scholar] [CrossRef]
- Brenner, A.C.; Blndschadler, R.A.; Thomas, R.H.; Zwally, H.J. Slope-induced errors in radar altimetry over continental ice sheets. J. Geophys. Res. Oceans 1983, 88, 1617–1623. [Google Scholar] [CrossRef]
- ESTEC. Cryosat Mission and Data Description; Technical Report 3; ESTEC: Noordwijk, The Netherlands, 2007. [Google Scholar]
- Csatho, B.M.; Schenk, A.F.; van der Veen, C.J.; Babonis, G.; Duncan, K.; Rezvanbehbahani, S.; Van Den Broeke, M.R.; Simonsen, S.B.; Nagarajan, S.; van Angelen, J.H. Laser altimetry reveals complex pattern of Greenland ice sheet dynamics. Proc. Natl. Acad. Sci. USA 2014, 111, 18478–18483. [Google Scholar] [CrossRef] [PubMed]
- Helm, V.; Humbert, A.; Miller, H. Elevation and elevation change of Greenland and Antarctica derived from cryosat-2. Cryosphere 2014, 8, 1539–1559. [Google Scholar] [CrossRef]
- Khan, S.A.; Aschwanden, A.; Wahr, J.; Kjeldsen, K.K. Greenland ice sheet mass balance: A review. Rep. Prog. Phys. Phys. Soc. 2015, 78, 046801. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Wang, Z.; Li, F.; An, J.; Yang, Y.; Liu, J. Estimation of present-day glacial isostatic adjustment, ice mass change and elastic vertical crustal deformation over the Antarctic ice sheet. J. Glaciol. 2017, 63, 703–715. [Google Scholar] [CrossRef]

| Bias (m year−1) | SD (m year−1) | Numbers | |
|---|---|---|---|
| Raw | −0.018 | 0.470 | 6535 |
| ICE1 | −0.015 | 0.303 | 6595 |
| ICE2 | −0.047 | 0.314 | 6585 |
| Sea Ice | −0.019 | 0.348 | 6548 |
| OCEAN | −0.004 | 0.365 | 6515 |
| All | SARIn | LRM | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Bias (m year−1) | RMSE (m year−1) | Number | Bias (m year−1) | RMSE (m year−1) | Number | Bias (m year−1) | RMSE (m year−1) | Number | |
| Raw | 0.18 | 0.60 | 13363 | 0.18 | 0.67 | 7291 | 0.18 | 0.50 | 6072 |
| ICE1 | 0.11 | 0.43 | 13604 | 0.12 | 0.47 | 7344 | 0.10 | 0.38 | 6260 |
| ICE2 | 0.18 | 0.50 | 13632 | 0.22 | 0.55 | 7455 | 0.12 | 0.41 | 6177 |
| Sea Ice | 0.11 | 0.46 | 13516 | 0.11 | 0.53 | 7300 | 0.11 | 0.37 | 6216 |
| OCEAN | 0.11 | 0.49 | 13417 | 0.12 | 0.55 | 7164 | 0.10 | 0.42 | 6253 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; Yang, Y.; Wang, Z.; Zhang, B.; Jiang, H. Elevation Change Derived from SARAL/ALtiKa Altimetric Mission: Quality Assessment and Performance of the Ka-Band. Remote Sens. 2018, 10, 539. https://doi.org/10.3390/rs10040539
Yang Q, Yang Y, Wang Z, Zhang B, Jiang H. Elevation Change Derived from SARAL/ALtiKa Altimetric Mission: Quality Assessment and Performance of the Ka-Band. Remote Sensing. 2018; 10(4):539. https://doi.org/10.3390/rs10040539
Chicago/Turabian StyleYang, Quanming, Yuande Yang, Zemin Wang, Baojun Zhang, and Hu Jiang. 2018. "Elevation Change Derived from SARAL/ALtiKa Altimetric Mission: Quality Assessment and Performance of the Ka-Band" Remote Sensing 10, no. 4: 539. https://doi.org/10.3390/rs10040539
APA StyleYang, Q., Yang, Y., Wang, Z., Zhang, B., & Jiang, H. (2018). Elevation Change Derived from SARAL/ALtiKa Altimetric Mission: Quality Assessment and Performance of the Ka-Band. Remote Sensing, 10(4), 539. https://doi.org/10.3390/rs10040539




