1. Introduction
Moving target tracking has become a key technique in many emerging research applications of Smart City, such as video surveillance, intrusion monitoring, activity control, and detection of approaching objects [
1]. For example, it has been successfully employed to monitor human activities so as to prevent theft in residential areas, banks parking lots, etc. During the past decades, target tracking with visible cameras has been deeply investigated and a number of effective methods were proposed [
2,
3,
4,
5]. However, this is obviously not suitable for the nighttime environment due to its high dependency on the illumination condition. In contrast, an infrared imaging system is much more robust to illumination changes and is able to work well in both daytime and nighttime. Therefore, infrared moving target tracking has attracted more and more attention in computer vision and has been gradually utilized from civil to military areas, e.g., precise guidance, early warning, and unmanned air vehicle navigation [
6]. Based on the afore-mentioned discussion, we consider that it is of great necessity and significance for us to further investigate a robust infrared moving target tracking algorithm under various backgrounds.
In spite of the advantage that infrared imaging system can work all day long, it does suffer from a fatal drawback that the information of target is not so ample as the one that was obtained from a visible camera [
7]. In general, the moving target is lacking color and texture information, which helps to describe the target more accurately due to the adverse influence of energy attenuation. Besides, sensor noise and background clutters lead to a low signal-to-noise ratio and thus the severe drift problem, which is a great challenge for robust target tracking, may easily occur. More seriously, partial or even full occlusion is another main obstacle for the success of long-term tracking. Hence, it is a critical task to establish an efficient model to precisely describe the appearance model of moving target for the infrared search and track system.
Given an initial target state in the first frame manually, the aim of a tracker is to predict or estimate the states of target in the following frames. The algorithms now available can be classified into three categories: generative approaches, discriminative approaches, and deep learning-based approaches. Generative methods aim to build an appearance model describing the target of interest and to search locally for the most similar image patch to the templates in each frame [
8]. Mean-shift (MS) tracker, which was originally designed by Comaniciu et al. [
9], employs an isotropic kernel function weighing the color or intensity histograms of template and candidate to measure their similarity quantitatively, after which the target in the current frame is located using a gradient descent method. However, the MS tracker cannot cope with the scale change of target and it has weaker robustness in infrared videos when compared with red-green-blue (RGB) videos. The conventional intensity histogram-based particle filtering (PF) tracker [
10], which is also known as Sequential Monte Carlo algorithm, is one of the most widely-used trackers nowadays. The posterior probability density function of the state space is recursively approximated by the Bayesian model using finite samples [
11]. During the past decades, many improved PF trackers, e.g., a hierarchical PF [
12] utilized for multiple target tracking and an appearance-adaptive model that is integrated with a PF tracker [
13] to achieve robust object tracking and recognition, have been developed. Xue et al. [
14] proposed a sparse representation based L
1 tracker under the PF framework. According to their study, the target of interest can be projected into a set of linearly independent basis, i.e., templates, with a sparse coefficient containing few non-zero entries, which denote the occlusion. The relevant experiments verify that the L
1 tracker can achieve satisfactory performances in video sequences with distinct occlusions, but the computational efficiency is poor due to its relatively complex optimization. To deal with the difficulties caused by appearance variation, some online models, such as incremental visual tracker (IVT) [
15], have been proposed. IVT can adapt online to the appearance change of target by means of incrementally learning a low-dimensional subspace representation and achieves promising computational efficiency in practice, but it turns out to be less effective on the condition that the occlusion is heavy or that the distortion is non-rigid due to its adopted holistic appearance model [
15,
16].
Discriminative methods regard the tracking problem as a binary classification task and are intended to distinguish the target from the background by means of determining a decision boundary [
8]. Recently, the compressive sensing (CS) theory has shown great advantages in constructing trackers. Zhang et al. presented a real-time compressive tracker (CT) [
17], as well as its improved version fast compressive tracker (FCT) [
18], with an appearance model based on the features that were extracted from the multi-scale image feature space with data-independent basis [
19], but there often exist a large number of samples, from which features need to be extracted for classification, thereby entailing computationally expensive operations [
18]. In light of the advances that have been acquired in face recognition, lots of boosting feature selection-based algorithms have been developed. Grabner et al. [
19] presented an online boosting feature selection method based on online ensemble approach, but the classifier is updated using only one positive sample, i.e., the resulting patch in the current frame, along with multiple negative samples. The following tracking process may fail when the current target location extracted by the current classifier is not accurate. Thus, the strategy that multiple positive samples are cropped around the target location while the negative ones are cropped far away from the target is utilized to update the classifier online [
20], which relieves the afore-mentioned problem to some extent. However, the classifier is easy to be confused when the ambiguity problem occurs. Fortunately, Zhang et al. [
21] proposed an online multiple instance learning (MIL) tracker by putting the positive samples and the negative ones into several positive and negative bags, after which a classifier is trained online, according to the bag likelihood function. Furthermore, a weighted multiple instance learning (WMIL) tracker was developed by integrating the sample importance into the learning procedure [
22].
On the other hand, deep learning-based trackers have been becoming more and more popular in intelligent surveillance. Generally speaking, the core of this kind of approaches is to learn a generic representation offline from large quantities of training images [
23], and it resorts to transfer learning and online fine-tuning strategy to adapt to the appearance variations of target [
24]. Wang et al. proposed a deep learning tracker (DLT), which integrates the philosophies behind both generative and discriminative trackers by using an effective image representation learned automatically as the first work on applying deep neural networks to visual tracking [
25]. Nam et al. developed a multi-domain convolutional neural networks-based tracker (MDNet), which learns domain-independent representations from pretraining and captures domain-specific information through online learning during the process of tracking [
26]. Besides, an online visual tracker that was built by modeling and propagating convolutional networks in a tree structure (TCNN) was also proposed by Nam et al. to achieve multi-modality and reliability of target appearances [
27]. The state of target is estimated by calculating a weighted average of scores from the multiple convolutional networks (CNNs), and the contribution of each CNN is determined by exploiting the tree structure also. Ma et al. presented a hierarchical convolutional features (HCF)-based tracker [
28]. They interpret the hierarchies of the convolution layers as a nonlinear counterpart of an image pyramid representation and exploit these multiple levels of abstraction for visual tracking. In order to get rid of the offline training with a large number of auxiliary data, Zhang et al. proposed a visual tracker with convolutional networks (CNT) [
23]. In their method, a simple two-layer feed-forward CNN is constructed to generate an effective representation for robust tracking. To denoise the representation, a soft shrinkage strategy is employed, and the representation is updated using an online scheme. Even so, the huge sample size and the low running efficiency are still the two main drawbacks of deep learning-based approaches.
Although trackers available have made much progress in Smart City, the robustness to appearance variation, image noise as well as other environmental disturbances is still a worthy topic to be studied. Fortunately, low-rank and sparse representation is an effective tool that is employed in many applications of computer vision, such as fore-and background separation [
26,
27,
28,
29,
30,
31,
32], fabric defect inspection [
33], face recognition [
34], act recognition [
35], and so on. Its basic principle is that the foreground occupies a small number of pixels and that the background images are linearly related in consecutive frames, meaning that the fore-and background patches can be treated as a low-rank matrix and a sparse matrix, respectively. Inspired by the huge success of low-rank and sparse decomposition theory in object detection and recognition, a TV-LRSMR tracker is proposed to cope with the particular tracking challenges in infrared videos. First of all, the observation matrix is decomposed into a low-rank matrix denoting the target and a sparse matrix denoting the occlusion so that the interference of partial occlusion is taken into consideration. Then, a total variation regularization term is implemented on the occlusion matrix in order to avoid the sensor noise being fitted into the occlusion term. To solve the afore-proposed convex optimization problem, principal component analysis (PCA) [
36,
37] and the accelerated proximal gradient (APG) [
38] methods are combined as an alternating algorithm to formulate a two-step optimization. Finally, the target location is calculated under the PF framework along with a dynamic model update mechanism. Experimental results verify an accurate and robust tracking performance.
In conclusion, the main contributions of our work can be summarized into the following aspects:
- (1)
a low-rank and sparse representation-based appearance model is proposed so that the tracking problem can be transformed into a convex optimization problem;
- (2)
a total variation regularization term is imposed on the sparse matrix in order to overcome the noise disturbance in infrared images;
- (3)
an alternating algorithm that integrates the PCA and APG methods is exploited to solve the optimization problem separately; and,
- (4)
a dynamic template update scheme is developed to further cope with the appearance change.
The remainder of this paper is organized as follows:
Section 2 briefly reviews the theory of PF framework; in
Section 3, the proposed tracker, including the appearance model, the algorithm to solve the optimization equation, and the template update mechanism, is introduced at great length; qualitative and quantitative evaluations and related discussions about the experimental results are given in
Section 4 to demonstrate the precision and robustness of our tracker; finally, a conclusion as well as the future work is summarized in
Section 5.
2. Related work about particle filtering
Let us define the position and affine parameters as a two-dimensional (2D) transition state
at time k, in which
and
represent the spatial coordinates;
,
,
, and
denote scale, aspect, rotation angle, and skew, respectively. Suppose that
is the all of the available observations of target from the beginning to time k, based on which the predicting distribution of
represented as
can be recursively calculated, as follows
where,
illustrates the state transition model and can be modeled by a Gaussian distribution:
where,
is a diagonal covariance matrix, the elements of which denote the variances of the affine parameter
, respectively.
Since the observation
at time k is available, the posteriori estimation of target state is updated based on the Bayes rule, as Equation (3).
where,
is the likelihood probability indicating the similarity between a candidate image patch and the target templates. When considering that
keeps constant, Equation (3) can be thus expressed as
In this work, n candidate samples (particles) are created by the state transition model
, and all of the six state variables
are seen as independent to each other. The likelihood probability
of a candidate sample is computed as
where,
is the reconstruction error matrix of the current candidate sample and the computing method of
is explained in
Section 3.2. In essence,
is governed by a Gaussian distribution, the mean of which is 0 and variance is
.
Lastly, the optimal state
for time k is obtained from the maximal approximate posterior probability, as
3. Model Establishment
In this section, we focus on explaining the infrared moving target tracking model using total variation regularization term-based low-rank and sparse representation. In
Section 3.1, the definitions of the notations mentioned in our model are simply introduced; then, the detailed theories about the appearance model represented by a joint optimization equation are discussed in
Section 3.2; next, an alternating algorithm is presented to solve the optimization problem in
Section 3.3; in
Section 3.4, a template update scheme is introduced and a summary of the presented tracker is made in
Section 3.5.
3.1. Definitions
Given n infrared image patches cropped around the target selected manually in the first frame, they make up of a template matrix , and represent the i-th patch in F, where every patch containing m pixels is stacked into a column vector. Note that the bounding box region of the moving target in each frame is regularized as sized, thus the total pixel number of every patch is . For each candidate sample , which is also regularized as sized in the current frame, it composes an observation matrix with the template matrix F. stands for the target matrix, which shares the same size with Y. In other words, each column of T estimates the target pixels in the corresponding vector column of Y. Similarly, we denote as the occlusion matrix, an arbitrary column Si of which corresponds to the estimation of occlusion pixels in .
Besides, three matrix norms are utilized in our algorithm: (1) represents norm; (2) represents nuclear norm, where r is the rank of matrix X and represents all of the non-zero singular values of X; (3) denotes Frobenius norm.
3.2. Appearance Model
In this paper, we propose that the observation matrix Y of an infrared sequence can be decomposed into a low-rank matrix T representing the moving target and a sparse matrix S representing the occlusion appearing in the sequence at times. When considering the troublesome noise in infrared images, the appearance model [
39] can be generally written as
where,
is the Gaussian noise.
In order to reconstruct the observation matrix Y with the target matrix T and the occlusion matrix S, a minimum error reconstruction through a regularized Frobenius norm minimization function is firstly proposed, as follows
For the sequential infrared images that were captured in a moderate or high frame rate, the moving targets in the adjacent frames have a strong linear correlation mainly because their intensity distributions as well as the shapes can approximately be seen as similar within a short time. To this end, the moving target regions can form a low-rank matrix when they are stacked into column vectors. Since no additional assumptions are made for the target matrix, the constraint that is imposed on our moving target model T is expressed as
where,
means calculating the rank of a matrix and K is a constant with a low value. Fortunately, it has been demonstrated that nuclear norm is a well-performed convex substitution of the rank operator [
40]. Hence, our appearance model can be further expressed as
where,
is a constant.
In addition, spatial or even full occlusions which may appear in any sizes and any part of the real target commonly exist in the procedure of infrared target tracking, always leading to the unexpected tracking errors. We argue that the occlusion can be regarded as outliers that cannot be fitted into the moving target model due to the lack of linear correlations. As a result, the occlusion part is depicted by a matrix S individually. A prior knowledge is that the occlusion region usually occupies few pixels with a relatively small size, which means that the occlusion matrix S should have the sparse property. It is known that
norm is extensively applied to describe the matrix sparsity, so the afore-discussed sparse term is added to our model, as follows
where,
is a constant.
However, test sequences are always contaminated by noise derived from infrared sensors, and it is easy to generate drift problems when the real infrared moving target is immersed in the noise. Noise is easy to be separated into S for the reason that the rank of target matrix T is limited and the noise which may distribute in any part of the image also possesses sparse property. In order to distinguish the noise from S, we introduce a total variation model that is used in image denoising [
41] and object detection [
42] to impose a more accurate regularization on S:
where,
and
represent the partial derivatives along x and y direction, respectively; P and Q are the difference matrices of the two directions:
Intended to make noise pixels separated into S as few as possible, it is equivalent to transforming this issue into limiting the total variation of S. Therefore, apart from the constraints in Equation (11), another total variation-based regularization term needs to be imposed on S as
where,
is a constant.
In our work, the observation matrix Y consists of n templates
and a current candidate sample
(
, N is the particle number of the particle filtering). The n templates are cropped around the target that is chosen in the first frame with certain Gaussian disturbances, and they are normalized to the same size as the target. For each frame, we apply the Gaussian distribution to model the state transition distribution
so that N corresponding candidate samples can be acquired. Further, for each sample, the reconstruction error matrix
is computed as
where,
,
and
are the observation, target, and occlusion matrixes that are corresponding to the current candidate sample
.
Then, the likelihood
of
that reflects the similarity between the candidate sample and the target templates can be calculated as Equation (5) introduced in
Section 2.
3.3. Solution
The objective function defined in Equation (14) is a convex optimization problem with the only solution. However, there exist two dependent variables in this function and it is hard to make a joint optimization over T and S simultaneously. Thus, we choose to separate the optimization procedure into two stages: T-stage and S-stage, through an alternating algorithm. Since both the T-stage and S-stage are convex optimization problems, the optimal solutions of T and S are able to be worked out efficiently.
3.3.1. Estimation of the Moving Target Matrix T
Given an estimate of the occlusion matrix
, Equation (14) can be simplified as
Equation (16) is a typical matrix completion problem that can be solved using a singular value threshold operator as
where,
stands for the estimation of T;
is the singular value matrix of
, i.e.,
;
is a shrink operator.
According to the solving process of Equation (17), we find that the rank of
is determined by the number of singular values of
that are larger than
. A lower
increases the complexity of background, thus we set
, according to the robust principal component analysis (RPCA) method [
35] in this paper.
3.3.2. Estimation of the Occlusion Matrix S
Once the target matrix
is computed, Equation (14) turns to be the following form:
It is noticeable that Equation (18) is made up of two parts:
- (1)
is a differentiable convex function with Lipschitz continuous gradient and its Lipschitz constant is ;
- (2)
is an L1 constraint term which is a non-smooth but convex function.
As a result, this optimization problem can be efficiently solved by APG approach with quadratic convergence [
43]. The main steps of estimating S by APG are listed in Algorithm 1, and the derivation of Lipschitz L and the key steps of APG approach are given in
Appendix A.
| Algorithm 1. Steps of estimating S by APG approach. |
| 1. Initialize , |
| 2. for i = 0, 1, 2, …, iterate until converge |
| (1) ; |
| (2) |
| (3) |
| 3. end for |
| 4. Output: |
3.4. Template Update Scheme
During the tracking process, the appearance of target (e.g., the shape and scale) as well as the tracking environment (e.g., the illumination and background pattern) may change at any time, which means that part of the templates would be no longer representative. Based on this consideration, it is of necessity for us to update the templates for a better observation, especially when the moving target encounters pose or illumination variations. However, it should be noticed that it is inappropriate to update the template too often because slight tracking errors would be introduced once the template is updated and the errors will be accumulated, causing the tracking result drifting from the ground truth. That is to say, the template matrix cannot be updated in the case that serious occlusion exists in the current frame or that the target is overlapped by the foreground object.
For the dynamic update of template matrix, the importance weight () is assigned to each entry of . In a direct way, the Frobenius norm of can be used as the weight for each template, where stands for the reconstruction error of the newly selected target in the k-th frame. An iterative strategy as is designed, where each weight is initialized as . When the sum of the (n+1)-th column vector in the current occlusion matrix S is larger than a threshold , then we argue that there are occlusions existing in the current frame and T will not be updated in this case. Motivated by the afore-discussed considerations, a template update scheme is presented in Algorithm 2.
| Algorithm 2. Template update mechanism. |
| 1. Initialize: (i = 1, 2, …, n), where n is number of templates; |
| 2. is the newly selected target using the method discussed above; |
| 3. and are the target matrix and occlusion matrix corresponding to ; |
| 4. Update the importance weight as ; |
| 5. , where denotes the arc-cosine function and is the target template which shares the most similar appearance with ; |
| 6. if and , where and denote the pre-defined thresholds; |
| 7. , where ; |
| 8. , where denotes computing the median value of a vector; |
| 9. end if |
| 10. Normalize ; |
| 11. Adjust to guarantee that ; |
| 12. Normalize the template matrix F again. |
Note that the conventional Euclidean distance is replaced by the arc-cosine function to describe the similarity between the currently selected target and the template in our algorithm. Absolutely, two column vectors are more similar when turns smaller. In conclusion, the least similar template vector needs to be substituted by the newly chosen target under the circumstances that the target deviates far from the templates and the occlusion is not too serious. What is more, a median weight of all the templates is given to the newly added template so as to prohibit it from playing a leading role in the next procedure of evaluating the candidate samples. Last but not least, the maximum template weight cannot be larger than 0.3 on account of the motivation of preventing skewing.
3.5. Summary of the Proposed Tracker
A summary of our presented IR moving target tracking algorithm using the total variation regularization term-based low-rank and sparse representation is listed in Algorithm 3. To sum up, the proposed tracker includes three main stages: state sampling, objective function optimization, and template updating.
| Algorithm 3. Complete steps of the proposed tracker. |
| 1. Input: the ground truth of target selected manually in the first frame; |
| 2. Initialize: template matrix and state vector ; |
| 3. for k = 2 to the last frame do |
| 4. for i = 1 to the last particle do |
| 5. Crop and normalize the candidate sample and compose the observation matrix ; |
| 6. Initialize: and ; |
| 7. Loop |
| 8. Estimate the target matrix T: ; |
| 9. Estimate the occlusion matrix S: ; |
| 10. Until converge |
| 11. end for |
| 12. Resample via the weight ; |
| 13. Output: ; |
| 14. end for |
4. Experiments and Discussions
In this part, the presented tracking algorithm is examined on several typical infrared sequences. Our tracker is compared with other state-of-the-art algorithms, both qualitatively and quantitatively. For each sequence, the target templates are all regularized to an appropriate size depending on the bounding box that is drawn manually in the first frame, and the affine parameter standard variances vary accordingly in different scenes. All of the codes are implemented using Matlab 2012b on a PC with a 2.60 GHz INTEL CPU and 4.0 GB installed memory (RAM).
4.1. Datasets
In our experiments, seven infrared sequences with different types of targets and backgrounds are utilized as the datasets. All of the sequences can be downloaded from [
44,
45]. The detailed information of the sequences is listed in
Table 1.
The seven sequences cover all of the afore-mentioned challenges in infrared moving target tracking: pose change, scale change, illumination change, occlusion, noise, small target size, etc. The first frame with the manually selected target of interest (marked with a red rectangle) of each sequence is presented in
Figure 1.
4.2. Results of the Proposed Tracker
In our algorithm, the particle number and the generated template number are set as 500 and 10 in all seven sequences. For the optimization function in Equation (14), there are totally three parameters , , and to be set in advance. As is mentioned above, , and . In addition, the angle threshold is set as , and the seven groups of affine parameter standard variances are: , , , , , , , respectively.
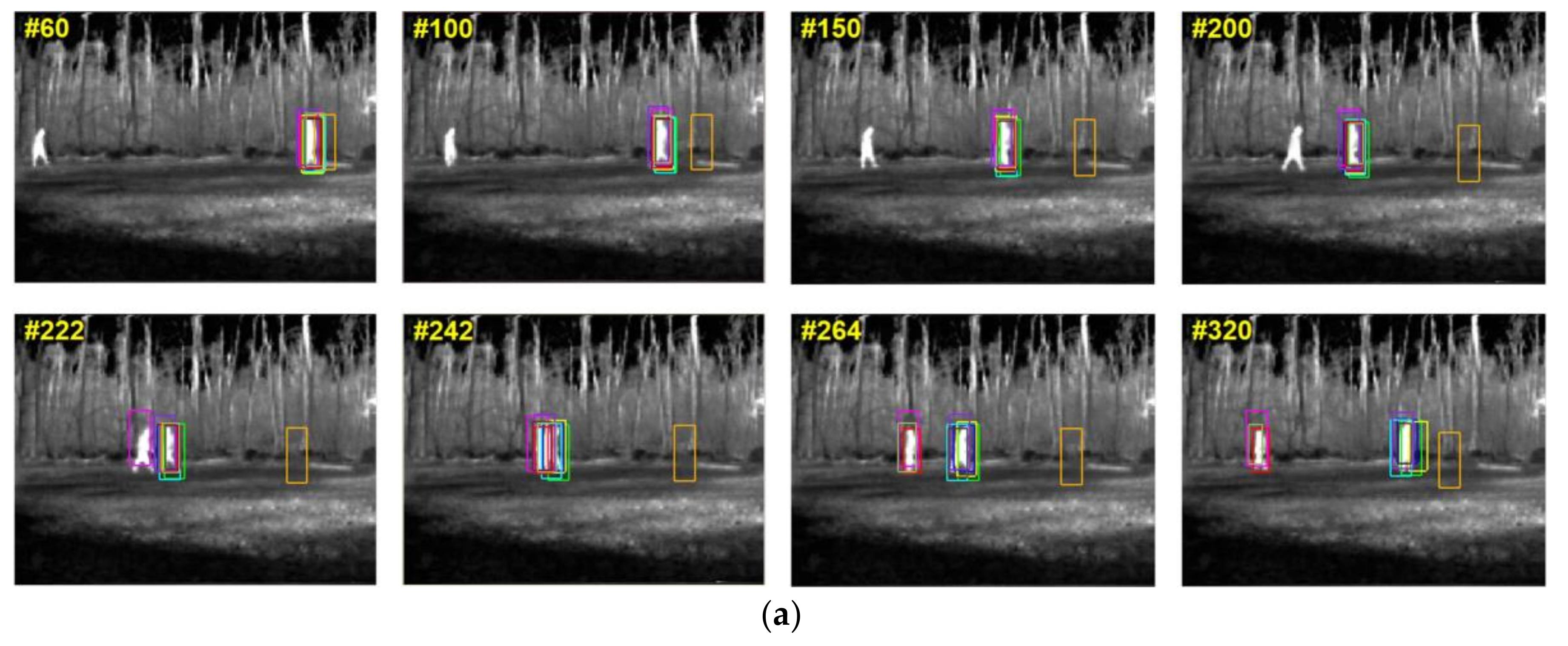
Five resulting images of each sequence are shown in
Figure 2 and the ten corresponding template images are also given at the bottom of each image. Note that the targets that were tracked by our algorithm are marked in red rectangles.
As we can see in
Figure 2a, the target of interest in Seq.1 does not have obvious intensity or pose changes, so the templates at the bottom are not replaced during the whole process. However, the occlusion that is caused by the overlap with another man around the 240-th frame is a big challenge. Owing to the occlusion term in our optimization function, this problem is easily solved and no drifts occur during the tracking.
The man in Seq.2 walks from the near to the distant, which results in severe scale variations. What is more, the background patterns within the tracking rectangle also vary a lot, leading to the template update around the 160-th frame, but the tracking performance is satisfactory as a whole because of the standard variance of scale parameter set in the state transition model.
Seq.3 is also a challenging sequence with pose variation that results from the dramatic rotation of the face. The appearance model of target is quite likely to change when its pose changes suddenly. Fortunately, as we can see in
Figure 2c, the templates are updated two times around the 150-th and 232-th frames, and thus the drifting phenomenon is avoided.
The targets in Seq.4 and Seq.5 both undergo occlusion disturbances. The telegraph pole and trees occlude the car at times in Seq.4, while the pedestrians as well as the street lamps cause partial or full occlusions in Seq.5. Besides, we argue that the moving targets in these two sequences are more difficult to track than Seq.1, because the target/background and target/occlusion contrasts are relatively weaker. Regardless of the afore-mentioned difficulties, the tracking results are of satisfaction according to
Figure 2d–e.
The target in Seq.6 is also a car driving on the highway. However, the car is blurred and the global contrast is much weaker than Seq.4. For the former half, the global illumination is weak, and both the car and the highway are dark; for the latter half, the illumination sharply rises, causing a high possibility of tracking failure around the 262-th frame. Because of the suitable frequency of template update, the illumination variation does not affect the tracking performance remarkably.
For Seq.7, there is a dim and small target to be tracked and the gray level distribution of the cloud background is inhomogeneous. On the one hand, the small target is lack of shape and texture information, and the local target/background is the weakest one among the seven sequences. Besides, Gaussian noise distributes around the whole image, making the small target dimmer and more difficult to be distinguished from the background. Another point that should be mentioned is that when the small target is immersed in the heavy cloud, the cloud can also be seen as occlusion. According to
Figure 2g, the tracking precision of this sequence is quite high, which, we consider, is a comprehensive result of the low-rank representation and the total variation regularization term.
4.3. Qualitative Comparisons
In this section, we qualitatively compare our tracker with other state-of-the-art trackers, including conventional gray level histogram-based particle filtering (PF) [
10], mean-shift (MS) [
9], incremental instance learning (IVT) [
15], weighted multiple instance learning (WMIL) [
21], accelerated proximal gradient L
1-tracker (L
1APG) [
14], fast compressive tracking (CT) [
17] and probability continuous outlier model (PCOM) [
46], deep learning tracker (DLT) [
25], and convolutional networks (CNT) [
23] methods on the seven test infrared sequences. For fair comparisons, all of the compared methods are evaluated with their default parameter settings. Note that the particle numbers of PF, IVT, L
1APG, DLT, and CNT are set to be 500 and their affine parameter standard variances are also the same as our tracker.
As is shown in
Figure 3, the tracking results of all the trackers are presented in the bounding boxes with different colors. The seven test sequences include almost all of the adverse conditions in infrared target tracking: occlusion, overlap, pose change, illumination change, scale change, weak contrast, noise, and small size. On account of the strategy that the occlusion is regarded as the outliers from target appearance and is distinguished from the inliers with high accuracy in our proposed algorithm, the state of moving target can be well estimated, regardless of the existence of occlusion. The posterior probability of target state is calculated via an affine subspace under the PF framework so that the scale and pose variations can be overcome. Besides, the total variation regularization term prevents the noise being separated into the occlusion matrix, so our tracker can achieve a robust performance under the noise condition.
PF and MS trackers can only achieve satisfactory performances when the target appearance keeps constant and the target/background is relatively high, mainly because they only use grayscale histogram to judge the similarity between the current candidate and the template. As a result, these two trackers are easy to fail in practice.
Since IVT tracker projects the moving target onto a PCA orthogonal subspace and quantizes the similarity between the candidate sample and the template using Mahalanobis distance, it is non-sensitive to partial occlusion and pose variation to a certain degree. As is shown in
Figure 3c,d,f, the tracking results of Seqs. (3, 4, 6) are quite good. However, this tracker fails when the real target is overlapped with another target with a similar appearance, which can be reflected in
Figure 3a,e.
PCOM tracker performs well on Seq. 2 and Seq.4 with pose variation and slight occlusion, because these kinds of appearance change can be estimated by the PCA subspace that is used in PCOM, but the PCOM tracker loses targets in other sequences. Drift is likely to happen on the condition that the neighboring background pixels are classified into the principal components, while part of the target pixels are recognized as the outliers instead.
CF and WMIL trackers are implemented based on classification models and the Haar-like feature utilized mainly represents the local structures, rather than the general view of target, so they can only track targets with conspicuous appearances, which means that the local contrast should be high enough if we want to achieve great tracking results. According to
Figure 3a,e,f, CF and WMIL totally fail in Seqs. (1, 5, 6) due to the serious overlap and weak contrast.
L
1APG combines the challenging interferences (such as occlusion, noise) into a set of trivial templates, so it performs quite well in most scenes, e.g., Seqs. (3, 4, 6). However, it would also lose the target (see
Figure 3a,e,g) because its L
1 optimization function may converge to an incorrect position due to the fact that the non-zero entries in the trivial templates are randomly distributed.
DLT and CNT trackers are both deep learning-based algorithms, so their tracking results depend on the features that were extracted from training samples to a great extent. Generally speaking, these two trackers are able to achieve relatively satisfactory performances in the test sequences when compared with other seven state-of-the-art trackers, but their robustness is weaker than our method. In regard to the DLT tracker, we find that it works quite well in Seq.3, because the size of face in Seq.3 is comparatively large and the target feature is easy to represent; however, its tracking results of Seq.1 are poor, mainly because the moving target in Seq.1 undergoes overlap with another person, proving that DLT does not possess robustness to appearance overlap. It is remarkable that CNT tracker succeeds in Seq.2, the object in which has severe scale changes, and Seq.6, the illumination in which varies from dark to bright. We consider it is owing to the fact that the first layer of the convolutional network is constructed by a set of cell feature maps which can not only preserve the local structure of the target, but also keep its global geometric layout, even when the illumination and target size changes.
It should be noted that all the algorithms, except our tracker, completely lose the target in Seq.7 at last, indicating that IR image noise is the most serious interference for most trackers.
4.4. Quantitative Comparisons
Two extensively accepted metrics, including center location error
and average overlap score (AOS) [
47], are employed to evaluate the performances of the above-mentioned trackers quantitatively.
The normalized center location error
is defined as the absolute Euclidian distance between two central points, which is normalized by the diagonal length of the ground truth rectangle
:
where,
is the center of the tracking result;
is the center of the ground truth.
Table 2 lists the average normal center location errors
and the last row of this table is the average error of each tracker over all of the sequences. It should be noticed that a smaller
means a more accurate tracking result.
In order to further verify the conclusions made in
Table 2, the precision plot curve is utilized to depict the precision rate of tracking. It is defined as the proportion of frames, the center location errors of which are smaller than a given threshold in pixel. As is shown in
Figure 4, the abscissa axis denotes the center error threshold and the vertical axis denotes the precision rate under each threshold.
It can be seen from
Table 2 and
Figure 4 that the tendencies that are reflected by the precision plot curves exactly match the statistical data provided by the table. First all, our tracker achieves the best performances in all the seven sequences when considering the fact that all the areas covered by the red curves in
Figure 4 are obviously much larger than others, and our average error is at least 32 times smaller than that of WMIL, which wins the second place in terms of the aggregate performance. To be more specific, PCOM,
, IVT, DLT, and CNT do well in Seq.2, Seq.3, and Seq.6, in which the
values are smaller than 1, whereas they sharply reach 2 in other sequences containing overlap or noise, indicating that they do not have satisfactory robustness to these disturbances. Besides, CF and WMIL can get relatively small
values and small areas covered by the precision curves in Seq.3 because the target (a moving face) occupies a large area in the image that is suited to the construction of a classifier. In addition, the
values of MS and PF are comparatively smaller despite of the existence of slight drifts, but it is absolutely cannot reach the standard of being precise because the resulting rectangles in Seq.1, Seq.5, and Seq.7 have already been far away from the ground truth intuitively. Most of the
values of DLT and CNT are smaller than 1, convincingly demonstrating that deep learning is a powerful tool in visual tracking. But we need to recognize that IR sequences are more challenging than RGB-based sequences for learning-based trackers due to lack of object feature. When the target size and target/background difference decrease (see Seq.7), or the number of disturbance targets increases (see Seq.5), the tracking error improves obviously. When considering that the
of DLT in Seq.1 increases to larger than 2, we argue that although DLT is robust to illumination and size changes, it fails when facing occlusion caused by disturbance target with a similar appearance. We emphasize that noise in IR image is a huge disturbance for DLT and CNT trackers, and this adverse factor is ignored by most of the deep learning-based trackers.
Another index, called the success plot, is applied to further evaluate the tracking results in this work. It is drawn based on the average overlap (AOS) that takes both the size and the scale of target into consideration. Given a tracked bounding box
and the ground-truth bounding box
of the target of interest, the overlap score (success rate) R [
48] is defined as Equation (20):
where,
and
denote the intersection and union operators, respectively, and
represents counting the pixel number in a certain region.
We judge whether a tracker is able to successfully track a moving target in each frame by means of examining whether R is larger than an AOS threshold
. The success rate falls down to 0 when
varies from 0 to 1. Normally, the average success rate with a fixed AOS threshold
is utilized to evaluate the overall performance of a tracker [
48].
As is revealed in
Figure 5, our tracker can achieve a success rate that is higher than 90% when
in all of the sequences, fully demonstrating its robustness in different infrared imaging conditions and various background types. Next, we would like to discuss other trackers at length. For Seq.1, only WMIL and CNT can get a success rate higher than 50%, which matches the fact in
Figure 3a that only the bounding boxes of these two trackers do not drift far away from the real target. All of the compared trackers, except for DLT and CNT, have poor success rates (<10%) in Seq.2 with the challenge of scale variation, which means that they all fail in this sequence. Besides, the success rates of IVT,
, PCOM, CF, DLT, and CNT in Seq.3 are satisfactory (>90%), and others are all higher than 70%. This is mainly because the area of face in Seq.3 is large and almost keep constant, only resulting in slight drifts for the most trackers. For Seq.4, only MS can keep the rate at a relatively high level (around 70%) while the ones of PF, L
1APG and WMIL drop down to 10% or even lower, and we argue that it is the frequent occlusions that decrease their values. The pedestrian in Seq.5 has a small size and other pedestrians, as well as the telegraph poles generate partial or full occlusions from time to time, so IVT, L
1APG, PCOM as well as DLT achieve almost the same poor performances where their rates are approximately around 30%, while MS and PF only possess a 5% success rate. More seriously, WMIL has completely lost the target since it starts in the 2nd frame, so its success rate keeps 0 all the time. Considering that L
1APG, DLT and CNT are robust to illumination variations to some extent, its success rate (>85%) is close to ours in Seq.6, but others, especially CF, WMIL, PF, and PCOM, do not have such kind of advantage. Seq.7 is the most difficult sequence to cope with among all of the test sequences due to the extremely small target size and the strong noise disturbance. It can be seen from
Figure 5g that except for L
1APG, all of the compared trackers immediately lose the small target immersed in the background clutters and noise. As a matter of fact, in the latter half of the sequence, L
1APG also fails and its success rate is dissatisfactory (around 25%), either.
Table 3 lists the running time of each tracker, and the average time over all of the sequences is shown in the last row. As we can see, PCOM achieves the fastest running speed which is almost 20 fps and the discriminative approaches, e.g., WMIL and CF, also perform well in terms of running efficiency. DLT and CNT get low running efficiencies on all the seven test sequences, which are approximately 0.3 fps and 1 fps, respectively. Actually, deep learning-based methods using PF framework always suffer from long running time, even though CNT has simplified the convolutional networks. The average running time of our tracker is 0.2311 s, so the frequency is around 5 fps, which still may not meet the standard of real-time running. We notice that the similar condition happens in MS, PF and L
1APG, which is mainly due to the fact that there are more iteration procedures for convergence in these kinds of trackers. However, we believe that our running efficiency can be greatly improved if the code optimization is exploited and a more appropriate running platform is used in the future.