Abstract
As speckle seriously restricts the applications of remote sensing images in many fields, the ability to efficiently and effectively suppress speckle in a coherent imaging system is indispensable. In order to overcome the over-smoothing problem caused by the speckle suppression algorithm based on classical sparse representation, we propose a non-local speckle suppression algorithm that combines the non-local prior knowledge of the image into the sparse representation. The proposed algorithm first applies shearlet to sparsely represent the input image. We then incorporate the non-local priors as constraints into the image sparse representation de-noising problem. The denoised image is obtained by utilizing an alternating minimization algorithm to solve the corresponding constrained de-noising problem. The experimental results show that the proposed algorithm can not only significantly remove speckle noise, but also improve the visual effect and retain the texture information of the image better.
1. Introduction
The ability to efficiently and effectively suppress speckle is indispensable, since speckle noise is generally serious. It causes difficulties for subsequent processing in coherent imaging systems, such as synthetic aperture radar (SAR) images and infrared target detection in remote sensing [1,2]. Generally, we can divide speckle noise reduction into two categories: (i) multi-look processing by averaging several looks (images) to suppress speckle during imaging process, and (ii) image filtering approach after imaging process [3,4]. The first method was widely used in the last century since it is straightforward and also has good noise reduction performance. However, one of its main drawbacks is that it seriously reduces azimuth resolution. Therefore, image filtering after imaging process has been utilized as an alternative approach to overcome this drawback.
One of the most commonly used filtering approaches to speckle suppression is via the wavelet transform [5,6]. The corresponding method decomposes images into different scale components by using wavelet transform. Then, it removes the high-frequency components generated by noise, and reconstructs the image to suppress noise. In order to obtain better de-noising methods, we should consider the effect of speckle on wavelet coefficients. Since wavelet technology has better time-frequency characteristics compared with Fourier analysis, it can effectively suppress noise and has better edge preservation. The frequency intervals that are supported by the wavelet are of different sizes of squares. With decreasing resolution, it can only use spots to approach a singular curve, and thus cannot optimally represent high-dimensional functions with a line or surface that contains singularity, which means the wavelet transform cannot represent images more sparsely. Furthermore, the 2D wavelet has limited directions [7], and it cannot effectively capture the direction information.
A potential approach to addressing the problems mentioned above is to utilize the multiscale geometric transforms. The dual-tree complex wavelet transform (DTCWT), contourlet, and curvelet transforms [8,9,10] have been commonly used in speckle noise reduction. However, these multiscale geometric transforms also have certain shortcomings. For example, DTCWT does not provide optimal sparse representations; contourlet is not a shift-invariant system; and curvelet is not constructed by a single base function, causing incompatibility with the multi-resolution framework and problems with discretization [11]. Therefore, there are some problems (e.g., blurred edge and texture, as well as artificial texture) when using the above transforms to suppress speckle.
In order to overcome the shortcomings mentioned above, Glenn et al. derived the shearlet transform based on the supported tight wavelet frames and strict logic mathematics. The image approximation order of this transform is the same as that of curvelet, but the implementation is simpler and more flexible [11,12]. Therefore, shearlet has been rapidly applied to general image de-noising, such as hard threshold de-noising in the shearlet domain [12] and total variation de-noising algorithm in the shearlet domain [13]. Moreover, the bivariate model has been applied in the wavelet to shearlet domain to de-noise [14]. Speckle suppression is also widely used in the shearlet transform. For example, the speckle suppression algorithm in a non-subsampled shearlet domain was proposed to avoid translation variability [15], and it achieved good results. In [16], we also proposed a speckle reduction method based on the context model in a shearlet domain by combining the statistical properties of speckles. Although these algorithms achieved a good de-noising effect, we realize that these algorithms based on statistical characteristics in shearlet domain would virtually limit the de-noising effect.
Recently, sparse representation has been widely adopted for signal processing [17,18], and results in excellent de-noising performance [19,20]. However, these methods need an optimal complete sparse dictionary, the construction of which is difficult and time-consuming. Consequently, Zhao et al. [21] proposed a new wavelet de-noising framework based on sparse representation, among which the de-noising problem was transformed into an optimization problem using steepest descent to iteratively recover the wavelet coefficients of the contaminated signals. Moreover, he also proved the uniqueness and unbiased estimation of the optimization problem. Therefore, the de-noising algorithm is efficient and works well. However, using the steepest descent method in this method leads to a limitation of the measurement matrix, increasing the difficulty of constructing the measurement matrix.
The previous analysis shows that the 2D discrete wavelet cannot provide an optimal sparse representation. Therefore, in [22], we replace wavelet transform by shearlet to implement image sparse decomposition. This can represent the image optimally. Since speckle is multiplicative noise, the coherent noise is usually converted into additive noise before using the de-noising algorithm. To reduce the speckle with the sparse model, it is popular [23,24] to directly transfer the multiplicative noise model into the additive noise model (see Equation (4) in Section 2.2) rather than by taking the logarithm transform, since after taking the logarithm transform, the image is probably not sparse in the conventional transforms (e.g., the wavelet transform). More importantly, the mean of the resulted additive noise model by taking the logarithm is not zero [23,24]. In order to adapt the noise reducing algorithm based on sparse representation, we adopt the noise model in [23,24] to turn the multiplicative noise into additive noise of zero mean. Then, the unconstrained optimization problem constructed by the sparse de-noising model can satisfy the convergence condition of the conjugate gradient method. Therefore, the conjugate gradient method is used to solve the optimal model, which can reduce the restrictions for the measurement matrix. The improved method has the same unbiased estimation as the original one, and its optimal solution is also a local minimum. Moreover, the convergence of the conjugate gradient method is better than the steepest descent method. We improve the selection of the threshold, the solution of noise variance, and the selection of the iterative initial value. Then, we propose a sparse de-noising model based on Bayesian in shearlet domain. The algorithm achieved good results.
It can be seen that all the de-noising algorithms mentioned above use the local prior knowledge of the image to suppress coherent noise, which largely limits the effect of speckle reduction of the natural image. The non-local means (NLM) image de-noising algorithm [25] can suppress noise by using a large amount of redundant information and non-local self-similarity of the natural image itself. There are many patches similar to each patch in a natural image. NLM can determine weighted coefficients by comparing the similarity of the neighborhood patches of each pixel. The estimated central pixels of the current window can be replaced by a weighted sum of the central pixels in the similar patches. NLM depends on the similarity between two patches rather than just relying on the relationship between pixels to estimate the image pixel gray values. Thus, the local neighborhood framework is broken by the weighted average process of each pixel. Instead, the similarity of the patch structure in the whole image has been taken into account, and the redundant information provided by the image is fully utilized. Thus, NLM can get a better filtering effect [25].
Although NLM has received extensive recognition and attention due to its excellent de-noising performance, the high computational complexity caused by weight calculation limits the application and development of NLM. Liu et al. proposed a fast non-local de-noising algorithm [26] which can partly address this problem. Although NLM achieved a good de-noising effect, the protection of the structural information of the original image is still insufficient. The authors of [27] proposed a block method of 3-dimension (BM3D) algorithm based on the similarity between blocks of the image. In BM3D, the image is first divided into blocks of a certain size. According to the similarity between blocks, the 2D image blocks with similar structure are combined to form a 3D array, and then the 3D array is processed by joint filtering method. Finally, the processed image is returned to the original image by inverse transform, and then the de-noised image is obtained. This method not only has a high signal-to-noise ratio, but also has a good visual effect. However, both the shape of the block and the joint filtering algorithm can be improved, such as the method in [28] which uses a polygon as the block shape and uses principal component analysis (PCA) to reduce the dimension to find the optimal sparse block. This can achieve better results. In addition, the de-noising algorithms based on NLM have also been rapidly used for speckle reduction. For example, Ref. [29] put forward a non-local speckle suppression algorithm based on variance stabilization transformation; Ref. [30] proposed a non-local speckle suppression algorithm based on the Bayesian theory; and Ref. [24] applied the BM3D framework to speckle suppression and proposed a block matching algorithm for coherent noise by using linear minimum-mean-square-error (LMMSE) filtering. According to the special distribution of coherent noise, Ref. [31] proposed a fast adaptive speckle suppression algorithm and achieved good results.
Although the non-local de-noising algorithm can be well applied to the speckle suppression, it is easy to produce artificial texture with the non-local de-noising algorithm due to the block effect, causing visual discomfort. The de-noising algorithm based on sparse representation can fix this problem by using sparse information. However, the sparse de-noising algorithm proposed in [22] did not use the non-local information of an image. It can be seen that if the non-local prior condition of the image is added into the speckle suppression by using the sparse representation, the ability of noise suppression and the visual effect of the de-noised image will be greatly improved. The main contributions of this paper are as follows. Firstly, the non-local prior information of an image is applied to the de-noising model based on sparse representation, and we can obtain a new speckle suppression algorithm in a sparse domain with non-local priors. Secondly, the alternating iterative algorithm is used to solve the de-noising model. The new algorithm can not only utilize the advantage of sparse representation, but also takes advantage of the non-local de-noising, which can provide a new idea for a de-noising algorithm based on sparse representation. Therefore, in order to overcome the disadvantages of the de-noising model based on sparse representation in shearlet domain, we propose a new speckle suppression model based on sparse representation combined with non-local image structure, and we transform the noise suppression into an optimization problem and propose an algorithm to solve it.
2. Speckle Suppression Model in Sparse Domain
2.1. Shearlet Transform
The shearlet transform overcomes the disadvantages that the wavelet cannot represent the image optimally and the difficulty of discretizing the curvelet. It also overcomes the flaw that contourlet does not conform to the multiscale geometric analysis (MGA) theory [11]. The approximation order of shearlet is the same as that of the Curvelet [11,12], but the implementation of shearlet is simpler and more flexible. When the dimension , the affine transformation system of the shearlet function is:
where and denote two-dimensional invertible square matrices, and . is the the set of all integer numbers and is the set of all real numbers. Let (d = 1, 2) be an anisotropic expansion matrix, and (d = 1, 2) be a shear matrix. Generally, , and . Similarly, let , . Then, a set of wavelet functions can be obtained:
Therefore, the shearlet transform of f is defined as:
where . The frequency supporting region of is a pair of trapezoid regions with a size of about and gradient about . In this paper, we use the shift-invariant shearlet transform mentioned in [12] to implement SAR image de-noising based on sparse representation. This discretization scheme is implemented by cascading non-sampling Laplace transform and shear transform. Because of the high redundancy, the sparse representation of the image is better; thus, the de-noising effect is better.
2.2. Noise Suppression Model in the Sparse Domain
Coherent speckle is generally assumed to obey the multiplicative noise model [22,23,24]:
where and represent the observed noisy image and the noise-free signal, respectively, and is the multiplicative noise and is assumed to be distributed with a Gamma distribution with mean equal to one [23]. Here is the pixel position.
To remove the multiplicative noise in Equation (4), a natural method is to transfer the multiplicative noise model into the additive noise model by taking the logarithm of . Logarithmic transformation attempts to turn multiplicative noise to familiar white Gaussian noise. After de-noising, index transform is used to turn the de-noised image into original statistical model. However, after logarithmic transform, the mean of the additive noise is not equal to zero. Additionally, in the scheme of solving the speckle suppression model with sparse representation method in [22], we need the mean of the additive noise model is zero. Moreover, in the case of a low number of looks, the de-noising error by logarithmic SAR image is very large. Thus, to reduce the speckle with the sparse representation method, it has been widely utilized [23,24] to directly transfer the multiplicative noise model into the additive noise model as
where now is a random variable with zero mean [23] and can be considered as additive noise. For a better description, we rewrite the above additive noise model as
where can be viewed as the additive noise. Though now is the re-scaled noise that also depends on the image , it is expected that the shearlet transform of the noise n is not sparse, while the shearlet transform of s is sparse, which is important in speckle suppression method based on sparse representation in [22]. Figure 1h shows the shearlet transform of the noise n.

Figure 1.
The original image and noise image: (a) Original image. (b) Noise image. (c) Noise . (d) Noise . (e) The shearlet coefficients of the noise image. (f) The shearlet coefficients of the de-noised image by our method. (g) The shearlet coefficients of noise by subtracting (e) from (f). (h) The shearlet coefficients of noise n.
As we explained before, for most natural images without noise, the shearlet coefficients obtained by shearlet transform are sparse [11]. That is, most of the coefficients after the shearlet transform are very small and almost close to zero. If the natural image is contaminated by noise, the sparsity of the shearlet coefficients will be greatly reduced, so the de-noising target is converted to recover the sparsity of the shearlet coefficients. Therefore, the de-noising process comes down to the optimization problem of recovering the sparsity of the shearlet coefficients [22]. Figure 1c,d give the noise images based on this noise model. This noise model can help to estimate the noise parameters to recover the signal by sparse representation, and the details can be found in [22]. Therefore, let the above shearlet transform coefficient be (see the schematic diagram in Figure 1e), where l represents the different directions of shearlet decomposition, j represents different scales, and represents different positions. For convenience, is used to represent the shearlet transform coefficient matrix of one direction in a scale (the size is ), and ( M less than N ) is a random measurement matrix of sparse representation ( should satisfy the uniform uncertainty principle (UUP) [20]). If , the optimal sparse coefficient matrix can be obtained by solving the following problems:
where is the variable in this optimization problem according to the coefficients of shearlet . is the optimum solution.
For the convenience of the solution, Equation (7) can be converted to Equation (8) to solve.
where is a zero norm (i.e., the number of non-zero elements). Although Formula (7) is an NP hard problem in numerical solution, it can also be solved by orthogonal matching pursuit (OMP), the steepest descent method, or conjugate gradient algorithm under certain conditions. The authors of [22] used the conjugate gradient algorithm to solve the optimal solution of Formula (8).
3. The Speckle Suppression Model Based on Non-Local Priors in a Sparse Domain
3.1. Non-Local De-Noising
Non-local-means filtering is a superior image de-noising algorithm. Its basic idea is to suppress noise by using the characteristic of repeated structure in images, overcome the over-smoothness of traditional algorithms, and improve the quality of images. The non-local self similarity of images is often described as a strong correlation between pixels or blocks in different positions, such as long edge, texture, and image with periodic structure. For a certain pixel in a noisy image sequence (where represents a noisy image and represents the pixel position), we define as a rectangular neighborhood centered at (generally, the length and width are all set to be M). Then, the weight of the similarity between pixel and pixel in image can be calculated as follows [25]:
where
is the normalized coefficient of weight and h is the smooth parameter of non-local smooth filtering. Parameter h controls the magnitude of the weight by controlling the attenuation of the exponential function so as to control the degree of smoothing noise. If h is small, the attenuation effect of the power function is significant, and the level of detail retention is relatively high, so the details of the image itself will be maintained. Since the similarity between pixel and pixel depend on the similarity degree of rectangle neighborhoods and , the rectangle neighborhood of the image is more similar when the weight is larger. At the same time, the weight satisfies the following conditions: and [25,31].
Although the non-local de-noising algorithm can be applied well to speckle suppression, the non-local de-noising algorithm easily produces artificial texture due to the block effect, causing visual discomfort (Figure 2c,e show that artificial texture is drawn into the de-noised image by the de-noised method based on NLM). However, the de-noising methods based on sparse representation can make good use of the sparse information of the image to solve this problem. Therefore, we combine two methods to suppress speckle.

Figure 2.
The de-noising images using different methods: (a) Lee filter. (b) Bayesian threshold shrinkage de-noising algorithm in shearlet domain based on sparse representation (BSS-SR). (c) Nonlocal synthetic aperture radar (SAR) image denoising algorithm based on local linear minimum-mean-square-error (LMMSE) wavelet shrinkage (SAR-BM3D). (d) Bayesian shrinkage de-noising algorithm in shearlet domain based on continuous cycle spinning (CS-BSR). (e) Blind de-noising algorithm based on weighted nuclear norm (BWNNM). (f) Speckle suppression algorithm based on sparse domain with non-local priors (NL-SR).
3.2. The Speckle Suppression Model
Let represent the shearlet transform, then . For convenience, the noise reduction process in the sparse domain is simplified as , and is used to represent the noise suppression model. is the variable in the function according to an image. By only applying non-local de-noising to Equation (6), we get
where is the result after image de-noising and is a search window in non-local de-noising. is the weight of two similar pixels, which is related to the location of two pixels and the definition of similarity function, and it can be designed according to the specific application. In order to incorporate the non-local prior knowledge into the sparse noise suppression model, it is necessary to convert Equation (11) to the following:
This is the non-local prior information of the image in sparse domain. Next, we add the non-local prior knowledge represented by Equation (12) to the sparse noise reduction model.
The speckle suppression method based on sparse representation only uses the local prior knowledge of the image to reduce noise. This largely limits the effect of speckle reduction. To overcome this weakness, the simplest method is to use Formula (12) as the constraints condition of model (7). That is,
where is the variable in this optimization problem, according to the coefficients of shearlet.
For a better solution, the Lagrange multiplier method can be used to turn Equation (13) into Equation (14). We then defined
where is the optimal solution derived previously (see the schematic diagram in Figure 1f). Note that the here is a constant factor, which can be determined experimentally. is the variable based on the non-local mean filtering of the coefficients of shearlet.
Since the condition of unconstrained optimization can be solved, it is clear that Formula (14) can be solved by using the Karush–Kuhn–Tucker (KKT) condition. The most direct algorithm is the fast alternating iterative algorithm.
3.3. The Alternating Algorithm for Speckle Suppression
The alternating iterative algorithm is used to solve the de-noising model mentioned above. There are three unknown parameters , , and in Equation (14). A practical strategy for solving this problem is the alternating iterative algorithm. The main idea is to keep one of the variables constant and optimize it over the other variables.
At the first step, we fix based on the definition of , and then the Formula (14) is converted into Equation (8). This is the same as the de-noising model proposed in [22], which can be solved by using the conjugate gradient method. The detailed solution algorithm can be seen in [22].
Then, is updated as the optimal solution of , defined as in the last step, which is converted into the following problem:
It can be seen that the form of Equation (15) is similar to the optimization model obtained in [32]. Thus, the optimal solution of this formula can be solved by the fast bivariate iteration algorithm shown in the literature [32].
Next, we can fix first and solve and . Then, fix and to solve and . Finally, the solution of the whole optimization problem is obtained. In our methods, we set the number of iterations to 50. The whole algorithm is presented in Algorithm 1.
In this processing, the windows of patches and the searches windows around the defined patches in NLM have an influence on the de-noising performance. In our paper, we first fix the windows of the patches, and then find the best search windows around the defined patches. Then we get the best windows of the patches by fixing the search windows in the experiment. Finally, the windows of the patches are , while the search windows are .
| Algorithm 1: The proposed SAR image de-noising method |
| the noisy SAR image |
| calculate by applying shearlet transform to image |
| obtain by |
| calculate and by Equation (9)– (12) |
| solve Equation (14) by alternating iterative algorithm |
| : let , the number of iterations N can be set to 50 |
| get by Equation (8) [22] |
| to N |
| 1: set , update and as |
| get and by using fast bivariate iteration algorithm in [32] |
| 2: fix , update and as |
| get and by using fast bivariate iteration algorithm in [32] |
| set |
| obtain de-noised image by applying inverse shearlet transform to |
| the de-noised image |
4. Experimental Results and Analysis
In order to verify the reliability and validity of the proposed algorithm, multiplicative noise was added to an original image, and each denoising method was used in the de-noising process. The de-noising algorithms were, respectively: Lee filter [4], the Bayesian threshold shrinkage de-noising algorithm in shearlet domain based on sparse representation in [22] (BSS-SR), the nonlocal SAR image denoising algorithm based on local LMMSE wavelet shrinkage in [24] (SAR-BM3D), the Bayesian shrinkage de-noising algorithm in shearlet domain based on continuous cycle spinning in [33] (CS-BSR), the blind de-noising algorithm based on weighted nuclear norm in [34] (BWNNM), and the speckle suppression algorithm based on sparse domain with non-local priors (NL-SR) proposed in this paper. Experimental results were obtained by using the authors’ own code, available online or run by the authors themselves on our test images. The window size of the Lee filter was . The decomposition levels of shearlet in BSS-SR, CS-BSR, and NL-SR were all two. There were four direction high-pass bands in the first level, and eight direction high-pass bands in the second level. In SAR-BM3D, we used the default parameters selected by the authors; that is, Daubechies-8 undecimated discrete wavelet transform with a three-level decomposition had fixed groups of dimension , the search area was . In BWNNM, the size of patches was . Figure 1a is the original image and Figure 1b is the noise image that added multiplicative noise with the number of observations . Figure 1c is the noise in our model, and Figure 1d is the speckle noise. Comparing Figure 1c to Figure 1d, we can find that they are different. The additive noise in our paper is zero mean, and its variance depends on signal. Figure 1e shows the four-direction shearlet coefficients at scale 2 of the noise image. Figure 1f shows the four-direction shearlet coefficients at scale 2 of the de-noised image by our method. Figure 1g shows the shearlet coefficients of noise by subtracting (e) from (f). Figure 1h shows the shearlet coefficients of noise in our model; we can easily see that it is not sparse. From Figure 1e–g, we can see that our method can hold back the edge information and effectively reduce the speckle. Figure 2 shows the experimental results.
From the experimental results, it can be seen that the image filtered by the Lee filter in Figure 2a still contains a lot of speckle noise. In Figure 2b, there is some blurring at the edges of the image de-noised by BSS-SR. Although the noise suppression performance of SAR-BM3D in Figure 2c shows that the speckle is effectively suppressed, a lot of details of the original image are lost. Although Figure 2d shows that CS-BSR can effectively suppress the blurring of the edge of the image in the process of de-noising, suppression noise ability is weakened. In Figure 2e, although BWNNM can further suppress the noise and retain the edge of the image better, there are still some residual noises. From Figure 2f, we can find that NL-SR has better visual effects than the BWNNM and SAR-BM3D. Compared with BSS-SR and the CS-BSR, the speckle noise is effectively suppressed, so it shows the best de-noising effect. This fully demonstrates the advantages of the combination of non-local priors and the de-noising model based on a sparse domain.
In order to better demonstrate the superiority of the algorithm proposed in this paper, four objective evaluation criteria were used to reveal the advantages of the NL-SR algorithm. These four objective evaluation criteria are: peak signal-to-noise ratio (PSNR) [22], equivalent numbers of looks (ENL) [22], edge preservation index (EPI) [22] and unassisted measure of quality based on first- and second-order descriptors of the ratio of the de-noised image of the natural image (UM) [35]. A larger PSNR indicates that the de-noising ability of the algorithm is stronger. A larger ENL shows that the visual effect of the algorithm is better. A larger EPI indicates that the edge-preserving ability of the algorithm is stronger. UM does not rely on the original image to evaluate the de-noised image, and a smaller UM shows that the performance of the speckle suppression algorithm is better. Table 1 shows the objective evaluation values of each de-noising algorithm for noisy images containing different quantities of noise. To show the performance of each method clearly, we highlight the best result in the table with bold font.

Table 1.
Objective evaluation of different de-noising methods. ENL: equivalent numbers of looks; EPI: edge preservation index; PSNR: peak signal-to-noise ratio; UM: unassisted measure of quality based on first- and second-order descriptors of the ratio of the de-noised image of the natural image.
From the objective evaluation criteria shown in Table 1, it can be proved that the non-local priors preserve the structure information of the image better than the simple noise suppression algorithm based on sparse domain, which makes the EPI of NL-SR and BWNNM algorithms better than that of BSS-SR and CS-BSR. The noise suppression based on the sparse domain can better suppress speckle, which is why PSNR of CS-BSR is higher than that of BWNNM and PSNR of BSS-SR is higher than that of SAR-BM3D. It can be seen that the NL-SR combined with non-local priors and sparse domain de-noising achieves the best de-noising effect, and it also shows that the combination of the two methods is suitable for speckle suppression.
Of course, we also test the proposed algorithm in actual coherent imaging. The test images we used are the SAR images of TerraSar-X, which are provided on the website of Federico II University in Naples, Italy. The test SAR images are shown in Figure 3.

Figure 3.
The natural SAR images: (a) The noise image of woods. (b) The noise image of an urban area. (c) The noise image of a lake.
Figure 3a shows a SAR image of woods. Figure 3b shows a SAR image of an urban area. Figure 3c shows a SAR image of a lake. They are de-noised by using the above noise suppression algorithms. Figure 4 shows the de-noised images of Figure 3a.

Figure 4.
The de-noised woods SAR images by using each de-noising method: (a) De-noised using Lee filter. (b) De-noised using BSS-SR. (c) De-noised using SAR-BM3D. (d) De-noised using CS-BSR. (e) De-noised using BWNNM. (f) De-noised using NL-SR.
From Figure 4, it can be seen that the effect is the worst by using Lee filter. BSS-SR and CS-BSR algorithms remove some edge texture when de-noising. BWNNM and SAR-BM3D de-noising algorithms produce some artificial textures. The proposed NL-SR algorithm can keep the edge and texture information better, and suppresses the artificial texture. When the image located in the white rectangular box is enlarged, we find that the de-noising effect of our method is best in the areas around the ditch. The de-noised images of other SAR images are shown in Figure 5 and Figure 6, respectively, in which Figure 5 is the de-noising result of the urban area SAR image in Figure 3b, and Figure 6 is the de-noising result of the lake SAR image in Figure 3c.

Figure 5.
The de-noised urban area SAR images by using each de-noising method: (a) De-noised using Lee filter. (b) De-noised using BSS-SR. (c) De-noised using SAR-BM3D. (d) De-noised using CS-BSR. (e) De-noised using BWNNM. (f) De-noised using NL-SR.

Figure 6.
The de-noised lake SAR images by using each method: (a) De-noised using Lee filter. (b) De-noised using BSS-SR. (c) De-noised using SAR-BM3D. (d) De-noised using CS-BSR. (e) De-noised using BWNNM. (f) De-noised using NL-SR.
From Figure 5 and Figure 6, it can be seen that the de-noising effect for both SAR images by using the six de-noising algorithms listed above are similar to those shown in Figure 4, and the de-noising effect of the proposed algorithm is the best. However, with neither a noiseless image nor an expert interpreter, it is difficult to decide whether such artifacts and edge blurring imply any loss of detail. Some help comes from the analysis of ratio images obtained, as mentioned in [24], as the pointwise ratio between the original SAR image and de-noised SAR images. Given a perfect de-noising, the ratio image should contain only speckle. On the contrary, the presence of geometric structures or details correlated to the original image indicates that the algorithm has removed not only noise, but also some information of interest. To highlight the better visual effect of our methods, we give the ratio images in Figure 7, Figure 8, Figure 9, and Figure 10.

Figure 7.
The ratio images by using each de-noised method for Figure 4: (a) Ratio image using Lee filter. (b) Ratio image using BSS-SR. (c) Ratio image using SAR-BM3D. (d) Ratio image using CS-BSR. (e) Ratio image using BWNNM. (f) Ratio image using NL-SR.
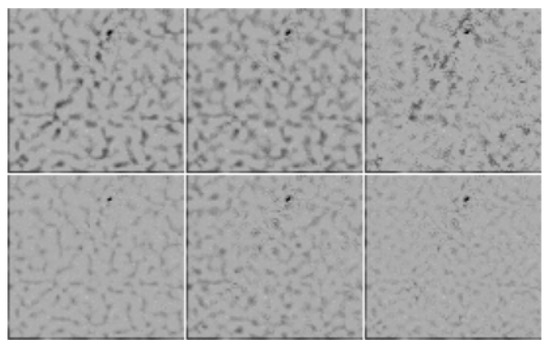
Figure 8.
The large ratio images in the black box in Figure 7.

Figure 9.
The ratio images by using each de-noised method for Figure 5: (a) Ratio image using Lee filter. (b) Ratio image using BSS-SR. (c) Ratio image using SAR-BM3D. (d) Ratio image using CS-BSR. (e) Ratio image using BWNNM. (f) Ratio image using NL-SR.

Figure 10.
The ratio images by using each de-noised method for Figure 6: (a) Ratio image using Lee filter. (b) Ratio image using BSS-SR. (c) Ratio image using SAR-BM3D. (d) Ratio image using CS-BSR. (e) Ratio image using BWNNM. (f) Ratio image using NL-SR.
From Figure 8, we can see that the ratio image of our method is more close to speckle. Figure 9 shows the ratio images from Figure 5.
From the ratio images in Figure 7, Figure 8, Figure 9 and Figure 10, we can find that the ratio image of our method has the least residual signal of the original images, and close to speckle. From this view, it can be seen that our method can achieve a better visual effect. In order to demonstrate the superiority of the proposed algorithm fully, we calculated several commonly-used noise suppression performance parameters of all the de-noising algorithms, including ENL, EPI, and UM. Table 2 demonstrates the experimental results of de-noising performance parameters for all three SAR images.

Table 2.
The performance parameters of de-nosing methods in SAR images.
From the performance parameters of all the de-noising methods shown in Table 2, the objective evaluation criteria of the proposed algorithm are better than that of other algorithms. Therefore, the speckle suppression algorithm proposed in this paper is also a good de-noising algorithm for the SAR image. Compared with the de-noising effect of forest SAR images with less texture, the values of the objective evaluation criteria of CS-BSR, BWNNM, and the proposed algorithm were much better than those of the other algorithms. Comparing the proposed algorithm to BWNNM, we can see that the proposed algorithm has the same edge-preserving ability as BWNNM from EPI in Table 2. However, the ENL of the proposed algorithm was 1.5 higher than BWNNM, and the UM of the proposed algorithm was 0.5 lower than BWNNM, which fully demonstrates the effectiveness of the de-noising framework based on a sparse domain. Comparing the proposed algorithm to CS-BSR, we can see that the algorithm improved on ENL and EPI, and reduced UM, which fully illustrates the importance of the non-local priors of the images. For urban areas (which require SAR image de-noising with more textures), from Table 2 we can see that the visual effects of the proposed algorithm were far better than the other algorithms. For the lake SAR images, with rich textures between woods and urban SAR images, the proposed algorithm also had the highest ENL and EPI, and the UM was smaller. Through the above analysis, we can see that the proposed algorithm not only has a strong ability to suppress speckle, but also has good visual effect after de-noising. It has strong edge preserving ability, and can better retain the texture information of the image.
In order to further verify the ability of the proposed algorithm to suppress speckle, the infrared images of power equipment monitoring provided by North China Electric Power University were used to test the above algorithms again. Figure 11 is the infrared monitoring image of power equipment provided by the North China Electric Power University. Figure 12 is the result of speckle suppression.

Figure 11.
The natural infrared image.

Figure 12.
The de-noised infrared images by using each de-noising method: (a) De-noised using Lee filter. (b) De-noised using BSSR. (c) De-noised using SAR-BM3D. (d) De-noised using BWNNM. (e) De-noised using CS-BSR. (f) De-noised using NL-SR.
Then, Figure 8 was used to analyze the effectiveness of the proposed algorithm in the suppression of speckle in infrared images of power equipment monitoring. From the experimental results shown in Figure 8, the effect of Figure 8a is the worst. This also shows that the Lee filter has a poor effect in suppressing the speckle of the infrared image, and there is still much noise in the de-noised image. Similarly, the de-noised image by SAR-BM3D shown in Figure 8c retains more image texture information, but the effect of speckle suppression becomes worse. The de-noised image by BWNNM in Figure 8d shows that BWNNM can suppress speckle effectively, while the edge and some details of the de-noised image are blurred. For example, the texture of the insulator above the transformer is very fuzzy, and we almost cannot see the shape of the insulator. In contrast to Figure 8b,e,f, the visual effect of Figure 8f is obviously better; that is, the NL-SR has better visual effect.
Table 3 gives the values of the objective evaluation criteria of each de-noising algorithm. It can be seen that the proposed algorithm was the best in every objective index, which fully demonstrates that the proposed algorithm can effectively suppress the speckle of the infrared image of the power equipment monitoring.

Table 3.
The performance parameters of de-nosing methods in an infrared image.
By de-noising the actual images of coherent imaging, the results show that the proposed algorithm has strong speckle suppression ability and better edge preserving ability. Therefore, it is a better speckle suppression algorithm.
5. Conclusions
This paper first reviewed the history of speckle suppression and the framework of de-noising based on a sparse domain. In image de-noising, texture loss and edge blur may be caused by the de-noising model based on sparse representation, while the artificial texture may be produced by the non-local de-noising algorithm. To overcome the above problems, we proposed a new speckle suppression method based on sparse representation with non-local priors. In this new method, we added the non-local priors as the constraint to the de-noising model based on sparse representation, which can make full use of the advantages of both types of de-noising algorithms. The new method can turn speckle suppression into an optimization problem, which can be solved by the alternating minimization algorithm. Experiments on SAR images and infrared images show that the proposed algorithm has a good noise suppression effect. However, the algorithm in this paper does not experiment on other kinds of coherent images. Therefore, we will study the universality of the algorithm in our next research.
Acknowledgments
This work was supported in part by the Natural Science Foundation of China under grants 61401308 and 61572063, the Natural Science Foundation of Hebei Province under grants F2016201142 and F2016201187, the Science research project of Hebei Province under grant QN2016085, the Natural Science Foundation of Hebei University under grant 2014-303, and the Post-graduate’s Innovation Fund Project of Hebei University under grant X201710.
Author Contributions
Shuaiqi Liu and Qi Hu conceived and designed the experiments; Chong Wang performed the experiments; Zhihui Zhu and Shuaiqi Liu analyzed the data; Jie Zhao and Pengfei Li contributed analysis tools; Shuaiqi Liu wrote the paper.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this article.
References
- Wang, Q.; Gao, J.; Yuan, Y. Embedding structured contour and location prior in siamesed fully convolutional networks for road detection. IEEE Trans. Intell. Transp. Syst. 2018, 19, 230–241. [Google Scholar] [CrossRef]
- Wang, Q.; Meng, Z.; Li, X. Locality adaptive discriminant analysis for spectral-spatial classification of hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2077–2081. [Google Scholar] [CrossRef]
- Touzi, R. A review of speckle filtering in the context of estimation theory. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2392–2404. [Google Scholar] [CrossRef]
- Di Martino, G.; Poderico, M.; Poggi, G.; Riccio, D.; Verdoliva, L. Benchmarking framework for SAR despeckling. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1596–1615. [Google Scholar] [CrossRef]
- Wang, B.H.; Zhao, C.Y.; Liu, Y.Y. An improved SAR interferogram denoising method based on principal component analysis and the Goldstein filter. Remote Sens. Lett. 2018, 9, 81–90. [Google Scholar] [CrossRef]
- Achim, A.; Tsakalides, P.; Bezerianos, A. SAR image denoising via Bayesian wavelet shrinkage based on heavy-tailed modeling. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1773–1784. [Google Scholar] [CrossRef]
- Do, M.N.; Vetterli, M. Contourlets: A directional multiresolution image representation. In Proceedings of the 2002 International Conference on Image Processing, Rochester, NY, USA, 22–25 September 2002; Volume 1, pp. 497–501. [Google Scholar]
- Ranjani, J.J.; Thiruvengadam, S. Dual-tree complex wavelet transform based SAR despeckling using interscale dependence. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2723–2731. [Google Scholar] [CrossRef]
- Gleich, D.; Kseneman, M.; Datcu, M. Despeckling of TerraSAR-X data using second-generation wavelets. IEEE Geosci. Remote Sens. Lett. 2010, 7, 68–72. [Google Scholar] [CrossRef]
- Shanthi, I.; Valarmathi, M. Comparison of wavelet, contourlet and curvelet transform with modified particle swarm optimization for despeckling and feature enhancement of SAR image. In Proceedings of the 2013 International Conference on Signal Processing Image Processing & Pattern Recognition (ICSIPR), Coimbatore, India, 7–8 February 2013; pp. 53–61. [Google Scholar]
- Easley, G.; Labate, D.; Lim, W.Q. Sparse directional image representations using the discrete shearlet transform. Appl. Comput. Harmon. Anal. 2008, 25, 25–46. [Google Scholar] [CrossRef]
- Lim, W.Q. The discrete shearlet transform: A new directional transform and compactly supported shearlet frames. IEEE Trans. Image Process. 2010, 19, 1166–1180. [Google Scholar] [PubMed]
- Easley, G.R.; Labate, D.; Colonna, F. Shearlet-based total variation diffusion for denoising. IEEE Trans. Image Process. 2009, 18, 260–268. [Google Scholar] [CrossRef] [PubMed]
- Cao, H.; Tian, W.; Deng, C. Shearlet-based image denoising using bivariate model. In Proceedings of the 2010 IEEE International Conference on Progress in Informatics and Computing (PIC), Shanghai, China, 10–12 December 2010; Volume 2, pp. 818–821. [Google Scholar]
- Hou, B.; Zhang, X.; Bu, X.; Feng, H. SAR image despeckling based on nonsubsampled shearlet transform. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 809–823. [Google Scholar] [CrossRef]
- Liu, S.; Shi, M.; Hu, S.; Xiao, Y. Synthetic aperture radar image de-noising based on Shearlet transform using the context-based model. Phys. Commun. 2014, 13, 221–229. [Google Scholar] [CrossRef]
- Peng, X.; Lu, J.; Yi, Z.; Yan, R. Automatic subspace learning via principal coefficients embedding. IEEE Trans. Cybern. 2017, 47, 3583–3596. [Google Scholar] [CrossRef] [PubMed]
- Peng, X.; Tang, H.; Zhang, L.; Yi, Z.; Xiao, S. A unified framework for representation-based subspace clustering of out-of-sample and large-scale data. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 2499–2512. [Google Scholar] [CrossRef] [PubMed]
- Tosic, I.; Olshausen, B.A.; Culpepper, B.J. Learning sparse representations of depth. IEEE J. Sel. Top. Signal Process. 2011, 5, 941–952. [Google Scholar] [CrossRef]
- Candes, E.J.; Tao, T. Near-optimal signal recovery from random projections: Universal encoding strategies? IEEE Trans. Inf. Theory 2006, 52, 5406–5425. [Google Scholar] [CrossRef]
- Zhao, R.; Liu, X.; Li, C.C.; Sclabassi, R.J.; Sun, M. Wavelet denoising via sparse representation. Sci. China Ser. F Inf. Sci. 2009, 52, 1371–1377. [Google Scholar] [CrossRef]
- Liu, S.Q.; Hu, S.H.; Xiao, Y.; An, Y.L. Bayesian Shearlet shrinkage for SAR image de-noising via sparse representation. Multidimens. Syst. Signal Process. 2014, 25, 683–701. [Google Scholar] [CrossRef]
- Dai, M.; Peng, C.; Chan, A.K.; Loguinov, D. Bayesian wavelet shrinkage with edge detection for SAR image despeckling. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1642–1648. [Google Scholar]
- Parrilli, S.; Poderico, M.; Angelino, C.V.; Verdoliva, L. A nonlocal SAR image denoising algorithm based on LLMMSE wavelet shrinkage. IEEE Trans. Geosci. Remote Sens. 2012, 50, 606–616. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J.M. A non-local algorithm for image denoising. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, CVPR 2005, San Diego, CA, USA, 20–25 June 2005; Volume 2, pp. 60–65. [Google Scholar]
- Liu, Y.L.; Wang, J.; Chen, X.; Guo, Y.W.; Peng, Q.S. A robust and fast non-local means algorithm for image denoising. J. Comput. Sci. Technol. 2008, 23, 270–279. [Google Scholar] [CrossRef]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef] [PubMed]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. BM3D image denoising with shape-adaptive principal component analysis. In Proceedings of the SPARS’09-Signal Processing with Adaptive Sparse Structured Representations, Saint Malo, France, 6–9 April 2009. [Google Scholar]
- Mäkitalo, M.; Foi, A.; Fevralev, D.; Lukin, V. Denoising of single-look SAR images based on variance stabilization and nonlocal filters. In Proceedings of the 2010 International Conference on Mathematical Methods in Electromagnetic Theory (MMET), Kyiv, Ukraine, 6–8 September 2010; pp. 1–4. [Google Scholar]
- Zhong, H.; Li, Y.; Jiao, L. SAR image despeckling using Bayesian nonlocal means filter with sigma preselection. IEEE Geosci. Remote Sens. Lett. 2011, 8, 809–813. [Google Scholar] [CrossRef]
- Cozzolino, D.; Parrilli, S.; Scarpa, G.; Poggi, G.; Verdoliva, L. Fast adaptive nonlocal SAR despeckling. IEEE Geosci. Remote Sens. Lett. 2014, 11, 524–528. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Figueiredo, M.A. A new TwIST: Two-step iterative shrinkage/thresholding algorithms for image restoration. IEEE Trans. Image Process. 2007, 16, 2992–3004. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Liu, M.; Li, P.; Zhao, J.; Zhu, Z.; Wang, X. SAR Image Denoising via Sparse Representation in Shearlet Domain Based on Continuous Cycle Spinning. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2985–2992. [Google Scholar] [CrossRef]
- Fang, J.; Liu, S.; Xiao, Y.; Li, H. SAR image de-noising based on texture strength and weighted nuclear norm minimization. J. Syst. Eng. Electron. 2016, 27, 807–814. [Google Scholar]
- Gomez, L.; Ospina, R.; Frery, A.C. Unassisted Quantitative Evaluation of Despeckling Filters. Remote Sens. 2017, 9, 389. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).