Figure 1.
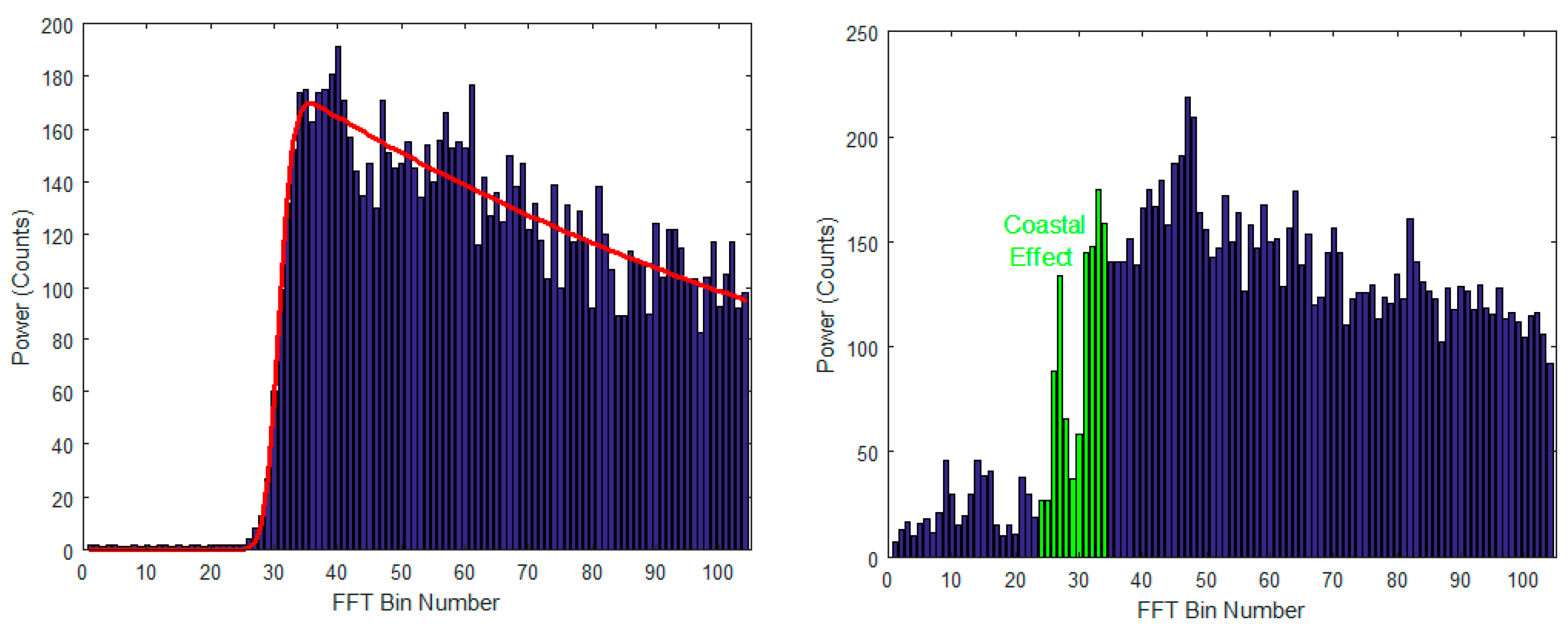
Examples of typical open ocean waveform (left; the red line corresponds to the fitted Brown model) and coastal ocean waveform (right).
Figure 1.
Examples of typical open ocean waveform (left; the red line corresponds to the fitted Brown model) and coastal ocean waveform (right).
Figure 2.
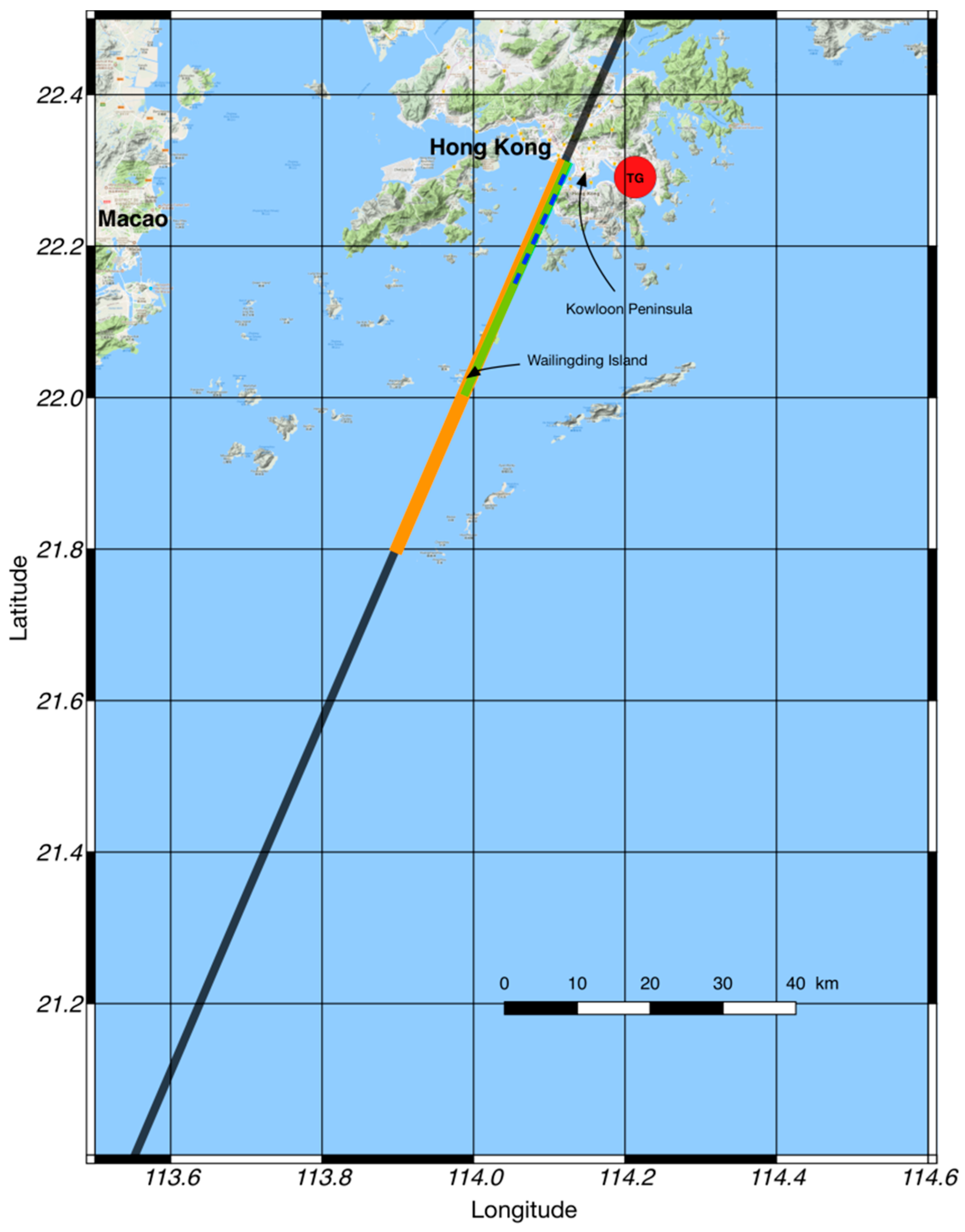
Map showing the study area, the selected Jason-2 pass 153 (black and colored line) and the Quarry Bay tide gauge (red circle). The latter is located ~10 km away from the Jason-2 pass. The along-track sections corresponding to study cases 1, 2, and 3 are also indicated (orange, green, and blue-green dashed lines, respectively). The background map is from Google Earth.
Figure 2.
Map showing the study area, the selected Jason-2 pass 153 (black and colored line) and the Quarry Bay tide gauge (red circle). The latter is located ~10 km away from the Jason-2 pass. The along-track sections corresponding to study cases 1, 2, and 3 are also indicated (orange, green, and blue-green dashed lines, respectively). The background map is from Google Earth.
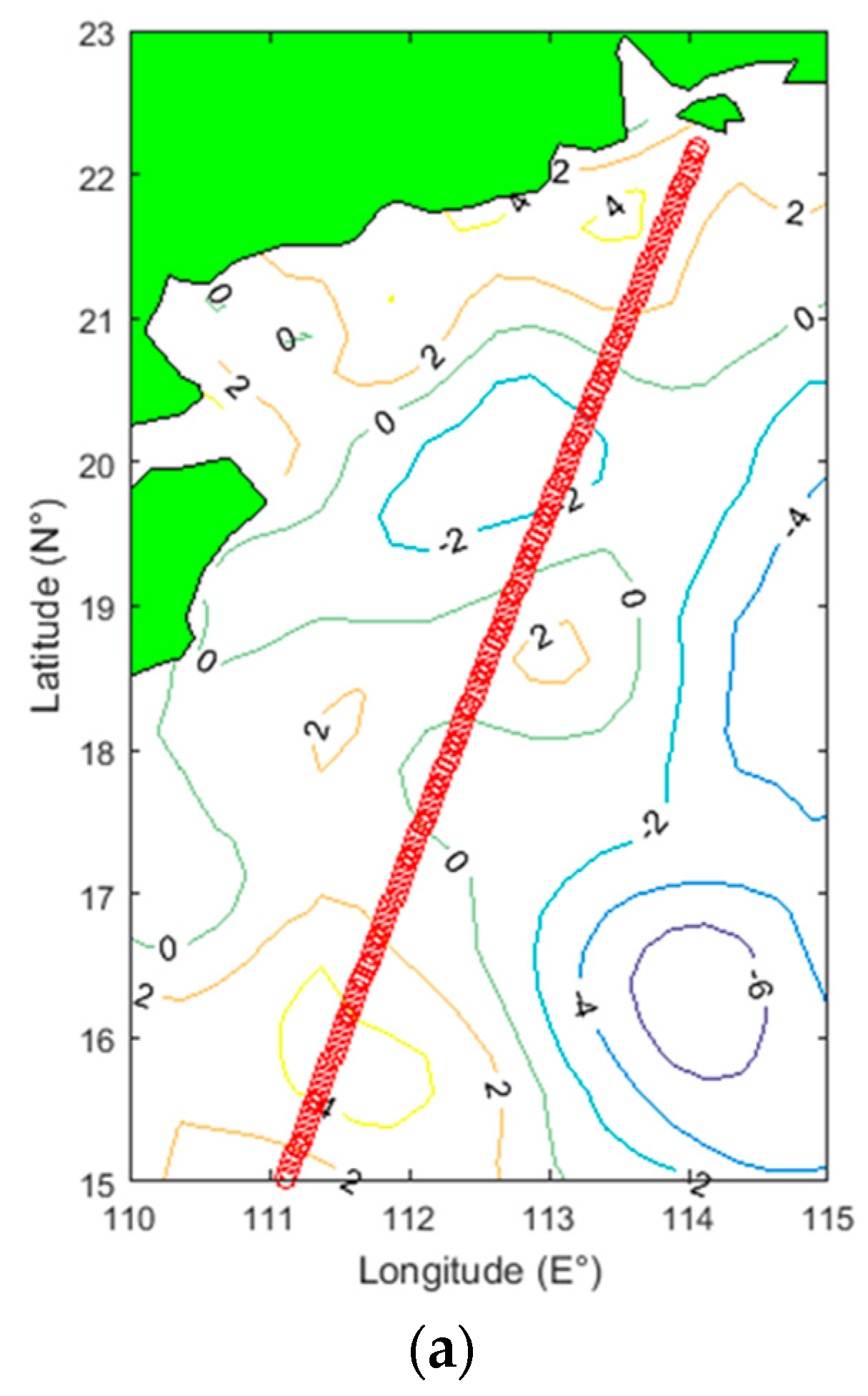
Figure 3.
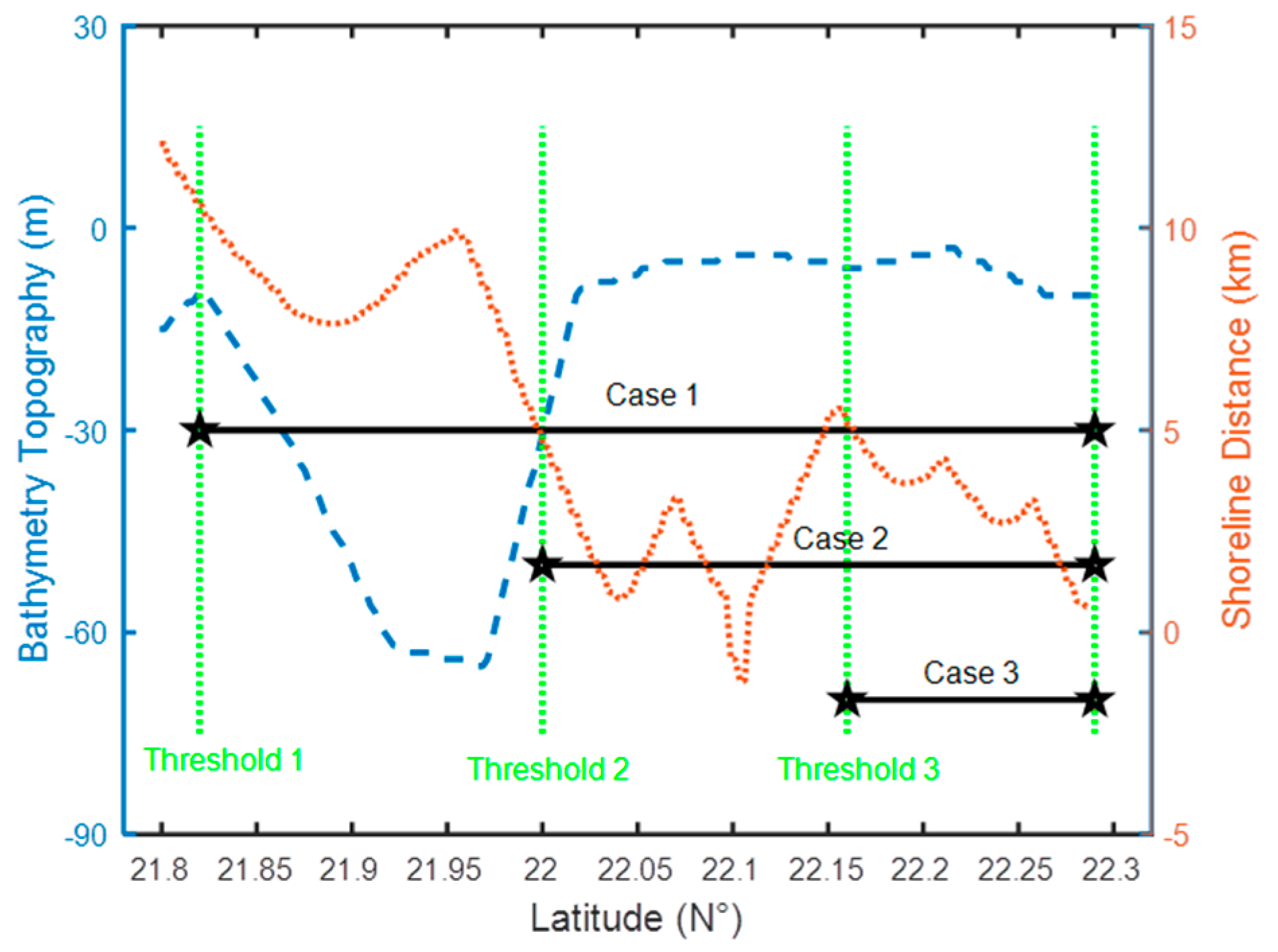
Bathymetry and shoreline distance at the Hong-Kong (HK) coast along 3 segments of the Jason-2 pass identified as cases 1, 2, and 3 (see location in
Figure 2).
Figure 3.
Bathymetry and shoreline distance at the Hong-Kong (HK) coast along 3 segments of the Jason-2 pass identified as cases 1, 2, and 3 (see location in
Figure 2).
Figure 4.
HK tide gauge sea level time series (in meters) interpolated to Jason-2 observations.
Figure 4.
HK tide gauge sea level time series (in meters) interpolated to Jason-2 observations.
Figure 5.
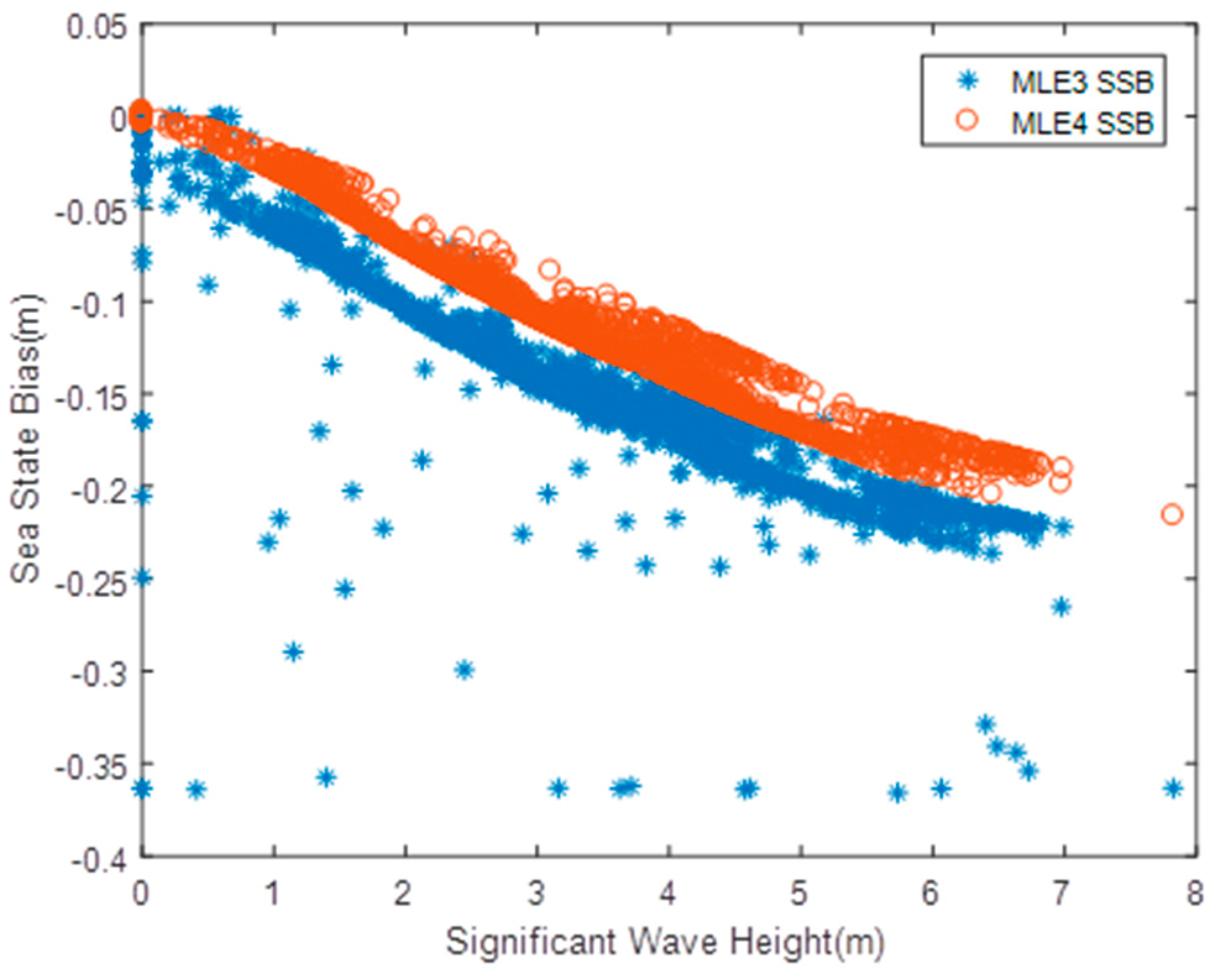
Sea state bias (SSB) difference with respect to Significant Wave Height.
Figure 5.
Sea state bias (SSB) difference with respect to Significant Wave Height.
Figure 6.
20-Hz sea level anomaly (SLA) before (left) and after (right) editing. Jason-2 cycle 5 is considered here.
Figure 6.
20-Hz sea level anomaly (SLA) before (left) and after (right) editing. Jason-2 cycle 5 is considered here.
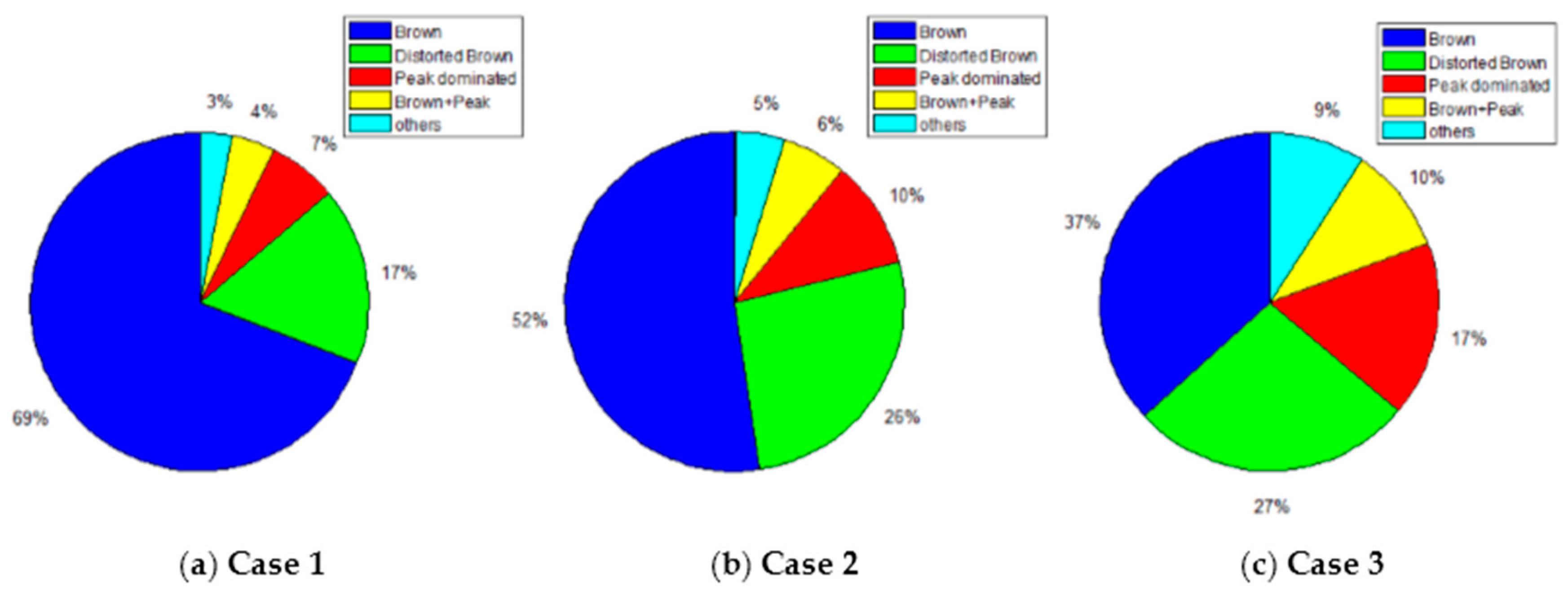
Figure 7.
Percentages of waveform categories in the 3 cases.
Figure 7.
Percentages of waveform categories in the 3 cases.
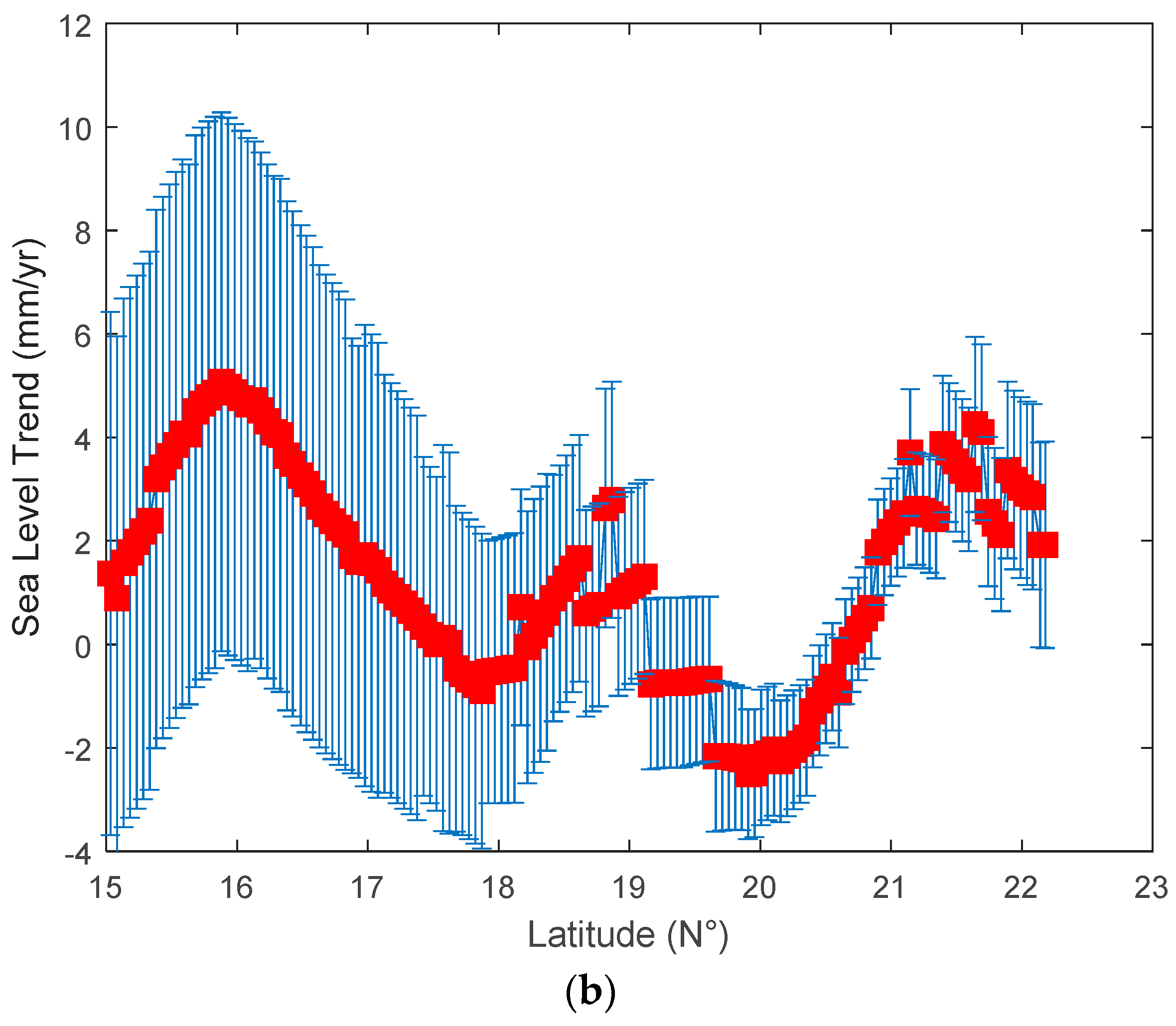
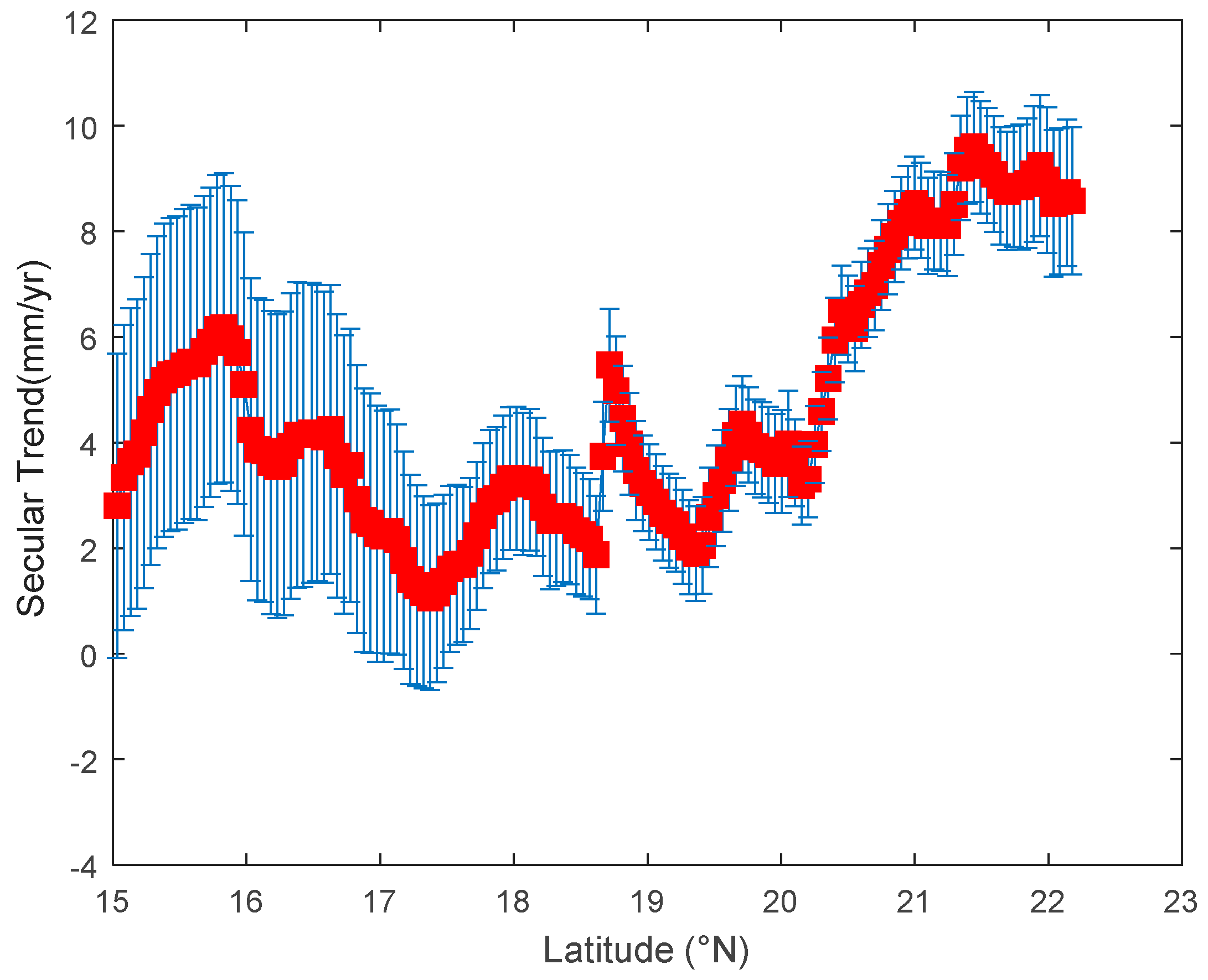
Figure 8.
Regional 6.5 yr-long trends in sea level derived from the CCI sea level data. (
a) using gridded data and (
b) interpolated along the Jason-2 pass 153. Vertical blue bars in
Figure 8b represent the uncertainty on the trend estimation.
Figure 8.
Regional 6.5 yr-long trends in sea level derived from the CCI sea level data. (
a) using gridded data and (
b) interpolated along the Jason-2 pass 153. Vertical blue bars in
Figure 8b represent the uncertainty on the trend estimation.
Figure 9.
Regional 6.5 yr-long trends in sea level derived from filtered X-TRACK data along the Jason-2 pass 153. Vertical blue bars represent the uncertainty on the trend estimation.
Figure 9.
Regional 6.5 yr-long trends in sea level derived from filtered X-TRACK data along the Jason-2 pass 153. Vertical blue bars represent the uncertainty on the trend estimation.
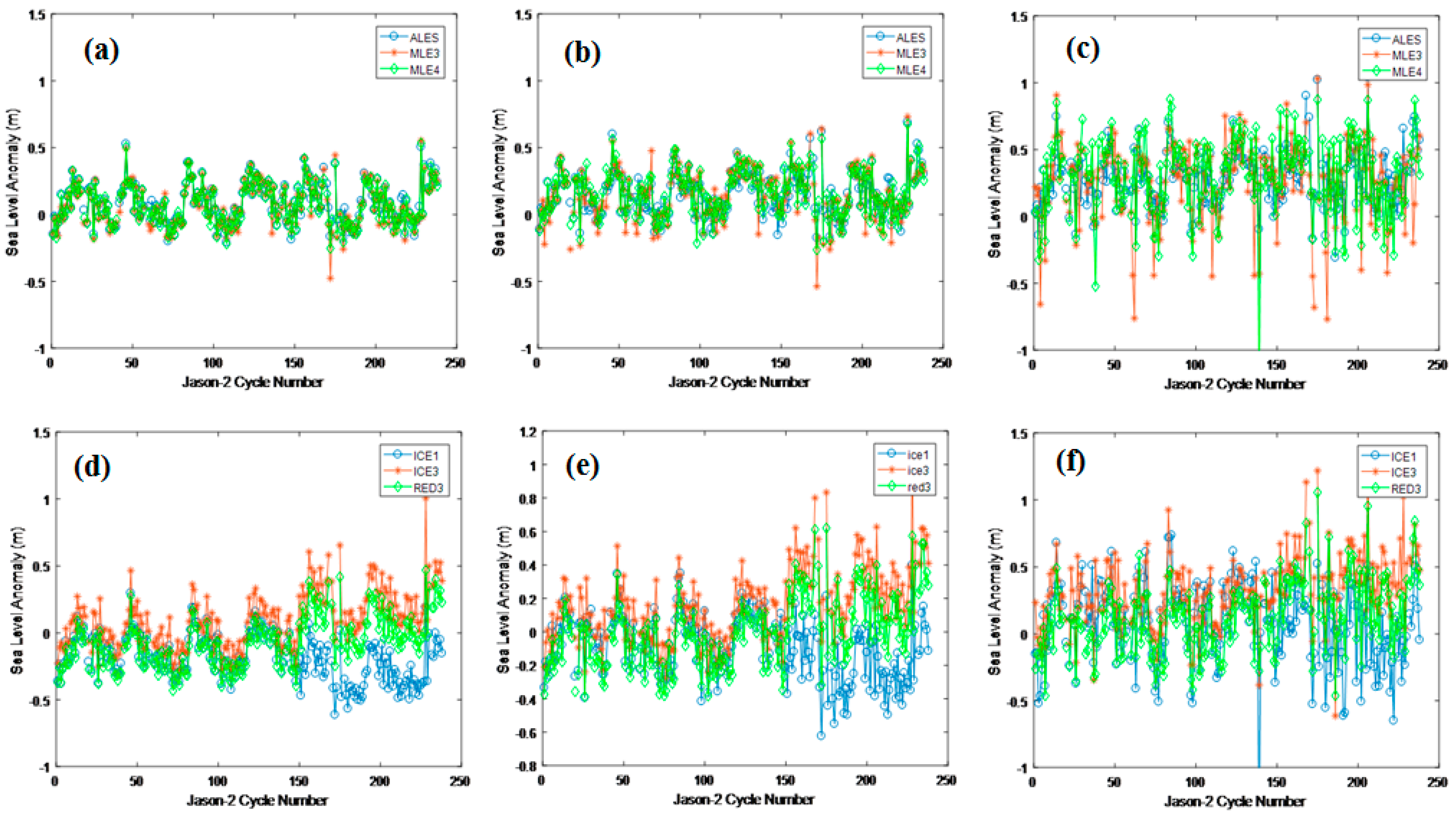
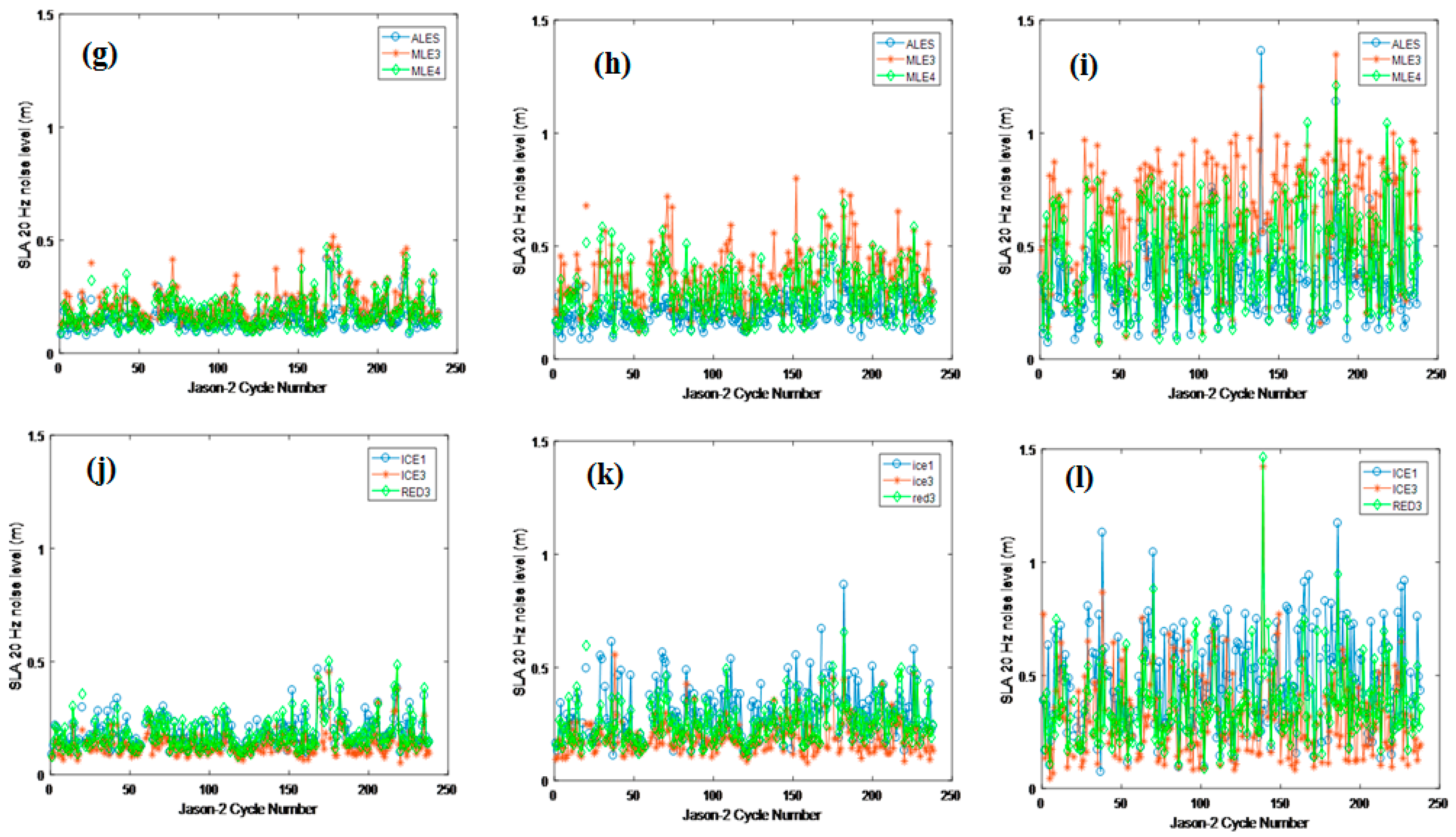
Figure 10.
SLA means and noise levels. (a) Case 1, mean SLA for ALES, MLE3 and MLE4; (b) Case 2, mean SLA for ALES, MLE3 and MLE4; (c) Case 3, mean SLA for ALES, MLE3 and MLE4; (d) Case 1, mean SLA for ICE1, ICE3 and RED3; (e) Case 2, mean SLA for ICE1, ICE3 and RED3; (f) Case 3, mean SLA for ICE1, ICE3 and RED3; (g) Case 1, noise levels for ALES, MLE3 and MLE4; (h) Case 2, noise levels for ALES, MLE3 and MLE4; (i) Case 3, noise levels for ALES, MLE3 and MLE4; (j) Case 1, noise levels for ICE1, ICE3 and RED3; (k) Case 2, noise levels for ICE1, ICE3 and RED3; (l) Case 3, noise levels for ICE1, ICE3 and RED3.
Figure 10.
SLA means and noise levels. (a) Case 1, mean SLA for ALES, MLE3 and MLE4; (b) Case 2, mean SLA for ALES, MLE3 and MLE4; (c) Case 3, mean SLA for ALES, MLE3 and MLE4; (d) Case 1, mean SLA for ICE1, ICE3 and RED3; (e) Case 2, mean SLA for ICE1, ICE3 and RED3; (f) Case 3, mean SLA for ICE1, ICE3 and RED3; (g) Case 1, noise levels for ALES, MLE3 and MLE4; (h) Case 2, noise levels for ALES, MLE3 and MLE4; (i) Case 3, noise levels for ALES, MLE3 and MLE4; (j) Case 1, noise levels for ICE1, ICE3 and RED3; (k) Case 2, noise levels for ICE1, ICE3 and RED3; (l) Case 3, noise levels for ICE1, ICE3 and RED3.
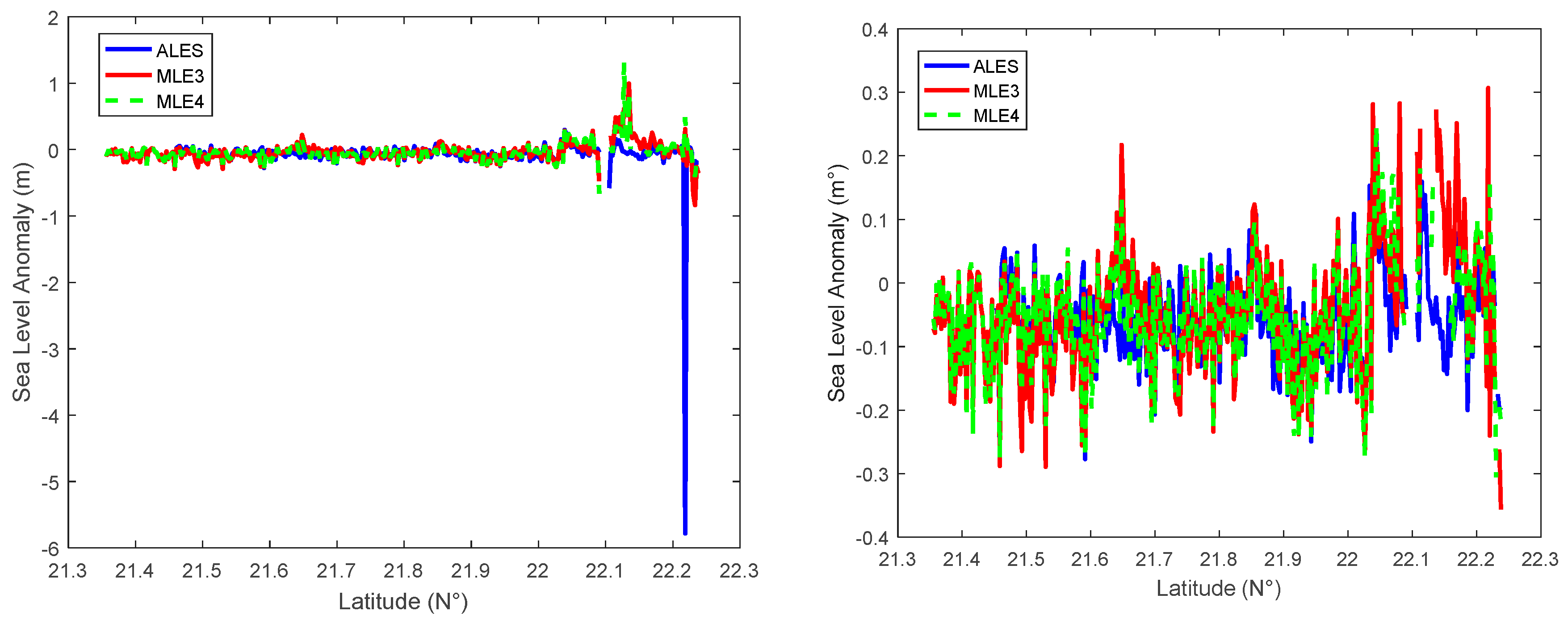
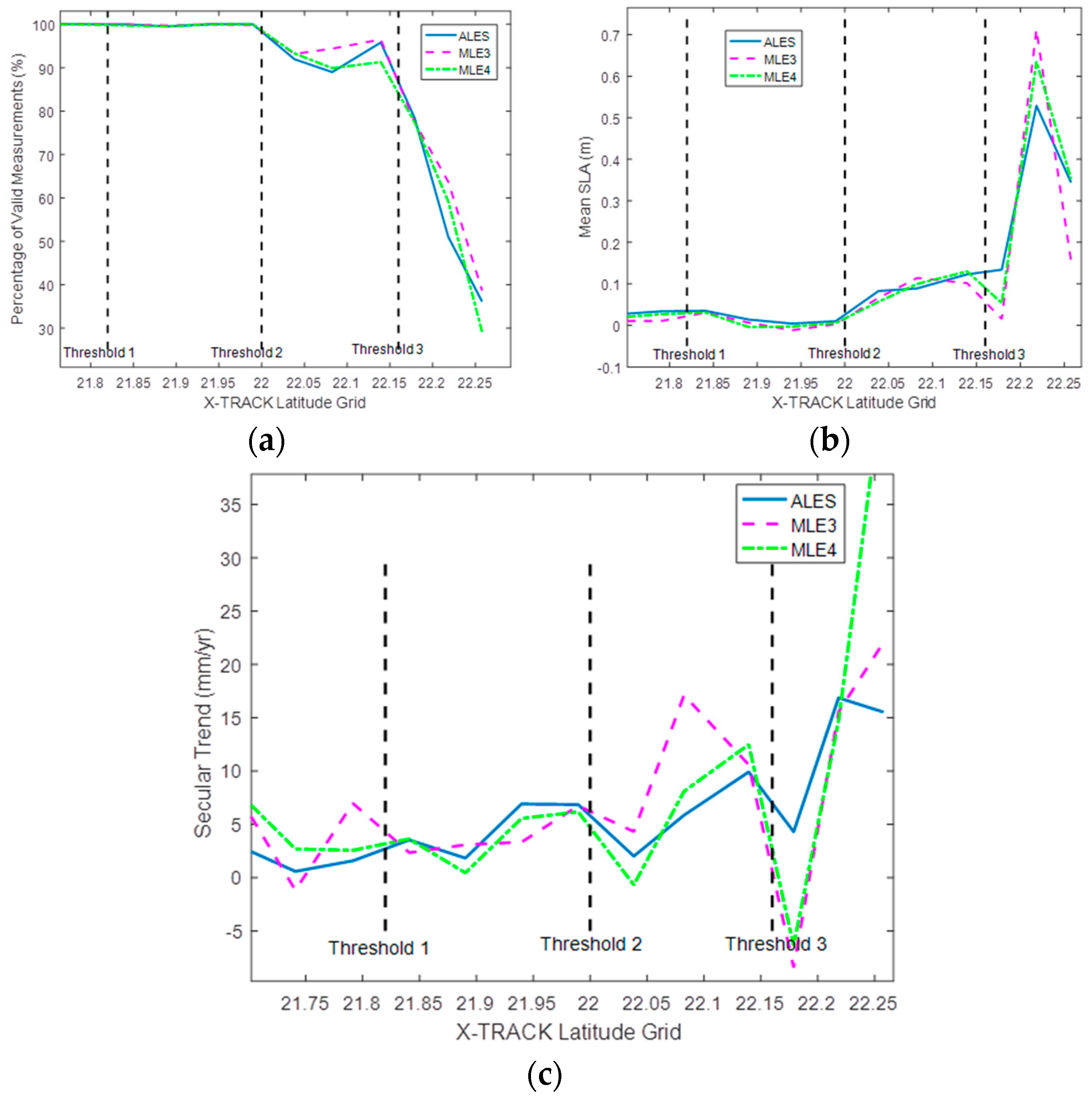
Figure 11.
(a) Percentage of valid measurements; (b,c) mean values and 6.5-yr trend estimates for ALES, MLE3, and MLE4 retrackers. Results are presented as a function of latitude.
Figure 11.
(a) Percentage of valid measurements; (b,c) mean values and 6.5-yr trend estimates for ALES, MLE3, and MLE4 retrackers. Results are presented as a function of latitude.
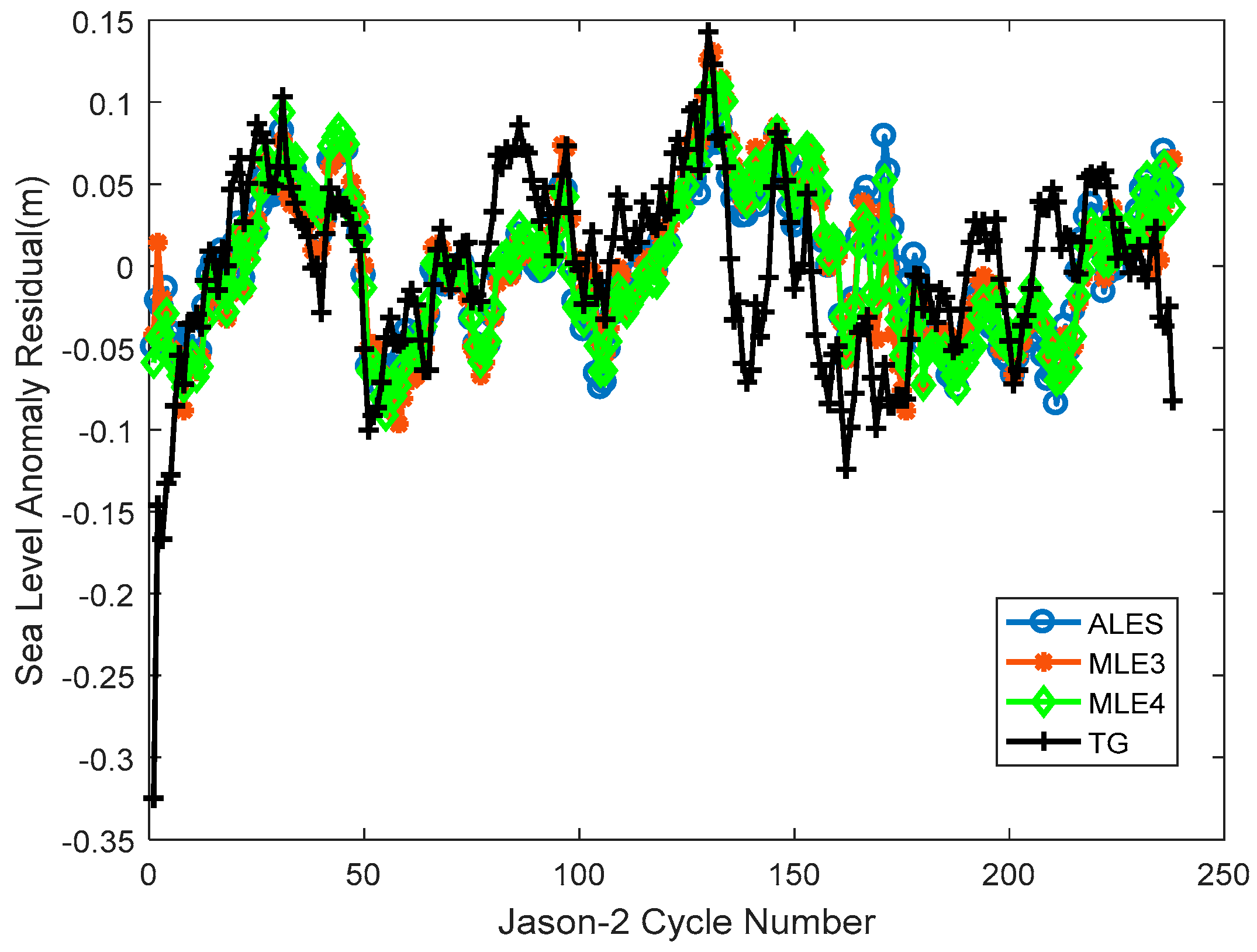
Figure 12.
Detrended and deseasoned SLA time series based on ALES, MLE3, and MLE4, with 3-month smoothing (tide gauge SLA—noted TG—is shown as reference).
Figure 12.
Detrended and deseasoned SLA time series based on ALES, MLE3, and MLE4, with 3-month smoothing (tide gauge SLA—noted TG—is shown as reference).
Table 1.
Overview of different retrackers applied in different altimetry products.
Table 1.
Overview of different retrackers applied in different altimetry products.
| Retracker | Product | Idea | Sub-Waveform | Comments |
|---|
| MLE4 | SGDR 1 | Brown model | No | Official standard retracker. |
| MLE3 | SGDR 1 | Brown model | No | |
| OCE3 | PISTACH | Brown model | No | Same as MLE3 |
| RED3 | PISTACH | Brown model | Fixed: bins: t0 + [−10:20] | Simplified version of ALES |
| ALES | ALES | Brown model | Adaptive to the SWH | Two-pass retracker |
| ICE1 | PISTACH | Modified threshold | No | |
| ICE3 | PISTACH | Modified threshold | Fixed: bins: t0 + [−10:20] | |
Table 2.
Overview of the five categories defined from the 16 PISTACH classes.
Table 2.
Overview of the five categories defined from the 16 PISTACH classes.
| Category | Waveform Characteristics | Possible Surface Observed | Retracking Strategy |
|---|
| Brown | The waveform is close to the Brown model. | The land contribution in the altimeter footprint is null or small. | MLE4 |
| Distorted Brown | The waveform is similar to the Brown model, but with distortions (either with an increasing plateau, or with a sharply decreasing plateau, or with a too broad noise floor). | There is land signature at the fringe of the altimeter footprint, with different reflection than over open ocean surface. | ALES |
| Peak dominated | One (or a few) large peak(s) dominate(s) the waveform; there may be a Brown shape in the waveform, but its maximum power is much lower than the peak(s). | There are one or a few strong bright targets (e.g., extremely calm water surface or effective corner reflector, see [34]) within the altimeter footprint. | MLE based on Gaussian model or improved threshold |
| Brown + Peak | The waveform is a mixture of Brown shape and one (or a few) peak(s) with comparable power levels. The location of the peak can be in the leading edge or the plateau. | The portions of ocean and land surfaces within the altimeter footprint are equivalent. | MLE based on BAGP (Brown with Asymmetric Gaussian Peak [35]) |
| Others | Unexplained waveform patterns (e.g., very noisy echoes or linear echoes). | Unexplainable surface features (e.g., very composite geomorphology or some extreme events). | Should be rejected. |
Table 3.
Estimated linear trend and associated uncertainty (mm/yr) as a function of sea level data source and case.
Table 3.
Estimated linear trend and associated uncertainty (mm/yr) as a function of sea level data source and case.
| Data Source | Case 1 | Case 2 | Case 3 |
|---|
| ALES | +5.9 ± 1.5 | +9.7 ± 1.6 | +17.3 ± 2.3 |
| MLE3 | +5.0 ± 1.6 | +8.1 ± 2.2 | +2.6 ± 3.1 |
| MLE4 | +4.2 ± 1.6 | +4.3 ± 2.2 | +5.5 ± 3.5 |
| ICE1 | −29.1 ± 2.4 | −27.5 ± 2.8 | −22.9 ± 4.0 |
| ICE3 | +57.5 ± 2.3 | +60.1 ± 2.5 | +52.9 ± 3.0 |
| RED3 | +55.3 ± 2.1 | +58.0 ± 2.3 | +58.5 ± 3.0 |
| XTRACK | +8.6 ± 2.2 |
| Tide Gauge (in-situ reference) | +5.2 ± 2.0 |
| Tide Gauge (After VLM correction) | +5.5 ± 2.0 |
| Regional trend from the CCI data | 2.7 ± 2.0 |
Table 4.
Estimated annual amplitude (cm) and phase (degree) as a function of sea level data source and case.
Table 4.
Estimated annual amplitude (cm) and phase (degree) as a function of sea level data source and case.
| Data Source | Case 1 | Case 2 | Case 3 |
|---|
| ALES | 13.05/344 | 12.49/348 | 11.19/2 |
| MLE3 | 13.29/338 | 12.39/339 | 13.17/343 |
| MLE4 | 12.96/339 | 11.44/340 | 11.12/348 |
| XTRACK | 13.23/338 |
| Tide Gauge | 11.46/311 |
Table 5.
Estimated semiannual amplitude (cm) and phase (degree) as a function of sea level data source and case.
Table 5.
Estimated semiannual amplitude (cm) and phase (degree) as a function of sea level data source and case.
| Data Source | Case 1 | Case 2 | Case 3 |
|---|
| ALES | 6.03/235 | 5.67/239 | 7.38/260 |
| MLE3 | 6.17/241 | 6.76/252 | 9.24/270 |
| MLE4 | 6.02/236 | 6.96/245 | 11.80/262 |
| XTRACK | 6.81/223 |
| Tide Gauge | 7.62/236 |
Table 6.
Deseasoned and detrended SLA standard deviation w.r.t. tide gauge sea level (cm) for case 1.
Table 6.
Deseasoned and detrended SLA standard deviation w.r.t. tide gauge sea level (cm) for case 1.
| SLA Series | ALES | MLE3 | MLE4 |
|---|
| Agreement | 5.12 | 4.82 | 4.88 |
Table 7.
Secular trend and associated uncertainty (mm/yr) for case 1, with different geophysical corrections choices. DAC = dynamic atmospheric correction.
Table 7.
Secular trend and associated uncertainty (mm/yr) for case 1, with different geophysical corrections choices. DAC = dynamic atmospheric correction.
| Choice | ALES | MLE3 | MLE4 |
|---|
| Standard choice (Table 4) | +5.9 ± 1.5 | +5.0 ± 1.6 | +4.2 ± 1.6 |
| composite wet delay | +6.1 ± 1.5 | +5.1 ± 1.6 | +4.3 ± 1.6 |
| FES 2004 ocean tide | +5.7 ± 1.5 | +4.6 ± 1.6 | +4.7 ± 1.6 |
| FES 2012 ocean tide | +9.1 ± 1.3 | +7.8 ± 1.5 | +7.1 ± 1.5 |
| No DAC applied | +6.3 ± 1.6 | +5.1 ± 1.8 | +4.5 ± 1.7 |
Table 8.
Residual SLA, standard deviation w.r.t. tide gauge-based sea level (cm), for case 1, after 3-month smoothing, with different geophysical corrections choices.
Table 8.
Residual SLA, standard deviation w.r.t. tide gauge-based sea level (cm), for case 1, after 3-month smoothing, with different geophysical corrections choices.
| Choice | ALES | MLE3 | MLE4 |
|---|
| Standard choice (Table 4) | 5.12 | 4.82 | 4.88 |
| composite wet delay | 5.02 | 4.80 | 5.01 |
| FES 2004 ocean tide | 4.87 | 4.76 | 4.82 |
| FES 2012 ocean tide | 4.89 | 4.56 | 4.88 |
| No DAC applied | 4.84 | 4.56 | 4.76 |
Table 9.
Correlations of different tide solutions with respect to the tide gauge tide height.
Table 9.
Correlations of different tide solutions with respect to the tide gauge tide height.
| Ocean Tide Solution | GOT 4.8 | FES 2004 | FES 2012 |
|---|
| Correlation | 0.91 | 0.89 | 0.95 |
Table 10.
20-Hz epoch noise (cm) for different singular value decomposition (SVD) configurations (cycle #100).
Table 10.
20-Hz epoch noise (cm) for different singular value decomposition (SVD) configurations (cycle #100).
| Threshold Percentage | No SVD | 90% SVD | 80% SVD |
|---|
| Far from the coast | 8.66 | 8.05 | 7.52 |
| Near the coast | 9.41 | 8.90 | 8.60 |
| The last ocean-like waveform | 39.17 | 36.18 | 34.68 |