Sensitivity Analysis of Arctic Sea Ice Extent Trends and Statistical Projections Using Satellite Data
Abstract
:1. Introduction
2. Data and Methods
3. Results
3.1. Sensitivity to Averaging Methods and Averaging Intervals
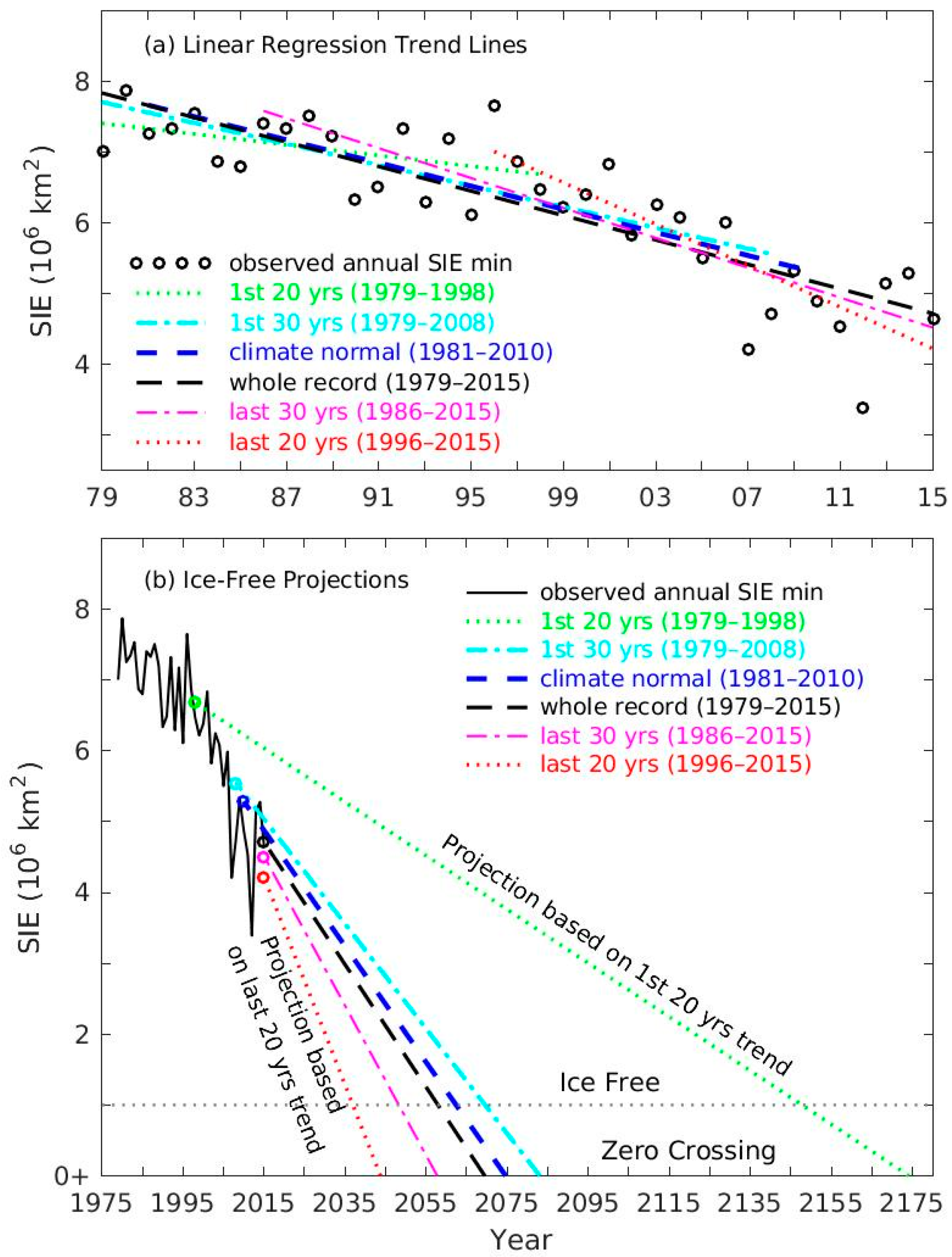
3.2. Sensitivity of Arctic Ice-Free Projection to Time Domain of Linear Regression
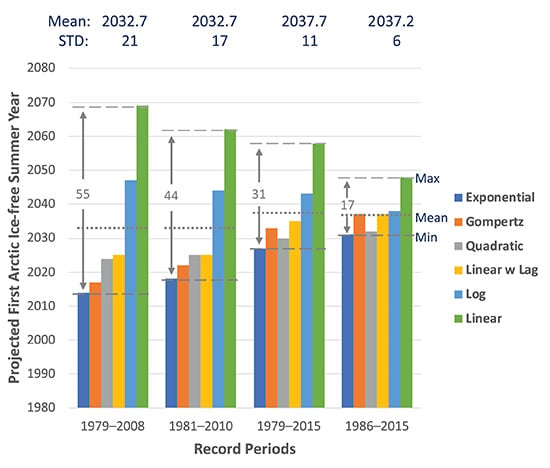
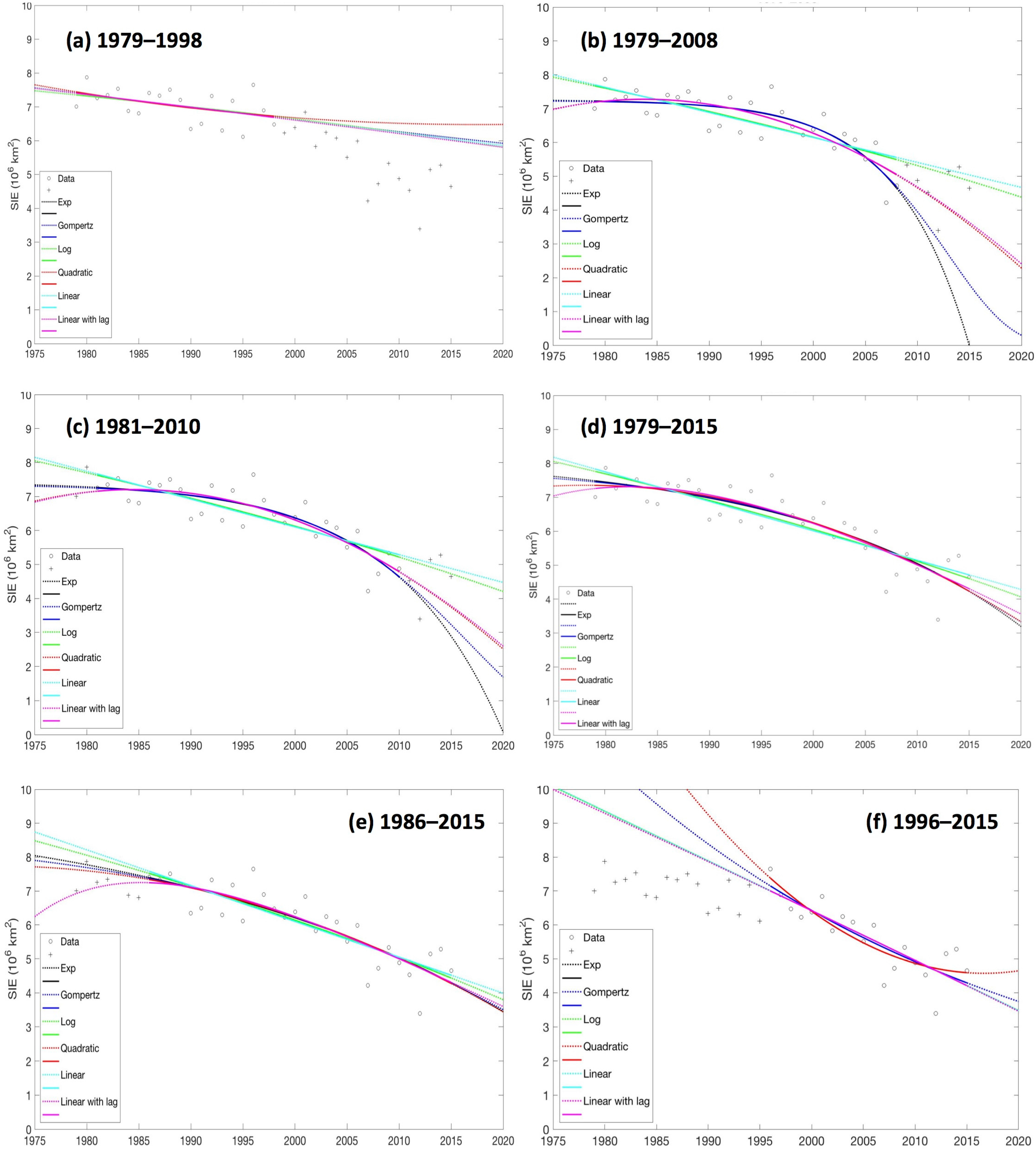
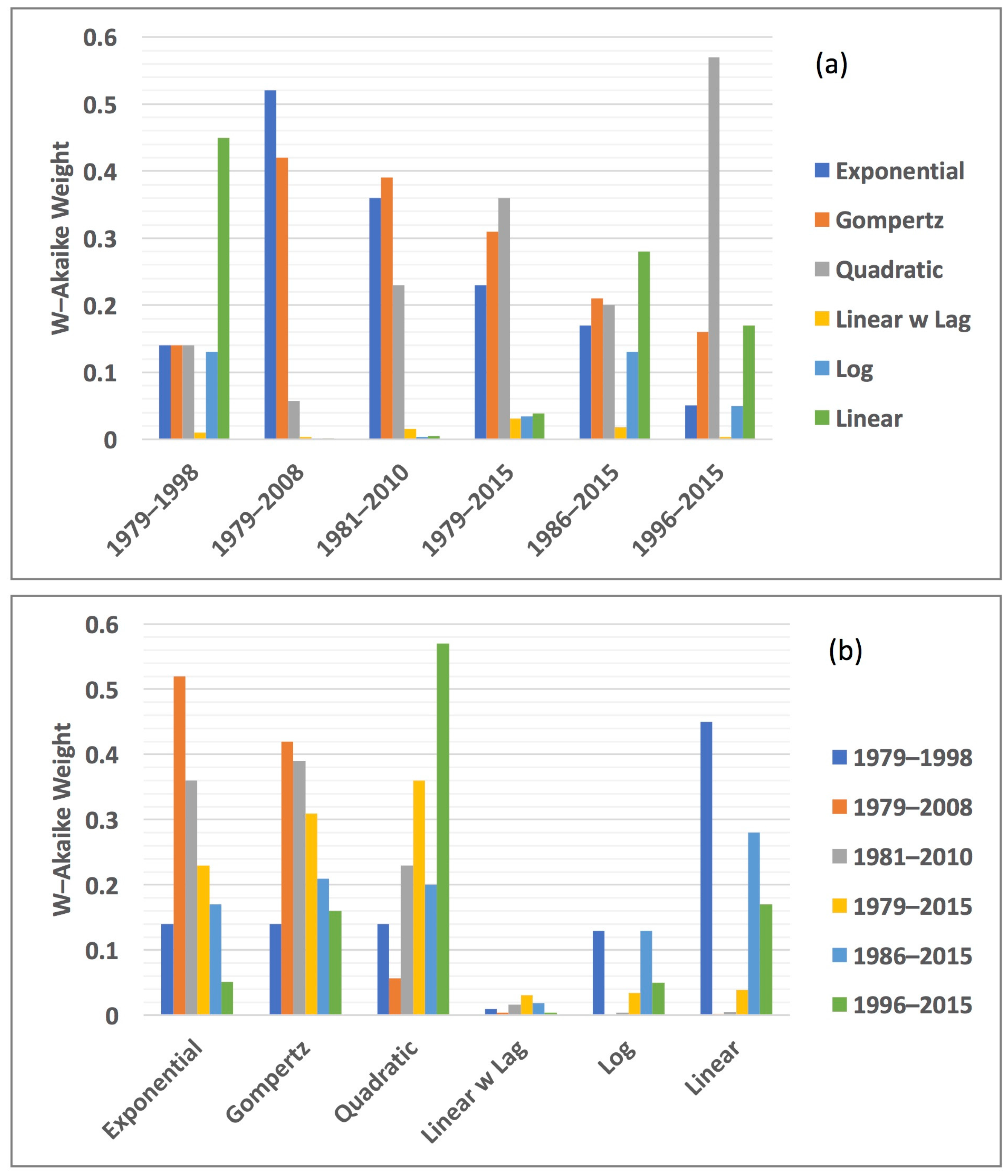
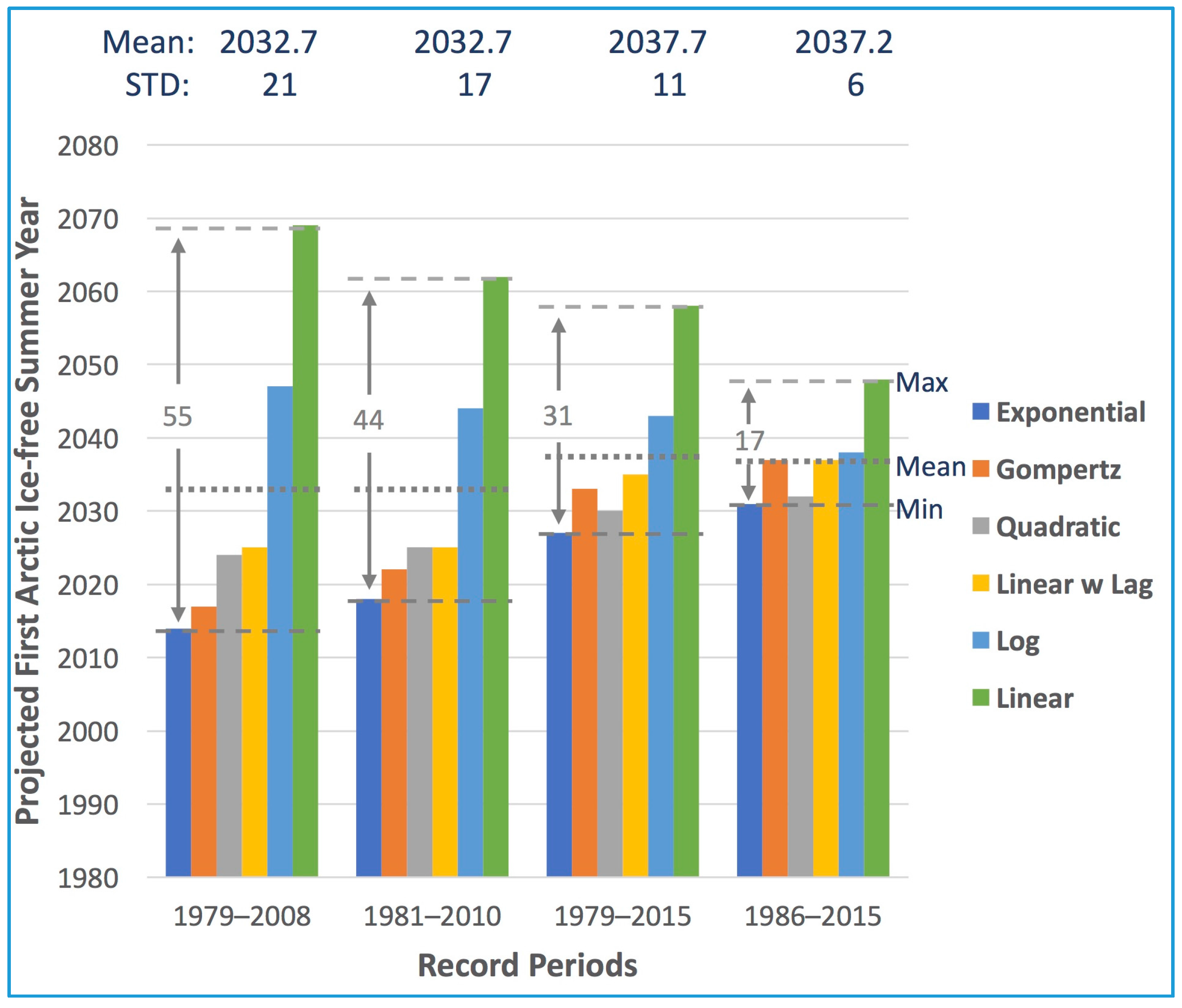
3.3. Sensitivity of Different Statistical Curve Fitting Functions
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Comiso, C.J.; Nishio, F. Trends in the sea ice cover using enhanced and compatible AMSR-E, SSM/I, and SMMR data. J. Geophys. Res. 2008, 113, C02S07. [Google Scholar] [CrossRef]
- Cavalieri, J.D.; Parkinson, L.C. Arctic sea ice variability and trends, 1979–2010. Cryosphere 2012, 6, 881–889. [Google Scholar] [CrossRef]
- Peng, G.; Meier, M.N.; Scott, D.J.; Savoie, M. A long-term and reproducible passive microwave sea ice concentration data record for climate studies and monitoring. Earth-Syst. Sci. Data 2013, 5, 311–318. [Google Scholar] [CrossRef]
- Serreze, M.C.; Stroeve, J. Arctic sea ice trends, variability and implications for seasonal ice forecasting. Phil. Trans. R. Soc. 2015, A373. [Google Scholar] [CrossRef] [PubMed]
- Overland, J.E.; Wang, M. When will the summer Arctic be nearly sea ice free? Geophys. Res. Lett. 2013, 40. [Google Scholar] [CrossRef]
- Stroeve, J.C.; Kattsov, V.; Barrett, A.; Serreze, M.; Pavlova, T.; Holland, M.; Meier, W.N. Trends in Arctic sea ice extent from CMIP5, CMIP3 and observations. Geophys. Res. Lett. 2012, 39, L16502. [Google Scholar] [CrossRef]
- Global Climate Change Blog. Historical analysis of Arctic Sea Ice Extent. AccuWeather, 2016. Available online: https://www.accuweather.com/en/weather-blogs/climatechange/historical-analysis-of-arctic/59342719 (accessed on 18 October 2016).
- Thompson, A. Arctic Sea Ice Sets Record-Low Peak for Third Year. Climate Central, 2017. Available online: www.climatecentral.org/news/arctic-sea-ice-sets-record-low-peak-for-3rd-year-21268 (accessed on 30 March 2017).
- Kwok, R.; Untersteiner, N. The thinning of Arctic sea ice. Phys. Today 2011, 64, 36–41. [Google Scholar] [CrossRef]
- Comiso, C.J. Large decadal decline of the Arctic multiyear ice cover. J. Clim. 2012, 25. [Google Scholar] [CrossRef]
- Arctic Climate Impact Assessment (ACIA). Impacts of a Warming Arctic—Arctic Climate Impact Assessment; Cambridge University Press: Cambridge, UK, 2004; 140p. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; 1535p. [Google Scholar]
- Meier, W.N.; Peng, G.; Scott, D.J.; Savoie, M. Verification of a new passive microwave sea ice concentration climate data record. Polar Res. 2014, 33. [Google Scholar] [CrossRef]
- Wohlleben, T.; Tivy, A.; Stroeve, J.; Meier, W.N.; Fetterer, F.; Wang, J.; Assel, R. Computing and Representing Sea Ice Trends: Toward a Community Consensus. Eos. Trans. AGU 2013, 94, 352. [Google Scholar] [CrossRef]
- Meier, W.N.; Stroeve, J.; Fetterer, F. Whither Arctic sea ice? A clear signal of decline regionally, seasonally and extending beyond the satellite record. Ann. Glaciol. 2007, 46, 428–434. [Google Scholar] [CrossRef]
- Dantzig, G. Origins of the Simplex Method; Tech. Report SOL 87-5; Stanford University: Stanford, CA, USA, 1987. [Google Scholar]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Cavanaugh, J.E. Unifying the derivations for the Akaike and corrected Akaike information criteria. Stat. Probab. Lett. 1997, 33, 201–208. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multi-Model Inference: A Practical Information-Theoretic Approach, 2nd ed.; Springer: New York, NY, USA, 2002; ISBN 0-387-95364-7. [Google Scholar]
- Boccolar, M.; Parmiggiani, F. Sea-ice area variability and trends in Arctic sectors of different morphology, 1996–2015. Eur. J. Remote Sens. 2017. [Google Scholar] [CrossRef]
- Peng, G.; Meier, W.N. Temporal and regional variability of Arctic sea ice coverage from satellite data. Ann. Glaciol. 2017. [Google Scholar] [CrossRef]
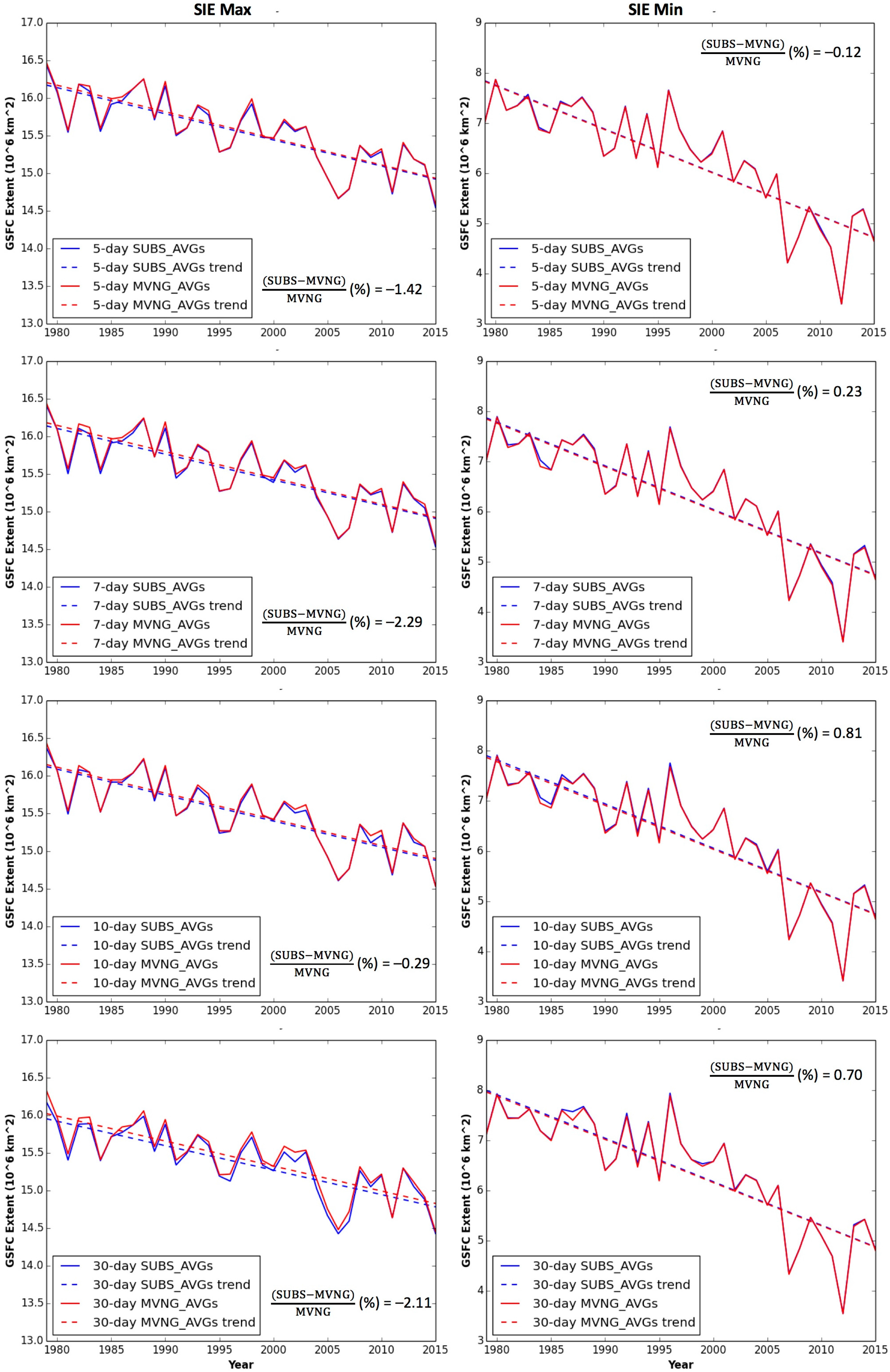
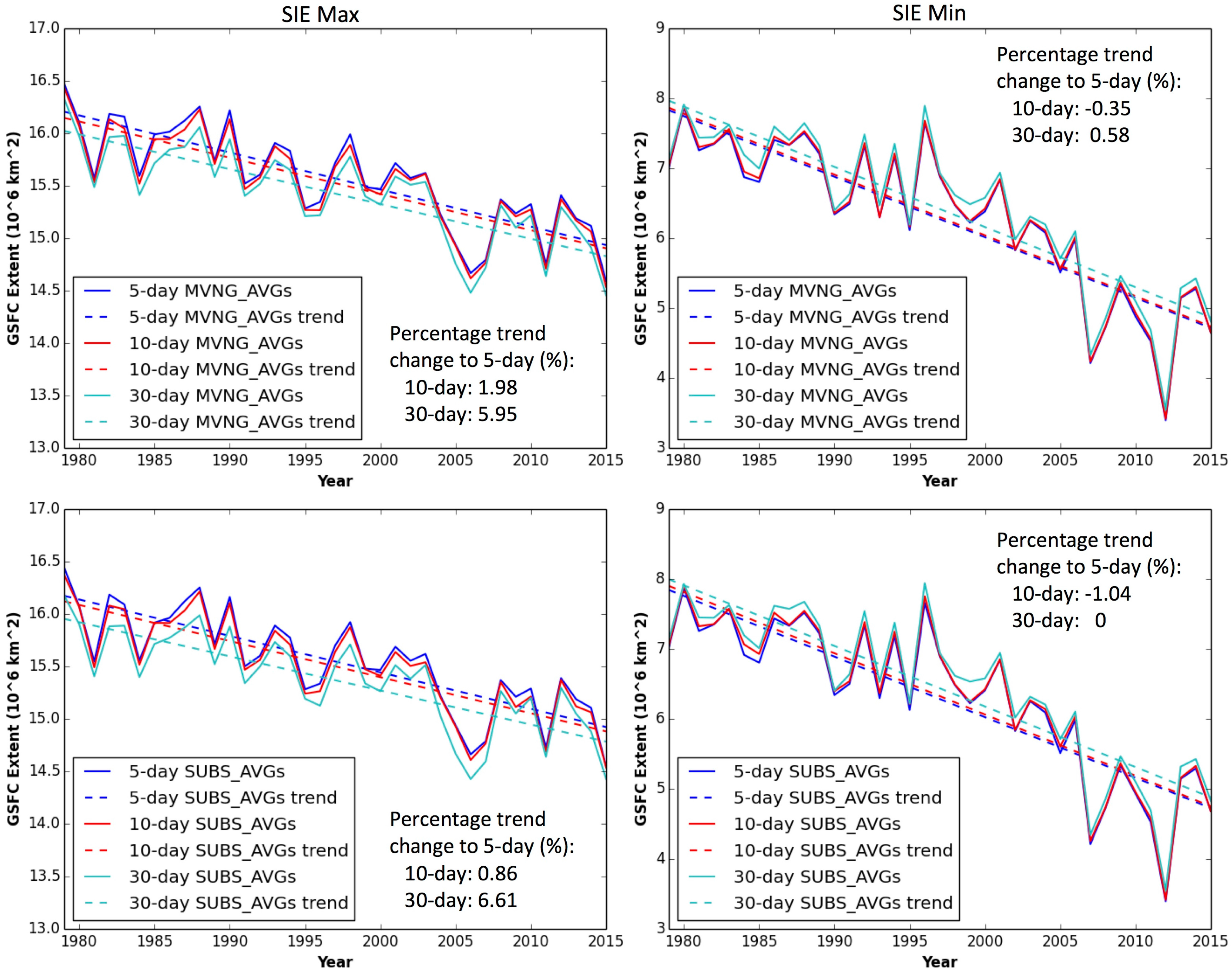
| Original | Moving Average Interval (in Days) | Subsetting Average Intervals (in Days) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 5 | 7 | 10 | 30 | 5 | 7 | 10 | 30 | ||
| SIE Decadal Trends in Annual Maximum (106 km2/decade) | −0.346 | −0.353 | −0.35 | −0.346 | −0.332 | −0.348 | −0.342 | −0.345 | −0.325 |
| Percentage Change to Original (%) | 0 | −2.02 | −1.16 | 0.00 | 4.05 | −0.58 | 1.16 | 0.29 | 6.07 |
| SIE Decadal Trends in Annual Minimum (106 km2/decade) | −0.868 | −0.866 | −0.868 | −0.869 | −0.861 | −0.867 | −0.87 | −0.876 | −0.867 |
| Percentage Change to Original (%) | 0 | 0.23 | 0.00 | −0.12 | 0.81 | 0.12 | −0.23 | −0.92 | 0.12 |
| Case ID | Data Period | Trend (106 km2/Decade) | Margin of Error (106 km2/Decade) * | First Ice-Free Summer (Year) | Zero-Crossing (Year) |
|---|---|---|---|---|---|
| First 20 years | 1979–1998 | −0.38 | 0.19 | 2147 | 2174 |
| First 30 years | 1979–2008 | −0.74 | 0.29 | 2069 | 2083 |
| Climate Normal | 1981–2010 | −0.82 | 0.32 | 2062 | 2074 |
| All years | 1979–2015 | −0.87 | 0.30 | 2058 | 2069 |
| Last 30 years | 1986–2015 | −1.06 | 0.41 | 2048 | 2057 |
| Last 20 years | 1996–2015 | −1.47 | 0.73 | 2036 | 2043 |
| Model | Exponential | Gompertz | Log | Quadratic | Linear | Linear w Lag | |
|---|---|---|---|---|---|---|---|
| Period | |||||||
| 1979–1998 (first 20 years) | RMSE (in) (106 km2) | 0.32 | 0.32 | 0.32 | 0.32 | 0.32 | 0.32 |
| RMSE (out) (106 km2) | 0.83 | 0.85 | 0.84 | 0.98 | 0.83 | 0.82 | |
| AICc [(106 km2)2] | −78.61 | −78.62 | −78.46 | −78.69 | −80.99 | −73.39 | |
| W [unitless] | 0.14 | 0.14 | 0.13 | 0.14 | 0.45 | 0.010 | |
| 1979–2008 (first 30 years) | RMSE (in) (106 km2) | 0.39 | 0.39 | 0.46 | 0.41 | 0.47 | 0.41 |
| RMSE (out) (106 km2) | 1.23 | 0.85 | 0.32 | 0.39 | 0.35 | 0.38 | |
| AICc [(106 km2)2] | −62.99 | −62.54 | −50.30 | −58.57 | −51.06 | −53.18 | |
| W [unitless] | 0.52 | 0.42 | 0.00091 | 0.057 | 0.0013 | 0.0039 | |
| 1981–2010 (climate normal) | RMSE (in) (106 km2) | 0.40 | 0.40 | 0.45 | 0.40 | 0.46 | 0.40 |
| RMSE (out) (106 km2) | 0.52 | 0.46 | 0.32 | 0.37 | 0.34 | 0.36 | |
| AICc [(106 km2)2] | −61.25 | −61.43 | −52.25 | −60.40 | −52.79 | −55.10 | |
| W [unitless] | 0.36 | 0.39 | 0.0039 | 0.23 | 0.0052 | 0.016 | |
| 1979–2015 (all years) | RMSE (in) (106 km2) | 0.52 | 0.52 | 0.55 | 0.52 | 0.57 | 0.51 |
| RMSE (out) (106 km2) | N/A | N/A | N/A | N/A | N/A | N/A | |
| AICc [(106 km2)2] | −41.26 | −41.83 | −38.16 | −42.15 | −37.69 | −37.22 | |
| W [unitless] | 0.23 | 0.31 | 0.034 | 0.36 | 0.039 | 0.031 | |
| 1986–2015 (last 30 years) | RMSE (in) (106 km2) | 0.50 | 0.49 | 0.50 | 0.49 | 0.50 | 0.49 |
| RMSE (out) (106 km2) | 0.22 | 0.20 | 0.31 | 0.18 | 0.36 | 0.18 | |
| AICc [(106 km2)2] | −45.31 | −45.64 | −44.66 | −45.58 | −46.23 | −40.76 | |
| W [unitless] | 0.17 | 0.21 | 0.13 | 0.20 | 0.28 | 0.018 | |
| 1996–2015 (last 20 years) | RMSE (in) (106 km2) | 0.41 | 0.40 | 0.41 | 0.38 | 0.41 | 0.41 |
| RMSE (out) (106 km2) | 0.96 | 1.57 | 0.95 | 2.62 | 0.96 | 0.93 | |
| AICc [(106 km2)2] | −59.51 | −61.75 | −59.48 | −64.35 | −61.88 | −54.15 | |
| W [unitless] | 0.051 | 0.16 | 0.050 | 0.57 | 0.17 | 0.0035 |
| Case ID | Data Period | Exponential | Gompertz | Log | Quadratic | Linear | Linear w Lag |
|---|---|---|---|---|---|---|---|
| First 20 years | 1979–1998 | >2100 | >2100 | 2077 | N/A | >2100 | >2100 |
| First 30 years | 1979–2008 | 2014 | 2017 | 2047 | 2024 | 2069 | 2025 |
| Climate Normal | 1981–2010 | 2018 | 2022 | 2044 | 2025 | 2062 | 2025 |
| All years | 1979–2015 | 2027 | 2033 | 2043 | 2030 | 2058 | 2035 |
| Last 30 years | 1986–2015 | 2031 | 2037 | 2038 | 2032 | 2048 | 2037 |
| Last 20 years | 1996–2015 | 2036 | 2067 | 2036 | N/A | 2036 | 2036 |
| Case ID | Data Period | Exponential | Gompertz | Log | Quadratic | Linear | Linear w Lag |
|---|---|---|---|---|---|---|---|
| First 20 years | 1979–1998 | >2100 | N/A | 2083 | N/A | >2100 | >2100 |
| First 30 years | 1979–2008 | 2015 | N/A | 2053 | 2027 | 2083 | 2028 |
| Climate Normal | 1981–2010 | 2020 | N/A | 2050 | 2028 | 2074 | 2029 |
| All years | 1979–2015 | 2030 | N/A | 2049 | 2034 | 2069 | 2041 |
| Last 30 years | 1986–2015 | 2035 | N/A | 2044 | 2036 | 2057 | 2044 |
| Last 20 years | 1996–2015 | 2043 | N/A | 2043 | N/A | 2043 | 2042 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, G.; Matthews, J.L.; Yu, J.T. Sensitivity Analysis of Arctic Sea Ice Extent Trends and Statistical Projections Using Satellite Data. Remote Sens. 2018, 10, 230. https://doi.org/10.3390/rs10020230
Peng G, Matthews JL, Yu JT. Sensitivity Analysis of Arctic Sea Ice Extent Trends and Statistical Projections Using Satellite Data. Remote Sensing. 2018; 10(2):230. https://doi.org/10.3390/rs10020230
Chicago/Turabian StylePeng, Ge, Jessica L. Matthews, and Jason T. Yu. 2018. "Sensitivity Analysis of Arctic Sea Ice Extent Trends and Statistical Projections Using Satellite Data" Remote Sensing 10, no. 2: 230. https://doi.org/10.3390/rs10020230
APA StylePeng, G., Matthews, J. L., & Yu, J. T. (2018). Sensitivity Analysis of Arctic Sea Ice Extent Trends and Statistical Projections Using Satellite Data. Remote Sensing, 10(2), 230. https://doi.org/10.3390/rs10020230