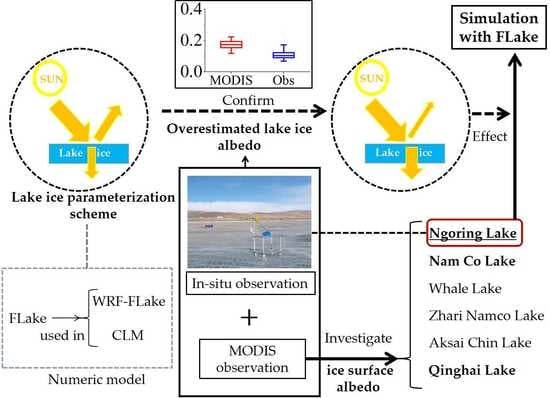
An Investigation of Ice Surface Albedo and Its Influence on the High-Altitude Lakes of the Tibetan Plateau
Abstract
1. Introduction
2. Study Area, Data and Method
2.1. Study Area and In-Situ Measurements
2.2. Data
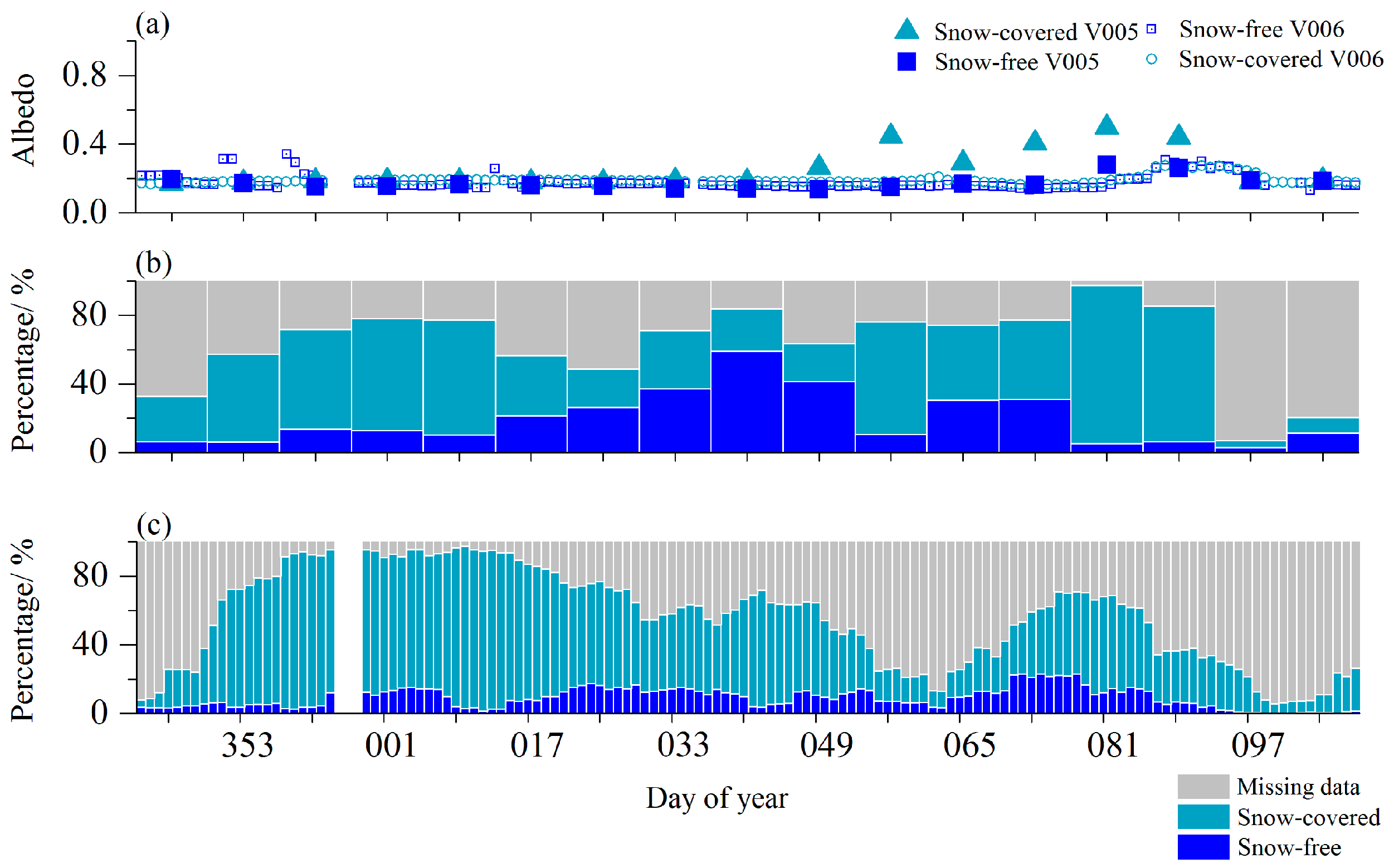
2.2.1. MODIS Albedo Products
2.2.2. MODIS Surface Temperature Product
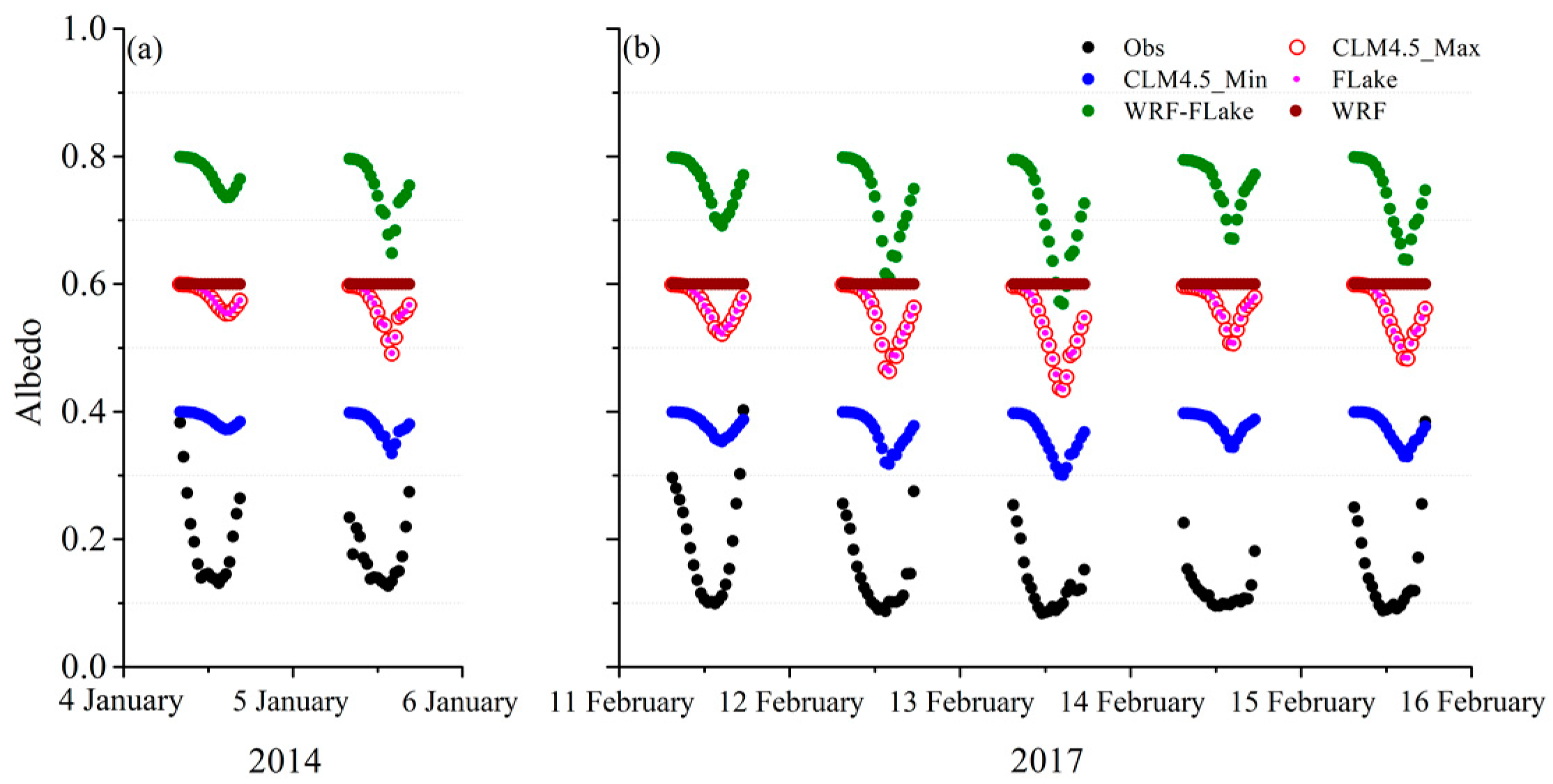
2.3. Lake Ice Albedo Parameterizations and the FLake Model
3. Results
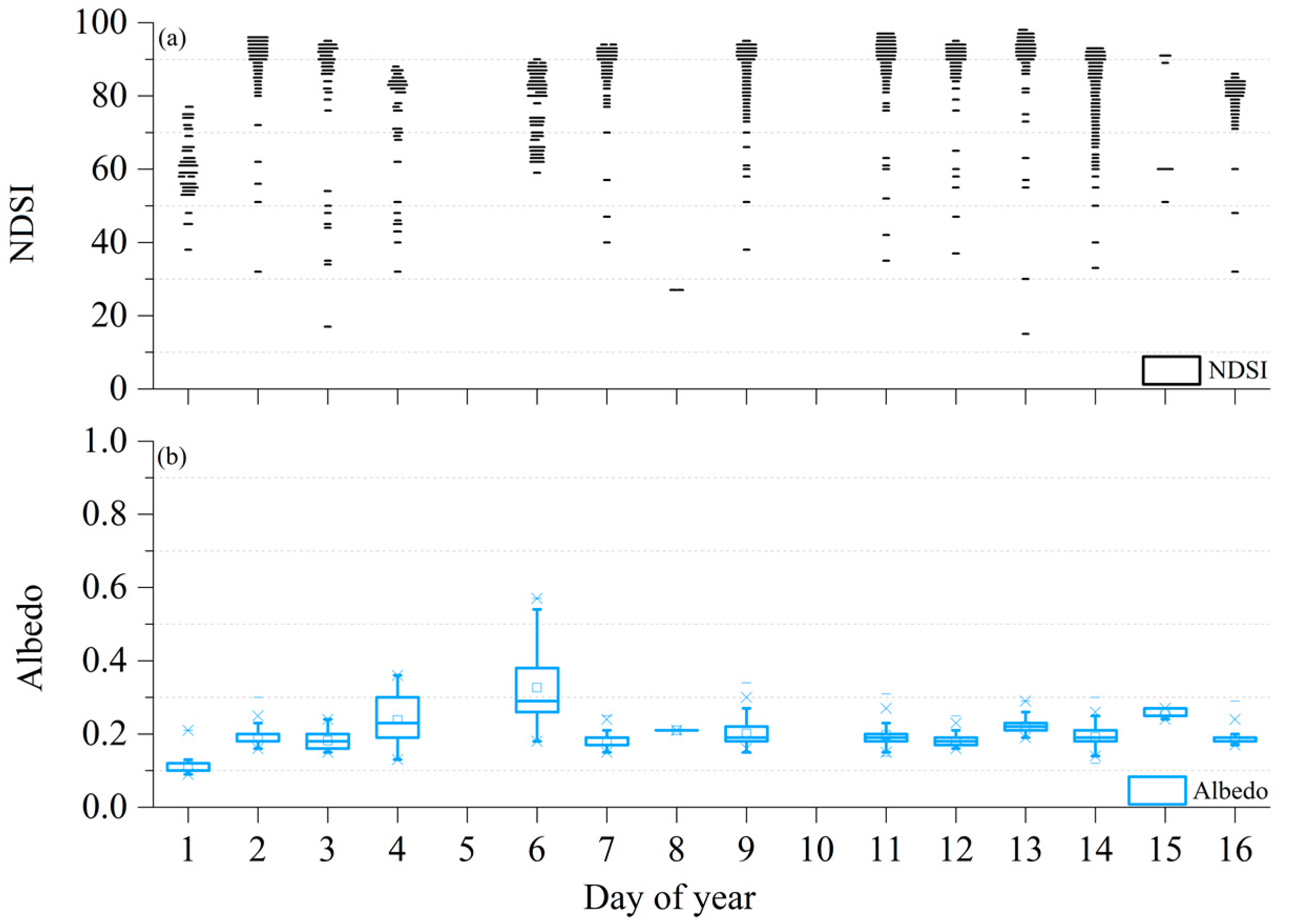
3.1. Albedo from MODIS, Observation and Parameterization-Drived
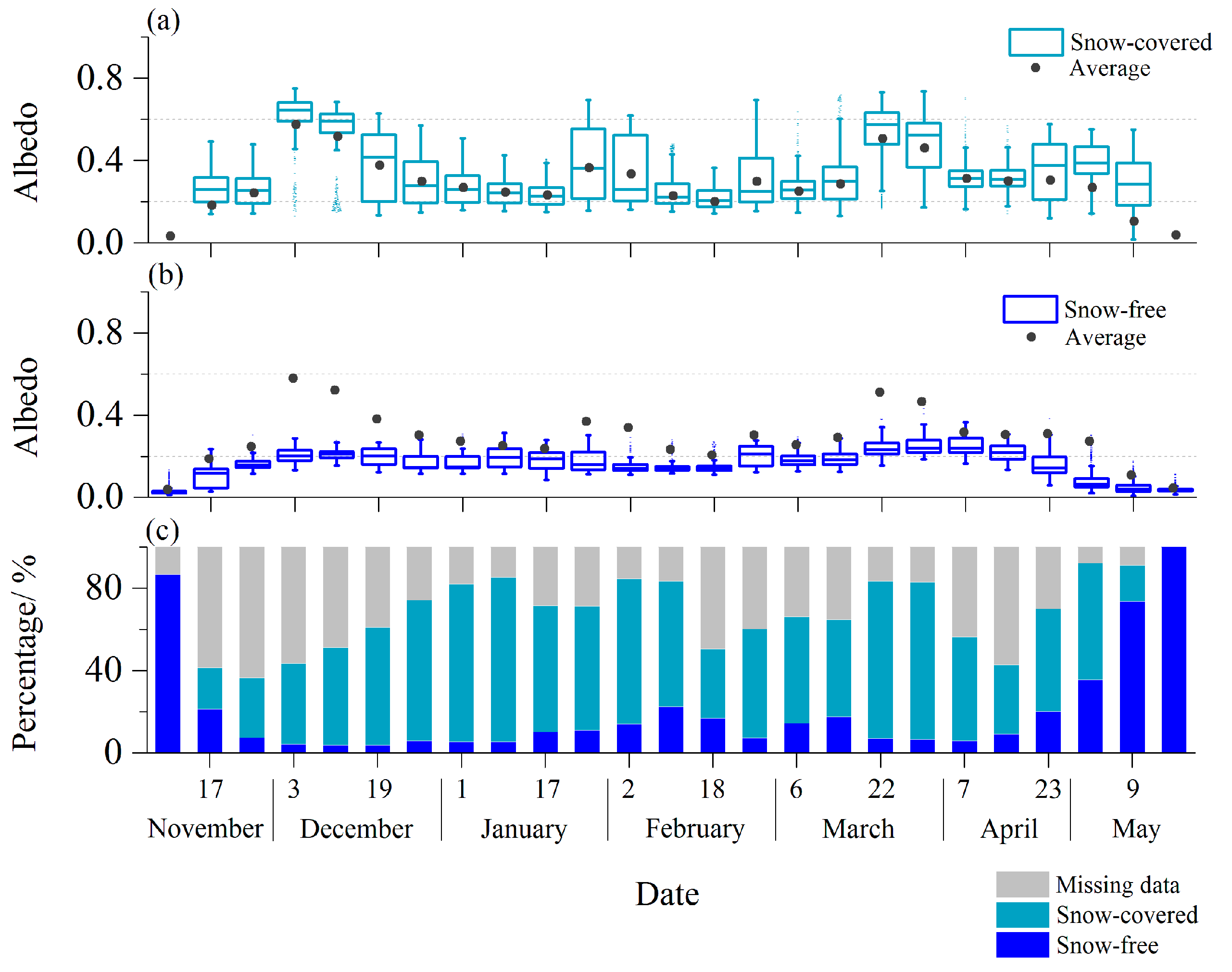
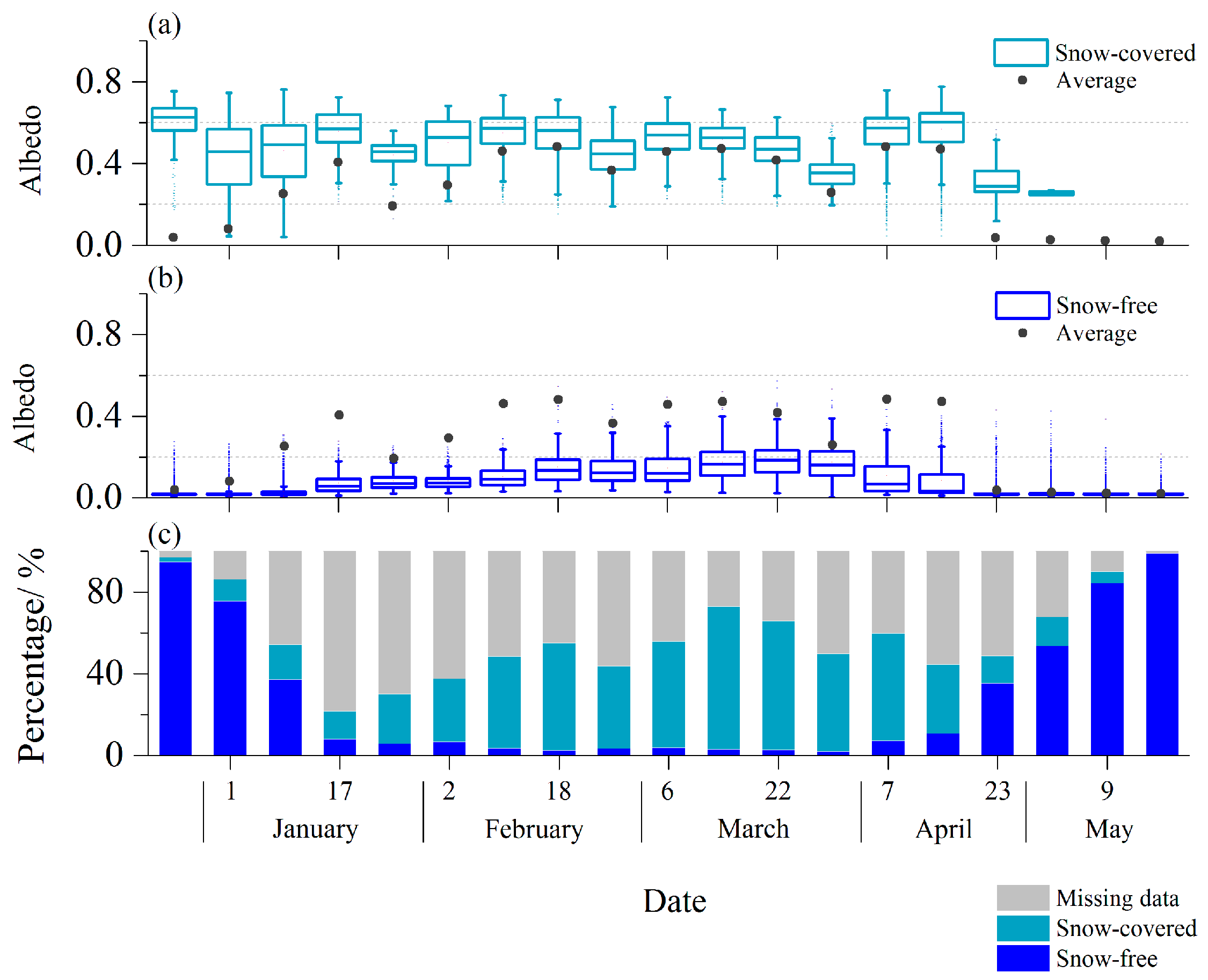
3.2. Lake Surface Albedo Characteristics during the Frozen Period Derived from MODIS Observation
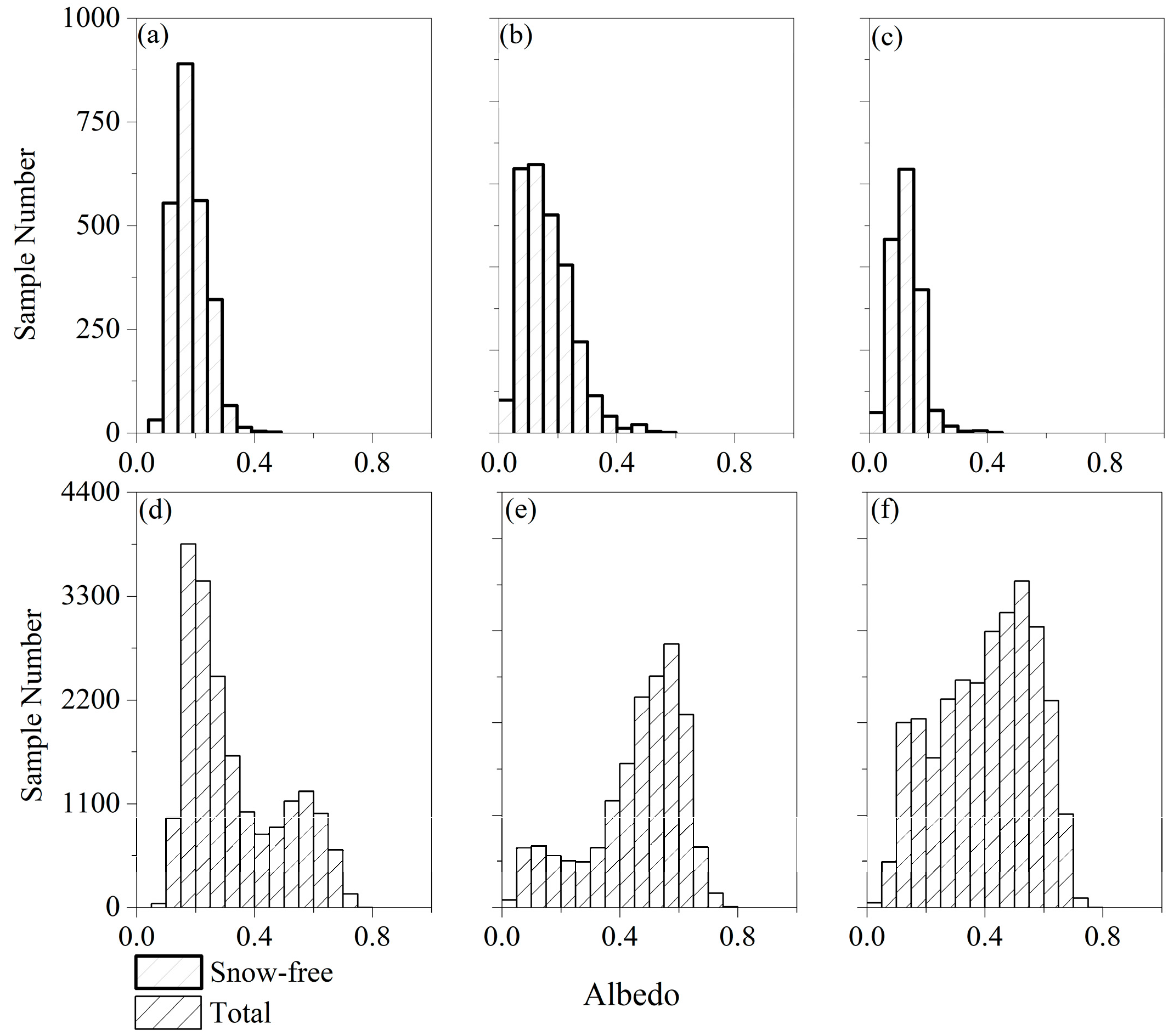
3.3. Distribution of the Albedo during the Frozen Period Derived from MODIS Observation
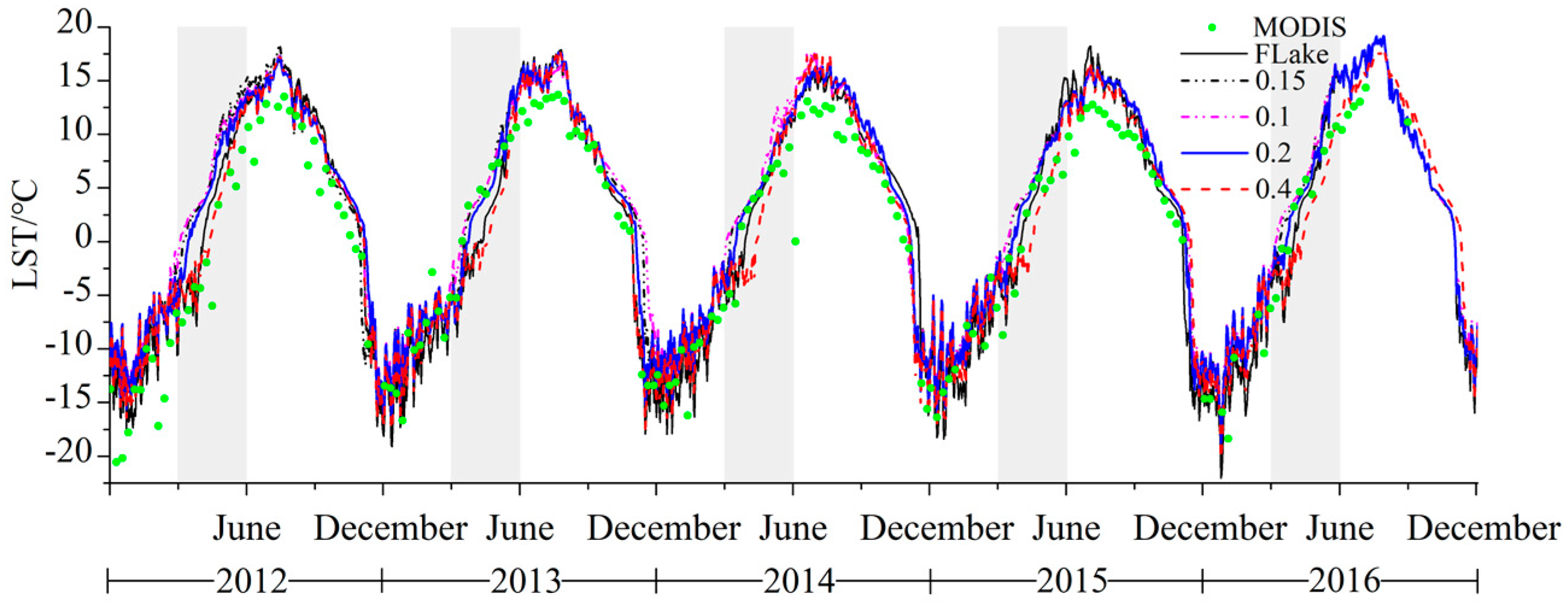
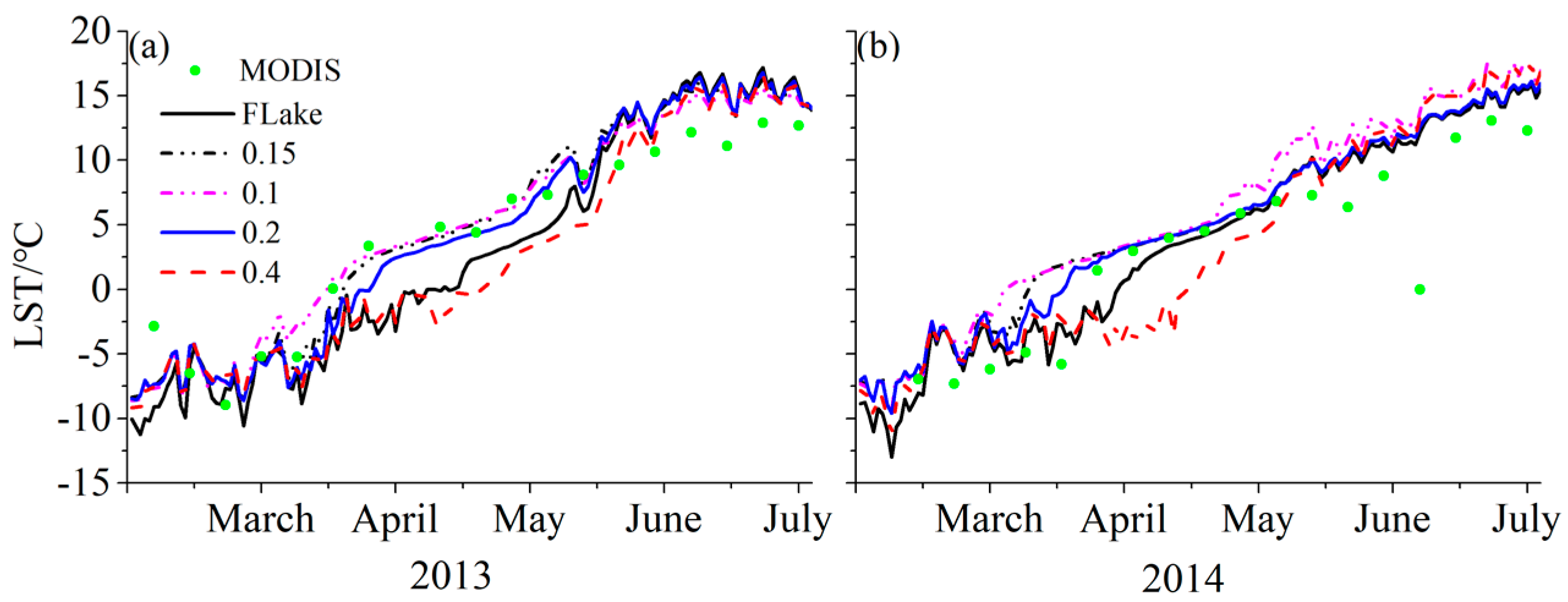
3.4. Influence of the Albedo Error in the Simulation with the Observation Data Derived from MODIS
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhang, G.; Yao, T.; Xie, H.; Zhang, K.; Zhu, F. Lakes’ state and abundance across the Tibetan Plateau. Chin. Sci. Bull. 2014, 59, 3010–3021. [Google Scholar] [CrossRef]
- Wang, Z.; Schaaf, C.B.; Strahler, A.H.; Chopping, M.J.; Román, M.O.; Shuai, Y.; Woodcock, C.E.; Hollinger, D.Y.; Fitzjarrald, D.R. Evaluation of MODIS albedo product (MCD43A) over grassland, agriculture and forest surface types during dormant and snow-covered periods. Remote Sens. Environ. 2014, 140, 60–77. [Google Scholar] [CrossRef]
- Chen, Y.; Zong, Y.; Li, B.; Li, S.; Aitchison, J.C. Shrinking lakes in Tibet linked to the weakening Asian monsoon in the past 8.2 Ka. Quat. Res. 2013, 80, 189–198. [Google Scholar] [CrossRef]
- Zhang, G.; Xie, H.; Kang, S.; Yi, D.; Ackley, S.F. Monitoring lake level changes on the Tibetan Plateau using ICESat altimetry data (2003–2009). Remote Sens. Environ. 2011, 115, 1733–1742. [Google Scholar] [CrossRef]
- Wang, X.; Gong, P.; Zhao, Y.; Xu, Y.; Cheng, X.; Niu, Z.; Luo, Z.; Huang, H.; Sun, F.; Li, X. Water-level changes in China’s large lakes determined from ICESat/GLAS data. Remote Sens. Environ. 2013, 132, 131–144. [Google Scholar] [CrossRef]
- Wan, W.; Long, D.; Hong, Y.; Ma, Y.; Yuan, Y.; Xiao, P.; Duan, H.; Han, Z.; Gu, X. A lake data set for the Tibetan Plateau from the 1960s, 2005, and 2014. Sci. Data 2016, 3. [Google Scholar] [CrossRef] [PubMed]
- Du, J.; Kimball, J.S.; Duguay, C.; Kim, Y.; Watts, J.D. Satellite microwave assessment of Northern Hemisphere lake ice phenology from 2002 to 2015. Cryosphere 2017, 11, 47–63. [Google Scholar] [CrossRef]
- Adrian, R.; O’Reilly, C.M.; Zagarese, H.; Baines, S.B.; Hessen, D.O.; Keller, W.; Livingstone, D.M.; Sommaruga, R.; Straile, D.; Van Donk, E. Lakes as sentinels of climate change. Limnol. Oceanogr. 2009, 54, 2283–2297. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Yao, T.; Xie, H.; Qin, J.; Ye, Q.; Dai, Y.; Guo, R. Estimating surface temperature changes of lakes in the Tibetan Plateau using MODIS LST data. J. Geophys. Res. Atmos. 2014, 119, 8552–8567. [Google Scholar] [CrossRef]
- Wang, S.-M.; Dou, H.S. Lakes in China; Science Press: Beijing, China, 1998. [Google Scholar]
- Austin, J.A.; Colman, S.M. Lake Superior summer water temperatures are increasing more rapidly than regional air temperatures: A positive ice-albedo feedback. Geophys. Res. Lett. 2007, 34, 47–63. [Google Scholar] [CrossRef]
- Hampton, S.E.; Izmest, E.; Lyubov, R.; Moore, M.V.; Katz, S.L.; Dennis, B.; Silow, E.A. Sixty years of environmental change in the world’s largest freshwater lake–lake Baikal, Siberia. Glob. Chang. Biol. 2008, 14, 1947–1958. [Google Scholar] [CrossRef]
- O’Reilly, C.M.; Sharma, S.; Gray, D.K.; Hampton, S.E.; Read, J.S.; Rowley, R.J.; Schneider, P.; Lenters, J.D.; McIntyre, P.B.; Kraemer, B.M. Rapid and highly variable warming of lake surface waters around the globe. Geophys. Res. Lett. 2015, 42. [Google Scholar] [CrossRef]
- Ingram, W.; Wilson, C.; Mitchell, J. Modelling climate change: An assessment of sea ice and surface albedo feedbacks. J. Geophys. Res. Atmos. 1989, 94, 8609–8622. [Google Scholar] [CrossRef]
- Efremova, T.; Pal’shin, N. Ice phenomena terms on the water bodies of Northwestern Russia. Russ. Meteorol. Hydrol. 2011, 36, 559–565. [Google Scholar] [CrossRef]
- Guo, Z.; Wang, N.; Jiang, X.; Mao, R.; Wu, H. Research progress on snow and ice albedo measurement, retrieval and application. Remote Sens. Technol. Appl. 2013, 28, 739–746. [Google Scholar]
- Bolsenga, S. Total albedo of great lakes ice. Water Resour. Res. 1969, 5, 1132–1133. [Google Scholar] [CrossRef]
- Wiscombe, W.J.; Warren, S.G. A model for the spectral albedo of snow. I: Pure snow. J. Atmos. Sci. 1980, 37, 2712–2733. [Google Scholar] [CrossRef]
- Heron, R.; Woo, M.-K. Decay of a high arctic lake-ice cover: Observations and modelling. J. Glaciol. 1994, 40, 283–292. [Google Scholar] [CrossRef]
- Gardner, A.S.; Sharp, M.J. A review of snow and ice albedo and the development of a new physically based broadband albedo parameterization. J. Geophys. Res. Earth Surf. 2010, 115. [Google Scholar] [CrossRef]
- Semmler, T.; Cheng, B.; Yang, Y.; Rontu, L. Snow and ice on Bear Lake (Alaska)—Sensitivity experiments with two lake ice models. Tellus A Dyn. Meteorol. Oceanogr. 2012, 64. [Google Scholar] [CrossRef]
- Svacina, N.; Duguay, C.; Brown, L. Modelled and satellite-derived surface albedo of lake ice—Part I: Evaluation of the albedo parameterization scheme of the Canadian Lake Ice Model. Hydrol. Process. 2014, 28, 4550–4561. [Google Scholar] [CrossRef]
- Shao, Z.-D.; Ke, C.-Q. Spring–summer albedo variations of Antarctic sea ice from 1982 to 2009. Environ. Res. Lett. 2015, 10. [Google Scholar] [CrossRef]
- Svacina, N.; Duguay, C.; King, J. Modelled and satellite-derived surface albedo of lake ice—Part II: Evaluation of MODIS albedo products. Hydrol. Process. 2014, 28, 4562–4572. [Google Scholar] [CrossRef]
- PÄRN, O.; Haapala, J. Occurrence of synoptic flaw leads of sea ice in the Gulf of Finland. Boreal Environ. Res. 2011, 16, 71–78. [Google Scholar]
- Dirmhirn, I.; Eaton, F.D. Some characteristics of the albedo of snow. J. Appl. Meteorol. 1975, 14, 375–379. [Google Scholar] [CrossRef]
- Warren, S.G. Optical properties of snow. Rev. Geophys. 1982, 20, 67–89. [Google Scholar] [CrossRef]
- Bolsenga, S. Short note: Preliminary observations on the daily variation of ice albedo. J. Glaciol. 1977, 18, 517–521. [Google Scholar] [CrossRef]
- Bolsenga, S. Spectral reflectances of snow and fresh-water ice from 340 through 1100 nm. J. Glaciol. 1983, 29, 296–305. [Google Scholar] [CrossRef]
- Mullen, P.C.; Warren, S.G. Theory of the optical properties of lake ice. J. Geophys. Res. Atmos. 1988, 93, 8403–8414. [Google Scholar] [CrossRef]
- Roesch, S.C. Modelling stress: A methodological review. J. Behav. Med. 1999, 22, 249–269. [Google Scholar] [CrossRef] [PubMed]
- Hall, A.; Qu, X. Using the current seasonal cycle to constrain snow albedo feedback in future climate change. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Pirazzini, R. Challenges in snow and ice albedo parameterizations. Geophysica 2009, 45, 41–62. [Google Scholar]
- Mallard, M.S.; Nolte, C.G.; Bullock, O.R.; Spero, T.L.; Gula, J. Using a coupled lake model with WRF for dynamical downscaling. J. Geophys. Res. Atmos. 2014, 119, 7193–7208. [Google Scholar] [CrossRef]
- Ye, Q.; Wei, Q.; Hochschild, V.; Duguay, C.R. Integrated observations of lake ice at Nam Co. on the Tibetan Plateau from 2001 to 2009. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Vancouver, BC, Canada, 24–29 July 2011; pp. 3217–3220. [Google Scholar]
- Huang, W.; Li, Z.; Han, H.; Niu, F.; Lin, Z.; Leppäranta, M. Structural analysis of thermokarst lake ice in Beiluhe Basin, Qinghai–Tibet Plateau. Cold Reg. Sci. Technol. 2012, 72, 33–42. [Google Scholar] [CrossRef]
- Huang, W.; Han, H.; Shi, L.; Niu, F.; Deng, Y.; Li, Z. Effective thermal conductivity of thermokarst lake ice in Beiluhe Basin, Qinghai–Tibet Plateau. Cold Reg. Sci. Technol. 2013, 85, 34–41. [Google Scholar] [CrossRef]
- Huang, W.; Li, R.; Han, H.; Niu, F.; Wu, Q.; Wang, W. Ice processes and surface ablation in a shallow thermokarst lake in the central Qinghai–Tibetan Plateau. Ann. Glaciol. 2016, 57, 20–28. [Google Scholar] [CrossRef]
- Schaaf, C.B.; Gao, F.; Strahler, A.H.; Lucht, W.; Li, X.; Tsang, T.; Strugnell, N.C.; Zhang, X.; Jin, Y.; Muller, J.-P. First operational BRDF, albedo nadir reflectance products from MODIS. Remote Sens. Environ. 2002, 83, 135–148. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, Q.; Wang, Z.; Schaaf, C.; Erb, A. Evaluation of VIIIRS daily BRDF, albedo, and NBAR product using the MODIS collection V006 product and in situ measurements. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 1962–1965. [Google Scholar]
- Hall, D.K.; Riggs, G.A. Accuracy assessment of the MODIS snow products. Hydrol. Process. 2007, 21, 1534–1547. [Google Scholar] [CrossRef]
- Crosman, E.T.; Horel, J.D. MODIS-derived surface temperature of the Great Salt Lake. Remote Sens. Environ. 2009, 113, 73–81. [Google Scholar] [CrossRef]
- Song, X.; Wang, Y.; Tang, B.; Leng, P.; Sun, C.; Peng, J.; Loew, A. Estimation of land surface temperature using FengYun-2E (FY-2E) data: A case study of the source area of the yellow river. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1–8. [Google Scholar] [CrossRef]
- Mironov, D.; Ritter, B. A New Sea Ice Model for GME; Technical Note; Deutscher Wetterdienst: Offenbach am Main, Germany, 2004. [Google Scholar]
- Subin, Z.M.; Riley, W.J.; Mironov, D. An improved lake model for climate simulations: Model structure, evaluation, and sensitivity analyses in CESM1. J. Adv. Model. Earth Syst. 2012, 4. [Google Scholar] [CrossRef]
- Mironov, D. Parameterization of Lakes in Numerical Weather Prediction. Part 1: Description of a Lake Model. Offenbach: Consortium for Small-Scale Modelling; Technical Report 11; Deutscher Wetterdienst: Offenbach am Main, Germany, 2003. [Google Scholar]
- Mironov, D.; Heise, E.; Kourzeneva, E.; Ritter, B.; Schneider, N.; Terzhevik, A. Implementation of the lake parameterisation saheme FLake into the numerical weather prediction model COSMO. Boreal Environ. Res. 2010, 15, 218–230. [Google Scholar]
- Perroud, M.; Goyette, S.; Martynov, A.; Beniston, M.; Annevillec, O. Simulation of multiannual thermal profiles in deep Lake Geneva: A comparison of one-dimensional lake models. Limnol. Oceanogr. 2009, 54, 1574–1594. [Google Scholar] [CrossRef]
- Kheyrollah Pour, H.; Duguay, C.; Martynov, A.; Brown, L. Simulation of surface temperature and ice cover of large northern lakes with 1-D models: A comparison with MODIS satellite data and in situ measurements. Tellus A Dyn. Meteorol. Oceanogr. 2012, 64. [Google Scholar] [CrossRef]
- Stepanenko, V.; Jöhnk, K.D.; Machulskaya, E.; Perroud, M.; Subin, Z.; Nordbo, A.; Mammarella, I.; Mironov, D. Simulation of surface energy fluxes and stratification of a small boreal lake by a set of one-dimensional models. Tellus A Dyn. Meteorol. Oceanogr. 2014, 66. [Google Scholar] [CrossRef]
- Gou, P.; Ye, Q.; Wei, Q. Lake ice change at the Nam Co. Lake on the Tibetan Plateau during 2000–2013 and influencing factors. Prog. Geogr 2015, 34, 1241–1249. [Google Scholar]
- Bengtsson, L. Spatial variability of lake ice covers. Geogr. Ann. Ser. A Phys. Geogr. 1986, 68, 113–121. [Google Scholar] [CrossRef]
- Petrov, M.; Terzhevik, A.Y.; Palshin, N.; Zdorovennov, R.; Zdorovennova, G. Absorption of solar radiation by snow-and-ice cover of lakes. Water Resour. 2005, 32, 496–504. [Google Scholar] [CrossRef]
- Jakkila, J.; Leppäranta, M.; Kawamura, T.; Shirasawa, K.; Salonen, K. Radiation transfer and heat budget during the ice season in Lake Pääjärvi, Finland. Aquat. Ecol. 2009, 43, 681–692. [Google Scholar] [CrossRef]
- Bernhardt, J.; Engelhardt, C.; Kirillin, G.; Matschullat, J. Lake ice phenology in Berlin-Brandenburg from 1947–2007: Observations and model hindcasts. Clim. Chang. 2012, 112, 791–817. [Google Scholar] [CrossRef]
- Salonen, K.; Pulkkanen, M.; Salmi, P.; Griffiths, R.W. Interannual variability of circulation under spring ice in a boreal lake. Limnol. Oceanogr. 2014, 59, 2121–2132. [Google Scholar] [CrossRef]
- Van Cleave, K.; Lenters, J.D.; Wang, J.; Verhamme, E.M. A regime shift in Lake Superior ice cover, evaporation, and water temperature following the warm EI Niñ winter of 1997–1998. Limnol. Oceanogr. 2014, 59, 1889–1898. [Google Scholar] [CrossRef]
- Donlon, C.J.; Minnett, P.J.; Gentemann, C.; Nightingale, T.J.; Barton, I.J.; Ward, B.; Murray, M.J. Toward improved validation of satellite sea surface skin temperature measurements for climate research. J. Clim. 2001, 15, 353–369. [Google Scholar] [CrossRef]
- Schaaf, C.; Wang, Z.; Shuai, Y.; Strahler, A. Daily operational MODIS BRDF, albedo and nadir reflectance products (V006). In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 3–7 December 2012. [Google Scholar]
- Chen, A.; Liang, X.; Bian, L.; Liu, Y. Analysis on MODIS albedo retrieval quality over the Qinghai-Tibet Plateau. Plateau Meteorol. 2016, 35, 277–284. [Google Scholar]
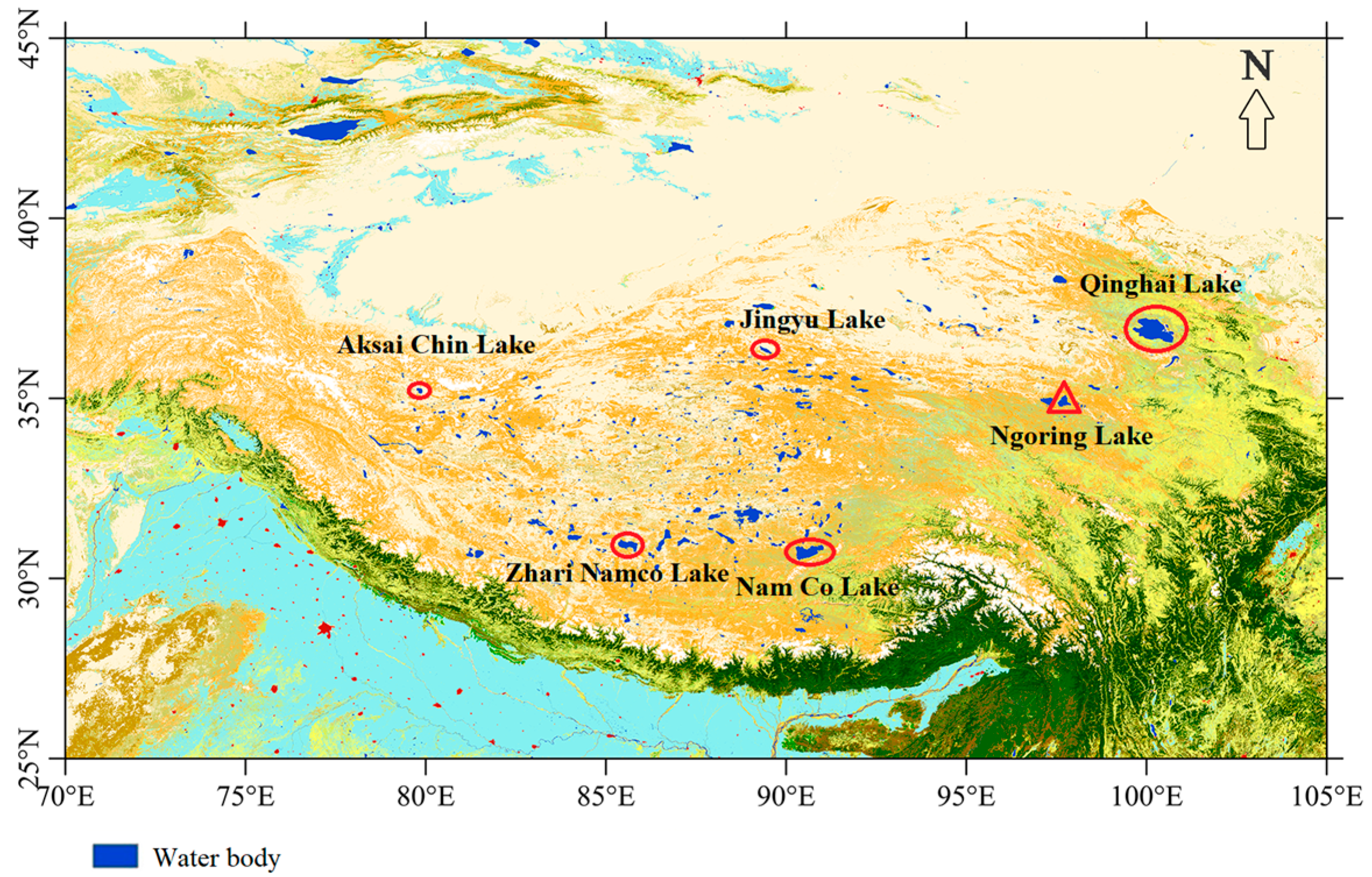



| Lake Names | Aksai Chin Lake | Nam Co Lake | Jingyu Lake | Zhari Namco Lake | Ngoring Lake | Qinghai Lake |
|---|---|---|---|---|---|---|
| Surface area (km2) | 184.9 | 2040.9 | 283.7 | 996.9 | 629.8 | 4254.9 |
| Altitude (m) | 4848 | 4718 | 4708 | 4613 | 4272 | 3260 |
| Lake Names | Aksai Chin Lake | Jingyu Lake | Zhari Namco Lake | Ngoring Lake | Nam Co Lake | Qinghai Lake | |
|---|---|---|---|---|---|---|---|
| Snow-covered | October | - | 0.12 | - | - | - | - |
| November | 0.23 | 0.32 | 0.23 | 0.22 | - | 0.22 | |
| December | 0.31 | 0.37 | 0.29 | 0.36 | - | 0.28 | |
| January | 0.25 | 0.40 | 0.40 | 0.41 | 0.40 | 0.29 | |
| February | 0.26 | 0.28 | 0.32 | 0.20 | 0.52 | 0.29 | |
| March | 0.35 | 0.44 | 0.27 | 0.38 | 0.54 | 0.23 | |
| April | 0.28 | 0.51 | 0.24 | 0.36 | 0.42 | - | |
| May | 0.27 | 0.47 | - | 0.23 | 0.31 | - | |
| June | - | 0.27 | - | - | - | - | |
| Mean | 0.28 | 0.35 | 0.29 | 0.31 | 0.44 | 0.26 | |
| SD | 0.04 | 0.11 | 0.06 | 0.08 | 0.08 | 0.03 | |
| Snow-free | October | - | 0.02 | - | - | - | - |
| November | 0.11 | 0.14 | 0.01 | 0.02 | - | 0.01 | |
| December | 0.21 | 0.21 | 0.03 | 0.10 | - | 0.05 | |
| January | 0.22 | 0.24 | 0.25 | 0.16 | 0.07 | 0.20 | |
| February | 0.20 | 0.20 | 0.30 | 0.14 | 0.14 | 0.16 | |
| March | 0.24 | 0.27 | 0.20 | 0.18 | 0.19 | 0.06 | |
| April | 0.22 | 0.34 | 0.05 | 0.10 | 0.14 | 0.02 | |
| May | 0.08 | 0.25 | - | 0.02 | 0.05 | - | |
| June | - | 0.04 | - | - | - | - | |
| Oct. | - | 0.12 | - | - | - | - | |
| Mean | 0.18 | 0.18 | 0.14 | 0.10 | 0.12 | 0.08 | |
| SD | 0.06 | 0.10 | 0.11 | 0.06 | 0.05 | 0.07 | |
| Ice Duration | Albedo Parameterized | Freezing Date | Melting Date | Ice Thickness | Coming Summer LST | LST in Winter |
|---|---|---|---|---|---|---|
| 2012–2013 | 0.1 | 5 December 2012 | 14 April 2013 | 0.48 | 15.11 | −9.17 |
| 0.15 | 30 November 2012 | 18 April 2013 | 0.56 | 15.44 | −10.24 | |
| 0.2 | 8 December 2012 | 14 April 2013 | 0.54 | 15.87 | −9.12 | |
| 0.4 | 5 December 2012 | 24 April 2013 | 0.69 | 15.68 | −10.58 | |
| FLake | 5 December 2012 | 12 May 2013 | 0.74 | 16.04 | −11.56 | |
| 2013–2014 | 0.1 | 17 December 2013 | 2 April 2014 | 0.43 | 15.52 | −7.49 |
| 0.15 | 13 December 2013 | 8 April 2014 | 0.52 | 14.86 | −8.35 | |
| 0.2 | 3 December 2013 | 16 April 2014 | 0.56 | 14.85 | −9.53 | |
| 0.4 | 29 November 2013 | 15 May 2014 | 0.66 | 15.42 | −11.36 | |
| FLake | 29 November 2013 | 28 April 2014 | 0.69 | 14.27 | −12.58 | |
| 2014–2015 | 0.1 | 2 December 2014 | 14 April 2015 | 0.5 | 14.33 | −9.3 |
| 0.15 | 5 December 2014 | 16 April 2015 | 0.54 | 14.31 | −9.15 | |
| 0.2 | 6 December 2014 | 20 April 2015 | 0.57 | 14.4 | −9.27 | |
| 0.4 | 4 December 2014 | 18 May 2015 | 0.66 | 13.99 | −10.51 | |
| FLake | 16 December 2015 | 2 May 2015 | 0.67 | 14.96 | −9.61 | |
| 2015–2016 | 0.1 | 12 December 2015 | 6 April 2016 | 0.53 | 16.97 | −9.17 |
| 0.15 | 9 December 2015 | 11 April 2016 | 0.58 | 16.97 | −9.61 | |
| 0.2 | 8 December 2015 | 20 April 2016 | 0.59 | 16.94 | −9.91 | |
| 0.4 | 15 December 2015 | 11 May 2016 | 0.66 | 15.39 | −9.92 | |
| FLake | 4 December 2015 | 30 April 2016 | 0.73 | 16.87 | −12.93 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lang, J.; Lyu, S.; Li, Z.; Ma, Y.; Su, D. An Investigation of Ice Surface Albedo and Its Influence on the High-Altitude Lakes of the Tibetan Plateau. Remote Sens. 2018, 10, 218. https://doi.org/10.3390/rs10020218
Lang J, Lyu S, Li Z, Ma Y, Su D. An Investigation of Ice Surface Albedo and Its Influence on the High-Altitude Lakes of the Tibetan Plateau. Remote Sensing. 2018; 10(2):218. https://doi.org/10.3390/rs10020218
Chicago/Turabian StyleLang, Jiahe, Shihua Lyu, Zhaoguo Li, Yaoming Ma, and Dongsheng Su. 2018. "An Investigation of Ice Surface Albedo and Its Influence on the High-Altitude Lakes of the Tibetan Plateau" Remote Sensing 10, no. 2: 218. https://doi.org/10.3390/rs10020218
APA StyleLang, J., Lyu, S., Li, Z., Ma, Y., & Su, D. (2018). An Investigation of Ice Surface Albedo and Its Influence on the High-Altitude Lakes of the Tibetan Plateau. Remote Sensing, 10(2), 218. https://doi.org/10.3390/rs10020218