Modelling Water Stress in a Shiraz Vineyard Using Hyperspectral Imaging and Machine Learning
Abstract
1. Introduction
2. Materials and Methods
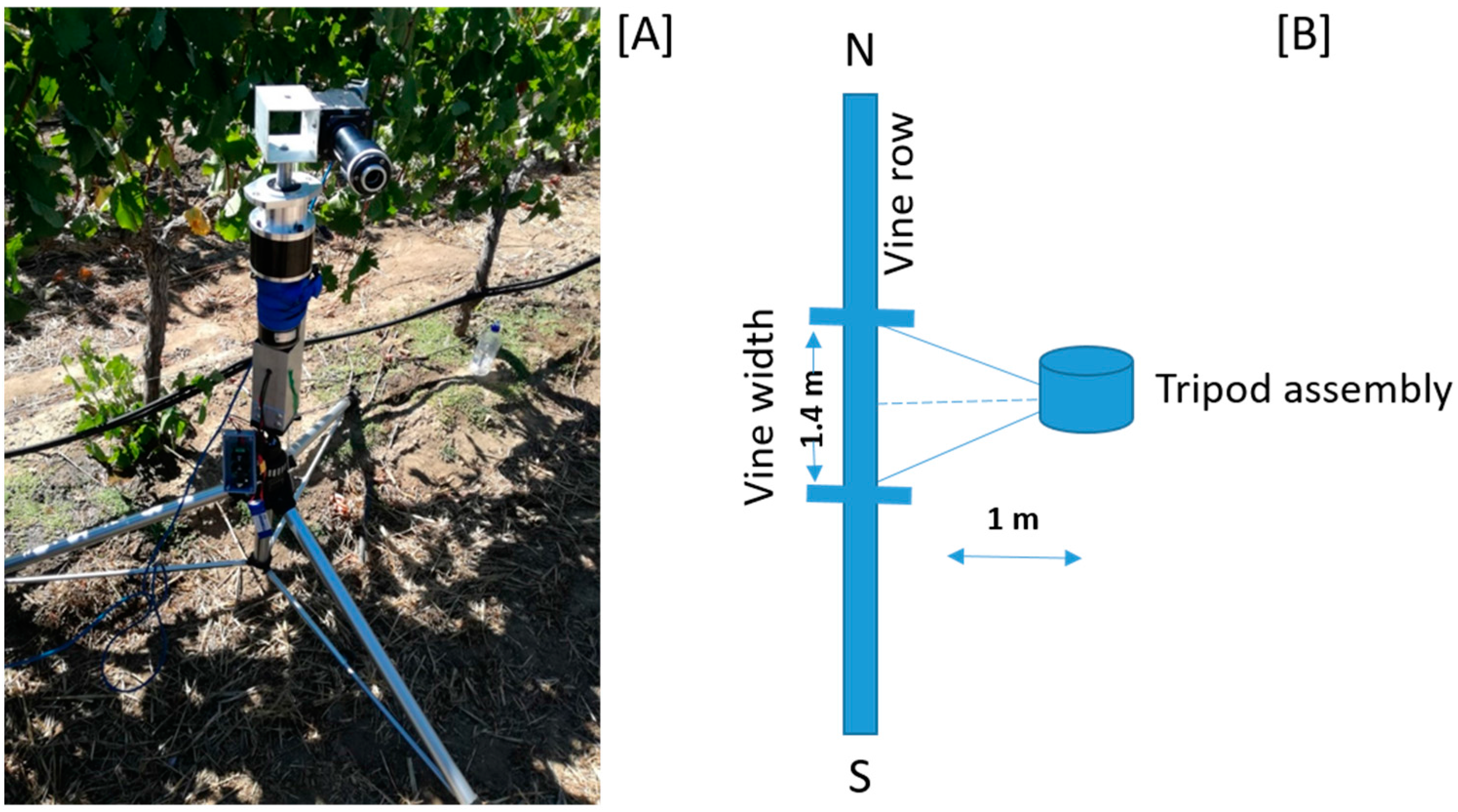
2.1. Study Site
2.2. Data Acquisition and Pre-Processing
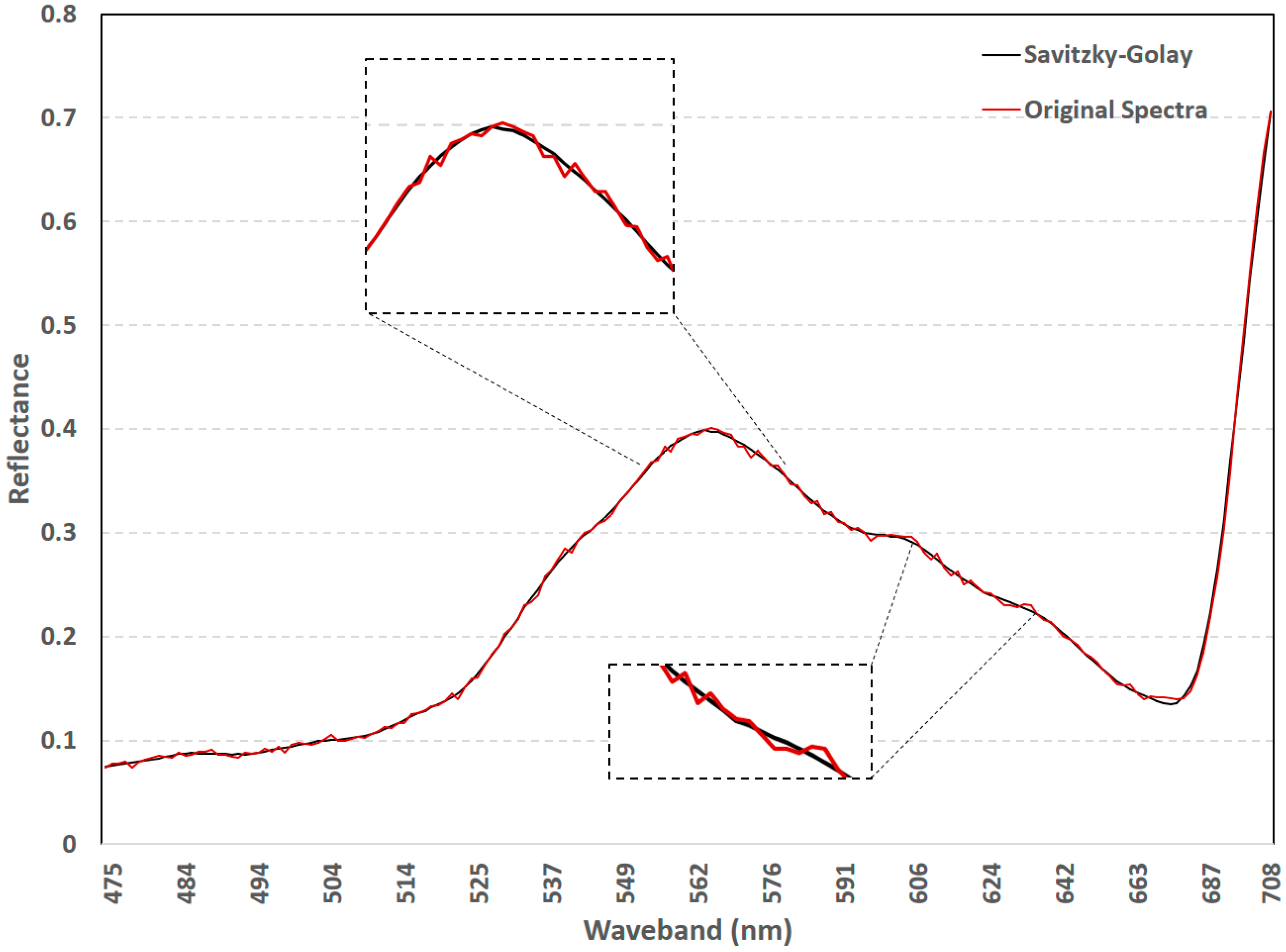
2.3. Spectral Smoothing
2.4. Classification
2.4.1. Random Forest (RF)
2.4.2. Extreme Gradient Boosting (XGBoost)
2.5. Dimensionality Reduction
2.6. Accuracy Assessment
3. Results
3.1. Spectral Smoothing Using the Savitzky-Golay Filter
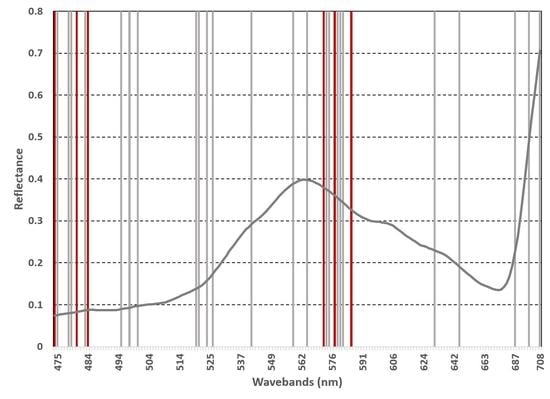
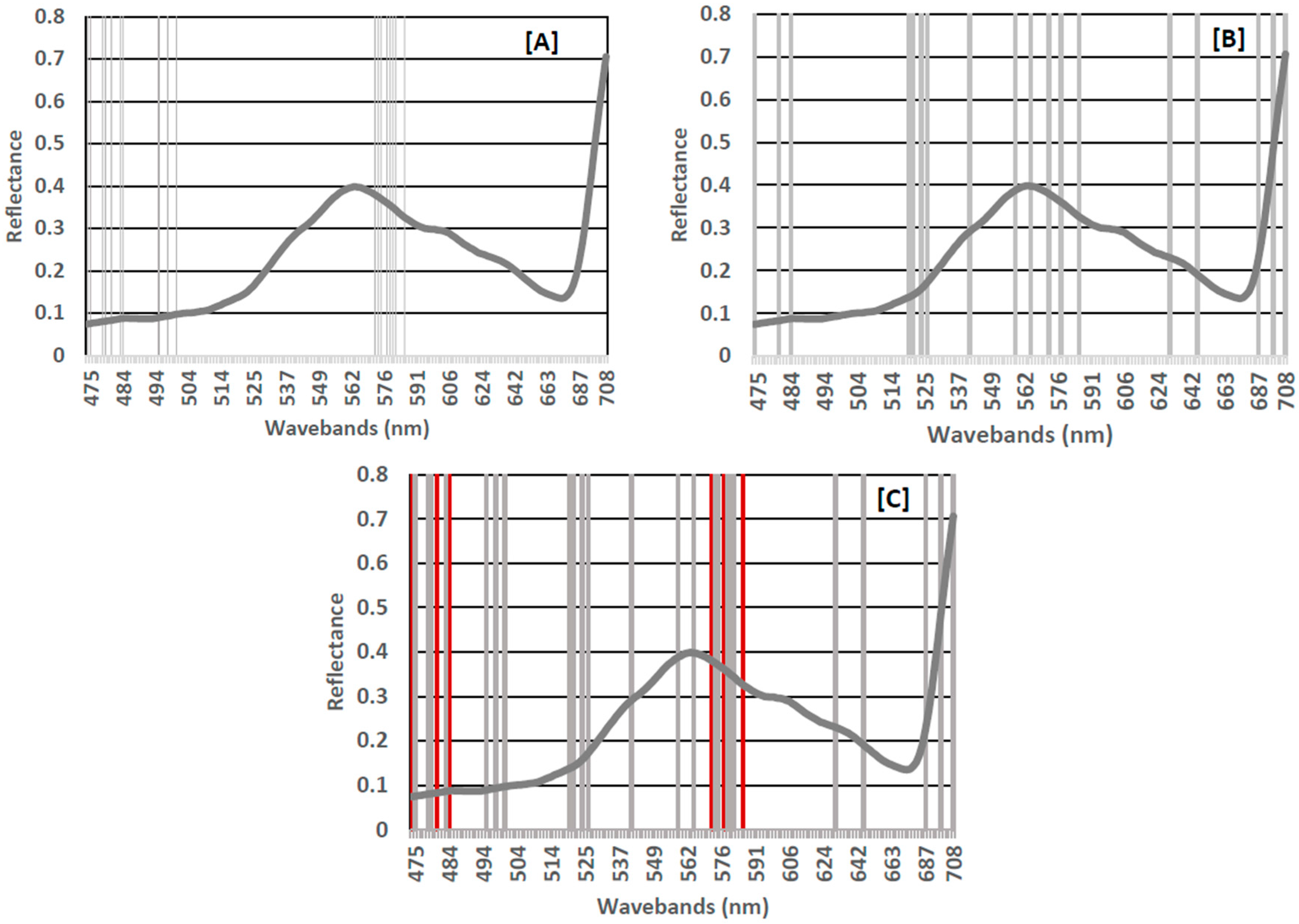
3.2. Important Waveband Selection
3.3. Classification Using Random Forest and Extreme Gradient Boosting
4. Discussion
4.1. Efficacy of the Savitzky-Golay Filter
4.2. Classification Using All Wavebands
4.3. Classification Using Subset of Important Wavebands
5. Conclusions
- Both RF and XGBoost may be utilised to model water stress in a Shiraz vineyard.
- Wavebands in the VIS region of the EM spectrum may be used to model water stress in a Shiraz vineyard.
- It is imperative that future studies carefully consider the impact of applying the Savitzky-Golay filter for smoothing spectral data.
- The developed framework requires further investigation to evaluate its robustness and operational capabilities.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Costa, J.M.; Vaz, M.; Escalona, J.; Egipto, R.; Lopes, C.; Medrano, H.; Chaves, M.M. Modern viticulture in southern Europe: Vulnerabilities and strategies for adaptation to water scarcity. Agric. Water Manag. 2016, 164, 5–18. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; González-Dugo, V.; Berni, J.A.J. Fluorescence, temperature and narrow-band indices acquired from a UAV platform for water stress detection using a micro-hyperspectral imager and a thermal camera. Remote Sens. Environ. 2012, 117, 322–337. [Google Scholar] [CrossRef]
- Kim, Y.; Glenn, D.M.; Park, J.; Ngugi, H.K.; Lehman, B.L. Hyperspectral image analysis for water stress detection of apple trees. Comput. Electron. Agric. 2011, 77, 155–160. [Google Scholar] [CrossRef]
- Maimaitiyiming, M.; Ghulam, A.; Bozzolo, A.; Wilkins, J.L.; Kwasniewski, M.T. Early Detection of Plant Physiological Responses to Different Levels of Water Stress Using Reflectance Spectroscopy. Remote Sens. 2017, 9, 745. [Google Scholar] [CrossRef]
- Bota, J.; Tomás, M.; Flexas, J.; Medrano, H.; Escalona, J.M. Differences among grapevine cultivars in their stomatal behavior and water use efficiency under progressive water stress. Agric. Water Manag. 2016, 164, 91–99. [Google Scholar] [CrossRef]
- Chirouze, J.; Boulet, G.; Jarlan, L.; Fieuzal, R.; Rodriguez, J.C.; Ezzahar, J.; Er-Raki, S.; Bigeard, G.; Merlin, O.; Garatuza-Payan, J.; et al. Intercomparison of four remote-sensing-based energy balance methods to retrieve surface evapotranspiration and water stress of irrigated fields in semi-arid climate. Hydrol. Earth Syst. Sci. 2014, 18, 1165–1188. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; González-Dugo, V.; Williams, L.E.; Suárez, L.; Berni, J.A.J.; Goldhamer, D.; Fereres, E. A PRI-based water stress index combining structural and chlorophyll effects: Assessment using diurnal narrow-band airborne imagery and the CWSI thermal index. Remote Sens. Environ. 2013, 138, 38–50. [Google Scholar] [CrossRef]
- González-Fernández, A.B.; Rodríguez-Pérez, J.R.; Marcelo, V.; Valenciano, J.B. Using field spectrometry and a plant probe accessory to determine leaf water content in commercial vineyards. Agric. Water Manag. 2015, 156, 43–50. [Google Scholar] [CrossRef]
- Baluja, J.; Diago, M.P.; Balda, P.; Zorer, R.; Meggio, F.; Morales, F.; Tardaguila, J. Assessment of vineyard water status variability by thermal and multispectral imagery using an unmanned aerial vehicle (UAV). Irrig. Sci. 2012, 30, 511–522. [Google Scholar] [CrossRef]
- Shimada, S.; Funatsuka, E.; Ooda, M.; Takyu, M.; Fujikawa, T.; Toyoda, H. Developing the Monitoring Method for Plant Water Stress Using Spectral Reflectance Measurement. J. Arid Land Stud. 2012, 22, 251–254. [Google Scholar]
- Govender, M.; Dye, P.; Witokwski, E.; Ahmed, F. Review of commonly used remote sensing and ground based technologies to measure plant water stress. Water SA 2009, 35, 741–752. [Google Scholar] [CrossRef]
- De Bei, R.; Cozzolino, D.; Sullivan, W.; Cynkar, W.; Fuentes, S.; Dambergs, R.; Pech, J.; Tyerman, S.D. Non-destructive measurement of grapevine water potential using near infrared spectroscopy. Aust. J. Grape Wine Res. 2011, 17, 62–71. [Google Scholar] [CrossRef]
- Diago, M.P.; Bellincontro, A.; Scheidweiler, M.; Tardaguila, J.; Tittmann, S.; Stoll, M. Future opportunities of proximal near infrared spectroscopy approaches to determine the variability of vineyard water status. Aust. J. Grape Wine Res. 2017, 23, 409–414. [Google Scholar] [CrossRef]
- Beghi, R.; Giovenzana, V.; Guidetti, R. Better water use efficiency in vineyard by using visible and near infrared spectroscopy for grapevine water status monitoring. Chem. Eng. Trans. 2017, 58, 691–696. [Google Scholar] [CrossRef]
- Pôças, I.; Rodrigues, A.; Gonçalves, S.; Costa, P.M.; Gonçalves, I.; Pereira, L.S.; Cunha, M. Predicting grapevine water status based on hyperspectral reflectance vegetation indices. Remote Sens. 2015, 7, 16460–16479. [Google Scholar] [CrossRef]
- Carreiro Soares, S.F.; Medeiros, E.P.; Pasquini, C.; de Lelis Morello, C.; Harrop Galvão, R.K.; Ugulino Araújo, M.C. Classification of individual cotton seeds with respect to variety using near-infrared hyperspectral imaging. Anal. Methods 2016, 8, 8498–8505. [Google Scholar] [CrossRef]
- Mulla, D.J. Twenty five years of remote sensing in precision agriculture: Key advances and remaining knowledge gaps. Biosyst. Eng. 2013, 114, 358–371. [Google Scholar] [CrossRef]
- Poona, N.K.; Van Niekerk, A.; Nadel, R.L.; Ismail, R. Random Forest (RF) Wrappers for Waveband Selection and Classification of Hyperspectral Data. Appl. Spectrosc. 2016, 70, 322–333. [Google Scholar] [CrossRef] [PubMed]
- Hughes, G.F. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef]
- Pedergnana, M.; Marpu, P.R.; Mura, M.D. A Novel Technique for Optimal Feature Selection in Attribute Profiles Based on Genetic Algorithms. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3514–3528. [Google Scholar] [CrossRef]
- Tong, Q.; Xue, Y.; Zhang, L. Progress in hyperspectral remote sensing science and technology in China over the past three decades. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 70–91. [Google Scholar] [CrossRef]
- Poona, N.K.; Ismail, R. Using Boruta-selected spectroscopic wavebands for the asymptomatic detection of fusarium circinatum stress. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3764–3772. [Google Scholar] [CrossRef]
- Abdel-Rahman, E.M.; Mutanga, O.; Adam, E.; Ismail, R. Detecting Sirex noctilio grey-attacked and lightning-struck pine trees using airborne hyperspectral data, random forest and support vector machines classifiers. ISPRS J. Photogramm. Remote Sens. 2014, 88, 48–59. [Google Scholar] [CrossRef]
- Corcoran, J.M.; Knight, J.F.; Gallant, A.L. Influence of multi-source and multi-temporal remotely sensed and ancillary data on the accuracy of random forest classification of wetlands in northern Minnesota. Remote Sens. 2013, 5, 3212–3238. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Abdel-Rahman, E.M.; Makori, D.M.; Landmann, T.; Piiroinen, R.; Gasim, S.; Pellikka, P.; Raina, S.K. The utility of AISA eagle hyperspectral data and random forest classifier for flower mapping. Remote Sens. 2015, 7, 13298–13318. [Google Scholar] [CrossRef]
- Adam, E.; Deng, H.; Odindi, J.; Abdel-Rahman, E.M.; Mutanga, O. Detecting the Early Stage of Phaeosphaeria Leaf Spot Infestations in Maize Crop Using In Situ Hyperspectral Data and Guided Regularized Random Forest Algorithm. J. Spectrosc. 2017, 2017. [Google Scholar] [CrossRef]
- Sandika, B.; Avil, S.; Sanat, S.; Srinivasu, P. Random forest based classification of diseases in grapes from images captured in uncontrolled environments. In Proceedings of the IEEE 13th International Conference, Signal Processing Proceedings, Chengdu, China, 6–10 November 2016; pp. 1775–1780. [Google Scholar]
- Knauer, U.; Matros, A.; Petrovic, T.; Zanker, T.; Scott, E.S.; Seiffert, U. Improved classification accuracy of powdery mildew infection levels of wine grapes by spatial-spectral analysis of hyperspectral images. Plant Methods 2017, 13. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Möller, A.; Ruhlmann-Kleider, V.; Leloup, C.; Neveu, J.; Palanque-Delabrouille, N.; Rich, J.; Carlberg, R.; Lidman, C.; Pritchet, C. Photometric classification of type Ia supernovae in the SuperNova Legacy Survey with supervised learning. J. Cosmol. Astropart. Phys. 2016, 12. [Google Scholar] [CrossRef]
- Torlay, L.; Perrone-Bertolotti, M.; Thomas, E.; Baciu, M. Machine learning–XGBoost analysis of language networks to classify patients with epilepsy. Brain Inform. 2017, 4, 159–169. [Google Scholar] [CrossRef] [PubMed]
- Fitriah, N.; Wijaya, S.K.; Fanany, M.I.; Badri, C.; Rezal, M. EEG channels reduction using PCA to increase XGBoost’s accuracy for stroke detection. AIP Conf. Proc. 2017, 1862, 30128. [Google Scholar] [CrossRef]
- Friedman, J. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Ren, X.; Guo, H.; Li, S.; Wang, S. A Novel Image Classification Method with CNN-XGBoost Model. In International Workshop on Digital Watermarking; Springer: Cham, Switzerland, 2017; pp. 378–390. [Google Scholar]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Mohite, J.; Karale, Y.; Pappula, S.; Shabeer, T.P.; Sawant, S.D.; Hingmire, S. Detection of pesticide (Cyantraniliprole) residue on grapes using hyperspectral sensing. In Sensing for Agriculture and Food Quality and Safety IX, Proceedings of the SPIE Commercial+ Scientific Sensing and Imaging Conference, Anaheim, CA, USA, 1 May 2017; Kim, M.S., Chao, K.L., Chin, B.A., Cho, B.K., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 2017. [Google Scholar]
- Conradie, W.J.; Carey, V.A.; Bonnardot, V.; Saayman, D.; Van Schoor, L.H. Effect of Different Environmental Factors on the Performance of Sauvignon blanc Grapevines in the Stellenbosch/Durbanville Districts of South Africa I. Geology, Soil, Climate, Phenology and Grape Composition. S. Afr. J. Enol. Vitic. 2002, 23, 78–91. [Google Scholar]
- Deloire, A.; Heyms, D. The leaf water potentials: Principles, method and thresholds. Wynboer 2011, 265, 119–121. [Google Scholar]
- Choné, X.; Van Leeuwen, C.; Dubourdieu, D.; Gaudillère, J.P. Stem water potential is a sensitive indicator of grapevine water status. Ann. Bot. 2001, 87, 477–483. [Google Scholar] [CrossRef]
- Myburgh, P.; Cornelissen, M.; Southey, T. Interpretation of Stem Water Potential Measurements. WineLand. 2016, pp. 78–80. Available online: http://www.wineland.co.za/interpretation-of-stem-water-potential-measurements/ (accessed on 26 January 2018).
- Aasen, H.; Burkart, A.; Bolten, A.; Bareth, G. Generating 3D hyperspectral information with lightweight UAV snapshot cameras for vegetation monitoring: From camera calibration to quality assurance. ISPRS J. Photogramm. Remote Sens. 2015, 108, 245–259. [Google Scholar] [CrossRef]
- Schmidt, K.S.; Skidmore, A.K. Smoothing vegetation spectra with wavelets. Int. J. Remote Sens. 2004, 25, 1167–1184. [Google Scholar] [CrossRef]
- Člupek, M.; Matějka, P.; Volka, K. Noise reduction in Raman spectra: Finite impulse response filtration versus Savitzky–Golay smoothing. J. Raman Spectrosc. 2007, 38, 1174–1179. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Liu, L.; Ji, M.; Dong, Y.; Zhang, R.; Buchroithner, M. Quantitative Retrieval of Organic Soil Properties from Visible Near-Infrared Shortwave Infrared Feature Extraction. Remote Sens. 2016, 8, 1035. [Google Scholar] [CrossRef]
- Prasad, K.A.; Gnanappazham, L.; Selvam, V.; Ramasubramanian, R.; Kar, C.S. Developing a spectral library of mangrove species of Indian east coast using field spectroscopy. Geocarto Int. 2015, 30, 580–599. [Google Scholar] [CrossRef]
- Ligges, U.; Short, T.; Kienzle, P.; Schnackenberg, S.; Billinghurst, S.; Borchers, H.-W.; Carezia, A.; Dupuis, P.; Eaton, J.W.; Farhi, E.; et al. Signal: Signal Processing. 2015. Available online: http://docplayer.net/24709837-Package-signal-july-30-2015.html (accessed on 26 January 2018).
- R Development Core Team, R. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar] [CrossRef]
- Poona, N.; van Niekerk, A.; Ismail, R. Investigating the utility of oblique tree-based ensembles for the classification of hyperspectral data. Sensors 2016, 16. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y. Xgboost: Extreme Gradient Boosting. 2017. Available online: https://cran.r-project.org/package=xgboost (accessed on 26 January 2018).
- Immitzer, M.; Atzberger, C.; Koukal, T. Tree species classification with Random forest using very high spatial resolution 8-band WorldView-2 satellite data. Remote Sens. 2012, 4, 2661–2693. [Google Scholar] [CrossRef]
- Belgiu, M.; Tomljenovic, I.; Lampoltshammer, T.J.; Blaschke, T.; Höfle, B. Ontology-based classification of building types detected from airborne laser scanning data. Remote Sens. 2014, 6, 1347–1366. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.-M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef]
- Kohavi, R.; Provost, F. Glossary of terms. Mach. Learn. 1998, 30, 271–274. [Google Scholar]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices, 2nd ed.; CRC Press: Boco Raton, FL, USA, 2008. [Google Scholar]
- Foody, G.M. Thematic map comparison: Evaluating the statistical significance of differences in classification accuracy. Photogramm. Eng. Remote Sens. 2004, 70, 627–633. [Google Scholar] [CrossRef]
- Gutiérrez, S.; Tardaguila, J.; Fernández-Novales, J.; Diago, M.P. Data mining and NIR spectroscopy in viticulture: Applications for plant phenotyping under field conditions. Sensors 2016, 16, 236. [Google Scholar] [CrossRef] [PubMed]
- Carvalho, A.A.; Rebello, J.M.A.; Sagrilo, L.V.S.; Camerini, C.S.; Miranda, I.V.J. MFL signals and artificial neural networks applied to detection and classification of pipe weld defects. NDT E Int. 2006, 39, 661–667. [Google Scholar] [CrossRef]
- Miao, X.; Heaton, J.S.; Zheng, S.; Charlet, D.A.; Liu, H. Applying tree-based ensemble algorithms to the classification of ecological zones using multi-temporal multi-source remote-sensing data. Int. J. Remote Sens. 2012, 33, 1823–1849. [Google Scholar] [CrossRef]
- Xu, L.; Li, J.; Brenning, A. A comparative study of different classification techniques for marine oil spill identification using RADARSAT-1 imagery. Remote Sens. Environ. 2014, 141, 14–23. [Google Scholar] [CrossRef]


| Parameter | Description | Default Value |
|---|---|---|
| max_depth | controls the maximum depth of each tree (used to control over-fitting) | 6 |
| subsample | specifies the fraction of observations to be randomly sampled at each tree (adds randomness) | 1 |
| eta | the learning rate | 0.3 |
| nrounds | the number of trees to be produced (similar to ntree) | 100–1000 |
| gamma | controls the minimum loss reduction required to make a node split (used to control over-fitting) | 0 |
| min_child_weight | Specifies the minimum sum of instance weight of all the observations required in a child (used to control over-fitting) | 1 |
| colsample_bytree | Specifies the number of features to consider when searching for the best node split (adds randomness) | 1 |
| VIS (473 nm–680 nm) | Red-Edge (680 nm–708 nm) | |||
|---|---|---|---|---|
| RF | 12 | 474.74, 478.09, 478.94, 483.2, 494.64, 497.36, 500.11, 573.31, 574.59, 578.48, 579.79, 581.11 | 0 | - |
| XGBoost | 9 | 520.31, 521.32, 524.36, 526.42, 541.34, 558.52, 564.56,630.23, 646.04 | 3 | 686.69, 698.39, 708.32 |
| Overlap | 6 | 473.92, 480.63, 484.06 572.04, 577.17, 585.12 | 0 | - |
| All Wavebands ( = 176) | Important Wavebands ( = 18) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | ||||||
| Accuracy (%) | Kappa | Accuracy (%) | Kappa | Accuracy (%) | Kappa | Accuracy (%) | Kappa | ||
| XGBoost | Unsmoothed | 85.0 | 0.70 | 78.3 | 0.57 | 90.0 | 0.80 | 80.0 | 0.60 |
| Smoothed | 83.3 | 0.67 | 77.6 | 0.53 | 86.7 | 0.73 | 78.3 | 0.57 | |
| RF | Unsmoothed | 90.0 | 0.80 | 83.3 | 0.67 | 93.3 | 0.87 | 83.3 | 0.67 |
| Smoothed | 90.0 | 0.80 | 81.7 | 0.63 | 91.7 | 0.83 | 81.7 | 0.63 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loggenberg, K.; Strever, A.; Greyling, B.; Poona, N. Modelling Water Stress in a Shiraz Vineyard Using Hyperspectral Imaging and Machine Learning. Remote Sens. 2018, 10, 202. https://doi.org/10.3390/rs10020202
Loggenberg K, Strever A, Greyling B, Poona N. Modelling Water Stress in a Shiraz Vineyard Using Hyperspectral Imaging and Machine Learning. Remote Sensing. 2018; 10(2):202. https://doi.org/10.3390/rs10020202
Chicago/Turabian StyleLoggenberg, Kyle, Albert Strever, Berno Greyling, and Nitesh Poona. 2018. "Modelling Water Stress in a Shiraz Vineyard Using Hyperspectral Imaging and Machine Learning" Remote Sensing 10, no. 2: 202. https://doi.org/10.3390/rs10020202
APA StyleLoggenberg, K., Strever, A., Greyling, B., & Poona, N. (2018). Modelling Water Stress in a Shiraz Vineyard Using Hyperspectral Imaging and Machine Learning. Remote Sensing, 10(2), 202. https://doi.org/10.3390/rs10020202