Abstract
Digital terrain models (DTMs) are a fundamental source of information in Earth sciences. DTM-based studies, however, can contain remarkable biases if limitations and inaccuracies in these models are disregarded. In this work, four freely available datasets, including Shuttle Radar Topography Mission C-Band Synthetic Aperture Radar (SRTM C-SAR V3 DEM), Advanced Spaceborne Thermal Emission and Reflection Radiometer Global Digital Elevation Map (ASTER GDEM V2), and two nationwide airborne light detection and ranging (LiDAR)-derived DTMs (at 5-m and 1-m spatial resolution, respectively) were analysed in three geomorphologically contrasting, small (3–5 km2) catchments located in Mediterranean landscapes under intensive human influence (Mallorca Island, Spain). Vertical accuracy as well as the influence of each dataset’s characteristics on hydrological and geomorphological modelling applicability were assessed by using ground-truth data, classic geometric and morphometric parameters, and a recently proposed index of sediment connectivity. Overall vertical accuracy—expressed as the root mean squared error (RMSE) and normalised median deviation (NMAD)—revealed the highest accuracy for the 1-m (RMSE = 1.55 m; NMAD = 0.44 m) and 5-m LiDAR DTMs (RMSE = 1.73 m; NMAD = 0.84 m). Vertical accuracy of the SRTM data was lower (RMSE = 6.98 m; NMAD = 5.27 m), but considerably higher than for the ASTER data (RMSE = 16.10 m; NMAD = 11.23 m). All datasets were affected by systematic distortions. Propagation of these errors and coarse horizontal resolution caused negative impacts on flow routing, stream network, and catchment delineation, and to a lower extent, on the distribution of slope values. These limitations should be carefully considered when applying DTMs for catchment hydrogeomorphological modelling.
1. Introduction
Digital terrain models (DTM) provide a continuous mathematical representation of the Earth’s bare surface [1]. In catchment hydrogeomorphological modelling, DTMs are the most important data inputs, as the accurate replication of landscape elements highly influences model accuracy [2,3,4,5]. Adequate representation of landscape elements is often limited by intrinsic errors related to the data acquisition process as well as preprocessing steps used to generate the DTM [6,7]. In fact, DTM dataset characteristics such as spatial resolution and vertical accuracy, as well as the accurate filtering of vegetation and human-made structures, may importantly affect terrain representation and subsequent modelling [8,9,10,11,12,13,14].
Most of the DTMs used in hydrogeomorphological applications are satellite-derived datasets, such as the SRTM DEM [15] and the ASTER GDEM [16], due to their nearly global topographic coverage and unrestricted availability. However, their spatial resolution is coarse (~30 m) and their targeted vertical accuracy is ~16 m [17] and ~17 m [18], respectively. Airborne light detection and ranging (LiDAR)-derived DTMs are recognised to overcome these restrictions in spatial resolution and vertical accuracy [19,20,21,22], but their spatial coverage is limited due to their cost-intensive acquisition and processing. Nationwide, LiDAR DTMs are becoming increasingly available for some regions (e.g., several countries in the European Union). However, the use of these datasets is frequently limited to small-scale landscape modelling, such as landslide and hillslope failure assessment [23,24,25]. A broader range of LiDAR DTM potential applications in catchment hydrology and landscape geomorphology has been identified [26,27].
At the catchment scale, studies focusing on vertical accuracy and DTM effects on hydrogeomorphological modelling have intensively applied satellite-derived SRTM and ASTER DTM data. These studies have been conducted in a wide range of geomorphologically contrasting study areas, including low-relief terrains [28,29,30] and steep-gradient areas [31,32,33], as well as different geographic regions, such as mid-latitude [34,35,36], tropical, and subtropical areas [37,38,39]. However, Mediterranean environments are clearly underrepresented in such validation and comparison studies, despite the few relatively old studies [40,41] and several more recent investigations about the detection of karst features in satellite-derived DTMs [42]. This underrepresentation must be seen as a critical point, as the Mediterranean region is arguably one of the most human-influenced areas on Earth. For instance, a major characteristic of this region is the massive presence of traditional soil and water conservation structures constructed since Roman times [43]. However, changes in traditional land use systems, such as urban expansion and increases in irrigated agriculture [44], have altered complex geoecosystems, thereby favouring the progress of land abandonment and further land degradation [45,46] as well as profound changes in hydrological systems [47].
In order to model current and future changes in the hydrogeomorphological behaviour of Mediterranean environments, the use of reliable and accurate DTM is fundamental. Accordingly, the objectives of this study were twofold. First, ground-truth assessment of the vertical accuracy of SRTM C-SAR DEM V3, ASTER GDEM V2 (spatial resolution 1 arcsecond ~ 30 m at the equator), and two airborne LiDAR DTM datasets with 5- and 1-m spatial resolution, respectively, was applied in the island of Mallorca (Spain) over three small catchments representative of characteristic Mediterranean landscapes with morphologies and land uses differently affected by a long-term history of human changes. Second, evaluation of the studied DTM data sources and dataset characteristics on hydrogeomorphological modelling applications was carried out over the analysed catchments by calculating widely used statistics and descriptors (e.g., hypsometry, slope–area relationships, stream network patterns, and distribution of the hillslope length and steepness factor values). Last, representative plots were selected within the catchments to investigate the role of characteristic landscape features, including human-made objects (e.g., agricultural terraces) and dominant geomorphological features (e.g., major rock outcrops), on the sediment connectivity index proposed by Borselli et al. [48] and improved by Cavalli et al. [49], providing critical assessment of small-detail patterns of water and sediment transference between different landscape compartments of the catchment. The results obtained by this study aim to expand the existing knowledge on the influence of DTM data sources and dataset characteristics on terrain representation for Mediterranean landscapes, while also providing valuable information about the application of remote-sensing-derived DTMs in small-catchment hydrogeomorphological modelling in and beyond Mediterranean environments.
2. Study Area
Three small contrasting catchments (Sa Font de la Vila, Es Fangar, and Es Telègraf; ranging from 3 to 5 km2) located in the Island of Mallorca (Spain) were selected for this study (Figure 1a). All three catchments are located in the alpine Tramuntana Range, although each of them is characterised by a unique underlying morphology with decreasing terrain complexity and land use intensity from the mountainous Es Telègraf and over the mixed Es Fangar to the terraced Sa Font de la Vila catchment. This gradient in terrain complexity and land use intensity is caused by the underlying geological settings of the Tramuntana Range, which is aligned in a NE to SW direction with several folds and thrusts with increasing relief energy and hillslope steepness to the northern part (Figure 1b; [50]).
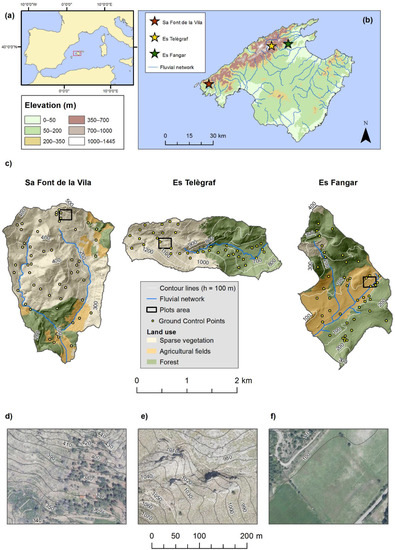
Figure 1.
(a) Location of Mallorca within the Western Mediterranean Sea. (b) Location of the three contrasting catchments (Island of Mallorca). (c) Detail of Sa Font de la Vila, Es Telègraf, and Es Fangar catchments illustrating the main land uses (following CORINE 2012), contour lines (height interval h = 100 m; numbers indicate minimum and maximum elevation in metres above sea level), and first-order streams (from the 5-m LiDAR DTM). (d–f) Images of the analysed representative plots at each catchment (d = Sa Font de la Fila, e = Es Telègraf, f = Es Fangar). LiDAR: light detection and ranging; DTM: digital terrain model.
The southernmost catchment is Sa Font de la Vila (4.8 km2). This catchment is located in the southwestern part of Mallorca (2°24′50″E, 39°35′20″N; Figure 1c). The relief of the catchment is complex due to the interaction of soft and hard lithology and different tectonics [50]. The catchment is characterised by the massive presence of traditional agricultural terraces, covering 37% of the whole catchment area and supported by 147 km of dry-stone walls [51]. Since the mid-twentieth century, the abandonment of traditional agriculture in these marginal areas caused an afforestation process with increased fuel availability [52]. As a result, two severe wildfires affected the catchment in 1994 and 2013. Current land use is dominated mainly by agriculture (44%), sparsely vegetated terrains (38%), and forests (18%).
The catchment with the highest relief energy and steepest hillslopes is the mountainous Es Telègraf catchment (2°51′0″E, 39°48′30″N; Figure 1c), which is located in the highest section of the Tramuntana Range (Figure 1b). The main geomorphological traits of the mountainous Es Telègraf catchment (ca. 3 km2) are aligned along a tectonic structure dominated by a NW-directed thrust system, including several cliffs and steep slopes. Vegetation shows a sharp contrast between the headwaters (25% of total area), dominated by sparse vegetation (culminal Balearic stage; [53]), and the lower parts (75% of total area), mostly covered by forest.
The mixed Es Fangar catchment (3.2 km2; 2°60′00″E, 39°50′10″N; Figure 1b) is characterised by a combination of thrust and normal faults and synclinal–anticlinal structures, as well as by the presence of different land use classes including forests (31%), sparsely vegetated areas (20%), and agricultural fields (49%), which are also affected by check-dam terraces and surface-leveled fields. Thus, the catchment shows a mosaic of different land uses and management practices as a result of a complex interaction between human and natural conditions [46].
Three small 5-ha plots, including characteristic landscape elements of the three catchments (Figure 1c), were selected to assess how accurate DTM representation of typical Mediterranean landscape elements—induced either by natural geomorphological conditions or human activities—can affect small-detail hydrogeomorphological modelling by using a morphometric hydrosedimentological connectivity index (see Section 3.3). The selected plot for the Sa Font de la Vila catchment is located in a terraced hillslope (Figure 1d). For the mountainous Es Telègraf catchment, the plot is selected in an area of high mountainous relief with bedrock outcrops and steep hillslopes of ca. ≥60% gradient slope (Figure 1e). This plot is centered on a massive bedrock outcrop formed by erosion-resistant limestone, while softer materials dominate the surrounding area. In the mixed Es Fangar catchment, the plot encompasses a flat agricultural field covered by rainfed herbaceous crops that are affected by traditional drainage systems, combining human-made artificial channels and subsurface tile drains [54] (Figure 1f).
3. Materials and Methods
3.1. DTM Datasets
The present study compares the widely used satellite-derived SRTM DEM V3 and ASTER GDEM V2 datasets as well as the nationwide, Spanish airborne LiDAR DTM datasets over the study catchments in the Island of Mallorca. SRTM data was acquired during February 2000 during an 11-day campaign of the National Aeronautics and Space Administration’s (NASA) space shuttle Endeavour, carrying both C-band (5.6 cm) and X-band (3.1 cm) synthetic aperture RADAR (SAR) devices as payload [15]. A first release of the SRTM C-SAR data was made available fpr public use by the government of the United States in 2003, providing nearly global topographic coverage with an initial horizontal resolution of 3 arcseconds (~90 m at the equator). Since 2014, the SRTM data has been available with the increased spatial resolution of 1 arcsecond (~27 m at Mallorca). The SRTM mission requirements have a targeted vertical accuracy of 16 m [55,56], but validation studies reported the actual vertical accuracy ranging between 3 and 12 m [29,30,31,32,33,35,39,57,58]. For use in this study, 1-arcsecond SRTM C-SAR version 3 data was downloaded from the USGS EROS, Earth Resources and Science Center at the United States Geological Survey.
Photogrammetry was employed in a collaborative effort of the NASA Jet Propulsion Laboratory (NASA-JPL) and the Japanese Ministry of Trade and Industry (METI) to produce the ASTER GDEM product from stereographic pairs of images in 1-arcsecond spatial resolution. A first release of the ASTER GDEM data was published in 2009 with an absolute vertical accuracy of 18.3 m. The second release of the dataset (ASTER GDEM V2) was published in 2011, with an improved vertical accuracy of 17 m [16]. Higher vertical accuracy was achieved by the inclusion of an additional number of 260,000 ASTER scenes and enhanced processing algorithms [18]. The reported vertical accuracy of the second release of ASTER GDEM was confirmed in the literature [38,39,58]. ASTER GDEM V2 was obtained for this study from the NASA tool. The number of stereographic pairs of ASTER images involved in DTM generation (stack number) for our study areas was between 11 and 27 in Sa Font de la Vila, between 2 and 7 in Es Telègraf, and between 5 and 9 in Es Fangar.
Airborne LiDAR data was acquired during an airborne campaign carried out by the Spanish National Institute of Geography (IGN) in 2014, covering the whole island of Mallorca [59]. The LiDAR dataset for the study areas is provided free of charge (i) as an already-processed DTM model with a spatial resolution of 5 m and as (ii) a preclassified point cloud by the Balearic Islands Autonomic Government and IGN. These nationwide IGN LiDAR datasets are just available for Spain, but are representative of most European airborne topographic LiDAR datasets, as evidenced by the European Union’s contribution to GMES (Global Monitoring for Environment and Security) services [60]. Minimum density of the point cloud is reported to be 0.5 points per m2 [59]. In this study, an average density of 1.65 points per m2 was calculated from the available LiDAR point cloud data of the catchments. Both 5-m DTM and point-cloud data was obtained from the IGN Geoinformatics webpage. Vertical accuracy of the 5-m DTM data is reported to be better than 0.2 m [59]. In order to generate a second LiDAR DTM model with 1-m spatial resolution, the preclassified point data was interpolated to a regularly spaced grid using multilevel B grid spline interpolation [61] with a threshold level of 0.0001 and a maximum level of 11 iterations. The resulting 1-m terrain model was smoothed by a multidirectional Lee filtering algorithm [62] to reduce the amount of noise.
Accordingly, four different datasets were analysed in this study: 1-arcsecond SRTM C-SAR DEM V3; 1-arcsecond ASTER GDEM V2; 5-m LIDAR IGN; and 1-m LIDAR IGN (hereafter referred to as SRTM, ASTER, IGN 5 m, and IGN 1 m, respectively). The datasets differ notably in their data source, spatial resolution, and vertical accuracy, so they provide an excellent study framework for investigating their applicability for catchment hydrogeomorphological modelling.
3.2. Vertical Accuracy Assesment
Vertical accuracy was assessed by collecting ground control points (GCPs) using a Real-Time Kinematic Global Positioning System (RTK-GPS, Leica GPS Series 1200) with a base station placed at central locations of the study catchments and absolute accuracy in the range of centimetres. Before surveying in September 2017, the initially established random spatial distribution of the GCPs was checked against the CORINE land use classes and 2012 cover data available from the COPERNICUS Land Monitoring Service and high-resolution (0.25 m/pixel) aerial imagery facilitated by the Government of the Balearic Islands. GCPs were adjusted manually later to ensure a representative proportion of densely vegetated (i.e., forest cover) and open field areas (i.e., sparse vegetation and agricultural land use cover classes) in the survey. At Sa Font de la Vila, 32 GCPs that were previously surveyed in January 2016 over terraced hillslopes using the same equipment and procedures were also included in this study. As a result, a total of 140 GCPs were included in our DTM accuracy assessments (Figure 1c).
After field acquisition, GPS measurements were rectified from ellipsoidal to orthometric height to ensure comparability with the DTM datasets that refer to the EGM1996 geoid (ASTER and SRTM) and the EGM2008-REDNAP geodetic vertical data (IGN data). The robustness of the accuracy assessment in terms of statistic measurements was ensured by applying a threshold of a maximum absolute vertical error of 7 cm in the GPS data, which is nearly 3 times more accurate than the accuracy given by IGN for the 5-m LiDAR data [59]. Under this condition, the derived DTM accuracy had an error of 5%, which is considered as tolerable [63].
Vertical accuracy of the DTM datasets was expressed as error statistics. In order to determine if the underlying distribution of elevation errors equals a normal distribution, histogram plots were examined visually. Robust measures such as the normalised median deviation (NMAD) and the 68.3% and 95.0% sample quantiles of the error between GPS- and DTM-derived elevation were computed. All these measures were reported by Höhle and Höhle [63] and Höhle [64] to be reliable even for non-normal distributions. NMAD is computed according to:
where denotes the median in elevation error , computed from the differences between GCP- and DTM-derived elevation values. For comparability with other accuracy assessments, the root mean squared error (RMSE) is also provided:
RMSE and NMAD values were provided at the levels of the DTM source (SRTM, ASTER, IGN 5 m, and 1 m), catchment (Sa Font de la Vila, Es Telègraf, and Es Fangar), and land use type (densely vegetated forest cover versus open-field agricultural plus sparse vegetation cover classes) for analysis.
3.3. Quality Assessment of DTMs for Hydrogeomorphological Modelling
All the different DTM datasets were projected to UTM Zone 31 N (ETRS89 ellipsoid) to ensure comparable geolocation. The original vertical data of the datasets remained unchanged as the difference in height between EGM1996 and EGM2008-REDNAP were <1 m in the study areas, which can be considered small if compared to the vertical resolution and precision of the satellite-derived DTMs. In order to correct the data for hydrogeomorphological purposes, the Planchon and Darboux [65] surface filtering algorithm was applied, imposing a minimum slope gradient between grid cells of 0.1%. The algorithm adds a virtual layer of water to the DTM data, filling all depressions up to the level of their outflow point. This results in a surface that ensures drainage even for flat areas. Comparison of elevation statistics before and after pit-filling was carried out to assess the influence of surface filtering.
A broad variety of hydrogeomorphological statistics and descriptors were analysed to explore the feasibility of the studied DTMs for hydrogeomorphological modelling in the three study catchments. These indicators encompassed basic terrain characteristics, widely used catchment geomorphometric parameters and relationships, and stream network and flowpath properties, as well as small-detail arrangement patterns of water and sediment fluxes (Table 1). Extraction of basic terrain characteristics, such as general elevation statistics, slope gradient and flow direction, upslope contributing area, and catchment area were computed using the ESRI ArcGIS (Version 10.3) spatial analyst toolbox. General flow accumulation for analysis was obtained by applying the deterministic nondispersive D8 algorithm [66] that simulates water flow in the direction of the strongest slope gradient.

Table 1.
Summary of statistics and descriptors applied to analyse the feasibility of the studied DTMs for catchment hydrogeomorphological modelling, and relevant references for the methods.
The hypsometric curve [67], slope–area relationship [68,69], cumulative area distribution function [70], and empirical hillslope length and slope steepness factor (LS factor [76,77]) were computed, providing geomorphometric evaluation criteria for analysis. The hypsometric curve relates relative catchment area to relative elevation and allows the estimation of dominant erosion processes [71] and landform maturity [72]. Thus, it is a simplistic measure of the mass and energy stored within a landscape. The slope–area relationship—defined by catchment mapping of the local slope gradient to the contributing area—and the cumulative area distribution—defined as the proportion of the catchment that has a contributing area greater than or equal to a specified drainage area—provide information about characteristic fluvial processes [69] and flow aggregation structures [70], respectively. In more detail, the analysis of slope–area plots generally reveals the emergence of an inflection point that separates relatively small catchment areas dominated by the action of diffusive erosion from larger catchment areas characterised by fluvial erosion and transport [69]. In theory, the shape of the slope–area plots of catchments is a “boomerang”, with the roll-over (inflection) point corresponding to the threshold in drainage area where hillslopes transition into channels [73]. Differently, the cumulative area relationship focuses on flow aggregation structures of hillslope elements and the stream network [74,75]. Herein, the leftmost section of the distribution curve is associated with flow aggregation at hillslopes, whereas the middle section describes channelised flow as a log–log linear straight line, and the rightmost section is related with boundary effects. Such an organisation of flow structures can be determined for all DTM datasets and catchments [74].
The empirical hillslope length and slope steepness factor (LS factor) provides critical information on the terrain morphological susceptibility to surface soil erosion. In its original formulation, as part of the universal soil loss equation (USLE) [76], the LS factor is determined as:
where accounts for the hillslope length (usually calculated from flowlength), is the standardised plot length applied in the USLE experiment (~22.1 m), Ɵ is the slope gradient (rad), and is the slope length exponent, which ranges between 0 and 1 and approaches 0 when the ratio of rill-to-interrill erosion is close to 0. Desmet and Govers [77] extended the classical LS approach to large-scale modelling applications in a Geographic Information System (GIS) by replacing hillslope flowlength by upslope contributing area. We applied the improved Desmet and Govers’ LS approach, assuming a rill-to-interrill erosivity ratio of 1 for LS calculation in SAGA GIS [78].
Differently from the above-described geomorphometric properties that describe the dominant erosion processes, landform maturity, flow aggregation structures, and terrain morphological susceptibility to surface erosion, stream network properties provide important clues for understanding the large-scale spatial arrangement of water and sediment fluxes. Flow routing differences between the different DTM models were analysed for each study catchment by exploring variations in stream network representation and flowpath length distribution. Stream networks were delineated from the derived D8 flow-accumulation raster maps of the catchments by imposing a minimum size of upslope contributing area of 30 ha, which produced the most realistic results when compared to field observations. In addition, the empirical inverse cumulative distribution function (iCDF) of derived flowlength values for each studied catchment and DTM were determined for analysis, following the approach of Moreno-de-las-Heras et al. [28].
Last, the connectivity index (IC) proposed by Borselli et al. [48] and modified by Cavalli et al. [49] was applied for exploring small-detail patterns of water and sediment transference between different landscape compartments of the study catchments, considering that a dynamic assessment of landscape connectivity can help to incorporate aspects of the process linkages that essentially drive water and sediment fluxes [79]. IC is a dynamic property of the catchment that indicates the probability of a particle at a certain location to reach a defined target area, which in this study, was established at the catchment outlet, with its effects being analysed at representative small-scale (5-ha) plots from each study catchment (Figure 1d–f). IC is calculated as:
where and are the up- and downslope components of the connectivity index, respectively, and represents the average percentage slope, A the size of the upslope contributing area, an averaged weighting factor represented by the terrain roughness, and di the length of the flowpath from the ith cell to the targeted outlet along the steepest downslope direction. IC was determined for this study using the freely available SedInConnect (Version 2.3) software developed by Crema and Cavalli [80].
4. Results
4.1. DTM Vertical Accuracy
Significant errors in elevation for all the analysed datasets were observed by comparing DTM-derived elevation values against those elevation values obtained in our dGPS-derived GCPs (Table 2). Accuracy increased from ASTER over SRTM to the 5-m and 1-m IGN LiDAR models. A systematic overestimation of elevation values was observed for all datasets, as indicated by the relative frequency distribution of (dGPS minus DTM) vertical errors (i.e., the error distributions are skewed to the left for all DTMs as shown in Figure 2).

Table 2.
Results of the vertical accuracy assessment expressed as root mean squared error (RMSE) and normalised median deviation (NMAD) between the GPS-measured elevation values and those values derived from the different DTM datasets (in metres).
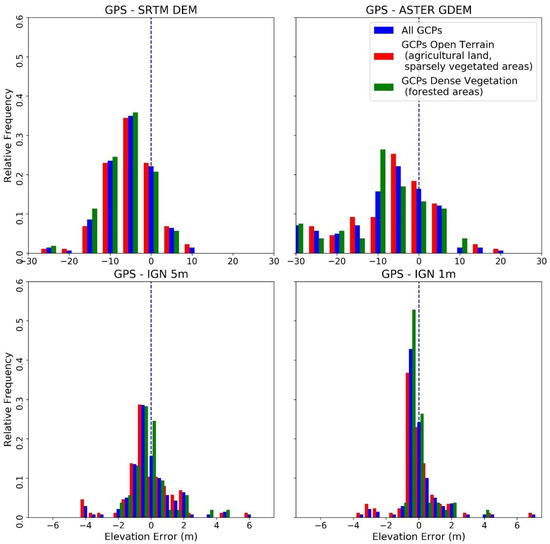
Figure 2.
Relative frequency distribution of elevation errors (i.e., RTK-GPS minus DTM elevations) binned to 5 m (for ASTER and SRTM data) and 0.5 m (for IGN 5-m and 1-m data) intervals. Blue bars indicate the distribution of all ground control points (GCPs, n = 140), whereas the red bars account for GCPs considered as open-terrain (agricultural landscapes and sparsely vegetated terrain, n = 87) and the green bars for densely vegetated GCPs (forest cover, n = 53). RTK-GPS: Real Time Kinematic Global Positioning System.
The SRTM data showed an overall accuracy of 6.98 m RMSE and 5.27 m NMAD (Table 2), also evidencing a strong tendency to overestimate surface elevation (up to 15–25 m; Figure 2). Among the three studied catchments, SRTM reached the lowest accuracy in terms of RMSE and NMAD (over 7.70 and 5.50 m, respectively) for the terraced Sa Font de la Vila catchment and the mountainous Es Telègraf catchment. The highest accuracy of the SRTM data was observed in the mixed Es Fangar catchment (RMSE = 4.06 m, NMAD = 2.98 m; Table 2). No clear influence of vegetation was observed in the SRTM errors, since the elevation bias showed the same relative distribution patterns (Figure 2) as well as similar RMSE and NMAD values (Table 2) for forest and open (agricultural and sparse vegetation cover) areas.
ASTER showed the lowest overall accuracy among all datasets, according to the obtained RMSE and NMAD values (16.10 and 11.23 m, respectively; Table 2). The frequency distribution of the elevation errors showed that ASTER values largely overestimated elevation (by up to 30 m), although significant underestimations were also identified for the dataset (Figure 2). The lowest accuracy was observed at the mountainous Es Telègraf catchment (RMSE = 26.77 m, NMAD = 12.17 m; Table 2). The mixed Es Fangar catchment showed the best accuracy in terms of RMSE (7.62 m), whilst the terraced Sa Font de la Vila catchment displayed the best NMAD performance (7.63 m). Comparing open and densely vegetated terrains, dense vegetation considerably increased the overestimation of elevation values (i.e., the histogram green bars are more skewed to the left than red bars in Figure 2), although both RMSE and NMAD values were similar for forest and open-terrain points (Table 2).
The vertical accuracy of the LiDAR-based IGN DTMs was considerably higher than for the SRTM and ASTER data. The IGN 5 m model showed a vertical accuracy of 1.73 and 0.84 m, expressed as RMSE and NMAD, respectively (Table 2). Differently to the SRTM and ASTER data, the vertical accuracy for the IGN 5 m increased from the terraced Sa Font de la Vila catchment (RMSE = 2.09 m, NMAD = 0.98 m) to the mountainous Es Telègraf (RMSE = 1.59, NMAD = 0.89) and the mixed Es Fangar (RMSE = 1.35, NMAD = 0.71 m) catchments. The IGN 1 m model, which was developed from the same LiDAR data cloud as the 5-m DTM, showed the best model performance in terms of vertical accuracy (RMSE = 1.55 m, NMAD = 0.44 m), performing slightly more accurately than the 5-m data (Table 2). Similarly to the IGN 5-m model, the results for the 1-m model showed the lowest accuracy in the terraced Sa Font de la Vila catchment (RMSE = 2.03 m, NMAD = 0.62 m), while reaching the best model performance in the mixed Es Fangar catchment (RMSE = 1.10 m, NMAD = 0.26 m). Both the IGN 5-m and 1-m models showed a slight tendency to overestimate elevation values, with densely vegetated areas showing slightly higher RMSE than open terrain (Table 2), but similar relative frequency distribution patterns of elevation errors for both (forest and open) land use classes (Figure 2).
4.2. DTM Hydrogeomorphic Modelling Performance
4.2.1. Basic Terrain Statistics
Descriptive statistics of minimum, maximum, and mean elevation values as well as average slope gradient values before and after applying surface filtering (i.e., pit-filling) are summarised in Table 3. Surface filtering did not significantly affect the terrain models, as the percentage of pit-filled areas was between 0.1 and 0.3% for SRTM, 0.6 and 1.7% for ASTER, and <0.1% for the IGN LiDAR models. Since the extension of the DTM-derived catchment areas was partly different (Table 3), the absolute values of relief (difference between maximum and minimum elevation) cannot be directly compared. For the mountainous Es Telègraf catchment, SRTM and ASTER data showed larger catchment areas (i.e., 3.55 and 3.17 km2, respectively) than the LiDAR models (i.e., 2.73 and 2.72 km2 for the 5-m and 1-m models, respectively). Conversely, the ASTER-derived catchment area for the terraced Sa Font de la Vila and the mixed Es Fangar catchment coincided well with the LiDAR-derived values. Among all datasets, SRTM showed the largest catchment extent for Sa Font de la Vila (5.06 km2) and the smallest catchment area for Es Fangar (3.04 km2). The differences between the two LiDAR models were negligible in all the studied catchments. In addition to the observed discrepancies regarding catchment area, a general increase in average slope gradient was detected from the SRTM model and over the ASTER data to the 5-m and 1-m LiDAR models (Table 3).

Table 3.
Descriptive statistics of the used DTM datasets. “Uncorr” refers to results before surface filtering and “Corr” after surface filtering “-” indicates not applicable measures.
4.2.2. Geomorphometric Parameters and Relationships
The values of both the hypsometric integral and LS factor decreased from the mountainous Es Telègraf catchment and over the terraced Sa Font de la Vila to the mixed Es Fangar catchment (Table 4). Differently, mean flowlength was largest at the Sa Font de la Vila catchment (Table 4), which also showed the largest catchment areas (Table 3). The hypsometric integral was nearly equivalent for all datasets, except for the mountainous Es Telègraf catchment, where SRTM showed a slightly higher integral value than the other models (Table 4). Differently, clear differences among the DTM datasets were detected for the (mean and SD) flowlength values of the catchments (Table 4). SRTM showed the smallest flowlength values in all catchments, followed by the ASTER data in Es Telègraf and Sa Font de la Vila, but not in the Es Fangar catchment. The IGN LiDAR models obtained the largest flowlength values in all catchments, except for the mixed Es Fangar catchment, where the ASTER model generated the largest value. A slight flowlength difference in the order of decametres was observed between the two IGN LiDAR models, with the 1-m dataset showing the highest (mean and SD) values (Table 4). Considering the LS factor, the LiDAR-based IGN data generated larger (mean and SD) values than the SRTM and ASTER datasets (Table 4). The LS values obtained by the IGN 1-m dataset in the studied catchments were (twofold) larger than those reached by the 5-m dataset (Table 4).

Table 4.
Geomorphological and hydrological characteristics of the studied datasets and catchments, including the hypsometric integral, mean flowlength, and LS factor and their corresponding standard deviation (SD). “-“ mean that the measure has no physical unit.
In agreement with the general patterns obtained using the values of the hypsometric integral, the hypsometric curves of the four elevation datasets showed a similar shape and trend for each of the three analysed catchments (Figure 3a). Differently, the slope–area and cumulative area distribution plots of the catchments showed important differences between DTMs. In fact, the slope–area plot showed the classic boomerang-like shape trend for the two (LiDAR-based) IGN models, separating the diffusive and fluvial-dominated section of the catchments (i.e., slope gradient slightly increased or kept constant values with contributing area in the 1 to 10³ m2 section and then decreased linearly in the log–log plot), but only showed the fluvial-dominated (negative log–log trend) section for the SRTM and ASTER datasets (Figure 3b). Similarly, the cumulative area distribution plots for the IGN datasets accurately separated the hillslope and stream-dominated areas in the study catchments (depicted by the change in the slope of the cumulative distribution at 102–103 m2 contributing area; Figure 3c). However, for the ASTER and SRTM datasets, a very small number of cells (leftmost section of the cumulative area plots) described the hillslope region of the catchments (Figure 3c).
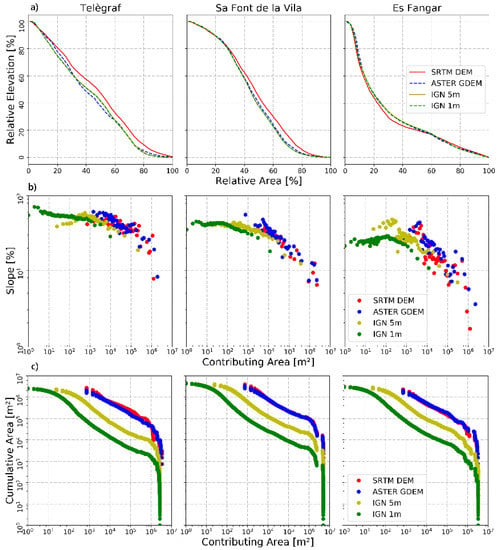
Figure 3.
(a) Hypsometric curves, (b) slope–area relationships, and (c) cumulative area distributions derived from DTMs.
4.2.3. Stream Networks
At the mountainous Es Telègraf catchment, SRTM produced straight-line stream features that did not reflect the actual terrain topography (Figure 4a). Furthermore, the satellite-derived SRTM and ASTER models indicated the existence of second-order streams that were not represented by the IGN LiDAR data for this catchment. It should be noted that Es Telègraf was also the catchment with the largest differences in delimited catchment area between the datasets (Table 2), where the SRTM and ASTER models largely failed to determine the actual boundary of the catchment, particularly in the southernmost contributing area region. In contrast, a better consistency between the models was obtained for the terraced Sa Font de la Vila catchment, despite some important shifts in the position of second-order streams at the headwaters and at the outlet point being detected (Figure 4a). The small area of interest represented in Figure 4a illustrates for this catchment how the streams derived from the IGN LiDAR data (green and yellow lines for the 5-m and 1-m IGN models, respectively) tended to reproduce the natural flow patterns of the landscape, following the valley floor as indicated by the 10-m contour lines, while the SRTM and ASTER streams (red and blue lines, respectively) partly deviated from those pathways. In the mixed Es Fangar catchment, the position of the outlet was identical for all DTMs, but again, remarkable differences were observed in the second-order streams, with the ASTER model showing the largest deviations (Figure 4a). Complementarily, the empirical inverse cumulative distribution function of flowlength probability (flowpath length iCDF; Figure 4b) revealed important differences among the datasets for Es Telègraf (i.e., shorter extreme flowpath lengths for the SRTM data) and Es Fangar (i.e., longer extreme flowpath lengths for the ASTER data).
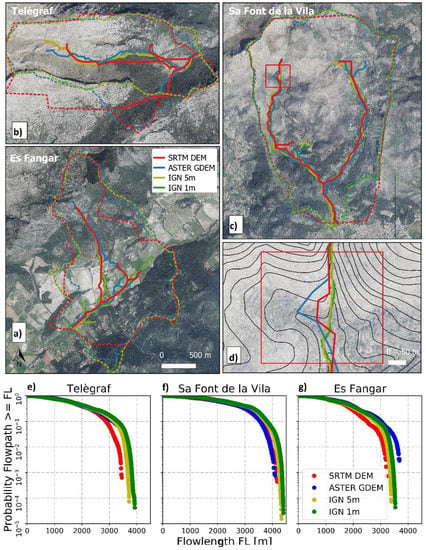
Figure 4.
Stream network patterns (solid lines) and catchment boundaries (dashed lines) derived from the DTM datasets showing the studied catchments (a–c). (d) Area of interest (AOI) selected in Sa Font de la Vila (solid black lines indicate height contours with Δh = 10 m). (e,f) Empirical inverse cumulative distribution function (iCDF) of the derived flowlength values for the three catchments.
4.2.4. Small-Detail Water and Sediment Connectivity
The coarser spatial resolution of the satellite-derived SRTM and ASTER models (~27 m) strongly limited the applicability of the analysed index of water/sediment connectivity (IC) for revealing small-detail surface flow patterns in the studied landscapes (Figure 5). Differently, the IC showed reliable surface flow patterns for the study sites using the LiDAR-based IGN DTMs, although the 1-m data considerably improved the details provided by the 5-m data (Figure 5). In accordance with these general results, a variety of differences characterised the IC performance of the SRTM, ASTER, and IGN LiDAR data for the small-detail 5-ha study plots. For example, for the mountainous Es Telègraf catchment, both the SRTM and LiDAR datasets showed a highly connected NW–SE flowpath that was enforced by the presence of a massive outcrop in the study site, while this dominant surface flow pathway was absent in the ASTER-derived IC map (Figure 5). The IC representation for this plot of the SRTM model was, however, limited as the high connectivity area appeared blurred and not as sharp as in the LiDAR-based IGN data. In Sa Font de la Vila, where the 5-ha small-detail plot was centred on a terraced hillslope, the SRTM and ASTER models failed to represent the effects caused by the presence of bench terraces on the surface flow patterns (Figure 5). The dendritic-like, highly connected network represented along the N–S direction by the IGN-derived maps of IC for this terraced site was replaced by a nearly uniform IC area in the SRTM and ASTER data. Furthermore, the effects of terracing on the IC patterns of this plot were better established by the 1-m data than the coarser 5-m LiDAR-based IGN model. Last, the IC results obtained in the 5-ha plot of Es Fangar again highlighted the severe difficulties of the ASTER model to reveal actual water and sediment pathways that are controlled by small-detail landscape objects. In this site, the small-detail plot was located in an agricultural field delimited by a road and a parallel artificial channel running along the SE corner of the landscape (Figure 5). Both the SRTM- and LiDAR-based IGN data showed a highly connected pathway running from NE to SW at the eastern border of the plot, reproducing the natural direction of the flow. Contrarily, the ASTER-derived IC values were highest along the northern part of the plot and did not show any sort of linear features associated to the actual water and sediment pathways of the landscape. Further comparisons of the SRTM- and LiDAR-derived IC patterns for this plot revealed that SRTM could not resolve minor features of the agricultural field (i.e., preferential flow patterns), indicating high connectivity crossing the plot from N to S. It should be also noted that even for the high-resolution 1-m LiDAR dataset, the position of the highest IC values did not exactly reproduce the actual position of the artificial channel in the landscape.

Figure 5.
Selected plots representing the connectivity index (IC) in the three catchments, including high-resolution aerial pictures of the selected plots and contour lines (Δh = 10 m).
5. Discussion
5.1. Vertical Accuracy
5.1.1. General Dataset Evaluation
The vertical accuracy results of the studied (SRTM and ASTER) satellite- and (LiDAR-based IGN) airborne-derived models (Table 2) were in good agreement with other similar studies in hilly and mountainous areas [31,32,81], despite the fact that they were mainly focused in regions characterised by very different climate, vegetation patterns, and land use systems in Mediterranean areas. SRTM was less affected by systematic errors than ASTER, as indicated by the corresponding histogram plots, and the errors tended to show minor deviations from the normal error distribution (Figure 2). The SRTM data clearly outperformed the ASTER datasets, showing lower RMSE and NMAD values for all catchments and land use cover classes (Table 2), which, overall, agreed with previous analyses of these global datasets [39,58].
The vertical accuracy of the (5-m and 1-m) IGN LiDAR models (about 1.6 m RMSE and <1 m NMAD) was considerably higher than that obtained from the SRTM and ASTER datasets (accounting for 7–16 m and 5–11 m RMSE and NMAD, respectively). However, our analysis indicated that the actual vertical accuracy of the IGN DTMs is considerably lower than the (0.2 m) reference vertical accuracy that is officially posted by the IGN [59] for these datasets. The error magnitude (RMSE and NMAD) of the studied LiDAR models was in agreement with Estornell et al. [82] and Simpson et al. [22], showing that the 1-m dataset had the lowest RMSE and NMAD for all study sites and land use/cover classes. The LiDAR data showed significant shifts of the distribution in elevation errors towards negative values (Figure 2), although the slight overestimation in elevation caused by these errors was notably lower than the large overestimations produced by the satellite-derived SRTM and ASTER models. The increase in spatial resolution from 5 to 1 m in the LiDAR-derived models did not involve remarkable changes in the frequency distribution and magnitude of the errors. This may be related to the fact that both LiDAR DTMs were generated from the same 3D point-cloud and predefined classification scheme to separate ground from nonground returns; thus, identical classification errors are likely to affect both models [83,84].
5.1.2. Assessing the Effects of Vegetation on the Datasets
Classification of elevation errors according to land use/cover type revealed further information about the structure of the DTM datasets. The presence of densely vegetated forest cover exacerbated the tendency of the ASTER dataset to overestimate elevation values, reaching deviations of up to 30 m (Figure 2). In this context, Li et al. [90] defined the ASTER data as a “first-return system”. In fact, ASTER, as an optical remote-sensing system, captures the top of the vegetation canopy. Consequently, a large offset to the true surface elevation is expected to be obtained for the ASTER data in densely covered areas. Interestingly, in spite of exacerbating the tendency to overestimate elevation values in the ASTER data, the absolute vertical accuracy of this dataset was very similar for both densely vegetated (forest) and open (agricultural fields and sparse vegetation areas) surfaces. The poor elevation accuracy of the ASTER data over the studied catchments (16 and 11 m RMSE and NMAD values, respectively; Table 3) could be more influenced by the low amount of stereographic pairs (or stack number) applied to generate the elevation data in these sites, which ranged between 2 and 27 pairs. The use of low stack numbers—particularly where applying fewer than 10 stereographic pairs—in the production of ASTER GDEM data is reported to very remarkably reduce the vertical accuracy of the elevation values, as the amount of residual artefacts in the data can be very large [18,28,93]. In fact, the inherent, large vertical errors that affect the analysed ASTER data over the study catchments very likely surpass the influence of vegetation in measured absolute vertical accuracy. For example, although some relatively tall (up to 20 m) pine forest patches can be found in the studied areas, forest cover for the analysed catchments is more widely dominated by relatively open xeric formations of holm oak trees of up to 6–8 m of tree height, which are largely below the obtained ~16 m RMSE for the analysed ASTER data.
No clear effects of vegetation cover were detected in the absolute vertical accuracy and the relative distribution of the vertical errors for the SRTM data. Kellndorfer et al. [87] and Ludwig and Schneider [35] reported that thick forest vegetation can generate negative bias (i.e., overestimation) in SRTM elevations when comparing model-derived elevation to in situ-derived values. This can be explained by the relatively short wavelength (i.e., 5.6 cm) of the C-band SAR used for DTM generation, which does not penetrate the tree canopy completely as it is affected by (back-) scattering by branches and leaves within the vegetation canopy [80,88,89]. Our SRTM results, however, did not show any clear increased tendency to overestimate elevation values under forest cover as compared to open (agricultural and sparse vegetation) areas (Figure 2). This may be due to the low tree height and relatively open structure that characterise the Mediterranean dry formations that dominate the forest cover in the studied catchments. Similarly to the analysed ASTER data, any elevation bias produced by the Mediterranean dry forest formations distributed within the studied catchments in the SRTM data may be largely surpassed by the large (~7 m RMSE) intrinsic vertical errors of this dataset.
For the development of LiDAR-based elevation models, last returns are usually taken from discrete waveform LiDAR cloud data to ensure that backscattering occurs as close as possible to the bare surface, maximizing DTM vertical accuracy. However, severely filtered LiDAR returns are reported to affect DTM accuracy [83]. In this study, the density of preclassified ground returns of the LiDAR data underlying the analysed (5-m and 1-m) IGN DTMs was 1.65 points per m2 in average for the three studied catchments, with the flat, open areas reaching up to 10 points per m2 and the steep, vegetated hillslopes reaching the lowest values (generally below 1 point per m2 on average). Data gap-filling techniques, such as the employed multilevel B-spline interpolation algorithm, are likely to produce artefacts in the production of high-resolution DTMs in the case that filling data gaps becomes necessary. Our results indicate that LiDAR DTM RMSE values slightly increased (by about 50 cm) for vegetated areas with low density of ground returns, as compared to flat, open areas (Table 2). Accordingly, previous studies indicated that gap filling can affect vegetated areas with low-density LiDAR ground returns, resulting in non-negligible errors in the resulting DTMs [85,86]. The analysed IGN LiDAR models showed a very similar relative distribution of elevation errors for both bare and vegetated areas (Figure 2). These results contrasted with Harding et al. [90], who observed higher underestimations in areas with dense vegetation compared to open terrain due to the dispersion of LiDAR pulses within the canopy. The results of the present work are more consistent with Clark et al. [83], who observed that the precision of LiDAR-based elevation models might vary where different patterns and vegetation types are combined with different slope gradients and morphological characteristics. Furthermore, Estornell et al. [82] reported that the effect of slope on the LiDAR DTM accuracy could largely surpass the direct effects caused by vegetation. In the studied Mediterranean catchments, the effect of vegetation on LiDAR-based DTM accuracy may be relatively small as compared to other error sources related to complex morphological features (e.g., terraces or artificial channels) and derived technical limitations related to filtering or interpolation processes in these complex areas.
5.1.3. Evaluating Terrain Morphology on DTM Accuracy
SRTM showed a low vertical accuracy at the mountainous Es Telègraf and the terraced Sa Font de la Vila catchments (Table 2), probably due to the presence of geometric distortions in the underlying C-band SAR imagery. Such distortions are caused by shadowing effects under extreme viewing conditions in very steep and fragmented areas [91,92]. These findings can also explain the observed straight-line stream features generated by the SRTM data in the mountainous Es Telègraf catchment (Figure 5), which are also likely to be related to severe intrinsic errors of the SRTM data in highly rugged, mountainous areas. Conversely, optical imagery is less affected by such relief distortions, as viewing angles are usually small. Nevertheless, the vertical accuracy of the ASTER model was extremely poor at the Telègraf catchment. Such poor performance can be directly related to the very low number of stack layers used for DTM generation, which was between 2 and 7 for the specific case of Es Telègraf. As previously discussed, the presence of large residual artefacts in the elevation data very importantly increases for areas where fewer than 10 stack layers were applied for ASTER GDEM production, inducing large errors and distortions in both steep [93] and low-gradient terrain [28]. Therefore, the insufficient amount of data available for the DTM generation largely conditioned the vertical accuracy of the ASTER data for this study, while the intrinsic errors of the underlying remotely sensed C-band SAR data represented for the SRTM dataset the main responsible factors affecting the poor performance of this synthetic aperture RADAR-based model in rugged terrain.
As mentioned above, a low density of ground returns for complex surfaces in the LiDAR data may be responsible for the observed small deviations in the vertical accuracy of the IGN DTMs. Model performance was relatively good for the mixed Es Fangar and the mountainous Es Telègraf catchment, although the data showed a poorer performance for the terraced Sa Font de la Vila catchment (Table 2). The relatively poor results obtained in Sa Font de la Vila are probably related to the highly fragmented topography that characterises this terraced catchment [94], which favours data oversampling in the flat areas of the terraces, but large data undersampling for the small-detail abrupt elevation changes aligned along the dry-stone walls of the terraces. This effect may be significantly increased by the presence of erroneously classified LiDAR returns in the datasets [82]. For the Es Telègraf and Es Fangar catchments, where the terrain is also complex, but less fragmented by human-made structures, these effects are also likely to be present, but to a lower extent.
5.2. Assessing Hydrogeomorphological Modelling Reliability
Hydrogeomorphological modelling reliability strongly depends on the ability of digital topographic models to accurately represent landscape morphology. In this study, very remarkable differences were identified between the descriptive statistics and hydrogeomorphological characteristics of the four assessed datasets.
5.2.1. Basic Terrain Attributes
Hypsometry did not show a high sensitivity to either DTM grid size or data source (Figure 4 and Table 4). Therefore, the ability of the DTMs to replicate general patterns of mass and energy stored within a landscape appears to be nearly independent of the horizontal resolution and dataset characteristics. The identified independencies are induced by the application of relative values of elevation and area that surpass the absolute differences [95]. Our results also showed consistent smoothing of the slope gradient values for the SRTM and ASTER datasets in all catchments (Table 3). The coarse spatial resolution of these models (i.e., 1 arcsecond) caused an oversimplification of the landscape elements, favouring the loss of hydrological and geomorphological details, which is in accordance with similar results obtained in other geographic regions [10,11,96]. Such coarse DTM resolution did not only simplified the landscape elements, but also affected subsequent catchment hydrogeomorphological modelling in terms of physical measures. In more detail, Zhang and Montgomery [8] reported the large implications of altered slope-gradient distributions on process-based hydrological modelling, as the laws of transport obtained from coarse-grained DTMs did not match those obtained from field studies, especially for small catchments.
Important differences in the distribution of the slope-gradient values were observed between datasets, showing a clear nonlinear relationship between the raster horizontal resolution and the derived terrain representation of hillslopes. Whilst the slope-gradient differences observed between the (1-m and 5-m) LiDAR models were tightly coupled to their differences in spatial resolution, slope-gradient differences identified between the (1-arcsecond) ASTER and SRTM datasets cannot be attributed to differences in horizontal grid resolution (Table 3). Thus, residual artefacts and errors associated with the intrinsic characteristics of these coarse-grained datasets were probably relevant not only in terms of vertical accuracy, but also in terms of landscape representation, such as slope gradient, stream network patterns, and catchment area delineation. In fact, these results were also supported by the large observed differences in flow routing characteristics (e.g., mean and SD flowlength) and catchment delineation of the coarse DTMs (Table 2 and Table 3).
5.2.2. Geomorphic Parameters and Relationships
In order to check the ability of the investigated DTMs to address hydrogeomorphological processes, different geomorphometric parameters and relationships were analysed, including the slope–area relationship and the cumulative area distribution (Figure 4) as well as the LS factor (Table 4). The obtained slope–area relationships and the cumulative area distributions for the satellite-derived SRTM and ASTER models reflected a poor landscape representation performance at the hillslope scale, and hence, a poor ability to assess soil erosion and flow aggregation processes. Contrarily, the LiDAR-based IGN models showed a good capacity to represent hillslope areas within the domain of diffusive and interrill erosion. This domain characterises effective catchment areas that contribute to the catchment conveyor belt [97]. Complete representation of hydrogeomorphological processes for meaningful assessment of catchment physical structure requires accurate DTM representation of dominant processes at different spatial and temporal scales. Thus, the SRTM and ASTER datasets provided insufficient information for hydrogeomorphological modelling in terms of water and sediment transfer processes in the studied small Mediterranean catchments. Both the SRTM and ASTER datasets showed very similar patterns in slope–area relationship and cumulative area distribution, whereas the 1-m IGN DTM induced changes in the position of critical (erosion-domain and flow aggregation) breaking points towards smaller values of contributing area (Figure 3). These results emphasise that the effect of the spatial resolution on the representation of different landscape features and erosion forms within the catchments was probably stronger than the effects caused by the intrinsic errors of the DTMs in the obtained geomorphological relationships. Differently to the slope–area relationship and the cumulative area distribution, the LS factor does not differentiate between regions or domains of erosion and flow aggregation within the catchments. A strong nonlinear dependency on raster resolution and derived slope gradient values was observed for our LS estimations, which largely agrees with the results obtained by Wu et al. [98], who assessed the influence of grid size on soil loss modelling in a mountainous catchment in Virginia (USA).
5.2.3. Stream Network Organisation
The residual artefacts and errors related to the intrinsic characteristics of the analysed datasets showed a strong effect on the organisation of stream networks (Figure 4). While differences in spatial resolution generally represent minor changes in the position of first-order streams [99], the residual artefacts and intrinsic errors of the studied satellite-derived SRTM and ASTER datasets induced the emergence of unrealistic fluvial networks (e.g., SRTM stream delineation for Es Telègraf; Figure 4a) and large uncertainties in stream network organisation and flowpath distribution (e.g., large ASTER deviations for Es Fangar; Figure 4b). Therefore, stream network delineation was directly affected by the propagation of errors in the input DTMs. Similar error propagation effects were reported by Oksanen and Sarjakoski [100], whereas Chaubey et al. [101] found that DTM grid size can significantly affect stream network and catchment delineation without invoking intrinsic elevation errors. Our analysis suggest that error propagation was more important than the grid size in this study, since stream network discrepancies between the LiDAR-based DTMs and the satellite-derived SRTM and ASTER models were relatively small for some of the study areas (e.g., Sa Font de la Vila catchment; Figure 4a).
5.2.4. Small-Detail Arrangement Patterns of Water and Sediment Fluxes
A relatively good consistency in the spatial pattern of modelled surface water and the sediment connectivity index (IC) was observed between the SRTM data and the two LiDAR-based models, while the patterns obtained from the ASTER data showed serious pitfalls for interpreting small-detail patterns of surface water and sediment flow. Since the ASTER imagery was collected with a ground-sampling distance of 15 m, small detail features remained within the subpixel range. Furthermore, the presence of large elevation inaccuracies and artefacts in the studied ASTER data strongly hindered the application of this dataset for detailed hydrogeomorphological analysis. Although more consistent within the SRTM data, the surface flow patterns obtained using this SAR-based DTM were considerably blurred, due to the coarse spatial resolution and lack of small-detail features of this dataset. In fact, the flow arrangement effects caused by microtopographic features such as concrete roads and preferential flow pathways were only captured within the 1-m LiDAR-based data (e.g., small detail plot at the mixed Es Fangar catchment; Figure 5), thereby highlighting the need for high-resolution (i.e., ≤5 m) DTMs in the application of small-detail hydrogeomorphological modelling.
Anthropogenic landscape features, such as small artificial drainage channels and ditches in agricultural fields, can significantly alter the hydrosedimentological functioning of traditional Mediterranean landscapes [102]. These artificial (metre- to submetre-wide) features were very likely underrepresented even for the 1-m LiDAR model. The coarser spatial resolution of the other analysed models made the detection of such traditional drainage systems largely unfeasible. Consequently, the model-derived stream networks and pathways of water and sediment connectivity obtained using the studied DTM sources approached a drainage pattern close to the “original” state of the system, but were unable to accurately reproduce the changes induced by human-made structures. This was probably true even for the analysed high-resolution 1-m LiDAR model. Therefore, the use of LiDAR-based models with very high resolution is recommended only if the underlying point density is high enough to reveal these small-detail features; otherwise, the consequent increases in computing time and required hardware resources cannot be justified in terms of increased accuracy and hydrogeomorphological modelling reliability.
6. Conclusions
This study examined the vertical accuracy of four DTMs (the 1-arcsecond SRTM C-SAR V3 and ASTER GDEM V2 datasets, as well as the 5- and 1-m LiDAR-based IGN models) with regard to data source, dataset characteristics, and terrain morphology in three small Mediterranean catchments. The reliability of these DTMs for subsequent hydrogeomorphological modelling purposes was also assessed. The results of this study can be summarised in the following keystone conclusions:
- The analysed LiDAR-based models and—to a lower extent—SRTM provided reliable sources for most of the discussed hydrological and geomorphological modelling aspects. However, SRTM notably failed to produce reliable results for highly rugged, mountainous areas due to intrinsic errors associated with topographic RADAR shadowing effects. For the analysed LiDAR-based models, attention should be also paid to the influence of data processing steps such as grid interpolation and point-cloud classification.
- ASTER showed the lowest vertical accuracy and considerable residual artefacts producing strong, non-normally distributed elevation errors that largely constrained the reliability of the ASTER elevation data. The presence of forest vegetation exacerbated the tendency of the ASTER dataset to overestimate elevation values (accounting for up to 30-m deviations), although the inherent, large vertical errors that affected this dataset largely surpassed the influence of Mediterranean dry forest vegetation in measured absolute vertical accuracy.
- Intrinsic errors and scarcity of the underlying DTM production data, vegetation patterns, and complex terrain morphology as well as relief fragmentation (especially for Mediterranean landscapes with traditional terraced structures) influenced the analysed datasets to different extents, resulting in significant deviations of elevation values.
- Both the vertical accuracy and horizontal resolution of the datasets were found to influence catchment hydrogeomorphological modelling in the studied sites. Error propagation impacted flow routing, stream network, and catchment delineation, and to a lower extent, the distribution of slope gradient values. Coarse horizontal raster resolution was found to reduce the degree of hydrological and geomorphological detail available from the DTMs and their reliability in representing processes at different spatial scales within the catchment.
The results presented in this study are transferable to other geographic regions dominated by fluvial processes and are not restricted to Mediterranean environments. Current trends in LiDAR-derived DTMs such as the use of unmanned aerial vehicles (UAV) and full-waveform LiDAR systems, as well as their possible gains in hydrogeomorphological modelling, should be addressed in future research.
Author Contributions
Conceptualisation, L.G., M.M.-d.-l.-H., M.R. and J.E.; Data curation, A.C., J.G.-C., J.F. and J.A.L.-T.; Formal analysis, L.G., J.G.-C. and J.F.; Funding acquisition, J.E.; Investigation, J.G.-C., J.F. and J.A.L.-T.; Methodology, L.G. and A.C.; Project administration, J.E.; Resources, M.R. and J.E.; Software, M.R. and A.C.; Supervision, M.M.-d.-l.-H. and M.R.; Validation, A.C., J.G.-C. and J.F.; Visualisation, J.G.-C. and J.F.; Writing—original draft, L.G., M.M.-d.-l.-H. and J.E.; Writing—review & editing, M.M.-d.-l.-H., J.A.L.-T. and J.E.
Funding
This research was supported by the research project CGL2017-88200-R “Functional hydrological and sediment connectivity at Mediterranean catchments: global change scenarios—MEDhyCON-2” funded by the State Research Agency of the Spanish Ministry of Science, Innovation and Universities as well as the European Regional Development Funds (ERDF, EU). Lukas Graf’s stay at the University of the Balearic Islands was funded by a research fellowship given by the German Academic Exchange Service (DAAD). Mariano Moreno-de-las-Heras is beneficiary of a Juan de la Cierva fellowship (IJCI-2015-26463) funded by the State Research Agency of the Spanish Ministry of Science, Innovation and Universities. Josep Fortesa has a contract funded by Ministry of Innovation, Research and Tourism of the Autonomous Government of the Balearic Islands (FPI/2048/2017). Aleix Calsamiglia acknowledges the support from the Spanish Ministry of Economy and Competitiveness through a pre-doctoral contract BES-2013-062887. Julián García-Comendador is in receipt of a pre-doctoral contract (FPU15/05239) funded by the Spanish Ministry of Education and Culture. José A. López-Tarazón has a post-doctoral Vicenç Mut contract (CAIB PD/038/2016) funded by the Vice-presidency and Ministry of Innovation, Research and Tourism of the Balearic Islands Autonomous Government.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Florinsky, I.V. An illustrated introduction to general geomorphometry. Prog. Phys. Geogr. 2017, 41, 723–752. [Google Scholar] [CrossRef]
- Quinn, P.F.B.J.; Beven, K.; Chevallier, P.; Planchon, O. The Prediction of Hillslope Flow Paths for Distributed Hydrological Modelling Using Digital Terrain Models. Hydrol. Process. 1991, 5, 59–79. [Google Scholar] [CrossRef]
- Brasington, J.; Richards, K. Interactions between model predictions, parameters and DTM scales for TOPMODEL. Comput. Geosci. 1998, 24, 299–314. [Google Scholar] [CrossRef]
- Casas, A.; Benito, G.; Thorndycraft, V.R.; Rico, M. The topographic data source of digital terrain models as a key element in the accuracy of hydraulic flood modelling. Earth Surf. Process. Landf. 2006, 31, 444–456. [Google Scholar] [CrossRef]
- Sanders, F.B. Evaluation of on-line DEMs for flood inundation modeling. Adv. Water Resour. 2007, 30, 1831–1843. [Google Scholar] [CrossRef]
- Moore, I.D.; Grayson, R.B.; Ladson, A.R. Digital Terrain Modeling: A Review of Hydrological Geomorphological and Biological Applications. Hydrol. Process. 1991, 5, 3–30. [Google Scholar] [CrossRef]
- Florinsky, I. Errors of signal processing in digital terrain modelling. Int. J. Geogr. Inf. Sci. 2002, 16, 475–501. [Google Scholar] [CrossRef]
- Zhang, W.; Montgomery, D.R. Digital elevation model grid size, landscape representation, and hydrological simulations. Water Resour. Res. 1994, 30, 1019–1028. [Google Scholar] [CrossRef]
- Armstrong, R.N.; Martz, L.W. Topographic parameterization in continental hydrology: A study in scale. Hydrol. Process. 2003, 17, 3763–3781. [Google Scholar] [CrossRef]
- Hancock, G.R. The use of digital elevation models in the identification and characterization of catchments over different grid scales. Hydrol. Process. 2005, 19, 1727–1749. [Google Scholar] [CrossRef]
- Wu, S.; Li, J.; Huang, G.H. A study on DEM-derived primary topographic attributes for hydrologic applications: Sensitivity to elevation data resolution. Appl. Geogr. 2008, 28, 210–223. [Google Scholar] [CrossRef]
- Kenward, T.; Lettenmaier, D.P.; Wood, E.F.; Fielding, E. Effects of digital elevation model accuracy on hydrologic prediction. Remote Sens. Environ. 2000, 74, 432–444. [Google Scholar] [CrossRef]
- Merwade, V.; Olivera, F.; Arabi, M.; Edleman, S. Uncertainty in Flood Inundation Mapping: Current Issues and Future Directions. J. Hydrol. Eng. 2008, 13, 608–620. [Google Scholar] [CrossRef]
- Guth, P.L. Geomorphometric Comparison of ASTER GDEM and SRTM. In Proceedings of the A Special Joint Symposium of ISPRS Technical Commission IV & AutoCarto in Conjunction with ASPRS/CaGIS 2010 Fall Specialty Conference, Orlando, FL, USA, 15–19 November 2010. [Google Scholar]
- van Zyl, J.J. The Shuttle Radar Topography Mission (SRTM): A breakthrough in remote sensing of topography. Acta Astronaut. 2001, 48, 559–565. [Google Scholar] [CrossRef]
- Tachikawa, T.; Hat, M.; Kaku, M.; Iwasaki, A. Characteristics of ASTER GDEM version 2. In Proceedings of the 2011 IEEE International Geosciences Remote Sensing Symposium (IGARSS), Vancouver, BC, Canada, 24–29 July 2011; pp. 3657–3660. [Google Scholar] [CrossRef]
- Rabus, B.; Eineder, M.; Roth, A.; Bamler, R. The shuttle radar topography mission—A new class of digital elevation models acquired by spaceborne radar. ISPRS J. Photogramm. Remote Sens. 2003, 57, 241–262. [Google Scholar] [CrossRef]
- ASTER-GDEM-Validation-Team. ASTER Global Digital Elevation Model Version 2—Summary of Validation Results; NASA - Earth Resources Observation and Science (EROS) Center: Sioux Falls, SD, USA, 2011.
- Hodgson, M.E.; Bresnahan, P. Accuracy of airborne LiDAR derived elevation: Empirical assessment and error budget. Photogramm. Eng. Remote Sens. 2004, 70, 331–339. [Google Scholar] [CrossRef]
- Heritage, G.L.; Milan, D.J.; Large, A.R.G.; Fuller, I.C. Influence of survey strategy and interpolation model on DEM quality. Geomorphology 2009, 112, 334–344. [Google Scholar] [CrossRef]
- Chen, Z.; Gao, B.; Devereux, B. State-of-the-Art: DTM Generation Using Airborne LIDAR Data. Sensors 2017, 17, 150. [Google Scholar] [CrossRef]
- Simpson, J.E.; Smith, T.E.L.; Wooster, M.J. Assessment of errors caused by forest vegetation structure in airborne LiDAR-derived DTMs. Remote Sens. 2017, 9, 1101. [Google Scholar] [CrossRef]
- Bossi, G.; Cavalli, M.; Crema, S.; Frigerio, S.; Quan Luna, B.; Mantovani, M.; Marcato, G.; Schenato, L.; Pasuto, A. Multi-temporal LiDAR-DTMs as a tool for modelling a complex landslide: A case study in the Rotolon catchment (eastern Italian Alps). Nat. Hazards Earth Syst. Sci. 2015, 15, 715–722. [Google Scholar] [CrossRef]
- Fernández, T.; Pérez, J.; Colomo, C.; Cardenal, J.; Delgado, J.; Palenzuela, J.; Irigaray, C.; Chacón, J. Assessment of the Evolution of a Landslide Using Digital Photogrammetry and LiDAR Techniques in the Alpujarras Region (Granada, Southeastern Spain). Geosciences 2017, 7, 32. [Google Scholar] [CrossRef]
- Kamps, M.T.; Bouten, W.; Seijmonsbergen, A.C. LiDAR and orthophoto synergy to optimize object-based landscape change: Analysis of an active landslide. Remote Sens. 2017, 9, 805. [Google Scholar] [CrossRef]
- Höfle, B.; Rutzinger, M. Topographic airborne LiDAR in geomorphology: A technological perspective. Z. Geomorphol. 2011, 55, 1–29. [Google Scholar] [CrossRef]
- Tarolli, P. Geomorphology High-resolution topography for understanding Earth surface processes: Opportunities and challenges. Geomorphology 2014, 216, 295–312. [Google Scholar] [CrossRef]
- Moreno-de-las-Heras, M.; Saco, P.M.; Willgoose, G.R. A Comparison of SRTM V4 and ASTER GDEM for Hydrological Applications in Low Relief Terrain. Photogramm. Eng. Remote Sens. 2012, 78, 7807. [Google Scholar] [CrossRef]
- Athmania, D.; Achour, H. External validation of the ASTER GDEM2, GMTED2010 and CGIAR-CSI-SRTM v4.1 free access digital elevation models (DEMs) in Tunisia and Algeria. Remote Sens. 2014, 6, 4600–4620. [Google Scholar] [CrossRef]
- Jarihani, A.A.; Callow, J.N.; McVicar, T.R.; Van Niel, T.G.; Larsen, J.R. Satellite-derived Digital Elevation Model (DEM) selection, preparation and correction for hydrodynamic modelling in large, low-gradient and data-sparse catchments. J. Hydrol. 2015, 524, 489–506. [Google Scholar] [CrossRef]
- Czubski, K.; Kozak, J.; Kolecka, N. Accuracy of SRTM-X and ASTER Elevation Data and its Influence on Topographical and Hydrological Modeling: Case Study of the Pieniny Mts. in Poland. Int. J. Geoinform. 2013, 9, 7–14. [Google Scholar]
- Mukherjee, S.; Joshi, P.K.; Mukherjee, S.; Ghosh, A.; Garg, R.D.; Mukhopadhyay, A. Evaluation of vertical accuracy of open source Digital Elevation Model (DEM). Int. J. Appl. Earth Obs. Geoinform. 2013, 21, 205–217. [Google Scholar] [CrossRef]
- Nascetti, A.; Di Rita, M.; Ravanelli, R.; Amicuzi, M.; Esposito, S.; Crespi, M. Free global DSM assessment on large scale areas exploiting the potentialities of the innovative google earth engine platform. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 627–633. [Google Scholar] [CrossRef]
- Gorokhovich, Y.; Voustianiouk, A. Accuracy assessment of the processed SRTM-based elevation data by CGIAR using field data from USA and Thailand and its relation to the terrain characteristics. Remote Sens. Environ. 2006, 104, 409–415. [Google Scholar] [CrossRef]
- Ludwig, R.; Schneider, P. Validation of digital elevation models from SRTM X-SAR for applications in hydrologic modeling. ISPRS J. Photogramm. Remote Sens. 2006, 60, 339–358. [Google Scholar] [CrossRef]
- Notebaert, B.; Verstraeten, G.; Govers, G.; Poesen, J. Qualitative and quantitative applications of LiDAR imagery in fluvial geomorphology. Earth Surf. Process. Landf. 2009, 34, 217–231. [Google Scholar] [CrossRef]
- Sharma, A.; Tiwari, K.N. A comparative appraisal of hydrological behavior of SRTM DEM at catchment level. J. Hydrol. 2014, 519, 1394–1404. [Google Scholar] [CrossRef]
- Tan, M.L.; Ficklin, D.L.; Dixon, B.; Ibrahim, A.L.; Yusop, Z.; Chaplot, V. Impacts of DEM resolution, source, and resampling technique on SWAT-simulated streamflow. Appl. Geogr. 2015, 63, 357–368. [Google Scholar] [CrossRef]
- Santillan, J.R.; Makinano-Santillan, M. Vertical accuracy assessment of 30-M. resolution ALOS, ASTER, and SRTM global DEMS over Northeastern Mindanao, Philippines. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 149–156. [Google Scholar] [CrossRef]
- Nikolakopoulos, K.G.; Kamaratakis, E.K.; Chrysoulakis, N. SRTM vs ASTER elevation products. Comparison for two regions in Crete, Greece. Int. J. Remote Sens. 2006, 27, 4819–4838. [Google Scholar] [CrossRef]
- de Vente, J.; Poesen, J.; Govers, G.; Boix-Fayos, C. The implications of data selection for regional erosion and sediment yield modelling. Earth Surf. Process. Landf. 2009, 34, 1994–2007. [Google Scholar] [CrossRef]
- de Carvalho Júnior, O.A.; Guimarães, R.F.; Montgomery, D.R.; Gillespie, A.R.; Gomes, R.A.T.; de Souza Martins, É.; Silva, N.C. Karst depression detection using ASTER, ALOS/PRISM and SRTM-derived digital elevation models in the Bambuí group, Brazil. Remote Sens. 2013, 6, 330–351. [Google Scholar] [CrossRef]
- Hooke, J.M. Human impacts on fluvial systems in the Mediterranean region. Geomorphology 2006, 79, 311–335. [Google Scholar] [CrossRef]
- Iglesias, A.; Garrote, L.; Flores, F.; Moneo, M. Challenges to manage the risk of water scarcity and climate change in the Mediterranean. Water Resour. Manag. 2007, 21, 775–788. [Google Scholar] [CrossRef]
- Calsamiglia, A.; Lucas-Borja, M.E.; Fortesa, J.; García-Comendador, J.; Estrany, J. Changes in Soil Quality and Hydrological Connectivity Caused by the Abandonment of Terraces in a Mediterranean Burned Catchment. Forests 2017, 8, 333. [Google Scholar] [CrossRef]
- Serra, P.; Pons, X.; Saurı, D. Land-cover and land-use change in a Mediterranean landscape: A spatial analysis of driving forces integrating biophysical and human factors. Appl. Geogr. 2008, 28, 189–209. [Google Scholar] [CrossRef]
- Buendia, C.; Bussi, G.; Tuset, J.; Vericat, D.; Sabater, S.; Palau, A.; Batalla, R.J. Effects of afforestation on runoff and sediment load in an upland Mediterranean catchment. Sci. Total Environ. 2015, 540, 144–157. [Google Scholar] [CrossRef] [PubMed]
- Borselli, L.; Cassi, P.; Torri, D. Prolegomena to sediment and flow connectivity in the landscape: A GIS and field numerical assessment. Catena 2008, 75, 268–277. [Google Scholar] [CrossRef]
- Cavalli, M.; Trevisani, S.; Comiti, F.; Marchi, L. Geomorphometric assessment of spatial sediment connectivity in small Alpine catchments. Geomorphology 2013, 188, 31–41. [Google Scholar] [CrossRef]
- Gelabert, B.; Sabat, F.; Rodriguez-Perea, A. A structural outline of the Serra de Tramuntana of Mallorca (Balearic Islands). Tectonophysics 1992, 203, 167–183. [Google Scholar] [CrossRef]
- Calsamiglia, A.; Fortesa, J.; García-Comendador, J.; Lucas-Borja, M.; Calvo-Cases, A.; Estrany, J. Spatial patterns of sediment connectivity in terraced lands: Anthropogenic controls of catchment sensitivity. Land Degrad. Dev. 2018, 29, 1198–1210. [Google Scholar] [CrossRef]
- Koutsias, N.; Arianoutsou, M.; Kallimanis, A.S.; Mallinis, G.; Halley, J.M.; Dimopoulos, P. Where did the fires burn in Peloponnisos, Greece the summer of 2007? Evidence for a synergy of fuel and weather. Agric. For. Meteorol. 2012, 156, 41–53. [Google Scholar] [CrossRef]
- Rosselló-Verger, V.M. The Serra de Tramuntana of Mallorca. Phys. Hum. Orig. Source: Catalan Soc. Sci. Rev. 2014, 4, 15–30. [Google Scholar] [CrossRef]
- Estrany, J.; Garcia, C.; Martínez-Carreras, N.; Walling, D.E. A suspended sediment budget for the agricultural Can Revull catchment (Mallorca, Spain). Z. Geomorphol. Suppl. 2012, 56, 169–193. [Google Scholar] [CrossRef]
- Eineder, M.; Bamler, R.; Werner, M.; Rabus, B.; Breit, H.; Adam, N.; Suchandt, S.; Holzner, J. SRTM/X-SAR CALIBRATION STATUS. In Proceedings of the CEOS WGCV-SAR Workshop, Sydney, NSW, Australia, 9–13 July 2001. [Google Scholar]
- Rosen, P.A.; Hensley, S.; Gurrola, E.; Rogez, F.; Chan, S.; Martin, J.; Rodriguez, E. SRTM C-Band Topographic Data: Quality Assessments and Calibration Activities. In Proceedings of the IEEE 2001 International Geoscience and Remote Sensing Symposium, Sydney, Ausralia, 9–13 July 2001; Volume 2. [Google Scholar]
- Reuter, H.I.; Nelson, A.; Strobl, P.; Mehl, W.; Jarvis, A. A first assessment of ASTER GDEM tiles for absolute accuracy, relative accuracy and terrain parameters. In Proceedings of the IGARSS 2009 International Geosciences Remote Sensing Symposium, Capetown, South Africa, 13–17 July 2009; Volume 5, pp. 240–243. [Google Scholar]
- Szabó, G.; Singh, S.K.; Szabó, S. Slope angle and aspect as influencing factors on the accuracy of the SRTM and the ASTER GDEM databases. Phys. Chem. Earth Parts 2015, 83–84, 137–145. [Google Scholar] [CrossRef]
- IGN. Instituto Geográfico Nacional—Centro Nacional de Información Geográfica [WWW Document]. 2018. Available online: http://www.ign.es/web/ign/portal (accessed on 13 February 2018).
- Bashfield, A.; Keim, A. Continent-wide DEM Creation for the European Union. In Proceedings of the 34th International Symposium on Remote Sensing of Environment—The GEOSS Era: Towards Operational Environmental Monitoring, Sydney, Australia, 10–15 April 2011; pp. 10–15. [Google Scholar]
- Lee, S.; Wolberg, G.; Shin, S.Y. Scattered Data Interpolation with Multilevel, B-Splines. IEEE Trans. Vis. Comput. Gr. 1997, 3, 228–244. [Google Scholar] [CrossRef]
- Lee, J.S. Digital image enhancement and noise filtering by use of local statistics. IEEE Trans. Pattern Anal. Mach. Intell. 1980, 2, 165–168. [Google Scholar] [CrossRef] [PubMed]
- Höhle, J.; Höhle, M. Accuracy assessment of digital elevation models by means of robust statistical methods. ISPRS J. Photogramm. Remote Sens. 2009, 64, 398–406. [Google Scholar] [CrossRef]
- Höhle, J. The Assessment of the Absolute Planimetric Accuracy of Airborne Laserscanning. ISPRS—Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 145–150. [Google Scholar] [CrossRef]
- Planchon, O.; Darboux, F. A fast, simple and versatile algorithm to fill the depressions of digital elevation models. Catena 2001, 46, 159–176. [Google Scholar] [CrossRef]
- O’Callaghan, J.F.; Mark, D.M. The extraction of drainage networks from digital elevation data. Comput. Vis. Gr. Image Process. 1984, 27, 247. [Google Scholar] [CrossRef]
- Strahler, A.N. Hypsometric (Area-Altitude) Analysis of Erosional Topography. Geol. Soc. Am. Bull. 1952, 63, 1117–1142. [Google Scholar] [CrossRef]
- Hancock, G.R.; Martinez, C.; Evans, K.G.; Moliere, D.R. A comparison of SRTM and high-resolution digital elevation models and their use in catchment geomorphology and hydrology: Australian examples. Earth Surf. Process. Landf. 2006, 31, 1384–1412. [Google Scholar] [CrossRef]
- Willgoose, G.R. A physical explanation for an observed area-slope-elevation relationship for declining catchments. Water Resour. Res. 1994, 30, 151–159. [Google Scholar] [CrossRef]
- Rodríguez-Iturbe, I.; Ijjász-Vásquez, E.; Bras, R.; Tarboton, D. Power law distributions of discharge mass and energy in River Basins. Water Resour. Res. 1992, 28, 1089–1093. [Google Scholar] [CrossRef]
- Vivoni, E.R.; Di Benedetto, F.; Grimaldi, S.; Eltahir, E.A. Hypsometric Control on Surface and Subsurface Runoff. Water Resour. Res. 2008, 44, 12502–12511. [Google Scholar] [CrossRef]
- Strahler, A.N. Quantitative analysis of watershed geomorphology. Trans. Am. Geophys. Union 1957, 38, 913–920. [Google Scholar] [CrossRef]
- Roering, J.J.; Perron, J.T.; Kirchner, J.W. Functional relationships between denudation andhillslope form and relief. Earth Planet. Sci. Lett. 2007, 264, 245–258. [Google Scholar] [CrossRef]
- Perera, H.; Willgoose, G.R. A physical explanation of the cumulative area distribution curve. Water Resour. Res. 1998, 34, 1335–1343. [Google Scholar] [CrossRef]
- Moglen, G.E.; Bras, R.L. The importance of spatially heterogeneous erosivity and the cumulative area distribution within a basin evolution model. Geomorphology 1995, 12, 173–185. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Predicting rainfall erosion losses A guide to conservation planning. Agric. Handb. 1978, 537. [Google Scholar]
- Desmet, P.J.; Govers, G. A GIS procedure for automatically calculating the USLE LS factor on topographically complex landscape units. J. Soil Water Conserv. 1996, 51, 427–433. [Google Scholar]
- Conrad, O.; Bechtel, B.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Boehner, J. System for Automated Geoscientific Analyses (SAGA) v. 2.1.4. Geosci. Model Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef]
- Wainwright, J.; Turnbull, L.; Ibrahim, T.G.; Lexartza-Artza, I.; Thornton, S.F.; Brazier, R.E. Linking environmental regimes, space and time: Interpretations of structural and functional connectivity. Geomorphology 2011, 126, 387–404. [Google Scholar] [CrossRef]
- Crema, S.; Cavalli, M. SedInConnect: A stand-alone, free and open source tool for the assessment of sediment connectivity. Comput. Geosci. 2018, 111, 39–45. [Google Scholar] [CrossRef]
- Li, P.; Shi, C.; Li, Z.; Muller, J.P.; Drummond, J.; Li, X.; Li, T.; Li, Y.; Liu, J. Evaluation of ASTER GDEM VER2 using GPS measurements and SRTM VER4.1 in China. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 1–4, 181–186. [Google Scholar] [CrossRef]
- Estornell, J.; Ruiz, L.A.; Velázquez-Martí, B.; Hermosilla, T. Analysis of the factors affecting lidar dtm accuracy in a steep shrub area. Int. J. Dig. Earth 2011, 4, 521–538. [Google Scholar] [CrossRef]
- Clark, M.L.; Clark, D.B.; Roberts, D.A. Small-footprint lidar estimation of sub-canopy elevation and tree height in a tropical rain forest landscape. Remote Sens. Environ. 2004, 91, 68–89. [Google Scholar] [CrossRef]
- Meng, X.; Currit, N.; Zhao, K. Ground filtering algorithms for airborne LiDAR data: A review of critical issues. Remote Sens. 2010, 2, 833–860. [Google Scholar] [CrossRef]
- Bater, C.W.; Coops, N.C. Evaluating error associated with lidar-derived DEM interpolation. Comput. Geosci. 2009, 35, 289–300. [Google Scholar] [CrossRef]
- Aguilar, F.J.; Mills, J.P.; Delgado, J.; Aguilar, M.A.; Negreiros, J.G.; Pérez, J.L. Modelling vertical error in LiDAR-derived digital elevation models. ISPRS J. Photogramm. Remote Sens. 2010, 65, 103–110. [Google Scholar] [CrossRef]
- Kellndorfer, J.; Walker, W.; Pierce, L.; Dobson, C.; Fites, J.A.; Hunsaker, C.; Vona, J.; Clutter, M. Vegetation height estimation from Shuttle Radar Topography Mission and National Elevation Datasets. Remote Sens. Environ. 2004, 93, 339–358. [Google Scholar] [CrossRef]
- Carabajal, C.C.; Harding, D.J. SRTM C-Band and ICEsat Laser Altimetry Elevation Comparisons as a Function of Tree Cover and Relief. Photogramm. Eng. Remote Sens. 2006, 72, 287–298. [Google Scholar] [CrossRef]
- Walker, W.S.; Kellndorfer, J.M.; Pierce, L.E. Quality assessment of SRTM C- and X-band interferometric data: Implications for the retrieval of vegetation canopy height. Remote Sens. Environ. 2007, 106, 428–448. [Google Scholar] [CrossRef]
- Harding, D.J.; Lefsky, M.A.; Parker, G.G.; Blair, J.B. Laser altimeter canopy height profiles methods and validation for closed-canopy, broadleaf forests. Remote Sens. Environ. 2001, 76, 283–297. [Google Scholar] [CrossRef]
- Eineder, M. Problems and Solutions for INSAR Digital Elevation Model Generation of Mountainous Terrain. In Proceedings of the FRINGE 2003 Workshop, Frascatti, Italy, 1–5 December 2003. [Google Scholar]
- Nascetti, A.; Capaldo, P.; Porfiri, M.; Pieralice, F.; Fratarcangeli, F.; Benenati, L.; Crespi, M. Fast terrain modelling for hydrogeological risk mapping and emergency management: The contribution of high-resolution satellite SAR imagery. Geomat. Nat. Hazards Risk 2015, 6, 554–582. [Google Scholar] [CrossRef]
- Arefi, H.; Reinartz, P. Accuracy enhancement of ASTER global digital elevation models using ICESat data. Remote Sens. 2011, 3, 1323–1343. [Google Scholar] [CrossRef]
- Liu, X. Airborne LiDAR for DEM generation: Some critical issues. Prog. Phys. Geogr. 2008, 32, 31–49. [Google Scholar] [CrossRef]
- Pérez-Peña, J.V.; Azañón, J.M.; Booth-Rea, G.; Azor, A.; Delgado, J. Differentiating geology and tectonics using a spatial autocorrelation technique for the hypsometric integral. J. Geophys. Res. Earth Surf. 2009, 114. [Google Scholar] [CrossRef]
- Kienzle, S. The Effect of DEM Raster Resolution on First Order, Second Order and Compound Terrain Derivatives. Trans. GIS 2004, 8, 83–111. [Google Scholar] [CrossRef]
- Fryirs, K.A. River sensitivity: A lost foundation concept in fluvial geomorphology. Earth Surf. Process. Landf. 2017, 42, 55–70. [Google Scholar] [CrossRef]
- Wu, S.; Li, J.; Huang, G. An evaluation of grid size uncertainty in empirical soil loss modeling with digital elevation models. Environ. Model. Assess. 2005, 10, 33–42. [Google Scholar] [CrossRef]
- McMaster, K.J. Effects of digital elevation model resolution on derived stream network positions. Water Resour. Res. 2002, 38. [Google Scholar] [CrossRef]
- Oksanen, J.; Sarjakoski, T. Error propagation analysis of DEM-based drainage basin delineation. Int. J. Remote Sens. 2005, 26, 3085–3102. [Google Scholar] [CrossRef]
- Chaubey, I.; Cotter, A.S.; Costello, T.A.; Soerens, T.S. Effect of DEM data resolution on SWAT output uncertainty. Hydrol. Process. 2005, 19, 621–628. [Google Scholar] [CrossRef]
- Calsamiglia, A.; Garcia-Comendador, J.; Fortesa, J.; López-Tarazón, J.A.; Crema, S.; Cavalli, M.; Calvo-Cases, A.; Estrany, J. Effects of agricultural drainage systems on sediment connectivity in a small Mediterranean lowland catchment. Geomorphology 2018, 318, 162–171. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).