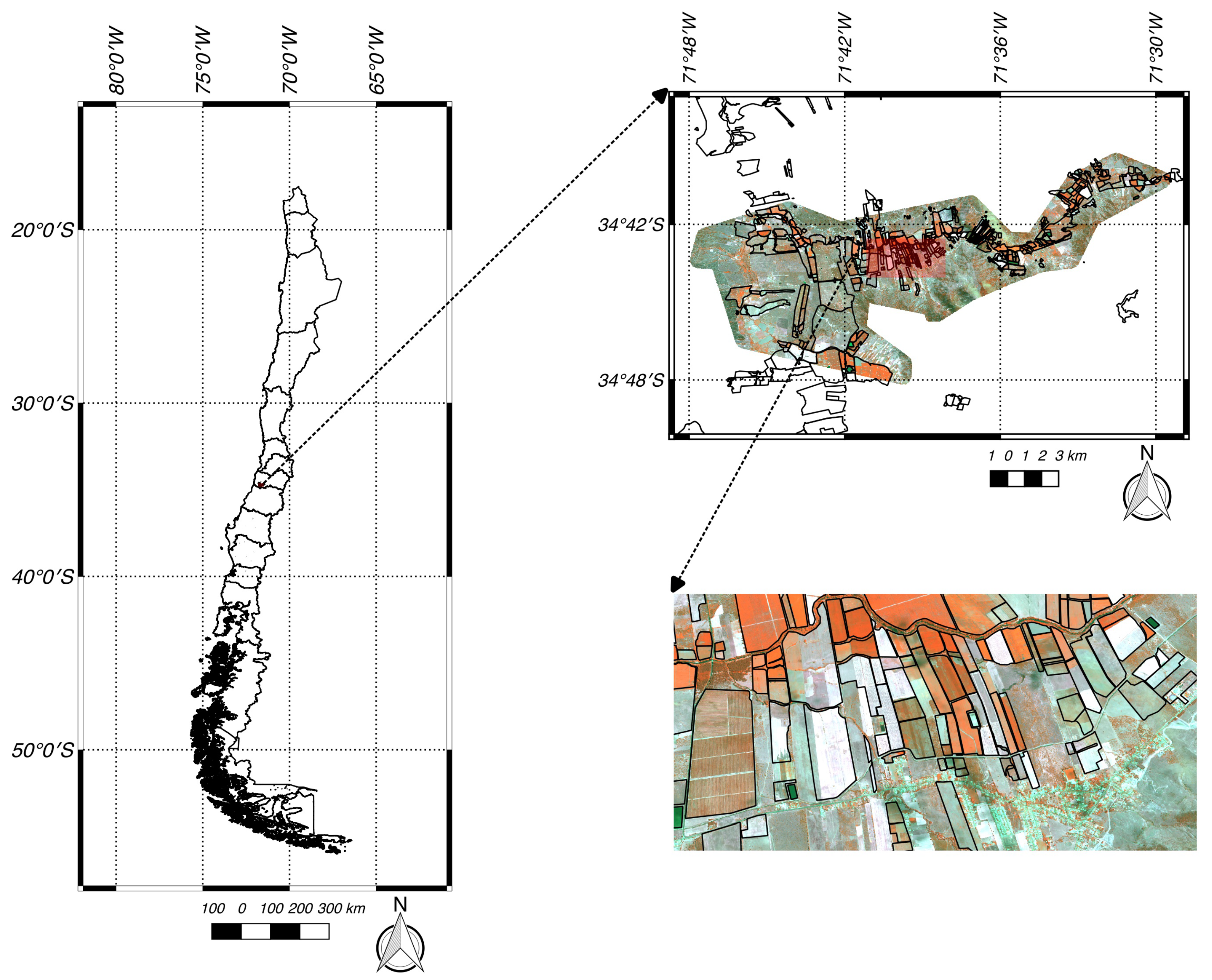
1. Introduction
The world’s population has tripled over the last 100 years and is still growing dramatically while resources have remained the same, causing changes in the outlook of food supply. According to the Food and Agriculture Organization (FAO), global food production will need to grow by 70% in order to satisfy the food and feed demand of a population of 9 billion people by 2050. The agriculture sector faces a critical overall challenge: to ensure access to safe, healthy, and nutritious food while using natural resources more sustainably and making an effective contribution to climate change adaptation and mitigation [
1].
This challenge implies a greater pressure than ever before on productive land. Accurate and up-to-date information about agricultural land, such as its status, acreage, ownership, and the type of crops, allows stakeholders to establish effective agricultural policies (e.g., for reducing greenhouse gas emissions, regulating water rights, and estimating subsidies and agriculture insurances) [
2,
3] and update agricultural geographical databases [
4], among other important tasks. In order to have up-to-date information on agricultural land, it is essential that the outlines of the plots are correct and can be quickly updated.
For the last 40 years, the outlining of plots in agricultural lands has been addressed through different initiatives around the world. In the United States, the National Research Council has published two reports that examine the situation of the land parcel data in the U.S. and provide a series of recommendations that would foster a national data system for storing plot information [
5,
6]. On the other hand, the European Union has promoted the use of a common Land Parcel Identification System (LPIS,
https://ec.europa.eu/jrc/en/scientific-tool/lpis-quality-assessment) among its members in order to maintain a record of the activities of farmers on their lands [
7]. The success of all these initiatives depends enormously on a precise outlining of the parcels.
Traditionally, the outlining of the parcels has been carried out manually using photointerpretation or field campaigns and documented by surveying sketches and textual documentation, all of which is very expensive both in time and financial resources.
The application of Information Technology tools, such as remote sensing and geographical information systems, improves efficiency in the agricultural sector, enabling planning and decision making based on the spatially and temporally distributed data provided by these tools [
8,
9]. The new generation of optical remote sensors placed on aircraft, satellite platforms, and drones offers accessible and useful data of very high resolution for monitoring agricultural fields at a plot level [
10,
11]. The task of processing this data while maintaining accuracy and meeting the time requirements becomes a real challenge.
Several methods have been proposed in the remote sensing literature to try to solve the automatic or semi-automatic parcel outlining problem. Most of them are based on image segmentation, edge detection algorithms, classification models, or combinations of these techniques. An object-based approach for extracting human-made objects, particularly agricultural fields from high-resolution images, was proposed in [
12]. This approach was able to extract regularly shaped objects by combining edge detection models with region-based segmentation. Da Costa et al. [
13] developed an algorithm to outline vine plots automatically from very high resolution images by exploiting their textural properties. To differentiate between vine and non-vine pixels, they applied a thresholding method to the texture attributes of the image. In [
14], a semi-automatic methodology for outlining field boundaries from satellite data was proposed. The authors first carried out segmentation using tonal and textural gradients, and the generated regions were then classified to obtain preliminary plot boundaries. Finally, they applied an active contour model [
15] to refine the geometry of these boundaries. Turker et al. used perceptual grouping for automatically detecting sub-boundaries within existing agricultural fields from satellite imagery [
16]. This approach combined field boundaries and image data to carry out a field-based analysis. A Canny edge detector was used to detect the edge pixels, and then lines were identified using a graph-based vectorization method.
From the analysis of the state of the art, it can be concluded that approaches based on segmentation methods have several drawbacks including that (1) they are sensitive to intra-plot variability, which can result in the production of more segmentation than desired, and (2) most of these methods depend heavily on the correct selection of parameters (e.g., the similarity measured used to group image pixels), which needs prior knowledge of the landscape or tuning by trial and error. Moreover, variability in the sizes and shapes of the plots means that certain configuration parameters do not allow plots with the different characteristics needed for a landscape to be outlined properly. Approaches based on edge detection tend to produce more of the desired edges, mainly due to the presence of spatial patterns and image noise. The oversegmentation problem presented by the two approaches is directly related to the high spatial resolution of the images used in the segmentation process. Nevertheless, in the case of outlining plots, a very high spatial resolution (VHSR) is critical for managing very differently shaped and sized parcels in the same scene. Methodologies based on the superpixel (SP) concept have been proposed to deal with VHSR. These methodologies aim to reduce the influence of noise and intra-class spectral variability, preserving most edges of the images and improving the computational speed of later steps, such as classification, clustering, and segmentation [
17]. In fact, some approaches to outlining plots based on SPs are found in the literature. The authors in [
18] combined a contour detection algorithm and simple linear iterative clustering (SLIC) to extract the cadastral boundaries from UAV orthoimages automatically. In [
19], the problem of outlining plots was addressed as a machine learning problem. The authors first oversegmented a VHSR image, then labeled each pair of segments according to whether they belonged to an agricultural plot, and, finally, they trained a classifier using this information. The trained classifier was then used to segment the agricultural plots of other regions in the image automatically. The oversegmentation problem has been addressed in other areas, such as computer vision [
20], video processing [
21], and medicine [
22], among others, by establishing a consensus between a set of different segments. This approach can also alleviate the parameter selection issue. Other works have addressed the problem of unsupervised parcel segmentation using time series. A procedure to identify different crops by combining information provided by an LPIS and a low spatial resolution image time series is presented in [
23]. However, LPISs are not always available; in fact, as has already mentioned, a suitable definition and update of an LPIS involve at least the semi-automatic outlining of the parcels. Nevertheless, some works in the literature that have applied time series for improving classification in agriculture. Thus, in [
24], an operational crop identification strategy based on the use of multispectral and multitemporal signatures was proposed for classification at the parcel level. It proposes a combination of synthetic-aperture radar (SAR) and optical data registered on particular dates with the objective of satisfying crop temporal constraints. The authors proved that the use of SAR time series reduces the crop classification delivery time when the optical image is replaced by several SAR images. The integration of spectral and temporal features was proposed in [
25] for annual cropland mapping. Even though the results presented in this paper showed that the methodology proposed is independent of in situ data and that it is capable of differentiating the croplands effectively, this methodology requires spatial baseline land cover information provided by different sources. A different crop classification approach is proposed in [
26]. Although an ensemble of multilayer perceptrons (MLPs) provides classified pixel-based and parcel-based maps from multitemporal satellite optical imagery, the labels of the training patterns were obtained through a ground survey. It should be noted that all these approaches are supervised, need additional information, and are not always available. To our knowledge, there is a lack of semi- or unsupervised methods that exploit temporal data for the purpose of outlining a high variety of parcels differing in size and shape. The use of temporal information to delineate agricultural plots appears promising since, during a growing season, plot boundaries in agricultural landscapes are relatively stable, while the phenological pattern of crops changes frequently [
27]. Some successful examples of combining superpixels and temporal information for change detection can be found in the literature [
28,
29]. However, in this case, the parcel outlining problem could be seen as a special case of change detection, in which the pattern (parcel edges) tends to remain constant over time.
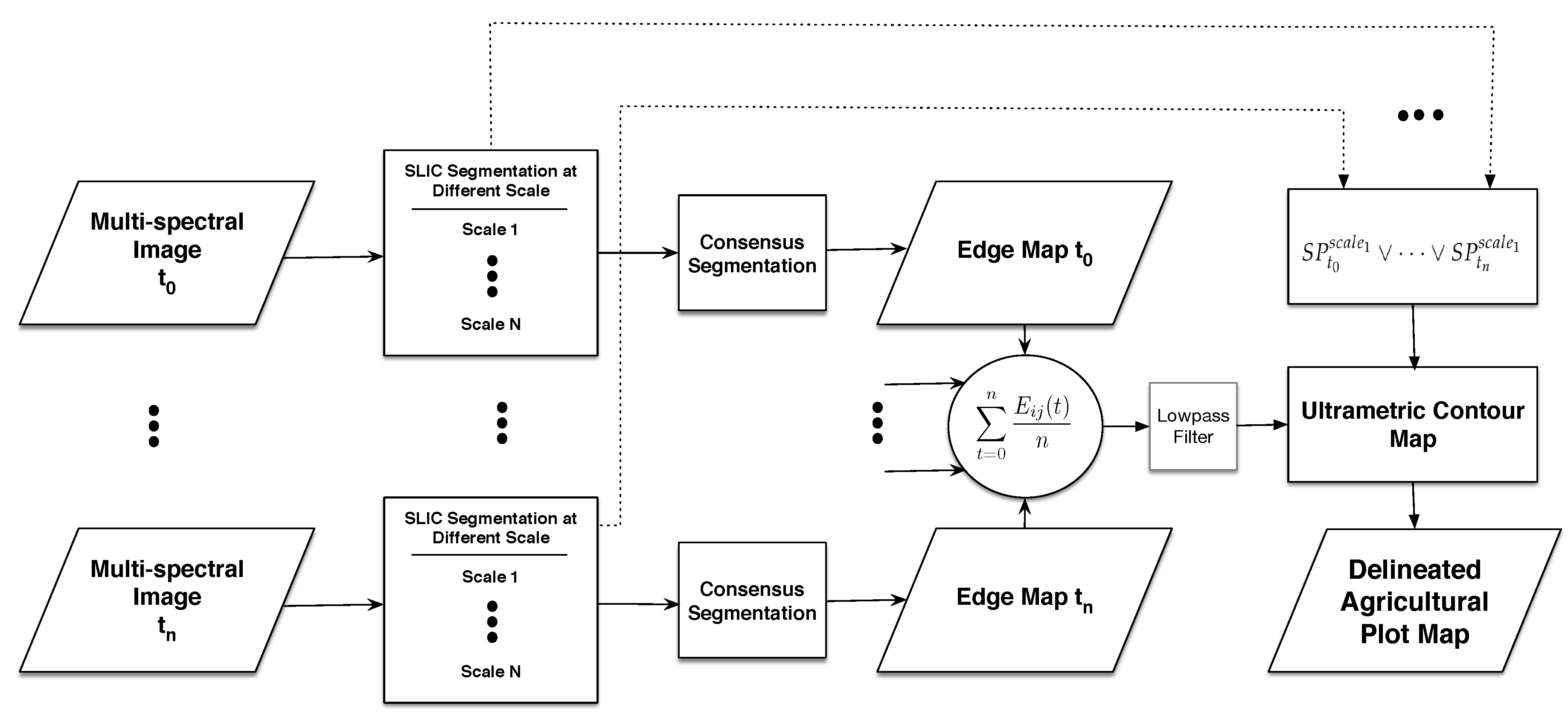
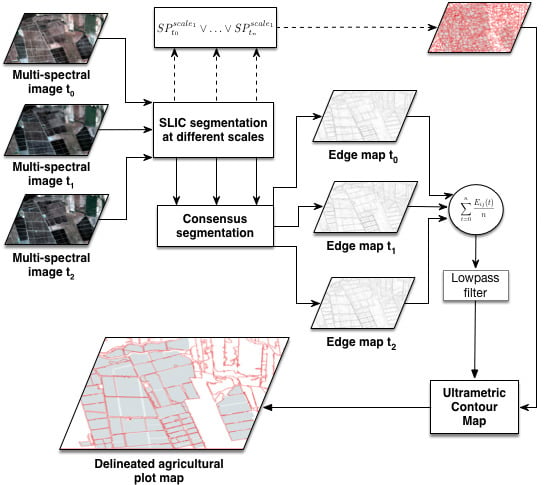
In this work, a new methodology based on consensus segmentation for outlining agricultural plots is presented. The proposed methodology combines segmentation on different scales—carried out using an SP method—with images registered on different dates to obtain a single segmentation of the agricultural plots.
This paper is organized as follows.
Section 2 describes the imagery used and the ground truth built for the evaluation of the methodology proposed, which is explained in detail in
Section 2.2. The results obtained are included and discussed in
Section 3. The conclusions derived from this work are presented in
Section 4.
3. Results and Discussion
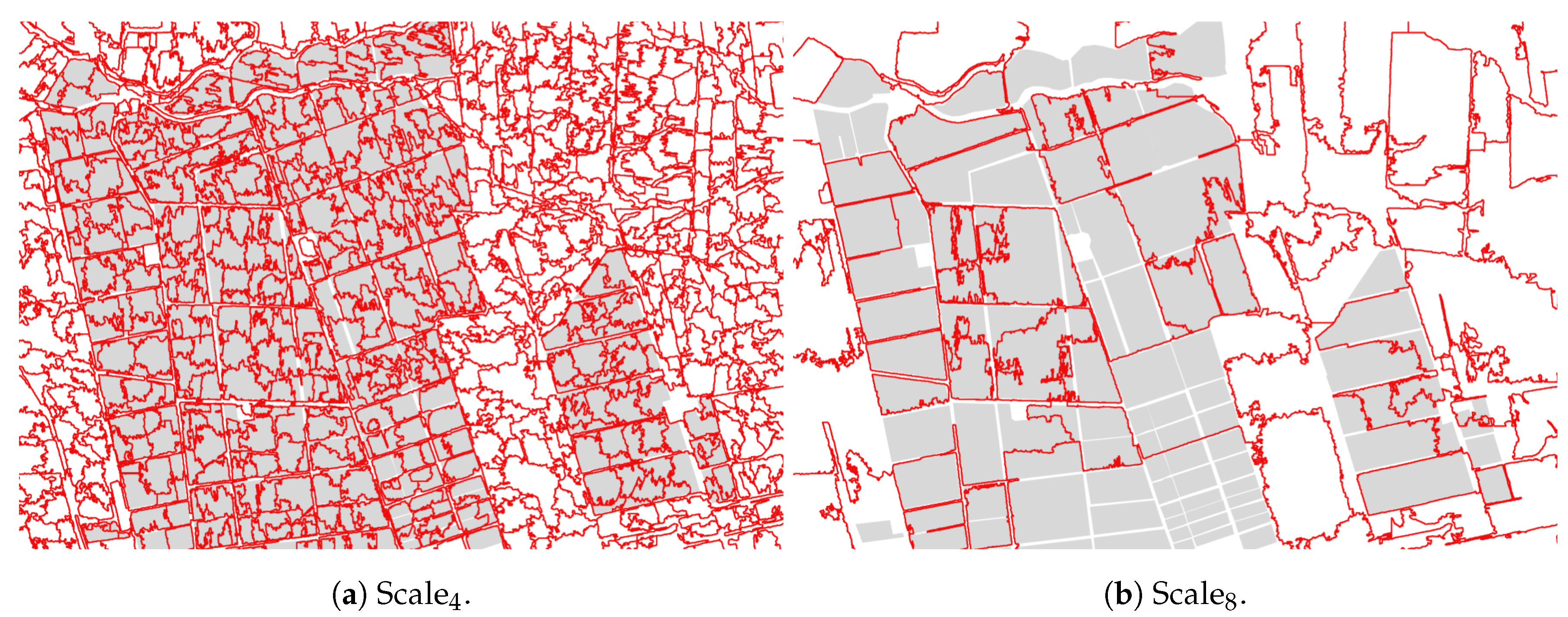
In
Figure 4, the SP segmentation obtained for the image registered on 30 January 2018 and corresponding to scale
and scale
is overlaid onto the color-composition image. It is possible to see the good adherence of the SPs to image objects in the three displayed cases. However, it can also be observed that the smaller the SP size (
Figure 4a), the better its adherence to the edges, as well as the homogeneity of the pixels that compose it. While, in the segmentation scales with larger SPs (
Figure 4a,b), the segments are less spectrally homogeneous, they still respect the borders between regions with a high contrast (the thickest edges).
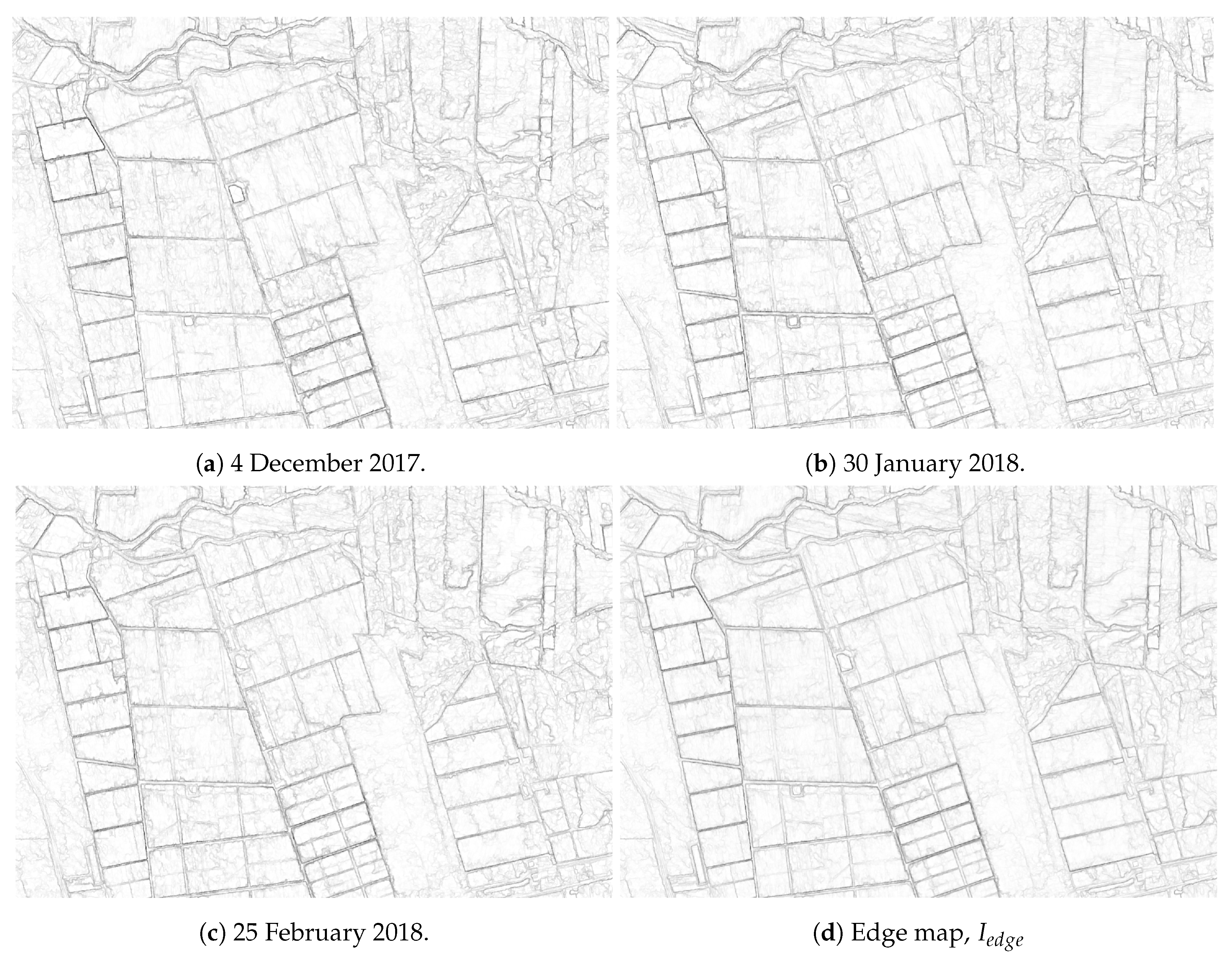
From the 10 segmentation scales for each date generated and consensus, the edge maps shown in
Figure 5a–c were obtained.
As can be seen in
Figure 5a–c, the edges of the plots tend to be more intense in all cases. In accordance with the methodology described, the next step is the integration of the three edge maps, one for each date, by calculating the average value. The average value is chosen as the basic form of integration because it allows for representing the information (borders) contained in all dates, thus reducing the effect of the appearance of borders in only one of the images, which is usually unusual for images of the same growing season (as mentioned in
Section 1). In addition, the edges that appear as a result of phenological changes tend to decrease. The edge map obtained (
Figure 5d) provides useful information for identifying the edges belonging to the plots; however, as mentioned above, it does not guarantee complete plots by applying a threshold, mainly due to edge-pixels not having the same value. Then, in order to obtain the final outlined agricultural plot map for the area considered, the UCM algorithm was applied to complete the edges.
Figure 6 shows the result of applying the UCM algorithm to the average of the three edge maps (
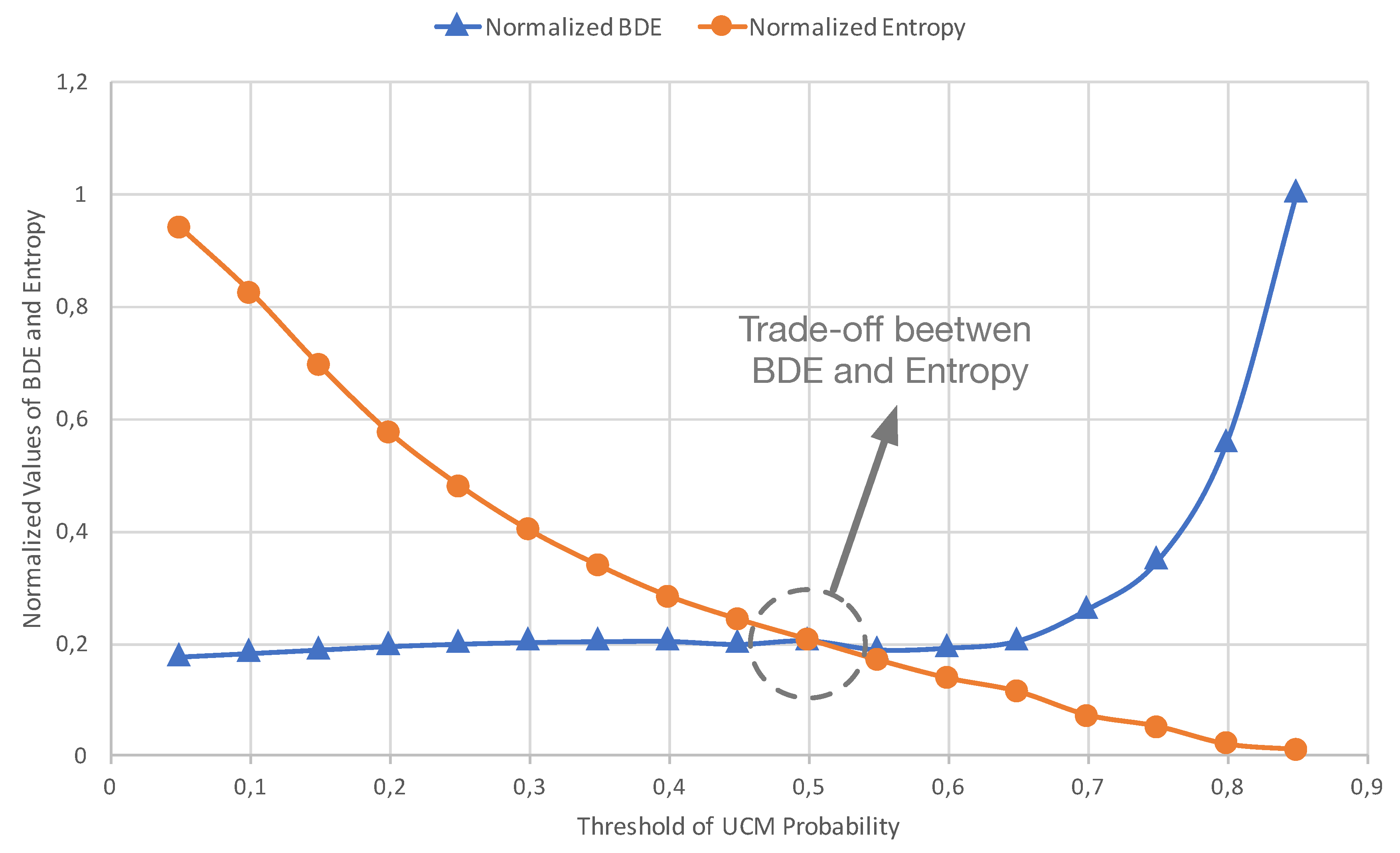
Figure 5d). As can be observed, even though all edges have been closed, there is a lot of noise inside each plot. This noise is due to the fact that in the UCM, the totality of the probabilities of occurrence of the edges is represented. This is why it is necessary to determine a threshold value of the probability above which an edge is considered as such. Two indicators were used to determine this value objectively. The first was an error metric of the calculated edges with respect to a ground truth called boundary displacement error (BDE) [
37,
38]; the second metric considers the Shannon entropy, which represents the information content present in a border image: in this case, it is the number of edges present at the UCM. The BDE index measures the difference between two segmented images by averaging the displacement of boundary pixels. Specifically, the distance (
) between a boundary pixel (
) in the obtained boundary image (
) and the closest pixel (
) in the ground-truth boundary image
is used to define the error (disagreement) of each boundary pixel. The BDE index can be mathematically defined as in Equation (
11).
where
represents the number of boundary pixels in image
B, and
is the Euclidean distance. The BDE index ranges within
, where the lower its value, the better. The BDE index is plotted against the edge entropy in
Figure 5d for each threshold value. As shown in
Figure 7, the smallest BDE metric error occurs for threshold values that are close to 1, while the worst values occur for values close to 0. Conversely, entropy behavior presents low values of information content for high threshold values and high information content for high threshold values. For the purpose of determining a specific threshold value, a compromise was established between the BDE value and the entropy value. As can be observed, a threshold value of 0.5 provides the balance between the error and the amount of edge information.
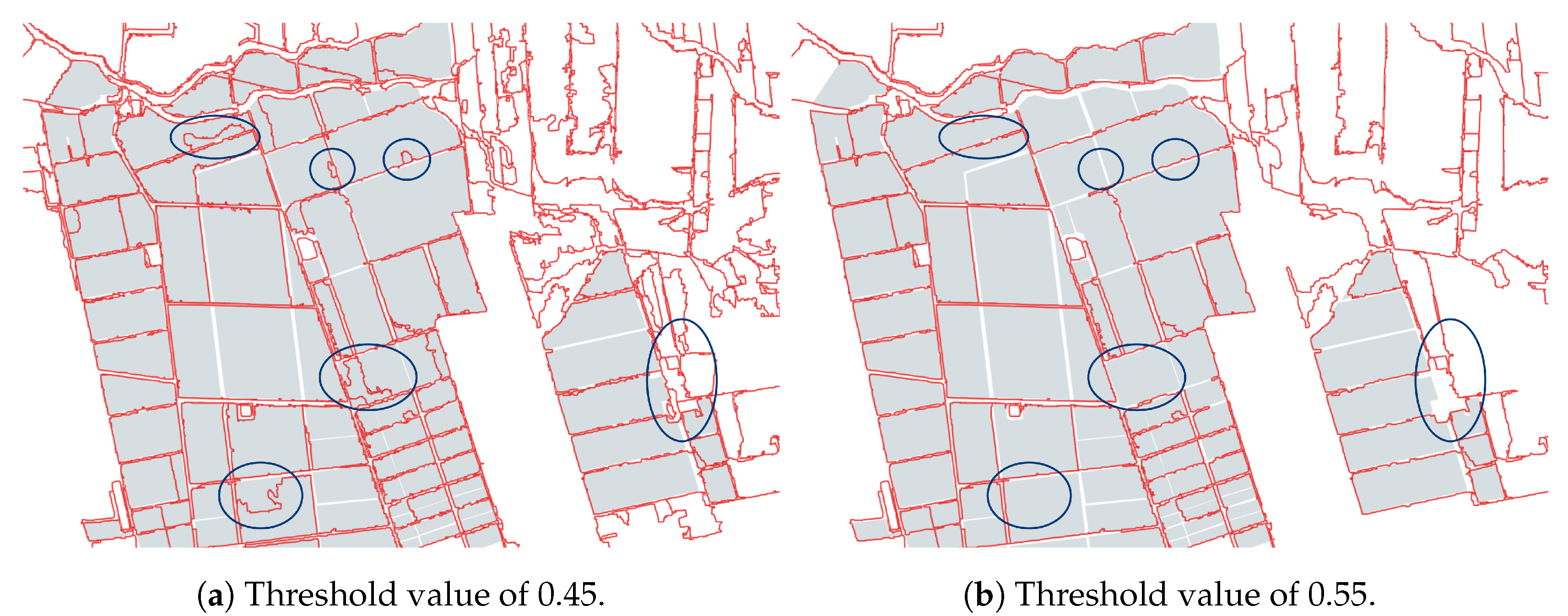
Figure 8 shows the final outlined plot maps obtained for two different threshold values overlaid onto the ground truth map.
As can be seen, most of the edges agree between the two maps (
Figure 8a,b), particularly in homogeneous areas with a high contrast between adjacent regions; however, discrepancies in plots with different tilled patterns can be also distinguished where the appearance of inner edges is present, as in plots within which anomalies are perceived due to poor agricultural practices, land heterogeneity, or crop diseases. As an example of the above, some areas where these changes occur are shown enclosed in circles. Consequently, only the edges stable over time—those that appear in the two images—remain in the final outlined plot map.