Inversion of Nearshore X-Band Radar Images to Sea Surface Elevation Maps
Abstract
1. Introduction
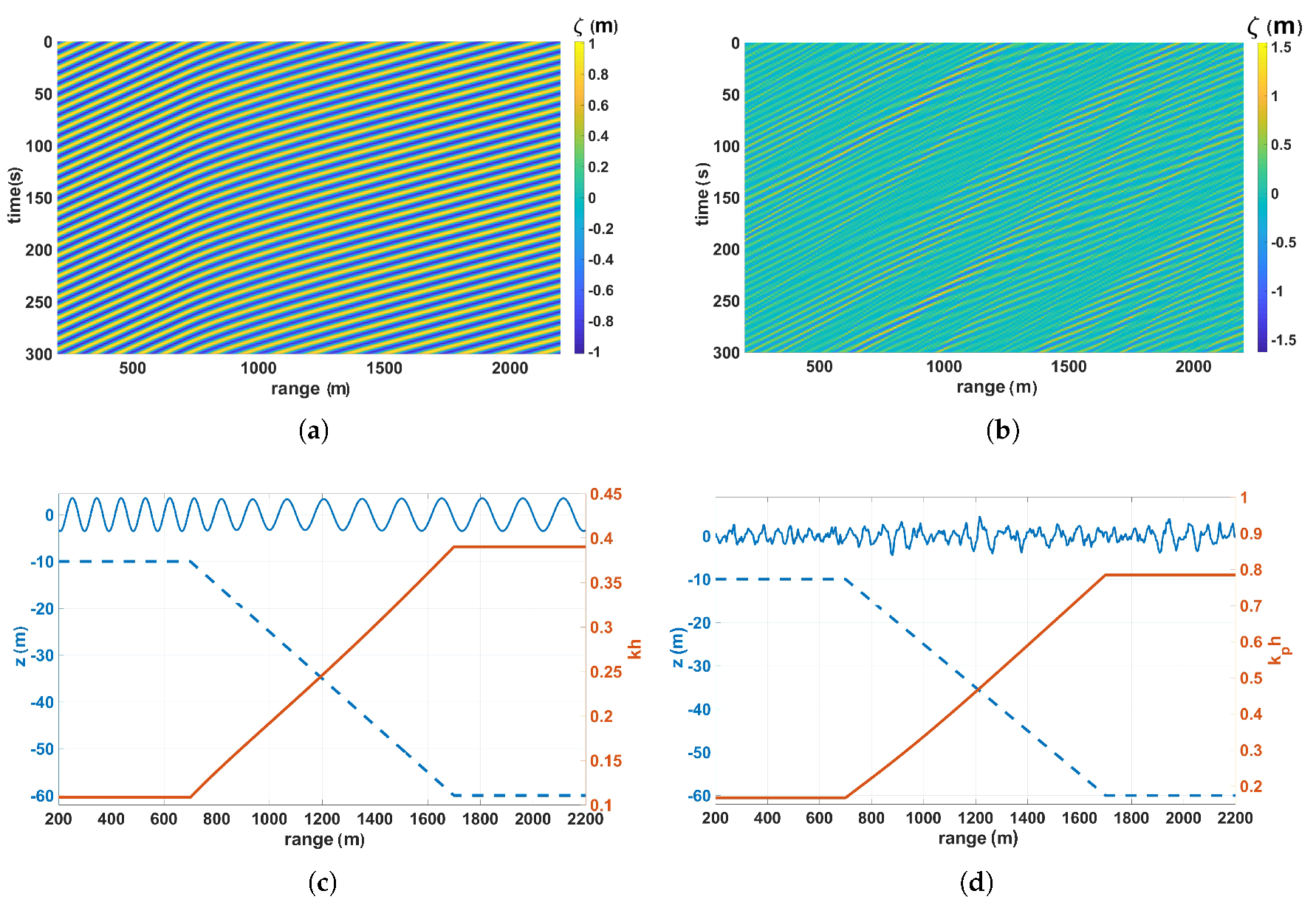
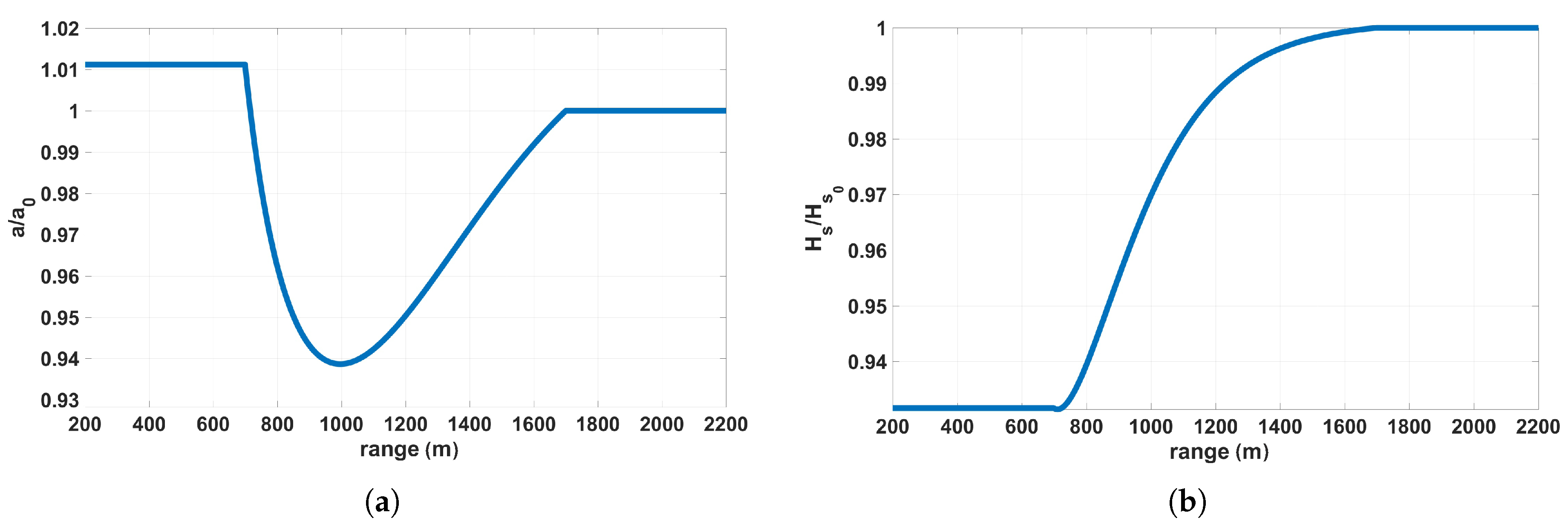
2. Inhomogeneous Sea Surface Simulation
Linear Shoaling for Monochromatic Waves and Spectra
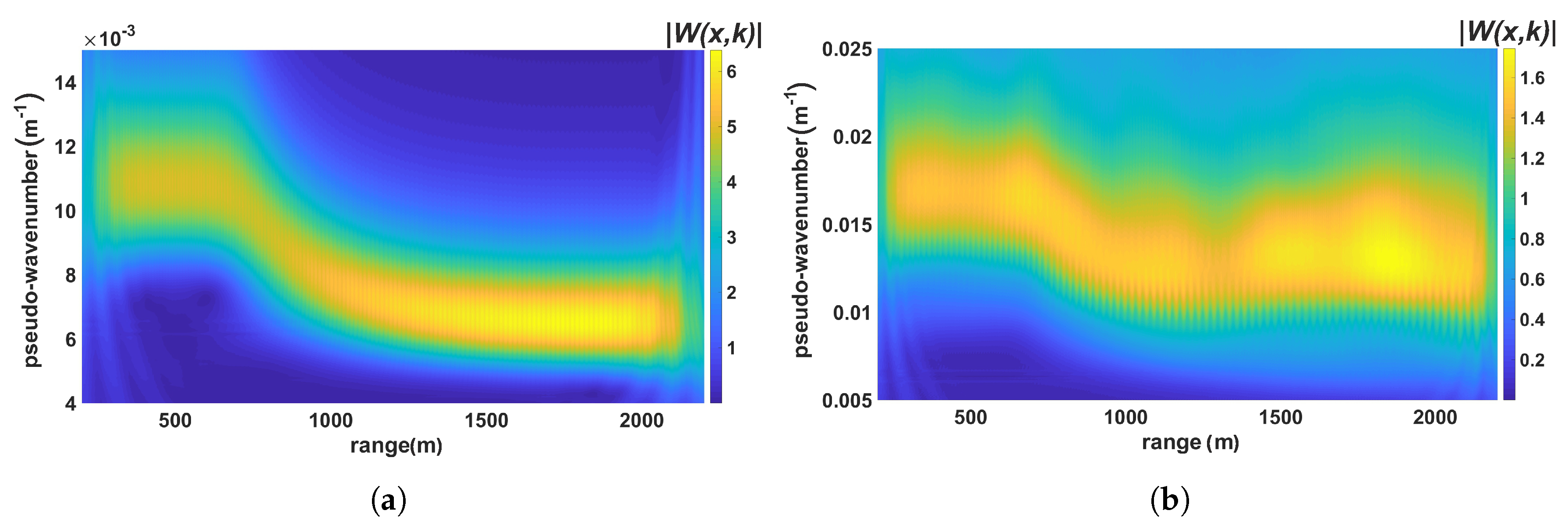
3. Wavelet Analysis of the Simulated Data
4. Basic Imaging Mechanisms—A Literature Summary
4.1. The Radar Equation
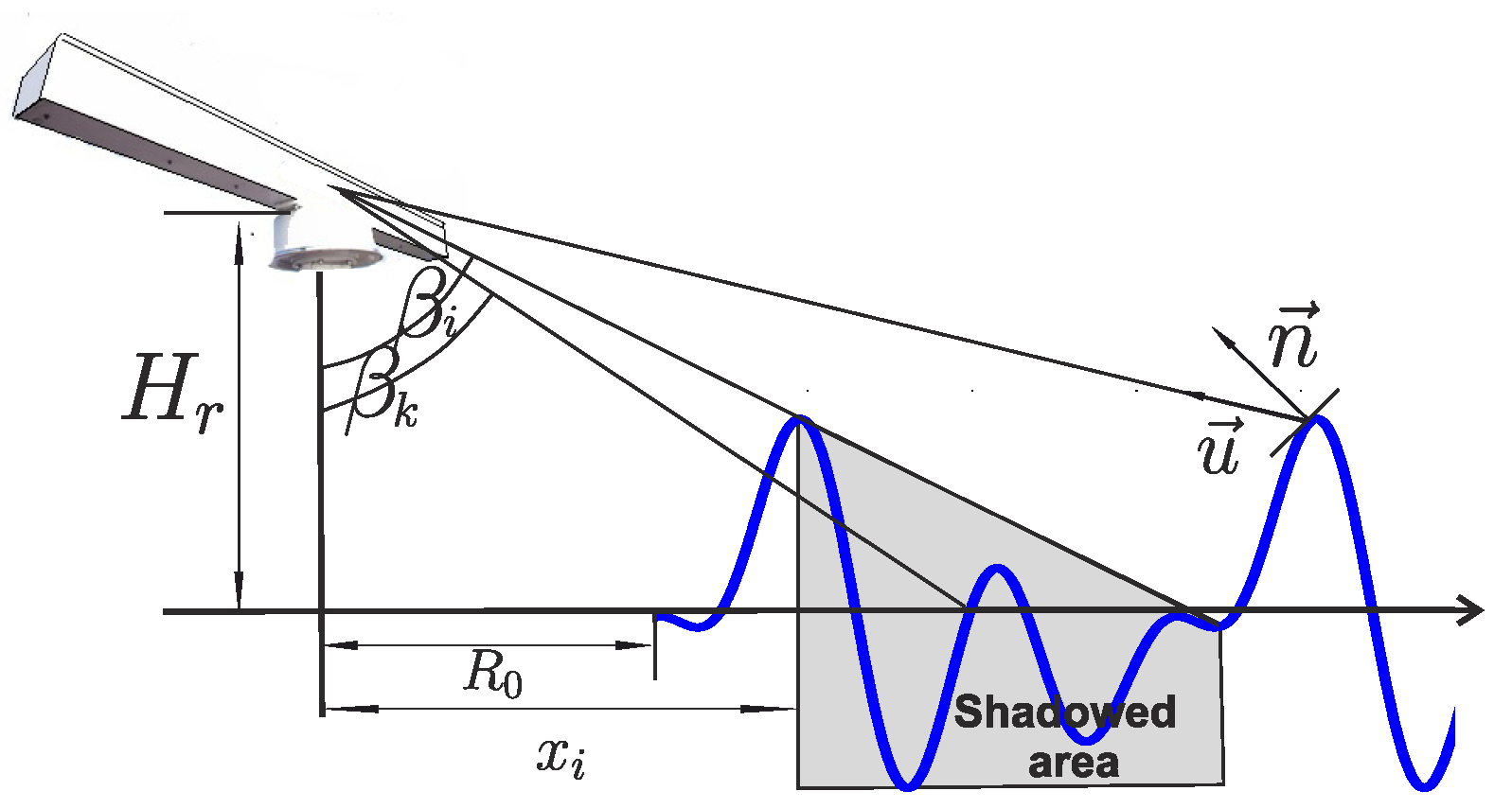
4.2. Shadowing
4.3. Speckle Noise
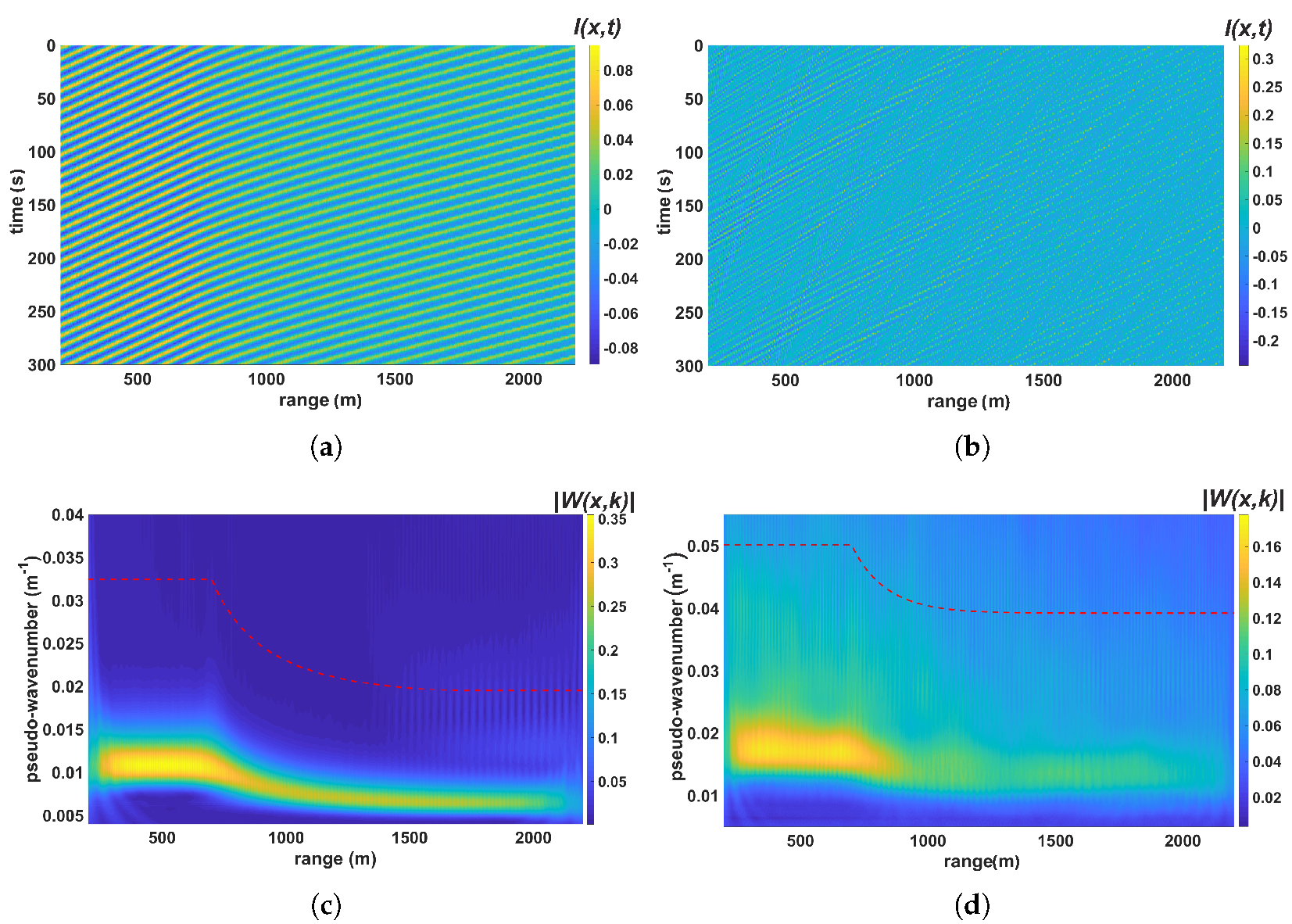
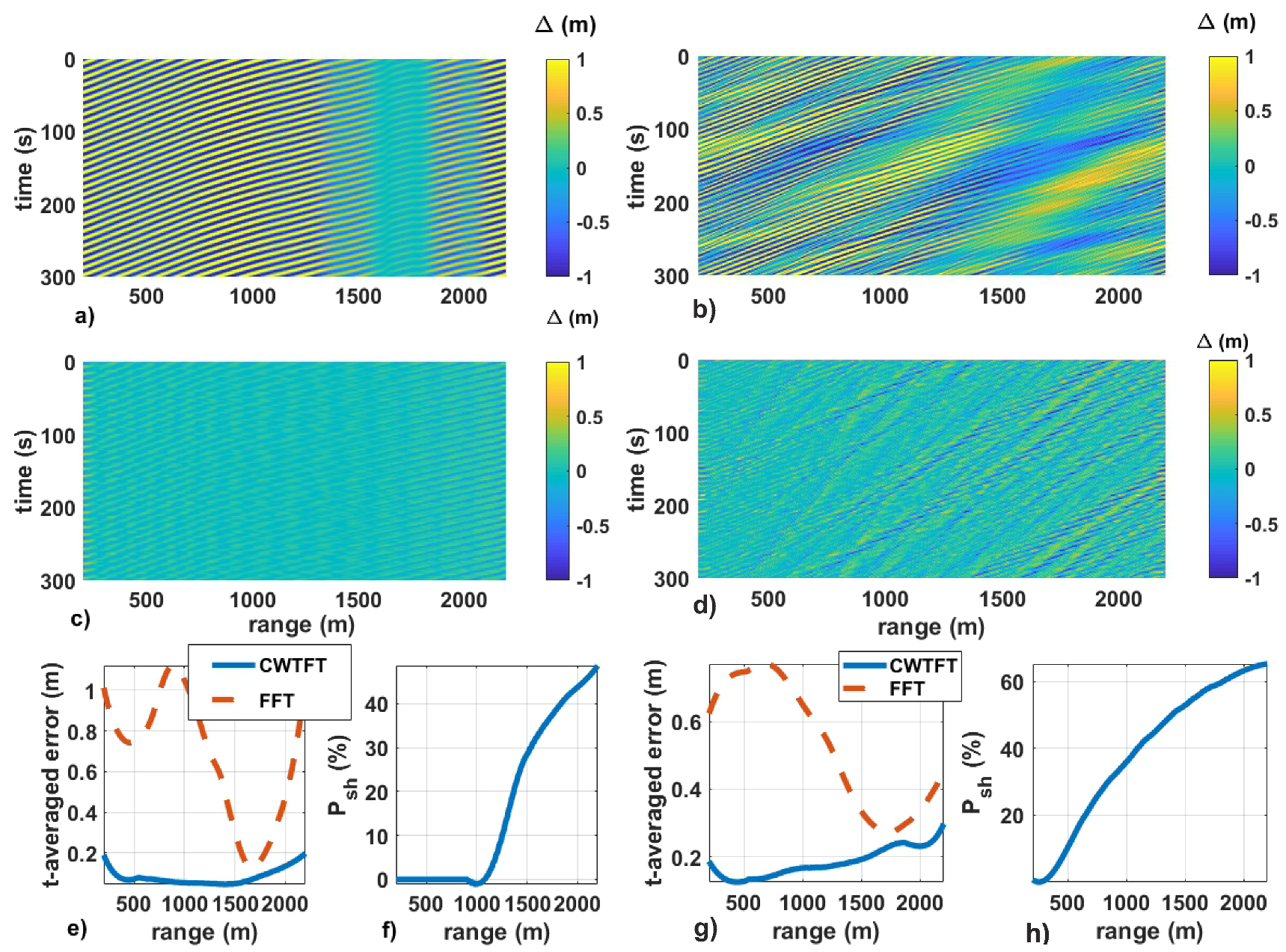
5. Simulation of the Sea Clutter Images and Their Wavelet Analysis
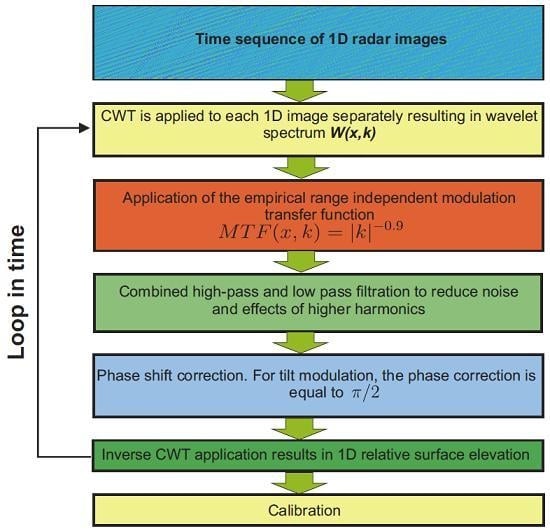
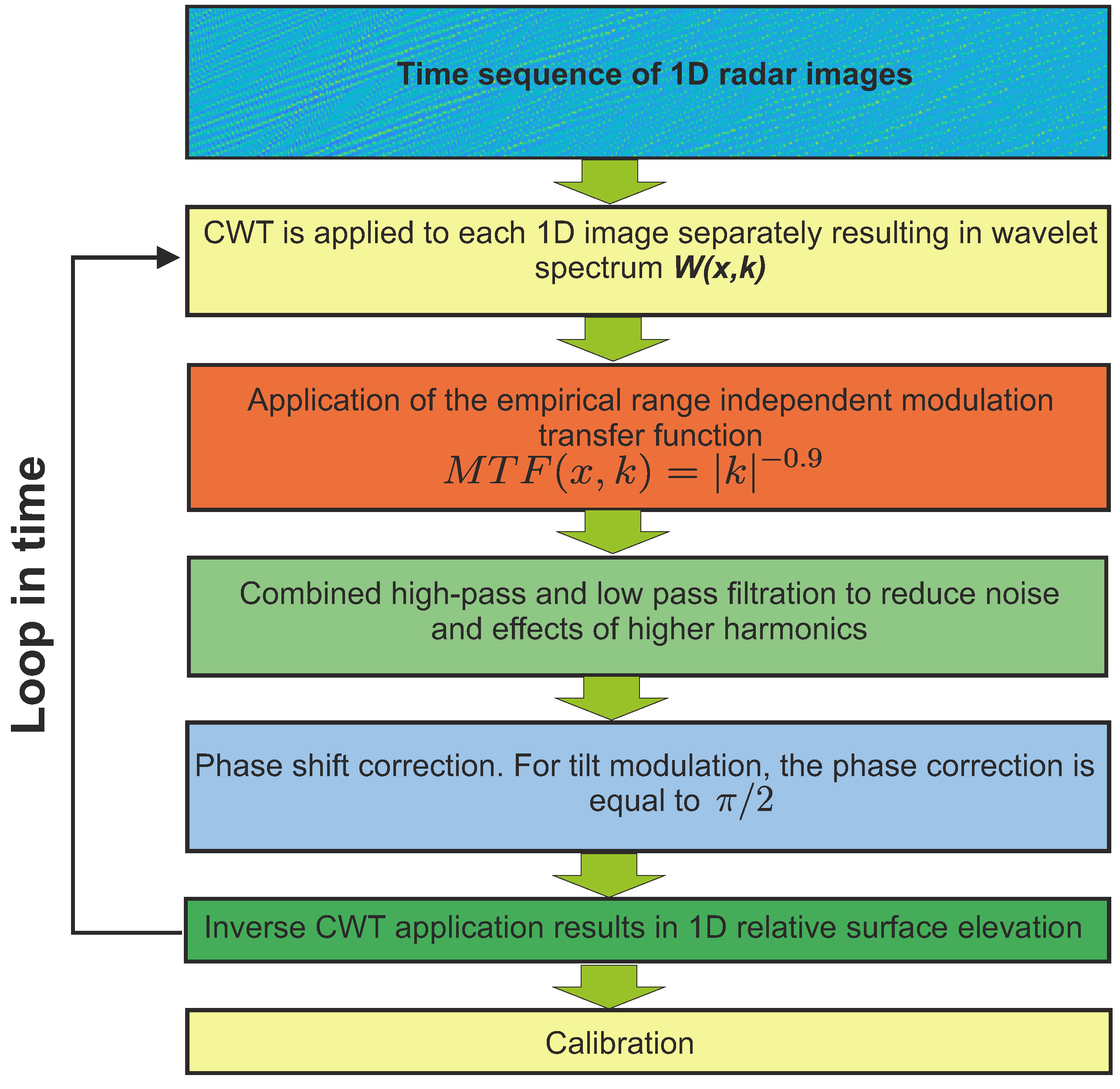
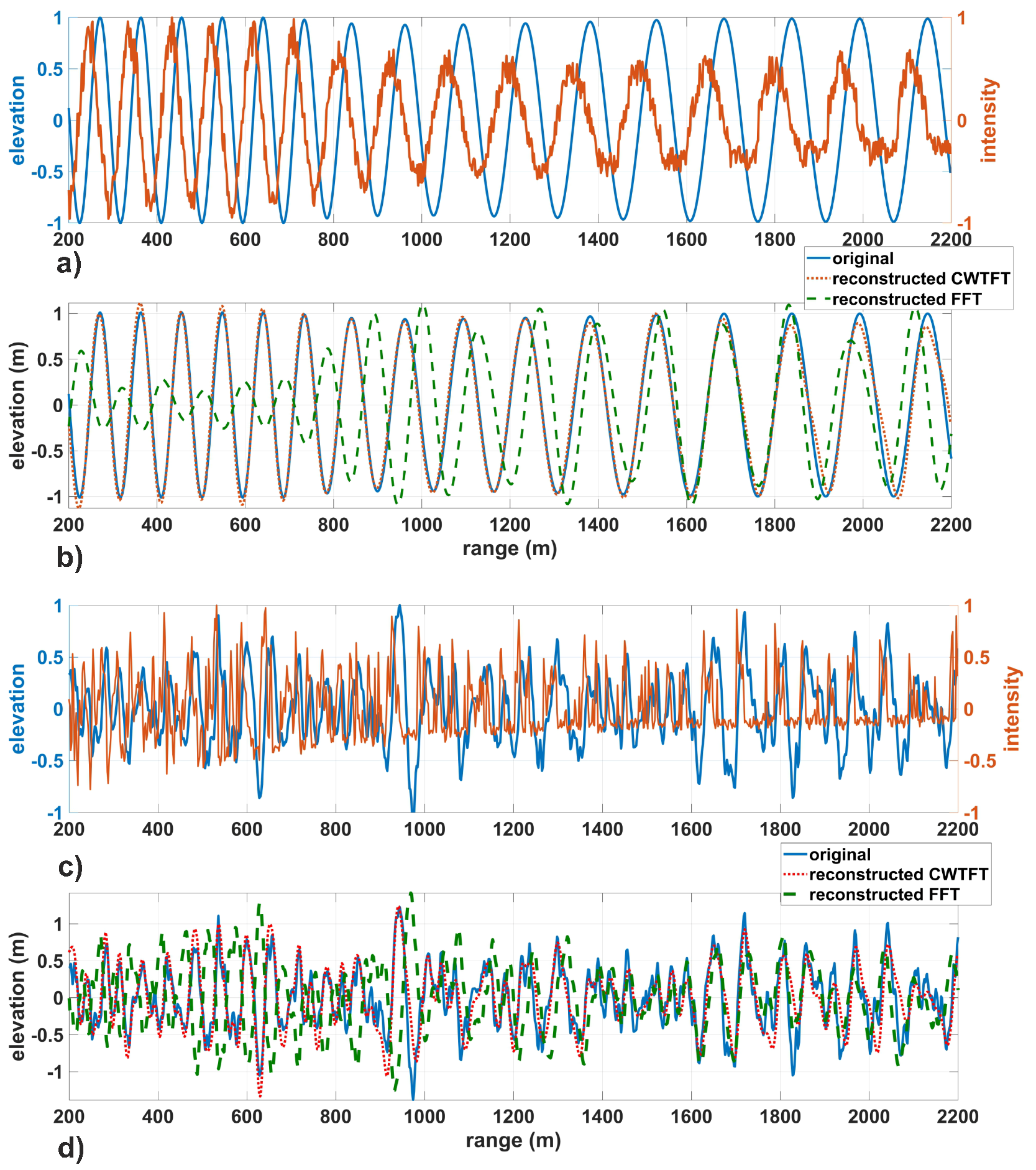
6. Inversion of the Simulated Radar Images into Surface Elevations (Wavelet Analysis)
- Estimation of the CWTFT coefficients of a radar image at a fixed time instance and calculation of the correspondent pseudo-wave numbers.
- Application of the empirical Modulation-Transfer Function (MTF) in a wave number-coordinate domain . The empirical power is set to 0.9 for all applications. The wavelet-based technique allows the to vary with the range; nevertheless, a range independent MTF is employed as a first approximation. The details of the MTF’s choice are discussed in Appendix C.
- Use of combined high-pass (HP) and LP filters F to reduce noise and influence of higher harmonics. The corresponding filter in the wave number-coordinate domain is defined as , where X denotes a characteristic function of a set of points, is constant in space (0.001 used in this paper), is the line of maximum energy in a wavelet spectral domain as a function of space, and l is an empirical constant. Here, the value is used for both monochromatic wave and spectrum cases. The filtered wavelet spectrum is further defined as .
- Phase shift correction: As geometrical mechanisms are used, a phase shift equal to is applied to every complex spectral wavelet component.
- Calculation of the inverse CWTFT and calibration: Denoting the ICWTFT as , the calibrated surface elevation is defined as , where is the time averaged standard deviation of a 2D array denoted as A in the range defined in Equation (16).
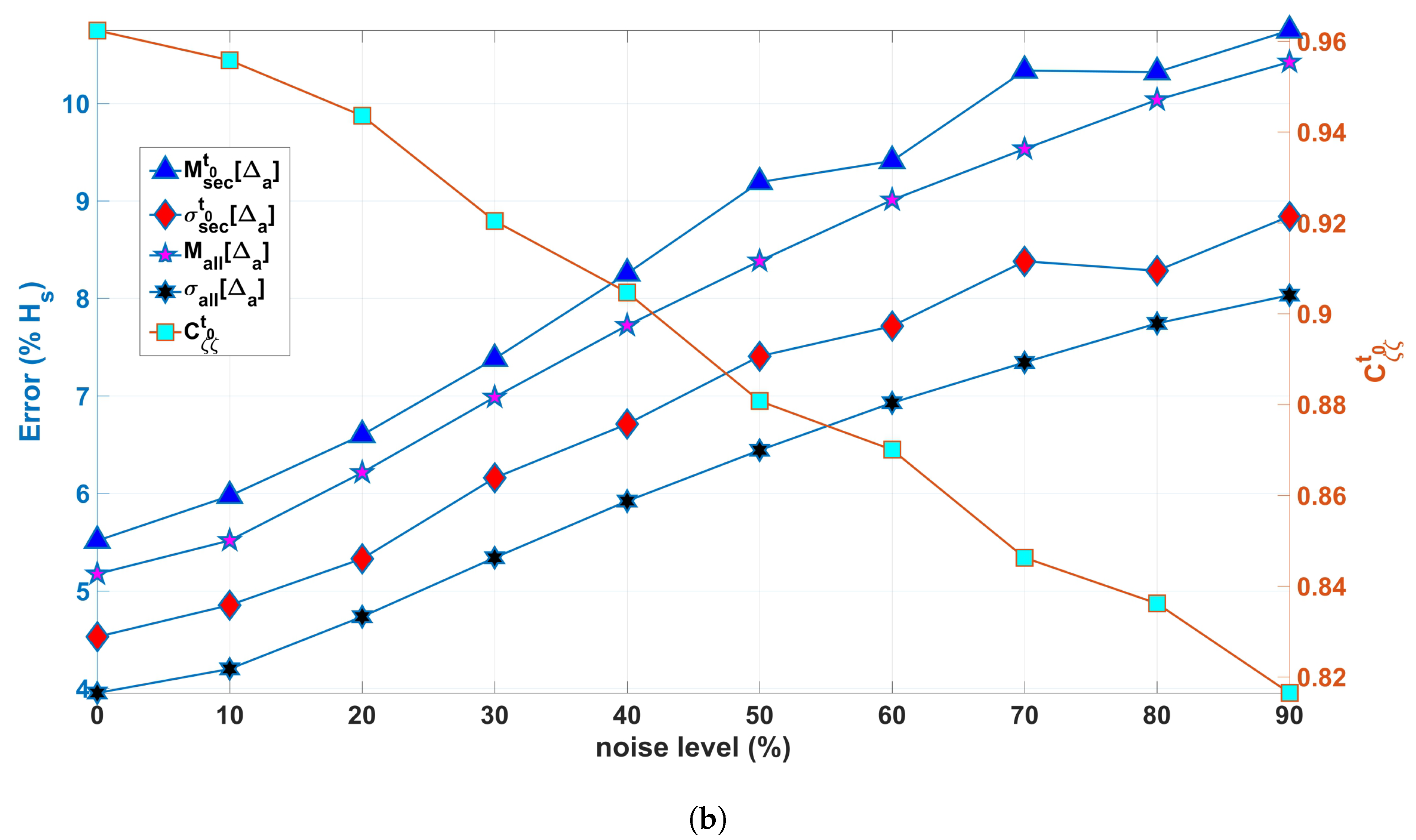
7. Analysis of the Results
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CWT | Continuous Wavelet Transform |
| CWTFT | Continuous Wavelet Transform with Fourier Transform |
| ICWTFT | Inverse Continuous Wavelet Transform with Fourier Transform |
| FFT | Fast Fourier Transform |
| MTF | Modulation Transfer Function |
| JONSWAP | JOint North Sea WAve Project |
| SAR | Synthetic Aperture Radar |
| LP | Low-Pass (filter) |
| HP | High-Pass (filter) |
Appendix A. The Shadowing Probability, Accounting for Linear Shoaling Conditions
Appendix B. Utilization of the Conventional Method for the Radar Image Sequences Inversion in 1D Case
- Estimation of the complex 2D Fourier spectrum of a 1D radar image sequence. To mitigate the aliasing effect, the area of the negative frequencies is cut and pasted above the Nyquist frequency.
- Application of the dispersion relation shell filter in order to separate the signals of wave modulations from the higher harmonics. The resulting filtered signal contains the following set of harmonics , where is the arithmetic average between the minimal and the maximal depth over the image area, U is the uniform current, and is the width of the filter.
- Application of the empirical Modulation-Transfer Function to the spectral amplitudes [9].
- HP filtration, which passes all the components higher than a certain limiting wave number and corresponding frequency . According to [34] it is plausible to take rad/s. The corresponding is calculated using the dispersion relation accounting for the minimal water depth ().
- Phase shift correction: As geometrical mechanisms are used, a phase shift equal to should be applied to every complex spectral component. The constant phase shift is applicable only in case of homogenous and periodic signals. In cases of linear shoaling, when the phase of the original signal is defined as in Equation (1), this step does not give the desired result and hence becomes optional.
- Calculation of the inverse FFT, taking the real part of the resulting array and calibration. The calibration is conducted using the same approach as described in the new method.
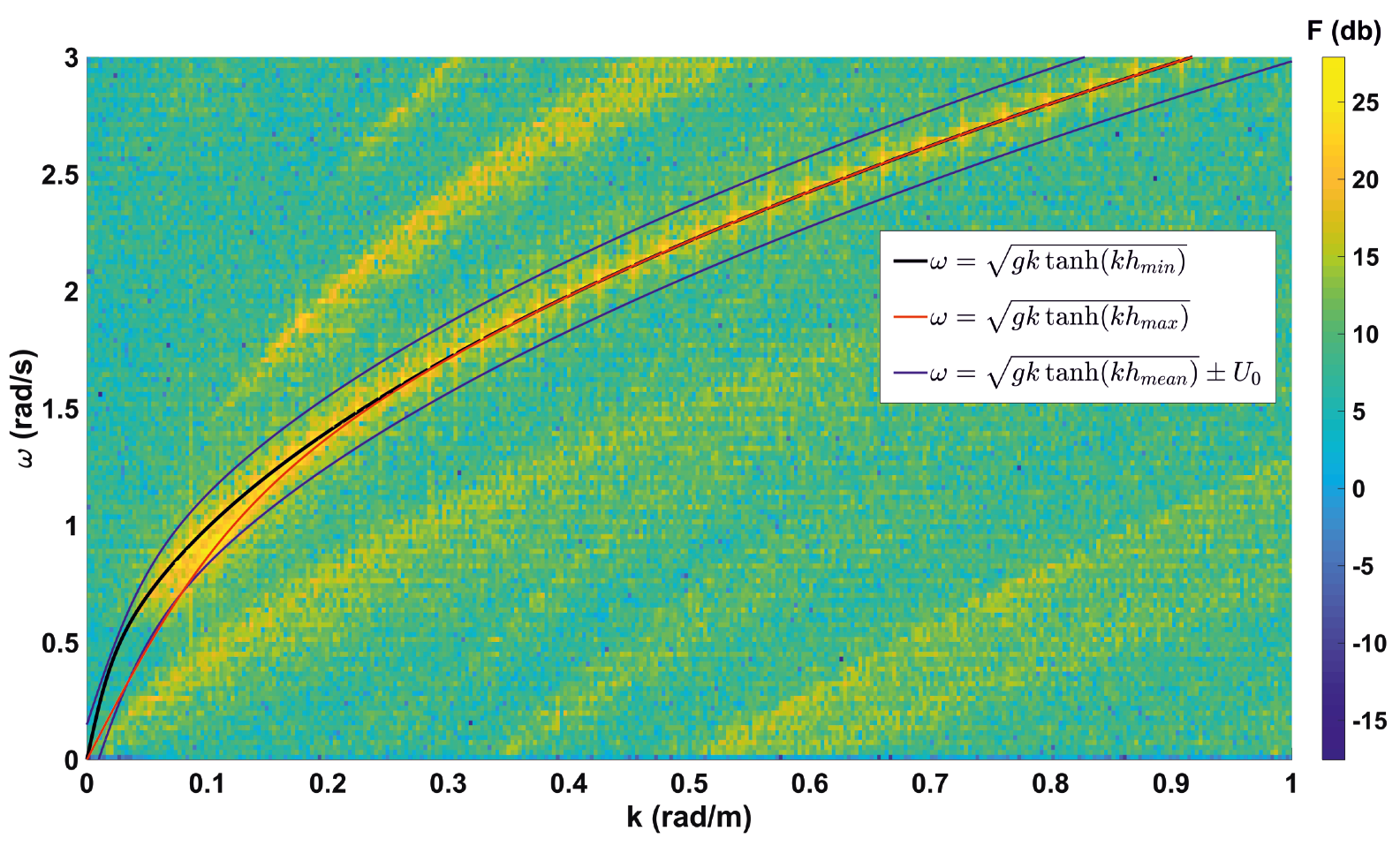
Appendix C. Modulation-Transfer Function Discussion
Appendix D. Bathymetry Profiles
References
- Borge, J.C.N.; Reichert, K.; Dittmer, J. Use of nautical radar as a wave monitoring instrument. Coast. Eng. 1999, 37, 331–342. [Google Scholar] [CrossRef]
- Nieto-Borge, J.; Hessner, K.; Jarabo-Amores, P.; de La Mata-Moya, D. Signal-to-noise ratio analysis to estimate ocean wave heights from X-band marine radar image time series. IET Radar Sonar Navig. 2008, 2, 35–41. [Google Scholar] [CrossRef]
- Senet, C.M.; Seemann, J.; Flampouris, S.; Ziemer, F. Determination of bathymetric and current maps by the method DiSC based on the analysis of nautical X-band radar image sequences of the sea surface (November 2007). IEEE Trans. Geosci. Remote Sens. 2008, 46, 2267–2279. [Google Scholar] [CrossRef]
- Serafino, F.; Lugni, C.; Nieto Borge, J.C.; Zamparelli, V.; Soldovieri, F. Bathymetry determination via X-band radar data: A new strategy and numerical results. Sensors 2010, 10, 6522–6534. [Google Scholar] [CrossRef] [PubMed]
- Lebedev, I.; Tomczak, M. Rainfall measurements with navigational radar. J. Geophys. Res. Ocean. 1999, 104, 13697–13708. [Google Scholar] [CrossRef]
- Dankert, H.; Horstmann, J.; Rosenthal, W. Ocean wind fields retrieved from radar-image sequences. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Kanevsky, M.B. Radar Imaging of the Ocean Waves; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Valenzuela, G.R. Theories for the interaction of electromagnetic and oceanic waves—A review. Bound.-Layer Meteorol. 1978, 13, 61–85. [Google Scholar] [CrossRef]
- Borge, J.C.N.; Rodríguez, G.R.; Hessner, K.; González, P.I. Inversion of marine radar images for surface wave analysis. J. Atmos. Ocean. Technol. 2004, 21, 1291–1300. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Borge, J.N.; Carro-Calvo, L.; Cuadra, L.; Hessner, K.; Alexandre, E. Significant wave height estimation using SVR algorithms and shadowing information from simulated and real measured X-band radar images of the sea surface. Ocean Eng. 2015, 101, 244–253. [Google Scholar] [CrossRef]
- Alpers, W.; Hasselmann, K. The two-frequency microwave technique for measuring ocean-wave spectra from an airplane or satellite. Bound.-Layer Meteorol. 1978, 13, 215–230. [Google Scholar] [CrossRef]
- Chernyshov, P.; Ivonin, D.; Khalikov, Z.; Myslenkov, S. Accuracy analysis of individual waves retrieval from X-band radar brightness images by implementation of stochastic modeling of rough sea surface. Sovremmennie Probl. Distansionnogo Zondirovaniya Zemli Iz Kosmosa 2016, 13, 68–78. (In Russian) [Google Scholar] [CrossRef]
- Wei, Y.; Zhang, J.K.; Lu, Z. A Novel Successive Cancellation Method to Retrieve Sea Wave Components from Spatio-Temporal Remote Sensing Image Sequences. Remote Sens. 2016, 8, 607. [Google Scholar] [CrossRef]
- Daubechies, I. The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Wu, L.C.; Chuang, L.Z.H.; Doong, D.J.; Kao, C.C. Ocean remotely sensed image analysis using two-dimensional continuous wavelet transforms. Int. J. Remote Sens. 2011, 32, 8779–8798. [Google Scholar] [CrossRef]
- An, J.; Huang, W.; Gill, E.W. A self-adaptive wavelet-based algorithm for wave measurement using nautical radar. IEEE Trans. Geosci. Remote Sens. 2015, 53, 567–577. [Google Scholar] [CrossRef]
- Chuang, L.Z.H.; Wu, L.C.; Doong, D.J.; Kao, C.C. Two-dimensional continuous wavelet transform of simulated spatial images of waves on a slowly varying topography. Ocean Eng. 2008, 35, 1039–1051. [Google Scholar] [CrossRef]
- Doong, D.J.; Wu, L.C.; Kao, C.C.; Chuang, H.; Zsu, L. Wavelet spectrum extracted from coastal marine radar images. In Proceedings of the The Thirteenth International Offshore and Polar Engineering Conference, Honolulu, HI, USA, 25–30 May 2003. [Google Scholar]
- Ludeno, G.; Brandini, C.; Lugni, C.; Arturi, D.; Natale, A.; Soldovieri, F.; Gozzini, B.; Serafino, F. Remocean system for the detection of the reflected waves from the costa concordia ship wreck. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3011–3018. [Google Scholar] [CrossRef]
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; World Scientific Publishing Co Inc.: Singapore, 1991; Volume 2. [Google Scholar]
- Agnon, Y.; Sheremet, A.; Gonsalves, J.; Stiassnie, M. Nonlinear evolution of a unidirectional shoaling wave field. Coast. Eng. 1993, 20, 29–58. [Google Scholar] [CrossRef]
- Hasselmann, K.; Barnett, T.; Bouws, E.; Carlson, H.; Cartwright, D.; Enke, K.; Ewing, J.; Gienapp, H.; Hasselmann, D.; Kruseman, P.; et al. Measurements of Wind-Wave Growth and Swell Decay During the Joint North Sea Wave Project (JONSWAP); Technical Report; Deutches Hydrographisches Institut: Hamburg, Germany, 1973. [Google Scholar]
- Daubechies, I. Ten Lectures on Wavelets; SIAM: Philadelphia, PA, USA, 1992. [Google Scholar]
- Alpers, W.R.; Ross, D.B.; Rufenach, C.L. On the detectability of ocean surface waves by real and synthetic aperture radar. J. Geophys. Res. Ocean. 1981, 86, 6481–6498. [Google Scholar] [CrossRef]
- Skolnik, M.I. Radar Handbook; McGraw-Hill Book Co.: New York, NY, USA, 1970. [Google Scholar]
- Plant, W.J.; Farquharson, G. Wave shadowing and modulation of microwave backscatter from the ocean. J. Geophys. Res. Ocean. 2012, 117, 1–14. [Google Scholar] [CrossRef]
- Gangeskar, R. An algorithm for estimation of wave height from shadowing in X-band radar sea surface images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3373–3381. [Google Scholar] [CrossRef]
- Liu, X.; Huang, W.; Gill, E.W. Comparison of Wave Height Measurement Algorithms for Ship-Borne X-Band Nautical Radar. Canadian J. Remote Sens. 2016, 42, 343–353. [Google Scholar] [CrossRef]
- Forouzanfar, M.; Moghaddam, H.A.; Dehghani, M. Speckle reduction in medical ultrasound images using a new multiscale bivariate Bayesian MMSE-based method. In Proceedings of the IEEE 15th Signal Processing and Communications Applications, Eskisehir, Turkey, 11–13 June 2007; pp. 1–4. [Google Scholar]
- Smith, B. Geometrical shadowing of a random rough surface. IEEE Trans. Antennas Propag. 1967, 15, 668–671. [Google Scholar] [CrossRef]
- Bass, F.; Fuks, I. Wave Scattering from Statistically Rough Surfaces: International Series in Natural Philosophy; Elsevier: Amsterdam, The Netherlands, 2013; Volume 93. [Google Scholar]
- Naaijen, P.; Blondel-Couprie, E. Reconstruction and Prediction of Short-Crested Seas Based on the Application of a 3D-FFT on Synthetic Waves. Part 1: Reconstruction. In Proceedings of the ASME 2012 31st International Conference on Ocean, Offshore and Arctic Engineering, Rio de Janeiro, Brazil, 1–6 July 2012; pp. 43–53. [Google Scholar]
- Blondel-Couprie, E.; Naaijen, P. Reconstruction and Prediction of Short-Crested Seas Based on the Application of a 3D-FFT on Synthetic Waves. Part 2: Prediction. In Proceedings of the ASME 2012 31st International Conference on Ocean, Offshore and Arctic Engineering, Rio de Janeiro, Brazil, 1–6 July 2012; pp. 55–70. [Google Scholar]
- Nieto Borge, J.C.; Guedes Soares, C. Analysis of directional wave fields using X-band navigation radar. Coast. Eng. 2000, 40, 375–391. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, B.; He, Y.; Qiu, Z.; Perrie, W. A new modulation transfer function for ocean wave spectra retrieval from X-band marine radar imagery. Chin. J. Oceanol. Limnol. 2015, 33, 1132–1141. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| fetch (F) | 500 (km) |
| wind speed (U) | 3.2, 9.2, 15.7 (m/s) |
| peak period () | 7, 10, 12 s |
| initial significant wave height () | 1.76, 4.53, 7.33 (m) |
| time step () | 2 (s) |
| spatial step () | 2 m |
| spectral resolution () | 0.031 (rad/s) |
| number of harmonics (N) | 100 |
| number of time samples () | 151 |
| number of range samples () | 1001 |
| Case | (m) | Mean | (m) | (m) | (m) | (m) | |
|---|---|---|---|---|---|---|---|
| monochromatic wave | 50 | 16 | 0.067 | 0.051 | 0.071 | 0.063 | 0.991 |
| spectrum | 50 | 39 | 0.164 | 0.147 | 0.169 | 0.142 | 0.872 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chernyshov, P.; Vrecica, T.; Toledo, Y. Inversion of Nearshore X-Band Radar Images to Sea Surface Elevation Maps. Remote Sens. 2018, 10, 1919. https://doi.org/10.3390/rs10121919
Chernyshov P, Vrecica T, Toledo Y. Inversion of Nearshore X-Band Radar Images to Sea Surface Elevation Maps. Remote Sensing. 2018; 10(12):1919. https://doi.org/10.3390/rs10121919
Chicago/Turabian StyleChernyshov, Pavel, Teodor Vrecica, and Yaron Toledo. 2018. "Inversion of Nearshore X-Band Radar Images to Sea Surface Elevation Maps" Remote Sensing 10, no. 12: 1919. https://doi.org/10.3390/rs10121919
APA StyleChernyshov, P., Vrecica, T., & Toledo, Y. (2018). Inversion of Nearshore X-Band Radar Images to Sea Surface Elevation Maps. Remote Sensing, 10(12), 1919. https://doi.org/10.3390/rs10121919