Decoupling Canopy Structure and Leaf Biochemistry: Testing the Utility of Directional Area Scattering Factor (DASF)
Abstract
1. Introduction
2. Theory and Model Description
2.1. Spectral Invariants Theory
2.2. Retrieval of DASF and Total Canopy Scattering (W)
3. Model Simulations
3.1. Baseline Experiment
3.2. Departures from Baseline Experiment
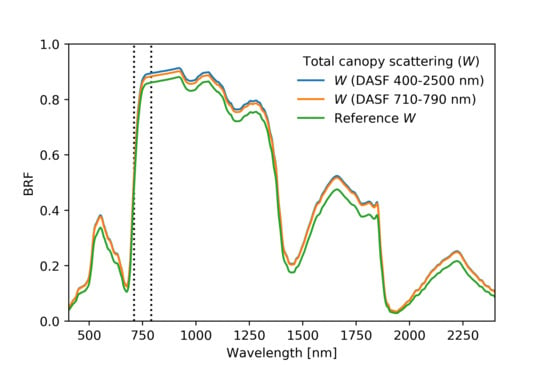
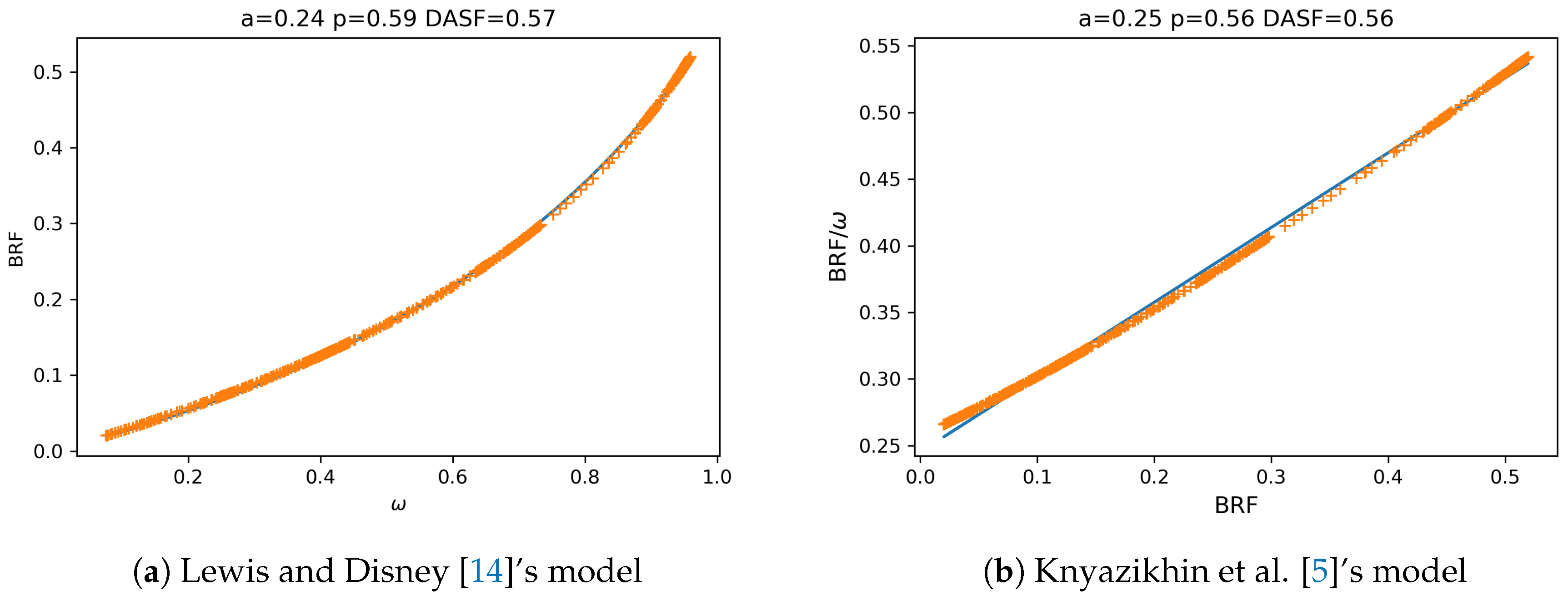
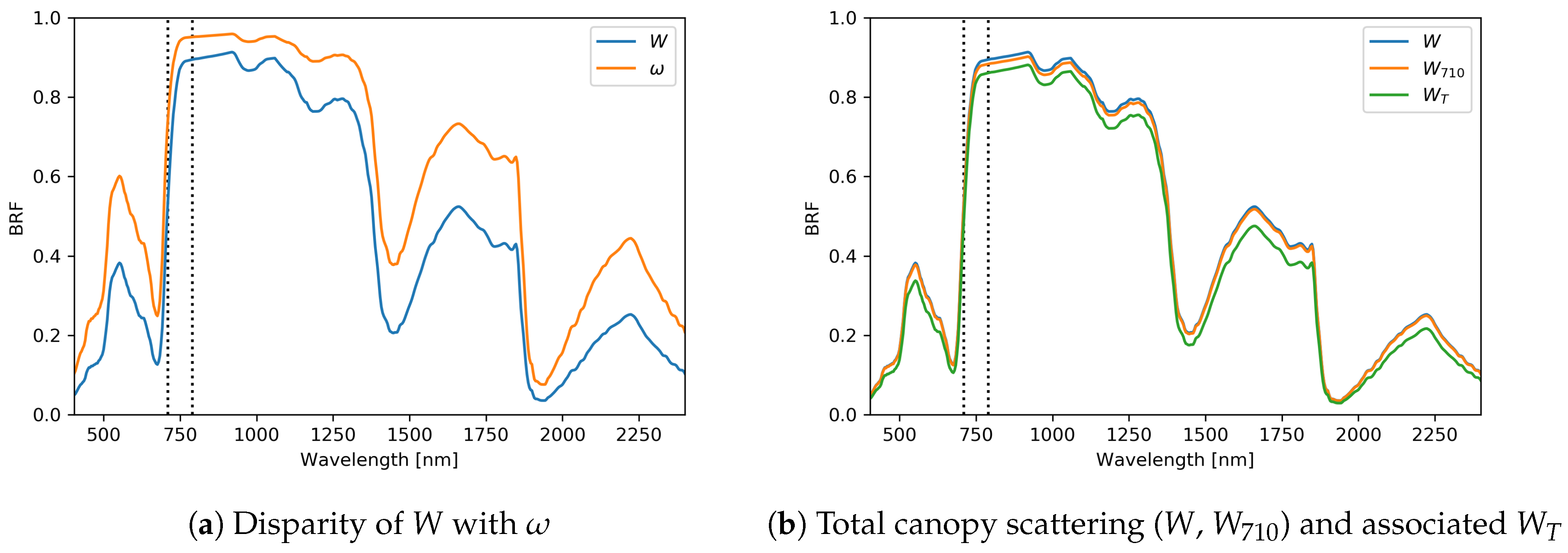
3.3. Deriving DASF and W
- Calculate the leaf single scattering albedo ()
- Given a BRF simulated by librat:
- Determine parameters a and p
- Calculate DASF using the ratio
- Extract total canopy scattering (W) by BRF/DASF
4. Results and Discussion
4.1. Baseline Experiment (Homogeneous): Known Single Scattering Albedo
4.2. Baseline Experiment (Heterogeneous): Known Single Scattering Albedo
4.3. Baseline Experiment: Unknown Single Scattering Albedo
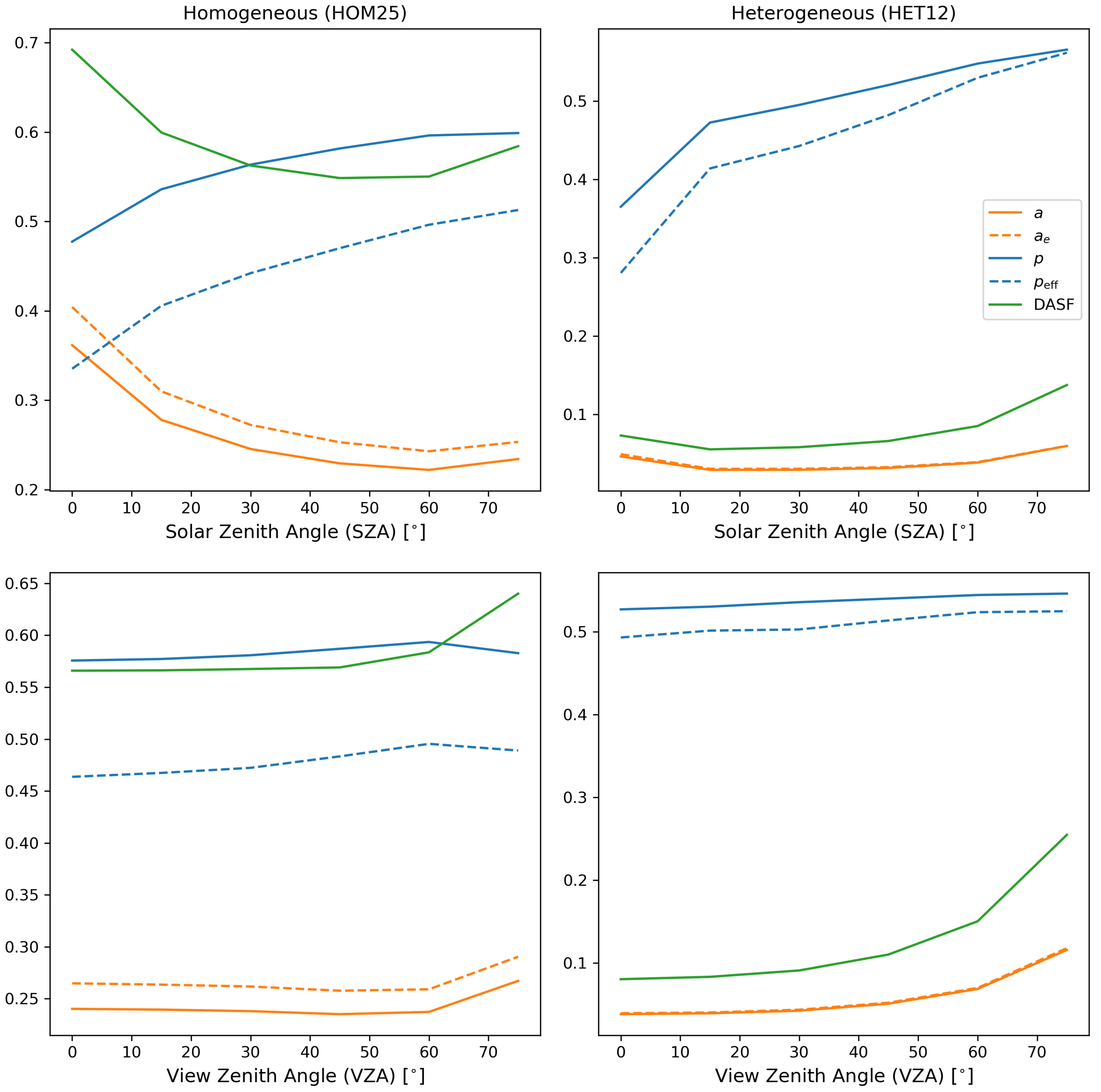
4.4. Departures from Baseline Experiment: VZA and SZA
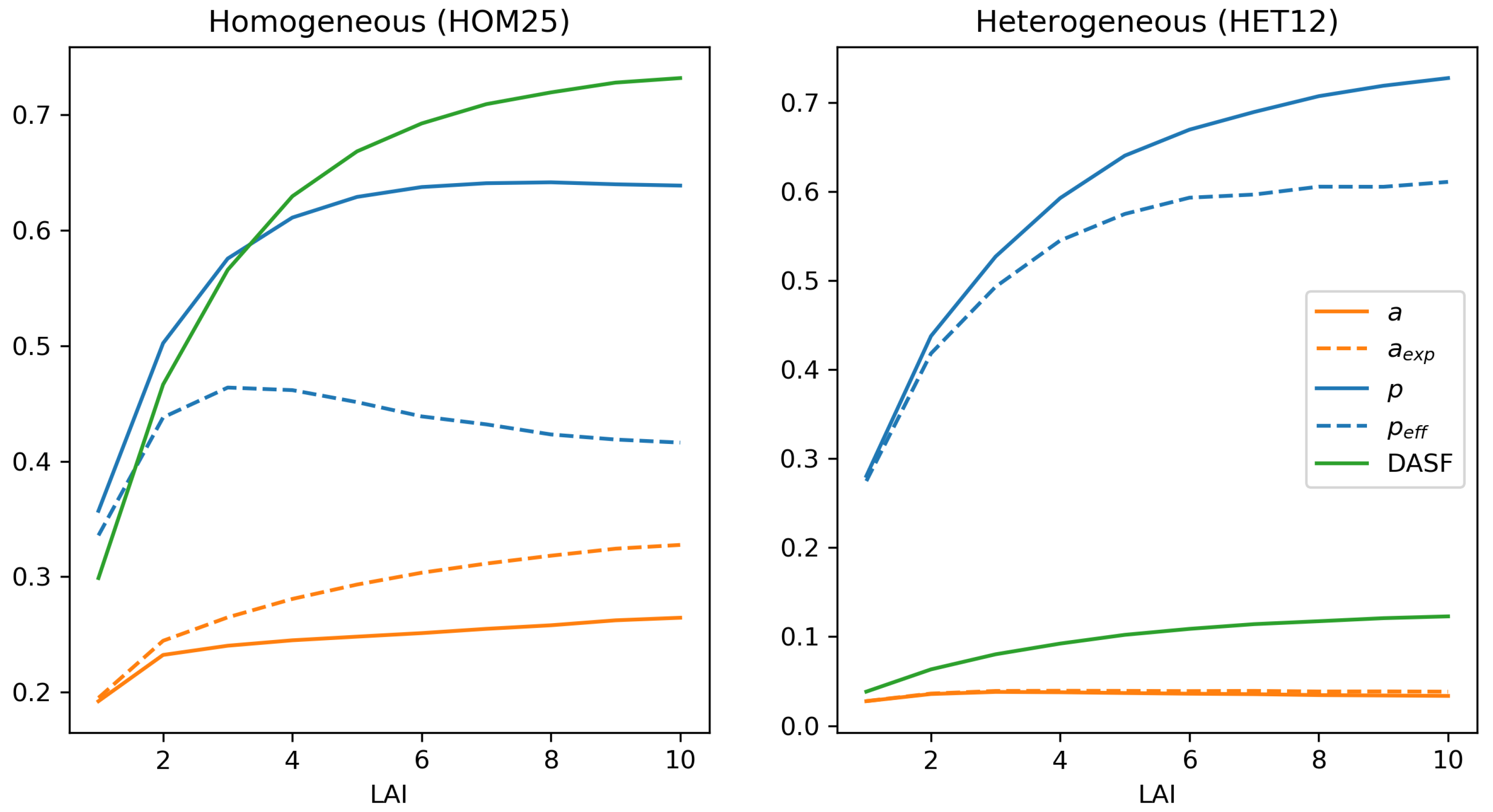
4.5. Departures from Baseline Experiment: LAI
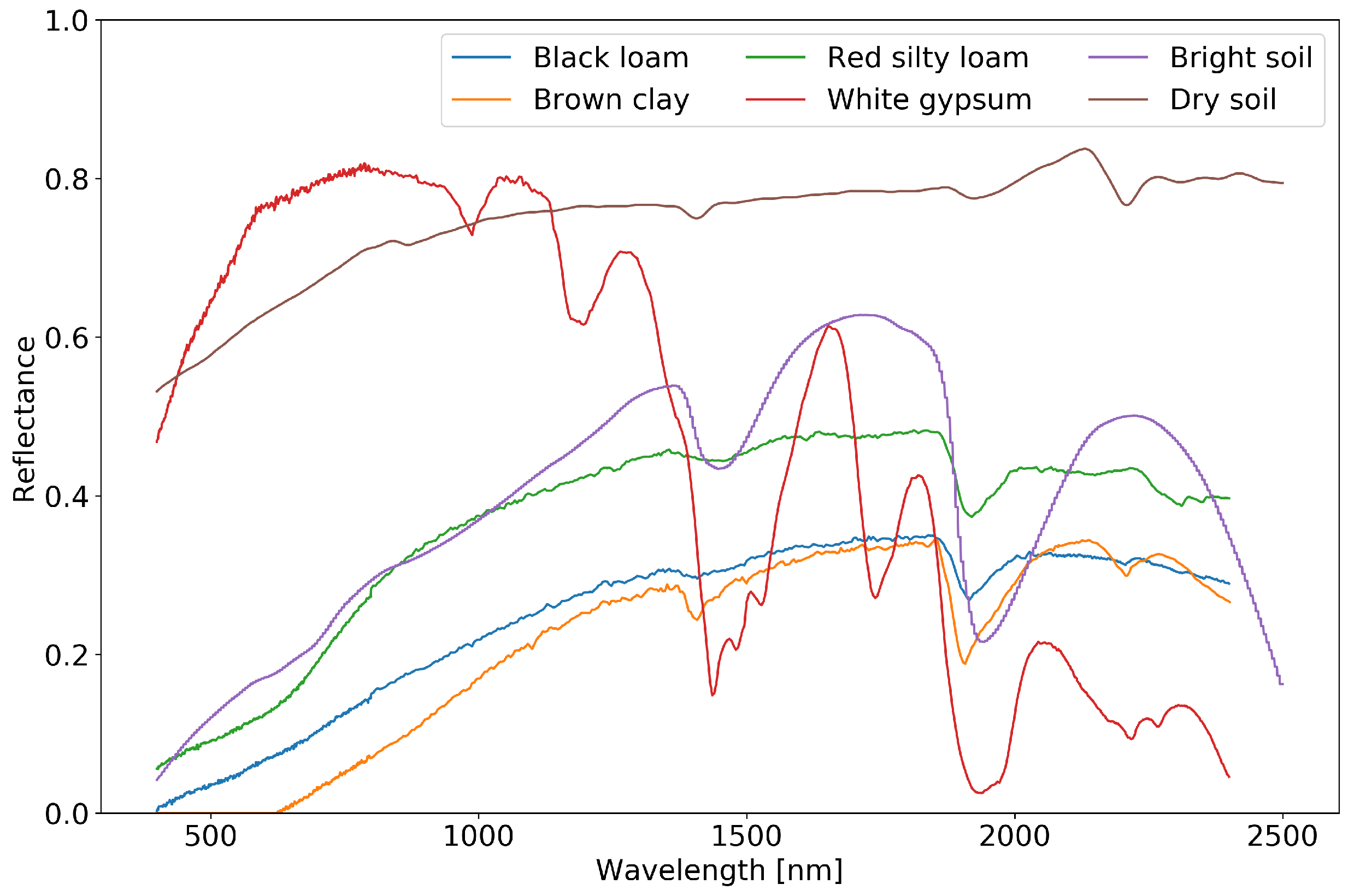
4.6. Departures from Baseline Experiment: Soil
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Ollinger, S.V.; Richardson, A.D.; Martin, M.E.; Hollinger, D.Y.; Frolking, S.E.; Reich, P.B.; Plourde, L.C.; Katul, G.G.; Munger, J.W.; Oren, R.; et al. Canopy nitrogen, carbon assimilation, and albedo in temperate and boreal forests: Functional relations and potential climate feedbacks. Proc. Natl. Acad. Sci. USA 2008, 105, 19336–19341. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Buermann, W.; Stenberg, P.; Smolander, H.; Häme, T.; Tian, Y.; Hu, J.; Knyazikhin, Y.; Myneni, R.B. A new parameterization of canopy spectral response to incident solar radiation: Case study with hyperspectral data from pine dominant forest. Remote Sens. Environ. 2003, 85, 304–315. [Google Scholar] [CrossRef]
- Smolander, S.; Stenberg, P. Simple parameterizations of the radiation budget of uniform broadleaved and coniferous canopies. Remote Sens. Environ. 2005, 94, 355–363. [Google Scholar] [CrossRef]
- Ustin, S.L. Remote sensing of canopy chemistry. Proc. Natl. Acad. Sci. USA 2013, 110, 804–805. [Google Scholar] [CrossRef] [PubMed]
- Knyazikhin, Y.; Schull, M.A.; Stenberg, P.; Mõttus, M.; Rautiainen, M.; Yang, Y.; Marshak, A.; Latorre Carmona, P.; Kaufmann, R.K.; Lewis, P.; et al. Hyperspectral remote sensing of foliar nitrogen content. Proc. Natl. Acad. Sci. USA 2013, 110, E185–E192. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Zeng, Y.; Kuusk, A.; Wu, B.; Dong, L.; Mao, K.; Chen, J. Inverting a forest canopy reflectance model to retrieve the overstorey and understorey leaf area index for forest stands. Int. J. Remote Sens. 2011, 32, 7591–7611. [Google Scholar] [CrossRef]
- Dawson, T.; Curran, P.; Plummer, S. LIBERTY—Modeling the Effects of Leaf Biochemical Concentration on Reflectance Spectra. Remote Sens. Environ. 1998, 65, 50–60. [Google Scholar] [CrossRef]
- Ganapol, B.D.; Johnson, L.F.; Hammer, P.D.; Hlavka, C.A.; Peterson, D.L. LEAFMOD: A New Within-Leaf Radiative Transfer Model. Remote Sens. Environ. 1998, 63, 182–193. [Google Scholar] [CrossRef]
- Wang, Z.; Skidmore, A.K.; Wang, T.; Darvishzadeh, R.; Heiden, U.; Heurich, M.; Latifi, H.; Hearne, J. Canopy foliar nitrogen retrieved from airborne hyperspectral imagery by correcting for canopy structure effects. Int. J. Appl. Earth Obs. Geoinf. 2017, 54, 84–94. [Google Scholar] [CrossRef]
- Yang, B.; Knyazikhin, Y.; Mõttus, M.; Rautiainen, M.; Stenberg, P.; Yan, L.; Chen, C.; Yan, K.; Choi, S.; Park, T.; et al. Estimation of leaf area index and its sunlit portion from DSCOVR EPIC data: Theoretical basis. Remote Sens. Environ. 2017, 198, 69–84. [Google Scholar] [CrossRef] [PubMed]
- Stenberg, P.; Manninen, T. The effect of clumping on canopy scattering and its directional properties: A model simulation using spectral invariants. Int. J. Remote Sens. 2015, 36, 5178–5191. [Google Scholar] [CrossRef]
- Huang, D.; Knyazikhin, Y.; Dickinson, R.E.; Rautiainen, M.; Stenberg, P.; Disney, M.; Lewis, P.; Cescatti, A.; Tian, Y.; Verhoef, W.; et al. Canopy spectral invariants for remote sensing and model applications. Remote Sens. Environ. 2007, 106, 106–122. [Google Scholar] [CrossRef]
- Marshak, A.; Knyazikhin, Y.; Chiu, J.C.; Wiscombe, W.J. Spectrally Invariant Approximation within Atmospheric Radiative Transfer. J. Atmos. Sci. 2011, 68, 3094–3111. [Google Scholar] [CrossRef]
- Lewis, P.; Disney, M. Spectral invariants and scattering across multiple scales from within-leaf to canopy. Remote Sens. Environ. 2007, 109, 196–206. [Google Scholar] [CrossRef]
- Knyazikhin, Y.; Schull, M.A.; Xu, L.; Myneni, R.B.; Samanta, A. Canopy spectral invariants. Part 1: A new concept in remote sensing of vegetation. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 727–735. [Google Scholar] [CrossRef]
- Stenberg, P. Simple analytical formula for calculating average photon recollision probability in vegetation canopies. Remote Sens. Environ. 2007, 109, 221–224. [Google Scholar] [CrossRef]
- Schull, M.; Knyazikhin, Y.; Xu, L.; Samanta, A.; Carmona, P.; Lepine, L.; Jenkins, J.; Ganguly, S.; Myneni, R. Canopy spectral invariants, Part 2: Application to classification of forest types from hyperspectral data. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 736–750. [Google Scholar] [CrossRef]
- Lewis, P.; Disney, M.; Knyazikhin, Y.; Quaife, T.; Schull, M. Modelling canopy reflectance with spectral invariants. In Proceedings of the 10th International Symposium on Physical Measurements and Signatures in Remote Sensing, Davos, Switzerland, 12–14 March 2007. [Google Scholar]
- Lewis, P. Three-dimensional plant modelling for remote sensing simulation studies using the Botanical Plant Modelling System. Agronomie 1999, 19, 185–210. [Google Scholar] [CrossRef]
- Widlowski, J.-L.; Pinty, B.; Lopatka, M.; Atzberger, C.; Buzica, D.; Chelle, M.; Disney, M.; Gastellu-Etchegorry, J.-P.; Gerboles, M.; Gobron, N.; et al. The fourth radiation transfer model intercomparison (RAMI-IV): Proficiency testing of canopy reflectance models with ISO-13528. J. Geophys. Res. Atmos. 2013, 118, 6869–6890. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Ustin, S.; Verdebout, J.; Schmuck, G.; Andreoli, G.; Hosgood, B. Estimating leaf biochemistry using the PROSPECT leaf optical properties model. Remote Sens. Environ. 1996, 56, 194–202. [Google Scholar] [CrossRef]
- Hosgood, B.; Jacquemoud, S.; Andreoli, G.; Verdebout, J.; Pedrini, G.; Schmuck, G. Leaf Optical Properties Experiment 93 (LOPEX93); Report EUR—16095-EN; Joint Research Centre, Institute for Remote Sensing Applications: Ispra, Italy; European Commission: Luxembourg, 1995. [Google Scholar]
- Price, J. On the information content of soil reflectance spectra. Remote Sens. Environ. 1990, 33, 113–121. [Google Scholar] [CrossRef]
- Baldridge, A.; Hook, S.; Grove, C.; Rivera, G. The ASTER spectral library version 2.0. Remote Sens. Environ. 2009, 113, 711–715. [Google Scholar] [CrossRef]
- Mõttus, S.; Stenberg, P.; Rautiainen, M. Photon recollision probability in heterogeneous forest canopies: Compatibility with a hybrid GO model. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Mõttus, M.; Stenberg, P. A simple parameterization of canopy reflectance using photon recollision probability. Remote Sens. Environ. 2008, 112, 1545–1551. [Google Scholar] [CrossRef]
- Kobayashi, H.; Ryu, Y.; Baldocchi, D.D.; Welles, J.M.; Norman, J.M. On the correct estimation of gap fraction: How to remove scattered radiation in gap fraction measurements? Agric. For. Meteorol. 2013, 174–175, 170–183. [Google Scholar] [CrossRef]
- Panferov, O.; Knyazikhin, Y.; Myneni, R.B.; Szarzynski, J.; Engwald, S.; Schnitzler, K.G.; Gravenhorst, G. The role of canopy structure in the spectral variation of transmission and absorption of solar radiation in vegetation canopies. IEEE Trans. Geosci. Remote Sens. 2001, 39, 241–253. [Google Scholar] [CrossRef]

| Known | Unknown | |
|---|---|---|
| Chlorophyll (g/cm) | 15.0 | 30.0 |
| Dry matter content (g/cm) | 0.0053 | 0.0106 |
| Equivalent water thickness (cm) | 0.0113 | 0.0226 |
| Homogeneous (HOM25) | Heterogeneous (HET12) | |||||||
|---|---|---|---|---|---|---|---|---|
| 400–2500 nm | 710–790 nm | 400–2500 nm | 710–790 nm | |||||
| Known | Unknown | Known | Unknown | Known | Unknown | Known | Unknown | |
| 0.24 | 0.53 | 0.22 | 0.45 | 0.05 | 0.10 | 0.05 | 0.12 | |
| 0.59 | 0.04 | 0.62 | 0.21 | 0.55 | 0.07 | 0.54 | −0.08 | |
| DASF | 0.57 | 0.56 | 0.58 | 0.57 | 0.11 | 0.11 | 0.11 | 0.11 |
| SSE | 0.64 | 1.12 | 0.45 | 0.50 | 0.02 | 0.03 | 0.03 | 0.019 |
| Homogeneous | Heterogeneous | |||
|---|---|---|---|---|
| LAI | SSE () | SSE () | SSE () | SSE () |
| 1 | 0.03 | 0.02 | 0.00 | 0.00 |
| 2 | 0.25 | 0.19 | 0.01 | 0.01 |
| 3 | 0.81 | 0.59 | 0.08 | 0.06 |
| 4 | 1.74 | 1.21 | 0.15 | 0.11 |
| 5 | 2.76 | 1.85 | 0.22 | 0.15 |
| 6 | 3.86 | 2.53 | 0.39 | 0.25 |
| 7 | 4.94 | 3.25 | 0.58 | 0.35 |
| 8 | 5.73 | 3.74 | 0.82 | 0.49 |
| 9 | 6.64 | 4.41 | 1.04 | 0.62 |
| 10 | 7.15 | 4.76 | 1.28 | 0.75 |
| LAI | Black Loam | Brown Clay | Red Silty-Loam | White Gypsum | Bright | Dry |
|---|---|---|---|---|---|---|
| HOM25 | ||||||
| 1 | 5.88 | 7.68 | 5.51 | 6.42 | 7.68 | 4.39 |
| 3 | 0.43 | 0.41 | 0.23 | 1.16 | 0.41 | 0.08 |
| 5 | 1.97 | 1.86 | 1.69 | 0.57 | 1.86 | 0.99 |
| 10 | 6.29 | 6.35 | 6.24 | 5.98 | 6.35 | 6.18 |
| HET12 | ||||||
| 1 | 150.42 | 92.74 | 115.08 | 18.90 | 92.74 | 115.86 |
| 3 | 112.78 | 85.66 | 95.66 | 14.05 | 85.66 | 112.68 |
| 5 | 108.22 | 90.88 | 97.45 | 14.82 | 90.88 | 123.57 |
| 10 | 119.55 | 107.88 | 114.13 | 21.74 | 107.89 | 152.06 |
| HET22 | ||||||
| 1 | 84.55 | 114.00 | 69.02 | 12.16 | 62.36 | 77.99 |
| 3 | 198.60 | 270.18 | 139.01 | 4.78 | 33.03 | 38.32 |
| 5 | 212.22 | 283.41 | 151.55 | 3.22 | 28.17 | 33.49 |
| 10 | 251.71 | 322.54 | 188.15 | 5.04 | 33.02 | 43.46 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adams, J.; Lewis, P.; Disney, M. Decoupling Canopy Structure and Leaf Biochemistry: Testing the Utility of Directional Area Scattering Factor (DASF). Remote Sens. 2018, 10, 1911. https://doi.org/10.3390/rs10121911
Adams J, Lewis P, Disney M. Decoupling Canopy Structure and Leaf Biochemistry: Testing the Utility of Directional Area Scattering Factor (DASF). Remote Sensing. 2018; 10(12):1911. https://doi.org/10.3390/rs10121911
Chicago/Turabian StyleAdams, Jennifer, Philip Lewis, and Mathias Disney. 2018. "Decoupling Canopy Structure and Leaf Biochemistry: Testing the Utility of Directional Area Scattering Factor (DASF)" Remote Sensing 10, no. 12: 1911. https://doi.org/10.3390/rs10121911
APA StyleAdams, J., Lewis, P., & Disney, M. (2018). Decoupling Canopy Structure and Leaf Biochemistry: Testing the Utility of Directional Area Scattering Factor (DASF). Remote Sensing, 10(12), 1911. https://doi.org/10.3390/rs10121911