Neural Network Based Kalman Filters for the Spatio-Temporal Interpolation of Satellite-Derived Sea Surface Temperature
Abstract
1. Introduction
2. Problem Statement and Related Work
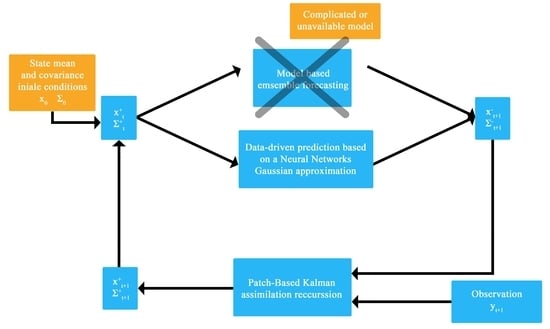
3. Proposed Interpolation Model
3.1. Neural-Network Gaussian Dynamical Prior
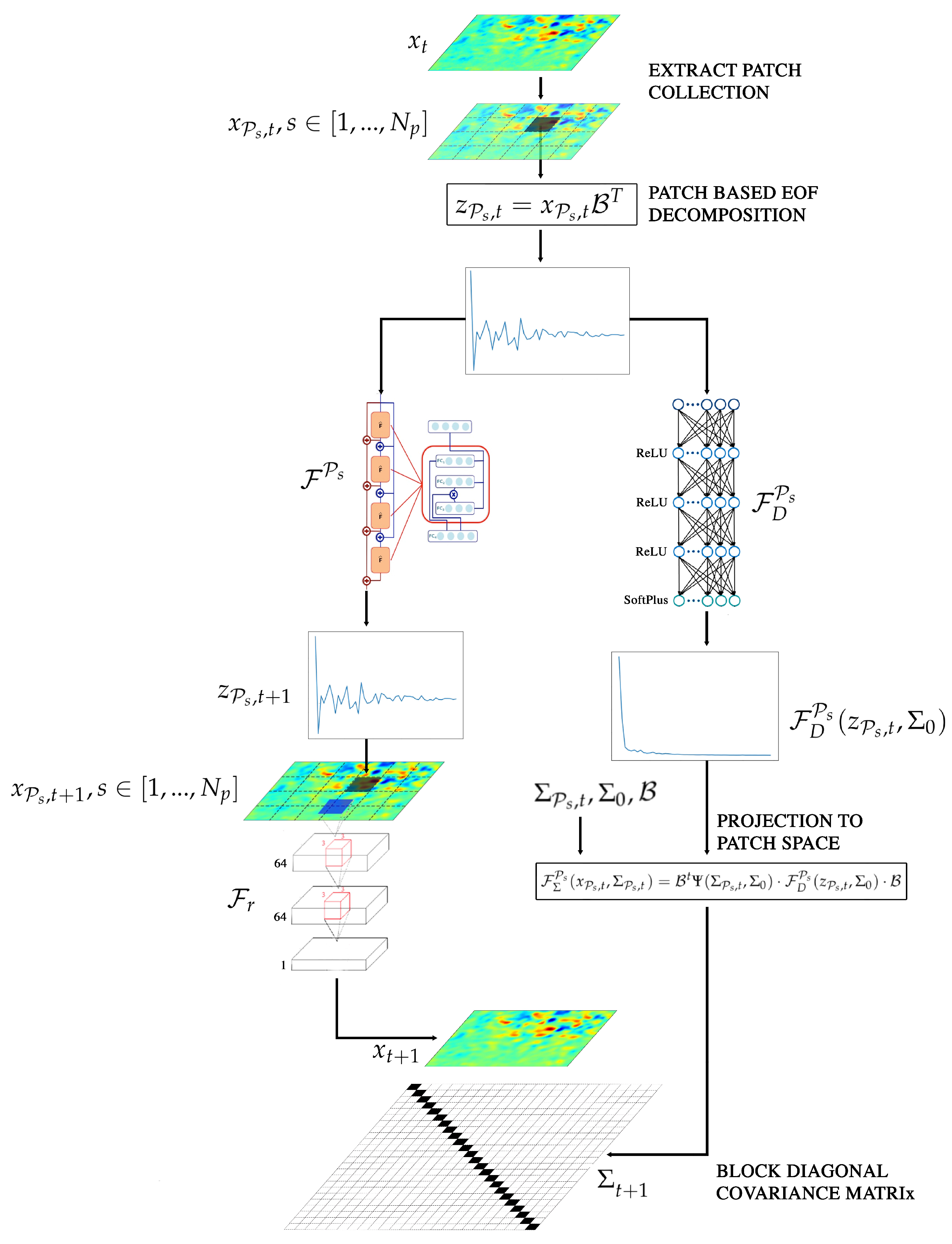
3.2. Patch-Based NN Architecture
- At a given time t, the first layer of the network, which is parameter-free in terms of training, comes to decompose an input field into a collection of patches , where P is the width and height of each patch and s the patch location in the global field. Each patch is decomposed onto an EOF basis according to:with the EOF decomposition of the patch . The EOF decomposition matrix is trained offline as preprocessing step; For each , we predict using an EOF-patch-based model . This model is implemented based on a residual architecture to mimic a numerical integration scheme (typically, an Euler or 4th-order Runge-Kutta scheme) of an approximate Ordinary Differential Equation (ODE) parametrized by the residual block of our residual network. By contrast to other neural networks models, This architecture grantee the physical interpretability of our dynamical model as stated in [27]. In order to enhance the modeling capabilities of our approximate model, The residual block is a classic Multilayer Perceptron (MLP) network with bilinear layers;
- The third layer is a reconstruction network . It combines the predicted patches to reconstruct the output field . This reconstruction network involves a convolution neural network [38].
3.3. Data Assimilation Procedure
| Algorithm 1 Patch-based NNKF reconstruction |
|
4. Data and Experimental Setting
4.1. Dataset Description
4.2. Experimental Setting
- Optimal interpolation (OI): We use a Gaussian kernel with a spatial correlation length of 100 km and a temporal resolution length of 3 days. These parameters were empirically tuned for the considered dataset using a cross-validation experiment.
- Analog data assimilation (Local Analog Forecasting(LAF)-EnKF, Global Analog Forecasting(GAF)-EnKF): We apply both the global and local analog data assimilation schemes, referred to as GAF-EnKF, LAF-EnKF [19,22]. Similarly to the proposed scheme, we consider patches and 50-dimensional EOF decomposition with an overlapping of 10 pixels. We let the reader refer to [19,22] for a detailed description of this data-driven approach, which relies on nearest-neighbor regression techniques.
- EOF based reconstruction (PB-VE-DINEOF): We also compare our approach to the state-of-the-art interpolation scheme based on the projection of our observations with missing data on an EOF basis [11]. The SST field is here decomposed as described in the analog data assimilation application into a collection of patches with a 10 pixels overlapping. Each patch is then reconstructed using the VE-DINEOF method.
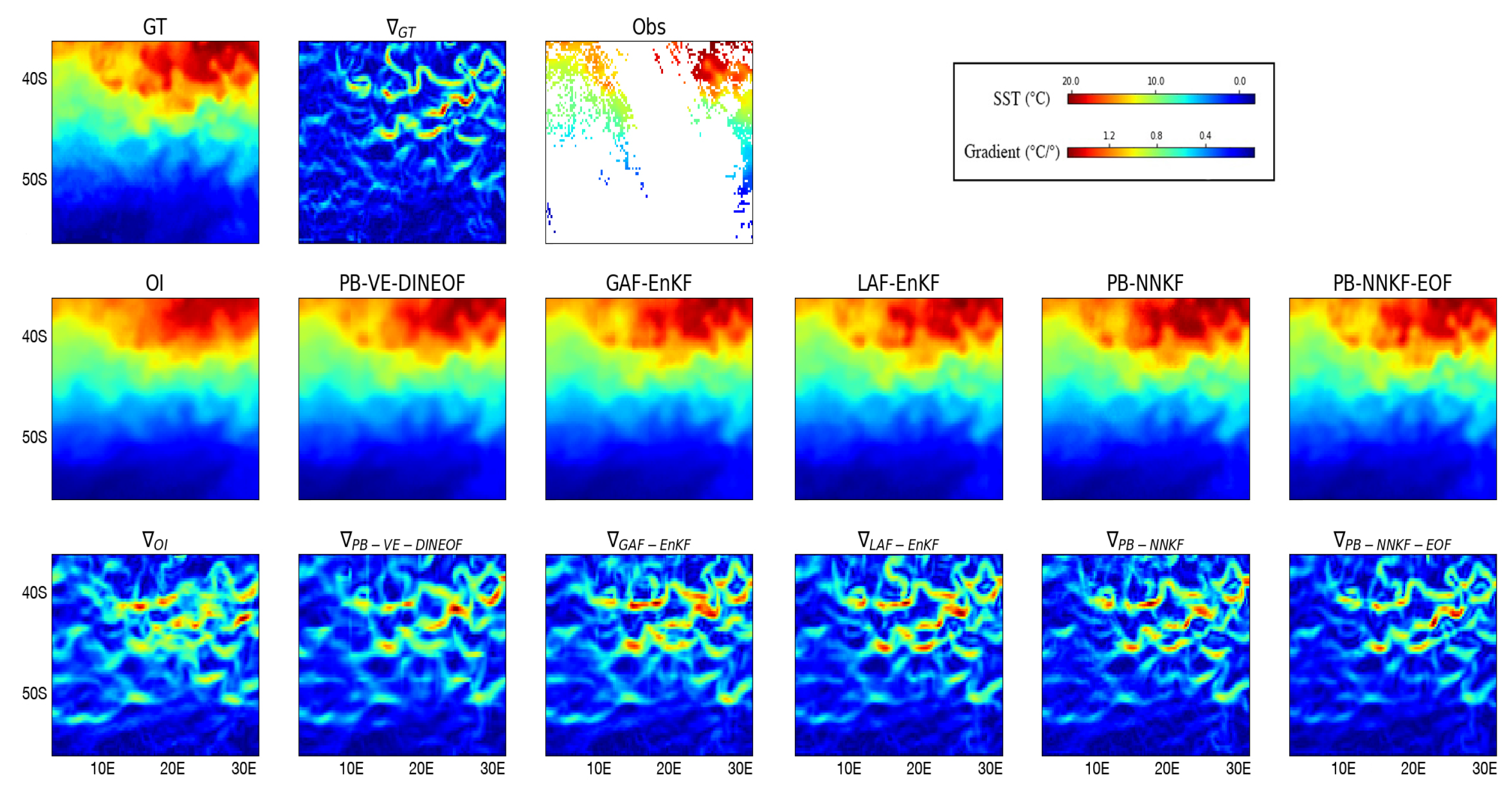
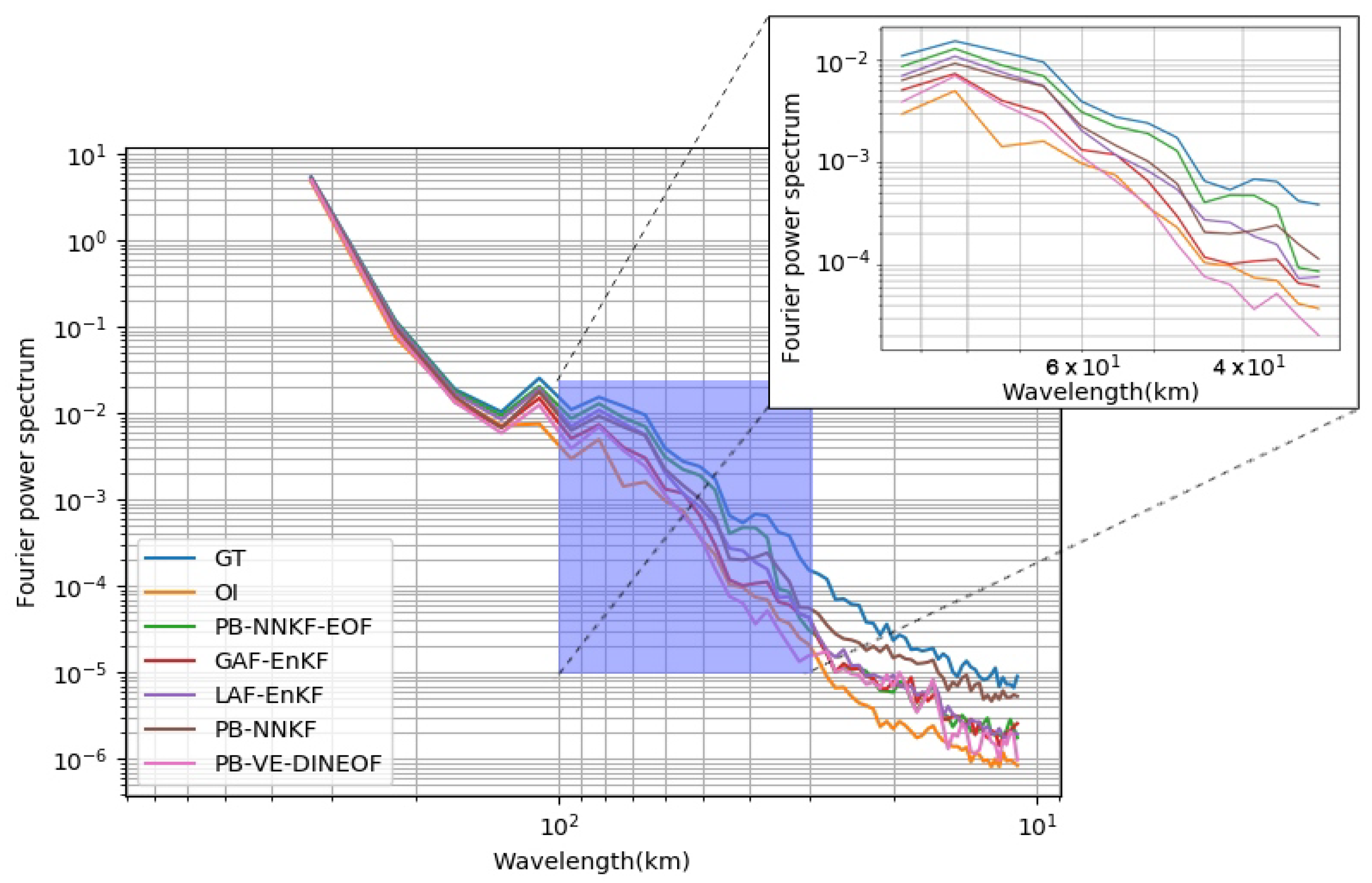
5. Results and Discussion
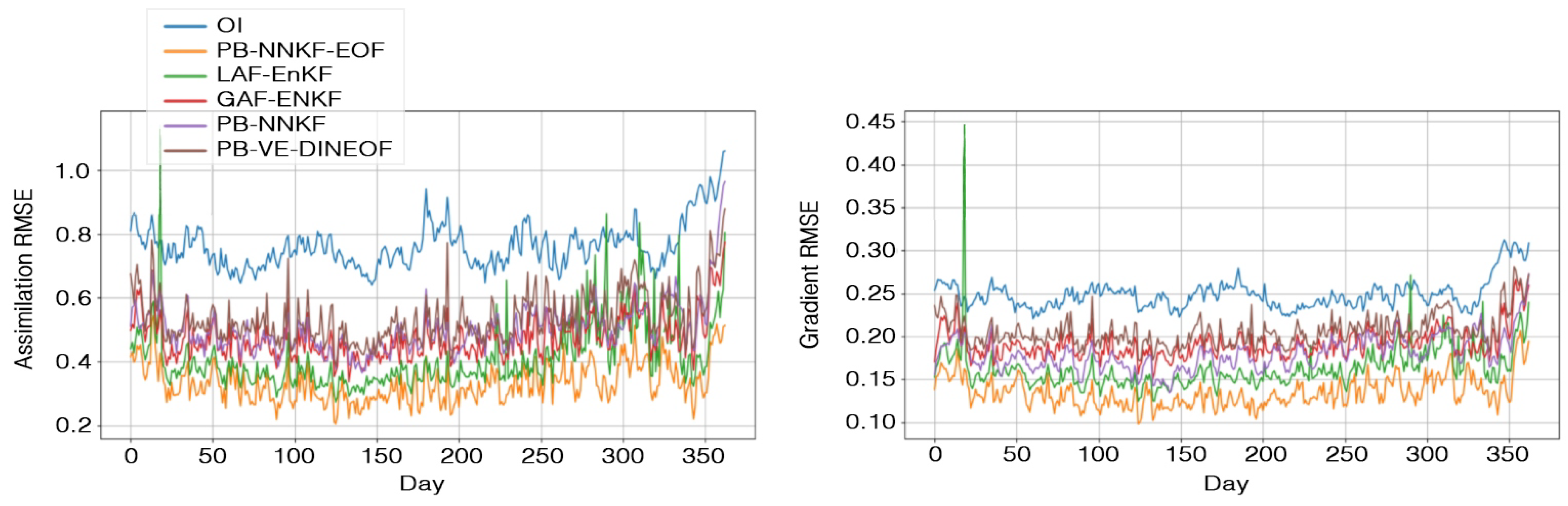
5.1. Patch-Level Interpolation Performance
5.2. Global Forecasting and Interpolation Performances
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hardman-Mountford, N.J.; Richardson, A.J.; Boyer, D.C.; Kreiner, A.; Boyer, H.J. Relating sardine recruitment in the Northern Benguela to satellite-derived sea surface height using a neural network pattern recognition approach. Prog. Oceanogr. 2003, 59, 241–255. [Google Scholar] [CrossRef]
- Le Traon, P.Y. Satellites and operational oceanography. In Operational Oceanography in the 21st Century; Springer: Berlin/Heidelberg, Germany, 2011; pp. 29–54. [Google Scholar]
- Von Schuckmann, K.; Le Traon, P.Y.; Alvarez-Fanjul, E.; Axell, L.; Balmaseda, M.; Breivik, L.A.; Brewin, R.J.; Bricaud, C.; Drevillon, M.; Drillet, Y. The copernicus marine environment monitoring service ocean state report. J. Oper. Oceanogr. 2016, 9, s235–s320. [Google Scholar] [CrossRef]
- Escudier, R.; Bouffard, J.; Pascual, A.; Poulain, P.M.; Pujol, M.I. Improvement of coastal and mesoscale observation from space: Application to the northwestern Mediterranean Sea. Geophys. Res. Lett. 2013, 40, 2148–2153. [Google Scholar] [CrossRef]
- Donlon, C.J.; Martin, M.; Stark, J.; Roberts-Jones, J.; Fiedler, E.; Wimmer, W. The Operational Sea Surface Temperature and Sea Ice Analysis (OSTIA) system. Remote Sens. Environ. 2012, 116, 140–158. [Google Scholar] [CrossRef]
- Le Traon, P.Y.; Nadal, F.; Ducet, N. An improved mapping method of multisatellite altimeter data. J. Atmos. Ocean. Technol. 1998, 15, 522–534. [Google Scholar] [CrossRef]
- Droghei, R.; Buongiorno Nardelli, B.; Santoleri, R. A New Global Sea Surface Salinity and Density Dataset From Multivariate Observations (1993–2016). Front. Mar. Sci. 2018, 5, 84. [Google Scholar] [CrossRef]
- Nardelli, B.B.; Pisano, A.; Tronconi, C.; Santoleri, R. Evaluation of different covariance models for the operational interpolation of high resolution satellite Sea Surface Temperature data over the Mediterranean Sea. Remote Sens. Environ. 2015, 164, 334–343. [Google Scholar] [CrossRef]
- Ducet, N.; Le Traon, P.Y.; Reverdin, G. Global high-resolution mapping of ocean circulation from TOPEX/Poseidon and ERS-1 and-2. J. Geophys. Res. Oceans 2000, 105, 19477–19498. [Google Scholar] [CrossRef]
- Gomis, D.; Ruiz, S.; Pedder, M.A. Diagnostic analysis of the 3D ageostrophic circulation from a multivariate spatial interpolation of CTD and ADCP data. Deep Sea Res. Part I Oceanogr. Res. Pap. 2001, 48, 269–295. [Google Scholar] [CrossRef]
- Ping, B.; Su, F.; Meng, Y. An Improved DINEOF Algorithm for Filling Missing Values in Spatio-Temporal Sea Surface Temperature Data. PLoS ONE 2016, 11, e0155928. [Google Scholar] [CrossRef] [PubMed]
- Olmedo, E.; Taupier-Letage, I.; Turiel, A.; Alvera-Azcárate, A. Improving SMOS Sea Surface Salinity in the Western Mediterranean Sea through Multivariate and Multifractal Analysis. Remote Sens. 2018, 10, 485. [Google Scholar] [CrossRef]
- Alvera-Azcárate, A.; Barth, A.; Parard, G.; Beckers, J.M. Analysis of SMOS sea surface salinity data using DINEOF. Remote Sens. Environ. 2016, 180, 137–145. [Google Scholar] [CrossRef]
- Beckers, J.M.; Rixen, M. EOF Calculations and Data Filling from Incomplete Oceanographic Datasets. J. Atmos. Ocean. Technol. 2003, 20, 1839–1856. [Google Scholar] [CrossRef]
- Bertino, L.; Evensen, G.; Wackernagel, H. Sequential Data Assimilation Techniques in Oceanography. Int. Stat. Rev. 2007, 71, 223–241. [Google Scholar] [CrossRef]
- Lorenc, A.C.; Ballard, S.P.; Bell, R.S.; Ingleby, N.B.; Andrews, P.L.F.; Barker, D.M.; Bray, J.R.; Clayton, A.M.; Dalby, T.; Li, D.; et al. The Met. Office global three-dimensional variational data assimilation scheme. Q. J. R. Meteorol. Soc. 2000, 126, 2991–3012. [Google Scholar] [CrossRef]
- Yablonsky, R.M.; Ginis, I. Limitation of One-Dimensional Ocean Models for Coupled Hurricane–Ocean Model Forecasts. Mon. Weather Rev. 2009, 137, 4410–4419. [Google Scholar] [CrossRef]
- van Leeuwen, P.J. Nonlinear data assimilation in geosciences: An extremely efficient particle filter. Q. J. R. Meteorol. Soc. 2010, 136, 1991–1999. [Google Scholar] [CrossRef]
- Lguensat, R.; Tandeo, P.; Ailliot, P.; Pulido, M.; Fablet, R. The Analog Data Assimilation. Mon. Weather Rev. 2017, 145, 4093–4107. [Google Scholar] [CrossRef]
- Tandeo, P.; Ailliot, P.; Chapron, B.; Lguensat, R.; Fablet, R. The analog data assimilation: Application to 20 years of altimetric data. In Proceedings of the 5th International Workshop on Climate Informatics, Boulder, CO, USA, 24–25 September 2015; pp. 1–2. [Google Scholar] [CrossRef]
- Lguensat, R.; Huynh Viet, P.; Sun, M.; Chen, G.; Fenglin, T.; Chapron, B.; Fablet, R. Data-Driven Interpolation of Sea Level Anomalies Using Analog Data Assimilation. 2017. Available online: https://hal.archives-ouvertes.fr/hal-01609851 (accessed on 22 November 2018).
- Fablet, R.; Viet, P.H.; Lguensat, R. Data-Driven Models for the Spatio-Temporal Interpolation of Satellite-Derived SST Fields. IEEE Trans. Comput. Imaging 2017, 3, 647–657. [Google Scholar] [CrossRef]
- Pannekoucke, O.; Emili, E.; Thual, O. Modelling of local length-scale dynamics and isotropizing deformations. Q. J. R. Meteorol. Soc. 2013, 140, 1387–1398. [Google Scholar] [CrossRef]
- Pannekoucke, O.; Ricci, S.; Barthelemy, S.; Ménard, R.; Thual, O. Parametric Kalman filter for chemical transport models. Tellus A Dyn. Meteorol. Oceanogr. 2016, 68, 31547. [Google Scholar] [CrossRef]
- Rezende, D.J.; Mohamed, S.; Wierstra, D. Stochastic Backpropagation and Approximate Inference in Deep Generative Models. arXiv, 2014; arXiv:1401.4082. [Google Scholar]
- Matthews, A.G.d.G.; Rowland, M.; Hron, J.; Turner, R.E.; Ghahramani, Z. Gaussian Process Behaviour in Wide Deep Neural Networks. arXiv, 2018; arXiv:1804.11271. [Google Scholar]
- Fablet, R.; Ouala, S.; Herzet, C. Bilinear residual Neural Network for the identification and forecasting of dynamical systems. arXiv, 2017; arXiv:1712.07003. [Google Scholar]
- Egmont-Petersen, M.; de Ridder, D.; Handels, H. Image processing with neural networks—A review. Pattern Recognit. 2002, 35, 2279–2301. [Google Scholar] [CrossRef]
- Braakmann-Folgmann, A.; Roscher, R.; Wenzel, S.; Uebbing, B.; Kusche, J. Sea Level Anomaly Prediction using Recurrent Neural Networks. arXiv, 2017; arXiv:1710.07099. [Google Scholar]
- Taormina, R.; Chau, K.W.; Sivakumar, B. Neural network river forecasting through baseflow separation and binary-coded swarm optimization. J. Hydrol. 2015, 529, 1788–1797. [Google Scholar] [CrossRef]
- Evensen, G. Data Assimilation; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Anderson, J.L.; Anderson, S.L. A Monte Carlo Implementation of the Nonlinear Filtering Problem to Produce Ensemble Assimilations and Forecasts. Mon. Weather Rev. 1999, 127, 2741–2758. [Google Scholar] [CrossRef]
- Houtekamer, P.L.; Mitchell, H.L. Data Assimilation Using an Ensemble Kalman Filter Technique. Mon. Weather Rev. 1998, 126, 796–811. [Google Scholar] [CrossRef]
- Gaspari, G.; Cohn, S.E. Construction of correlation functions in two and three dimensions. Q. J. R. Meteorol. Soc. 1999, 125, 723–757. [Google Scholar] [CrossRef]
- Houtekamer, P.L.; Mitchell, H.L. A Sequential Ensemble Kalman Filter for Atmospheric Data Assimilation. Mon. Weather Rev. 2001, 129, 123–137. [Google Scholar] [CrossRef]
- Bocquet, M. Localization and the iterative ensemble Kalman smoother. Q. J. R. Meteorol. Soc. 2016, 142, 1075–1089. [Google Scholar] [CrossRef]
- Cohn, S.E. Dynamics of Short-Term Univariate Forecast Error Covariances. Mon. Weather Rev. 1993, 121, 3123–3149. [Google Scholar] [CrossRef]
- LeCun, Y.; Haffner, P.; Bottou, L.; Bengio, Y. Object Recognition with Gradient-Based Learning. In Shape, Contour and Grouping in Computer Vision; Forsyth, D.A., Mundy, J.L., di Gesú, V., Cipolla, R., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1999; pp. 319–345. [Google Scholar] [CrossRef]
- Ouala, S.; Herzet, C.; Fablet, R. Sea surface temperature prediction and reconstruction using patch-level neural network representations. arXiv, 2018; arXiv:1806.00144. [Google Scholar]
- Fablet, R.; Verron, J.; Mourre, B.; Chapron, B.; Pascual, A. Improving Mesoscale Altimetric Data From a Multitracer Convolutional Processing of Standard Satellite-Derived Products. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2518–2525. [Google Scholar] [CrossRef]
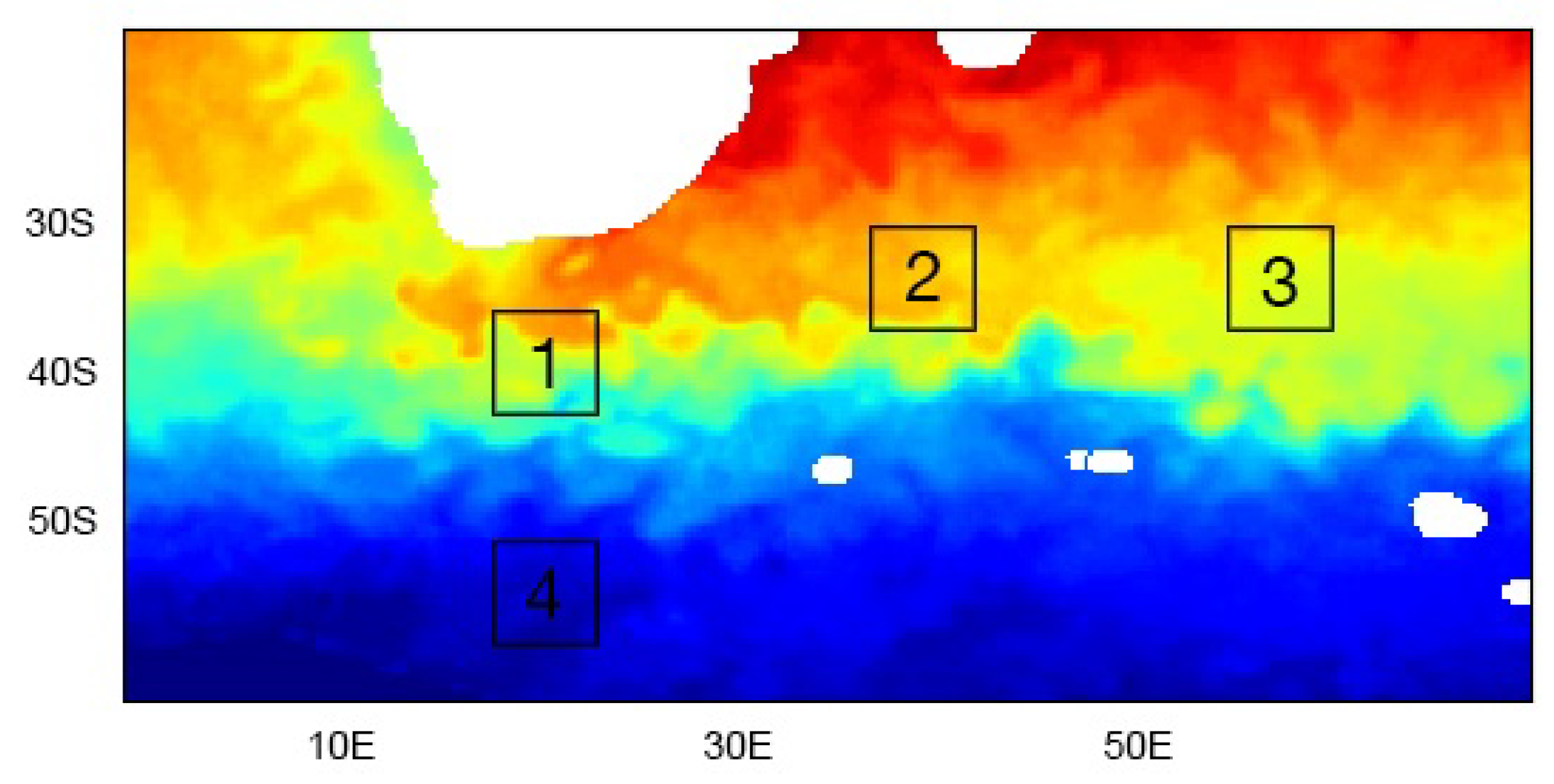
| Assimilation Method | Considered Patch RMSE (°C) | |||
|---|---|---|---|---|
| Patch 1 | Patch 2 | Patch 3 | Patch 4 | |
| LAF EnKF | 0.50 | 0.25 | 0.22 | 0.39 |
| Bi-NN-EnKF | 0.55 | 0.23 | 0.22 | 0.30 |
| Bi-NN-NNKF-EOF | 0.46 | 0.20 | 0.19 | 0.27 |
| Model | Forecasting RMSE (°C) | ||
|---|---|---|---|
| t+h | t+4h | t+8h | |
| PB-NN | 0.48 | 0.60 | 0.63 |
| LAF | 0.50 | 0.68 | 0.76 |
| GAF | 0.61 | 0.74 | 0.76 |
| Model | Entire Map | Missing Data Areas | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | Correlation | RMSE | Correlation | |||||
| PB-NNKF-EOF | 0.33 | 0.13 | 99.87% | 89.30% | 0.35 | 0.10 | 99.85% | 93.49% |
| PB-NNKF | 0.51 | 0.18 | 99.75% | 81.24% | 0.51 | 0.18 | 99.71% | 81.50% |
| LAF-EnKF | 0.43 | 0.16 | 99.79% | 84.41% | 0.42 | 0.15 | 99.77% | 86.73% |
| GAF-EnKF | 0.48 | 0.19 | 99.74% | 79.12% | 0.48 | 0.18 | 99.72% | 80.74% |
| PB-VE-DINEOF | 0.54 | 0.20 | 99.68% | 75.30% | 0.54 | 0.21 | 99.66% | 74.71% |
| OI | 0.76 | 0.25 | 99.37% | 60.31% | 0.75 | 0.27 | 99.37% | 55.73% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouala, S.; Fablet, R.; Herzet, C.; Chapron, B.; Pascual, A.; Collard, F.; Gaultier, L. Neural Network Based Kalman Filters for the Spatio-Temporal Interpolation of Satellite-Derived Sea Surface Temperature. Remote Sens. 2018, 10, 1864. https://doi.org/10.3390/rs10121864
Ouala S, Fablet R, Herzet C, Chapron B, Pascual A, Collard F, Gaultier L. Neural Network Based Kalman Filters for the Spatio-Temporal Interpolation of Satellite-Derived Sea Surface Temperature. Remote Sensing. 2018; 10(12):1864. https://doi.org/10.3390/rs10121864
Chicago/Turabian StyleOuala, Said, Ronan Fablet, Cédric Herzet, Bertrand Chapron, Ananda Pascual, Fabrice Collard, and Lucile Gaultier. 2018. "Neural Network Based Kalman Filters for the Spatio-Temporal Interpolation of Satellite-Derived Sea Surface Temperature" Remote Sensing 10, no. 12: 1864. https://doi.org/10.3390/rs10121864
APA StyleOuala, S., Fablet, R., Herzet, C., Chapron, B., Pascual, A., Collard, F., & Gaultier, L. (2018). Neural Network Based Kalman Filters for the Spatio-Temporal Interpolation of Satellite-Derived Sea Surface Temperature. Remote Sensing, 10(12), 1864. https://doi.org/10.3390/rs10121864