1. Introduction
Mountain forests provide a wide range of ecosystem services in terms of protective, productive, social and economic functions. Therefore, the timely information on the state and the change of land-use and forest cover, productivity, and structure is crucial for different stakeholders from local to regional scales. To quantify the provided forest services, detailed forest information is required with high spatial and temporal resolutions. Among the forest metrics, canopy height, which describes the top of the vegetated canopy, is the basis for deriving other parameters such as forest gaps, crown coverage, canopy density, volume, and biomass. For deriving canopy height at wide spatial coverage i.e., at the landscape scale, remote sensing observations with fine spatial resolutions are required. Current remote sensing systems that fulfil this requirement include airborne laser scanning (ALS) and multi-view aerial or very high resolution (VHR) satellite imagery [
1]. Since the last decade, airborne laser scanning (ALS) has been the primary data source for three-dimensional (3D) information on forest vertical structure [
2,
3,
4]. The main advantage of ALS for forest applications is the capability to penetrate through the vegetation and thus to obtain the top height, the forest vertical structure, and the bare-earth, with the latter being needed to define the terrain height. By contrast, passive optical sensors can provide only the topmost surface of forest canopies, where at least two images (a so-called image stereo pair) share a common area in the scene [
5]. Both aerial and satellite images have been used to record forest change for more than 30 years. In the last decade, thanks to great technological improvements, the gap between aerial and VHR satellite imagery has become smaller in terms of image resolution (up to 30 cm ground sample distance (GSD)). However, in comparison with airborne remote sensing, VHR satellite imagery has the benefits of worldwide availability without any access restrictions, large area coverage and high temporal resolutions of only a few days.
Forest mapping over large spatial extents with VHR satellites started with IKONOS in 1999 [
6,
7]. Since then, several VHR satellites have been launched such as QuickBird, GeoEye-1, WorldView-1, -2, and -3, Ziyuan-3A, and the Pléiades satellites. WorldView multispectral stereo imagery was largely used to analyse forest structure [
8,
9], the size of tree crowns [
10] and for the 3D modelling of forest canopies [
1,
11,
12].
Among the available VHR satellite systems, we consider Pléiades imagery over mountain regions for deriving DSMs. This first European VHR satellite system is comprised of two identical satellites, Pléiades-1A (PHR1A) and Pléiades-1B (PHR1B), which were launched in December 2011 and in December 2012, respectively. Both satellites fly at an altitude of 694 km in sun-synchronous orbits with 98.2° inclination and an offset of 180° from each other, which provides a daily revisit capability [
13]. An outstanding feature of the Pléiades system is the great agility of its sensors that allows for optimised acquisitions of areas of interest, with stereo angles varying from ~6° to ~28° [
14]. The time difference between along-track images is in the range of a few seconds only, which guarantees almost constant sun illumination conditions, limited changes in the scene and similar cloud coverages in all of them [
15]. Moreover, the sensor is designed to acquire panchromatic and multispectral images, which are delivered at nominal resolutions of 0.5 m and 2 m, respectively, in stereo (forward-, backward-view) and tri-stereo (forward-, nadir-, and backward-view) modes along-track.
To explore the full potential of Pléiades images over forest mountain areas, an investigation of the relationship between DSM accuracy and imaging geometry, such as tri-stereo imagery, convergence angle and across-track angle, is essential for an optimal image acquisition planning. Therefore, we focus on answering the question of which combination and acquisition setting of tri-stereo or stereo pairs of Pléiades images can produce the highest DSM accuracy over Alpine forest regions.
4. Results
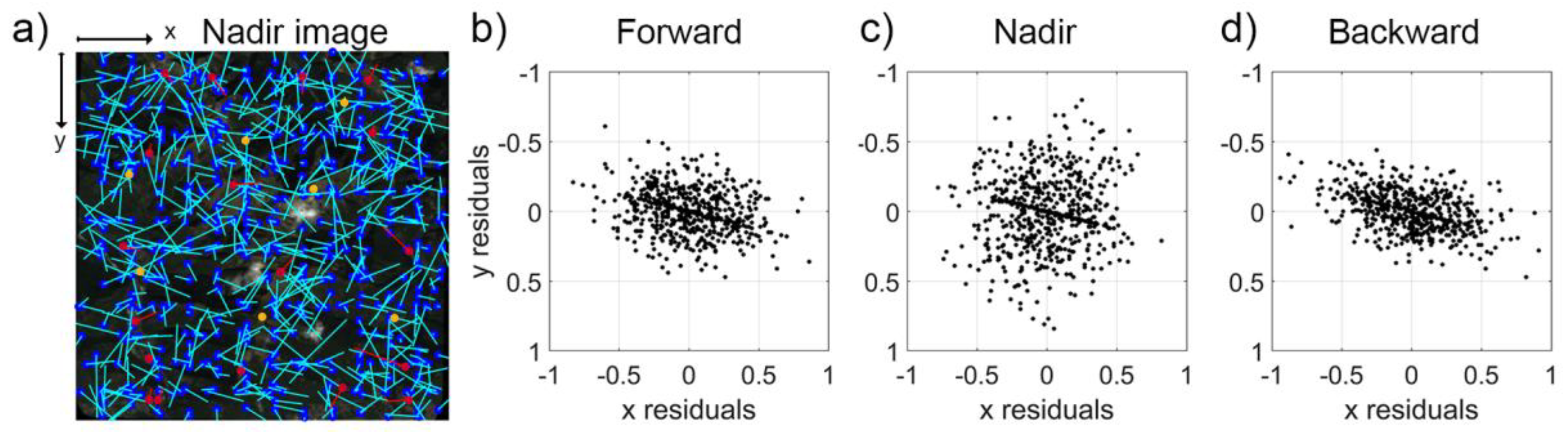
For each study area, the image orientation refinement was performed jointly for all available images. In Ticino, the bundle adjustment was performed with all three images in a single block. Automatic tie point extraction identified ~580 points. The RMSE of the GCPs is in the range of a decimetre both in the horizontal and vertical directions. At the CPs, a similar accuracy is achieved in planimetry, whereas with 1.04 m, the RMSE results were much larger in the vertical direction (
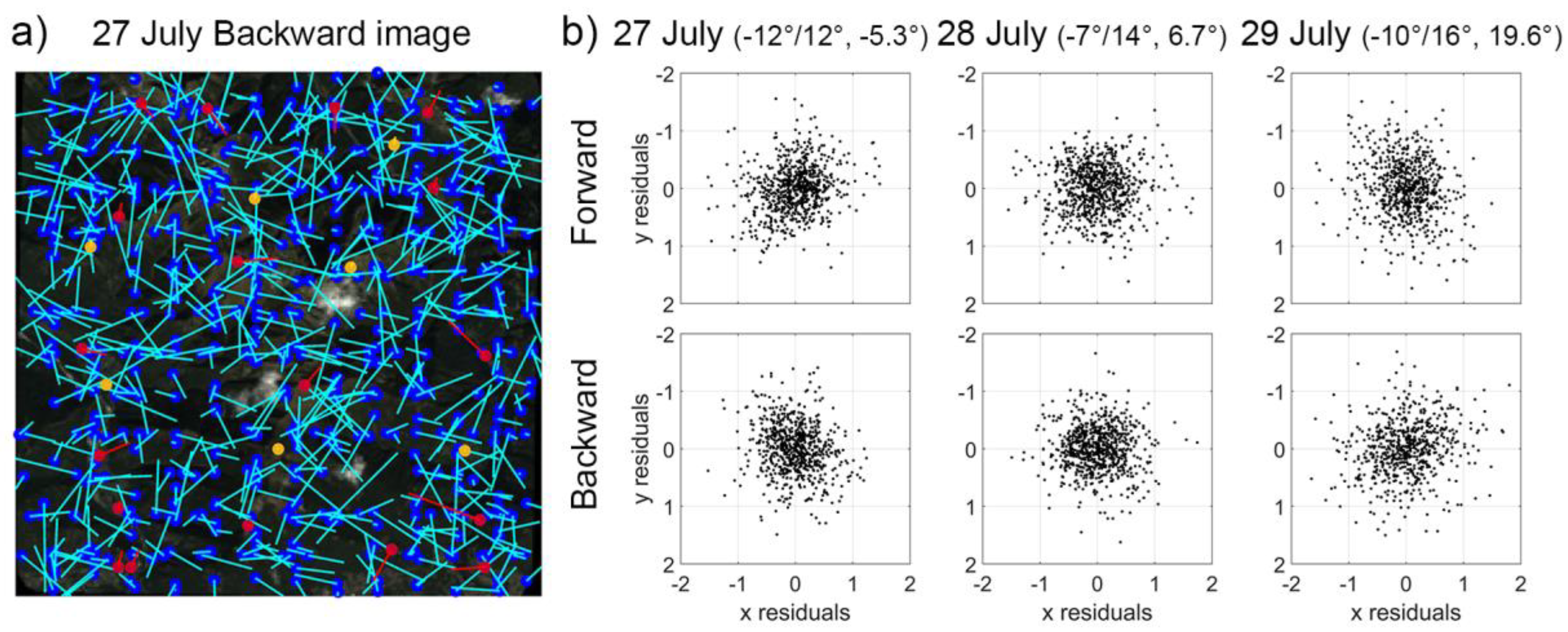
Table A1). In Ljubljana, the RPCs of the six images were improved simultaneously in one single block using 18 GCPs and automatically extracted tie points. The number of the automatically extracted tie points ranges between 690 and 806. The standard deviation of the tie point residuals ranges between 0.39 and 0.52 pixel. In the vertical direction, the RMSE of the ground coordinates is 0.80 m at the CPs, whereas at the GCPs it is 0.17 m. In planimetry, the accuracy at the GCPs and CPs is almost the same (
Table A2). For details of adjustment results, see
Appendix A for Ticino and Ljubljana, respectively.
Dense image matching was successful on forest areas (
Figure 3). With ~1362 million points, FNB over Ticino provided a larger point cloud than each of the three stereo pairs, having ~700 (FN), ~696 (NB), and ~657 (FB) million points. For each of the Ljubljana stereo pairs, around 2000 million points were matched, where the lowest number of points was generated for the stereo pair with the widest angle of convergence.
Over the entire scene, the interpolation ensured an almost complete reconstruction of the void areas since those areas were small enough to be reliably filled by the used grid interpolation with 3 m search radius. In all Pléiades DSMs, less than 1.5% of pixels result as void, being located within or close to the clouds or, for Ticino, on the lake surface. Despite this, the image triplet reduced the missing height values by up to 0.7 percentage points when compared to the standard stereo FB DSM. Concerning Ljubljana, the image pair with the widest angle of convergence resulted in a notably larger amount of missing data than the other pairs (
Table 2).
4.1. Impact of the Tri-Stereo Acquisition on the Quality of the Derived Products in Ticino
4.1.1. Accuracy Assessment of the VHR nDSMs Over Stable Areas and of the VHR-CHMs
The GCPs and CPs were employed to assess the vertical accuracy of the DSM before and after LSM for each image combination (
Table 3). The total RMSE of the DSMs before LSM at the GCPs and CPs ranged between 0.79 m (FB) and 1.25 m (FN). When the GCPs were not used within the bundle adjustment, the vertical accuracy of the tri-stereo DSM resulted with an offset of approximately 37 m at the GCP and CP locations. Nevertheless, this vertical offset was completely removed by application of LSM, resulting in the same accuracy achieved with GCPs. The LSM transformation slightly reduced the total RMSEs for each image combination, ranging between 0.68 m (FB) and 1.10 m (FN).
The spatial distribution of the normalised elevation (nDSM) for the tri-stereo and the aerial images are shown in
Figure 4 before and after LSM.
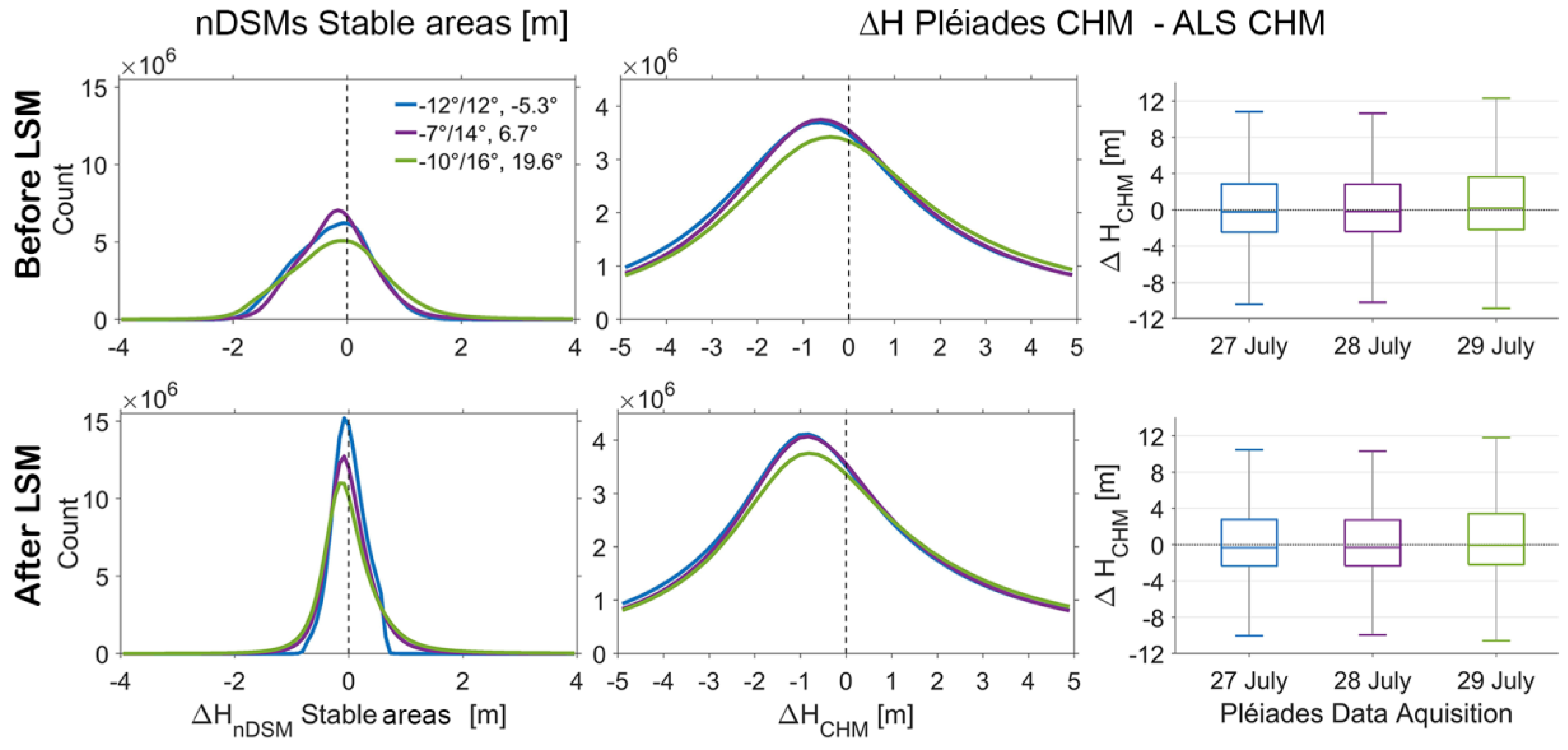
According to visual analysis, both positive and negative biases are visible on the stable areas for both Pléiades and aerial nDSMs before and after the LSM transformation. Before LSM, the vertical error distributions of the Pléiades nDSMs feature medians between 0.14 m and 0.43 m, with a maximum σ
MAD of 1.30 m (
Table 4).
The highest accuracy was achieved by the standard stereo FB, although after LSM the accuracy is practically the same for all image combinations and comparable with the results from aerial image matching. LSM improved the accuracy of the Pléiades DSMs on the stable areas, which yielded a median close to zero for each scene combination, and a σMAD below 1 m. Only the FN stereo pair exceeds this value slightly. Moreover, the ratio of Pléiades cells with an absolute accuracy of better than 1 m increases by around 10 percentage points due to application of LSM. Nevertheless, both Pléiades and aerial nDSMs after LSM show a negative shift in the frequency distribution histograms.
The distributions of ΔH between the Pléiades and aerial CHMs before and after LSM are reported in
Figure 5 by means of a map of the differences, histograms, and boxplots.
For all image combinations, the histograms reveal unimodal symmetric distributions of the height differences, similar to normal distributions, and they feature negative shifts. The two stereo pairs involving the nadir image provided the lowest accuracy, whereas the tri-stereo and FB combinations resulted in similar error distributions. After LSM, the histograms show a slightly lower dispersion around zero, but the ratio of cells that fall in the range of ±1 m increase only by approximately 5 percentage points. The statistics of each scene combination are reported in
Table 5.
Overall, the tri-stereo and nadir stereo Pléiades DSMs underestimated the canopy height, with medians of around 20 cm, whereas the FB combination shows a median of almost zero. The dispersion in terms of σ
MAD is about 2 m for each scene combination. The correlation between the Pléiades CHM errors and the canopy height itself, as given by the reference CHM, was calculated. In order to remove the spatial variation of the canopy height, a standard deviation moving window of 20 m was applied over the aerial CHM and subsequently pixels with a standard deviation greater than 5 m were excluded from the calculation. The time gap of two years can justify the positive ∆H of Pléiades CHMs for young trees with heights below 10 m (
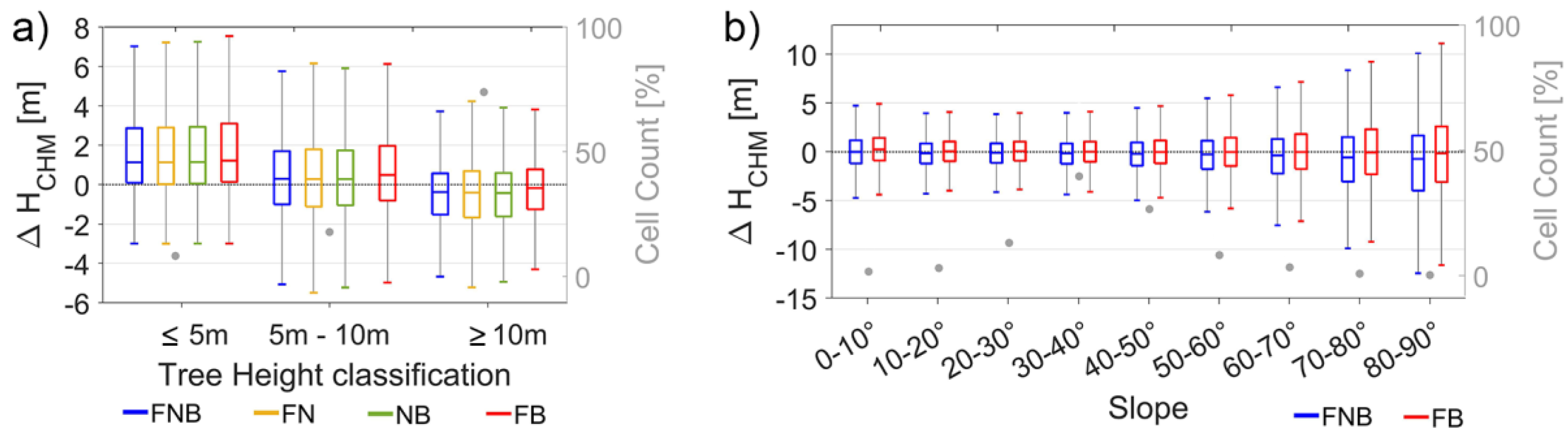
Figure 6a), although young trees occupied only about 8% of the entire area. For this tree height class, the median values of ∆H range from 0.29 m to 1.22 m, whereas negative values between −0.42 m and −0.17 m are identified for tree heights greater than 10 m. No significant correlation was identified between ∆H and forest roughness, quantified by the RMSE of the height values to a fitting a plane. Contrary, grouping the data by slope classes of 10° width, a rapid increase in the variance of ∆H was observed for the steep classes with slopes larger than 60°, which, however, represents a small proportion of the investigated area (14%) (
Figure 6b).
4.1.2. Accuracy Assessment of the VHR nDSMs for a Selected Area
The profiles in the insets in
Figure 7 show that with Inpho Match-T, there is no benefit of using three images i.e., FNB, because the resulting point cloud is simply the union of those of the two nadir stereo pairs.
However, the questions which remain are: (1) if a better DSM than FNB can be derived by computing the three stereo point clouds independently (i.e., for FN, NB, FB after LSM), and then interpolate them into a tri-stereo DSM (FB-NB-FN) using the method described above, and (2) if selecting the locally best of the three stereo DSMs (MinAbs∆H) improves upon the DSMs computed so far. As the locally best DSM, we used the one with the minimum absolute error. To answer the above questions, we derived the histogram of the absolute errors for each of the corresponding CHMs, shown in
Figure 8a. The generation of the DSM considering simultaneously the point clouds from the three stereo pairs (FB-NB-FN) does not provide significantly better results than the FB stereo pair. The optimum selection provided a significant improvement. However, no clear systematic pattern can be identified from the spatial distribution of the stereo pairs with the locally minimum absolute error (
Figure 8b). Moreover, examining the influences of the canopy height and forest roughness on the absolute error, no significant relationships were identified. Nevertheless, for deriving an automatic approach to optimally select the best height of these three stereo results, a reference data surveyed at the same time should be considered.
4.2. Impact of the Viewing Angles on the Quality of the Derived Product in the Area of Ljubljana
4.2.1. Accuracy Assessment of the VHR nDSM over Stable Areas and the VHR-CHMs
The vertical accuracy of the Pléiades DSMs in terms of the total RMSE at the GCPs and CPs is around 0.70 m (
Table 6). The application of the LSM transformation led to a lower RMSE in the Z-direction, which ranges between 0.14 m and 0.27 m. The worst result is shown by the DSM derived from the stereo pair with the largest angle of convergence and across-track angle. The vertical accuracy of Pléiades DSMs over the entire scene was assessed by calculating the distribution of ∆H using the reference ALS dataset i.e., the ALS DTM for the stable areas, and the ALS CHM for the forested areas.
Figure 9 allows for a visual comparison of the Pléiades nDSMs for each stereo scene before and after LSM, together with the ALS nDSM, and the orthophoto. Compared to the ALS nDSM, the spatial distribution of the Pléiades nDSMs over stable areas appears clustered before LSM and more homogeneous after LSM. The spatial pattern observed in the Pléiades nDSM suggests a tilt of around ±1 m in north-east/south-west direction between the Pléiades DSM and the ALS DTM, which, however, was significantly reduced by applying a full LSM transformation.
According to the histograms of Pléiades nDSMs in stable areas and ∆H (in forest areas) (
Figure 10), the improvement of the accuracy of the CHMs due to LSM is not as significant as in the stable areas, where a considerable reduction of dispersion around zero is visible.
The statistics and the box plots of each stereo pair confirm this observation. Overall, after LSM, nDSM heights in stable areas have a median of almost zero, with a σ
MAD below 0.50 m, whereas CHM errors show a considerably higher dispersion, with a σ
MAD around 4 m (
Table 7).
In order to investigate the correlation between the accuracy of the Pléiades CHMs and the reference canopy height, the latter was divided into three height classes, and CHM cells with high variation, i.e., larger than 5.0 m standard deviation within 20 m moving window were excluded (
Figure 11a). For all stereo pairs, the CHM errors for tree heights greater than 10 m displays negative median values ranging from −0.58 m to −0.82 m. This can be explained by the tree growth during the two years gap between the Pléiades and ALS data capture. Conversely, the accuracy of the Pléiades CHMs for tree heights below 10 m shows overall positive differences and a considerably higher dispersion for the tree heights smaller than 5 m (
Figure 11b). Those trees occupied about 10% of the entire forest area and they are mainly distributed within managed forests areas, as shown in the spatial distribution of the ALS CHM grouped by the three height classes. For this study area, the effect of slope on the accuracy of the Pléiades CHMs cannot be assessed since less than 1% of it reveals a slope greater than 50°.
4.2.2. Accuracy Assessment of the VHR CHMs for the Selected Areas
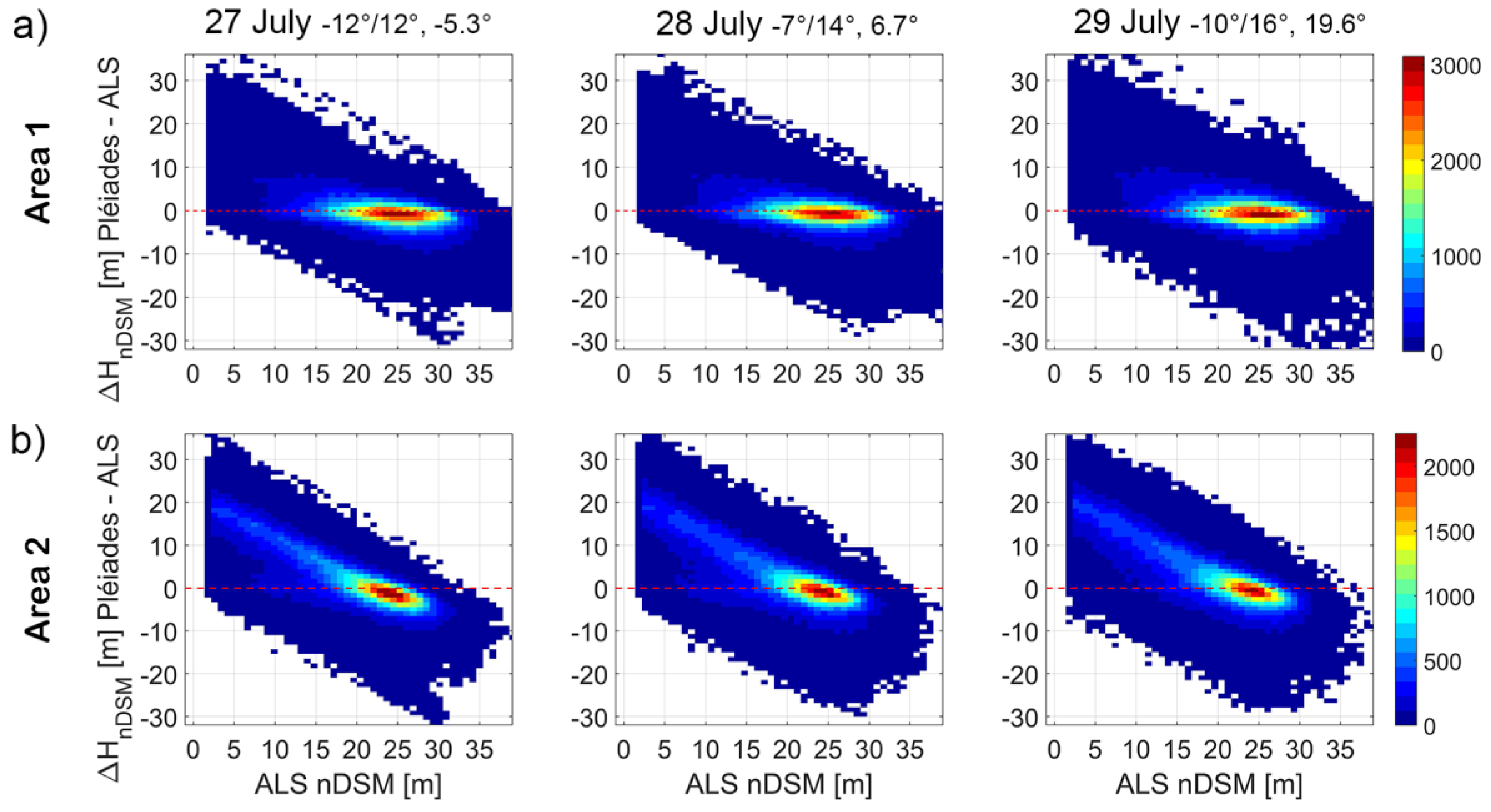
The quality of the Pléiades CHMs varies according to forest density and forest height. A detailed investigation on the Pléiades CHMs for the two selected areas shows that Pléiades CHMs provided comparable results to the ALS data for a homogenous forest canopy (
Figure 12a). Conversely, distinct canopy height patterns that can be seen in the ALS canopy height map cannot be discerned in the Pléiades map where the tree crowns are significantly wider and less defined (
Figure 12b). It is worth noting that those differences in the canopy gap characteristics can be attributed to forest management activities, but most likely to the severe freezing rain event that hit Slovenian forests in 2014, damaging 40% forest areas throughout the country [
37]. Indeed, the orthophoto acquired simultaneously to ALS data (2015) shows larger canopy gaps than those visible in the Pleiades orthophoto (2013) (
Figure 12c).
These qualitative results are confirmed by the distribution of Pleiades CHM height errors, where a clear correlation exists with low forest heights (
Figure 13b, area 2). Moreover, the trend also demonstrates that young forest (height < 5 m), which is typically underestimated by image matching [
23], is completely missing in the Pleiades results, validating the differences in forest structure at the points in time of Pléiades and ALS data capture. The larger across-track angle shows a wider error dispersion for both areas i.e., forest types.
5. Discussion
This work focuses on analysing the accuracy of Pléiades DSMs over forest mountain regions in order to identify the optimal acquisition planning in terms of stereo or tri-stereo data and incidence angle along- and across-track. Tri-stereo (FNB) images were requested in 2017 over Ticino forest area in Switzerland. The angle of convergence of the forward-backward (FB) images was about 12°, with an average across track-angle of −5°. The three stereo pairs with different across- and along-track angles were acquired in 2013 over the same area in Ljubljana (Slovenia), one day apart from each other. Those images had an angle of convergence of about 24°, 22°, and 27°, respectively, with about −5°, +6° and +20° in across-track direction.
In this study, we focus on the reconstruction of the surface height from pan-sharpened Pléiades images. As reported by Reference [
26], if only tree heights are of interest, there is a limited reimbursement of also acquiring and processing spectral and textural data, because multispectral and colour information typically does not contribute to the matching performance [
38]. Therefore, in this work, the fourth band was only exploited to generate the NDVI map which was used to derive the tree mask for the Ticino study area and for removing the lake and river surfaces from the stable area mask. The surface covered by clouds was excluded from the analyses in post-processing based on the nDSM.
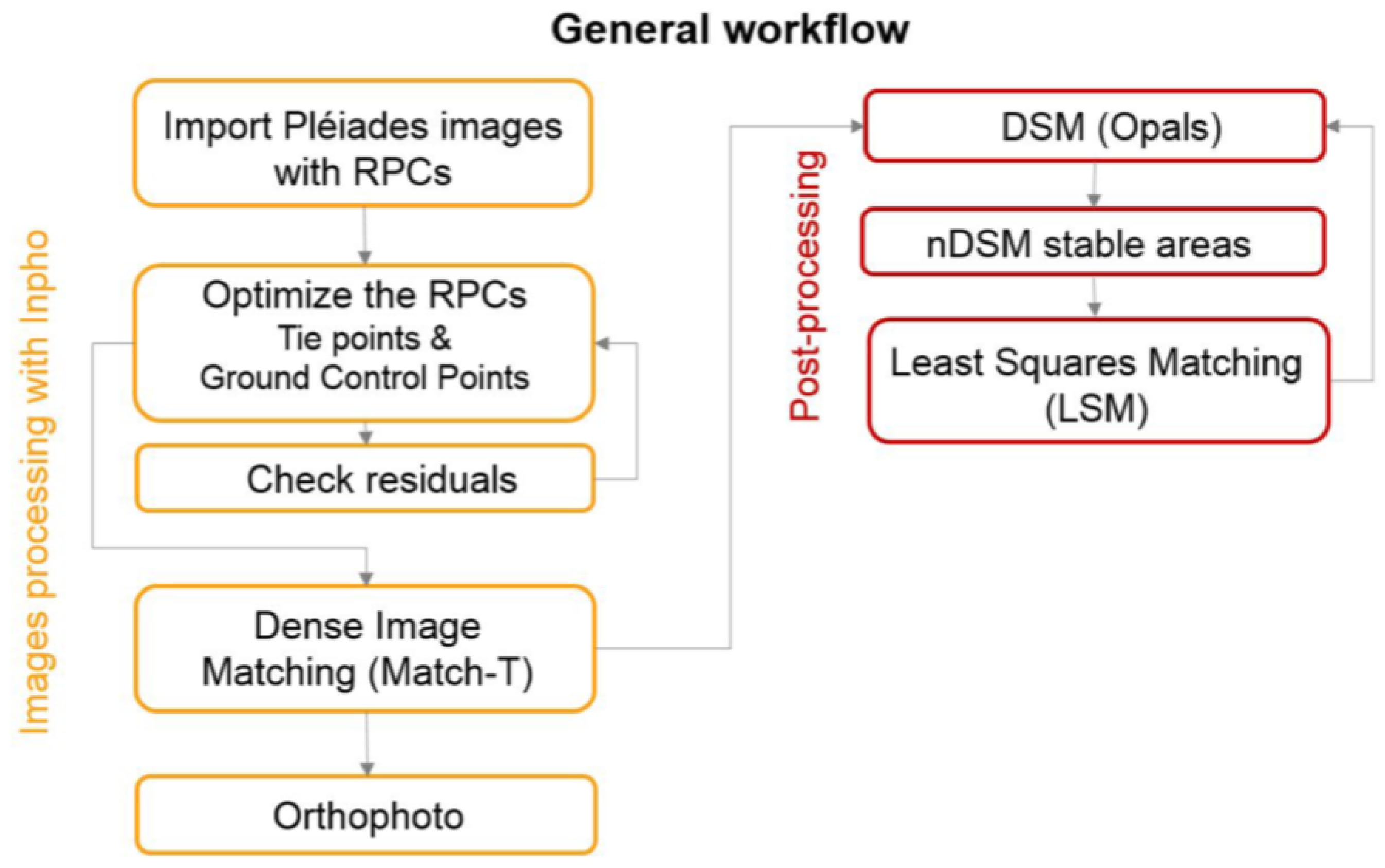
Processing in Inpho Match-T is highly automated. It requires only limited information to be entered by users, consisting of manually observing GCPs in the images, checking the residuals of tie points to remove blunders, and setting some parameters for the dense point cloud computation e.g., the type of filtering and the spatial resolution (in our work, one point per pixel). The GCPs were employed to achieve sub-meter accuracy. A high number of GCPs improves the accuracy, but no significant improvement can be reached by increasing the number of GCPs from 10 to 40 [
39,
40]. For both study areas we used 18 GCPs to refine the RPC in combination with automatically extracted tie points. For the tie points, we obtained a precision of better than 0.3 pixels for the tri-stereo images in Ticino and around 0.5 pixels for the three stereo images in Ljubljana. For both study areas, there is a good agreement between the horizontal RMSE of the adjusted coordinates of the GCPs and the CPs on the ground, but high discrepancies can be found in the vertical direction, where the RMSE of the CPs is about 1.0 m (Ticino) and 0.80 m (Ljubljana) in comparison to one decimetre of the GCPs. Because the GCPs were used within the bundle adjustment, only the CPs residuals represent external accuracy. Indeed, this result is validated by the vertical RMSE of the DSM at the GCPs and CPs, which is in total about 0.90 m and 0.70 m for Ticino and Ljubljana, respectively. For the area of Ticino, the vertical DSM RMSE of the CPs is almost twice as large as the one of the GCPs, which suggests a sub-optimal distribution of the GCPs. However, the large forest coverage and the steep terrain limited the selection of GCPs and CPs within this area.
To generate DSMs from dense point clouds, a moving plane interpolation was chosen that consider all the points within a 3 m search radius. This approach was found to be the optimal compromise between minimizing the number of void pixels, preservation of detail, and noise filtering. Considering that the vertical accuracy of photogrammetric DSMs largely depends on the target land cover [
11], we assessed the global accuracy of Pléiades DSMs separately for stable areas and for forest areas (CHM) by comparison with the reference data. In stable areas, the Pléiades DSMs elevation errors showed a clustered bias for both study areas. Consequently, the application of an affine transformation estimated by LSM reduced them. However, to derive globally optimal transformation parameters using LSM, the common stable areas in the master and slave surfaces should be homogeneously distributed over the entire scene, which can be hard to achieve in forest mountain areas. Despite this limitation, we demonstrated that for both study areas, LSM improved the geolocation accuracy by removing the clustered error, especially over the flat area of Ljubljana. Moreover, in Ticino, LSM removed the 35 m geolocation error resulting from the original RPCs delivered with the imageries. This accuracy corresponds to the results reported by Reference [
39], who estimated an RMSE of the absolute height of the Pléiades DSMs between 35.6 m and 41.9 m when using the original RPCs. Our results indicate that sub-meter geolocation accuracy can be achieved without the time-consuming measurement of GCPs by applying an LSM transformation, if a high-resolution DTM and stable areas are available. In Ticino, some clustered errors were still present after LSM, likely due to the low quality of the reference DTM, which showed abrupt terrain discontinuities. This is confirmed by similar distributions of the nDSMs in stable areas for Pléiades (σ
MAD = 0.82 (FB)) and aerial image matching (σ
MAD = 0.80), where the same DTM was used for normalisation. The application of LSM in Ljubljana significantly removed the tilt effect in the flat stable areas: For the images of 29 July, 74% of the cells fell in the range ±1 m before LSM, whereas the percentage increased to 92% after LSM. The improvement due to LSM of the Pléiades DSM accuracies in forest areas is not as significant as in stable areas. If we quantify this improvement as the percentage of Pléiades DSM cells with height errors within the range of ±1 m, then LSM increases the accuracy by 5 and 4 percentage points for Ticino and Ljubljana, respectively. However, note that in both study areas there is a considerable time gap between the acquisition of the reference data and the Pléiades image.
After LSM, the vertical error distribution of the Pléiades CHMs in Ticino and Ljubljana show good agreement in terms of their median, ranging between 0.02 m (FB) and −0.20 m (NB) for Ticino and between −0.04 m and −0.32 m for Ljubljana. In contrast, their dispersions differ significantly, with a σ
MAD of about 4 m for Ljubljana, as opposed to 2 m for Ticino. This larger dispersion of the error distribution can be attributed to the different forest types and managements of the two study areas. In Ticino, the forest areas were more homogeneous, containing mainly adult trees (87%, >10 m) in broadleaf forest. The height of lower trees was generally overestimated by Pléiades image matching, contrary to the conclusion of Reference [
26]. However, in our study, this overestimation can be attributed to tree growth between the time of aerial (2015) and Pléiades (2017) images acquisitions. However, in Ljubljana, only 76% of the canopy cover revealed heights greater than 10 m, and it consists of managed forests, several vegetated urban areas, and single trees in flat areas. Tree growth between the Pléiades (2013) and ALS (2015) data acquisitions can explain the negative differences between Pléiades and ALS CHMs for tree heights greater than 10 m. Younger trees were significantly overestimated by Pleiades CHMs in comparison to ALS. However, note that between these two data acquisitions, the Slovenian forests were hit by a strong ice storm, which caused severe damage. Consequently, many of the canopy gaps formed during this event and the younger trees due to forest regeneration were not yet present at the time of the Pléiades image. This was confirmed by visual comparison of a Pléiades orthophoto and an aerial one acquired at the time of ALS data acquisition. An additional aspect to consider in the comparison of the results for the two study areas is the different kinds of data used to compute the reference DSMs: ALS in Ljubljana versus aerial images in Ticino. Hence, two image sensors (with GSDs of 0.50 m for the aerial and of 0.70 m for the Pleiades images) were compared, which have similar issues concerning gap detection, because the same point has to be visible in at least two images. Hence, accurate CHM reconstruction in mountain areas remains difficult due to strong elevation contrast between trees and the surrounding ground, which results in occlusions. Therefore, we confirm that the ability to accurately measure points between trees heavily depends on the GSD, the base length of stereo images, dominating tree heights and the density of the forest [
41]. The analysis of the height profiles confirms that the Pléiades DSMs follow well the aerial DSM (
Figure 7) and the ALS DSM (
Figure 12c) for homogenous canopy cover and adult trees, but overestimates the height between single trees close to each other and within canopy gaps. This result matches the expectation that stereo-photogrammetry reconstructions yield a relatively smooth surface in which height discontinuity between trees and their surrounding are represented by gradual changes [
39,
42]. The median of Pléiades CHM errors is not influenced by slope, but a rapid increase of its dispersion was observed for steep areas in Ticino (>60°).
When analysing the quality of Pléiades DSMs regarding the acquisition mode in Ticino, i.e., tri-stereo vs. stereo, we observed in a profile (
Figure 7) that the nadir image increases completeness, reducing the data void left out by FB matching in steep forest areas, because of fewer occlusions, and larger image similarity. Anyway, the small angle of convergence (12°) of the FB stereo pair resulted in small unreconstructed areas only that were mostly filled by DSM interpolation. The study shows a limitation of the used software in the dense matching of from tristereo images: The resulting FNB dense point cloud is simply a subset of the two-nadir stereo (FN and NB) point clouds, without any contribution of the FB stereo pair. FB provided the highest accuracy in comparison to the tri-stereo and the two nadir stereo pairs, albeit differences are rather small. Among the two nadir stereo pairs, FN had the smaller angle of convergence, and it provided the worst results, as expected. The reached accuracy of the height model based on all three images (i.e., FN-NB-FB) is slightly better than for FB, as also observed by Reference [
42]. Selecting the locally best of the three stereo results (i.e., with minimum local height error) yields an improved model. This selection is straightforward when having reference data at hand that was acquired at the same time as the satellite imagery. Without reference data, however, according selection criteria still remain an open question.
Incidence angles, both across- and along-track, affect DSM accuracy, although our results showed only moderate differences, especially within forest areas. When comparing the accuracies of the study areas, we observed that the larger angle of convergence (>24° of Ljubljana versus 12° in Ticino) provided a σ
MAD in stable areas that was two times smaller. However, this might also be attributed to the more mountainous topography in Ticino and the more homogeneous distribution of the GCPs in Ljubljana. Nevertheless, the median values of the nDSMs in stable areas is close to zero for both study areas, which suggests that a narrow angle of convergence doesn’t constitute a major limiting factor for the quality of the Pléiades DSMs [
39]. By contrast, based on the assumption that a wider angle of convergence (>15°) would help to enhance the accuracy of the measured heights [
15,
43], our results suggest that a wider across-track angle (20°) has a negative impact on the vertical accuracy of the DSM. Furthermore, the error dispersion is more affected by steep terrain than by small across-track angles (±6°).
6. Conclusions
Pléiades satellite images compared to other VHR sensors have the main advantages of a great agility, daily revisit capability, smaller time intervals between the image acquisition and the possibility to acquire a nadir-looking view. Considering these characteristics and if a digital terrain model (DTM) is available, the system offers a great potential for providing a high spatial resolution canopy height model (CHM), which can be used for supporting forest inventory and monitoring programs at the regional and national level. Therefore, to take this system into consideration, an important challenge is to understand the accuracy of the derived products. Specifically, since the acquisition mode (Tri-stereo/stereo) and the incidence angles can be planned for the new Pléiades images acquisitions, this work wants to answer the following two questions: (1) what is the benefit of using tri-stereo images and (2) what is the impact of different incidence angles along- and across-track on the image matching performance and on the accuracy of the DSM. In order to derive the height above the ground (i.e., the nDSM), available DTM was subtracted from the DSMs. The image orientation implied the use of GCPs and tie points to refine the RPC. However, in order to remove systematic errors on the generated DSMs, an affine transformation (LSM) was successfully applied to the dense point cloud. We demonstrated that by applying an LSM transformation sub-meter geolocation accuracy without the time-consuming GCPs measurements could be achieved.
Our results suggest that the differences between tri-stereo and stereo matching are rather small and the stereo forward-backward canopy height showed slightly higher accuracies than the tristereo results and the two nadir stereo pairs. In terms of completeness, the nadir image can minimize the issues of stereo matching in steep forest areas, but the adopted interpolation method and the narrow angle of convergence of the forward-backward pair yielded to small unreconstructed areas. Both incidence angles, across- and along-track are important parameters for determining DSM accuracy of a stereo pair, although our results do not show dramatic differences. However, a large across-track angle (19°) reduces the quality of Pléiades CHMs/nDSMs.