A Novel Integrated Approach of Relevance Vector Machine Optimized by Imperialist Competitive Algorithm for Spatial Modeling of Shallow Landslides
Abstract
:1. Introduction
2. Study Area and Data Acquisition
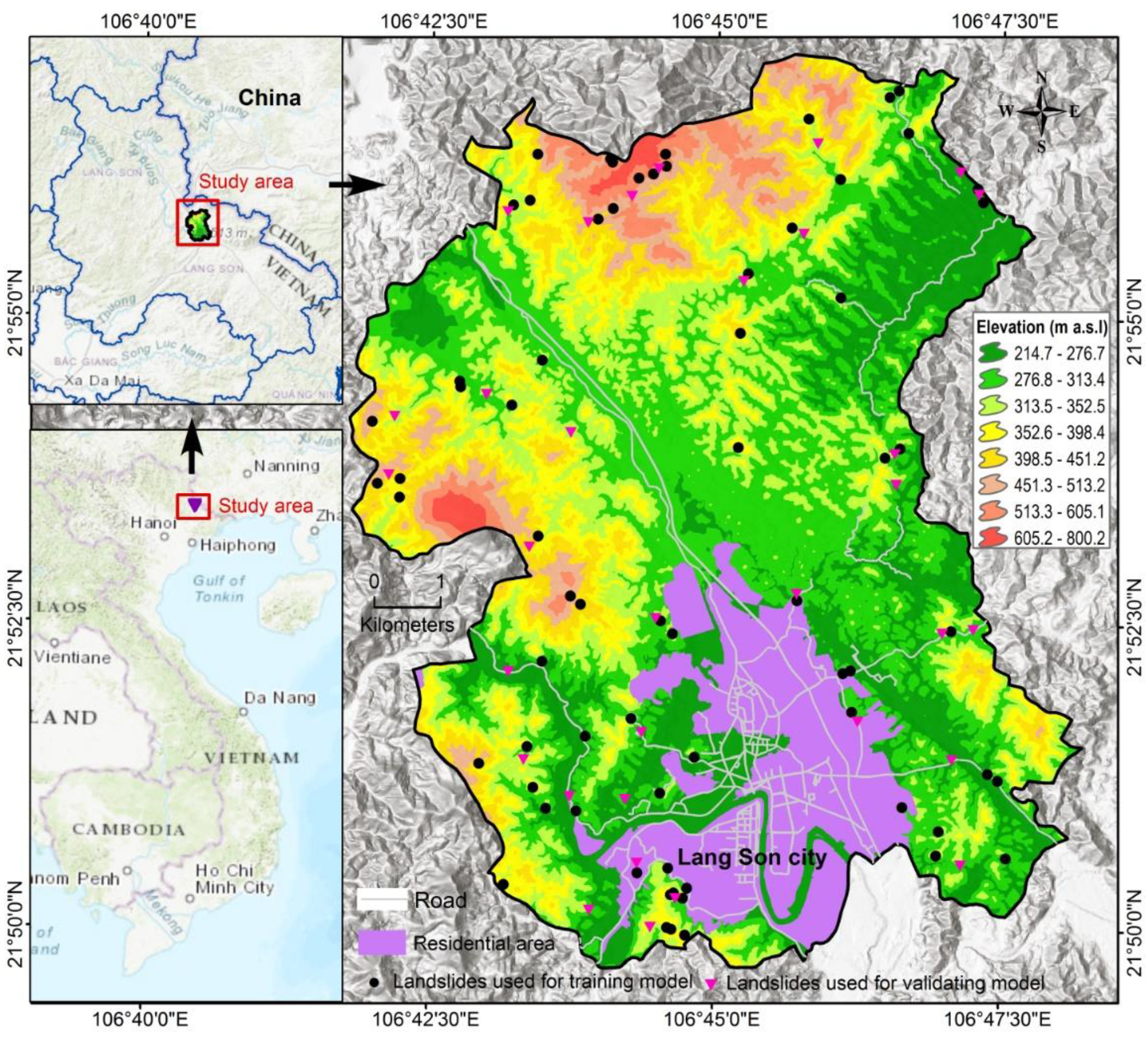
2.1. Description of the Study Area
2.2. Data Preparation
2.2.1. Landslide Inventory Map
- (i)
- The locations of landslides, occurring before the year 2003, are identified by the interpretation of aerial photographs with resolution of about 1 m (obtained from the Aerial Photo-Topography Company, 2003) and field survey data.
- (ii)
- (iii)
- Some recent landslide locations were identified during field works by Nguyen et al. [88].
2.2.2. Landslide Conditioning Factors
3. Methodology
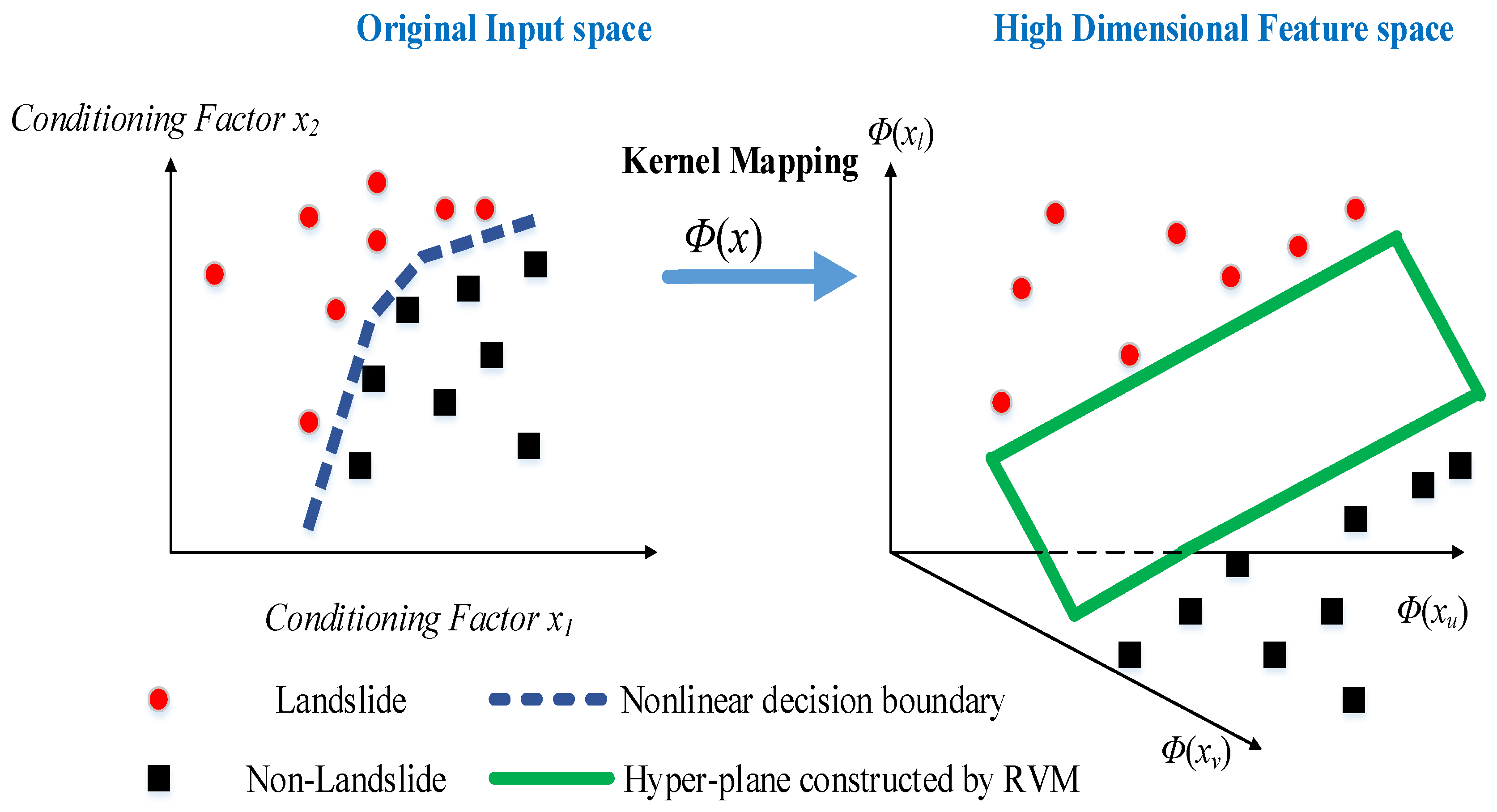
3.1. Relevance Vector Machine
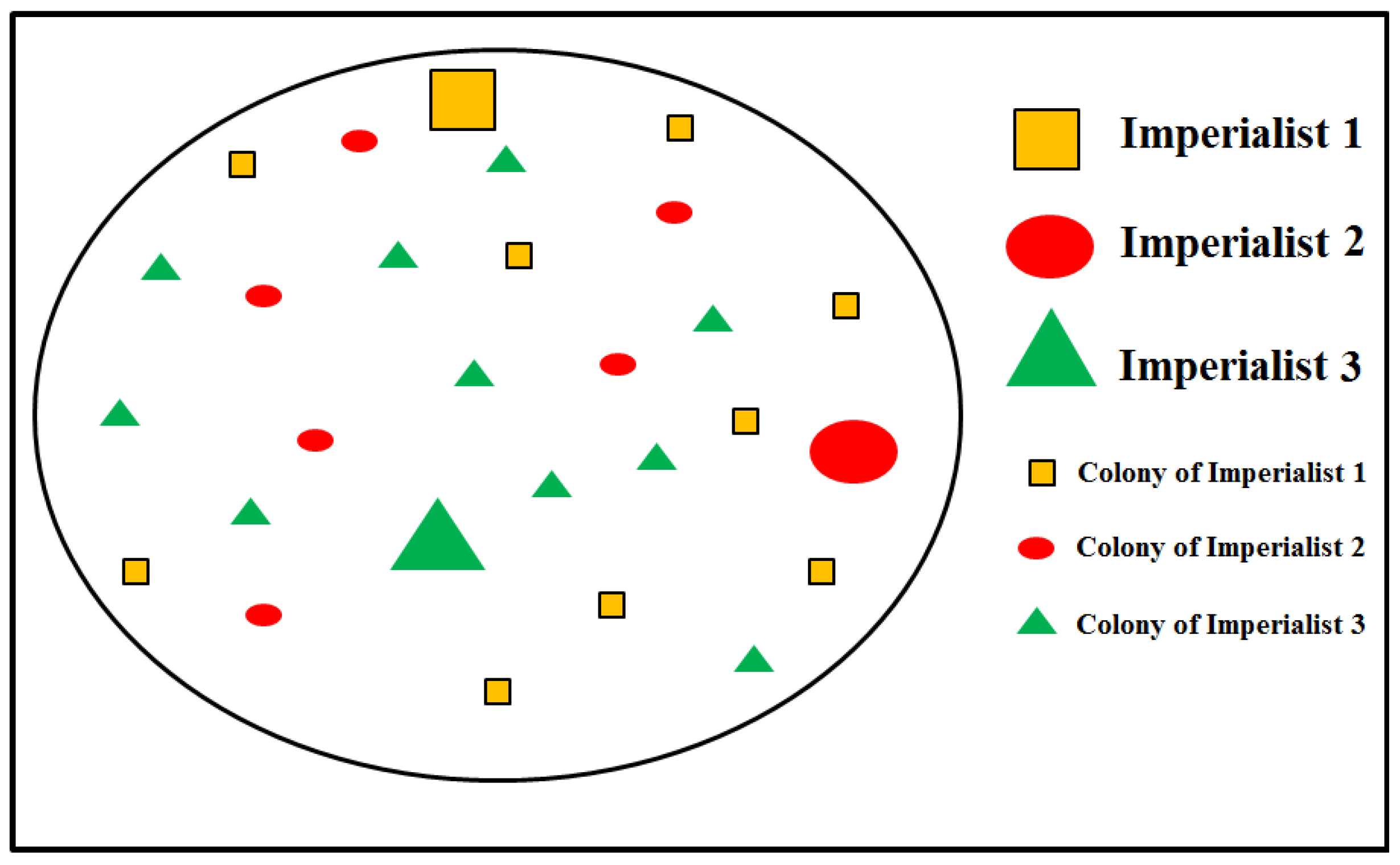
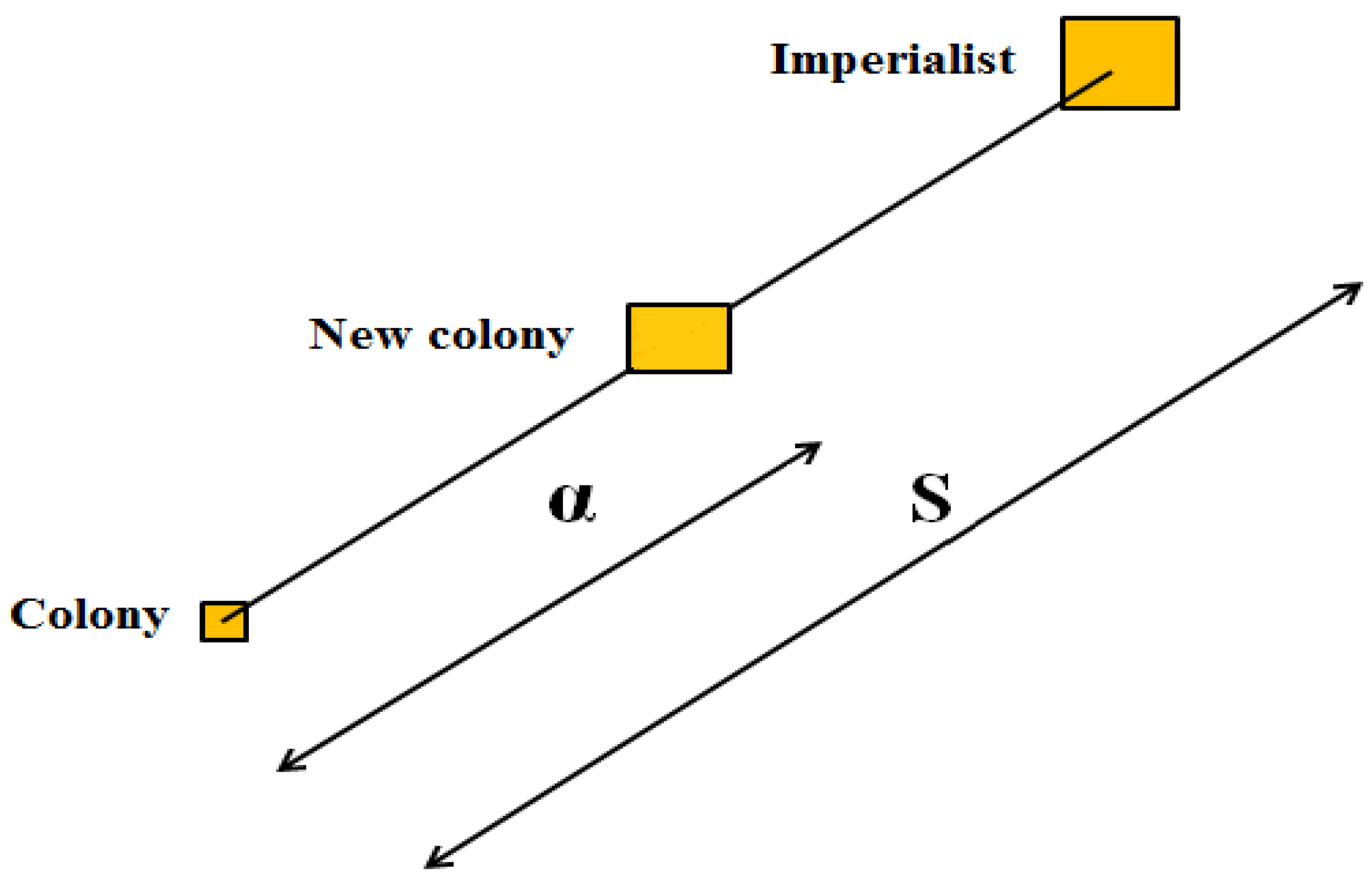
3.2. Imperialist Competitive Algorithm (ICA)
3.3. Performance Evaluation
3.3.1. Statistical-Based Measures
3.3.2. Receiver Operating Characteristic (ROC) Curve
3.4. The Proposed Integration Approach Based on RVM and ICA for Spatial Modeling of Rainfall-Induced Shallow Landslides
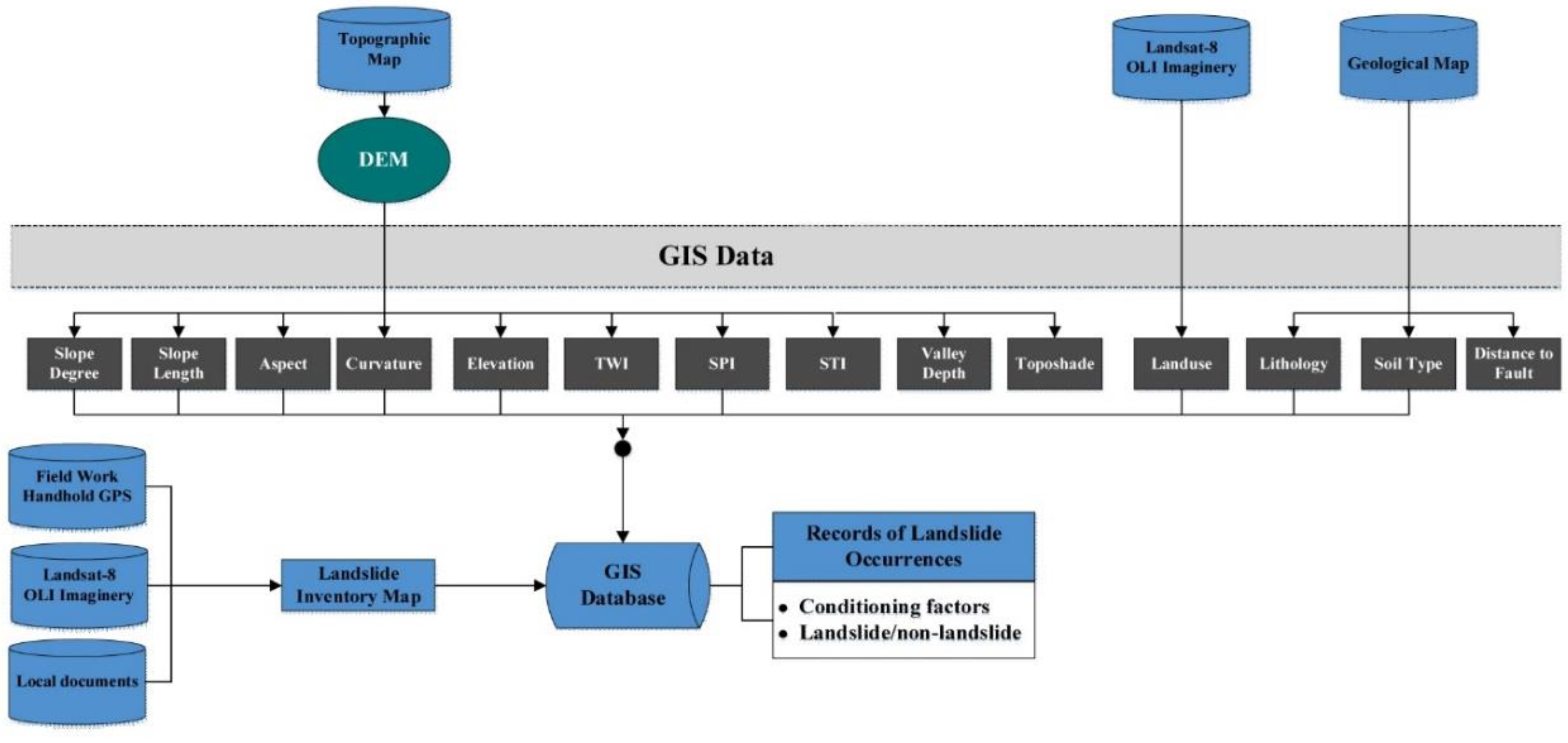
3.4.1. GIS Database, Training and Validation Datasets
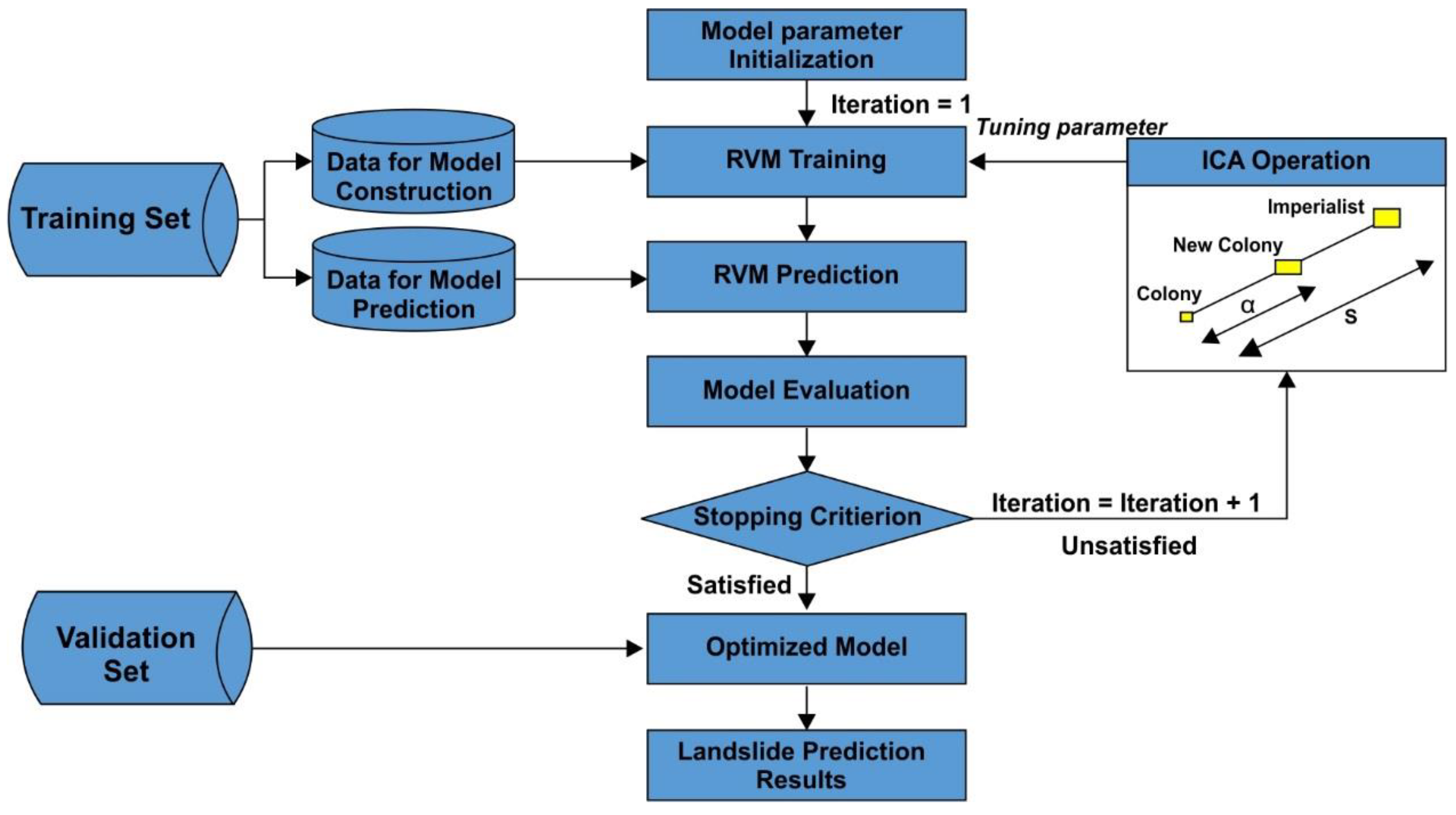
3.4.2. The Proposed Model Structure
4. Results and Analysis
4.1. Factor Selection Using Information Gain Ratio (IGR)
4.2. Training and Validation Process
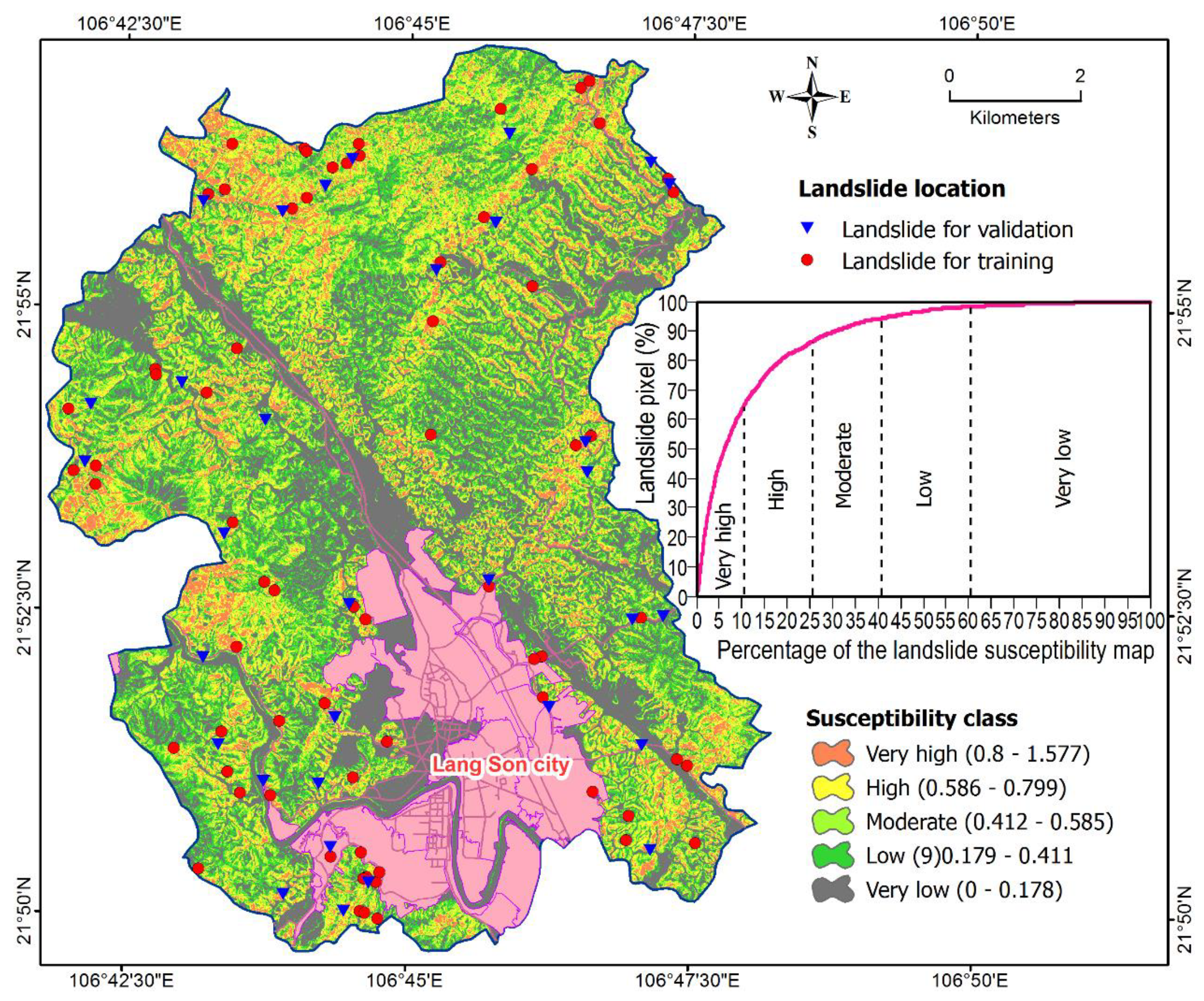
4.3. Construction of the Susceptibility Map
4.4. Model Comparison
5. Discussion
6. Concluding Remark
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Varnes, D.J. Slope movement types and processes. Spec. Rep. 1978, 176, 11–33. [Google Scholar]
- Dai, F.; Lee, C.; Ngai, Y.Y. Landslide risk assessment and management: An overview. Eng. Geol. 2002, 64, 65–87. [Google Scholar] [CrossRef]
- Guzzetti, F.; Reichenbach, P.; Ardizzone, F.; Cardinali, M.; Galli, M. Estimating the quality of landslide susceptibility models. Geomorphology 2006, 81, 166–184. [Google Scholar] [CrossRef]
- Shirzadi, A.; Bui, D.T.; Pham, B.T.; Solaimani, K.; Chapi, K.; Kavian, A.; Shahabi, H.; Revhaug, I. Shallow landslide susceptibility assessment using a novel hybrid intelligence approach. Environ. Earth Sci. 2017, 76, 60–78. [Google Scholar] [CrossRef]
- Malamud, B.D.; Turcotte, D.L.; Guzzetti, F.; Reichenbach, P. Landslide inventories and their statistical properties. Earth Surf. Process. Landf. 2004, 29, 687–711. [Google Scholar] [CrossRef]
- Chau, K.; Sze, Y.; Fung, M.; Wong, W.; Fong, E.; Chan, L. Landslide hazard analysis for hong kong using landslide inventory and gis. Comput. Geosci. 2004, 30, 429–443. [Google Scholar] [CrossRef]
- Van Den Eeckhaut, M.; Verstraeten, G.; Poesen, J. Morphology and internal structure of a dormant landslide in a hilly area: The collinabos landslide (Belgium). Geomorphology 2007, 89, 258–273. [Google Scholar] [CrossRef]
- Shahabi, H.; Hashim, M. Landslide susceptibility mapping using gis-based statistical models and remote sensing data in tropical environment. Sci. Rep. 2015, 5, 9899. [Google Scholar] [CrossRef] [PubMed]
- Van Westen, C.J.; Castellanos, E.; Kuriakose, S.L. Spatial data for landslide susceptibility, hazard, and vulnerability assessment: An overview. Eng. Geol. 2008, 102, 112–131. [Google Scholar] [CrossRef]
- Remondo, J.; Bonachea, J.; Cendrero, A. A statistical approach to landslide risk modelling at basin scale: From landslide susceptibility to quantitative risk assessment. Landslides 2005, 2, 321–328. [Google Scholar] [CrossRef]
- Maharaj, R.J. Landslide processes and landslide susceptibility analysis from an upland watershed: A case study from St. Andrew, Jamaica, West Indies. Eng. Geol. 1993, 34, 53–79. [Google Scholar] [CrossRef]
- Hoang, N.-D.; Tien Bui, D. Spatial prediction of rainfall-induced shallow landslides using gene expression programming integrated with gis: A case study in Vietnam. Nat. Hazards 2018, 92, 1871–1887. [Google Scholar] [CrossRef]
- Martha, T.R.; Roy, P.; Govindharaj, K.B.; Kumar, K.V.; Diwakar, P.; Dadhwal, V. Landslides triggered by the June 2013 extreme rainfall event in parts of Uttarakhand state, India. Landslides 2015, 12, 135–146. [Google Scholar] [CrossRef]
- Thanh, L.N.; De Smedt, F. Application of an analytical hierarchical process approach for landslide susceptibility mapping in a luoi district, thua thien hue province, Vietnam. Environ. Earth Sci. 2012, 66, 1739–1752. [Google Scholar] [CrossRef]
- Barry, R.G.; Chorley, R.J. Atmosphere, Weather and Climate; Routledge: Abingdon, UK, 2009. [Google Scholar]
- Salinger, M.J. Climate variability and change: Past, present and future—An overview. In Increasing Climate Variability and Change; Springer: Berlin, Germany, 2005; pp. 9–29. [Google Scholar]
- Lima, P.; Steger, S.; Glade, T.; Tilch, N.; Schwarz, L.; Kociu, A. Landslide Susceptibility Mapping at National Scale: A First Attempt for Austria; Springer International Publishing: Cham, Switzerland, 2017; pp. 943–951. [Google Scholar]
- Jaiswal, P.; van Westen, C.J.; Jetten, V. Quantitative landslide hazard assessment along a transportation corridor in southern India. Eng. Geol. 2010, 116, 236–250. [Google Scholar] [CrossRef]
- Nilsen, T.H. Relative Slope Stability and Land-Use Planning in the San Francisco Bay Region, California; US Government Printing Office: Washington, DC, USA, 1979; Volume 944.
- Nilsen, T.H.; Brabb, E.E. Current slope-stability studies in the san francisco bay region. J. Res. US Geol. Surv. 1973, 1, 327–431. [Google Scholar]
- Nilsen, T.; Brabb, E.E. Slope stability studies in the san francisco bay region, California. Geol. Soc. Am. Rev. Eng. Geol. 1977, 3, 235–243. [Google Scholar]
- Kienholz, H. Maps of geomorphology and natural hazards of Grindelwald, Switzerland: Scale 1:10,000. Arct. Alp. Res. 1978, 10, 169–184. [Google Scholar] [CrossRef]
- Fell, R.; Corominas, J.; Bonnard, C.; Cascini, L.; Leroi, E.; Savage, W.Z. Guidelines for landslide susceptibility, hazard and risk zoning for land use planning. Eng. Geol. 2008, 102, 85–98. [Google Scholar] [CrossRef] [Green Version]
- Moosavi, V.; Niazi, Y. Development of hybrid wavelet packet-statistical models (WP-SM) for landslide susceptibility mapping. Landslides 2016, 13, 97–114. [Google Scholar] [CrossRef]
- Chen, J.; Zeng, Z.; Jiang, P.; Tang, H. Application of multi-gene genetic programming based on separable functional network for landslide displacement prediction. Neural Comput. Appl. 2016, 27, 1771–1784. [Google Scholar] [CrossRef]
- Meinhardt, M.; Fink, M.; Tünschel, H. Landslide susceptibility analysis in central Vietnam based on an incomplete landslide inventory: Comparison of a new method to calculate weighting factors by means of bivariate statistics. Geomorphology 2015, 234, 80–97. [Google Scholar] [CrossRef]
- Ballabio, C.; Sterlacchini, S. Support vector machines for landslide susceptibility mapping: The staffora river basin case study, Italy. Math. Geosci. 2012, 44, 47–70. [Google Scholar] [CrossRef]
- Matin, M.A.; Chitale, V.S.; Murthy, M.S.R.; Uddin, K.; Bajracharya, B.; Pradhan, S. Understanding forest fire patterns and risk in nepal using remote sensing, geographic information system and historical fire data. Int. J. Wildl. Fire 2017, 26, 276–286. [Google Scholar] [CrossRef]
- Tien Bui, D.; Hoang, N.D. A bayesian framework based on a gaussian mixture model and radial-basis-function fisher discriminant analysis (baygmmkda v1.1) for spatial prediction of floods. Geosci. Model Dev. 2017, 10, 3391–3409. [Google Scholar] [CrossRef]
- Samodra, G.; Chen, G.; Sartohadi, J.; Kasama, K. Comparing data-driven landslide susceptibility models based on participatory landslide inventory mapping in purwosari area, Yogyakarta, Java. Environ. Earth Sci. 2017, 76, 184–203. [Google Scholar] [CrossRef]
- Dehnavi, A.; Aghdam, I.N.; Pradhan, B.; Varzandeh, M.H.M. A new hybrid model using step-wise weight assessment ratio analysis (Swara) technique and adaptive neuro-fuzzy inference system (Anfis) for regional landslide hazard assessment in iran. Catena 2015, 135, 122–148. [Google Scholar] [CrossRef]
- Ahmed, B. Landslide susceptibility mapping using multi-criteria evaluation techniques in chittagong metropolitan area, bangladesh. Landslides 2015, 12, 1077–1095. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Blaschke, T. An uncertainty and sensitivity analysis approach for gis-based multicriteria landslide susceptibility mapping. Int. J. Geogr. Inf. Sci. 2014, 28, 610–638. [Google Scholar] [CrossRef] [PubMed]
- Shirzadi, A.; Saro, L.; Joo, O.H.; Chapi, K. A gis-based logistic regression model in rock-fall susceptibility mapping along a mountainous road: Salavat abad case study, Kurdistan, Iran. Nat. Hazards 2012, 64, 1639–1656. [Google Scholar] [CrossRef]
- Shahabi, H.; Hashim, M.; Ahmad, B.B. Remote sensing and gis-based landslide susceptibility mapping using frequency ratio, logistic regression, and fuzzy logic methods at the central Zab Basin, Iran. Environ. Earth Sci. 2015, 73, 8647–8668. [Google Scholar] [CrossRef]
- Othman, A.A.; Gloaguen, R.; Andreani, L.; Rahnama, M. Improving landslide susceptibility mapping using morphometric features in the mawat area, Kurdistan region, NE Iraq: Comparison of different statistical models. Geomorphology 2018, 319, 147–160. [Google Scholar] [CrossRef]
- Shahabi, H.; Ahmad, B.; Khezri, S. Evaluation and comparison of bivariate and multivariate statistical methods for landslide susceptibility mapping (case study: Zab basin). Arab. J. Geosci. 2013, 6, 3885–3907. [Google Scholar] [CrossRef]
- Süzen, M.L.; Doyuran, V. A comparison of the gis based landslide susceptibility assessment methods: Multivariate versus Bivariate. Environ. Geol. 2004, 45, 665–679. [Google Scholar] [CrossRef]
- Shahabi, H.; Khezri, S.; Ahmad, B.B.; Hashim, M. Landslide susceptibility mapping at central zab basin, iran: A comparison between analytical hierarchy process, frequency ratio and logistic regression models. Catena 2014, 115, 55–70. [Google Scholar] [CrossRef]
- Komac, M. A landslide susceptibility model using the analytical hierarchy process method and multivariate statistics in perialpine Slovenia. Geomorphology 2006, 74, 17–28. [Google Scholar] [CrossRef]
- Wang, L.-J.; Guo, M.; Sawada, K.; Lin, J.; Zhang, J. Landslide susceptibility mapping in mizunami city, Japan: A comparison between logistic regression, bivariate statistical analysis and multivariate adaptive regression spline models. Catena 2015, 135, 271–282. [Google Scholar] [CrossRef]
- Felicísimo, Á.M.; Cuartero, A.; Remondo, J.; Quirós, E. Mapping landslide susceptibility with logistic regression, multiple adaptive regression splines, classification and regression trees, and maximum entropy methods: A comparative study. Landslides 2013, 10, 175–189. [Google Scholar] [CrossRef]
- Tan, Y.; Guo, D.; Xu, B. A geospatial information quantity model for regional landslide risk assessment. Nat. Hazards 2015, 79, 1385–1398. [Google Scholar] [CrossRef]
- Lee, S.; Choi, J. Landslide susceptibility mapping using gis and the weight-of-evidence model. Int. J. Geogr. Inf. Sci. 2004, 18, 789–814. [Google Scholar] [CrossRef]
- Bui, D.T.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar]
- Chen, W.; Shahabi, H.; Shirzadi, A.; Li, T.; Guo, C.; Hong, H.; Li, W.; Pan, D.; Hui, J.; Ma, M. A novel ensemble approach of bivariate statistical-based logistic model tree classifier for landslide susceptibility assessment. Geocarto Int. 2018, 1–23. [Google Scholar] [CrossRef]
- Althuwaynee, O.F.; Pradhan, B.; Lee, S. Application of an evidential belief function model in landslide susceptibility mapping. Comput. Geosci. 2012, 44, 120–135. [Google Scholar] [CrossRef]
- He, S.; Pan, P.; Dai, L.; Wang, H.; Liu, J. Application of kernel-based fisher discriminant analysis to map landslide susceptibility in the qinggan river delta, three gorges, china. Geomorphology 2012, 171, 30–41. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Peng, J.; Shahabi, H.; Hong, H.; Bui, D.T.; Duan, Z.; Li, S.; Zhu, A.-X. Gis-based landslide susceptibility evaluation using a novel hybrid integration approach of bivariate statistical based random forest method. Catena 2018, 164, 135–149. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, S.; Li, R.; Shahabi, H. Performance evaluation of the gis-based data mining techniques of best-first decision tree, random forest, and naïve bayes tree for landslide susceptibility modeling. Sci. Total Environ. 2018, 644, 1006–1018. [Google Scholar] [CrossRef]
- Ngoc-Thach, N.; Ngo, D.B.-T.; Xuan-Canh, P.; Hong-Thi, N.; Thi, B.H.; NhatDuc, H.; Dieu, T.B. Spatial pattern assessment of tropical forest fire danger at thuan chau area (vietnam) using gis-based advanced machine learning algorithms: A comparative study. Ecol. Inform. 2018, 46, 74–85. [Google Scholar] [CrossRef]
- Ercanoglu, M.; Dağdelenler, G.; Özsayin, E.; Alkevlı, T.; Sönmez, H.; Özyurt, N.N.; Kahraman, B.; Uçar, İ.; Çetınkaya, S. Application of chebyshev theorem to data preparation in landslide susceptibility mapping studies: An example from yenice (Karabük, Turkey) region. J. Mt. Sci. 2016, 13, 1923–1940. [Google Scholar] [CrossRef]
- Mandal, S.; Mandal, K. Modeling and mapping landslide susceptibility zones using gis based multivariate binary logistic regression (LR) model in the rorachu river basin of eastern Sikkim Himalaya, India. Model. Earth Syst. Environ. 2018, 4, 69–88. [Google Scholar] [CrossRef]
- Hong, H.; Pradhan, B.; Xu, C.; Bui, D.T. Spatial prediction of landslide hazard at the yihuang area (China) using two-class kernel logistic regression, alternating decision tree and support vector machines. Catena 2015, 133, 266–281. [Google Scholar] [CrossRef]
- Hong, H.; Liu, J.; Zhu, A.-X.; Shahabi, H.; Pham, B.T.; Chen, W.; Pradhan, B.; Bui, D.T. A novel hybrid integration model using support vector machines and random subspace for weather-triggered landslide susceptibility assessment in the wuning area (China). Environ. Earth Sci. 2017, 76, 652. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Jones, S.; Shabani, F.; Martínez-Álvarez, F.; Bui, D.T. A novel ensemble modeling approach for the spatial prediction of tropical forest fire susceptibility using logitboost machine learning classifier and multi-source geospatial data. Theor. Appl. Climatol. 2018, 1–17. [Google Scholar] [CrossRef]
- Pradhan, B.; Sezer, E.A.; Gokceoglu, C.; Buchroithner, M.F. Landslide susceptibility mapping by neuro-fuzzy approach in a landslide-prone area (cameron highlands, Malaysia). IEEE Trans. Geosci. Remote Sens. 2010, 48, 4164–4177. [Google Scholar] [CrossRef]
- Chen, W.; Panahi, M.; Tsangaratos, P.; Shahabi, H.; Ilia, I.; Panahi, S.; Li, S.; Jaafari, A.; Ahmad, B.B. Applying population-based evolutionary algorithms and a neuro-fuzzy system for modeling landslide susceptibility. Catena 2019, 172, 212–231. [Google Scholar] [CrossRef]
- Tien Bui, D.; Khosravi, K.; Li, S.; Shahabi, H.; Panahi, M.; Singh, V.; Chapi, K.; Shirzadi, A.; Panahi, S.; Chen, W. New hybrids of anfis with several optimization algorithms for flood susceptibility modeling. Water 2018, 10, 1210. [Google Scholar] [CrossRef]
- Shadman Roodposhti, M.; Aryal, J.; Shahabi, H.; Safarrad, T. Fuzzy shannon entropy: A hybrid gis-based landslide susceptibility mapping method. Entropy 2016, 18, 343. [Google Scholar] [CrossRef]
- Pham, B.T.; Bui, D.T.; Pourghasemi, H.R.; Indra, P.; Dholakia, M. Landslide susceptibility assesssment in the uttarakhand area (India) using gis: A comparison study of prediction capability of naïve bayes, multilayer perceptron neural networks, and functional trees methods. Theor. Appl. Climatol. 2017, 128, 255–273. [Google Scholar] [CrossRef]
- Shirzadi, A.; Chapi, K.; Shahabi, H.; Solaimani, K.; Kavian, A.; Ahmad, B.B. Rock fall susceptibility assessment along a mountainous road: An evaluation of bivariate statistic, analytical hierarchy process and frequency ratio. Environ. Earth Sci. 2017, 76, 152–169. [Google Scholar] [CrossRef]
- Chen, W.; Shirzadi, A.; Shahabi, H.; Ahmad, B.B.; Zhang, S.; Hong, H.; Zhang, N. A novel hybrid artificial intelligence approach based on the rotation forest ensemble and naïve bayes tree classifiers for a landslide susceptibility assessment in langao county, China. Geomat. Nat. Hazards Risk 2017, 8, 1955–1977. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Pradhan, B.; Chen, W.; Khosravi, K.; Panahi, M.; Bin Ahmad, B.; Saro, L. Land subsidence susceptibility mapping in south korea using machine learning algorithms. Sensors 2018, 18, 2464. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Peng, J.; Hong, H.; Shahabi, H.; Pradhan, B.; Liu, J.; Zhu, A.-X.; Pei, X.; Duan, Z. Landslide susceptibility modelling using gis-based machine learning techniques for chongren county, Jiangxi province, China. Sci. Total Environ. 2018, 626, 1121–1135. [Google Scholar] [CrossRef] [PubMed]
- Fatemi Aghda, S.M.; Bagheri, V.; Razifard, M. Landslide susceptibility mapping using fuzzy logic system and its influences on mainlines in lashgarak region, Tehran, Iran. Geotech. Geol. Eng. 2018, 36, 915–937. [Google Scholar] [CrossRef]
- Pham, B.T.; Tien Bui, D.; Prakash, I. Bagging based support vector machines for spatial prediction of landslides. Environ. Earth Sci. 2018, 77, 146–161. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, L. Review on landslide susceptibility mapping using support vector machines. Catena 2018, 165, 520–529. [Google Scholar] [CrossRef]
- Pham, B.T.; Tien Bui, D.; Prakash, I. Landslide susceptibility assessment using bagging ensemble based alternating decision trees, logistic regression and J48 decision trees methods: A comparative study. Geotech. Geol. Eng. 2017, 35, 2597–2611. [Google Scholar] [CrossRef]
- Wang, L.-J.; Guo, M.; Sawada, K.; Lin, J.; Zhang, J. A comparative study of landslide susceptibility maps using logistic regression, frequency ratio, decision tree, weights of evidence and artificial neural network. Geosci. J. 2016, 20, 117–136. [Google Scholar] [CrossRef]
- Bishop, C. Pattern Recognition and Machine Learning; Springer Science + Business Media: Singapore, 2006. [Google Scholar]
- Tien Bui, D.; Tuan, T.A.; Hoang, N.-D.; Thanh, N.Q.; Nguyen, D.B.; Van Liem, N.; Pradhan, B. Spatial prediction of rainfall-induced landslides for the lao cai area (Vietnam) using a hybrid intelligent approach of least squares support vector machines inference model and artificial bee colony optimization. Landslides 2016, 14, 447–458. [Google Scholar] [CrossRef]
- Hoang, N.-D.; Tien Bui, D.; Liao, K.-W. Groutability estimation of grouting processes with cement grouts using differential flower pollination optimized support vector machine. Appl. Soft Comput. 2016, 45, 173–186. [Google Scholar] [CrossRef]
- Xue, X. Prediction of slope stability based on hybrid PSO and LSSVM. J. Comput. Civ. Eng. 2017, 31, 04016041. [Google Scholar] [CrossRef]
- Prayogo, D.; Susanto, Y.T.T. Optimizing the prediction accuracy of friction capacity of driven piles in cohesive soil using a novel self-tuning least squares support vector machine. Adv. Civ. Eng. 2018, 2018, 1–9. [Google Scholar] [CrossRef]
- Qi, C.; Fourie, A.; Ma, G.; Tang, X.; Du, X. Comparative study of hybrid artificial intelligence approaches for predicting hangingwall stability. J. Comput. Civ. Eng. 2018, 32, 04017086. [Google Scholar] [CrossRef]
- Hong, H.; Tsangaratos, P.; Ilia, I.; Liu, J.; Zhu, A.X.; Xu, C. Applying genetic algorithms to set the optimal combination of forest fire related variables and model forest fire susceptibility based on data mining models. The case of Dayu county, China. Sci. Total Environ. 2018, 630, 1044–1056. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Panahi, M.; Pourghasemi, H.R. Performance evaluation of gis-based new ensemble data mining techniques of adaptive neuro-fuzzy inference system (ANFIS) with genetic algorithm (GA), differential evolution (DE), and particle swarm optimization (PSO) for landslide spatial modelling. Catena 2017, 157, 310–324. [Google Scholar] [CrossRef]
- Hoang, N.-D.; Tien-Bui, D. A novel relevance vector machine classifier with cuckoo search optimization for spatial prediction of landslides. J. Comput. Civ. Eng. 2016, 30, 04016001. [Google Scholar] [CrossRef]
- Tipping, M.E. The relevance vector machine. Adv. Neural Inf. Process. Syst. 2000, 12, 652–658. [Google Scholar]
- Atashpaz-Gargari, E.; Lucas, C. Imperialist Competitive Algorithm: An Algorithm for Optimization Inspired by Imperialistic Competition. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 4661–4667. [Google Scholar]
- Imani, M.; Kao, H.-C.; Lan, W.-H.; Kuo, C.-Y. Daily sea level prediction at chiayi coast, taiwan using extreme learning machine and relevance vector machine. Glob. Planet. Chang. 2018, 161, 211–221. [Google Scholar] [CrossRef]
- Bui, D.T.; Pradhan, B.; Revhaug, I.; Tran, C.T. A comparative assessment between the application of fuzzy unordered rules induction algorithm and J48 decision tree models in spatial prediction of shallow landslides at lang son city, Vietnam. In Remote Sensing Applications in Environmental Research; Springer: Berlin, Germnay, 2014; pp. 87–111. [Google Scholar]
- Quoc, N.D.; Hung, L.; Huyen, D.T. Geological Map; Institute of Geosciences and Mineral Resources: Hanoi, Vietnam, 1992. [Google Scholar]
- Bui, D.T.; Pradhan, B.; Revhaug, I.; Nguyen, D.B.; Pham, H.V.; Bui, Q.N. A novel hybrid evidential belief function-based fuzzy logic model in spatial prediction of rainfall-induced shallow landslides in the lang son city area (Vietnam). Geomat. Nat. Hazards Risk 2015, 6, 243–271. [Google Scholar] [CrossRef]
- Tam, V.; Tuy, P.; Nam, N.; Tuan, L.; Tuan, N.; Trung, N.; Thang, D.; Ha, P. Geohazard Investigation in Some Key Areas of the Northern Mountainous Area of Vietnam for the Planning of Socio-Economic Development; Vietnam Institute of Geosciences and Mineral Resources: Hanoi, Vietnam, 2006; Volume 83, pp. 56–62. [Google Scholar]
- Nguyen, Q.-K.; Tien Bui, D.; Hoang, N.-D.; Trinh, P.; Nguyen, V.-H.; Yilmaz, I. A novel hybrid approach based on instance based learning classifier and rotation forest ensemble for spatial prediction of rainfall-induced shallow landslides using gis. Sustainability 2017, 9, 813. [Google Scholar] [CrossRef]
- Jebur, M.N.; Pradhan, B.; Tehrany, M.S. Using alos palsar derived high-resolution dinsar to detect slow-moving landslides in tropical forest: Cameron highlands, Malaysia. Geomat. Nat. Hazards Risk 2015, 6, 741–759. [Google Scholar] [CrossRef]
- Hung, L.Q.; Van, N.T.H.; Duc, D.M.; Van Son, P.; Khanh, N.H.; Binh, L.T. Landslide susceptibility mapping by combining the analytical hierarchy process and weighted linear combination methods: A case study in the upper lo river Catchment (Vietnam). Landslides 2016, 13, 1285–1301. [Google Scholar] [CrossRef]
- Huang, S.L.; Yamasaki, K. Slope failure analysis using local minimum factor-of-safety approach. J. Geotech. Eng. 1993, 119, 1974–1989. [Google Scholar] [CrossRef]
- Yalcin, A. Gis-based landslide susceptibility mapping using analytical hierarchy process and bivariate statistics in ardesen (Turkey): Comparisons of results and confirmations. Catena 2008, 72, 1–12. [Google Scholar] [CrossRef]
- Gomez, H.; Kavzoglu, T. Assessment of shallow landslide susceptibility using artificial neural networks in jabonosa river basin, venezuela. Eng. Geol. 2005, 78, 11–27. [Google Scholar] [CrossRef]
- Clerici, A.; Perego, S.; Tellini, C.; Vescovi, P. A gis-based automated procedure for landslide susceptibility mapping by the conditional analysis method: The baganza valley case study (Italian Northern Apennines). Environ. Geol. 2006, 50, 941–961. [Google Scholar] [CrossRef]
- Ohlmacher, G.C. Plan curvature and landslide probability in regions dominated by earth flows and earth slides. Eng. Geol. 2007, 91, 117–134. [Google Scholar] [CrossRef]
- Walker, L.R.; Shiels, A.B. Landslide Ecology; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Wilson, J.P.; Gallant, J.C. Terrain Analysis: Principles and Applications; John Wiley & Sons: Mississauga, ON, Canada, 2000. [Google Scholar]
- Ozdemir, A. Landslide susceptibility mapping using bayesian approach in the Sultan Mountains (Akşehir, Turkey). Nat. Hazards 2011, 59, 1573–1607. [Google Scholar] [CrossRef]
- Poudyal, C.P.; Chang, C.; Oh, H.-J.; Lee, S. Landslide susceptibility maps comparing frequency ratio and artificial Neural networks: A case study from the Nepal Himalaya. Environ. Earth Sci. 2010, 61, 1049–1064. [Google Scholar] [CrossRef]
- Moore, I.D.; Wilson, J.P. Length-slope factors for the revised universal soil loss equation: Simplified method of estimation. J. Soil Water Conserv. 1992, 47, 423–428. [Google Scholar]
- Pradhan, A.M.S.; Kim, Y.-T. Relative effect method of landslide susceptibility zonation in weathered granite soil: A case study in Deokjeok-ri creek, South Korea. Nat. Hazards 2014, 72, 1189–1217. [Google Scholar] [CrossRef]
- Devkota, K.C.; Regmi, A.D.; Pourghasemi, H.R.; Yoshida, K.; Pradhan, B.; Ryu, I.C.; Dhital, M.R.; Althuwaynee, O.F. Landslide susceptibility mapping using certainty factor, index of entropy and logistic regression models in gis and their comparison at mugling–narayanghat road section in Nepal Himalaya. Nat. Hazards 2013, 65, 135–165. [Google Scholar] [CrossRef] [Green Version]
- Jebur, M.N.; Pradhan, B.; Tehrany, M.S. Optimization of landslide conditioning factors using very high-resolution airborne laser scanning (Lidar) data at catchment scale. Remote Sens. Environ. 2014, 152, 150–165. [Google Scholar] [CrossRef]
- Hong, H.; Chen, W.; Xu, C.; Youssef, A.M.; Pradhan, B.; Tien Bui, D. Rainfall-induced landslide susceptibility assessment at the chongren area (China) using frequency ratio, certainty factor, and index of entropy. Geocarto Int. 2016, 32, 139–154. [Google Scholar] [CrossRef]
- Caniani, D.; Pascale, S.; Sdao, F.; Sole, A. Neural networks and landslide susceptibility: A case study of the urban area of Potenza. Nat. Hazards 2008, 45, 55–72. [Google Scholar] [CrossRef]
- Ercanoglu, M.; Kasmer, O.; Temiz, N. Adaptation and comparison of expert opinion to analytical hierarchy process for landslide susceptibility mapping. Bull. Eng. Geol. Environ. 2008, 67, 565–578. [Google Scholar] [CrossRef]
- Zhao, C.; Chen, W.; Wang, Q.; Wu, Y.; Yang, B. A comparative study of statistical index and certainty factor models in landslide susceptibility mapping: A case study for the Shangzhou district, shaanxi province, China. Arab. J. Geosci. 2015, 8, 9079–9088. [Google Scholar] [CrossRef]
- Ayalew, L.; Yamagishi, H. The application of gis-based logistic regression for landslide susceptibility mapping in the Kakuda-Yahiko mountains, central Japan. Geomorphology 2005, 65, 15–31. [Google Scholar] [CrossRef]
- Yesilnacar, E.; Topal, T. Landslide susceptibility mapping: A comparison of logistic regression and neural networks methods in a medium scale study, Hendek region (Turkey). Eng. Geol. 2005, 79, 251–266. [Google Scholar] [CrossRef]
- Nefeslioglu, H.A.; Duman, T.Y.; Durmaz, S. Landslide susceptibility mapping for a part of tectonic Kelkit Valley (Eastern Black sea region of Turkey). Geomorphology 2008, 94, 401–418. [Google Scholar] [CrossRef]
- Gorum, T.; Fan, X.; van Westen, C.J.; Huang, R.Q.; Xu, Q.; Tang, C.; Wang, G. Distribution pattern of earthquake-induced landslides triggered by the 12 may 2008 wenchuan earthquake. Geomorphology 2011, 133, 152–167. [Google Scholar] [CrossRef]
- Tipping, M.E. Sparse bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Pardo, B.A. Professional employment. IEEE Trans. Signal Process. 2014, 62, 4298–4310. [Google Scholar]
- Bishop, C.M.; Tipping, M.E. Variational relevance vector machines. In Proceedings of the Sixteenth Conference on Uncertainty in Artificial Intelligence, San Francisco, CA, USA, 30 June–3 July 2000; pp. 46–53. [Google Scholar]
- Hosseini, S.; Al Khaled, A. A survey on the imperialist competitive algorithm metaheuristic: Implementation in engineering domain and directions for future research. Appl. Soft Comput. 2014, 24, 1078–1094. [Google Scholar] [CrossRef]
- Sadowski, L.; Nikoo, M. Corrosion current density prediction in reinforced concrete by imperialist competitive algorithm. Neural Comput. Appl. 2014, 25, 1627–1638. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rao, R.V. Teaching-learning-based optimization algorithm. In Teaching Learning Based Optimization Algorithm; Springer: Berlin, Germany, 2016; pp. 9–39. [Google Scholar]
- Kaveh, A.; Talatahari, S. Optimum design of skeletal structures using imperialist competitive algorithm. Comput. Struct. 2010, 88, 1220–1229. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to roc analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Pham, B.T.; Shirzadi, A.; Bui, D.T.; Prakash, I.; Dholakia, M. A hybrid machine learning ensemble approach based on a radial basis function neural network and rotation forest for landslide susceptibility modeling: A case study in the Himalayan area, India. Int. J. Sediment Res. 2018, 33, 157–170. [Google Scholar] [CrossRef]
- Pham, B.T.; Bui, D.T.; Prakash, I.; Nguyen, L.H.; Dholakia, M. A comparative study of sequential minimal optimization-based support vector machines, vote feature intervals, and logistic regression in landslide susceptibility assessment using gis. Environ. Earth Sci. 2017, 76, 371. [Google Scholar] [CrossRef]
- Micheletti, N.; Foresti, L.; Robert, S.; Leuenberger, M.; Pedrazzini, A.; Jaboyedoff, M.; Kanevski, M. Machine learning feature selection methods for landslide susceptibility mapping. Math. Geosci. 2014, 46, 33–57. [Google Scholar] [CrossRef]
- Forman, G. An extensive empirical study of feature selection metrics for text classification. J. Mach. Learn. Res. 2003, 3, 1289–1305. [Google Scholar]
- Abedini, M.; Ghasemian, B.; Shirzadi, A.; Shahabi, H.; Chapi, K.; Pham, B.T.; Bin Ahmad, B.; Tien Bui, D. A novel hybrid approach of bayesian logistic regression and its ensembles for landslide susceptibility assessment. Geocarto Int. 2018, 14, 447–458. [Google Scholar] [CrossRef]
- Lee, S. Comparison of landslide susceptibility maps generated through multiple logistic regression for three test areas in Korea. Earth Surf. Process. Landf. J. Br. Geomorphol. Rese. 2007, 32, 2133–2148. [Google Scholar] [CrossRef]
- Chung, C.J.F.; Fabbri, A.G. Validation of spatial prediction models for landslide hazard mapping. Nat. Hazards 2003, 30, 451–472. [Google Scholar] [CrossRef]
- Chung, C.-J.F.; Fabbri, A.G.; Van Westen, C.J. Multivariate regression analysis for landslide hazard Zonation. In Geographical Information Systems in Assessing Natural Hazards; Springer: Berlin, Germany, 1995; pp. 107–133. [Google Scholar]
- Ohlmacher, G.C.; Davis, J.C. Using multiple logistic regression and gis technology to predict landslide Hazard in Northeast Kansas, USA. Eng. Geol. 2003, 69, 331–343. [Google Scholar] [CrossRef]
- Pham, B.T.; Pradhan, B.; Tien Bui, D.; Prakash, I.; Dholakia, M.B. A comparative study of different machine learning methods for landslide susceptibility assessment: A case study of uttarakhand area (India). Environ. Model. Softw. 2016, 84, 240–250. [Google Scholar] [CrossRef]



| No. | Factors | Classes |
|---|---|---|
| 1 | Slope (degree) | (1) 0–8.1; (2) 8.2–15.1; (3) 15.2–24.3; (4) 24.4–31.5; (5) 31.6–41.1; (6) 41.2–80.4 |
| 2 | Slope length (m) | (1) 0–8.6; (2) 8.7–34.8; (3) 34.9–61.1; (4) 61.2–84.9; (5) 85–774.2 |
| 3 | Aspect | (1) Flat; (2) N; (3) NE; (4) E; (5) SE; (6) S; (7) SW; (8) W; (9) NW |
| 4 | Curvature | (1) >−2.1; (2) −2–−0.1; (3) −0.1–0.1; (4) 0.1–2.1; (5) <2.1 |
| 5 | Elevation (m) | (1) 214.7–269.7; (2) 269.8–295.6; (3) 295.7–326.5; (4) 326.6–373.6; (5) 373.7–413.9; (6) 432–553.4; (7) 553.5–800.2 |
| 6 | TWI | (1) 1.3–4.2; (2) 4.3–5.3; (3) 5.4–6.4; (4) 6.5–8.1; (5) 8.2–9.4; (6) 9.5–20.8 |
| 7 | SPI | (1) 0–20.2; (2) 20.3–80.8; (3) 80.9–151.8; (4) 151.9–211.8; (5) 211.9–270.1; (6) >270.1 |
| 8 | STI | (1) 0–6.8; (2) 6.9–22; (3) 22.1–38.2; (4) 38.3–44.2; (5) 44.3–72.9; (6) >72.9 |
| 9 | Valley depth (m) | (1) −128.8–−12.1; (2) −12–13.4; (3) 13.5–32.2; (4) 32.3–53.7; (5) 53.8–85.9; (6) 86–213.4 |
| 10 | Toposhade | (1) Ridge; (2) Saddle; (3) Flat; (4) Ravine; (5) Convex hillside; (6) Saddle hillside; (7) Slope hillside; (8) Concave hillside; (9) Inflection hillside; (10) Unknown hillside |
| 11 | Land use | (1) RA; (2) PTL; (3) PDL; (4) PL; (5) BL; (6) PCL; (7) WSL |
| 12 | Soil type | (1) FA; (2) DG; (3) PA; (4) WS; (5) DF; (6) EF; (7) RF; (8) RMS |
| 13 | Lithology | (1) Tuff; (2) Sandstone; (3) Siltstone; (4) Quaternary; (5) Basalt; (6) Conglomerate |
| 14 | Distance to fault (m) | (1) 0–100; (2) 100–200; (3) 200–300; (4) 300–400; (5) >400 |
| No | Conditioning Factor | Average Predictive Ability | Standard Deviation |
|---|---|---|---|
| 1 | Slope (degree) | 0.601 | 0.002 |
| 2 | STI | 0.378 | 0.005 |
| 3 | Aspect | 0.230 | 0.003 |
| 4 | SPI | 0.217 | 0.004 |
| 5 | TWI | 0.215 | 0.003 |
| 6 | Land use | 0.155 | 0.002 |
| 7 | Curvature | 0.152 | 0.003 |
| 8 | Toposhade | 0.121 | 0.002 |
| 9 | Lithology | 0.118 | 0.002 |
| 10 | Elevation (m) | 0.119 | 0.001 |
| 11 | Slope length (m) | 0.072 | 0.003 |
| 12 | Distance to fault (m) | 0.068 | 0.002 |
| 13 | Soil type | 0.055 | 0.001 |
| 14 | Valley depth (m) | 0.023 | 0.001 |
| Statistical Index | Relevance Vector Machine | Logistic Regression | Support Vector Machine |
|---|---|---|---|
| True positive | 2338 | 2200 | 2319 |
| True negative | 2061 | 2040 | 2109 |
| False positive | 72 | 209 | 91 |
| False negative | 349 | 370 | 301 |
| Sensitivity (%) | 87.0 | 85.6 | 88.5 |
| Specificity (%) | 96.6 | 90.7 | 95.9 |
| Accuracy (%) | 91.3 | 88.0 | 91.9 |
| Statistical Index | Relevance Vector Machine | Logistic Regression | Support Vector Machine |
|---|---|---|---|
| True positive | 945 | 798 | 857 |
| True negative | 867 | 869 | 911 |
| False positive | 90 | 246 | 187 |
| False negative | 178 | 176 | 135 |
| Sensitivity (%) | 84.1 | 81.9 | 86.4 |
| Specificity (%) | 90.6 | 77.9 | 83.0 |
| Accuracy (%) | 87.1 | 79.8 | 84.6 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tien Bui, D.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Hoang, N.-D.; Pham, B.T.; Bui, Q.-T.; Tran, C.-T.; Panahi, M.; Bin Ahmad, B.; et al. A Novel Integrated Approach of Relevance Vector Machine Optimized by Imperialist Competitive Algorithm for Spatial Modeling of Shallow Landslides. Remote Sens. 2018, 10, 1538. https://doi.org/10.3390/rs10101538
Tien Bui D, Shahabi H, Shirzadi A, Chapi K, Hoang N-D, Pham BT, Bui Q-T, Tran C-T, Panahi M, Bin Ahmad B, et al. A Novel Integrated Approach of Relevance Vector Machine Optimized by Imperialist Competitive Algorithm for Spatial Modeling of Shallow Landslides. Remote Sensing. 2018; 10(10):1538. https://doi.org/10.3390/rs10101538
Chicago/Turabian StyleTien Bui, Dieu, Himan Shahabi, Ataollah Shirzadi, Kamran Chapi, Nhat-Duc Hoang, Binh Thai Pham, Quang-Thanh Bui, Chuyen-Trung Tran, Mahdi Panahi, Baharin Bin Ahmad, and et al. 2018. "A Novel Integrated Approach of Relevance Vector Machine Optimized by Imperialist Competitive Algorithm for Spatial Modeling of Shallow Landslides" Remote Sensing 10, no. 10: 1538. https://doi.org/10.3390/rs10101538
APA StyleTien Bui, D., Shahabi, H., Shirzadi, A., Chapi, K., Hoang, N.-D., Pham, B. T., Bui, Q.-T., Tran, C.-T., Panahi, M., Bin Ahmad, B., & Saro, L. (2018). A Novel Integrated Approach of Relevance Vector Machine Optimized by Imperialist Competitive Algorithm for Spatial Modeling of Shallow Landslides. Remote Sensing, 10(10), 1538. https://doi.org/10.3390/rs10101538











