2.1. Study Area and Field Measurement
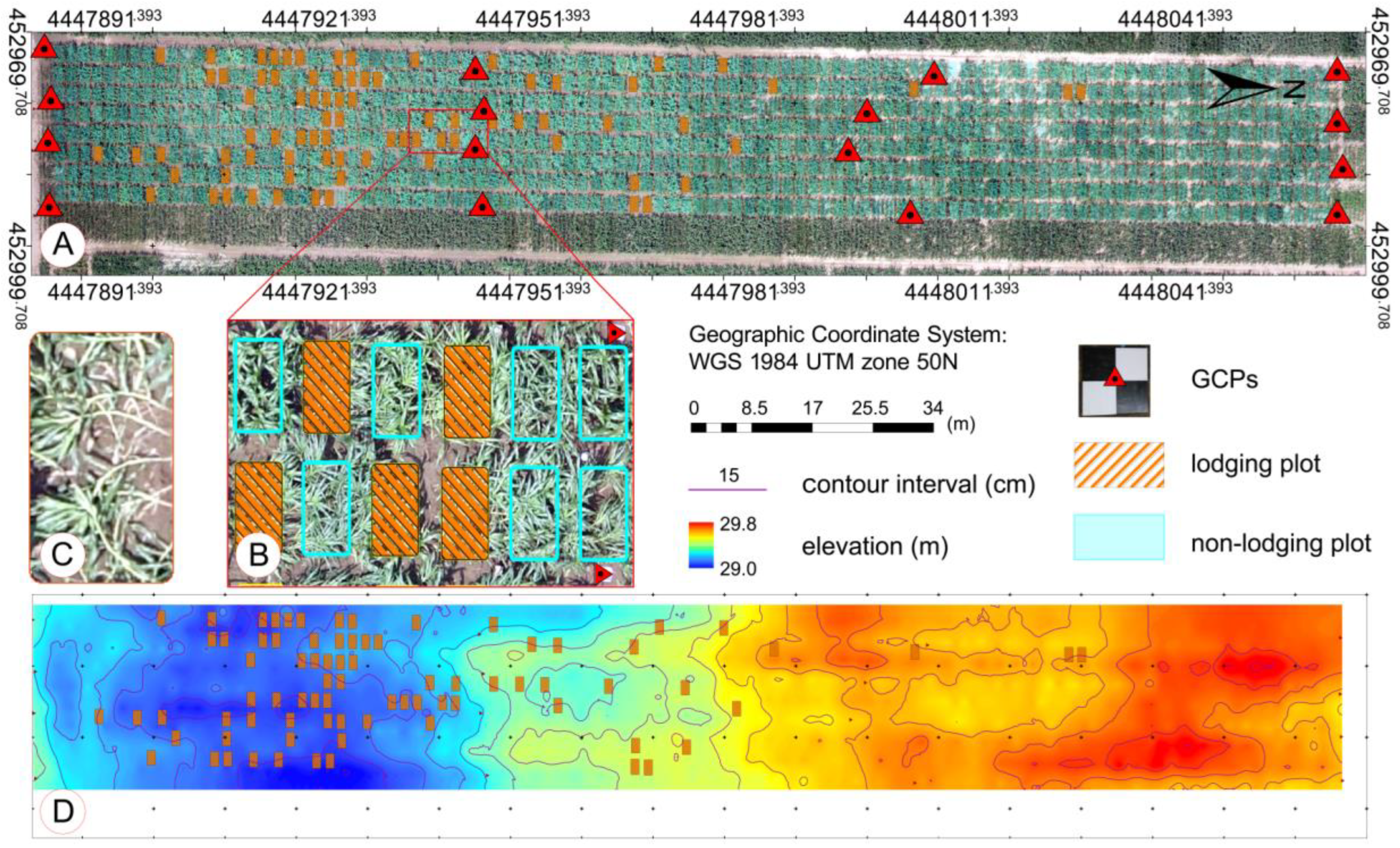
The field trial was conducted at the research station of Xiao Tangshan National Precision Agriculture Research Center of China, which covers an area of about two square kilometers and is located in the Changping District of Beijing City. The trial area was approximately 210 m from north to south and approximately 27 m from east to west. A single factor breeding trial with the randomized block design was adopted in this study. Maize seeds of different genetic backgrounds with differences in growth period and stalk stiffness were sown on 15 May 2017. Eight hundred maize breeding plots with a size of 2.4 m × 2 m were arranged in 100 rows and 8 columns and used to observe the phenotypic expression of maize. These plots were planted using a seeding density of 6 plants/m
2 and a row spacing of 0.6 m. To extract the plant height from UAV images accurately, 16 ground control points (GCPs) were distributed evenly within the field (
Figure 1) and measured with a differential global positioning system (DGPS, South Surveying & Mapping Instrument Co., Ltd., Shenzhen, China) with millimeter accuracy. The GCPs were marked with 50 cm × 50 cm, black and white, square planks were nailed to a stake stably fixed in the ground. Meteorological data were acquired from QT-1060 open-path eddy-covariance systems (Channel Technology Group Limited, Beijing, China) in the field. From 1 to 10 July, there were several strong winds and rainfall, and the daily average precipitation reached 7.6 mm, which resulted in the lodging of maize on 11 July 2017. It was then that maize in the trial area was at the growth stage 19 (BBCH-scale) [
26].
In 72 sampling plots, plant height was measured manually by a telescopic leveling rod. Avoiding the influence of marginal effects and growth competition, the average of the three plants in the center of each sampling plot was counted as the representative value for the ground truth of plant height. Removing 11 sampling plots affected by lodging from 72 sampling plots, 61 sampling plots were used to validate plant height extraction accuracy.
2.2. UAV Flight and Image Processing
A Sony Cyber-shot DSC-QX100 (Sony Electronics Inc., Tokyo, Japan) camera (resolution: 5472 × 3648 pixels) served as an optical sensor to record RGB images and a Parrot Sequoia (MicaSense Inc., Seattle, WA, USA) camera (resolution: 1280 × 960 pixels, four different spectral bands: green (wavelength 550 nm; bandwidth 40 nm), red (wavelength 660 nm; bandwidth 40 nm), red-edge (wavelength 735 nm; bandwidth 10 nm) and near infrared (wavelength 790 nm; bandwidth 40 nm)) served as a multispectral sensor to acquire spectral images, were mounted on a DJI Spreading Wings S1000 (SZ DJI Technology Co., Shenzhen, China) simultaneously. The radiometric calibration images of the Parrot Sequoia camera were captured by using a calibrated reflectance panel (MicaSense Inc., Seattle, WA, USA) on the ground before and after each flight. The flight altitude above ground level on 8 June 2017, and 11 July 2017, were set to 40 m and 60 m, yielding the ground sampling distance (GSD) of 0.72 cm and 1.3 cm, respectively. The forward overlap was 80% and the lateral overlap was 75%. Each flight speed was set to 6 m per second. ISO and shutter speed were set to a fixed value (i.e., 160 and 1/2000, respectively). A total of 287 digital images and 110 per band multi-spectral images were collected.
According to Reference [
27], Agisoft PhotoScan (full-featured trial version 1.3, Agisoft LLC, St. Petersburg, Russia) software implementing a structure-from-motion (SFM) algorithm was used to stitch digital images. The key steps of this process included the image geolocation, GCPs import, image alignment, building a dense point cloud, and building a digital surface model (DSM) and orthoimage. For multispectral images, besides the above key steps, radiation correction and vegetation index calculations were also included. A Pix4Dmapper Pro (version 4.0, PIX4D, Lausanne, Switzerland) was used to reconstruct multispectral images. Radiometric calibration was done by using radiometric calibration images with known reflectance values provided by Micasense. Using the index calculator in the Pix4D software, an NDVI map was produced. We used an Otsu algorithm [
28] to determine a threshold and transformed the NDVI image into a binary image. The binary image was used to distinguish between plants and the soil background. ArcMap (version 10.2, Esri Inc., Redlands, CA, USA) was used to create areas of interest (AOIs) in the binary image with covered plants, and to extract the average NDVI for each plot.
The crop surface model (CSM) was normalized by subtracting the digital elevation model (DEM) from the DSM [
29,
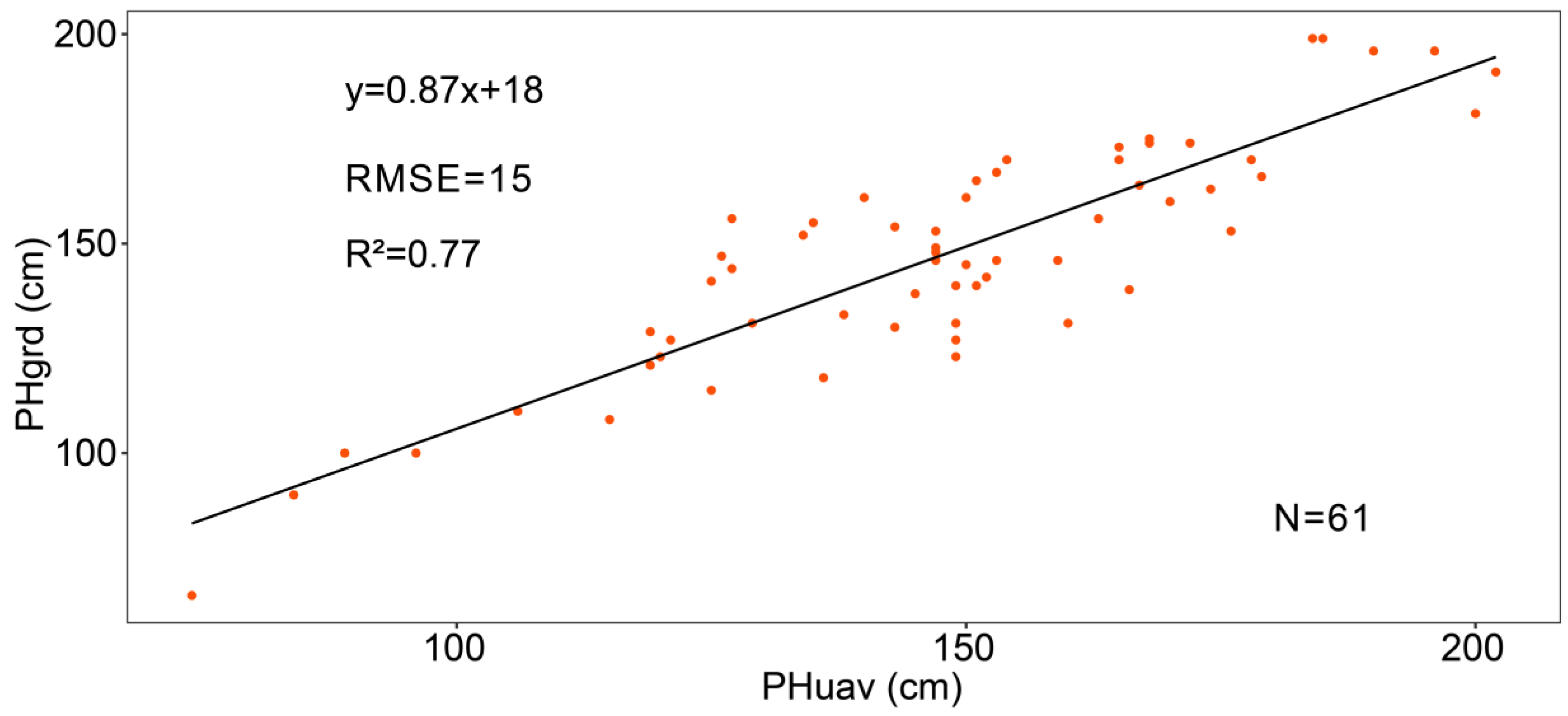
30]. DSMs were the model output from the Agisoft Photoscan Pro software by using images captured on 8 June and 11 July, respectively. On 8 June, maize was about at growth stage 13 (BBCH-scale) and the average plant height of the plots was less than 20 cm. We extracted 1332 elevation points from the DSM on 8 June that were not covered with vegetation. The DEM was interpolated from these 1332 points with the ordinary Kriging spatial interpolation method by using ArcMap. Using AOIs (only cover vegetation), we extracted plant height information on 11 11 July from the CSM by the ENVI software (version 4.5, Esri Inc., Redlands, CA, USA). A linear fitting model was developed to test the relationship of the plant height between UAV observations and manual measurements. This model explained 77% of the variations in maize plant height, with a root mean square error (RMSE) of 15 cm (
Figure 2).
In the stitching processing, 16 GCPs were used to optimize the camera position and orientation, which allowed for the improvement of the georeferenced accuracy of the DSM and orthoimage. The contents listed in
Table 1 were used to evaluate the accuracy of DSMs and orthoimage.
2.3. Potential Factors for Maize Lodging
Before and after the lodging, canopy structure, texture, and spectral characteristics of the maize population changed to varying degrees, which were regarded as feature factors of maize lodging identification in this study. The genetic background was reported to be related to the lodging resistance of maize [
31,
32], so the genetic background (G) was considered as a potential factor. Although previous studies had shown that planting density had an impact on crop lodging [
33], this trial adopted uniform standard mechanized planting, averaging about 24 plants in a plot, so planting density factor was not considered.
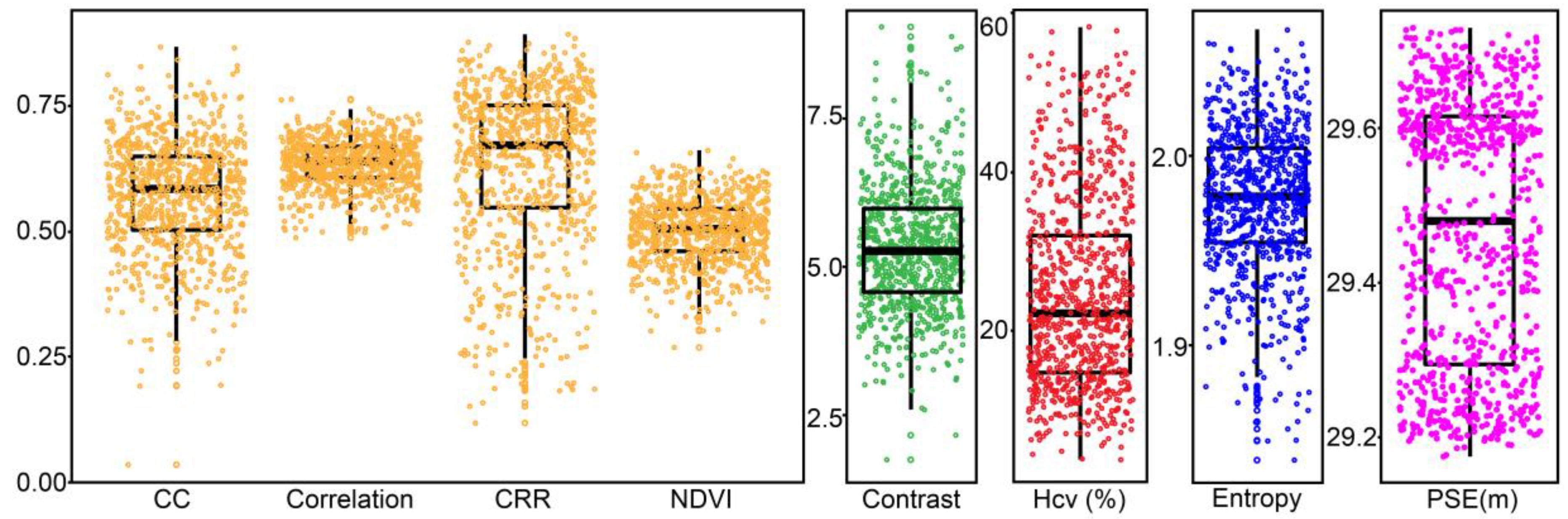
Since the plot was small and flat, the surface elevation (PSE) of a plot could be represented by one single numeric value. PSE is an average value calculated by the elevation values at four corners and center of a plot. These elevation values were extracted from the DEM. After multiple rainfalls, terrain may cause spatial variability in the soil moisture, leading to waterlogging in parts of the study area. Therefore, the PSE revealed terrain changes at the plot scale, which was considered a potential factor for lodging identification.
In this study, the canopy structure was described in two dimensions: horizontal and vertical. Canopy cover (CC) was regarded as an indicator of the development of the canopy structure in the horizontal direction, implicating information on maize leaf density and planting area. According to Reference [
34], green and non-green pixels in the orthoimage were segmented by using the excess green index (EXG) proposed by Woebbecke et al. [
35]. CC was calculated as the ratio of the area between green pixels and total pixels within a plot. Canopy elevation relief ratio (CRR) and the coefficient of variation of canopy height (Hcv) were the metrics of the vertical canopy structure. Hcv is defined as the ratio of the canopy height standard deviation (Hstd) to the mean (Hmean), which has been confirmed by multiple studies to effectively describe the heterogeneity of the canopy plant height in the vertical direction [
10,
36,
37,
38]. CRR is commonly used as a metric that describes the relative shape of the canopy in forestry studies, which can be calculated with minimum (Hmin), maximum (Hmax), and mean (Hmean) of the plant height. CRR represents the degree to which the outer canopy surfaces are in the upper (CRR > 0.5) or in the lower (CRR < 0.5) portions of the height range [
39,
40].
Gray-co-occurrence matrices (GLCM) were frequently used to quantitatively evaluate texture features that can be used for image classification and target recognition [
41]. Previous studies had shown no redundancy between Entropy, Contrast, and Correlation in many GLCM textural parameters [
42]. Therefore, the three texture feature parameters were considered as potential factors. Minarno et al. [
43] had introduced the extraction method of texture feature parameters in detail.
According to Reference [
14], the normalized difference vegetation index (NDVI) had a good indication of the lodging identification, where the relative increase of the canopy spectral reflectance in the visible light band was higher than that in the near-infrared band after lodging. Therefore, NDVI as a spectral feature parameter participated in the lodging recognition and factor analysis. Potential feature factors and parameters are summarized in
Table 2.
Pij is element i,j of the normalized symmetrical GLCM. N is the number of gray levels in the image as specified by the number of levels under quantization on the GLCM texture page of the variable properties dialog box. is the GLCM mean, and is calculated using: . is the variance of the intensities of all reference pixels in the relationships that contributed to the GLCM, and is calculated using: . EXG is the excess green index, NDVI is the normalized difference vegetation index, CC is the canopy cover, and CRR is the canopy elevation relief ratio. , , , and represent the minimum, maximum, mean, and standard deviation of the plant height at the plot scale, respectively. indicates the calculation of areas, and and are the reflectances for near-infrared and red bands, respectively. represents the elevation at five sampling points of a plot.
These feature parameter acquisitions were repeated for each plot based on the 11 July data and divided into two groups, namely, the lodging group and non-lodging group. We combined a field investigation and image-based visual interpretation to determine the ground truth; namely, whether lodging occurs in a plot. Before and after lodging, the change of stem-to-leaf ratio at the plot scale was the main visual discrimination criterion. Stalks of maize in the lodging plots were clearly observed from the orthoimage (
Figure 1C part). The non-lodging group treated as a control group was created using stratified random sampling according to row number. When modeling, CC, CRR, Hcv, NDVI, Entropy, Contrast, and Correlation were treated as continuous variables, and PSE and G were treated as categorical variables. Therefore, PSE needed to be discretized and converted into categorical variables so that it was easier to interpret the results. In this study, the R package “apcluster” (version 1.4.5) [
48] was used to implement the affinity propagation (AP) clustering algorithm [
49], which could automatically determine the optimal number of clusters. The clustering result was divided into two grades, high and low, which represented the difference in terrain within the study area.
2.4. Predictors Selection and Modeling
Predictors (i.e., feature parameters) should have significant differences between the lodging and non-lodging group. In order to preliminarily filter some potential predictors that were not relevant for modeling, testing for significant differences between the two groups was performed. According to different data distribution conditions (normal or non-normal distribution) and types of predictor variables (continuous or categorical variables), different test methods were used. A Shapiro and Wilk test at the 0.05 level was applied to check whether continuous predictor variables followed a normal distribution [
50]. If the continuous predictor variables followed the normal distribution, the mean and standard deviation was used to describe the distribution of predictors, and the
t-test was used to compare the difference between groups; otherwise, the median and interquartile was used to describe the distribution of predictors, and a Mann Whitney U test was used to compare the difference between groups. No statistically significant continuous predictor variables (
p-value > 0.05) were removed and no longer involved in modeling [
51]. A χ
2 test was applied to check for categorical predictor variables, and no statistically significant categorical predictor variables (
p-value > 0.05) were retained [
24].
Univariate logistic regression analysis was used to examine whether predictor variables had an independent effect on maize lodging and preliminarily determined predictors relevant for modeling [
52]. Multivariate logistic regression analysis was used to further explore confounding predictors and discover the underlying association between the outcome and the selected predictors [
53]. Backward selection procedures applying asymptotic significant correlations for the log-likelihood ratio test (
p-value < 0.001) were used to select the predictors in the logistic regression analysis.
In this study, the binary logistic regression model was created to estimate the probability of a binary outcome (i.e., non-lodging or lodging) based on multiple selected predictors. Lodging was coded as “1”, and a contrary outcome (i.e., non-lodging) was coded as “0”. Following this, a binary outcome named “Islodging” was defined for modeling:
Islodging = 0, the negative outcome, if a non-lodging event occurred in a plot
Islodging = 1, the positive outcome, if a lodging event occurred in a plot
The probability of a positive outcome is
P and that of a negative outcome is
Q (
Q = 1 −
P). Then, the logit for multivariable logistic regression given by the equation below:
The lodging probability is:
where
is the intercept,
are regression coefficients, and Hcv, NDVI, PSE, and so on are the predictors.
and
were estimated using the maximum likelihood method, which is designed to maximize the likelihood of reproducing the data given the parameter estimates [
54]. A Hosmer–Lemeshow test (
p-value > 0.05 indicating good fit) was performed to test the fitting degree of logistic regression model and to ensure that all the factors in the model were adequately utilized [
55].
The ratio of
P to
Q is defined as the odds ratio (OR). The outcome of a logistic regression model is the logarithm of the OR, which is linearly related to the weighted sum of multiple predictors. The odds ratios and 95% confidence intervals (CI) were calculated. The interpretation of final logistic regression model for maize lodging was rendered using the OR-value of predictors. When
> 0 and OR > 1 in the models, the predictor variable was deemed as a risk factor. When
< 0 and OR < 1 in the models, the predictor variable was deemed as a protective factor [
56,
57].
2.5. Nomogram Construction and Evaluation
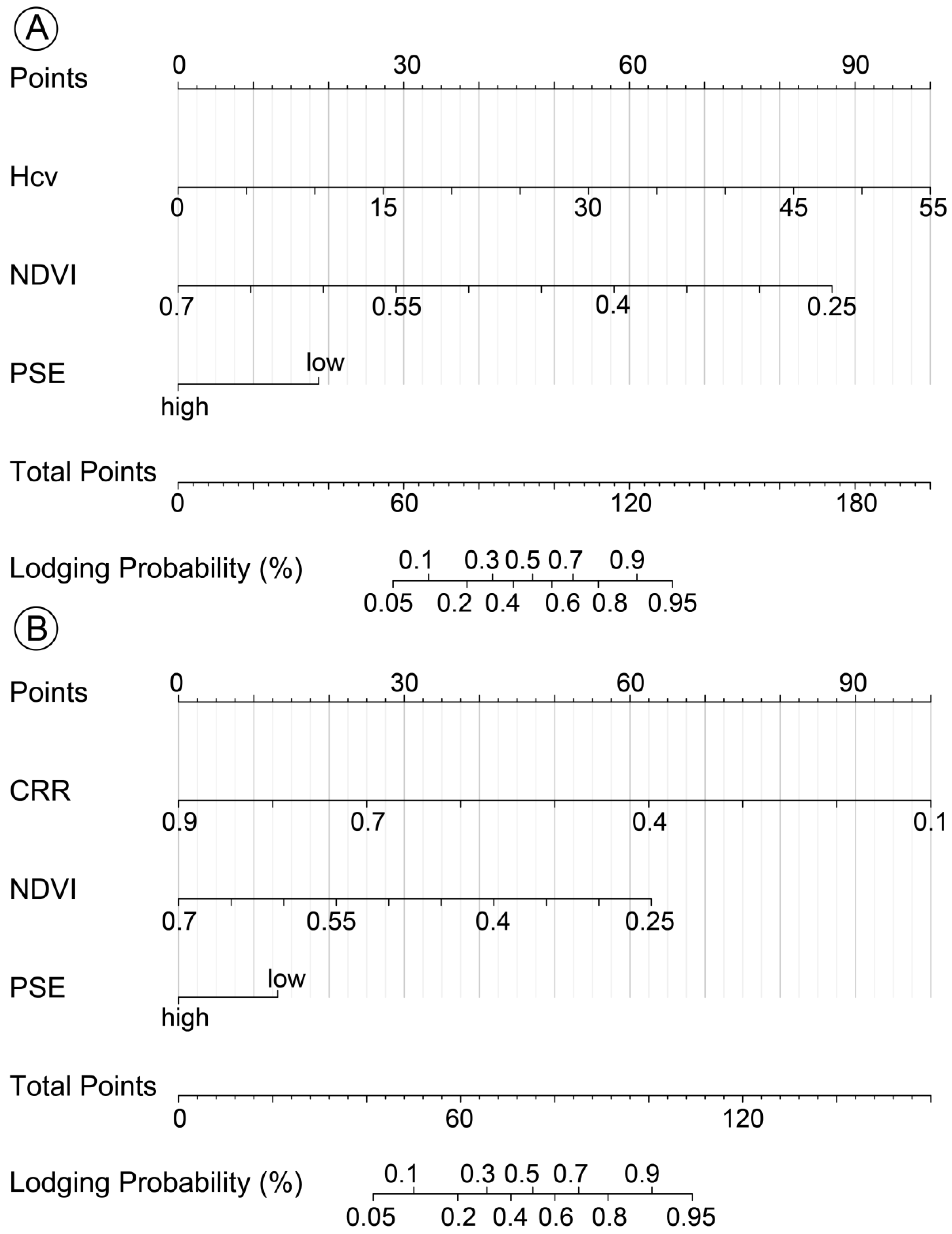
Nomograms were constructed to evaluate the lodging probability and the strength effect of each predictor. In the nomogram, the point corresponding to a predictor variable was converted from the fitting coefficient of the regression model. The predictor with the largest strength effect on lodging was taken as the reference and all points were rescaled to values between 0 and 100 [
25]. Longer horizontal lines represent larger points and indicate the larger effects on lodging. Total points at the bottom scale provided insight into the likelihood that a maize plot will be lodging.
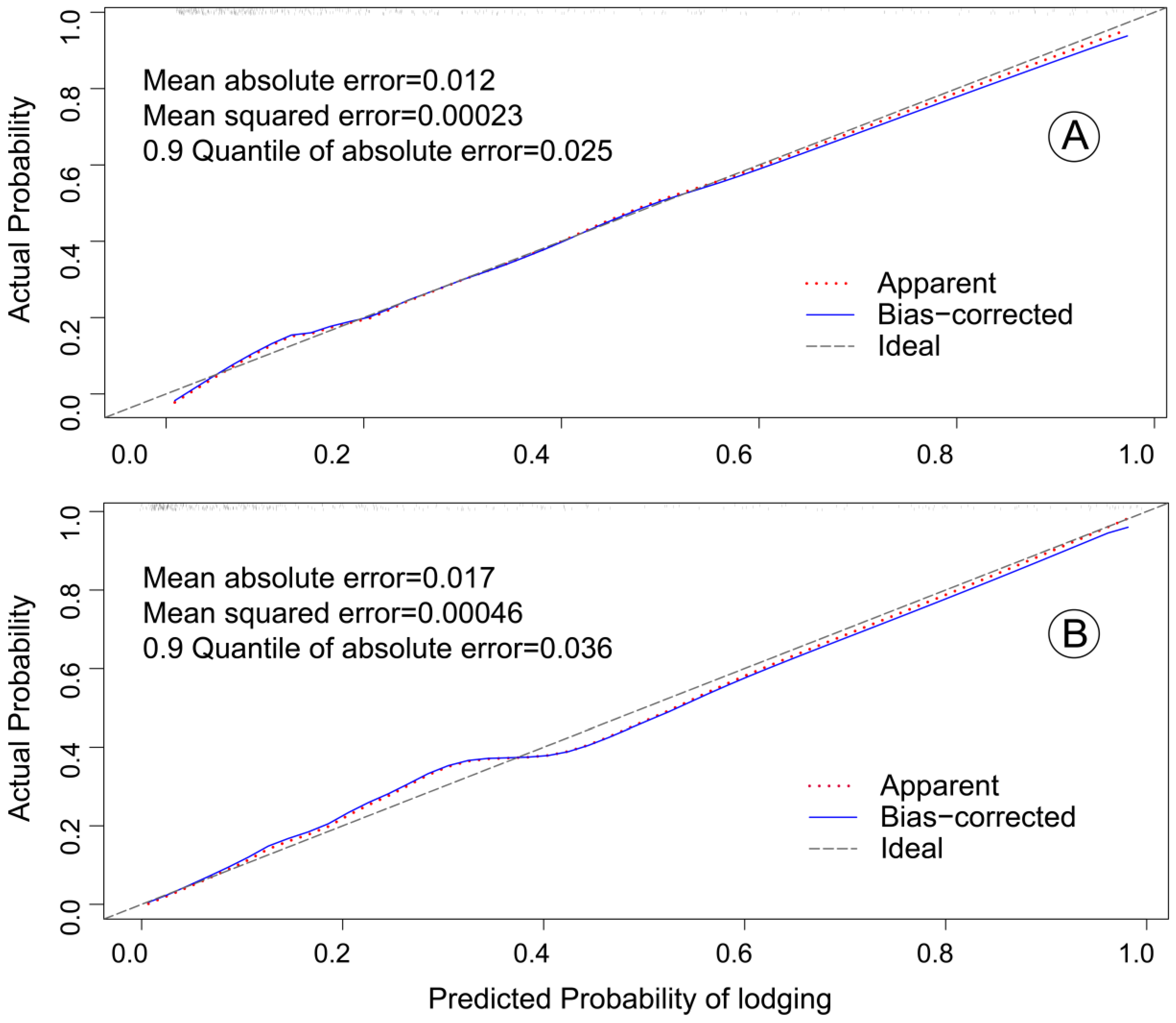
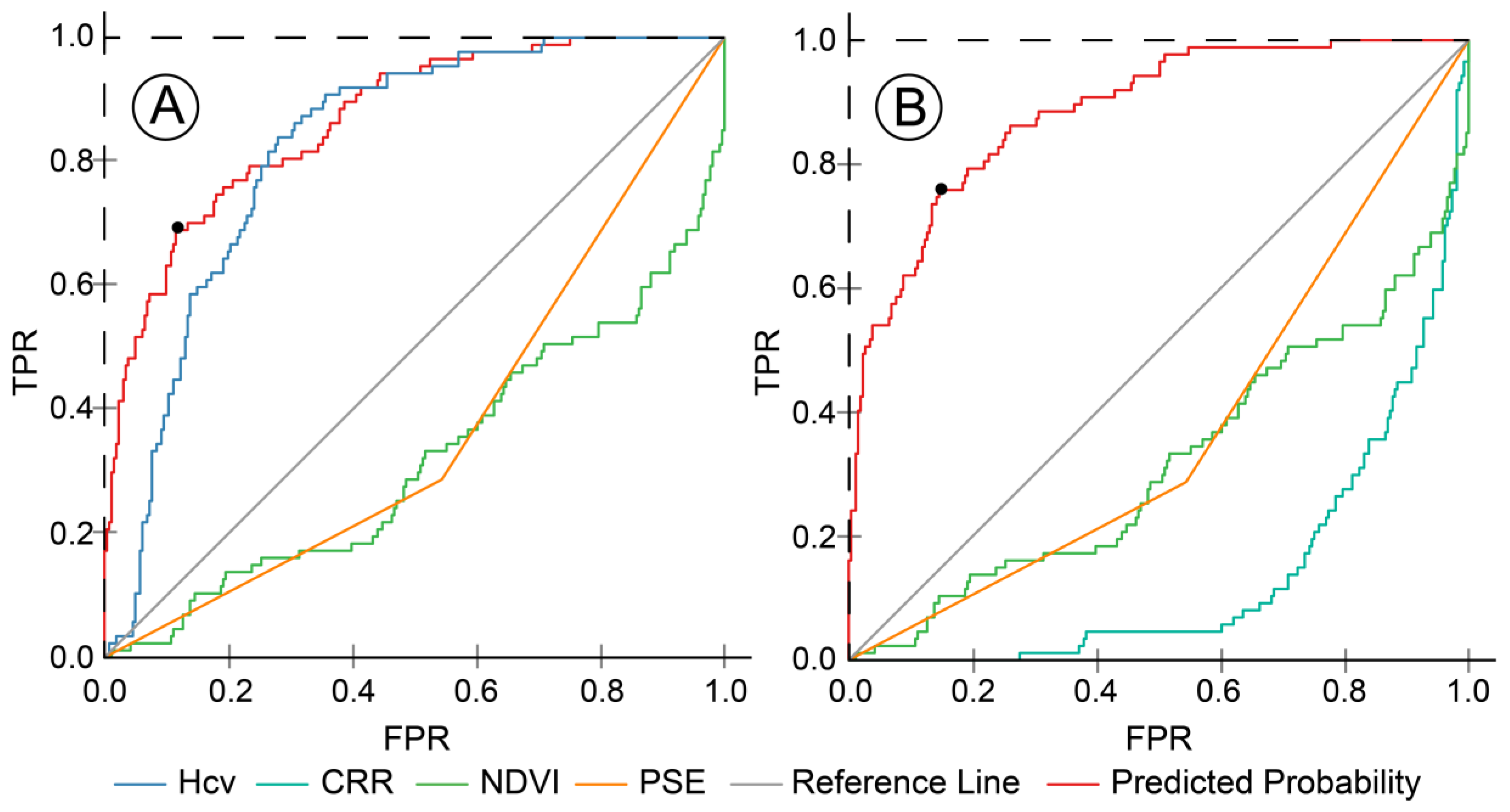
The effectiveness evaluation of the model included two indicators, namely discrimination and calibration, which were performed by the area under receiver operating characteristic (ROC) curve and a calibration method, respectively [
58]. The true positive rate (TPR) and false positive rate (FPR) are the vertical axis and horizontal axis of the ROC, respectively. TPR, also known as sensitivity, referred to the percentage that an actual lodging was correctly judged as lodging. FPR, also known as (1 − specificity), referred to the percentage that non-lodging was incorrectly judged as lodging. The area under the ROC curve (AUC) was developed as a discrimination criterion. According to Hosmer and Lemeshow, AUC = 0.5 corresponds to randomly guess and AUC > 0.7 corresponds to a reasonable recognition [
59,
60]. Calibration measures the model’s ability to generate predictions that are on average closer to the average observed outcome, which is used to validate the robustness of the models [
61]. A visual calibration plot was used to illustrate the correlation between the actual probability and the predicted probability by a bootstrapping method [
24,
62].
Youden’s J statistic is another main summary statistic of the ROC curve used interpret and evaluate the performance of the model [
63], which ranged between 0 and 1, with values close to 1 indicating that the model’s effectiveness was relatively large and values close to 0 indicating limited effectiveness [
64]. The maximum value of the Youden’s J statistic was used as a criterion for selecting the optimum cutoff point [
65]. J is defined as J = sensitivity + specificity − 1 [
66].
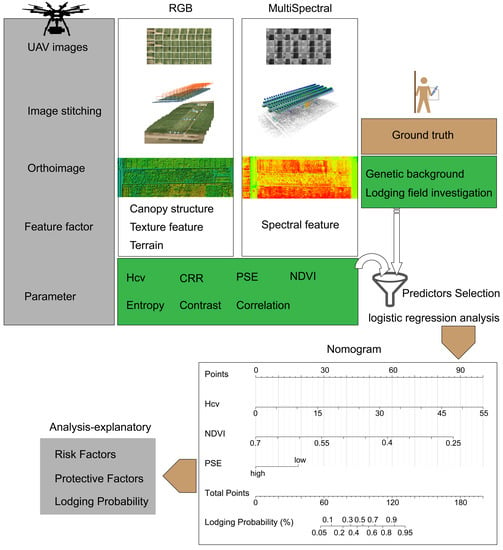
Statistical analysis, modeling, and evaluation were carried out using an R software version 3.4.3 for Windows (
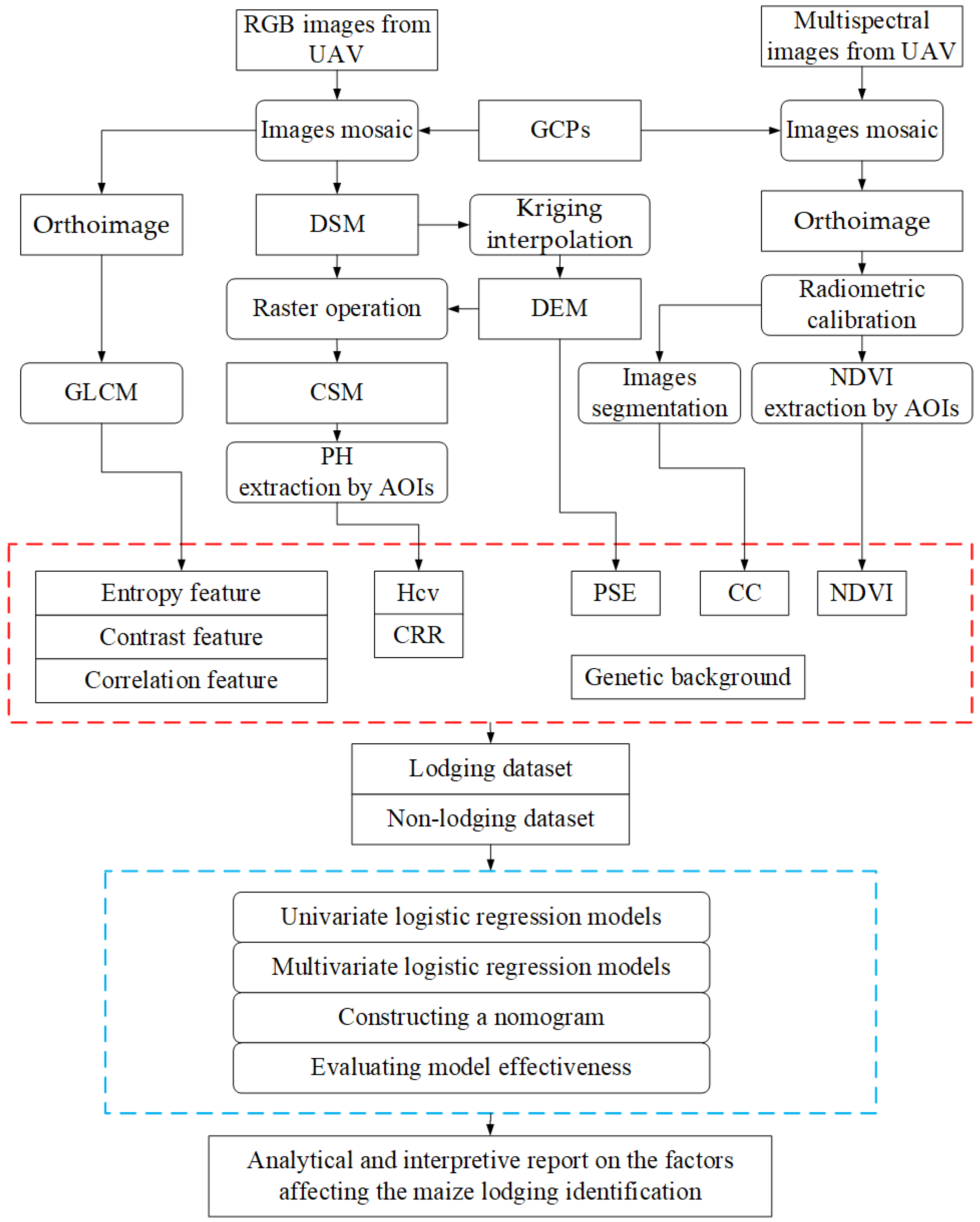
https://www.r-project.org) with R packages (apcluster, ggplot2, rms, and pROC). The schematic diagram of data processing and analysis procedure for maize lodging recognition is illustrated in
Figure 3.