Sun Glint Correction of High and Low Spatial Resolution Images of Aquatic Scenes: a Review of Methods for Visible and Near-Infrared Wavelengths
Abstract
:1. Introduction
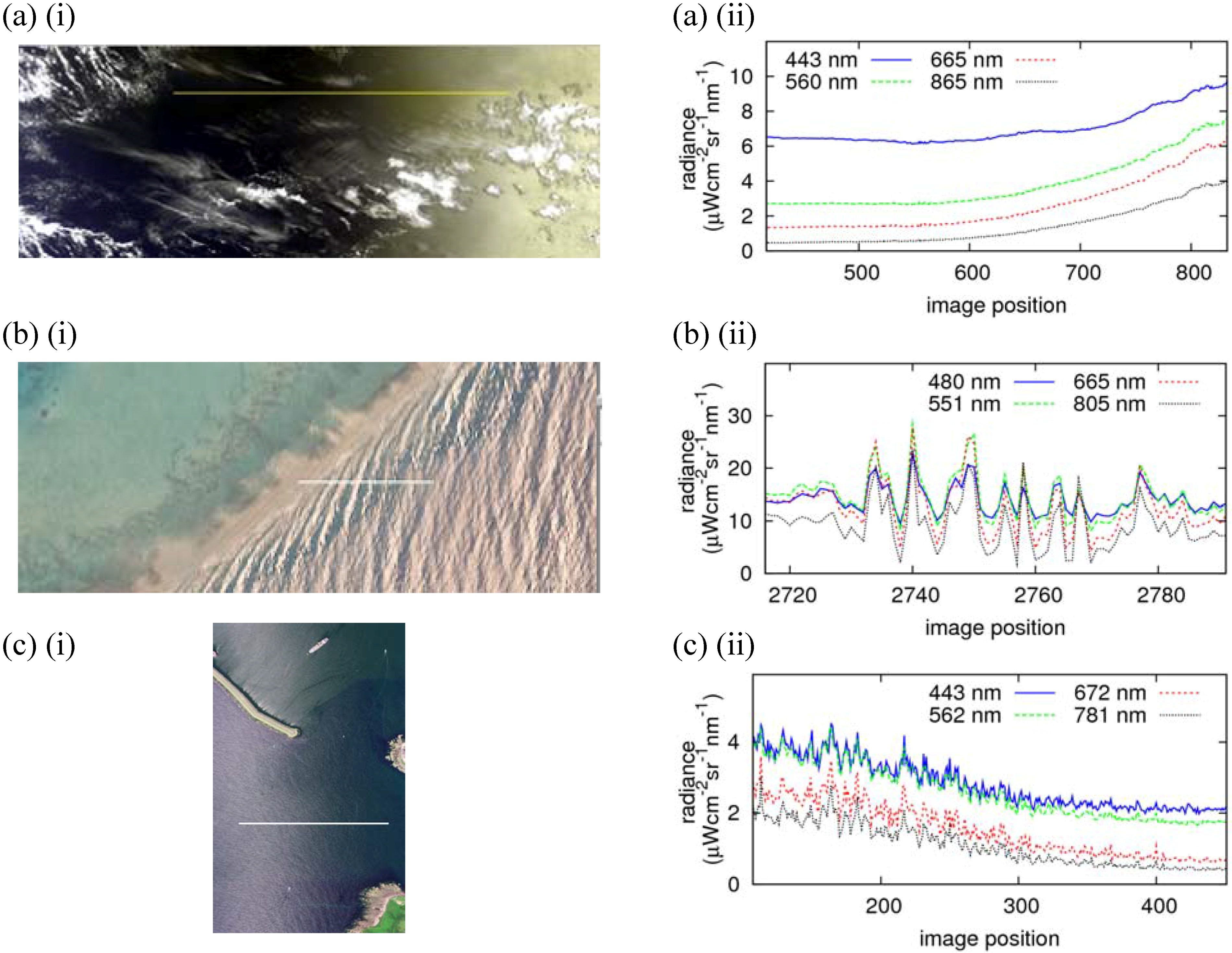
- Methods of the first category are used for open ocean imagery with resolutions on the scale of 100–1,000 m. Statistical models of the sea surface, such as that of Cox and Munk [4,5], are used to calculate the probability that the sea surface will be orientated to cause glint, depending on the wind speed and direction. This probability is then used to predict the amount of glint for a given wind vector, sun and sensor position. Variations on this method are used for a number of operational ocean color instruments [6,7,8]. However, they can only correct moderate glint and large errors remain in the brightest glint areas.
- A separate set of methods is used for coastal images with pixel sizes less than about 10 m. These use data from the near-infrared (NIR) to give an indication of the amount of glint in the received signal. This is based on the assumption that the water-leaving radiance in this part of the spectrum is negligible and so any NIR signal remaining after atmospheric correction must be due to sun glint. The spectrum for a deep water part of the image is examined and used to establish the relationship between the NIR and glint radiances [1,2,9,10]. These methods can improve data retrieval for bathymetry or habitat classification, but the assumption of no water-leaving radiance in the NIR is not valid for very shallow or turbid water or where vegetation reaches the surface.
| Instrument name | Dates in orbit | Satellite | Band information | Tilting? | Resolution (m) |
|---|---|---|---|---|---|
| Sea-viewing Wide Field-of-view Sensor (SeaWiFS) [11] | 1997–present | OrbView-2 (also called SeaStar) | 8 bands in the visible and NIR | Y | 1100/4500 |
| Global Imager (GLI) [12] | 2002–2003 | ADEOS-II | 36; 23 in visible and near-infrared | Y | 1000 |
| Medium Resolution Imaging Spectrometer (MERIS) [13] | 2002–present | Envisat | 15, ranging from 412.5 to 900 nm | N | 300/1200 |
| Moderate Resolution Imaging Spectroradiometer (MODIS) [14] | 1999 (Terra) /2002 (Aqua)–present | Aqua (EOS PM) & Terra (EOS AM) | 36; 8 bands in the visible and NIR are used for ocean colour, other bands extend up to 14 μm | N | 1000 |
| IKONOS multispectral imager [15] | 1999–present | IKONOS | 4 bands, visible and NIR, each about 70–100 nm wide | N | 4 |
| Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) [16] | Flights since 1992 | Airborne, 20 km altitude | 224 bands, visible to infrared (400–2,500 nm) | N | 20 |
| Compact Airborne Spectral Imager-2 (CASI-2)* [17] | Flights since 1989 | Airborne | 18–288 band in the range 405–950 nm, number of bands and band frequencies are tunable | N | <1–10 |
| Coastal Zone Color Scanner (CZCS) [18] | 1978–1986 | Nimbus 7 | 6 Band centres: 443, 520, 550, 670, 750, 11500 | Y | 825 |
| Ocean color and Temperature Sensor (OCTS) [19] | 1996–1997 | ADEOS | 12; 8 bands in visible and near-infrared | Y | 700 |
| Polarization and Directionality of the Earth’s Reflectances (POLDER) [20] | 1996–1997 2002–2003 | ADEOS ADEOS-II | 8, 443, 490, 565, 665, 763, 765, 865 and 910 | N | 7000 |
| Ocean and Land Colour Instrument (OCLI) [21] | Due for launch in 2012 | Sentinel-3 | 21, 400–1,020 nm | Y | 300 m |
2. Theoretical Background
2.1. Radiative Transfer Processes
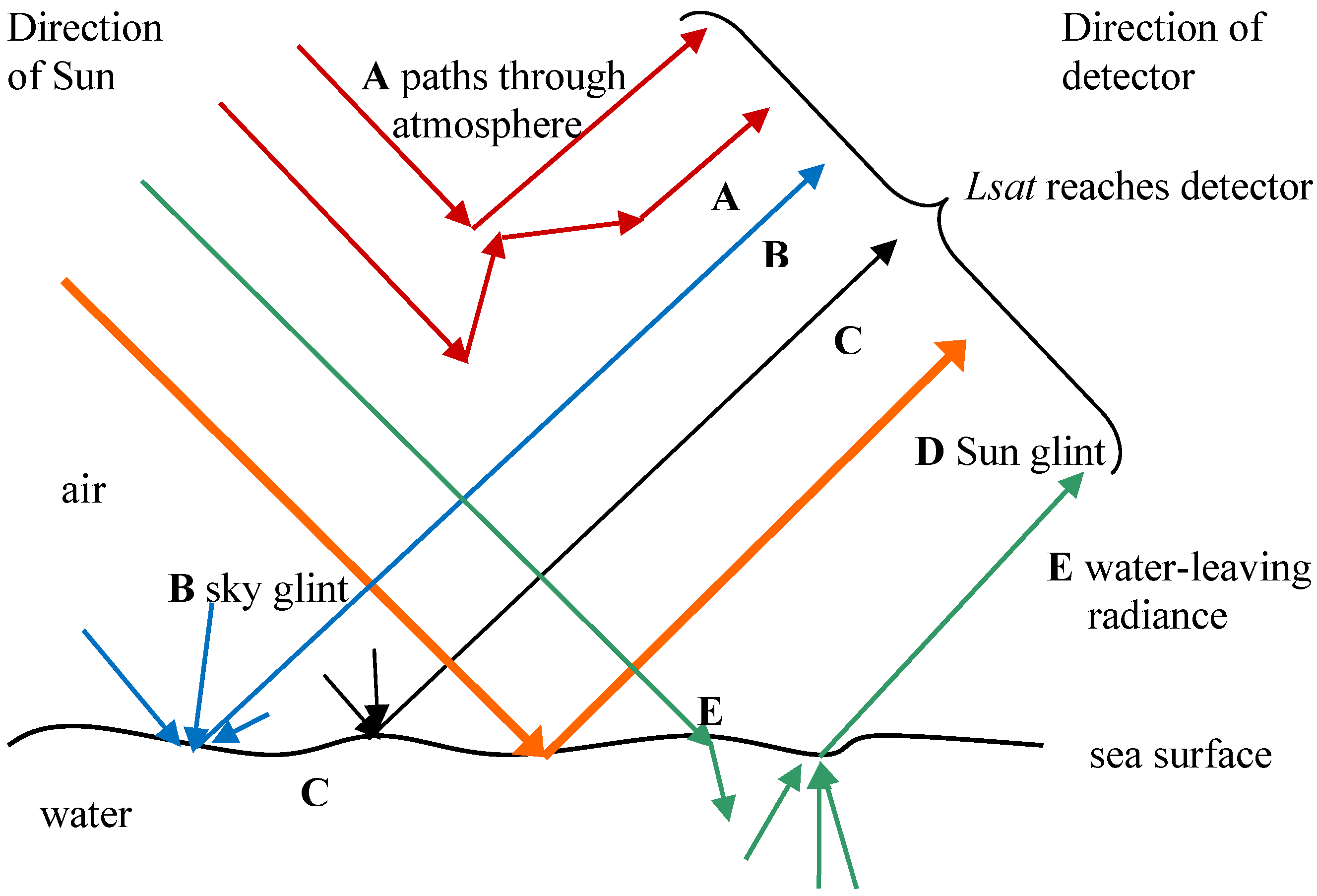
- A
- Single or multiple scattering in the atmosphere, by molecules or aerosols
- B
- Scattering from the atmosphere to the water surface and then reflection to the detector—often termed “sky glint”
- C
- Reflection from whitecaps on the sea surface
- D
- Specular reflection from water surface, with direct transmission through the atmosphere from the sun to the surface and from the surface to the detector—this is termed ‘sun glint’ in the context of this review.
- E
- Transmission through the atmosphere and air-water interface followed by scattering or reflection below the water surface and transmission back through the atmosphere to the detector.
| Lsensor | total radiance reaching a sensor |
| Latm | radiance reaching the sensor via single or multiple scattering in the atmosphere (path radiance) |
| Lglint | radiance just above the water surface for light reaching the sensor by specular reflection at the surface and direct transmission through the atmosphere: sun glint |
| Lsky | radiance just above the water surface for light scattered from the atmosphere and then reflected from the water surface to the sensor (“sky glint”) |
| Lwhitecap | radiance just above the water surface for light reflected from whitecaps on the water surface |
| Lwater | radiance just above the water surface for light transmitted into the water and then scattered or reflected to the sensor |
| LRayleigh | radiance reaching the sensor due to Rayleigh scattering from molecules in the atmosphere |
| Laerosol | radiance reaching the sensor due to scattering from aerosols in the atmosphere |
| Lra | radiance reaching the sensor due to Rayleigh-aerosol interaction |
| LGN | normalized sun glint radiance, used in the SeaWiFS scheme: the glint radiance that would be received if there was no atmosphere and the solar irradiance were 1 (Equation 26) |
| Fo(λ) | the extraterrestrial solar irradiance |
| To(λ) | the atmospheric direct transmittance along the path from the sun to the water surface |
| T(λ), t(λ) | direct and diffuse transmittance of the atmosphere between the water surface and the sensor, i.e., the proportion of the radiance leaving the surface that reaches the sensor; diffuse transmittance includes light scattered into the path. |
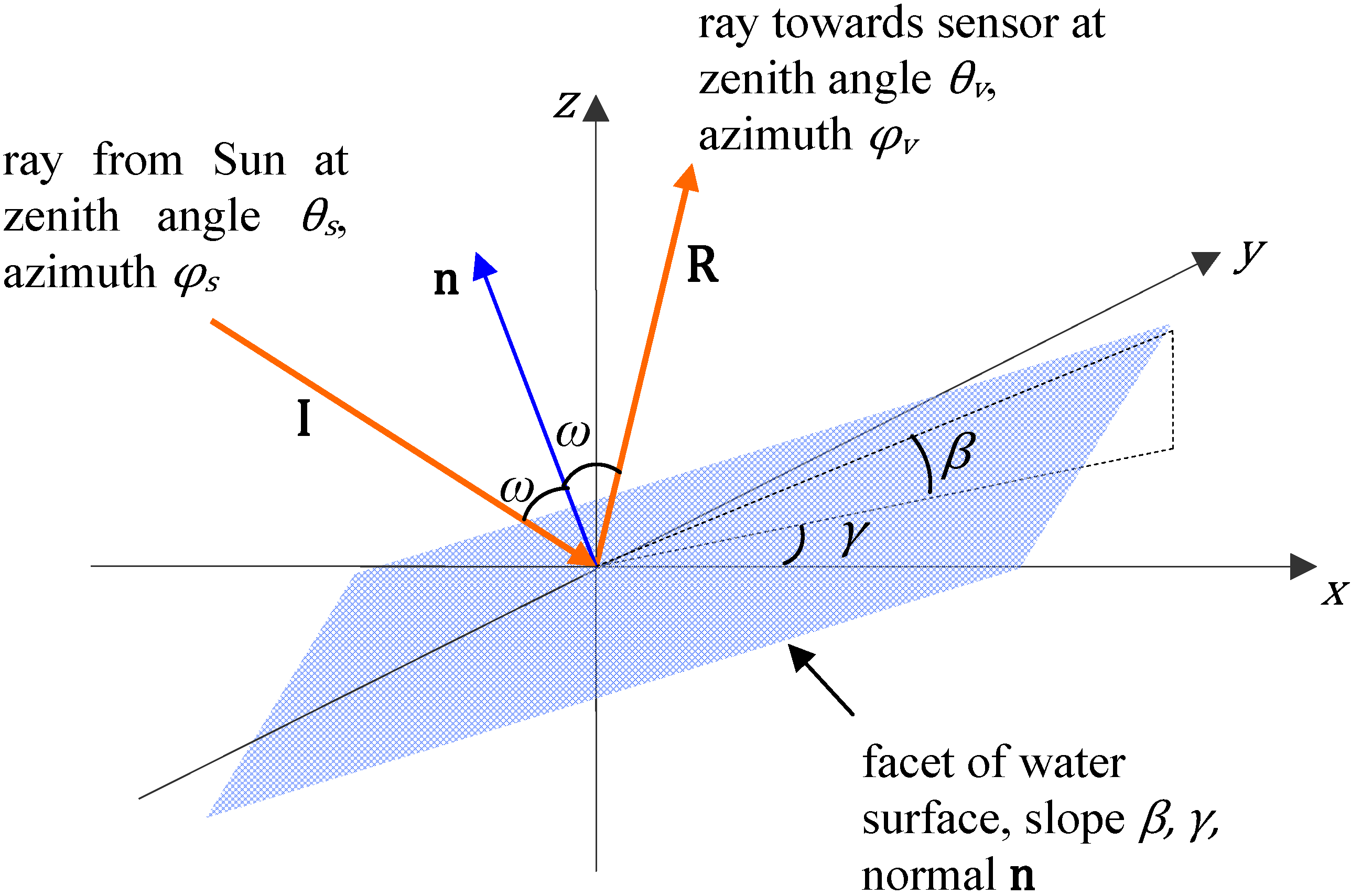
| ω, ω’ | the angle of incidence and refraction of a light ray at the water surface |
| β, γ | steepest slope and azimuth of a facet of the water surface |
| θs, φs | solar zenith and azimuth angles |
| θv, φv | sensor zenith and azimuth angles |
| x, y, z | a right-handed axis system with x in the downwind direction, y in the crosswind direction and z vertically upwards from the equilibrium position of the sea surface |
| zx, zy | facet slope ∂z/∂x, ∂z/∂y |
| E | solar irradiance at the surface |
| ρ(ω,λ) | Fresnel reflectance at the water surface |
| p(zx,zy) | probability distribution function of the sea surface slope |
| σw, σc | root mean square slopes in the downwind and crosswind directions |
| ξ, η | normalized surface slopes zx/ σw and zy/ σc |
| mss | mean square slope (of the sea surface) |
| U10 | the wind speed at 10 m above mean sea level |
| W | surface wind vector, measured at 10 m |
| τaerosol, τRayleigh | the aerosol and Rayleigh optical thicknesses of the atmosphere |
| Wavelength (nm) | % contribution to received signal | |||||
| Clear water | Turbid water | |||||
| Air paths (A) | Reflected paths (C and D) | Water-leaving paths (E) | Air paths (A) | Reflected paths (C and D) | Water-leaving paths (E) | |
| 440 | 84.4 | 1.2 | 14.4 | 80.8 | 1.1 | 18.1 |
| 520 | 81.2 | 1.3 | 17.5 | 66.6 | 1.1 | 32.3 |
| 550 | 84.2 | 1.3 | 14.5 | 64.1 | 1.0 | 34.9 |
| 670 | 96.3 | 1.5 | 2.2 | 82.4 | 1.2 | 16.4 |
| 750 | 97.0 | 1.9 | 1.1 | 97.4 | 1.5 | 1.1 |
- both processes have only a weak dependence on wavelength, so do not leave a distinctive spectral signature. The wavelength dependence of sun glint is through variation in the refractive index (see Equations 12 and 28)—for pure water this varies from 1.339 at 400 nm to 1.328 at 900 nm [27], while for sea water it varies from 1.35 at 400 nm to 1.34 at 700 nm [28]. The aerosol reflectance varies as λα, where α is the Angström exponent, whose value varies from about +1 to −2 depending on environmental conditions [26]. Typical maritime values are 0.3–1.0 [29]; for low values, corresponding to large aerosols, the wavelength dependence is weak.
- the atmospheric transmittance, T, depends on aerosol scattering, so the radiance term TLglint inevitably involves both glint and aerosol processes. Without knowing the concentration and size of aerosol in the path T cannot be calculated; the aerosol quantities can vary significantly over time scales of days and space scales of a few kilometers [26].
2.2. Geometric Estimation and Prediction of Sun Glint
2.3. Avoidance of Sun Glint
3. Summary of Current Glint Correction Techniques
| Method type | Authors and ref. | Demonstration instrument | Outline of method | Assumptions | Examples of use | Before/after atmospheric correction |
|---|---|---|---|---|---|---|
| Open ocean | Wang & Bailey [6] Wang et al. [31] | SeaWiFS POLDER OCTS | Glint is predicted from wind speed (NCEP data) and subtracted from radiance where it falls between 2 thresholds. Glint and aerosol are estimated together. | Cox and Munk model of the sea surface; neglects effects of wind direction, multiple scattering. | Ocean color | Together with aerosol scattering, Rayleigh scattering separately |
| Open ocean | Montagner, Billat & Belanger [7] | MERIS | Glint is predicted from wind speed and direction (ECMWF data) and subtracted from reflectance where it falls between 2 thresholds. | Cox and Munk model of the sea surface; neglects effects of multiple scattering, aerosol. | Ocean color | Before |
| Open ocean | Fukushima et al. [40] | GLI | Similar to SeaWiFS, but with wind speed from SeaWinds microwave scatterometer on the same satellite (ADEOS-II). | Cox and Munk model of the sea surface; neglects effects of wind direction, multiple scattering. | Ocean color | Together with aerosol scattering, Rayleigh scattering separately |
| Open ocean | Ottaviani et al. [41] | SeaWiFS | Uses a solution of the full radiative transfer equation to include the effect of multiple scattering, multiple reflection and shadowing. | Cox and Munk model of the sea surface; neglects effects of wind direction. | Ocean color | Together |
| Open ocean –but a different approach | Steinmetz, Deschamps & Ramon [3] | MERIS | Aerosol and glint correction are made together by matching reflectance using a neural network or iterative mean square minimization method. | Polynomial model of glint and atmospheric factors. | Ocean color | Together with aerosol scattering, Rayleigh scattering separately |
| Open ocean –another alternative | Doerffer et al. [42] | MERIS | A neural network is used to correct both glint and atmospheric effects. Wind speed is not used. | No explicit assumptions, but the neural network is trained using data from radiative transfer simulations, which will have built-in assumptions. | Ocean color | Together |
| Shallow waters | Hochberg, Andrefouet & Tyler [2] | IKONOS | NIR is used to find the spatial variation of glint across the image, by scaling depending on the brightest and darkest points (NIR). | Refractive index is independent of wavelength; low NIR water-leaving radiance. | Sub-surface imaging (e.g., reef, estuary) | After |
| Shallow waters | Hedley, Harborne and Mumby [10] | IKONOS | Refined the method of Hochberg et al. [2] using a group of pixels that have similar underlying brightness (e.g., deep water) rather than just two. | Refractive index is independent of wavelength; low NIR water-leaving radiance. | Sub-surface imaging (e.g., reef, estuary) | After |
| Shallow waters | Lyzenga, Malinas and Tanis [9] | IKONOS | Sun glint correction factor for a given band is based on covariance of radiance in that band and in NIR for a deep water area. | No upwelling radiance for deep water. | Bathymetry | After |
| Shallow waters | Philpot [38] | AVIRIS | Use of info from a glint-contaminated and non-contaminated pixel pair to calculate glint radiance. This is then extended to nearby pixels using NIR. | Uniform atmosphere across the region where glint correction is applied No water-leaving radiance for NIR. No glint in dark pixel. | Bathymetry and water properties in shallow water | Before |
| Shallow waters | Goodman, Lee & Ustin [1] | AVIRIS | At each wavelength an offset is added, depending on difference between reflectance at 640 and 750 nm. | Method is based on a radiative transfer model. | Bathymetry and water properties in shallow water | After |
| Shallow waters | Kutser, Vahtmäe & Praks [43] | AISA | The depth of the 760 nm oxygen absorption band is used to indicate the amount of glint. | Glint is the only process affecting the absorption depth; depth is proportional to amount of glint. | Bathymetry and water properties in shallow water | After |
4. Correction Methods Based on Statistical Models of the Sea Surface State
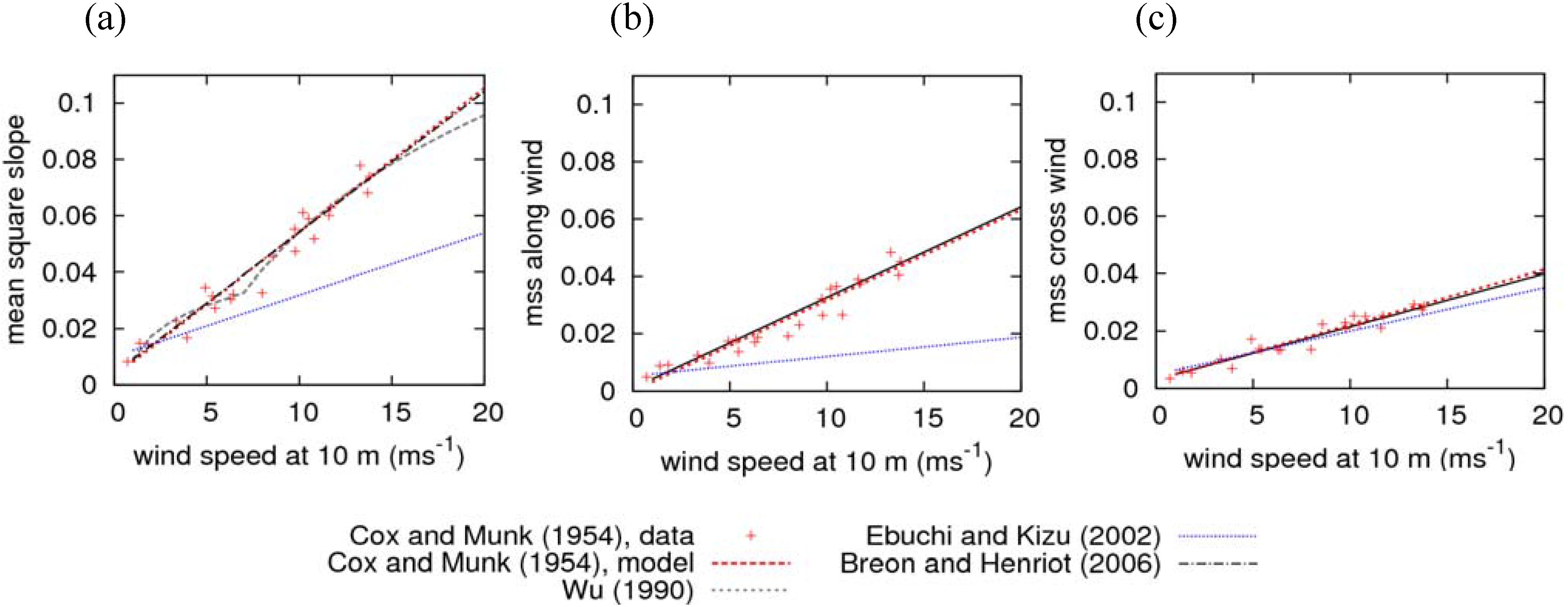
4.1. The Cox and Munk Statistical Model of the Sea Surface State
4.2. The SeaWiFS Correction Method
4.3. Other Methods Using Sea Surface Slope Statistics: MERIS and GLI

- a new aerosol correction method, which allows for absorption as well as scattering;
- sun glint correction by calculating a glint reflectance and subtracting it from the received value; it is not clear whether this is done before or after the atmospheric correction;
- wind data taken from the SeaWinds microwave scatterometer mounted on the same satellite as GLI, instead of from the Japanese Meteorological Agency.
4.4. Limitations of the SeaWiFS and MERIS Schemes
4.5. New Methods Based on Neural Networks
5. Methods for Shallow Water, High Resolution Images
5.1. Theoretical Background
5.2. The Method of Hedley et al. [10]; Figure 7(b), Figure 8(b)
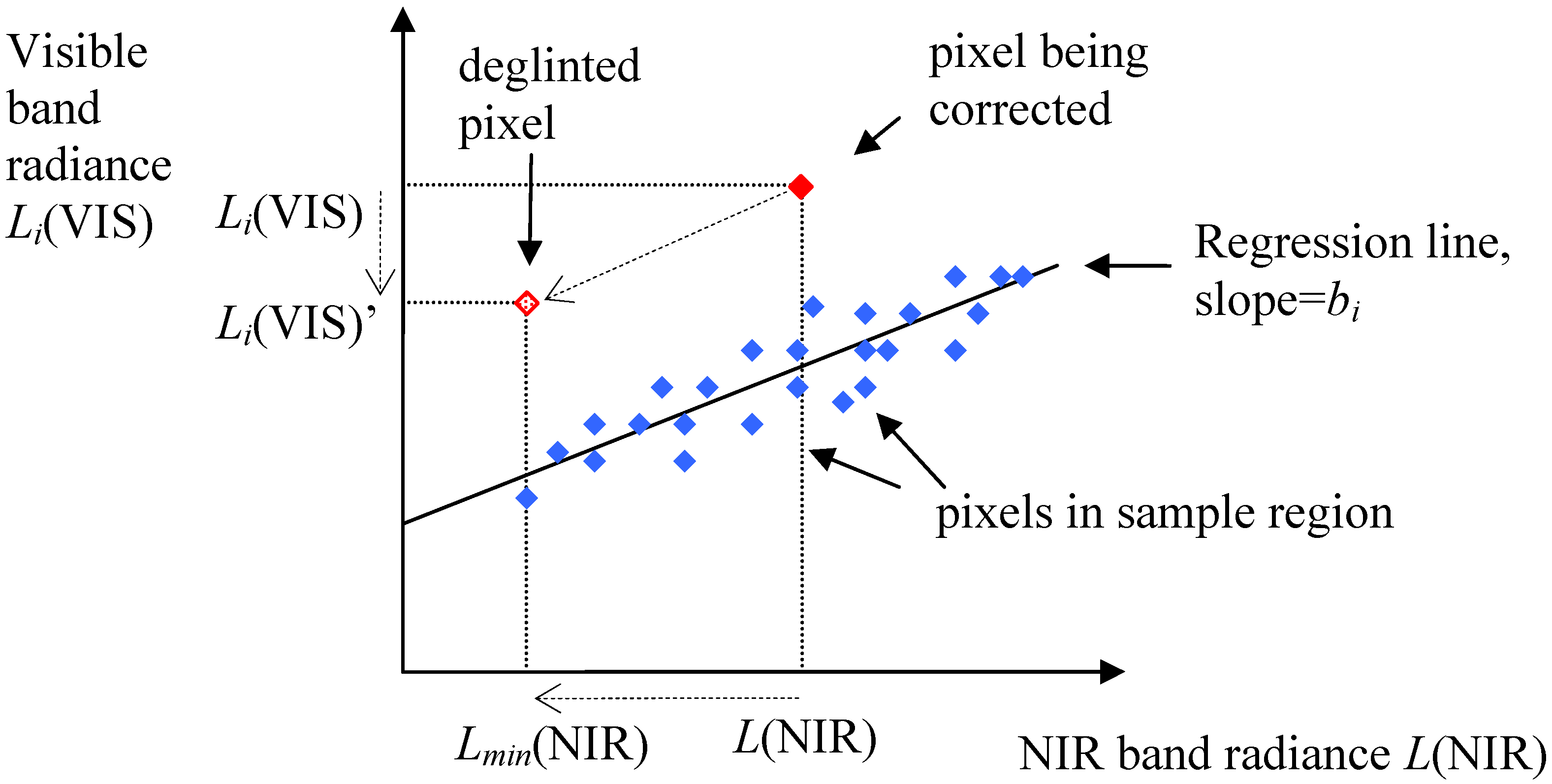
5.3. The Method of Lyzenga et al. [9]; Figure 7(c), Figure 8(c)
5.4 The method of Goodman et al. [1]; Figure 7(d), Figure 8(d)
5.5. The Method of Kutser et al.
5.6. Comments on the Methods
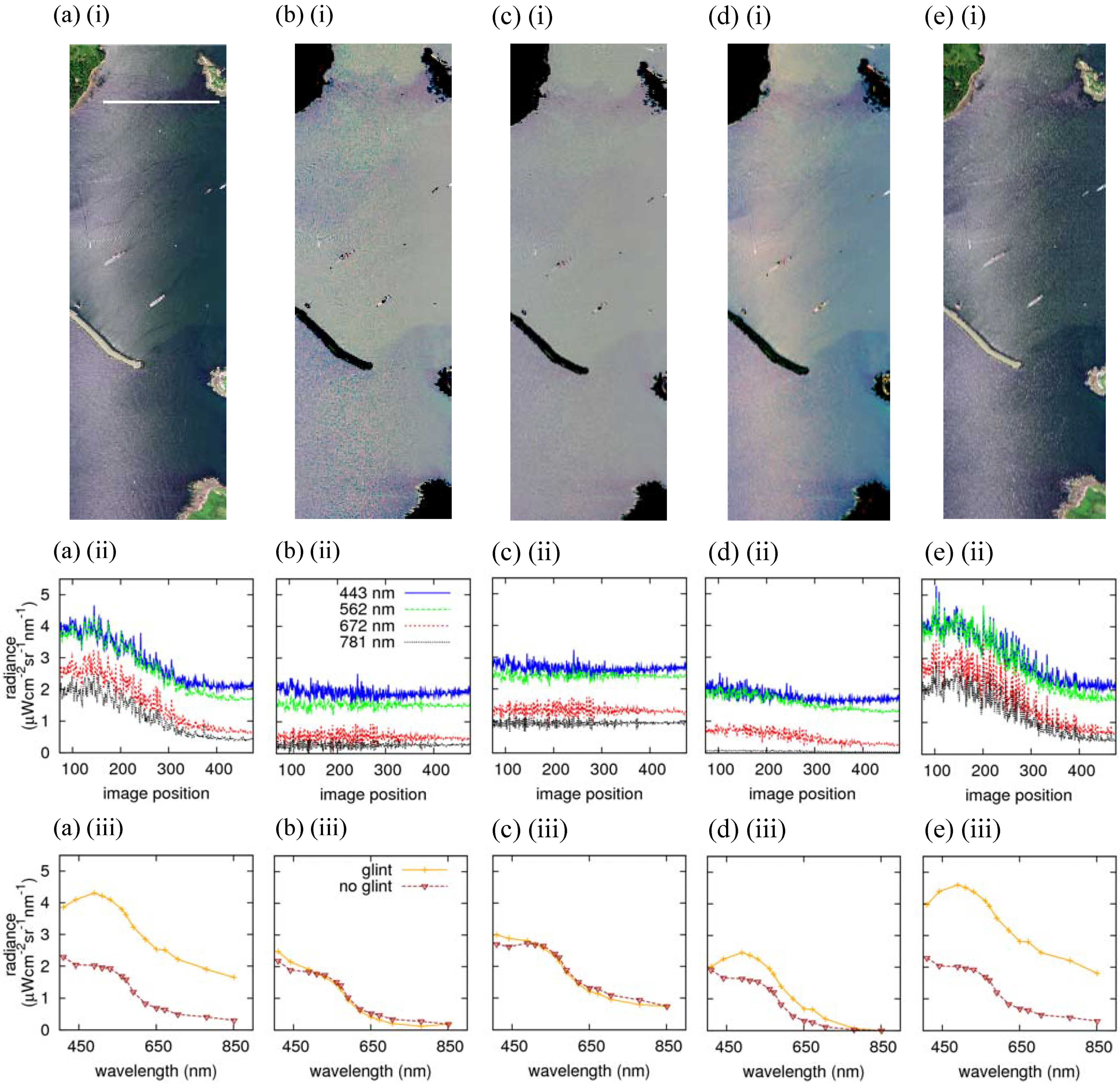
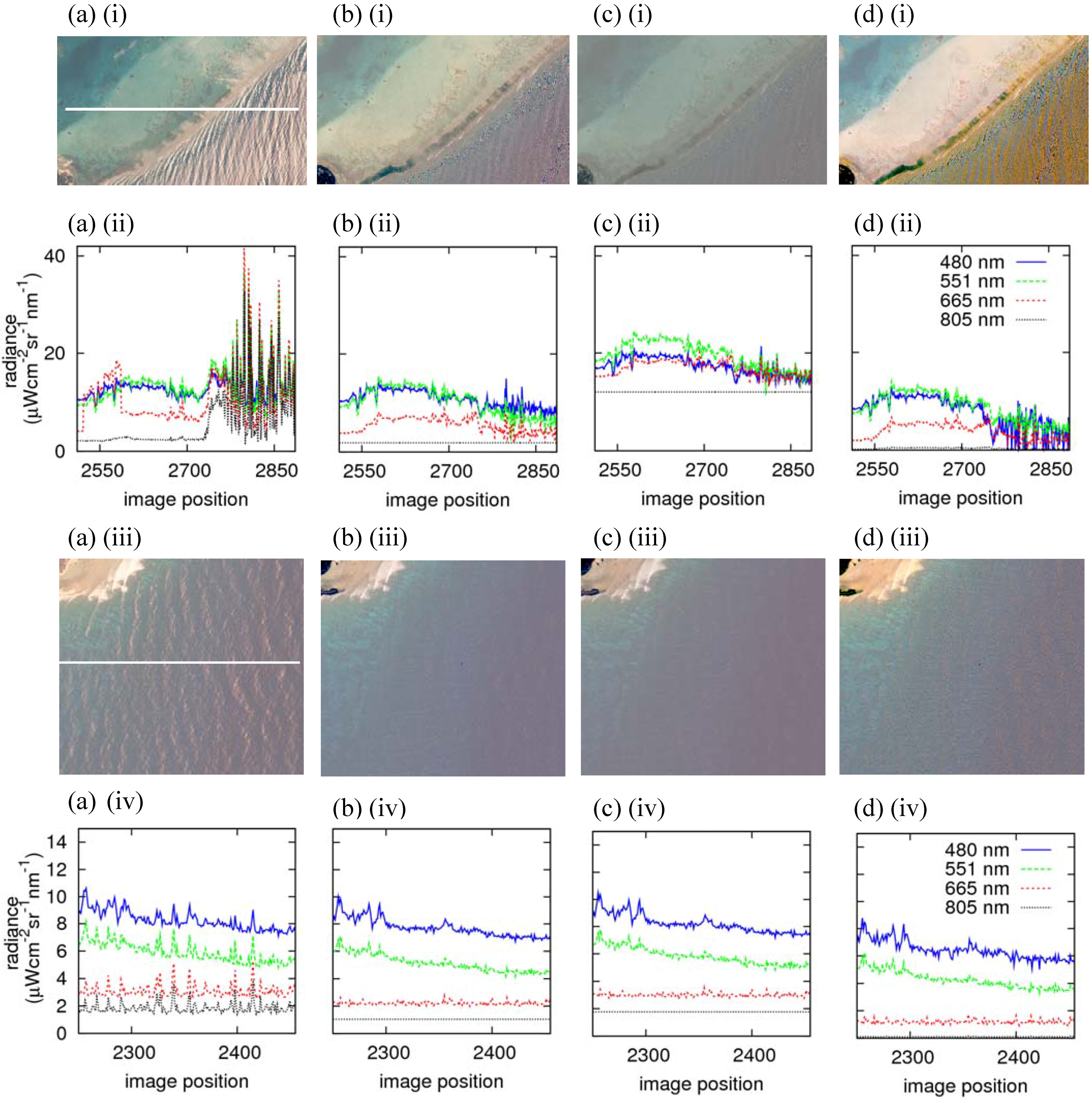
5.7. Limitations of These Methods
6. Wavelengths Outside the Visible and NIR
7. Useful Glint
8. Summary and Prospects for Further Development
Acknowledgments
References and Notes
- Goodman, J.A.; Lee, Z.; Ustin, S.L. Influence of Atmospheric and Sea-Surface Corrections on Retrieval of Bottom Depth and Reflectance Using a Semi-Analytical Model: A Case Study in Kaneohe Bay, Hawaii. Appl. Opt. 2008, 47, F1–F11. [Google Scholar] [CrossRef] [PubMed]
- Hochberg, E.; Andrefouet, S.; Tyler, M. Sea Surface Correction of High Spatial Resolution Ikonos Images to Improve Bottom Mapping in Near-Shore Environments. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1724–1729. [Google Scholar] [CrossRef]
- Steinmetz, F.; Deschamps, P.; Ramon, D. Atmospheric Correction in Presence of Sun Glint: Application to MERIS. In Presented at the 2nd MERIS-(A)ATSR workshop, Frascati, Italy, 22–26 September 2008; Available online: http://earth.esa.int/cgi-bin/confm8.pl?abstract=75 (accessed 17 December 2008).
- Cox, C.; Munk, W. Statistics of the Sea Surface Derived from Sun Glitter. J. Mar. Res. 1954, 13, 198–227. [Google Scholar]
- Cox, C.; Munk, W. Measurement of the Roughness of the Sea Surface from Photographs of the Suns Glitter. J. Opt. Soc. Am. 1954, 44, 838–850. [Google Scholar] [CrossRef]
- Wang, M.; Bailey, S. Correction of Sun Glint Contamination on the SeaWiFS Ocean and Atmosphere Products. Appl. Opt. 2001, 40, 4790–4798. [Google Scholar] [CrossRef] [PubMed]
- Montagner, F.; Billat, V.; Belanger, S. MERIS ATBD 2.13 Sun Glint Flag Algorithm. Available online: http://envisat.esa.int/instruments/meris/atbd/atbd_2_13.pdf (accessed 5 November 2008).
- Gordon, H.; Voss, K. MODIS Normalized Water-Leaving Radiance Algorithm Theoretical Basis Document (MOD 18); Version 5; NASA: Washington, DC, 2004. Available online: http://modis.gsfc.nasa.gov/data/atbd/atbd_mod18.pdf (accessed 19 March 2009).
- Lyzenga, D.; Malinas, N.; Tanis, F. Multispectral Bathymetry Using a Simple Physically Based Algorithm. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2251–2259. [Google Scholar] [CrossRef]
- Hedley, J.; Harborne, A.; Mumby, P. Simple and Robust Removal of Sun Glint for Mapping Shallow-Water Benthos. Int. J. Remote Sens. 2005, 26, 2107–2112. [Google Scholar] [CrossRef]
- SeaWiFS Project - Homepage. http://oceancolor.gsfc.nasa.gov/SeaWiFS/ (accessed 6 May 2009).
- Earth Observation Satellite—Global Imager. http://www.eorc.jaxa.jp/en/hatoyama/satellite/sendata/gli_e.html (accessed 6 May 2009).
- ESA Earthnet: The Medium Resolution Imaging Spectrometer Instrument. http://envisat.esa.int/object/index.cfm?fobjectid=1665 (accessed 6 May 2009).
- MODIS Website. http://modis.gsfc.nasa.gov/about/ (accessed 6 May 2009).
- GeoEye - IKONOS. http://www.geoeye.com/CorpSite/products/imagery-sources/Default.aspx#ikonos (accessed 6 May 2009).
- AVIRIS Home Page. http://aviris.jpl.nasa.gov/ (accessed 6 May 2009).
- NERC Airborne Research and Survey Facility - CASI. http://arsf.nerc.ac.uk/instruments/casi.asp (accessed 6 May 2009).
- NASA—Coastal Zone Color Scanner. http://nssdc.gsfc.nasa.gov/nmc/experimentDisplay.do?id=1978-098A-03 (accessed 6 May 2009).
- Earth Observation Satellite—Ocean Color and Temperature Sensor. http://www.eorc.jaxa.jp/en/hatoyama/satellite/sendata/octs_e.html (accessed 6 May 2009).
- Earth Observation Satellite—Polarization and Directionality of the Earth's Reflectances. http://www.eorc.jaxa.jp/ en/hatoyama/satellite/sendata/polder_e.html (accessed 6 May 2009).
- ESA—Living Planet Programme - GMES - Sentinel-3. http://www.esa.int/esaLP/SEMTST4KXMF_LPgmes_0.html (accessed 5 May 2009).
- Sturm, B. The Atmospheric Correction of Remotely Sensed Data and the Quantitative Determination of Suspended Matter in Marine Water Surface Layers. In Remote Sensing in Meteorology, Oceanography and Hydrology; Cracknell, A.P., Ed.; Ellis Horwood Ltd: Chichester, UK, 1981; pp. 163–197. [Google Scholar]
- Mobley, C.D. Light and Water: Radiative Transfer in Natural Waters; Academic Press: San Diego, CA, USA, 1994. [Google Scholar]
- Gordon, H.; Wang, M. Retrieval of Water-Leaving Radiance and Aerosol Optical-Thickness Over the Oceans with Seawifs—a Preliminary Algorithm. Appl. Opt. 1994, 33, 443–452. [Google Scholar] [CrossRef] [PubMed]
- Siegel, D.A.; Wang, M.; Maritorena, S.; Robinson, W. Atmospheric Correction of Satellite Ocean Color Imagery: The Black Pixel Assumption. Appl. Opt. 2000, 39, 3582–3591. [Google Scholar] [CrossRef] [PubMed]
- Lavender, S.; Pinkerton, M.; Moore, G.; Aiken, J.; Blondeau-Patissier, D. Modification to the Atmospheric Correction of SeaWiFS Ocean Colour Images Over Turbid Waters. Cont. Shelf Res. 2005, 25, 539–555. [Google Scholar] [CrossRef]
- Hale, G.; Querry, M. Optical-Constants of Water in 200-Nm to 200-Mum Wavelength Region. Appl. Opt. 1973, 12, 555–563. [Google Scholar] [CrossRef] [PubMed]
- Quan, X.; Fry, E. S. Empirical Equation for the Index of Refraction of Seawater. Appl. Opt. 1995, 34, 3477–3480. [Google Scholar] [CrossRef] [PubMed]
- Smirnov, A.; Holben, B.N.; Kaufman, Y.J.; Dubovik, O.; Eck, T.F.; Slutsker, I.; Pietras, C.; Halthorne, R.N. Optical Properties of Atmospheric Aerosol in Maritime Environments. J. Atmos. Sci. 2002, 59, 501–523. [Google Scholar] [CrossRef]
- Cox, C.; Munk, W. Slopes of the Sea Surface Deduced from Photographs of Sun Glitter. Scripps Inst. Oceanogr. Bull. 1956, 6, 401–488. [Google Scholar]
- Wang, M.; Isaacman, A.; Franz, B.; McClain, C. Ocean-Color Optical Property Data Derived from the Japanese Ocean Color and Temperature Scanner and the French Polarization and Directionality of the Earth's Reflectances: A Comparison Study. Appl. Opt. 2002, 41, 974–990. [Google Scholar] [CrossRef] [PubMed]
- Gordon, H.; Wang, M. Surface-Roughness Considerations for Atmospheric Correction of Ocean Color Sensors. 1. The Rayleigh-Scattering Component. Appl. Opt. 1992, 31, 4247–4260. [Google Scholar] [CrossRef] [PubMed]
- Seawifs Overflight Prediction Information. http://oceancolor.gsfc.nasa.gov/SUPPORT/Overflight_Info.html (accessed 5 May 2009).
- Wolter, P.; Johnston, C.; Niemi, G. Mapping Submergent Aquatic Vegetation in the US Great Lakes Using Quickbird Satellite Data. Int. J. Remote Sens. 2005, 26, 5255–5274. [Google Scholar] [CrossRef]
- Dekker, A.; Byrne, G.; Brando, V.; Anstee, J. Hyperspectral Mapping of Intertidal Rock Platform Vegetation as a Tool for Adaptive Management; CSIRO Land and Water: Canberra, Australia, 2003. [Google Scholar]
- Mustard, J.; Staid, M.; Fripp, W. A Semianalytical Approach to the Calibration of AVIRIS Data to Reflectance Over Water Application in a Temperate Estuary. Remote Sens. Environ. 2001, 75, 335–349. [Google Scholar] [CrossRef]
- Mobley, C. Estimation of the Remote-Sensing Reflectance from Above-Surface Measurements. Appl. Opt. 1999, 38, 7442–7455. [Google Scholar] [CrossRef] [PubMed]
- Philpot, W. Estimating Atmospheric Transmission and Surface Reflectance from a Glint-Contaminated Spectral Image. IEEE Trans. Geosci. Remote Sens. 2007, 45, 448–457. [Google Scholar] [CrossRef]
- Mount, R. Acquisition of Through-Water Aerial Survey Images: Surface Effects and the Prediction of Sun Glitter and Subsurface Illumination. Photogramm. Eng. Rem. S. 2005, 71, 1407–1415. [Google Scholar] [CrossRef]
- Fukushima, H.; Toratani, M.; Murakami, H.; Deschamps, P.; Frouin, R.; Tanaka, A. Evaluation of ADEOS-II GLI Ocean Color Atmospheric Correction Using SIMBADA Handheld Radiometer Data. J. Oceanogr. 2007, 63, 533–543. [Google Scholar] [CrossRef]
- Ottaviani, M.; Spurr, R.; Stamnes, K.; Li, W.; Su, W.; Wiscombe, W. Improving the Description of Sunglint for Accurate Prediction of Remotely Sensed Radiances. J. Quant. Spectrosc. Radiat. Transf. 2008, 109, 2364–2375. [Google Scholar] [CrossRef]
- Doerffer, R.; Schiller, H.; Fischer, J.; Preusker, R.; Bouvet, M. The Impact of Sun Glint on the Retrieval of Water Parameters and Possibilities for the Correction of MERIS Scenes. In Proceedings of the 2nd MERIS-(A)ATSR workshop, Frascati, Italy, September 22–26, 2008.
- Kutser, T.; Vahtmäe, E.; Praks, J.A. Sun Glint Correction Method for Hyperspectral Imagery Containing Areas with Non-Negligible Water Leaving NIR Signal. Remote Sens. Environ. 2009, 113, 2267–2274. [Google Scholar] [CrossRef]
- Munk, W. An Inconvenient Sea Truth: Spread, Steepness, and Skewness of Surface Slopes. Annu. Rev. Mar. Sci. 2009, 1, 377–415. [Google Scholar] [CrossRef] [PubMed]
- Plant, W. A New Interpretation of Sea-Surface Slope Probability Density Functions. J. Geophys. Res. 2003, 108, C9, 3295, 11:1–11:4. [Google Scholar] [CrossRef]
- Wu, J. Mean-Square Slopes of the Wind-Disturbed Water-Surface, Their Magnitude, Directionality, and Composition. Radio Sci. 1990, 25, 37–48. [Google Scholar] [CrossRef]
- Fukushima, H.; Suzuki, K.; Li, L.; Suzuki, N.; Murakami, H. Improvement of the ADEOS-II/GLI Sun-Glint Algorithm Using Concomitant Microwave Scatterometer-Derived Wind Data. Adv. Space Res. 2009, 43, 941–947. [Google Scholar] [CrossRef]
- Ebuchi, N.; Kizu, S. Probability Distribution of Surface Wave Slope Derived Using Sun Glitter Images from Geostationary Meteorological Satellite and Surface Vector Winds from Scatterometers. J. Oceanogr. 2002, 58, 477–486. [Google Scholar] [CrossRef]
- Bréon, F.; Henriot, N. Spaceborne Observations of Ocean Glint Reflectance and Modeling of Wave Slope Distributions. J. Geophys. Res. 2006, 111, C06005:1–C06005:10. [Google Scholar] [CrossRef]
- Fox, D.; Gonzalez, E.; Kahn, R.; Martonchik, J. Near-Surface Wind Speed Retrieval from Space-Based, Multi-Angle Imaging of Ocean Sun Glint Patterns. Remote Sens. Environ. 2007, 107, 223–231. [Google Scholar] [CrossRef]
- Gatebe, C.; King, M.; Lyapustin, A.; Arnold, G.; Redemann, J. Airborne Spectral Measurements of Ocean Directional Reflectance. J. Atmos. Sci. 2005, 62, 1072–1092. [Google Scholar] [CrossRef]
- SeaDAS Home Page. http://oceancolor.gsfc.nasa.gov/seadas/ (accessed 5 May 2009).
- Franz, B. Overview of MODIS Processing Within The Ocean Color Discipline Processing System (OCDPS); NASA: Washington, DC, June 2003. Available online: http://oceancolor.gsfc.nasa.gov/DOCS/modis_processing_overview.pdf (accessed 10 March 2009).
- Ocean Color Announcement. http://oceancolor.gsfc.nasa.gov/forum/oceancolor/topic_show.pl?tid=356 (accessed 8 May 2009).
- ACRI. MERIS Level 1 Detailed Processing Model. Available online: http://earth.esa.int/pub/ESA_DOC/ENVISAT/MERIS/MERIS_DPML1b_i7r1.pdf (accessed 26 February 2009).
- ACRI. MERIS Level 2 Detailed Processing Model. Available online: http://earth.esa.int/pub/ESA_DOC/ENVISAT/MERIS/MERIS_DPML2_i7r2A_re-issued.pdf (accessed 26 February 2009).
- Hwang, P.; Shemdin, O. The Dependence of Sea-Surface Slope on Atmospheric Stability and Swell Conditions. J. Geophys. Res. 1988, 93, 13903–13912. [Google Scholar] [CrossRef]
- Shaw, J.; Churnside, J. Scanning-Laser Glint Measurements of Sea-Surface Slope Statistics. Appl. Opt. 1997, 36, 4202–4213. [Google Scholar] [CrossRef] [PubMed]
- Hwang, P. A. Observations of Swell Influence on Ocean Surface Roughness. J. Geophys. Res. 2008, 113, C12024:1–C12024:14. [Google Scholar] [CrossRef]
- Fischer, J.; Preusker, R.; Doerffer, R.; Bouvet, M. Atmospheric Correction of Sun Glint Contaminated MERIS Observations. In Proceedings of the 2nd MERIS-(A)ATSR workshop, Frascati, Italy, September 22–26, 2008.
- Heege, T.; Fischer, J. Sun Glitter Correction in Remote Sensing Imaging Spectrometry. In Proceedings of SPIE Ocean Optics XV Conference, Monaco, October 16–20, 2000.
- Carder, K.; Steward, R. A Remote-Sensing Reflectance Model of a Red-Tide Dinoflagellate Off West Florida. Limnol. Oceanogr. 1985, 30, 286–298. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.; Mobley, C.; Steward, R.; Patch, J. Hyperspectral Remote Sensing for Shallow Waters: 2. Deriving Bottom Depths and Water Properties by Optimization. Appl. Opt. 1999, 38, 3831–3843. [Google Scholar] [CrossRef] [PubMed]
- Joyce, K.E. A Method for Mapping Live Coral Cover Using Remote Sensing. Ph.D. thesis, University of Queensland, Brisbane, Australia, 2004. [Google Scholar]
- Bertels, L.; Vanderstraete, T.; van Coillie, S.; Knaeps, E.; Sterckx, S.; Goossens, R.; Deronde, B. Mapping of Coral Reefs Using Hyperspectral CASI Data; a Case Study: Fordata, Tanimbar, Indonesial. Int. J. Remote Sens. 2008, 29, 2359–2391. [Google Scholar] [CrossRef]
- Goodman, J.; Ustin, S. Classification of Benthic Composition in a Coral Reef Environment Using Spectral Unmixing. J. Appl. Remote Sens. 2007, 1, 011501:1–011501:17. [Google Scholar]
- Hooker, S.; Lazin, G.; Zibordi, G.; McLean, S. An Evaluation of Above- and in-Water Methods for Determining Water-Leaving Radiances. J. Atmos. Ocean. Tech. 2002, 19, 486–515. [Google Scholar] [CrossRef]
- Gordon, H.R. A Preliminary Assessment of the Nimbus-7 CZCS Atmospheric Correction Algorithm in a Horizontally Inhomogeneous Atmosphere. In Oceanography from Space; Gower, J.F.R., Ed.; Plenum Press: New York, NY, USA, 1981; pp. 257–266. [Google Scholar]
- Bukata, R.P.; Jerome, J.H.; Kondrattyev, K.Y.; Pozdnyakov, D.V. Optical Properties and Remote Sensing of Inland and Coastal Waters; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Zavody, A.; Birks, A. Sun Glint Contamination in ATSR-2 Data: Comparison of Observations and Values Calculated from the Measured 1.6-Mu M M Reflectivities. J. Atmos. Ocean. Tech. 2004, 21, 787–798. [Google Scholar] [CrossRef]
- Simpson, J.; Tsou, Y.; Schmidt, A.; Harris, A. Analysis of Along Track Scanning Radiometer-2 (ATSR-2) Data for Clouds, Glint and Sea Surface Temperature Using Neural Networks. Remote Sens. Environ. 2005, 98, 152–181. [Google Scholar] [CrossRef]
- Dinnat, E.; Le Vine, D. Impact of Sun Glint on Salinity Remote Sensing: An Example with the Aquarius Radiometer. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3137–3150. [Google Scholar] [CrossRef]
- Reul, N.; Tenerelli, J.; Chapron, B.; Waldteufel, P. Modeling Sun Glitter at L-Band for Sea Surface Salinity Remote Sensing with SMOS. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2073–2087. [Google Scholar] [CrossRef]
- Zavody, A.; Watts, P.; Smith, D.; Mutlow, C. A Novel Method for Calibrating the ATSR-2 1.6-Mu M Channel Using Simultaneous Measurements Made in the 3.7-Mu M Channel in Sun Glint. J. Atmos. Ocean. Tech. 1998, 15, 1243–1252. [Google Scholar] [CrossRef]
- Hagolle, O.; Nicolas, J.; Fougnie, B.; Cabot, F.; Henry, P. Absolute Calibration of VEGETATION Derived from an Interband Method Based on the Sun Glint Over Ocean. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1472–1481. [Google Scholar] [CrossRef]
- Nicolas, J.; Deschamps, P.; Hagolle, O. Radiometric Calibration of the Visible and Near-Infrared Bands of SEVIRI Using Rayleigh Scattering and Sun-Glint Over Oceans. In Proceedings of the 3rd MSG RAO Workshop, Helsinki, Finland, June 15, 2006; pp. 19–24.
- Aoki, T.; Aoki, T.; Fukabori, M. Path-Radiance Correction by Polarization Observation of Sun Glint Glitter for Remote Measurements of Tropospheric Greenhouse Gases. Appl. Opt. 2002, 41, 4945–4957. [Google Scholar] [CrossRef] [PubMed]
- Gao, B.; Kaufman, Y. Water Vapor Retrievals Using Moderate Resolution Imaging Spectroradiometer (MODIS) Near-Infrared Channels. J. Geophys. Res. 2003, 108, D13, 4389 ACH 4-1 to 4-10. [Google Scholar] [CrossRef]
- Ross, V.; Dion, D. Sea Surface Slope Statistics Derived from Sun Glint Radiance Measurements and Their Apparent Dependence on Sensor Elevation. J. Geophys. Res. 2007, 112, C09015:1–C09015:11. [Google Scholar] [CrossRef]
- Jackson, C. Internal Wave Detection Using the Moderate Resolution Imaging Spectroradiometer (MODIS). J. Geophys. Res. 2007, 112, C11012:1–C11012:13. [Google Scholar] [CrossRef]
- Elfouhaily, T.; Chapron, B.; Katsaros, K.; Vandemark, D. A Unified Directional Spectrum for Long and Short Wind-Driven Waves. J. Geophys. Res. 1997, 102, 15781–15796. [Google Scholar] [CrossRef]
- Heron, M.; Skirving, W.; Michael, K. Short-Wave Ocean Wave Slope Models for Use in Remote Sensing Data Analysis. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1962–1973. [Google Scholar] [CrossRef]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kay, S.; Hedley, J.D.; Lavender, S. Sun Glint Correction of High and Low Spatial Resolution Images of Aquatic Scenes: a Review of Methods for Visible and Near-Infrared Wavelengths. Remote Sens. 2009, 1, 697-730. https://doi.org/10.3390/rs1040697
Kay S, Hedley JD, Lavender S. Sun Glint Correction of High and Low Spatial Resolution Images of Aquatic Scenes: a Review of Methods for Visible and Near-Infrared Wavelengths. Remote Sensing. 2009; 1(4):697-730. https://doi.org/10.3390/rs1040697
Chicago/Turabian StyleKay, Susan, John D. Hedley, and Samantha Lavender. 2009. "Sun Glint Correction of High and Low Spatial Resolution Images of Aquatic Scenes: a Review of Methods for Visible and Near-Infrared Wavelengths" Remote Sensing 1, no. 4: 697-730. https://doi.org/10.3390/rs1040697
APA StyleKay, S., Hedley, J. D., & Lavender, S. (2009). Sun Glint Correction of High and Low Spatial Resolution Images of Aquatic Scenes: a Review of Methods for Visible and Near-Infrared Wavelengths. Remote Sensing, 1(4), 697-730. https://doi.org/10.3390/rs1040697




