Non-parametric Methods for Soil Moisture Retrieval from Satellite Remote Sensing Data
Abstract
:1. Introduction
2. Study Area and Data Sets
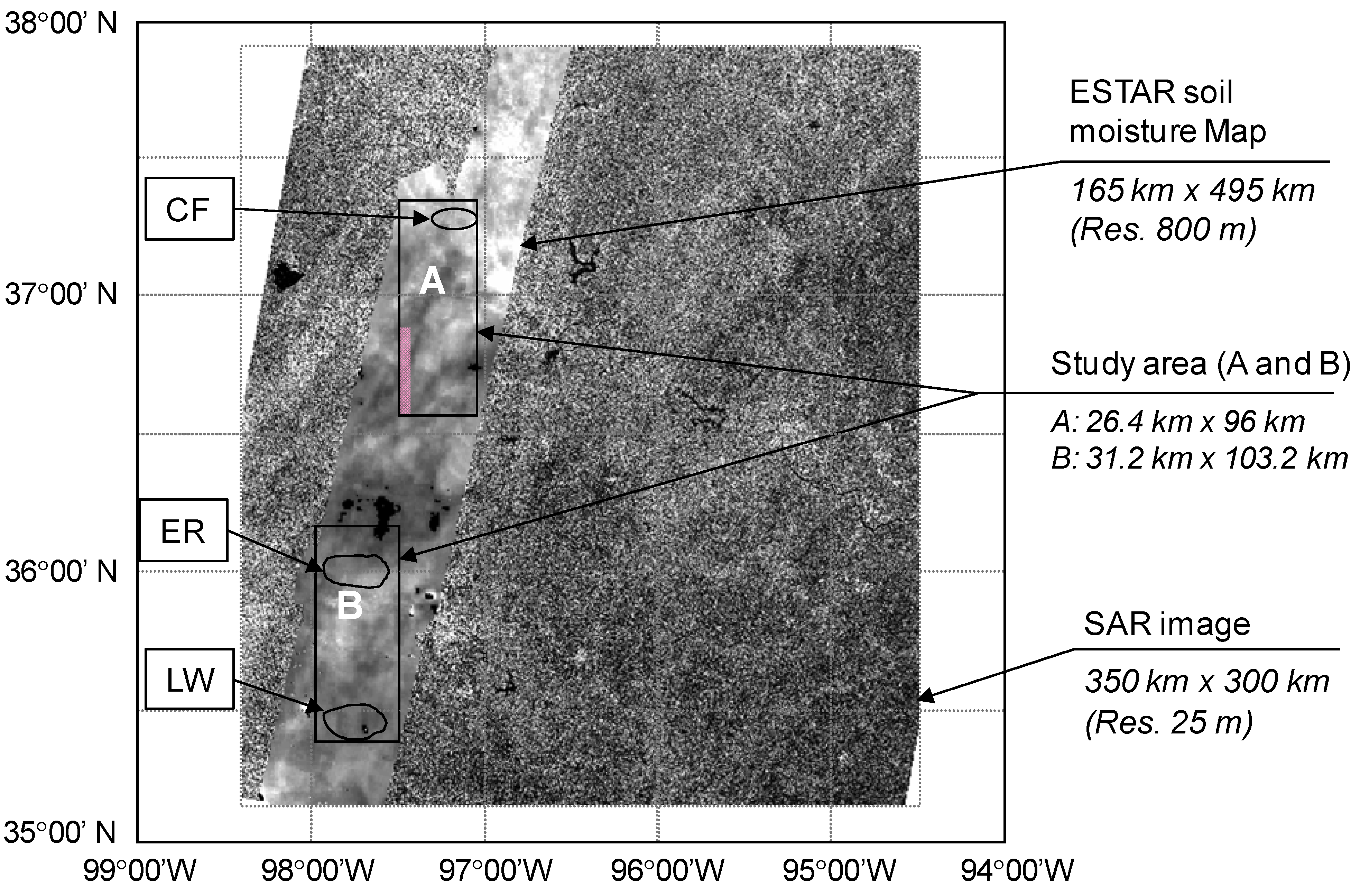
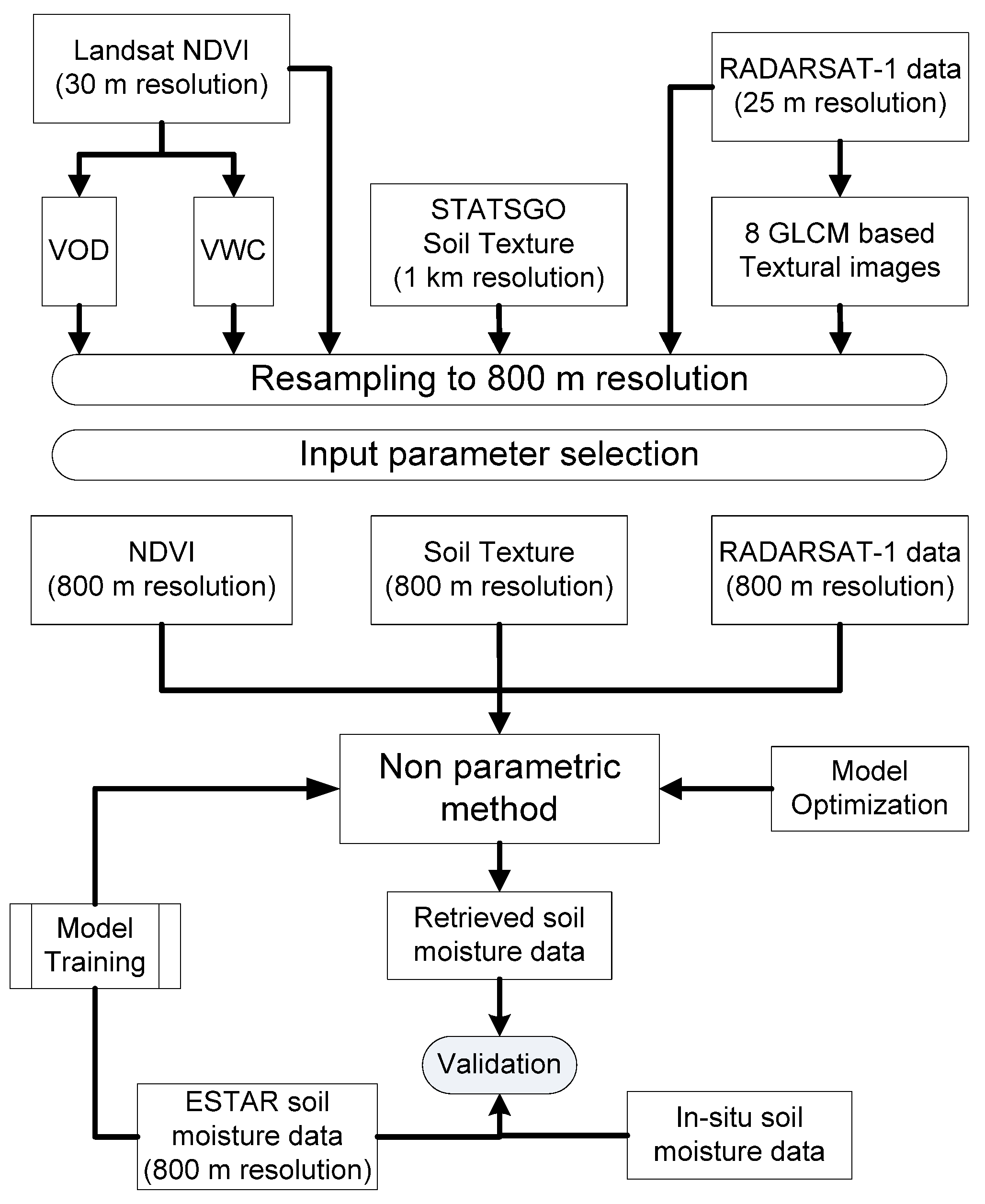
3. Methodology
3.1 Input Variable Selection approach
| Sr. No. | Data | Data Source | Spatial Resolution |
|---|---|---|---|
| 1 | Active microwave SAR data | RADARSAT-1 images | 25 m * 25 m (aggregated to 800 m * 800 m) |
| 2 | Soil moisture | ESTAR based brightness temperature | 800 m * 800 m |
| 3 | Soil moisture | Field Measurement | Point measurements |
| 4 | Normalized Difference Vegetation Index (NDVI) | Landsat images (Visible and Near Infrared band) | 30 m * 30 m (aggregated to 800 m * 800 m) |
| 5 | Vegetation Water Content (VWC) | Algorithm given by Jackson et al (1999) using NDVI | 800 m * 800 m |
| 6 | Vegetation Optical Depth (VOD) | Algorithm given in Jackson et al (1999) using NDVI | 800 m * 800 m |
| 7 | SAR textural images (Homogeneity, Contrast, Dissimilarity, Mean, Variance, Entropy, Angular Second Moment, and Correlation) | RADARSAT-1 images | 25 m * 25 m (aggregated to 800 m * 800 m) |
| 8 | Soil texture (percent of sand) | STATSGO of USDA | 1 km * 1 km (re-sampled to 800 m * 800 m) |
| Textural images | Homogeneity | Contrast | Dissimilarity | Mean | Variance | Entropy | AS-Moment | Correlation |
|---|---|---|---|---|---|---|---|---|
| Homogeneity | 1 | 0.647 | 0.848 | 0.303 | 0.053 | 0.949 | 0.870 | 0.544 |
| Contrast | 0.647 | 1 | 0.948 | 0.308 | 0.413 | 0.700 | 0.481 | 0.565 |
| Dissimilarity | 0.848 | 0.949 | 1 | 0.089 | 0.302 | 0.868 | 0.667 | 0.612 |
| Mean | 0.303 | 0.308 | 0.089 | 1 | 0.194 | 0.252 | 0.324 | 0.152 |
| Variance | 0.053 | 0.413 | 0.302 | 0.194 | 1 | 0.298 | 0.096 | 0.509 |
| Entropy | 0.949 | 0.700 | 0.868 | 0.252 | 0.298 | 1 | 0.859 | 0.372 |
| AS Moment | 0.870 | 0.481 | 0.667 | 0.324 | 0.096 | 0.859 | 1 | 0.337 |
| Correlation | 0.544 | 0.565 | 0.612 | 0.152 | 0.509 | 0.372 | 0.337 | 1 |
3.2 Multiple Regression Analysis
3.3 Neural Network
3.4 Fuzzy Logic
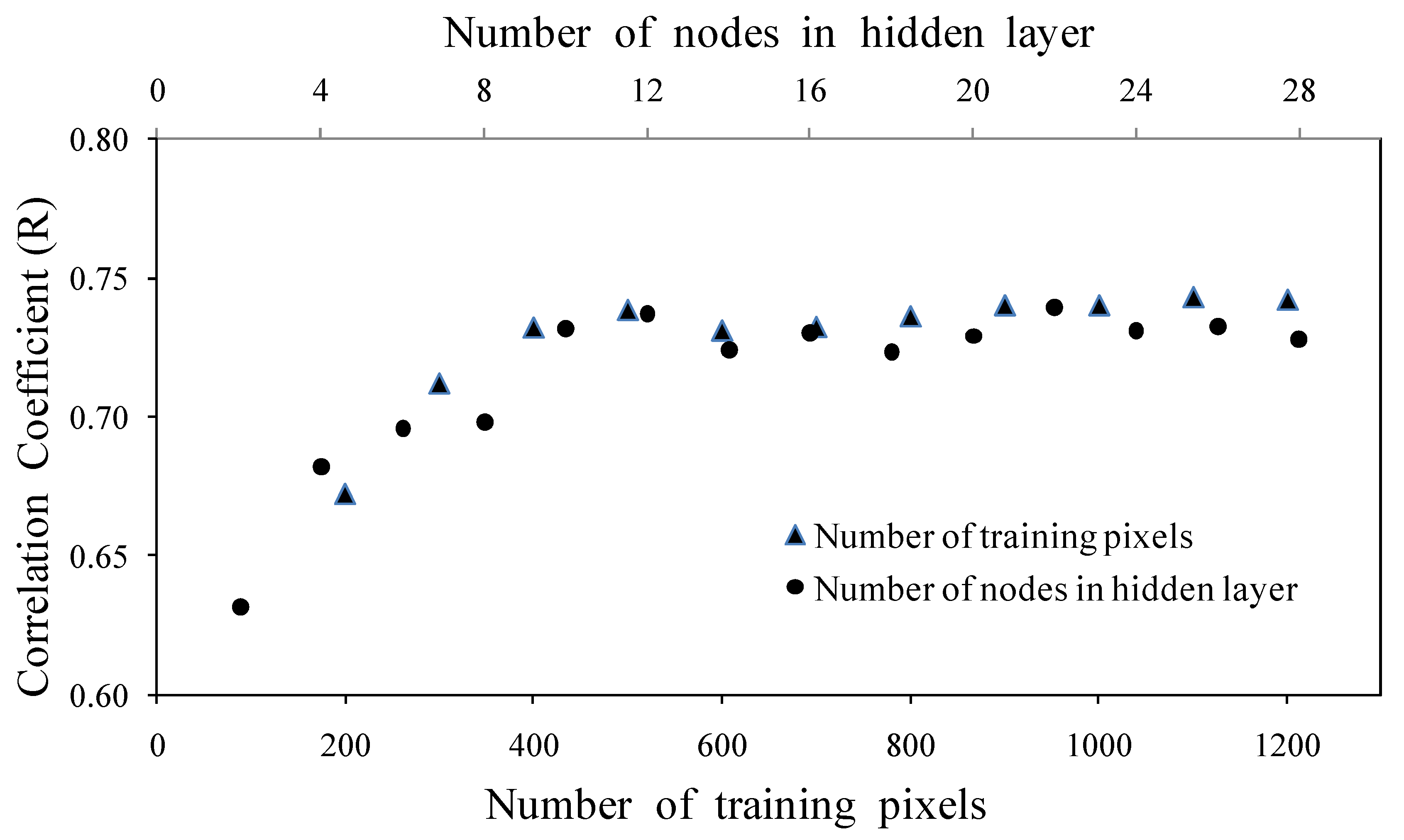
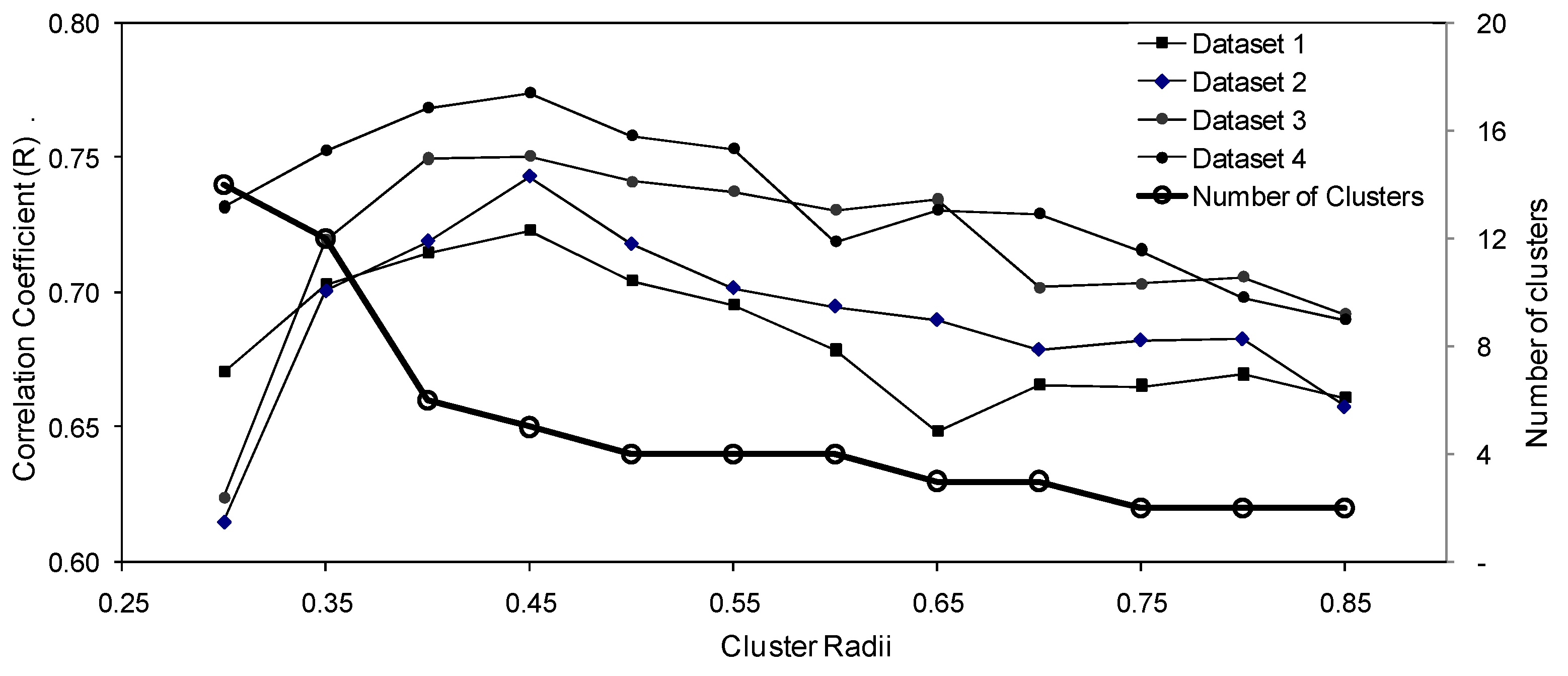
4. Results and Discussion
4.1 Comparison of Results
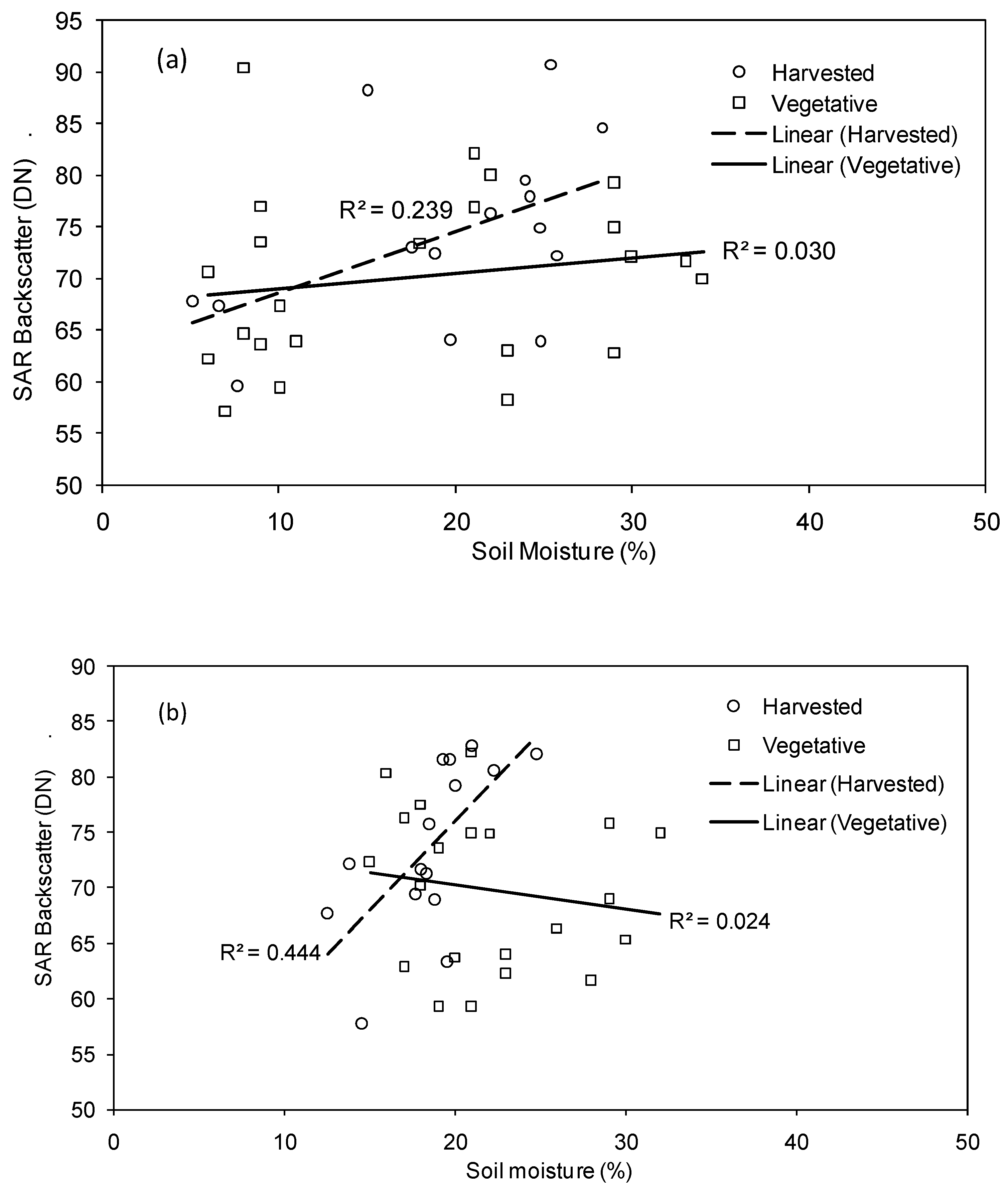
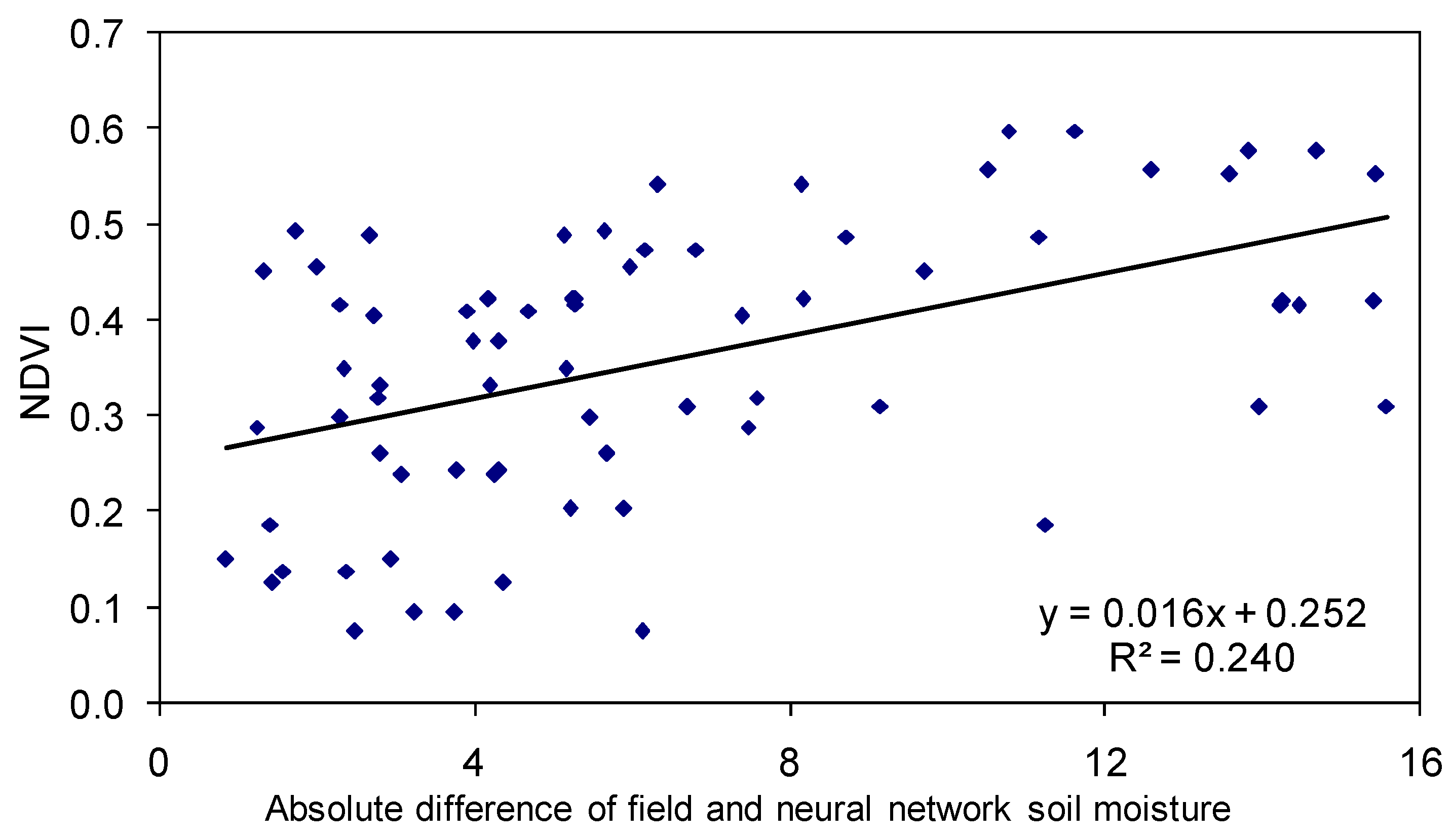
4.2 Effect of Vegetation and Soil Characteristics

| Date | Area | Neural Network Model | Fuzzy Logic Model | Multiple Regression Model | |||
|---|---|---|---|---|---|---|---|
| RMSE | R | RMSE | R | RMSE | R | ||
| 2nd July | A | 7.967 | 0.414 | 5.763 | 0.493 | 6.696 | 0.523 |
| B | 8.294 | 0.397 | 6.195 | 0.448 | 5.834 | 0.405 | |
| 12nd July | A | 3.621 | 0.715 | 3.722 | 0.702 | 4.570 | 0.665 |
| B | 4.493 | 0.458 | 3.853 | 0.504 | 4.822 | 0.483 | |
| Data Input | Neural Network Model | Fuzzy Logic Model | Multiple Regression Model | |||
|---|---|---|---|---|---|---|
| RMSE | R | RMSE | R | RMSE | R | |
| SAR | 4.847 | 0.620 | 4.506 | 0.645 | 7.436 | 0.591 |
| SAR+NDVI | 3.940 | 0.716 | 4.075 | 0.693 | 5.421 | 0.653 |
| SAR+PS | 4.344 | 0.660 | 3.955 | 0.684 | 5.631 | 0.634 |
| SAR+NDVI+PS | 3.396 | 0.767 | 3.454 | 0.759 | 4.482 | 0.719 |
5. Conclusions
Acknowledgments
References and Notes
- Jackson, T.J.; Vine, D.L.; Hsu, A.Y.; Oldak, A.; Starks, P.; Swift, C.; Isham, J.; Haken, M. Soil moisture mapping at regional scales using microwave radiometry: the Southern Great Plains Hydrology Experiment. IEEE Transactions on Geoscience and Remote Sensing 1999, 37, 2136–2151. [Google Scholar] [CrossRef]
- Jacobs, J.M.; Myers, D.A.; Whitfield, B.M. Improved Rainfall/Runoff Estimates Using Remotely Sensed Soil Moisture. Journal of the American Water Resources Association 2003, 39, 313–324. [Google Scholar] [CrossRef]
- Paige, G.B.; Keefer, T.O. Comparison of Field Performance of Multiple Soil Moisture Sensors in a Semi-Arid Rangeland. Journal of the American Water Resources Association 2008, 44, 121–135. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.; Fung, A. Microwave Remote Sensing Active and Passive From Theory to Applications; 1986; Artech House Norwood MA. [Google Scholar]
- Engman, E.T.; Chauhan, N. Status of microwave soil moisture measurements with remote sensing. Remote Sensing of Environment 1995, 51, 189–198. [Google Scholar] [CrossRef]
- Li, J.; Islam, S. On the estimation of soil moisture profile and surface fluxes partitioning from sequential assimilation of surface layer soil moisture. Journal of Hydrology 1999, 220, 86–103. [Google Scholar] [CrossRef]
- Houser, P.R.; Shuttleworth, W.J.; Gupta, H.V.; Famiglietti, J.S.; Syed, K.H.; Goodrich, D.C. Integration of Soil Moisture Remote Sensing and Hydrologic Modeling using Data Assimilation. Water Resources Research 1998, 34, 3405–3420. [Google Scholar] [CrossRef]
- Govind, A.; Chen, J.M.; Margolis, H.; Ju, W.; Sonnentag, O.; Giasson, M.-A. A spatially explicit hydro-ecological modeling framework (BEPS-TerrainLab V2.0): Model description and test in a boreal ecosystem in Eastern North America. Journal of Hydrology 2009, 367, 200–216. [Google Scholar] [CrossRef]
- Moran, M.S.; Watts, J.M.; Peters-Lidard, C.D.; McElroy, S.A. Estimating soil moisture at the watershed scale with satellite-based radar and land surface models. Canadian Journal of Remote Sensing 2004, 30, 805–826. [Google Scholar] [CrossRef]
- Cao, M.; Woodward, F.I. Dynamic responses of terrestrial ecosystem carbon cycling to global climate change. Nature 1998, 393, 249–252. [Google Scholar] [CrossRef]
- Harmsen, E.W.; Mesa, S.E.G.; Cabassa, E.; Ramirez-Beltran, N.D.; Pol, S.C.; Kuligowski, R. J.; Vasquez, R. Satellite Sub-Pixel Rainfall Variability. International Journal of Systems Applications, Engineering & Development 2008, 2, 91–100. [Google Scholar]
- Wagner, W.; Pathe, C.; Doubkova, M.; Sabel, D.; Bartsch, A.; Hasenauer, S.; Blöschl, G.; Scipal, K.; Martínez-Fernández, J.; Löw, A. Temporal Stability of Soil Moisture and Radar Backscatter Observed by the Advanced Synthetic Aperture Radar (ASAR). Sensors 2008, 8, 1174–1197. [Google Scholar] [CrossRef]
- Jeu, R.D.; Wagner, W.; Holmes, T.; Dolman, A.; Giesen, N.v.d.; Friesen, J. Global Soil Moisture Patterns Observed by Space Borne Microwave Radiometers and Scatterometers. Surveys in Geophysics 2008, 29, 399–420. [Google Scholar] [CrossRef]
- Jackson, T.J.; Schmugge, T. Vegetation effects on the microwave emission of soils. Remote Sensing of Environment 1991, 36, 203–212. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Allen, C.T.; Eger, G.; Kanemasu, H. Relating the microwave backscattering coefficient to leaf area index. Remote Sensing of Environment 1984, 14, 113–133. [Google Scholar] [CrossRef]
- Wang, C.; Qi, J.; Moran, S.; Marsett, R. Soil moisture estimation in a semiarid rangeland using ERS-2 and TM imagery. Remote Sensing of Environment 2004, 90, 178–189. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Dobson, M.; Bradley, G. Radar reflectivity of bare and vegetation covered soil. Advanced Space Research 1981, 1, 91–104. [Google Scholar] [CrossRef]
- Wang, J.R.; Hsu, A.; Shi, J.C.; O’Neill, P.E.; Engman, E.T. A Comparison of soil moisture retrieval models using SIR-C measurements over the Little Washita River Watershed. Remote Sensing of Environment 1997, 59, 308–320. [Google Scholar] [CrossRef]
- Ulaby, F.T. Radar measurement of soil moisture content. IEEE Transaction on Antennas and Propagation 1974, 22, 257–265. [Google Scholar] [CrossRef]
- Bernard, R.; Martin, P.H.; Thony, J.L.; Vauclin, M.; Vidal-Madjar, D. C-band radar for determining surface soil moisture. Remote Sensing of Environment 1982, 12, 189–200. [Google Scholar] [CrossRef]
- Wood, E.F.; Lin, D.S.; Mamcini, M.; Thongs, D.; Troch, P.A.; Jackson, T.J.; Famiglietti, J.S.; Engman, E.T. Inter-comparisons between passive and active microwave remote sensing and hydrological modeling for soil moisture. Advanced Space Research 1993, 13, 167–175. [Google Scholar] [CrossRef]
- Meade, N.; Hinzman, L.; Kane, D. Spatial estimation of soil moisture using synthetic aperture radar in Alaska. Advanced Space Research 1999, 24, 935–940. [Google Scholar] [CrossRef]
- Quesney, A.; Hégarat-Mascle, S.L.; Taconet, O.; Vidal-Madjar, D.; Wigneron, J.P.; Loumagne, C.; Normand, M. Estimation of watershed soil moisture index from ERS/SAR data. Remote Sensing of Environment 2000, 72, 290–303. [Google Scholar] [CrossRef]
- Moeremans, B.; Dautrebande, S. Soil moisture evaluation by means of multi-temporal ERS SAR PRI images and interferometric coherence. Journal of Hydrology 2000, 234, 162–169. [Google Scholar] [CrossRef]
- Glenn, N.F.; Carr, J.R. The use of geo-statistics in relating soil moisture to RADARSAT-1 SAR data obtained over the Great Basin, Nevada, USA. Computers and Geosciences 2003, 29, 577–586. [Google Scholar] [CrossRef]
- Srivastava, H.S.; Patel, P.; Manchanda, M.L.; Adiga, S. Use of multi-incidence angle RADARSAT-1 SAR data to incorporate the effect of surface roughness in soil moisture estimation. IEEE Transactions on Geoscience and Remote Sensing 2003, 41, 1638–1640. [Google Scholar] [CrossRef]
- Kasischke, E.; Smith, K.; Bourgeau-Chavez, L.; Romanowicz, E.; Brunzell, S.; Richardson, C. Effects of seasonal hydrologic patterns in south Florida wetlands on radar backscatter measured from ERS-2 SAR imagery. Remote Sensing of Environment 2003, 88, 423–441. [Google Scholar] [CrossRef]
- Geng, H.; Hugh, Q.; Gwyn, J.; Brisco, B.; Boisvert, J.; Brown, R. Mapping of Soil Moisture from C-Band Radar Images. Canadian Journal of Remote Sensing 1996, 22, 117–126. [Google Scholar] [CrossRef]
- Pultz, T.; Leconte, R.; Brown, R.; Brisco, B. Quantitative soil moisture extraction from airborne SAR data. Canadian Journal of Remote Sensing 1990, 16, 56–62. [Google Scholar] [CrossRef]
- Wang, Q.; Adiku, S.; Tenhunen, J.; Granier, A. On the relationship of NDVI with leaf area index in a deciduous forest site. Remote Sensing of Environment 2005, 94, 244–255. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Tatnall, A.R.L. Neural networks in remote sensing. International Journal of Remote Sensing 1997, 18, 699–709. [Google Scholar] [CrossRef]
- Benz, U.C.; Hofmann, P.; Willhauck, G.; Lingenfelder, I.; Heynen, M. Multi-resolution, object-oriented fuzzy analysis of remote sensing data for GIS-ready information. ISPRS Journal of Photogrammetry and Remote Sensing 2004, 58, 239–258. [Google Scholar] [CrossRef]
- Satalino, G.; Mattia, F.; Davidson, M.W.J.; Toan, T.L.; Pasquariello, G.; Borgeaud, M. On current limits of soil moisture retrieval from ERS-SAR data. IEEE Transactions on Geoscience and Remote Sensing 2002, 40, 2438–2447. [Google Scholar] [CrossRef]
- Ghedira, H.; Bernier, M.; Ouarda, T.B.M.J. Application of neural networks for wetland classification in Radarsat SAR imagery. IEEE International Geosciences and Remote Sensing Symposium, IGARSS’2000 2000, 2, 675–677. [Google Scholar]
- Benediktsson, J.; Swain, P.; Ersoy, O.K. Neural network approaches versus statistical methods in classification of multi-source remote sensing data. IEEE Transactions on Geoscience and Remote Sensing 1990, 28, 540–552. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Kouyate, F.; Brisco, B.; Williams, T.H.L. Textural information in SAR images. IEEE Transactions on Geoscience and Remote Sensing 1986, 24, 235–245. [Google Scholar] [CrossRef]
- Haralick, R.M. Statistical and structural approaches to texture. Proceedings of the IEEE 1979, 67, 786–804. [Google Scholar] [CrossRef]
- Soares, J.V.; Renno, C.D.; Formaggio, A.R.; Costa, C.F.Y.; Frery, A.C. An investigation of the selection of texture features for crop discrimination using SAR imagery. Remote Sensing of Environment 1997, 59, 234–247. [Google Scholar] [CrossRef]
- Soh, K.L.; Tsatsoulis, C. Texture analysis of SAR sea ice imagery using gray level co-occurrence matrices. Geoscience and Remote Sensing, IEEE Transactions on 1999, 37, 780–795. [Google Scholar] [CrossRef]
- Nystuen, J.A.; Garcia, F.W. Sea ice classification using SAR backscatter statistics. Geoscience and Remote Sensing, IEEE Transactions on 1992, 30, 502–509. [Google Scholar] [CrossRef]
- Sung, H.A. Ranking importance of input parameters of neural networks. Expert Systems with Applications 1998, 15, 405–411. [Google Scholar] [CrossRef]
- Almeida, J.S. Predictive non-linear modeling of complex data by artificial neural networks. Current Opinion in Biotechnology 2002, 13, 72–76. [Google Scholar] [CrossRef]
- Gilfilian, E.; Page, D. Use of Multivariate Statistical Techniques to Associate Biologically Active Stressors with Observed Effects in Multiple Stressor Situations. OCEANS 1986, 18, 953–959. [Google Scholar]
- Khoshgoftaar, T.M.; Szabo, R.M.; Guasti, P.J. Exploring the behaviour of neural network software quality models. Software Engineering Journal 1995, 10, 89–96. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Machine Learning 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Quinlan, J.R. Data mining tools See5 and C5.0. [cited 17 March 2009]. Available from: http://www.rulequest.com/see5-info.html.
- Cohen, J.; West, S.G. Applied Multiple Regression/correlation Analysis for the Behavioral Sciences, 3 ed.; 2003; Lawrence Erlbaum Associates. [Google Scholar]
- Paola, J.; Schowengerdt, R.A. A review and analysis of back-propagation neural networks for classification of remotely-sensed multi-spectral imagery. International Journal of Remote Sensing 1995, 16, 3033–3058. [Google Scholar] [CrossRef]
- Low, H.K.; Chuah, H.T.; Ewe, H.T. A neural network land use classifier for SAR images using textural and fractal information. Geocarto International 1999, 14, 66–73. [Google Scholar] [CrossRef]
- Carpenter, G.A.; Gopal, S.; Macomber, S.; Martens, S.; Woodcock, C.E.; Franklin, J. A neural network method for efficient vegetation mapping. Remote Sensing of Environment 1999, 70, 326–338. [Google Scholar] [CrossRef]
- Zainuddin, Z.; Pauline, O. Function Approximation Using Artificial Neural Networks. International Journal of Systems Applications, Engineering & Development 2007, 1, 173–178. [Google Scholar]
- Dias, F.M.; Antunes, A. Test error versus training error in artificial neural networks for systems affected by noise. International Journal of Systems Applications, Engineering & Development 2008, 2, 83–90. [Google Scholar]
- Augustejin, M.; Clemens, L.; Shaw, K. Performance evaluation of texture measures for ground cover identification in satellite images by means of a neural network classifier. IEEE Transactions on Geoscience and Remote Sensing 1995, 33, 616–626. [Google Scholar] [CrossRef]
- Chiu, S.L. An Efficient Method for Extracting Fuzzy Classification Rules from High Dimensional Data. Journal of Advanced Computational Intelligence 1997, 1, 1–7. [Google Scholar]
- Hayajneh, M.T.; Radaideh, S.M. Modeling Surface Finish in End Milling Using Fuzzy Subtractive Clustering-Based System Identification Method. Materials and Manufacturing Processes 2003, 18, 653–665. [Google Scholar] [CrossRef]
- Nedeljkovic, I. Image classification based on fuzzy logic. In The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences; 2004. [Google Scholar]
- Legleiter, C.J.; Goodchild, M.F. Alternative representations of in-stream habitat: classification using remote sensing, hydraulic modeling, and fuzzy logic. International Journal of Geographical Information Science 2005, 19, 29–50. [Google Scholar] [CrossRef]
- Jackson, T.J.; Chen, D.; Cosh, M.; Li, F.; Anderson, M.; Walthall, C.; Doraiswamy, P.; Hunt, E.R. Vegetation water content mapping using Landsat data normalized difference water index (NDWI) for corn and soybean. Remote Sensing of Environment 2004, 92, 475–482. [Google Scholar] [CrossRef]
- Famiglietti, J.S.; Devereaux, J.A.; Laymon, C.A.; Tsegaye, T.; Houser, P.R.; Jackson, T.J.; Graham, S.T.; Rodell, M.; Oevelen, P.J. Ground-based investigation of soil moisture variability within remote sensing footprints during the Southern Great Plains 1997 (SGP97) Hydrology Experiment. Water Resources Research 1999, 35, 1839–1851. [Google Scholar] [CrossRef]
- Crow, W.T.; Ryu, D.; Famiglietti, J.S. Upscaling of field-scale soil moisture measurements using distributed land surface modeling. Advances in Water Resources 2005, 28, 1–14. [Google Scholar] [CrossRef]
- Jacobs, J.M.; Mohanty, B.P.; Hsu, E.-C.; Miller, D. SMEX02: Field scale variability, time stability and similarity of soil moisture. Remote Sensing of Environment 2004, 92, 436–446. [Google Scholar] [CrossRef]
- Bindlish, R.; Barros, A.P. Sub-pixel variability of remotely sensed soil moisture: an inter-comparison study of SAR and ESTAR. Remote Sensing of Environment 2002, 40, 326–337. [Google Scholar]
- Marsett, R.C.; Qi, J.; Heilman, P.; Biedenbender, S.H.; Watson, M.C.; Amer, S.; Weltz, M.; Goodrich, D.; Marsett, R. Remote Sensing for Grassland Management in the Arid Southwest. Rangeland Ecology & Management 2006, 59, 530–540. [Google Scholar]
- Qi, J.; Marsett, R.C.; Moran, M.S.; Goodrich, D.C.; Swain, P.; Kerr, Y.H.; Dedieu, G.; Chehbouni, A.; Zhang, X.X. Spatial and temporal dynamics of vegetation in the San Pedro River basin area. Agricultural and Forest Meteorology 2000, 105, 55–68. [Google Scholar] [CrossRef]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lakhankar, T.; Ghedira, H.; Temimi, M.; Sengupta, M.; Khanbilvardi, R.; Blake, R. Non-parametric Methods for Soil Moisture Retrieval from Satellite Remote Sensing Data. Remote Sens. 2009, 1, 3-21. https://doi.org/10.3390/rs1010003
Lakhankar T, Ghedira H, Temimi M, Sengupta M, Khanbilvardi R, Blake R. Non-parametric Methods for Soil Moisture Retrieval from Satellite Remote Sensing Data. Remote Sensing. 2009; 1(1):3-21. https://doi.org/10.3390/rs1010003
Chicago/Turabian StyleLakhankar, Tarendra, Hosni Ghedira, Marouane Temimi, Manajit Sengupta, Reza Khanbilvardi, and Reginald Blake. 2009. "Non-parametric Methods for Soil Moisture Retrieval from Satellite Remote Sensing Data" Remote Sensing 1, no. 1: 3-21. https://doi.org/10.3390/rs1010003
APA StyleLakhankar, T., Ghedira, H., Temimi, M., Sengupta, M., Khanbilvardi, R., & Blake, R. (2009). Non-parametric Methods for Soil Moisture Retrieval from Satellite Remote Sensing Data. Remote Sensing, 1(1), 3-21. https://doi.org/10.3390/rs1010003






