Temperature Estimation for Photovoltaic Array Using an Adaptive Neuro Fuzzy Inference System
Abstract
:1. Introduction
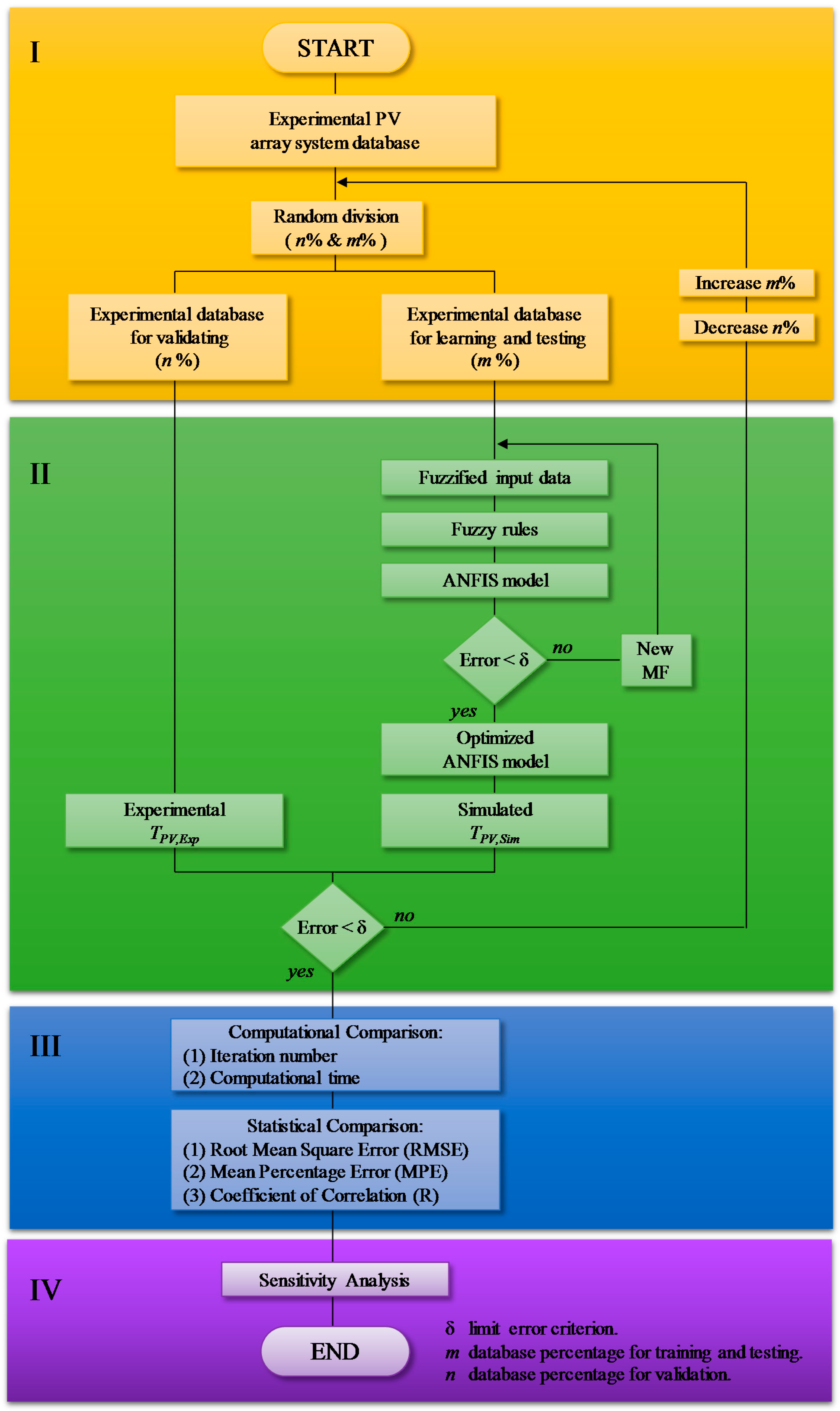
2. Materials and Methods
2.1. PV Module Performance
- Effect of environmental temperature. Similar to other semiconductor devices, solar cells are sensitive to temperature. An increase in temperature reduces the band gap of a semiconductor, affecting most of the semiconductor material parameters. The decrease in the band gap of a semiconductor with increasing temperature can be viewed as an energy increase in the material’s electrons. Lower electronic energy is therefore needed to break the bond, yielding lower current values. In the bond model of a semiconductor band gap, reduction in the bond energy also reduces the band gap. Therefore, increasing the temperature reduces the band gap and consequently its performance. It has been proven that the conversion efficiency of PV modules drops progressively as dust is accumulated on its surface in the simultaneous presence of high temperature [15].
- Effect of solar radiation. Solar radiation is under constant changes throughout the day. It varies depending on geographical location, sun angle, cloudiness, month of the year, etc. An increment of solar radiation improves the module power output, but also increases its temperature, reducing the efficiency [40].
- Effect of wind. The wind lowers the module’s temperature, which helps to reduce the cell temperature, which is crucial to maintaining PV conversion efficiency [16].
- Effect of atmospheric pressure. Atmospheric pressure is a combination of air molecules with weight and movement. The change of air pressure causes the change of airflow on the surface of PV modules, which affects heat dissipation and causes module temperature fluctuation [17].
2.2. Experimental System Description
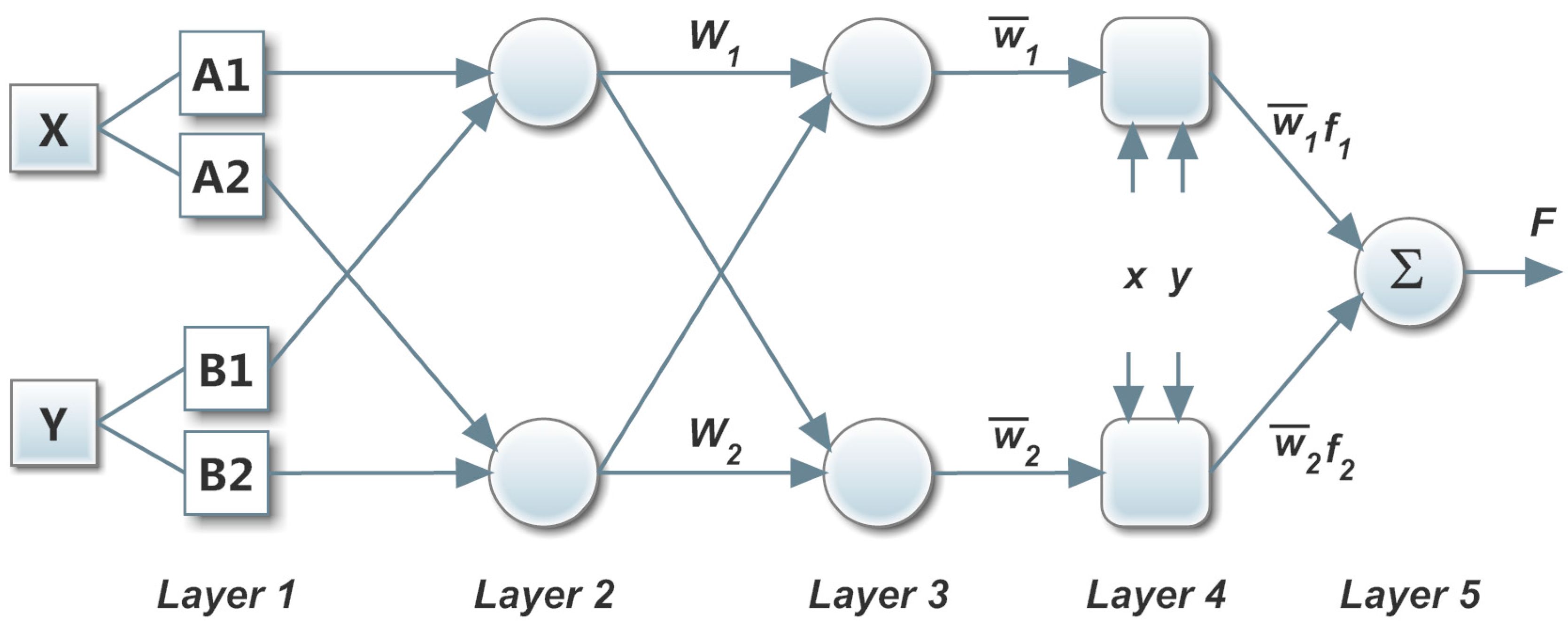
2.3. Adaptive Neuro-Fuzzy Inference System (ANFIS)
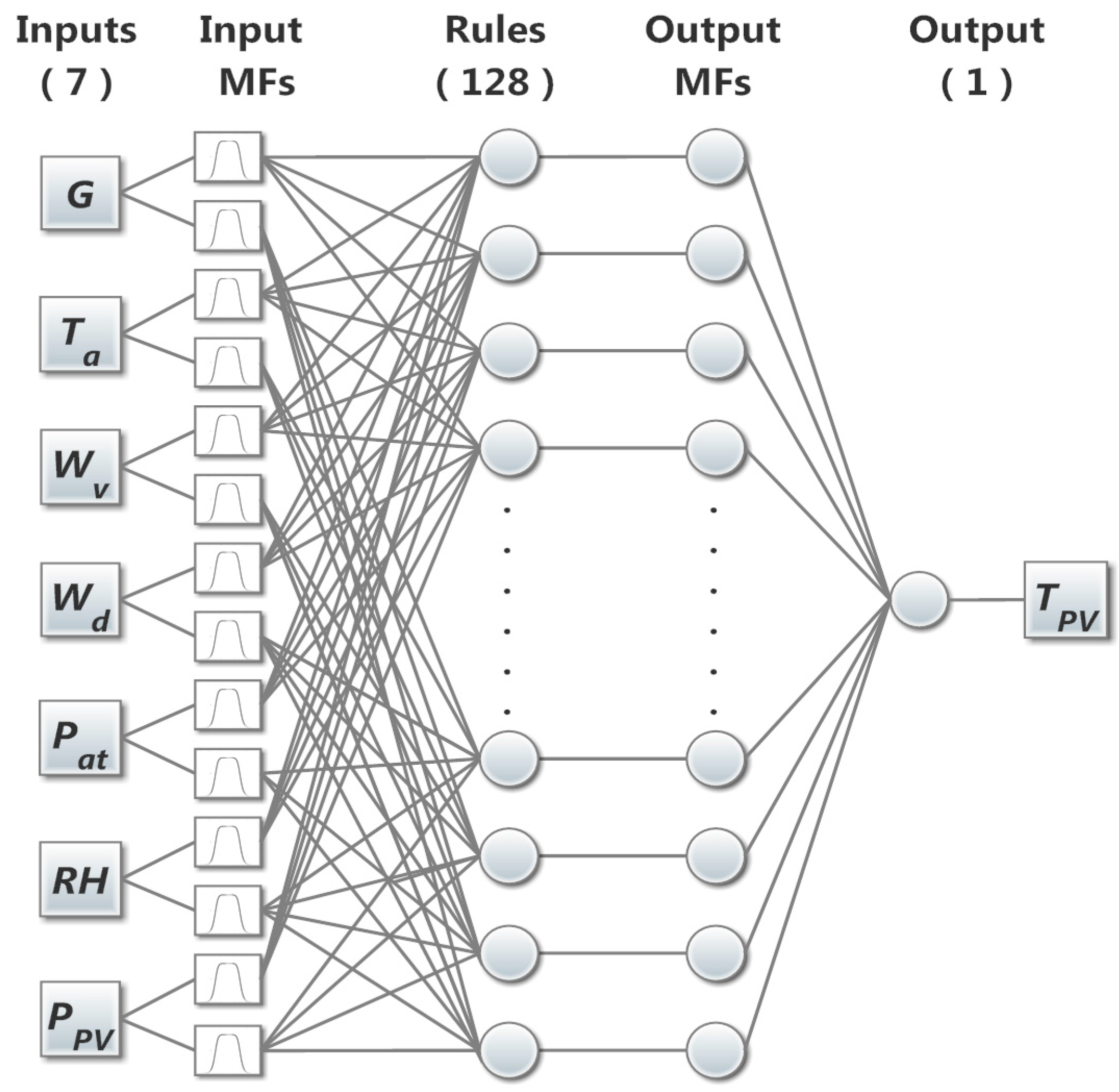
3. ANFIS PV Module Modeling
4. Results and Discussion
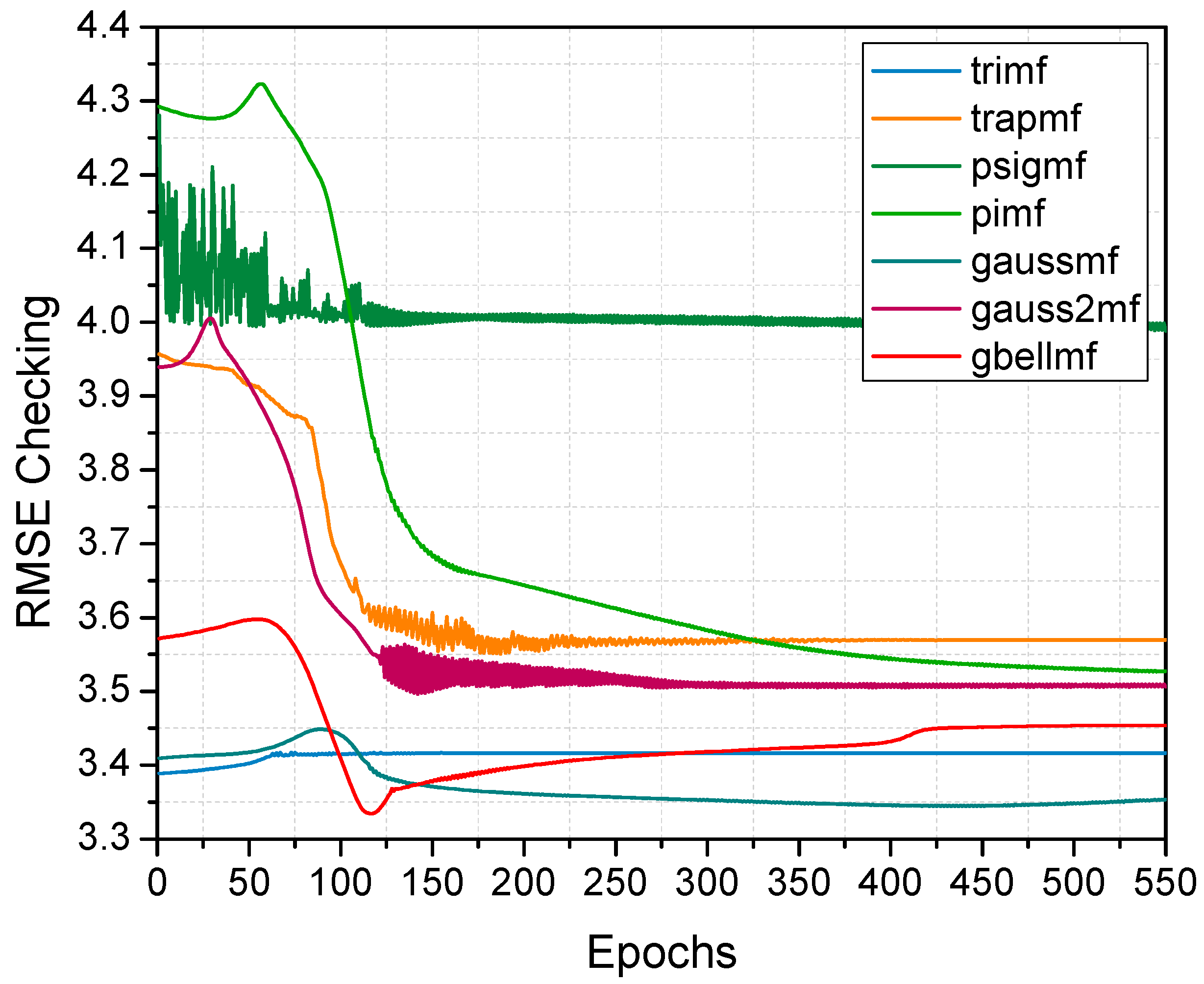
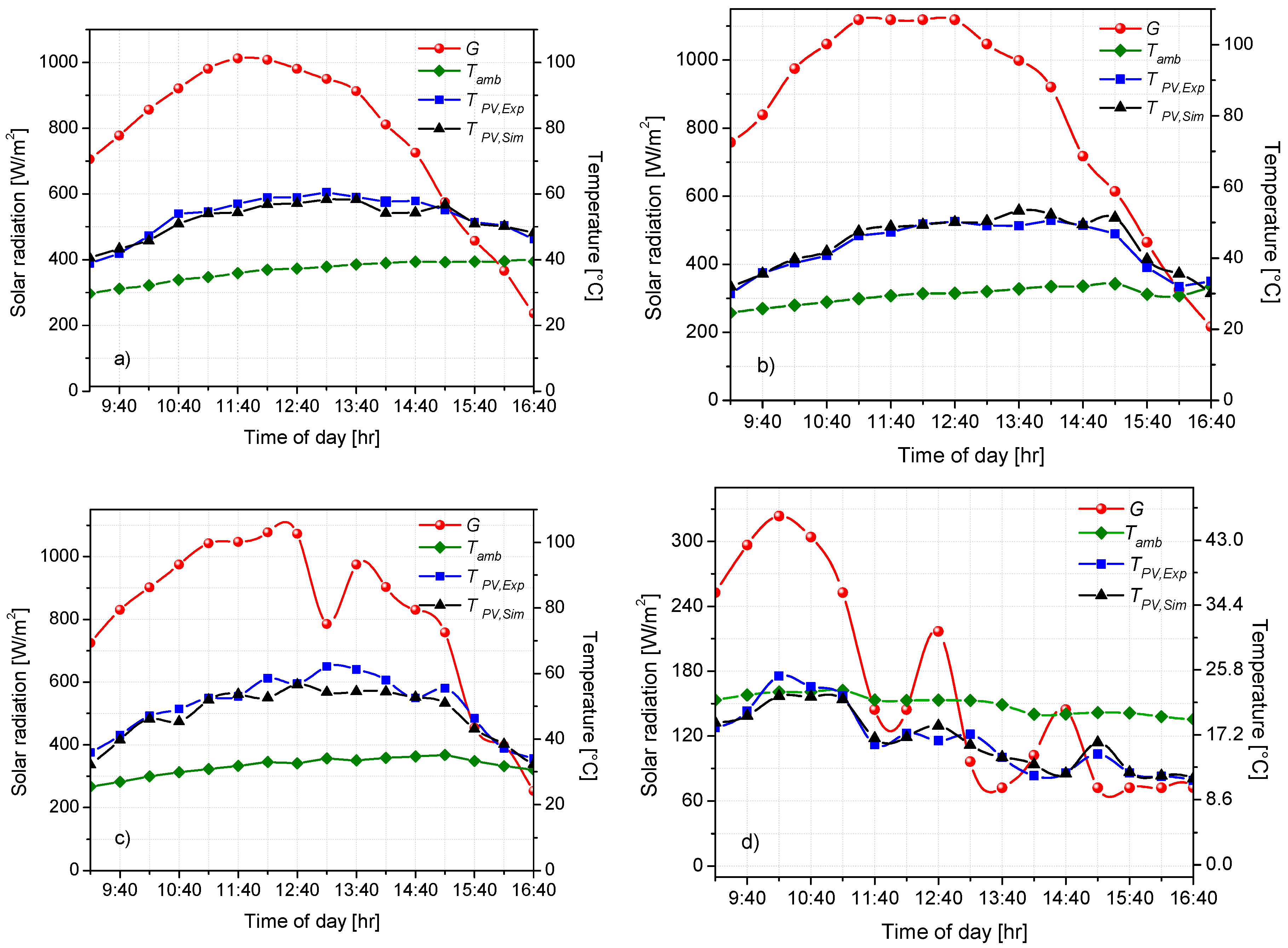
4.1. ANFIS Simulation Results
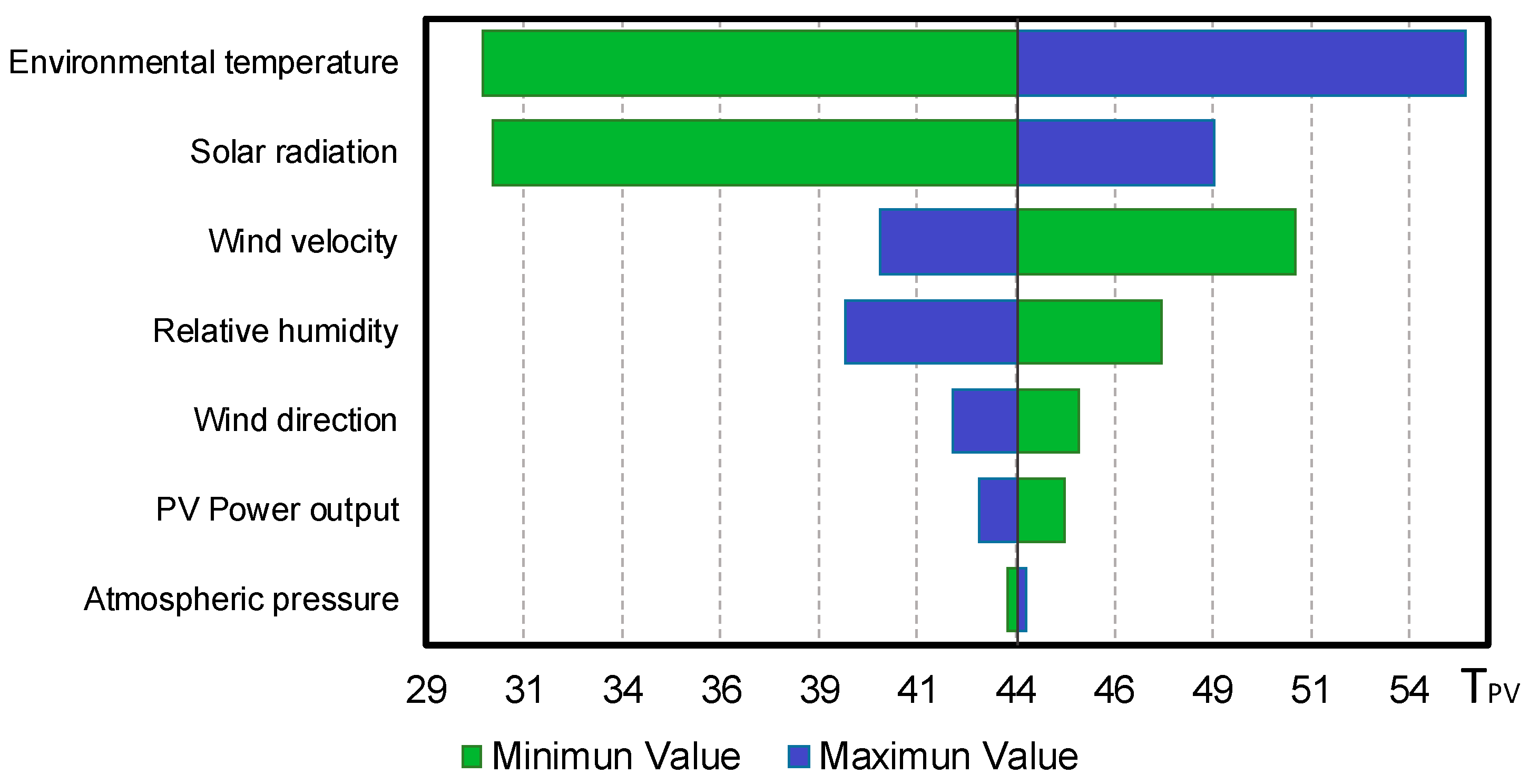
4.2. Sensitivity Analysis Results
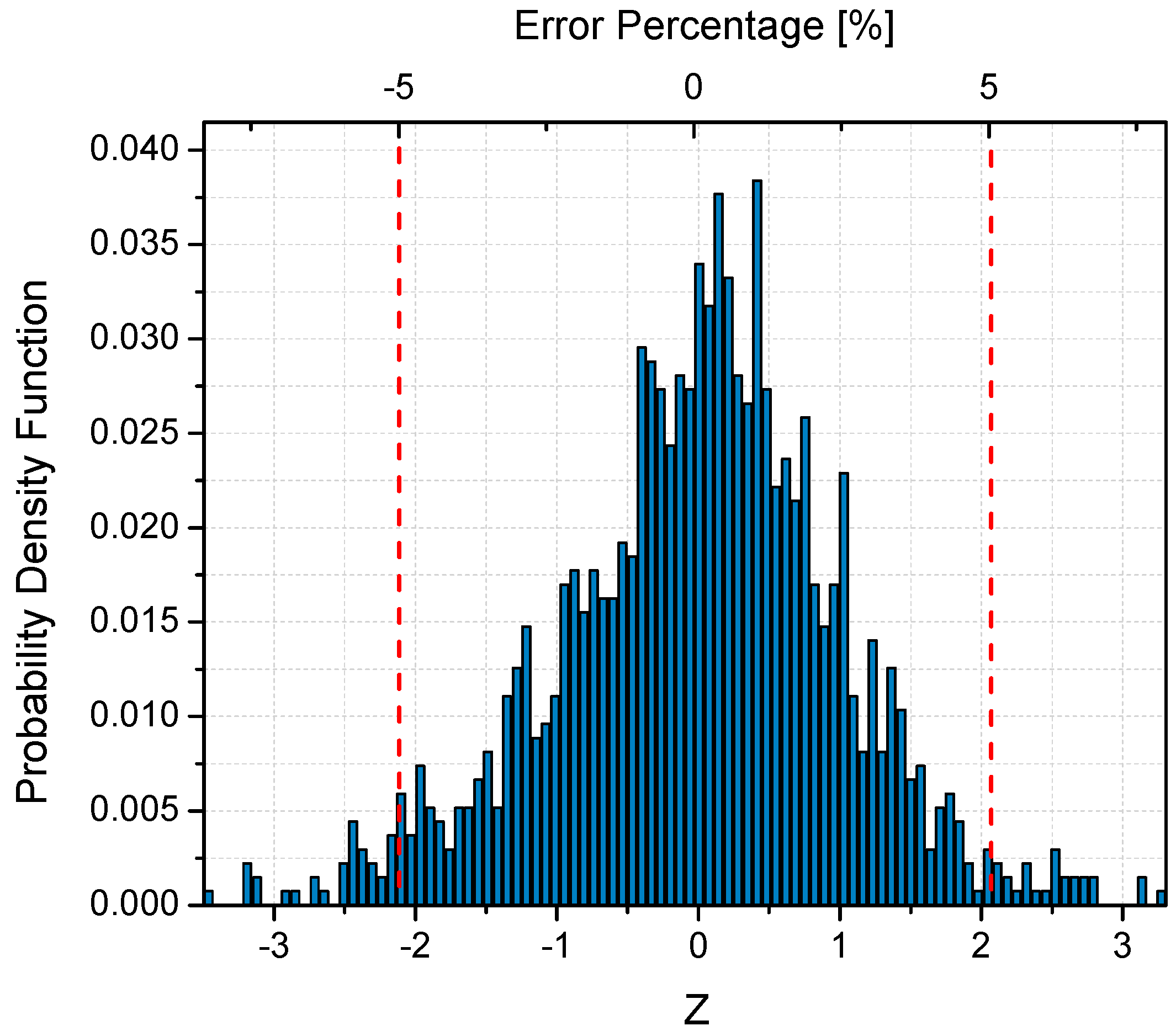
4.3. Evaluation of the ANFIS Model
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Calise, F.; Figaj, R.D.; Vanoli, L. Experimental and Numerical Analyses of a Flat Plate Photovoltaic/Thermal Solar Collector. Energies 2017, 10, 491. [Google Scholar] [CrossRef]
- Tzuc, O.M.; Bassam, A.; Flota-Bañuelos, M.; Ordoñez, E.E.; Ricalde-Cab, L.; Quijano, R.; Vega Pasos, A.E. Thermal Efficiency Prediction of a Solar Low Enthalpy Steam Generating Plant Employing Artificial Neural Networks. In Intelligent Computing Systems; Springer International: Mérida, Yucatán, Mexico, 2016; Volume 4113, pp. 61–73. [Google Scholar]
- Song, A.; Lu, L.; Liu, Z.; Wong, M.S. A Study of Incentive Policies for Building-Integrated Photovoltaic Technology in Hong Kong. Sustainability 2016, 8, 769. [Google Scholar] [CrossRef]
- Cucchiella, F.; Adamo, I.D.; Gastaldi, M. Economic Analysis of a Photovoltaic System: A Resource for Residential Households. Energies 2017, 10, 814. [Google Scholar] [CrossRef]
- Seyboth, K.; Sverrisson, F.; Appavou, F.; Brown, A.; Epp, B.; Leidreiter, A.; Lins, C.; Musolino, E.; Murdock, H.E.; Petrichenko, K.; et al. Renewables 2016 Global Status Report; REN21: Paris, France, 2016. [Google Scholar]
- Kim, S.; Yoon, S.; Choi, W.; Choi, K. Application of Floating Photovoltaic Energy Generation Systems in South Korea. Sustainability 2016, 8, 1333. [Google Scholar] [CrossRef]
- Ceylan, I.; Erkaymaz, O.; Gedik, E.; Gurel, A.E. The prediction of photovoltaic module temperature with artificial neural networks. Case Stud. Therm. Eng. 2014, 3, 11–20. [Google Scholar] [CrossRef]
- Vera, J.T.; Laukkanen, T.; Sirén, K. Multi-objective optimization of hybrid photovoltaic-thermal collectors integrated in a DHW heating system. Energy Build. 2014, 74, 78–90. [Google Scholar] [CrossRef]
- Bahaidarah, H.M.S.; Baloch, A.A.B.; Gandhidasan, P. Uniform cooling of photovoltaic panels: A review. Renew. Sustain. Energy Rev. 2016, 57, 1520–1544. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, Z. Design and Research of the Movable Hybrid Photovoltaic-Thermal (PVT) System. Energies 2017, 10, 507. [Google Scholar] [CrossRef]
- King, D.L.; Kratochvil, J.A.; Boyson, W.E. Temperature coefficients for PV modules and arrays: Measurement/nmethods, difficulties, and results. In Proceedings of the Conference Record of the Twenty Sixth IEEE Photovoltaic Specialists Conference, Anaheim, CA, USA, 29 September–3 October 1997; pp. 1183–1186. [Google Scholar]
- Jordehi, A.R. Parameter estimation of solar photovoltaic (PV) cells: A review. Renew. Sustain. Energy Rev. 2016, 61, 354–371. [Google Scholar] [CrossRef]
- Yordanov, G.H.; Midtgård, O.M.; Saetre, T.O. Series resistance determination and further characterization of c-Si PV modules. Renew. Energy 2012, 46, 72–80. [Google Scholar] [CrossRef]
- Skoplaki, E.; Palyvos, J.A. On the temperature dependence of photovoltaic module electrical performance: A review of efficiency/power correlations. Sol. Energy 2009, 83, 614–624. [Google Scholar] [CrossRef]
- Quaschning, V. Understanding Renewable Energy Systems; Earthscan: London, UK, 2005; Volume 67. [Google Scholar]
- Abiola-Ogedengbe, A.; Hangan, H.; Siddiqui, K. Experimental investigation of wind effects on a standalone photovoltaic (PV) module. Renew. Energy 2015, 78, 657–665. [Google Scholar] [CrossRef]
- Cheng, X.; Chen, F.; Yu, B.; Zhang, X. The method for photovoltaic module temperature ultra-short-term forecasting based on RBF neural network. In Proceedings of the 2016 China International Conference on Electricity Distribution (CICED), Xi’an, China, 10–13 August 2016; pp. 1–5. [Google Scholar]
- Mekhilef, S.; Saidur, R.; Kamalisarvestani, M. Effect of dust, humidity and air velocity on efficiency of photovoltaic cells. Renew. Sustain. Energy Rev. 2012, 16, 2920–2925. [Google Scholar] [CrossRef]
- Dzib, J.T.; Alejos Moo, E.J.; Bassam, A.; Flota-Bañuelos, M.; Escalante Soberanis, M.A.; Ricalde, L.J.; López-Sánchez, M.J. Photovoltaic Module Temperature Estimation: A Comparison Between Artificial Neural Networks and Adaptive Neuro Fuzzy Inference Systems Models. In Intelligent Computing Systems; Springer: Cham, Switzerland, 2016; Volume 597, pp. 46–60. [Google Scholar]
- Schwingshackl, C.; Petitta, M.; Wagner, J.E.; Belluardo, G.; Moser, D.; Castelli, M.; Zebisch, M.; Tetzlaff, A. Wind effect on PV module temperature: Analysis of different techniques for an accurate estimation. Energy Procedia 2013, 40, 77–86. [Google Scholar] [CrossRef]
- Raza, M.Q.; Khosravi, A. A review on artificial intelligence based load demand forecasting techniques for smart grid and buildings. Renew. Sustain. Energy Rev. 2015, 50, 1352–1372. [Google Scholar] [CrossRef]
- Mellit, A.; Benghanem, M.; Kalogirou, S.A. Modeling and simulation of a stand-alone photovoltaic system using an adaptive artificial neural network: Proposition for a new sizing procedure. Renew. Energy 2007, 32, 285–313. [Google Scholar] [CrossRef]
- May Tzuc, O.; Bassam, A.; Escalante Soberanis, M.A.; Venegas-Reyes, E.; Jaramillo, O.A.; Ricalde, L.J.; Ordoñez, E.E.; El Hamzaoui, Y. Modeling and optimization of a solar parabolic trough concentrator system using inverse artificial neural network. J. Renew. Sustain. Energy 2017, 9, 13701. [Google Scholar] [CrossRef]
- Yaïci, W.; Entchev, E. Performance prediction of a solar thermal energy system using artificial neural networks. Appl. Therm. Eng. 2014, 73, 1348–1359. [Google Scholar] [CrossRef]
- Yaïci, W.; Entchev, E. Adaptive Neuro-Fuzzy Inference System modelling for performance prediction of solar thermal energy system. Renew. Energy 2016, 86, 302–315. [Google Scholar] [CrossRef]
- Gao, Y.; Qu, C.; Zhang, K. A Hybrid Method Based on Singular Spectrum Analysis, Firefly Algorithm, and BP Neural Network for Short-Term Wind Speed Forecasting. Energies 2016, 9, 757. [Google Scholar] [CrossRef]
- Zhang, F.; Dong, Y.; Zhang, K. A Novel Combined Model Based on an Artificial Intelligence Algorithm—A Case Study on Wind Speed Forecasting in Penglai, China. Sustainability 2016, 8, 555. [Google Scholar] [CrossRef]
- Bassam, A.; Santoyo, E.; Andaverde, J.; Hernández, J.A.; Espinoza-Ojeda, O.M. Estimation of static formation temperatures in geothermal wells by using an artificial neural network approach. Comput. Geosci. 2010, 36, 1191–1199. [Google Scholar] [CrossRef]
- Petković, D.; Pavlović, N.T.; Ćojbašić, Ž. Wind farm efficiency by adaptive neuro-fuzzy strategy. Int. J. Electr. Power Energy Syst. 2016, 81, 215–221. [Google Scholar] [CrossRef]
- Mellit, A.; Kalogirou, S.A.; Hontoria, L.; Shaari, S. Artificial intelligence techniques for sizing photovoltaic systems: A review. Renew. Sustain. Energy Rev. 2009, 13, 406–419. [Google Scholar] [CrossRef]
- Mohanty, S. ANFIS based Prediction of Monthly Average Global Solar Radiation over Bhubaneswar (State of Odisha). Int. J. Ethics Eng. Manag. Educ. 2014, 1, 2–6. [Google Scholar]
- Mellit, A.; Kalogirou, S.A. ANFIS-based modelling for photovoltaic power supply system: A case study. Renew. Energy 2011, 36, 250–258. [Google Scholar] [CrossRef]
- Aldobhani, A.M.S.; Robert, J. Maximum power point tracking of PV system using ANFIS prediction and fuzzy logic tracking. In Proceedings of the International MultiConference of Engineers and Computer Scientists, Hong Kong, 19–21 March 2008; Vol. II, pp. 19–21. [Google Scholar]
- Vafaei, S.; Gandomkar, M.; Rezvani, A.; Izadbakhsh, M. Enhancement of grid-connected photovoltaic system using ANFIS-GA under different circumstances. Front. Energy 2015, 9, 322–334. [Google Scholar] [CrossRef]
- Kharb, R.K.; Shimi, S.L.; Chatterji, S. Improved Maximum Power Point Tracking for Solar PV Module using ANFIS. Int. J. Curr. Eng. Technol. 2013, 3, 1878–1885. [Google Scholar]
- Notton, G.; Cristofari, C.; Mattei, M.; Poggi, P. Modelling of a double-glass photovoltaic module using finite differences. Appl. Therm. Eng. 2005, 25, 2854–2877. [Google Scholar] [CrossRef]
- Chow, T.T.; He, W.; Ji, J. Hybrid photovoltaic-thermosyphon water heating system for residential application. Sol. Energy 2006, 80, 298–306. [Google Scholar] [CrossRef]
- Micheli, D.; Alessandrini, S.; Radu, R.; Casula, I. Analysis of the outdoor performance and efficiency of two grid connected photovoltaic systems in northern Italy. Energy Convers. Manag. 2014, 80, 436–445. [Google Scholar] [CrossRef]
- Humada, A.M.; Hojabri, M.; Hamada, H.M.; Samsuri, F.B.; Ahmed, M.N. Performance evaluation of two PV technologies (c-Si and CIS) for building integrated photovoltaic based on tropical climate condition: A case study in Malaysia. Energy Build. 2016, 119, 233–241. [Google Scholar] [CrossRef]
- Marion, B.; Adelstein, J.; Boyle, K.; Hayden, H.; Hammond, B.; Fletcher, T.; Canada, B.; Narang, D.; Kimber, A.; Mitchell, L.; et al. Performance parameters for grid-connected PV systems. In Proceedings of the 2005 Conference Record of the Thirty-first IEEE Photovoltaic Specialists Conference, Lake Buena Vista, FL, USA, 3–7 January 2005; pp. 1601–1606. [Google Scholar]
- Elminir, H.K.; Benda, V.; Tousek, J. Effects of solar irradiation conditions on the outdoor performance of photovoltaic modules. J. Electr. Eng. 2001, 52, 125–133. [Google Scholar]
- Lim, L.H.I.; Ye, Z.; Yang, D. Non-contact measurement of POA irradiance and cell temperature for PV systems. In Proceedings of the IECON 2015—41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 386–391. [Google Scholar]
- Jang, J.S.R. ANFIS: Adaptive-Network-Based Fuzzy Inference System. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Mohammadi, K.; Shamshirband, S.; Petkovic, D.; Yee, P.L.; Mansor, Z. Using ANFIS for selection of more relevant parameters to predict dew point temperature. Appl. Therm. Eng. 2016, 96, 311–319. [Google Scholar] [CrossRef]
- Abraham, A. Adaptation of fuzzy inference system using neural learning. Fuzzy Syst. Eng. 2005, 83, 53–83. [Google Scholar]
- Mohammadi, K.; Shamshirband, S.; Kamsin, A.; Lai, P.C.; Mansor, Z. Identifying the most signi ficant input parameters for predicting global solar radiation using an ANFIS selection procedure. Renew. Sustain. Energy Rev. 2016, 63, 423–434. [Google Scholar] [CrossRef]
- Loucks, D.P.; van Beek, E.; Stedinger, J.R.; Dijkman, J.P.M.; Villars, M.T. Water Resources Systems Planning and Management and Applications: An Introduction to Methods, Models and Applications; UNESCO: Paris, France, 2005; Volume 51. [Google Scholar]
- Mathworks, C. Fuzzy Logic ToolboxTM User’s Guide R 2014 b; The MathWorks, Inc.: Natick, MA, USA, 2014. [Google Scholar]
- Spiegel, M.; Stephens, L.J. Theory and Problems of Statistics; McGraw Hill: New York, NY, USA, 2009. [Google Scholar]
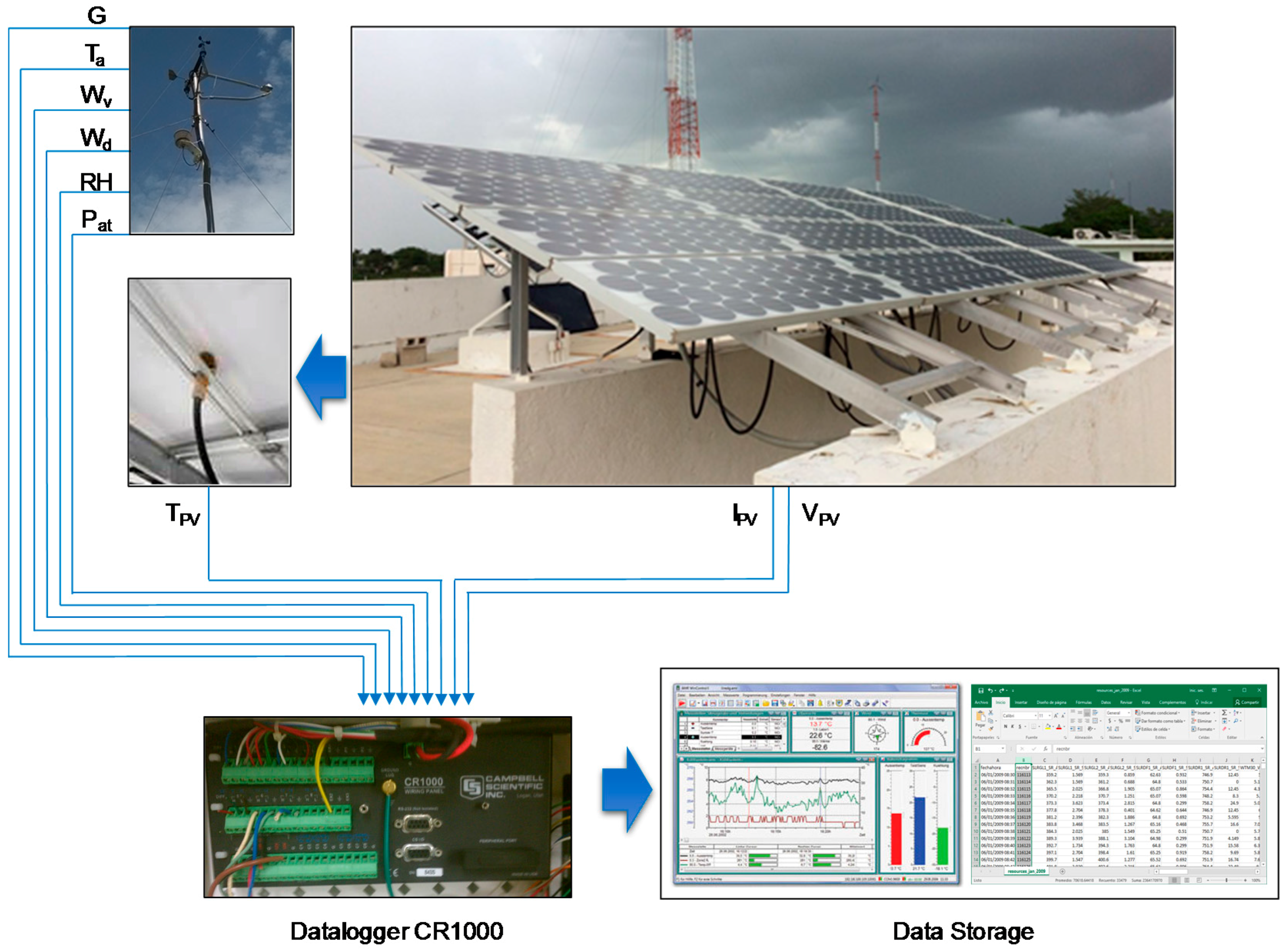
| Property | Value |
|---|---|
| Latitude (°) | 20°56′ N |
| Longitude (°) | 89°36′ W |
| Tilt angle (°) | 21°00′ |
| Incident area (m2) | 14.16 |
| Nominal output voltage (V) * | 17.7 |
| Nominal output current (A) * | 5.6 |
| Variable | Sensor | Uncertainty |
|---|---|---|
| Solar radiation (G) | Campbell CS300-L Pyrometer | ±5% |
| Environmental temperature (Ta) | Campbell CS215-L | ±4% |
| Wind velocity (Wv) | WINDSONIC4-L | ±2% |
| Wind direction (Wd) | WINDSONIC4-L | ±3% |
| Relative humidity (RH) | Campbell CS215-L | ±4% |
| Atmospheric pressure (Pat) | Campbell CS100 | ±1.0 mb |
| PV voltage (VPV) | TI LM747 | ±5% |
| PV current (IPV) | FW BELL NT-50 | ±0.30% |
| PV temperature module (TPV) | Sensor K-Type | ±0.75% |
| Parameters | Minimum | Nominal | Maximum | ±SD | Units | |
|---|---|---|---|---|---|---|
| Inputs: | ||||||
| Solar radiation * | (G) | 100 | 987 | 1367 | 10.130 | [W/m2] |
| Temperature | (Ta) | 9.56 | 28.73 | 39.53 | 5.1000 | [°C] |
| Wind velocity | (Wv) | 0.30 | 4.20 | 9.80 | 0.0572 | [m/s] |
| Wind direction | (Wd) | 0 | 133 | 360 | 21.12 | [°] |
| Relative humidity | (RH) | 25 | 57 | 97 | 1.7288 | [%] |
| Atmospheric pressure | (Pat) | 100 | 101.4 | 103.2 | 0.5370 | [hPa] |
| PV output power ** | (PPV) | 17.07 | 326.2 | 356 | 0.4821 | [W] |
| Output: | ||||||
| PV temperature modules | (TPV) | 9.97 | 37.6 | 62.8 | 4.3000 | [°C] |
| Statistical Criteria | Function |
|---|---|
| Root Mean Square Error | |
| Mean Absolute Error | |
| Coefficient of Correlation |
| Membership Function | Computational Parameter Criteria | Statistical Analysis | ||||
|---|---|---|---|---|---|---|
| Epochs | Time (s) | (MAE) | (RMSE) | (R) | Best Linear Equation | |
| Trimf | 001 | 0.65000 | 0.07529 | 3.68524 | 0.94293 | Y = 5.99700 + 0.8508X |
| Trapmf | 187 | 93.4484 | 0.07666 | 3.68152 | 0.94314 | Y = 5.99700 + 0.8505X |
| Psigmf | 550 | 386.149 | 0.08790 | 4.26082 | 0.92299 | Y = 5.99717 + 0.8508X |
| Pimf | 550 | 386.950 | 0.07720 | 3.75127 | 0.94080 | Y = 4.56403 + 0.8866X |
| Gaussmf | 437 | 84.2374 | 0.07163 | 3.54318 | 0.94738 | Y = 4.06859 + 0.8996X |
| Gauss2mf | 142 | 69.9605 | 0.07286 | 3.58801 | 0.94425 | Y = 4.12820 + 0.8795X |
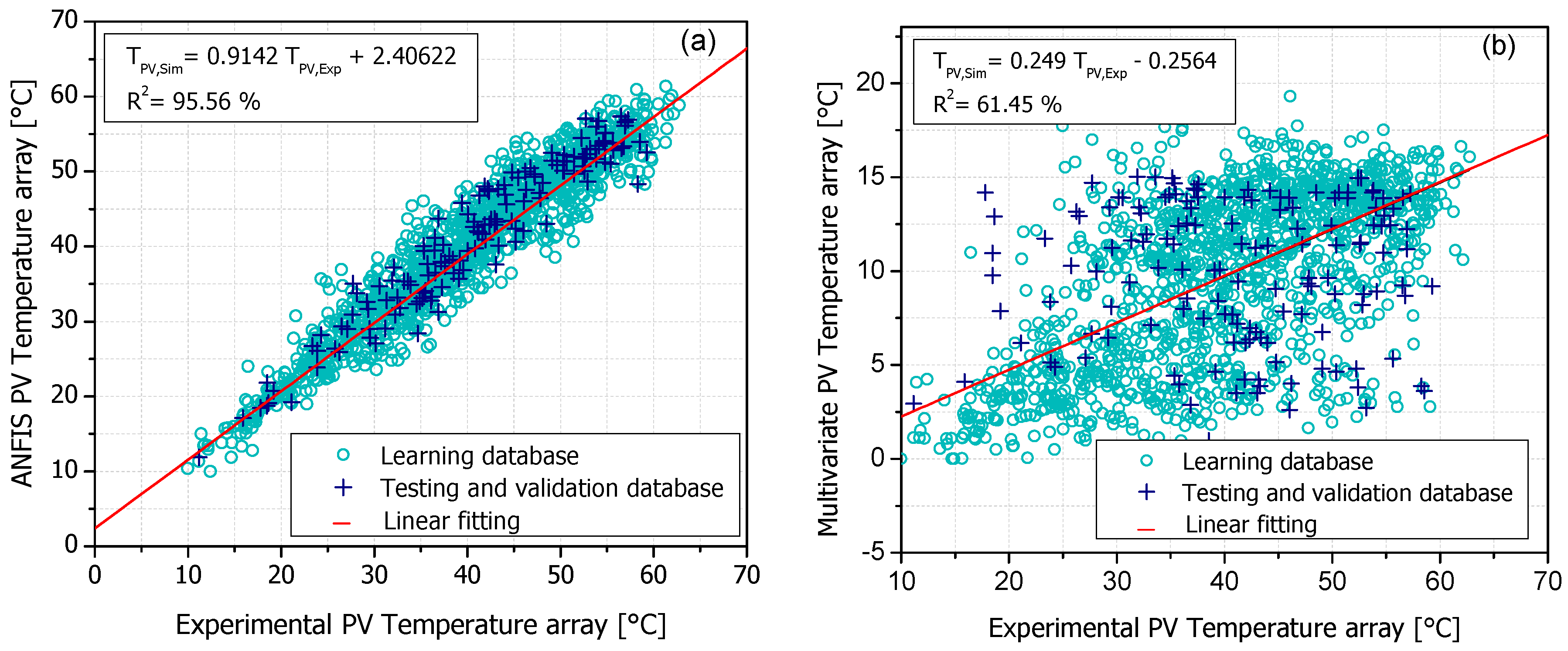
| Gbellmf | 115 | 55.7117 | 0.06729 | 3.45530 | 0.95563 | Y = 2.40622 + 0.9142X |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bassam, A.; May Tzuc, O.; Escalante Soberanis, M.; Ricalde, L.J.; Cruz, B. Temperature Estimation for Photovoltaic Array Using an Adaptive Neuro Fuzzy Inference System. Sustainability 2017, 9, 1399. https://doi.org/10.3390/su9081399
Bassam A, May Tzuc O, Escalante Soberanis M, Ricalde LJ, Cruz B. Temperature Estimation for Photovoltaic Array Using an Adaptive Neuro Fuzzy Inference System. Sustainability. 2017; 9(8):1399. https://doi.org/10.3390/su9081399
Chicago/Turabian StyleBassam, A., O. May Tzuc, M. Escalante Soberanis, L. J. Ricalde, and B. Cruz. 2017. "Temperature Estimation for Photovoltaic Array Using an Adaptive Neuro Fuzzy Inference System" Sustainability 9, no. 8: 1399. https://doi.org/10.3390/su9081399
APA StyleBassam, A., May Tzuc, O., Escalante Soberanis, M., Ricalde, L. J., & Cruz, B. (2017). Temperature Estimation for Photovoltaic Array Using an Adaptive Neuro Fuzzy Inference System. Sustainability, 9(8), 1399. https://doi.org/10.3390/su9081399







