Abstract
Considering a supply chain with fashion products comprising of a supplier and a retailer, we study the sustainability of the supply chain with alternative power structures (either the supplier or the retailer has the option of acting as a leader to make the decisions first). We also examine the impact of the supplier’s attitudes to loss on the supply chain’s sustainability and profitability. We build game theoretical modes to characterize one property of the fashion industry: the wide use of buy-back contract, and obtain the following results: (1) Compared to wholesale price contract, buy-back contract reduces the sustainability of the supply chain, and this result is robust with alternative power structures. (2) Under alternative power structure, the sustainability index is increasing in the buy-back price in the supplier-as-the-leader scenario, while decreasing in the retailer-as-the-leader scenario. That is, the relationships between sustainability and buy-back price is completely reversed when the leader is changed. (3) The sustainability is improved when the supplier acts as the leader and the buy-back price is lower than a threshold, but the contrary holds when the buy-back price is high. (4) Buy-back contract helps to improve the sustainability of the supply chain when supplier is extremely loss-averse, because the loss-averse supplier has the incentives to reduce the ordering quantity as well as the overstocking risk.
1. Introduction
Over the past decades, there are increasing concerns about sustainable operations as people are becoming more aware of the possible economic disruption from short-sighted development and environment pollution. This induces many industries to control carbon emission [1,2,3]. Among all industries, the fashion and apparel industry raises most concerns due to lots of related issues: the overuse of energy and water, the toxic dye, the waste of raw materials, etc. A European Commission on the environmental impact of products shows that clothing alone is responsible for 2 to 10% of the EU’s life-cycle environmental impacts [4].
With this trend of growing concerns, many apparel manufacturers and retailers have adopted some policies to improve the sustainability of their operations and become more eco-friendly. For example, famous fashion companies H&M, Levi Strauss, Nike, GAP, and Muji, have increased their investments in sustainable fashion collections. This helps them “reduce the side effects to the environment and project a positive brand image” [5]. Admittedly, sustainable fashion induces the fashion companies to concern more about sustainability-oriented objectives, however, they are also aware of that intracompany effort is limited [1,2,6] and insufficient and attempting to exert more intercompany effort in the supply chain level. In a recent survey conducted by the United States Fashion Industry Association, 33% respondents rate “unmet social and environmental compliance” as having a high impact on their supply chains, which is much higher than concerns for other supply chain risks (United States Fashion Industry Association [7]. The sustainability of a supply chain with fashion products has become an important issue besides its profitability.
In particular, the sustainability issue is highly related to some important issue in the supply chain, e.g., the power structure of the supply chain. It is common that there is power imbalance among a supply chain’s members and one becomes a dominant one, in other words, the leader of the supply chain. For example, WalMart and Tesco are often referred as “powerful retailers” as they have strong influences on their suppliers’ decisions [8]. On the contrary, in the apparel industry, many manufacturers who also own designers act as leading roles in their supply chains, e.g., Zara, Nike, H&M, and Mango [9,10]. It is well recognized that the power structure of the supply chain significantly affects its members’ decisions and the channel dynamics. However, the relation between a supply chain’s sustainability and its power structure is still under investigation. Another related issue is the supply chain members’ attitude to loss. Due to the highly uncertain demand in the fashion industry, buy-back contracts are widely provided by the suppliers, i.e., the unsold inventory of the retailer at the end of the selling season can be returned to the supplier [9,10,11]. Then, the demand risk is shared between the supplier and the retailer, and the supplier’s attitude towards loss becomes important [12].
In this paper, we aim to investigate the interplay of these three issues and find out the best sustainable operational model. We develop a stylized supply chain model including one apparel manufacturer (a supplier) and a retailer, and analyze two possible power structures: the supplier-as-the-leader and the retailer-as-the-leader. In each one, we assume that they make the agreements under a buy-back contract, and we compare the results to a benchmark scenario in which they only sign a wholesale price contract. Our findings are as follows. First, we show that, although buy-back contract may coordinate the supply chain [13], it also reduces the sustainability of the supply chain, regardless of the supply chain power structures. Second, we find that the relationships between sustainability and buy-back price is completely reversed when the leader is changed. That is, with alternative power structure, the sustainability index may be either increasing (supplier-as-the-leader) or decreasing (retailer-as-the-leader) in the buy-back price. Furthermore, we find that, it is more sustainable when the supplier is a leader and the buy-back price is below a unique threshold, but the contrary holds when the buy-back price is sufficiently high.
We then take the supplier’s attitude to loss into consideration, and find that the sustainability analysis becomes more complicated and strongly depends on the magnitude of loss-averseness. When the supplier is mildly loss-averse, the results are similar to the previous ones. However, when the supplier is extremely loss-averse, we show that buy-back contract can improve the sustainability of the supply chain compared to wholesale price contract. This is because the loss-averse supplier will try to control the production/ordering quantity to reduce the overstocking risk, so that the adverse effect of buy-back contract can be offset and the sustainability is improved.
The paper is organized as follows. We provide a literature review for related studies in Section 2, and present our model and some preliminary results in Section 3, as well as three sustainability indexes. Our analysis and main findings are placed in Section 4, and finally concluded in Section 5. The detail derivations of formulas and technical proofs can be found in the Appendix A.
2. Literature Review
First, our work is closely related to the studies on sustainable analysis and its applications in fashion industry. In other industries, general sustainability analysis are usually related to government involvement and low carbon emission. For example, Reference [14] formulate the government’s cap-and-trade regulation, and discuss how to improve environmental sustainability under this regulation via sustainability investment. Reference [1] analyze the effects of the cost of carbon emission, unequal lot sizes, and setup cost on the supply chain’s decisions. Reference [2] further investigate how to reduce the setup cost in an integrated supply chain with carbon emission. In a recent work, a three-tier supply chain with carbon emission is studied with the consideration of variable transportation [3]. In fashion industry, supply chain coordination and contract choice are widely studied to improve supply chain sustainability. Reference [9] define three sustainability indexes: (1) the expected quantity of goods leftover, (2) the ratio of expected sales to expected quantity of goods leftover, (3) the expected rate of return on investment, and conduct sustainability analysis of fashion retailing. Reference [15] investigate several channel structures (direct or indirect channels) of a remanufacturer, and find that the channel choice may be inefficient when considering social welfare and environmental protection. Reference [16] depicts the structure of sustainable supply chain with fashion products, and analyzes the sustainability of H&M’s supply chain. Reference [5] clarify main concerns of sustainable fashion as (1) sustainable production and remanufacturing, (2) green marketing, (3) green information sharing, and (4) green attitude and education. Reference [17] adopt the sustainability indexes defined in [9] to study a supply chain with fashion products under retail outsourcing where the unsold products can be returned to the supplier. They also study issues about supply chain contracts by comparing the performances of return policy (i.e., buy-back contract) and wholesale price contract. Reference [18] develop a dual-channel model by incorporating demand uncertainty and channel competition. Similarly, they adopt the sustainability indexes defined in [9] to analyze the environmental sustainability and economic sustainability. They find that a well-designed buy-back contract can coordinate the supply chain. Following their steps, we study a two-stage supply chain with fashion products by considering the impact of power structure and the supplier’s attitude to loss under buy-back contract. We study two alternative power structures: supplier-as-a-leader, and retailer-as-a-leader, and also compare the performances under buy-back contract and wholesale price contract.
A second closely related research stream is the studies on supply chain power structures. This issue has been extensively studied in economics, marketing and operations management in many different aspects, especially in the area of supply chain management, but there are still many problems deserving investigation. Reference [19] analyzes the competitions among two manufacturers of identical powers and a common retailer in which the leaders in the game can dominate the channels, and he finds that the results depend critically on the form of the demand function. Reference [20,21] study how the power structure of a supply chain affects firms’ preference on one ordering time over another. In their work, power structure is modeled based on who has the power to set the wholesale price. Reference [22] study the agents’ behaviors under two situations (the supplier-as-leader and the retailer-as-leader), and find that when the supplier is the leader, the seller tends to under-price and the buyer to over-order, when the retailer is the leader, the seller tends to over-produce and the buyer to under-price. Reference [23] study the contract choice and design decisions of a dominate supplier, who is powerful in the channel but dose not know the upstream manufacturer’s production cost information. Reference [24] further study the joint pricing and timing of effort investment decisions of a dominant retailer. They study two pricing schemes (dollar markup and percentage markup), and both ex-ante and ex-post effort-investment sequences. Reference [8] focus on three supply chain power structures: supplier-dominate, retailer-dominate, and equal-power, and compare the supply chain performance and customer surplus with price-sensitive uncertain demand. Compared to the foregoing works, our work is to examine the impact of power structure on supply chain sustainability, which is new in this stream of literature. Furthermore, we focus on buy-back contract and find out new insights about the relationship between the sustainability index and the buy-back price. This differs our work from previous works such [8,23], where wholesale price contract is the focus.
Our work is also closely related to the studies on fashion products’ supply chain management and buy-back contract. Reference [25] is among the earliest research of analyzing supply chain coordination with buy-back contract, and the following studies comprehensively extend this direction with many different issues. For example, [26] consider a supply chain of fashion products where there are one retailer and two complementary suppliers and find that supply chain coordination can be achieved when both suppliers offer buy-back contracts. Reference [27] analyze the possibility of supply chain coordination with wholesale price decisions, channel rebates and return policies (i.e., buy-back contract) simultaneously by examining both additive and multiplicative price-dependent demand models. Reference [10] also analyze return policies in a supply chain with fast fashion products by using mean-variance risk measurements, and show that these policies can indeed coordinate the supply chain. Reference [28] investigate how the uncertainty level embedded in market demand affects the applicability of buy-back contracts in a supplier-retailer supply chain. Reference [12] empirically compare the performance of supply chain coordination of a supply chain with revenue sharing contract and that with buy-back contract when the supplier is loss-averse. Reference [6] studies supply chain coordination by considering variable back orders, inspections and discount policy. More related studies can be found in the references therein. In this paper, we also consider the interplay of buy-back contract and supplier’s attitude to loss, but our main focus is the sustainability of supply chain rather than the coordination; and adding the issue of alternative channel power structures into this stream of research is also a new approach. For the ease of presentation, we summarize the contribution of the references cited above in Table 1.

Table 1.
Contribution of different authors.
3. The Model
We consider a typical supply chain with fashion products comprising of two supply chain parties: a supplier who manufactures brand name apparel, and a retailer who sells them to the end customers. The supplier offers its brand name apparel to the retailer at a contracted wholesale price, and the retailer faces to the uncertain demand in the consumer market. The retail price is assumed to be exogenous and be the market price [12], and the salvage value is assumed to be zero (This assumption can be reasonable because fast-fashion products are innovative, fast-changing and have a short selling season. Previous literature on fashion supply chain has widely made this assumption, e.g., [9,29,30]). At the end of the selling season, the unsold inventory will be returned to the supplier at a buy-back price. Therefore, we adopt a Newsvendor model for the retailer. Similar to [22], we investigate the different channel power structures of this supply chain: (1) If the supplier is the leader, she determines the wholesale price and the retailer accordingly decides the ordering quantity; (2) If the retailer is the leader, he determines the wholesale price and the supplier accordingly decides the production quantity. The illustration of these two types of supply chain structure are shown in Figure 1.
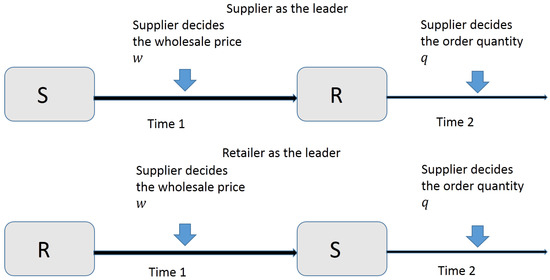
Figure 1.
Illustration of two supply chain structures with different channel powers.
Because the supplier allows the retailer to return the unsold inventory, it bears the major part of the risk of demand uncertainty as it still has to deal with the leftover apparel. Thus, our analysis can be divided into two cases according to the supplier’s attitude to loss: loss-neutral and loss-averse which is similar to [12]. Then, there are in total four scenarios with the combination of the channel power structures and the supplier’s attitude to loss, as shown in the Table 2:

Table 2.
Four scenarios with the combination of the channel power structures and the supplier’s attitude to loss.
We aim to analyze the sustainability of the fashion products’ supply chain among different scenarios, based on that both the supplier and the retailer are profit maximizers, and also compare with a benchmark scenario: “Supplier-as-a-Leader under Wholesale Price Contract Only” (Scenario H). Without a buy-back contract, the supplier bears little risk and thus we do not consider its attitude to loss. Furthermore, the scenario “Retailer-as-a-Leader and Wholesale Price Contract Only” is infeasible because the retailer must set zero wholesale price and the supplier has no profit.
In the first stage, the supplier decides a wholesale price w to maximize her profit, and then the retailer decides an order quantity q to maximize his excepted profit (see Figure 2). Their object functions are, respectively:
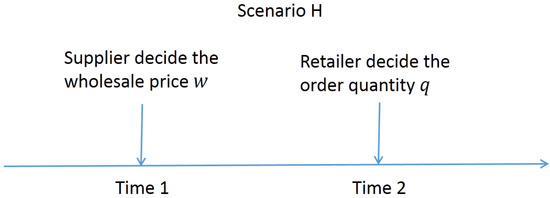
Figure 2.
Illustration of the decision sequence under Scenario H.
When the supplier and the retailer signs a wholesale price contract without buy-back agreement, their profits can be expressed as follows:
where is the random demand, w is the wholesale price and q is the ordering quantity. represents the satisfiable demand at the retailer. Without loss of generality, we assume that follows an IGFR (increased generalized failure rate) distribution [27,31,32]. (The failure rate of a probability distribution is defined by . An IGFR distribution means is increasing in x and . Most commonly used distribution, e.g., Uniform, Exponential, Normal, Gamma, Weibull, etc., are all IGFR distributions. This assumption is widely used in the literature of supply chain management.) This is a typical Newsvendor problem for the retailer and its ordering quantity should satisfy:
Putting it into the supplier’s profit function, we show that the optimal wholesale price should satisfy
and then the corresponding ordering quantity should satisfy:
where stands for the ease of presentation.
Sustainability Indexes
According to [9], three sustainability indexes are often used: the expected quantity of goods leftover , the ratio of expected sales to expected quantity of goods leftover , and the expected rate of return on investment . [9] also provide the following theorem:
Theorem 1.
(Choi and Chiu, 2012)
- 1.
- is an increasing function of q;
- 2.
- is a decreasing function of q, ;
- 3.
- is a decreasing function of q, .
It is not difficult to see that the ordering quantity q is the only determinant of all these three sustainability indexes: A larger ordering quantity leads to lower sustainability of the supply chain. This is consistent with people’s intuition: A larger ordering/production quantity causes heavier pollution and more wastes during the manufacturing process, and the amount of expected leftover inventory is also increased. Thus, in the following analysis, we compare the optimal quantities in each scenario to investigate the sustainability.
The Benchmark Case: Scenario H.
4. Sustainability Analysis
In this section, we analyze the sustainability of the fashion products’ supply chain in the four scenarios. We first consider the two scenarios where the supplier is loss-neutral, and then turn to the other two where the supplier is loss-averse.
4.1. Loss-Neutral Supplier
When the supplier is loss-neutral, the profit functions of the supplier and the retailer are as follows:
Here is the expected amount of leftover inventory, and , , are the buy-back prices. It is possible that the buy-back prices are different when the leader changes, so we use for the one when the supplier is the leader and for the one when the retailer is the leader. We still assume the buy-back prices are exogenously given, as the market price.
In the first stage, the supplier decides a wholesale price w to maximize her profit, and then the retailer decides an order quantity q to maximize his excepted profit (see Figure 3). Their object functions are, respectively:
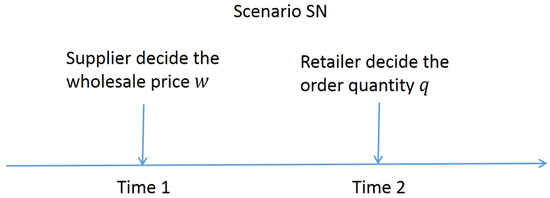
Figure 3.
Illustration of the decision sequence under Scenario SN.
When the supplier is the leader, the decision sequence is very similar to that of Scenario H. By backward induction, we first calculate the best response function of q of the retailer for a given wholesale price w:
Then, we have . When the supplier decides the optimal wholesale price, the ordering quantity is also determined by this formula. Therefore, we can plug it into and calculate the first-order derivative w.r.t. q:
Then, the optimal ordering quantity satisfies:
Scenario SN
In the first stage, the retailer decides a wholesale price w to maximize his excepted profit, and then the supplier decides an production quantity q to maximize her profit (see Figure 4). Their object functions are, respectively:
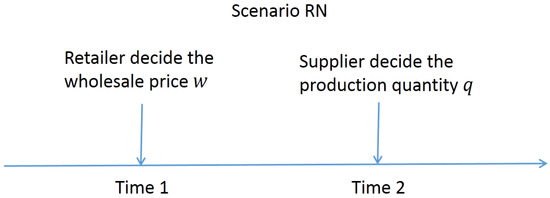
Figure 4.
Illustration of the decision sequence under Scenario RN.
When the retailer is the leader, it first determines the wholesale price and then the supplier decides the production quantity. Therefore, by backward induction, we first calculate the best response function of q of the supplier:
That is, . Then, we plug it into the retailer’s profit function and calculate its first-order derivative w.r.t. q:
Then, the optimal production quantity satisfies:
We now compare the optimal quantities and in these two scenarios.
Scenario RN
Proposition 1.
is increasing in , and is decreasing in .
It is interesting to find that the relationship between the ordering/production quantity and the buy-back price is completely reversed in the two scenarios. That is, the sustainability index q is increasing in the buy-back price in the supplier-as-the-leader scenario, while decreasing in the buy-back price in the retailer-as-the-leader scenario. The reason is that, a higher buy-back price means that the supplier bears higher risk in the supply chain, while the retailer bears lower risk. In Scenario SN, the ordering quantity is decided by the retailer, and therefore the retailer will order more when it bears lower demand risk; In Scenario RN, it is the supplier who decides the production quantity , and thus it will produce less when it bears higher demand risk.
Corollary 1.
if , and vice versa.
From Proposition 1, we can also compare the optimal quantities in the two scenarios. As the buy-back price increases, the optimal ordering quantity in Scenario SN increases, while the optimal production quantity in Scenario RN decreases. Therefore, there must exist a unique threshold of the buy-back price such that , and we find that the threshold is just the market price p. Especially, if there is no difference on the buy-back prices between the two scenarios, i.e., , then the threshold is exactly . That is, when the supplier bears higher demand risk, Scenario SN is less sustainable than Scenario RN; otherwise, when the retailer bears higher demand risk, Scenario RN is less sustainable than Scenario SN. In summary, to make the supply chain more sustainable, the one who bears lower demand risk should act as the leader.
Finally, we compare the two optimal quantities with the one in the benchmark scenario, Scenario H, and we have the following proposition.
Proposition 2.
- 1.
- , for any ;
- 2.
- , for any .
We show that, no matter who is the leader in the fashion products’ supply chain, the optimal quantity is always higher than . That is, a supply chain with a buy-back contract is always less sustainable than that with a wholesale price contract only. Note that the demand risk is shared between the supplier and the retailer with a buy-back contract, while it is solely borne by the retailer with a wholesale price contract only. Therefore, a buy-back contract can make the supply chain member who decides the ordering/production quantity more aggressive but less concerned about sustainability.
4.2. Loss-Averse Supplier
We then analyze the two scenarios where the supplier is loss-averse. Similar to [12], we formulate the supplier’s utility function as
where measures the magnitude of loss-averseness of the supplier. In these two scenarios, the supplier aims to maximize its utility rather than the actual profit . One can also easily see that if , the supplier is loss-neutral and , so this assumption is consistent between different scenarios.
In the first stage, the supplier decides a wholesale price w to maximize her profit, and then the retailer decides an order quantity q to maximize his excepted profit (see Figure 5). Their object functions are, respectively:
Figure 5.
Illustration of the decision sequence under Scenario SA.
When the supplier is the leader, because the retailer still aims to maximize its profit, the optimal ordering quantity still satisfies the best response function in Scenario SN, i.e., . Plugging it into the supplier’s utility function and calculate the first order derivative, we then obtain:
Then, the optimal ordering quantity should satisfy:
Scenario SA
In the first stage, the retailer decides a wholesale price w to maximize his excepted profit, and then the supplier decides an production quantity q to maximize her profit (see Figure 6). Their object functions are, respectively:
Figure 6.
Illustration of the decision sequence under Scenario RA.
When the retailer is the leader, we first calculate the best response function of the supplier by calculating the first order derivative of w.r.t. q:
which yields the equation of the optimal production quantity and the wholesale price . Plugging it into the retailer’s profit function and calculate the first order derivative, we then obtain:
Then, the optimal production quantity should satisfy:
We first show that in both scenarios, the optimal quantities are decreasing as the supplier becomes more loss-averse.
Scenario RA
Proposition 3.
Both and are decreasing in λ.
In Scenario SA, when the supplier is more loss-averse, it can set a higher wholesale price so that the retailer will reduce its ordering quantity. By doing that, the supplier is able to indirectly control the demand risk. In Scenario RA, the loss-averse supplier can directly produce less to reduce the demand risk it will bear. Therefore, in either scenario, the optimal quantities decreases in the magnitude of loss-averseness of the supplier. This result also implies that the supply chain with a loss-averse supplier is more sustainable.
Similar to Proposition 1, we investigate the relation between the optimal ordering/production quantity and the buy-back price. Interestingly, we find that is not necessarily increasing in . Reorganizing the formulation of , we have
By the implicit function theorem, . Furthermore,
However, the signs of these derivatives cannot be easily determined since they depend on and the demand distribution. To further analyze the relation between and , we focus on a special case in which is uniformly distributed in , and then we have the following proposition.
Proposition 4.
If ,
- 1.
- is increasing in when ; and
- 2.
- is decreasing in when .
Compared to Proposition 1, we find that, although a higher buy-back price will encourage the retailer to order more, the supplier may not be willing to accept a large order from the retailer if it is extremely loss-averse. Then, the supplier will set a very high wholesale price to discourage the retailer, and finally the ordering quantity will be even decreasing in the buy-back price. This result also implies that the sustainability of the supply chain can be improved with a higher buy-back price when the supplier is extremely loss-averse.
In Scenario RA, we find that the optimal production quantity is still decreasing in the buy-back price when the supplier is loss-averse.
Proposition 5.
is decreasing in .
Recall that in Scenario RN, the supplier produces a smaller amount of apparel as the buy-back price increases, because the demand risk it bears increases. In Scenario RA, this risk is even enlarged by . Thus, the supplier will further decrease its production quantity when it is loss-averse. Again, the sustainability of the supply chain can be improved with a higher buy-back price. Combing the two propositions, we obtain the comparison between and .
Corollary 2.
If the two scenarios (SA, RA) are under the same risk sharing structure (i.e., ),
- 1.
- , when ;
- 2.
- , when .
Due to the complexity of the relation between and , we have to assume that the buy-back prices are identical in the two scenarios to obtain clearer results. Under this assumption, the result is similar to Corollary 1: when the buy-back price is below a certain threshold, the optimal ordering quantity in Scenario SA is smaller and hence, this scenario is more sustainable; otherwise, when the buy-back price is above this threshold, Scenario RA is more sustainable. Furthermore, when the supplier is loss-averse and , the threshold is smaller (), so that Scenario SA is less likely to outperform Scenario RA in the respect of sustainability.
Finally, we compare the optimal quantities to the one in the benchmark scenario. Again, the result is affected by the demand distribution, and we focus on the special case that follows a uniform distribution.
Proposition 6.
Suppose that . Then,
- 1.
- in Scenario SA,
- (a)
- , when ;
- (b)
- , when ;
- 2.
- in Scenario RA,
- (a)
- , when ;
- (b)
- , when .
Different from Proposition 2, we show that the optimal quantities in the two scenarios when the supplier is loss-averse can be both lower than the one in Scenario H. According to Proposition 3, and both decreases in , while is not affected. Thus, when is large enough, the optimal quantities in the two scenarios can both be smaller than . This also implies that, when the supplier is loss-averse, the sustainability of the supply chain with a buy-back agreement can be even higher than that with a wholesale price contract only.
5. Conclusions
In the fashion industry, sustainability is a critical issue because it is common for a fashion company to produce products exceeding consumer demand, especially given that in practice buy-back contract is widely used and the uncertain overstocking risk is shared by the upstream fashion supplier and the downstream fashion retailer. Intuition tells us that rearrangement of supply chain power structure can change the total output and influence the supply chain sustainability [9], and this intuition can be even stronger under a buy-back contract. Therefore, in this paper, we first analyze the order quantities under alternative power structures: supplier-as-a-leader vs. retailer-as-a-leader, so as to examine the harm of buy-back contract in the sense of supply chain sustainability, compared to wholesale price contract.
An interesting finding that we obtain is, the impact of a high buy-back price on the supply chain sustainability is totally reversed with alternative power structures. That is, supply chain sustainability is increasing in the buy-back price in the supplier-as-the-leader scenario, while decreasing in the buy-back price in the retailer-as-the-leader scenario. This motivates us to further study how the supply chain sustainability can be improved, given buy-back contract performs worse than wholesale price contract in the sense of sustainability. We show that, sustainability improvement can be achieved when the supplier is the leader and the buy-back price is lower than a threshold.
In order to further improve supply chain sustainability, we examine the role of the fashion manufacturer/supplier’s attitude to loss. We apply a similar definition of loss-averseness to [12], and find that supplier’s loss-averseness helps to improve supply chain sustainability, especially when the supplier is extremely loss-averse. A possible reason for this is that the supplier may not be willing to receive a large order from the retailer which in turn raises its overstocking risk, if it is extremely loss-averse. This induces the supplier to set a very high wholesale price to discourage the retailer from ordering too much. Our findings are summarized as follows:
- Supply chain sustainability is increasing (decreasing) in the buy-back price in the supplier-as-the-leader (retailer-as-the-leader) scenario.
- With loss neutral supplier, the buy-back contract results in a lower sustainability than the wholesale price contract.
- Supplier’s loss-averseness helps to improve supply chain sustainability.
Finally, we point out several possible research directions to conclude this paper. First, we have assumed the buy-back price is exogenously given, which can be reasonable when the buy-back price is determined a long time before the actual ordering, or, the competition in the buy-back market is extensive. Having said that, in practice, the buy-back price can be negotiated by the supplier and the retailer, which requires a totally new modelling approach and hence, goes beyond the scope of this paper. Second, it can be interesting to study the impact of the retailer’s attitude to loss, because it faces to uncertain demand directly. We predict that our main findings will not be qualitatively changed under this new setting, but the impact of the supplier’s attitude to loss can be either weakened or strengthened, when the attitude to loss of the supplier and the retailer are considered simultaneously. In addition, we assume the salvage value is zero, and the impact of a positive salvage value can be a research direction. We can also consider other items such as the delay in payments, imperfect production, probabilistic deterioration, and the setup cost [33,34,35,36,37].
Acknowledgments
The authors are grateful to the managing editor and the two anonymous reviewers for their helpful comments and suggestions. This research was supported by the National Natural Science Foundation of China (No. 71571194, 71301032, 71201175), Foundation for the Excellent Youth Scholars of Guangdong Universities and Colleges (No. YQ2015014, YQ2015078) and Grants from the Hong Kong Polytechnic University (Project No. G-UA7Y).
Author Contributions
Baozhuang Niu designed the research framework. Lei Chen, Baozhuang Niu and Jie Zhang performed the research and Jie Zhang wrote the paper. All authors read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Proof of Proposition 1
Proof.
Note that satisfies
Let
then
Since follows an IGFR distribution, also increases in q, and then . Therefore,
Similarly, note that satisfies
Let
then
Therefore,
Hereby we finish the proof. ☐
Proof of Corollary 1
Proof.
Note that
One can easily find that if , i.e., . Then, by Proposition 1, we have the comparison result. ☐
Proof of Proposition 2
Proof.
Note that
and
Therefore, if , and if . Since and always hold, by Proposition 1, we have the comparison result. ☐
Proof of Proposition 3
Proof.
Note that satisfies
Let
then
Since follows an IGFR distribution, by its definition, , i.e., . Therefore,
Furthermore,
Thus,
Similarly, note that satisfies
Let
then
and
Thus,
Hereby we finish the proof. ☐
Proof of Proposition 4
Proof.
If , and . Then,
So the result is obvious. ☐
Proof of Proposition 5
Proof.
Following the proof of Proposition 3, we have
and . Furthermore,
and thus
Hereby we finish the proof. ☐
Proof of Corollary 2
Proof.
Note that when , and satisfies
They can also be represented as , . If ,
That is, .
From the proof of Proposition 3, , and thus . Similarly, we can show that if . ☐
Proof of Proposition 6
Proof.
If , from the proof of Proposition 4, , and
It is also easy to have
Then, the comparison result is obvious. ☐
References
- Sarkar, B.; Saren, S.; Sinha, D.; Hur, S. Effect of Unequal Lot Sizes, Variable Setup Cost, and Carbon Emission Cost in a Supply Chain Model. Math. Probl. Eng. 2015. [Google Scholar] [CrossRef]
- Sarkar, B.; Saren, S.; Sarkar, M.; Seo, Y.W. A Stackelberg Game Approach in an Integrated Inventory Model with Carbon-Emission and Setup Cost Reduction. Sustainability 2016, 8, 1244. [Google Scholar] [CrossRef]
- Sarkar, B.; Ganguly, B.; Sarkar, M.; Pareek, S. Effect of variable transportation and carbon emission in a three-echelon supply chain model. Trans. Res. Part E 2016, 91, 112–128. [Google Scholar] [CrossRef]
- European Commission (EC). Environmental Impact of Products. Available online: http://ec.europa.eu/environment/ipp/pdf/eipro_report.pdf (accessed on 26 February 2017).
- Shen, B.; Zheng, J.; Chow, P.; Chow, K. Perception of fashion sustainability in online community. J. Text. Inst. 2014, 9, 971–979. [Google Scholar] [CrossRef]
- Sarkar, B. Supply Chain Coordination with Variable Backorder, Inspections, and Discount Policy for Fixed Lifetime Products. Math. Probl. Eng. 2016. [Google Scholar] [CrossRef]
- United States Fashion Industry Association (USFIA). 2016. Available online: http://www.usfashionindustry.com/pdf_files/USFIA-2016-Fashion-Industry-Benchmarking-Study.pdf (accessed on 26 February 2017).
- Xue, W.; Demirag, O.C.; Niu, B.Z. Supply chain performance and consumer surplus under alternative structures of channel dominance. Eur. J. Oper. Res. 2014, 239, 130–145. [Google Scholar] [CrossRef]
- Choi, T.M.; Chiu, C.H. Mean-downside-risk and mean-variance newsvendor models: Implications for sustainable fashion retailing. Int. J. Prod. Econ. 2012, 135, 552–560. [Google Scholar] [CrossRef]
- Li, J.; Choi, T.M.; Cheng, T.C.E. Mean variance analysis of fast fashion supply chains with returns policy. IEEE Trans. Syst. Man Cybern. Syst. 2014, 44, 422–434. [Google Scholar] [CrossRef]
- Choi, T.M. Optimal return service charging policy for a fashion mass customization program. Serv. Sci. 2013, 5, 56–68. [Google Scholar] [CrossRef]
- Zhang, Y.; Donohue, K.; Cui, T.H. Contract preferences and performance for the loss-averse supplier: Buyback vs. revenue sharing. Manag. Sci. 2015, 62, 1734–1754. [Google Scholar] [CrossRef]
- Cachon, G. Supply chain coordination with contracts. Handb. Oper. Res. Manag. Sci. 2003, 11, 227–339. [Google Scholar]
- Dong, C.; Shen, B.; Chow, P.S.; Yang, L.; Ng, C.T. Sustainability investment under cap-and-trade regulation. Ann. Oper. Res. 2016, 240, 509–531. [Google Scholar] [CrossRef]
- Wang, K.; Zhao, Y.; Cheng, Y.; Choi, T.M. Cooperation or competition? Channel choice for a remanufacturing fashion supply chain with government subsidy. Sustainability 2014, 6, 7292–7310. [Google Scholar] [CrossRef]
- Shen, B. Sustainable Fashion Supply Chain: Lessons from H&M. Sustainability 2014, 6, 6239–6249. [Google Scholar]
- Shen, B.; Li, Q. Impact of returning unsold products in retail outsourcing fashion supply chain: A sustainability analysis. Sustainability 2015, 7, 1172–1185. [Google Scholar] [CrossRef]
- Wang, F.; Zhuo, X.; Niu, B.; Rosen, M.A. Sustainability analysis and buy-back coordination in a fashion supply chain with price competition and demand uncertainty. Sustainability 2017, 9, 25. [Google Scholar] [CrossRef]
- Choi, S.C. Price competition in a channel structure with a common retailer. Mark. Sci. 1991, 10, 271–296. [Google Scholar] [CrossRef]
- Ferguson, M.E. When to commit in a serial supply chain with forecast updating. Nav. Res. Logist. 2003, 50, 917–936. [Google Scholar] [CrossRef]
- Ferguson, M.E.; DeCroix, G.A.; Zipkin, P. Commitment decisions with partial information updating. Nav. Res. Logist. 2005, 52, 780–795. [Google Scholar] [CrossRef]
- Wang, Y.; Zipkin, P. Agents’ incentives under buy-back contracts in a two-stage supply chain. Int. J. Prod. Econ. 2009, 120, 525–539. [Google Scholar] [CrossRef]
- Wang, J.C.; Lau, A.H.L.; Lau, H.S. Practical and effective contracts for the dominant retailer of a newsvendor product with price-sensitive demand. Int. J. Prod. Econ. 2012, 138, 46–54. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Wang, J.C.; Shou, B. Pricing and effort investment for a newsvendor-type product. Eur. J. Oper. Res. 2013, 229, 422–432. [Google Scholar] [CrossRef]
- Donohue, K.L. Efficient supply chain contracts for fashion goods with forecast updating and two production modes. Manag. Sci. 2000, 46, 1397–1411. [Google Scholar] [CrossRef]
- Yang, D.; Choi, T.M.; Xiao, T.; Cheng, T.C.E. Coordinating a two-supplier and one-retailer supply chain with forecast updating. Automatica 2011, 47, 1317–1329. [Google Scholar] [CrossRef]
- Chiu, C.H.; Choi, T.M.; Tang, C.S. Price, rebate, and returns supply contracts for coordinating supply chains with price-dependent demands. Prod. Oper. Manag. 2011, 20, 81–91. [Google Scholar] [CrossRef]
- Zhao, Y.; Choi, T.M.; Cheng, T.C.E.; Sethi, S.; Wang, S. Buyback contracts with price-dependent demands: Effects of demand uncertainty. Eur. J. Oper. Res. 2014, 239, 663–673. [Google Scholar] [CrossRef]
- Kurata, H.; Yue, X. Trade promotion mode choice and information sharing in fashion retail supply chains. Int. J. Prod. Econ. 2008, 114, 507–519. [Google Scholar] [CrossRef]
- Liang, C.; Cakanyildirim, M.; Sethi, S.P. Analysis of Product Rollover Strategies in the Presence of Strategic Customers. Manag. Sci. 2014, 60, 1033–1056. [Google Scholar] [CrossRef]
- Lariviere, M.A. A Note on Probability Distributions with Increasing Generalized Failure Rate. Oper. Res. 2006, 53, 602–604. [Google Scholar] [CrossRef]
- Wang, Y.; Niu, B.; Guo, P. The Comparison of two vertical outsourcing structures under push and pull contracts. Prod. Oper. Manag. 2014, 23, 610–625. [Google Scholar] [CrossRef]
- Sarkar, B. An EOQ model with delay in payments and stock dependent demand. Appl. Math. Comput. 2012, 218, 8295–8308. [Google Scholar]
- Sarkar, B. An EOQ model with delay in payments and time varying deterioration rate. Math. Comput. Model. 2012, 55, 367–377. [Google Scholar] [CrossRef]
- Sarkar, B. An inventory model with reliability in an imperfect production process. Appl. Math. Comput. 2012, 218, 4881–4891. [Google Scholar] [CrossRef]
- Sarkar, B. A production-inventory model with probabilistic deterioration in two-echelon supply chain management. Appl. Math. Model. 2013, 37, 3138–3151. [Google Scholar] [CrossRef]
- Sarkar, B.; Majumder, A. Integrated vender-buyer supply chain model with vendor’s setup cost reduction. Appl. Math. Comput. 2013, 224, 362–371. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).