Assessment Method for Substation Capacity Credit of Generalized Power Source Considering Grid Structure
Abstract
:1. Introduction
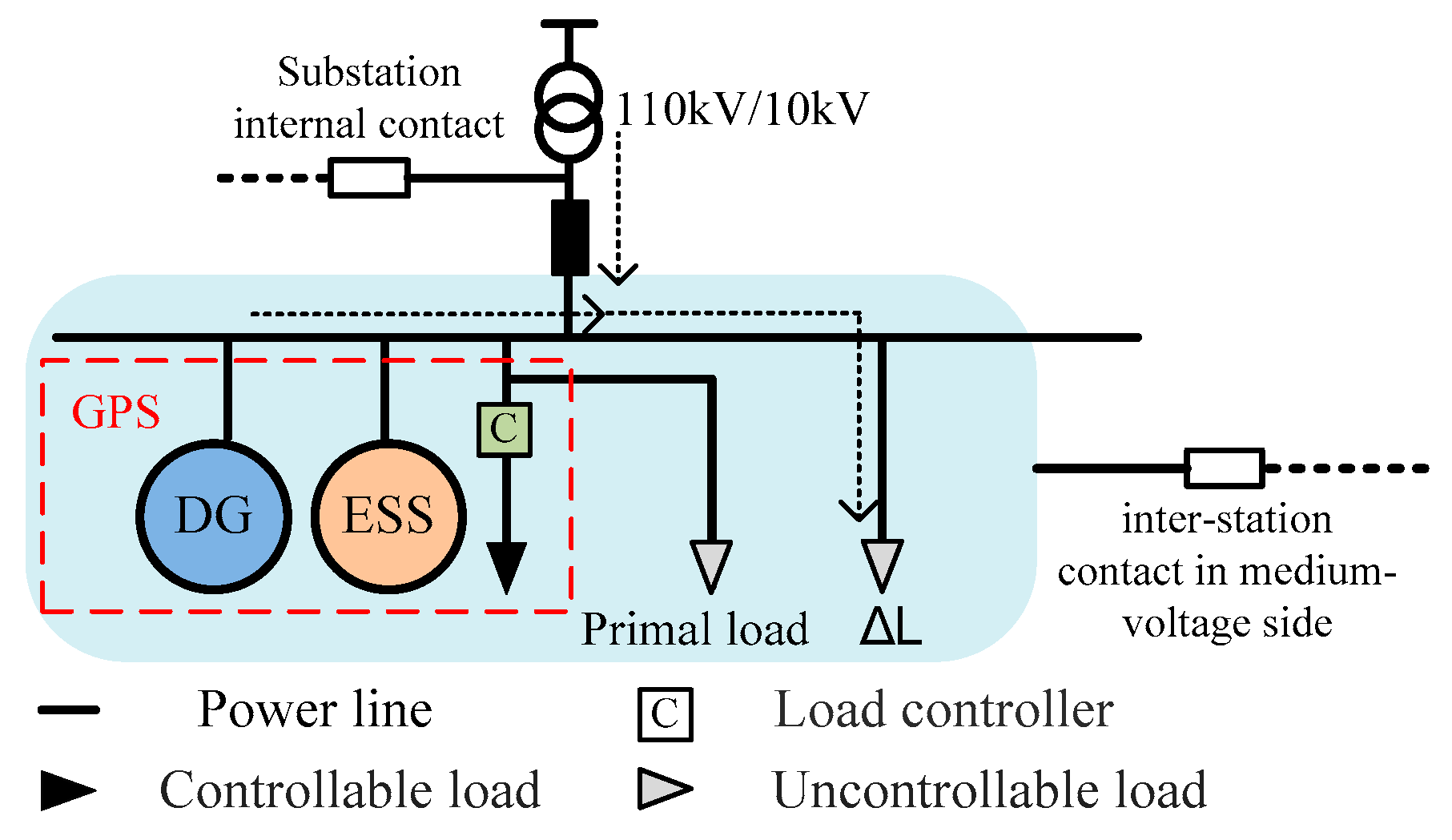
2. Definition of Substation Credible Capacity of GPS in an Active Distribution Network
- Generation credible capacity refers to the capacity of the traditional generating units that can be equivalently replaced by the new energy resources unit at the transmission grid level under the same generation reliability, which can be applied to the power balance of power system planning.
- Substation credible capacity refers to the capacity that can be equivalently replaced by GPS at the high-voltage distribution grid level, under the premise of obeying the equivalent reliability principle, considering the faults of main transformers, 110 kV lines, and circuit breakers. The substation credible capacity can be applied to the overall planning of substation capacity.
- Feeder credible capacity refers to the line capacity replaced by the power sources at the distribution network level under the condition of a 10 kV line fault, considering the line power flow constraint and ensuring the reliability of a power supply. The line selection is known, and the calculation result is equivalent to the number of standard lines.
3. GPS Output Model
3.1. Distributed Generator Modeling
3.2. Energy Storage System Modeling
3.3. Controllable Load
4. Reliability Calculation of High-Voltage Distribution Network Considering Grid Structure
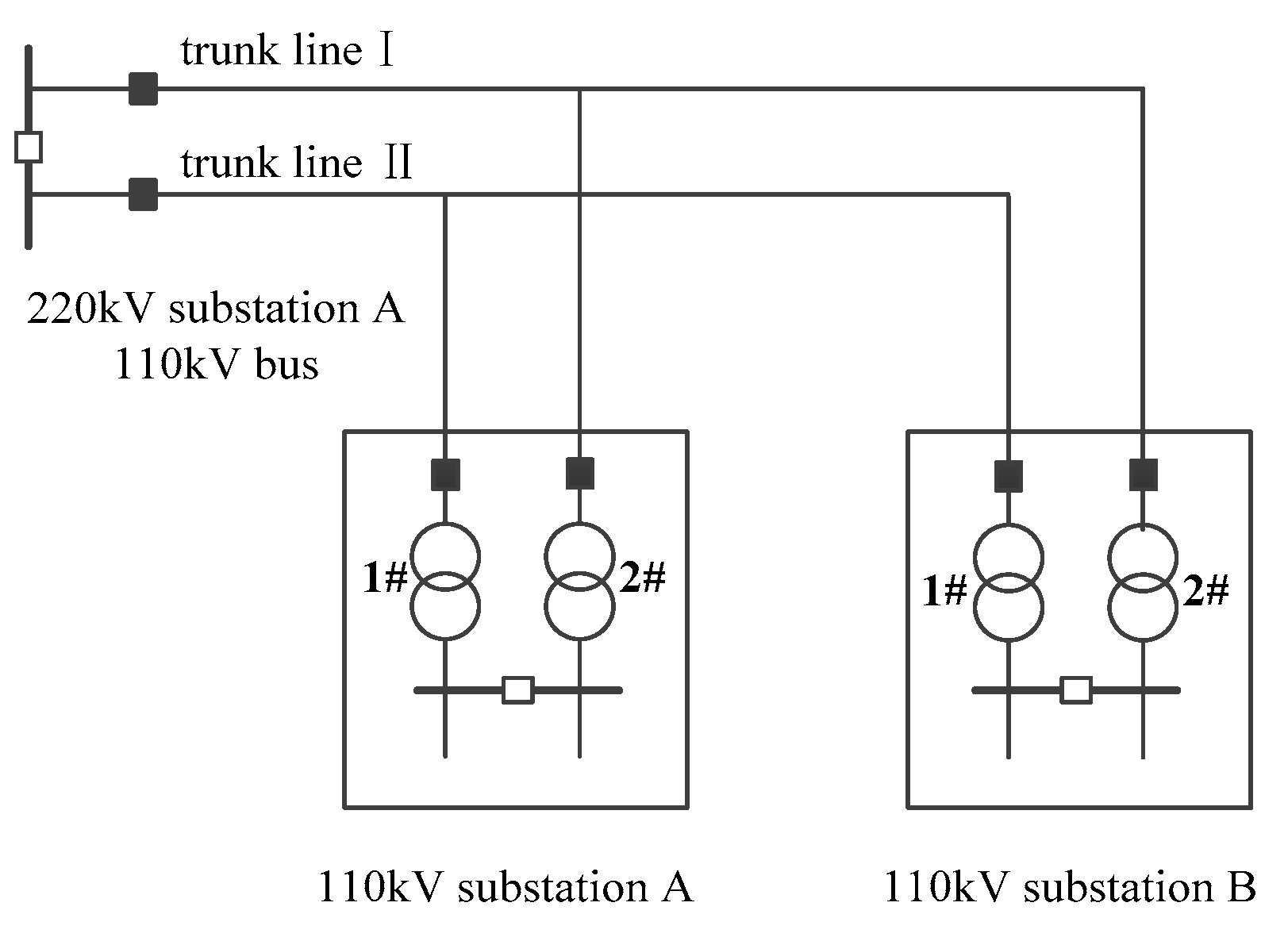
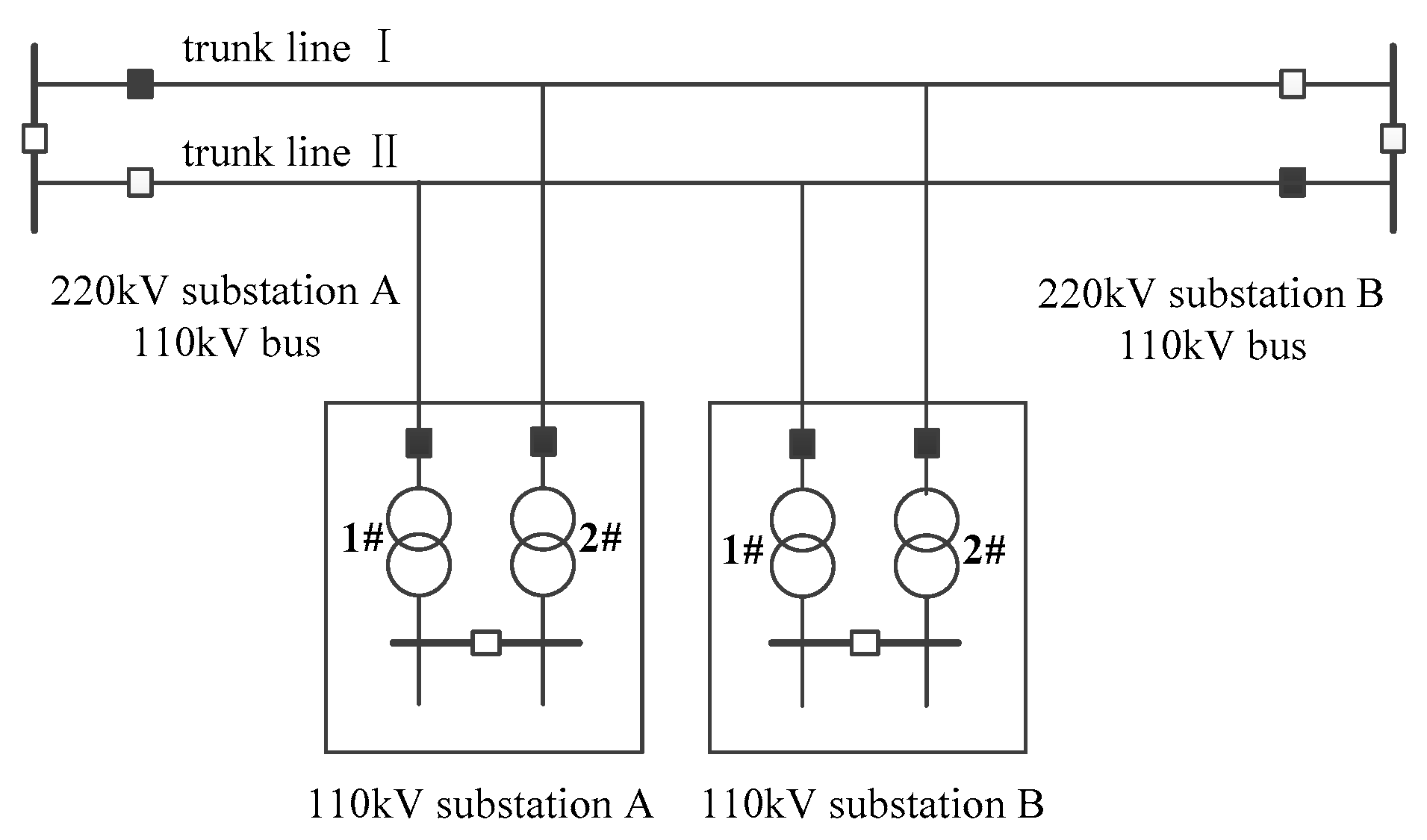
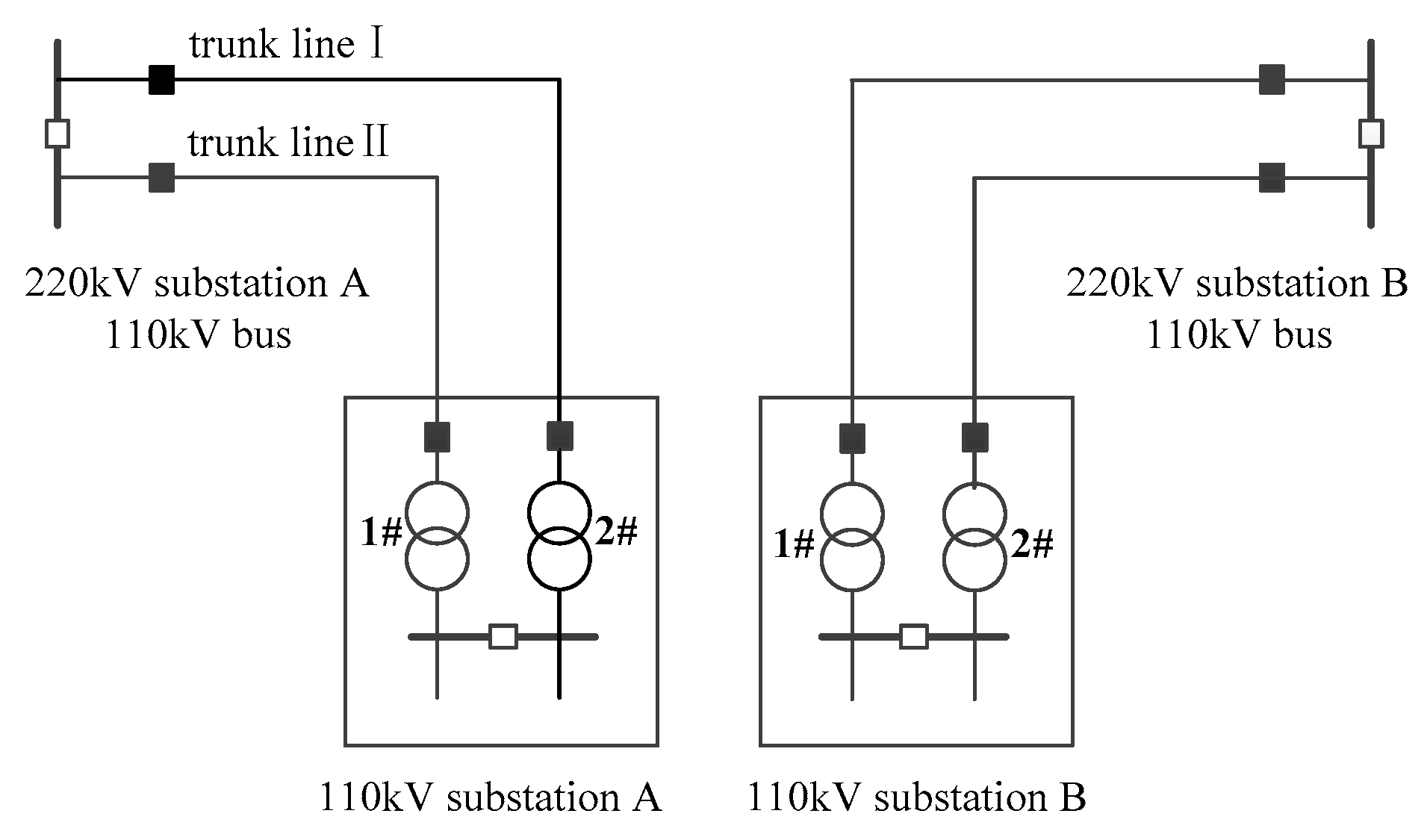
4.1. Analysis of Typical Power Supply Mode and Transfer Mode of High Voltage Distribution Network
4.2. Reliability Calculation
- Step 1:
- Generate sequential change sequences. According to the WTG and PV output models, the sequential sequence of WTG and PV are generated in the range of total simulation time T. According to the operation strategy under the normal ESS operation states, the state of charge (SOC) sequential change sequences of the ESS are generated. The load sequence is constant and is set as the maximum safety load.
- Step 2:
- Generate fault state sequences. Perform sequential simulations of GPS components and circuit components in the system, regardless of double and above failures. When the circuit component fault condition occurs, proceed to step 3a and p plus 1. When the fault condition of the GPS component is present, proceed to step 3b and q plus 1.
- Step 3:
- Fault evaluation. According to different fault component, the evaluation methods are divided into two types:
- (a)
- When the circuit component fails, look at the failure mode table to determine the loss of load area. Following this, according to the DG output sequence obtained in Step 1, the output condition of DG in the power loss area during the system failure is determined. Determine the size of the load to be transferred and the transfer path: when the transfer fails to complete, conduct a fault operation strategy on the energy storage in the power loss area to supply part of the load. If the total supplement of power for the entire load is not satisfied, determine the quantity of controllable load that needs to be reduced. After all the measures above, the load that still fails to be restored is the dead load of this failure. Record the power shortage for this fault state, Ens.n.
- (b)
- When the GPS component fails, determine the fault area and remove the fault power. According to the DG output sequence obtained in Step 1, the output of the remaining DG in the fault area is determined. The rest of the processing is the same as step 3a.
- Step 4:
- Indicator evaluation. The reliability indicator of the system after the GPS integration can be obtained by unifying the GPS component and circuit component fault state calculation indicators, as shown in Equation (10).
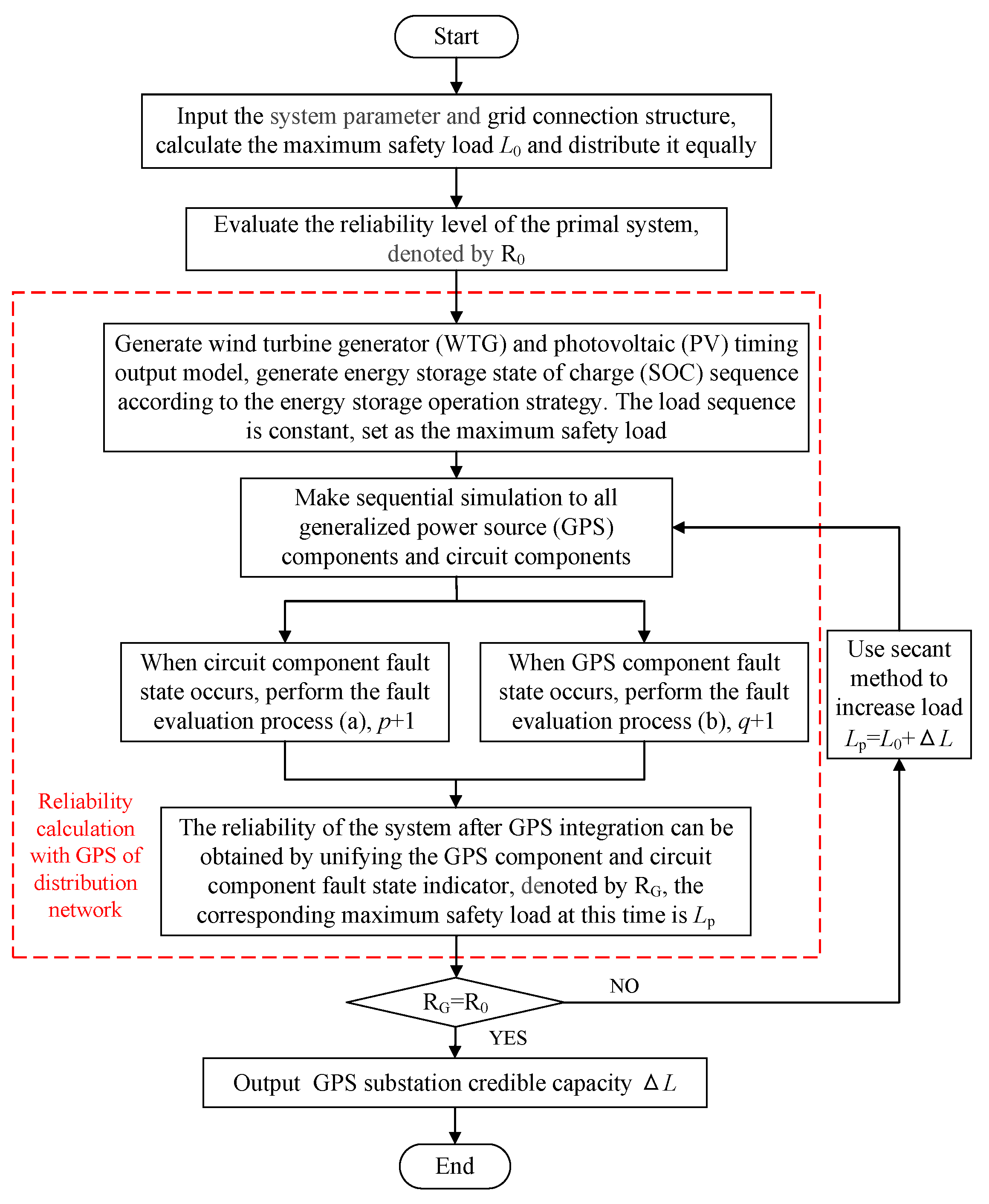
5. Method for Evaluating the Substation Credible Capacity of GPS
- Step 1:
- Input the grid connection structure of the HV distribution network and the inter-station contact constraint of the substation. According to the previous literature [20], the maximum safety load of the system under the wiring structure is obtained by linear optimization. Through the automatic traversing of the computer, a failure impact analytical table of all circuit components is established and the modes of transferring are determined.
- Step 2:
- Calculate the reliability level R0 in the primal system when the GPS is not integrated.
- Step 3:
- Calculate the distribution network reliability level RG with GPS integration using the Monte Carlo simulation method as described in Section 4.2.
- Step 4:
- Using the secant method to adjust load (primal load is the maximum safety load L0), make the system reliability RG after the GPS integration equal to the primal system reliability R0. Obtain the corresponding maximum safety load Lp at this time. The difference between Lp and L0 is the increment of the load, ΔL, which is exactly the substation credible capacity of the accessed GPS.
6. Case Study
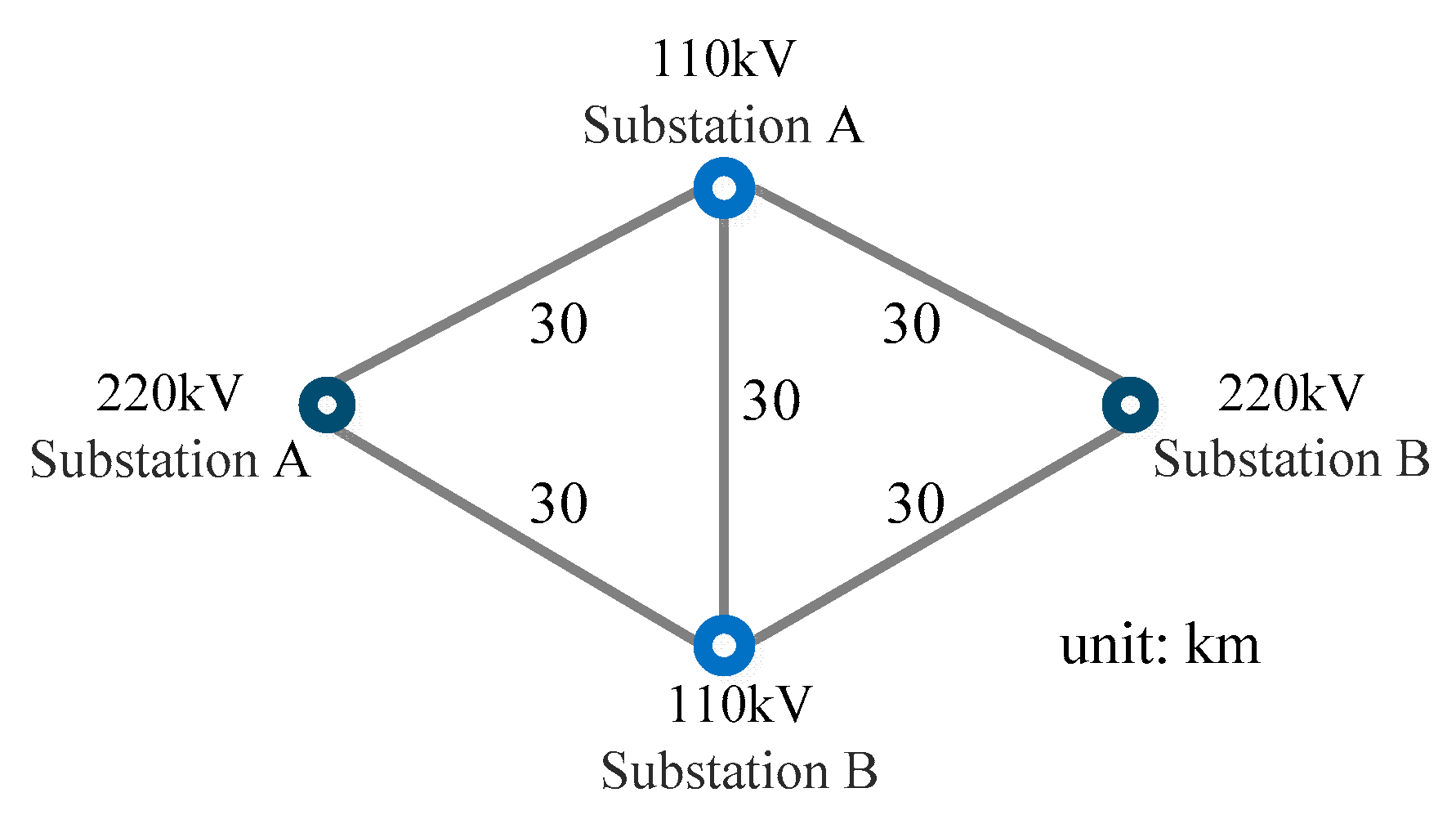
6.1. System Parameters
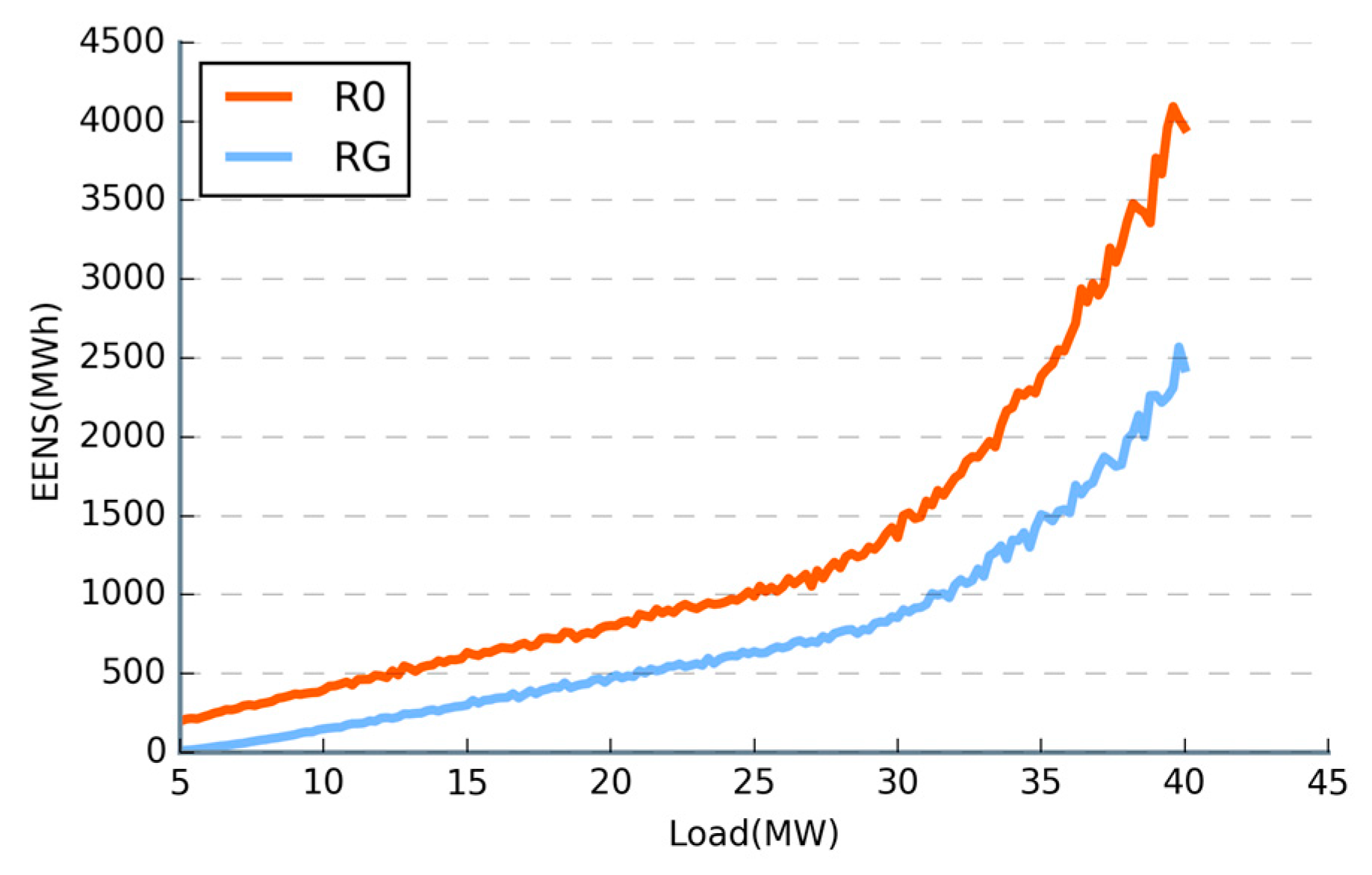
6.2. Impact of GPS Integration on System Reliability
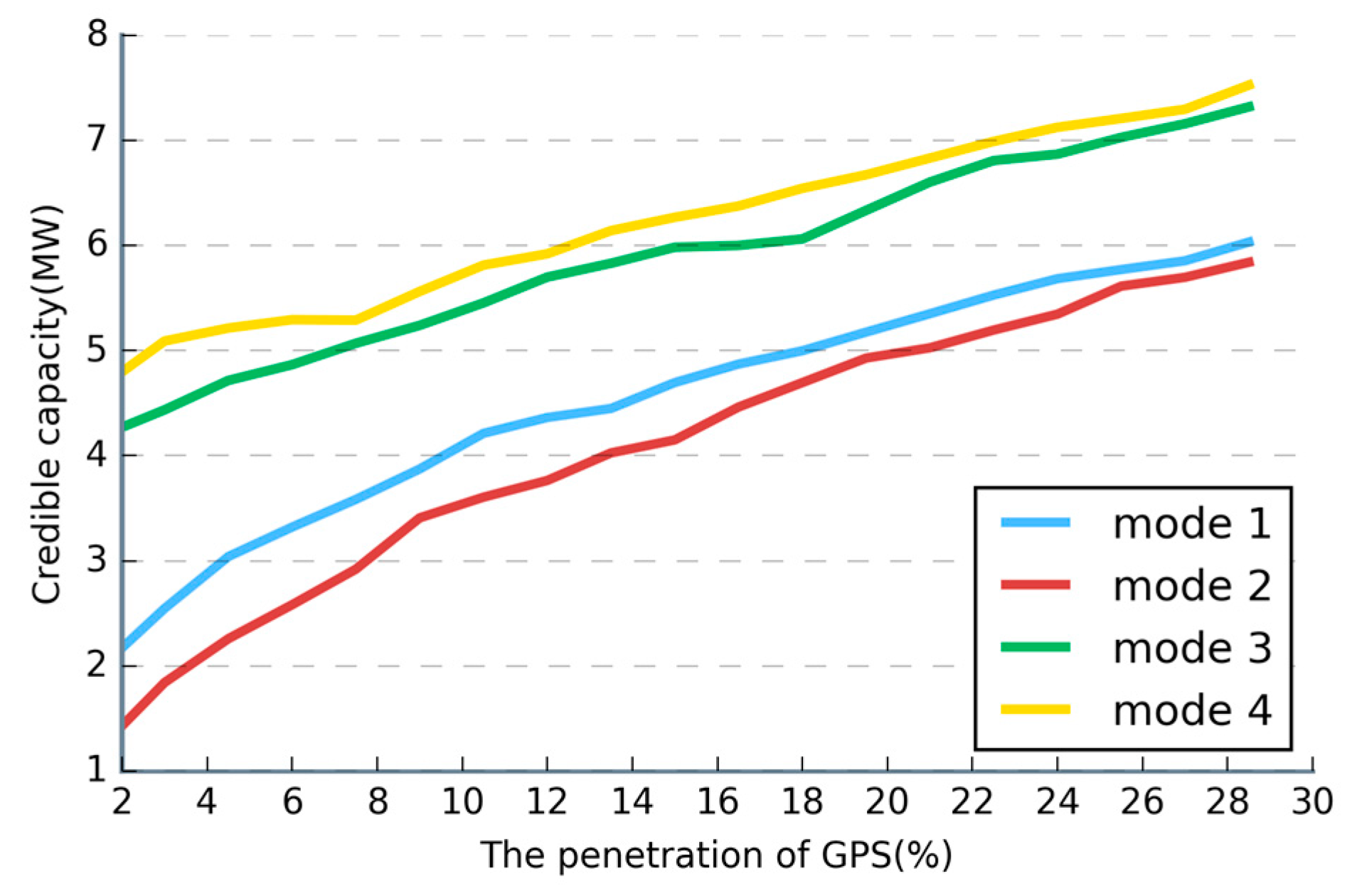
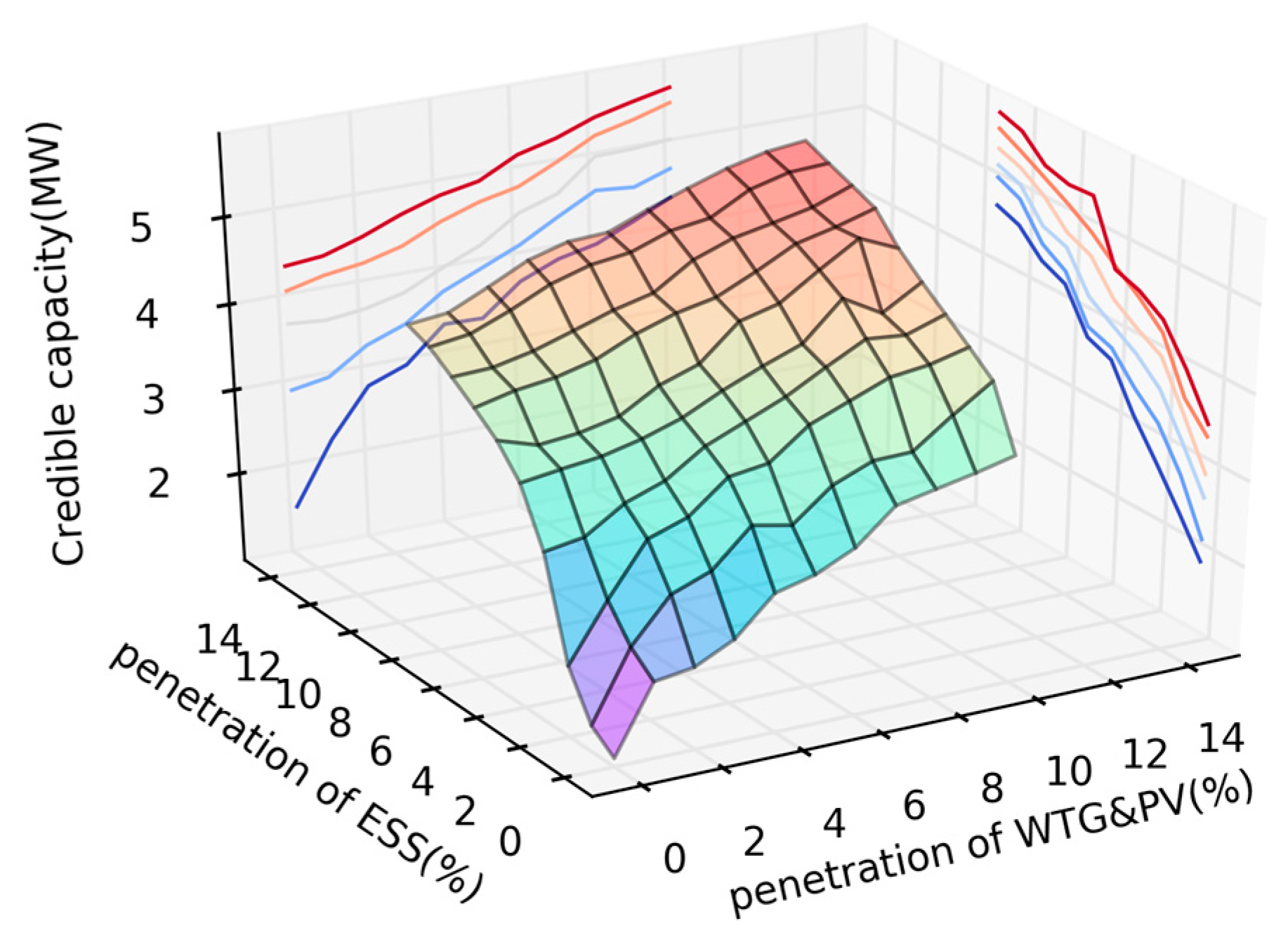
6.3. Substation Credible Capacity of GPS under Different Wiring Modes
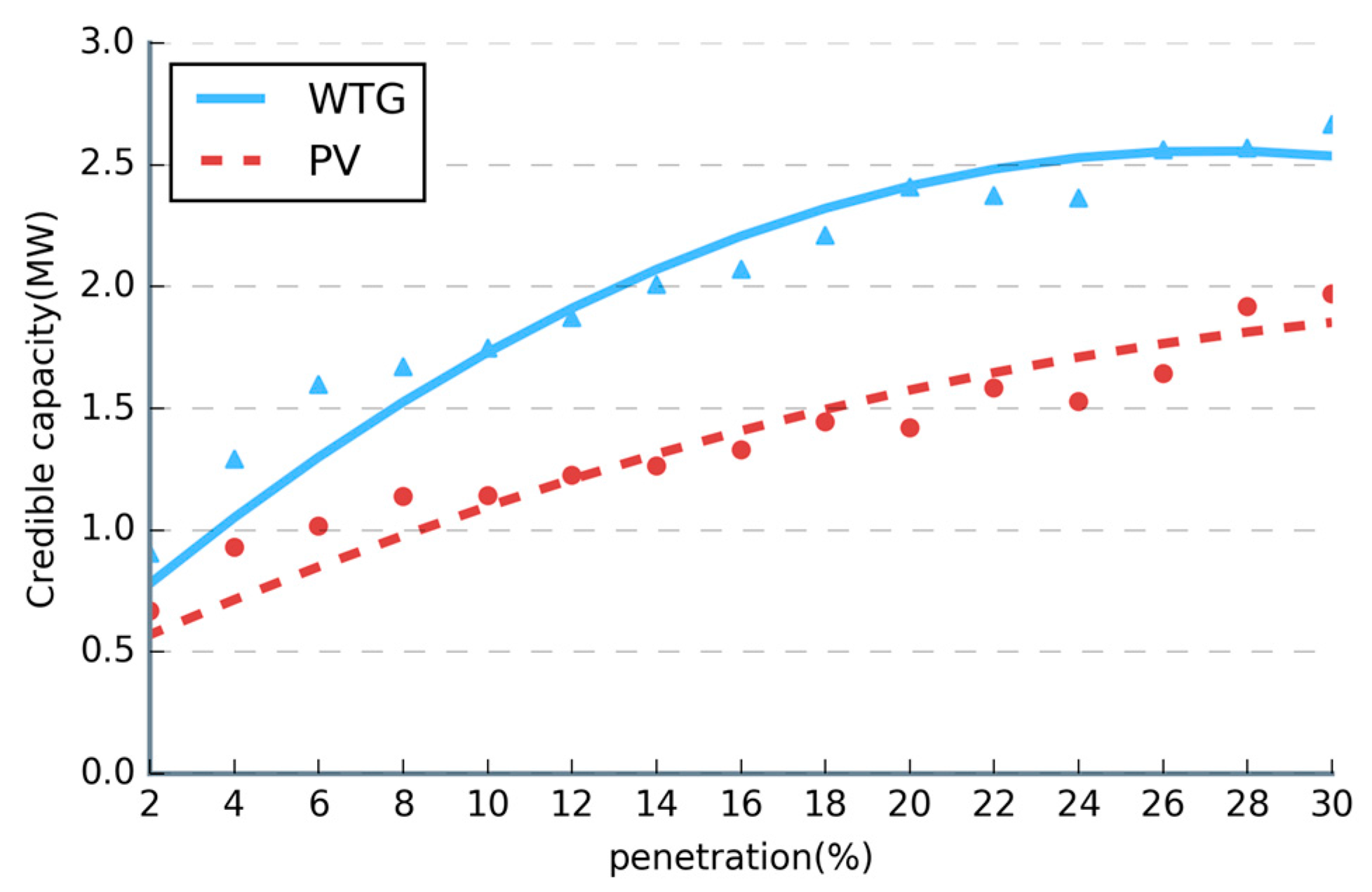
6.4. Substation Credible Capacity of GPS under Different GPS Types
7. Conclusions
- GPS in the distribution network can replace substation capacity. The access of GPS can reduce the shortage of power supply and improve the reliability of the system.
- It is necessary to consider the influence of the different grid structures on substation credible capacity of GPS in order to improve reliability calculation accuracy and provide reference for the substation capacity planning of GPS integration in an active distribution network.
- The contribution of the controllable load to substation credible capacity is the most obvious. The influence of the ESS is smaller than that of the controllable load. Due to the intermittency and fluctuation of the PV and WTG, ESS coordination is needed to maximize the substation credible capacity of GPS.
Author Contributions
Conflicts of Interest
Abbreviations
| DG | Distributed Generator |
| DR | Demand response |
| GPS | Generalized Power Source |
| CF | Capacity factor method |
| HV | High Voltage |
| ESS | Energy Storage System |
| CL | Controllable Load |
| ELCC | Effective Load Carrying Capacity |
| EENS | Expected energy not supplied |
| LOEE | Loss of energy expectation |
| SAIDI | System average interruption duration indicator |
| WTG | Wind Turbine Generator |
| PV | Photovoltaic |
| DLC | Direct Load Control |
| IL | Interruptible load |
| DSB | Demand-side bidding |
| EDR | Emergency demand response |
| CASP | Capacity/ancillary service program |
| SOC | State of Charge |
| kV | kilovolt |
| MW | Megawatt |
| MVA | Megavolt-ampere(s) |
| ACSR | Aluminum cable steel reinforced |
Appendix A


- (1)
- Assuming that there is at most one component failure in the same time period, the probability of a failure of a single component in time ts is satisfied with the Poisson distribution , where represents the failure rate of components in one hour.
- (2)
- To calculate the substation credible capacity of GPS, set to constant here. That is, during the calculation process in 8760 h of a year, remains unchanged to remove the impact of load fluctuations.
- (3)
- GPS components only fail in the working state, with the power loss in a failure equal to the rated output of the fault component.
- The process of obtaining the reliability R using the Monte Carlo simulation method:
- (1)
- Enter the component parameters, set the current time as = 0, the year k = 0, and the total failure power loss = 0.
- (2)
- Calculate the fault probability of the five components.
- (3)
- When k < N and ti is equal to 8760, reset ti = 0. When k < N and ti < 8760, calculate the WTG/PV output at time k and determine the SOC status of the ESS according to the size of , , , and transfer load PT. At time ti, five random numbers (j = 1, 2, 3, 4, 5) that are uniformly distributed are generated. The probability of failure is compared with the corresponding random number.
- (4)
- If , no failure, return to the third step to calculate the next moment ti + 1.
- (5)
- If and j is not a GPS component, j fails and the system switches to the circuit component failure state. The fault lasts for hours.
- (i)
- Calculate the sum of the GPS outputs, including , , , and , and compare with load to determine the size of the controllable load to be reduced.
- (ii)
- If there is still a load to be supplied after all the controllable load resources are used, the remaining load at this time is the power failure load . During the time to + 1, the total blackout is updated to .
- (iii)
- In the event of a fault duration , if + < 8760, repeat steps (1) and (2). Otherwise, return to step (3).
- (iv)
- When the fault is over, return to step (3).
- (6)
- If and j is a GPS component, GPS component j fails, and the system enters the GPS component failure state. The fault lasts for hours.
- (i)
- Calculate the lack of power supply PG for the GPS component.
- (ii)
- During the time to + 1, update the total power loss .
- (iii)
- In the event of a fault duration , if + < 8760, go back to step (6i). Otherwise, return to step (3). After the fault, return to step (3).
- (7)
- When k = N, stop the calculation of the total amount of power loss and calculate the annual average loss of power . When N is large enough, of the system at this time.
- Use the secant method to calculate the credible capacity:
- (1)
- Enter the system parameters (including the GPS penetration at this time) and set the initial system maximum power supply load as .
- (2)
- Use the Monte Carlo method to calculate the original system reliability level R0 without GPS.
- (3)
- Calculate the reliability level RG of the system, corresponding to the maximum supply load level under GPS.
- (4)
- Use the secant method to adjust LP and repeat step (3). Finally, make RG = R0.
- (5)
- Calculate according to the ELCC method, with the substation credible capacity at this level of GPS being ΔL.
References
- Liu, W.; Niu, S.; Shi, D.; Xie, J.; Xu, H. Optimal allocation of ADS battery energy storage considering operation strategy and investment subject benefit. Power Syst. Technol. 2015, 10, 2697–2704. [Google Scholar]
- Gholizadeh-Roshanagh, R.; Najafi-Ravadanegh, S.; Hosseinian, S. A Framework for Optimal Coordinated Primary-Secondary Planning of Distribution Systems Considering MV Distributed Generation. IEEE Trans. Smart Grid. 2016. [CrossRef]
- Tanaka, I.; Ohmori, H. Scenario generation with clustering for optimal allocation of renewable DG. In Proceedings of the 2016 IEEE Innovative Smart Grid Technologies-Asia (ISGT-Asia), Melbourne, Australia, 28 November–1 December 2016; pp. 966–971. [Google Scholar]
- Ding, M.; Xu, Z. Empirical Model for Capacity Credit Evaluation of Utility-Scale PV Plant. IEEE Trans. Sustain. Energy 2017, 8, 94–103. [Google Scholar] [CrossRef]
- Sallam, A.; El-Khattam, W.; El-Salmawy, H. Economic impact of Capacity Credit evaluation for Wind Energy Conversion Systems projects in Egypt. In Proceedings of the Power Systems Conference (MEPCON), 2016 Eighteenth International Middle East, Cairo, Egypt, 27–29 December December 2016; pp. 664–669. [Google Scholar]
- Zhou, Y.; Mancarella, P.; Mutale, J. Framework for capacity credit assessment of electrical energy storage and demand response. IET Gener. Transm. Distrib. 2016, 10, 2267–2276. [Google Scholar] [CrossRef]
- Ge, S.; Wang, S.; Lu, Z.; Liu, H.; Feng, Z.; Lu, Z. Substation Optimization planning method based on capacity credit evaluation of distributed generator. Autom. Electr. Power Syst. 2015, 19, 61–67. [Google Scholar]
- Ge, S.; Wang, S.; Lu, Z. Substation planning method in an active distribution network under low-carbon economy. Mod. Power Syst. Clean Energy 2015, 3, 468–474. [Google Scholar] [CrossRef]
- Ziadi, Z.; Taira, S.; Oshiro, M.; Funabashi, T. Optimal power scheduling for smart grids considering controllable loads and high penetration of photovoltaic generation. IEEE Trans. Smart Grid 2014, 5, 2350–2359. [Google Scholar] [CrossRef]
- Liu, W.; Niu, S.; Xu, H. Optimal planning of battery energy storage considering reliability benefit and operation strategy in active distribution system. Mod. Power Syst. Clean Energy 2017, 5, 177–186. [Google Scholar] [CrossRef]
- Billinton, R.; Bai, G. Generating capacity adequacy associated with wind energy. IEEE Trans. Energy Convers. 2004, 19, 641–646. [Google Scholar] [CrossRef]
- Billinton, R.; Chen, H.; Ghajar, R. Time-series models for reliability evaluation of power systems including wind energy. Microelectron. Reliab. 1996, 36, 1253–1261. [Google Scholar] [CrossRef]
- Cha, S.T.; Jeon, D.H. Reliability evaluation of distribution system connected photovoltaic generation considering weather effects. In Proceedings of the 8th International Conference on Probability Methods Applied to Power Systems, Ames, IA, USA, 12–16 September 2004; pp. 451–456. [Google Scholar]
- State Grid Corporation of China. The Code of Planning and Design of Urban. Electric Network; China Electric Power Press: Beijing, China, 2007; p. 14. ISBN 155083.1604. [Google Scholar]
- Ge, S.; Guo, Y.; Liu, H.; Ma, K.; Liu, J. Load Supply Capability Based Analysis of HV Distribution Network Connection Mode. Power Syst. Technol. 2014, 2, 405–411. [Google Scholar]
- Ge, S.; Wang, H. Reliability Evaluation of Distribution Networks Including Distributed Generations Based on System State Transition Sampling. Autom. Electr. Power Syst. 2013, 2, 28–35. [Google Scholar]
- Gami, D.; Sioshansi, R.; Denholm, P. Data Challenges in Estimating the Capacity Value of Solar Photovoltaics. Available online: https://ise.osu.edu/isefaculty/sioshansi/papers/pv_cv_subhour.pdf (accessed on 20 May 2017).
- Liang, S.; Hu, X.; Zhang, D.; Zhang, H.Y.; Wang, H.H. Capacity credit evaluation of wind generation considering wind speed variation characteristics. Proc. CSEE 2013, 33, 18–26. [Google Scholar]
- Zhang, L.; Wu, Y.; Lou, S.; Yang, Y.; Wang, Y. Photovoltaic generation capacity credit evaluation method considering its daily output characteristics. In Proceedings of the 2014 International Conference on Power System Technology, Chengdu, China, 20–22 October 2014; pp. 2763–2768. [Google Scholar]
- Chen, K.; Wu, W.; Zhang, B.; Djokic, S.; Harrison, G.P. A method to evaluate total supply capability of distribution systems considering network reconfiguration and daily load curves. IEEE Trans. Power Syst. 2016, 31, 2096–2104. [Google Scholar] [CrossRef]

| Parameter | 110 kV Overhead Lines | 10 kV Circuit Breakers | 110 kV Circuit Breakers | 110/10 kV Transformers |
|---|---|---|---|---|
| Failure rate | 0.01/t·(a·km)−1 | 0.005/t·(a·u)−1 | 0.02/t·(a·u)−1 | 0.005/t·(a·u)−1 |
| Repair time (h) | 12 | 4 | 7.5 | 48 |
| Parameter | WTG | PV |
|---|---|---|
| Fault probability (%/u) | 8.68 | 3.1 |
| Repair time (h) | 5 | 5 |
| Transfer Ways When 110 kV Circuit Breaker on Trunk Line I Fail | Reliability | |
|---|---|---|
| mode 1 | In-station + inter-station transfer | — |
| mode 2 | In-station transfer only | Lower than mode 1 |
| mode 3 | Close contralateral breaker, quickly restored | Higher than mode 1 and 2 |
| mode 4 | Isolate the faulty line | Highest |
| Penetration% | Mode 1 | Mode 2 | Mode 3 | Mode 4 |
|---|---|---|---|---|
| 2 | 2.3249 | 1.5143 | 4.3188 | 4.8913 |
| 4 | 2.9845 | 2.1590 | 4.6632 | 5.1839 |
| 6 | 3.3213 | 2.5824 | 4.8665 | 5.2943 |
| 8 | 3.7321 | 3.1089 | 5.1240 | 5.3563 |
| 10 | 4.1130 | 3.5056 | 5.3889 | 5.8032 |
| 12 | 4.3637 | 3.7645 | 5.6991 | 5.9209 |
| 14 | 4.5497 | 4.0938 | 5.9010 | 6.1892 |
| 16 | 4.7719 | 4.3850 | 5.9933 | 6.3257 |
| 18 | 4.9989 | 4.6959 | 6.0621 | 6.5443 |
| 20 | 5.2417 | 4.9392 | 6.4457 | 6.7315 |
| 22 | 5.4867 | 5.1257 | 6.7352 | 6.9637 |
| 24 | 5.6845 | 5.3471 | 6.8693 | 7.1246 |
| 26 | 5.7915 | 5.6427 | 7.0727 | 7.2218 |
| 28 | 6.0632 | 5.7976 | 7.2695 | 7.4959 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Liu, Y.; Niu, S.; Liu, Z. Assessment Method for Substation Capacity Credit of Generalized Power Source Considering Grid Structure. Sustainability 2017, 9, 928. https://doi.org/10.3390/su9060928
Liu W, Liu Y, Niu S, Liu Z. Assessment Method for Substation Capacity Credit of Generalized Power Source Considering Grid Structure. Sustainability. 2017; 9(6):928. https://doi.org/10.3390/su9060928
Chicago/Turabian StyleLiu, Wenxia, Yicong Liu, Shuya Niu, and Zongqi Liu. 2017. "Assessment Method for Substation Capacity Credit of Generalized Power Source Considering Grid Structure" Sustainability 9, no. 6: 928. https://doi.org/10.3390/su9060928
APA StyleLiu, W., Liu, Y., Niu, S., & Liu, Z. (2017). Assessment Method for Substation Capacity Credit of Generalized Power Source Considering Grid Structure. Sustainability, 9(6), 928. https://doi.org/10.3390/su9060928






