1. Introduction
In recent years, with the continued deterioration of the global warming crisis, it has caused a disastrous impact on natural resources and ecological environment. The intense pressure of global warming and the shortage of natural resources highlight the importance of low-carbon supply chain management. Meanwhile, Low-carbon supply chain receives more attention from the governments, enterprises and consumers. Many governments around the world have developed and applied relevant policies to curb carbon emissions, such as carbon tax and low-carbon subsidies. Some researchers have proven that carbon tax [
1,
2] and low-carbon subsidies [
3,
4] are effective ways to curb carbon emissions. In reality, Tesco and Wal-Mart have leverage to insist that their suppliers reduce carbon emissions in production and transportation. Moreover, as consumers’ environmental consciousness is improving gradually, more and more consumers are willing to pay more for low-carbon products [
5,
6]. Although consumers’ environmental consciousness and government policy are important drivers for enterprises to implement low-carbon strategy, enterprises have to face a higher cost to adopt low-carbon technologies, and low-carbon products are usually costlier to produce than normal products, as a result low-carbon products are more expensive [
7]. The key issue is whether the increased profit can cover the investment of adopting production process improvements; otherwise, enterprises are unwilling to choose low-carbon strategy. That is enterprises make decisions by measuring the investment and profit of the low-carbon strategy, the legislation and policies of the government and low-carbon preferences of the consumers. In order to solve the issues, the government may subsidize those low-carbon producers if the increased profits cannot cover the additional costs.
In actual operation, a supply chain is a complex network consisting of individual members with different objectives that often conflict with each other. The individual members only try to maximize their own profits which may cause channel conflict. Furthermore, there are different power structures in real-world supply chains. According to Waldman et al. [
8], channel power structure, which defined as an agent’s ability to control decision-making process in supply chains, has been regarded as an important contributor to competitive advantage and organizational success. In particular, there is a leader–follower relationship between the manufacturers and retailers. Traditionally, the manufacturers should be the channel leader, but some retailers may be the leaders of channels. For example, Wal-Mart, Tesco and Home Depot are usually referred to as power retailers, while Caterpillar and Apple are viewed as power manufacturers. It is well known that all channel members want to be leaders so that they can make decisions first. This is consistent with some research findings that there is a first-mover advantage in the market. For example, Choi and Fredj [
9] discuss a first-mover advantage, and their finding show that there is a first-mover advantage for the retailer when the market is fully covered. The key issue is whether the leaders always yield more profits than the followers after emission reduction. Meanwhile, it is common to see several similar products in supermarkets, large malls and big-box stores. Producing and selling Styrofoam cups versus biodegradable paper cups is a well-known example of substitutable products. Under consumers’ low-carbon preference and government subsidies, we try to ask the following research questions (RQ).
RQ1. Under what conditions are channel members motivated to implement low-carbon strategy?
RQ2. What is the influence of channel power structures and product substitutability on the performance of channel members and the entire supply chain?
RQ3. Is there a power structure always ensuring the entire supply chain getting the best performance under different supply chain structures?
To understand how different power structures and product substitutability affect manufacturers’, retailers’ and the entire supply chain’s pricing and emission reduction strategy. This paper investigates two game scenarios under symmetric and asymmetric related channel status. Manufacturer Stackelberg (MS) represents the manufacturer is more powerful in setting the wholesale price. Likewise, Retailer Stackelberg (RS) means the retailer is more powerful in setting the sale price. We first examine a single channel which consists of a single manufacturer and a single retailer. Then, we expand it to a dual exclusive channel where each manufacturer chooses a single exclusive retailer who sells substitutable goods. Many studies investigate the problem of low-carbon supply chains, our paper follows this trend but from a different angle. In the following passages, we only review the studies highly related to our paper.
Many studies focus on power structures; the relevant studies are as follows. In a seminal paper on channel power structures, Choi [
10] demonstrates the differences among three game settings (two Stackelberg games and a vertical Nash) of a duopoly common retailer channel model. Ertek and Griffin [
11] developed MS and RS games to discuss the impact of the power structures in a two-stage supply chain. Edirisinghe et al. [
12] develop a model, which comprises one retailer and two suppliers, to study the impact of channel power on performance and structure dominance. Their research finding indicates that power imbalance causes significant declines in supply chain profits. In a recent discussion, Luo et al. [
13] and Zhang et al. [
14] study three game scenarios (MS, RS and Nash games) of a dual channel. The following literature is related to power structures. Ji et al. [
15] study the emission reduction behaviors for the channel members in both retail-channel and dual-channel cases using the Stackelberg game model. Liu et al. [
16] develop Stackelberg game models to analyze the impact of consumers’ environmental awareness on supply chains, their finding suggests that as consumers’ environmental awareness increase, retailers and manufacturers with superior eco-friendly are better off than the inferior eco-friendly firm.
From the product substitutability perspective, McGuire and Staelin [
17] provide a seminal work on chain to chain competition. They investigate the effect of product substitutability on the Nash equilibrium distribution structures, and find that both manufacturers prefer the decentralized structure when product substitutability is relatively high. Liu et al. [
18] examine the cost sharing considering a model of two competing supply chains and, according to their research, the supply chain is more efficient with retailer advertising if product substitutability is low. Xu et al. [
19] investigate the production and pricing problems in a make-to-order supply chain which consists of a manufacturer who produces two substitutable products and a retailer. They point out that the optimal production quantities of the two products may be decreasing in the cap. Hafezalkotob [
20] examines the effects of government’s tariffs on the players’ optimal strategies and find that there are specific boundaries for tariffs which guarantee a stable competitive market. Indeed, many studies on product substitutability have been widely discussed in recent years. For instance, Zhu and He [
21] investigate the green product development problems with different supply chain structures, and they demonstrate that the greenness competition reduces the equilibrium product greenness and the price competition may increase the equilibrium product greenness. Wang et al. [
22] study the channel selection in a supply chain with a multi-channel retailer who sells two horizontally differentiated products. Then, Hafezalkotob [
23] investigates two green supply chains consisting of two manufacturers and two retailers who sell partially substitutable product.
Regarding green supply chain, a large volume of relevant studies has been published in recent years. Mitra and Webster [
24] examine the impact of government subsidies on remanufacturing activity in a single channel and demonstrate that subsidy sharing creates incentives for the manufacturer to design a more suitable product for remanufacturing. By building a revenue sharing mechanism to facilitate the cooperation among supply chain members, Zhang and Liu [
25] report that the supply chain is better off in cooperation decision-making than in non-cooperative decision-making. Then, Tian et al. [
26] develop a system dynamics model to analyze the relationships of government, enterprises and consumers, and they suggest that the subsidy for the manufacturer is an effective way to promote green supply chain management. Ghosh and Shah [
27] investigate the impact of cost sharing contract on the decisions of a green supply chain and demonstrate that low-carbon cost sharing contract is an effective way to improve the efficiency of the entire supply chain. Lee et al. [
28] suggest that carbon emissions persistently decrease firm value. Li et al. [
29] develop Stackelberg game model to investigate the pricing and greening strategies for the chain members under both decentralized and centralized scenarios. They point out that manufacturer will not add a direct channel if the greening cost satisfies certain conditions. Zhang et al. [
30] focus on the green supply chain performance in a single channel. Their results show that feedback equilibrium is beneficial to the manufacturer, while is harmful to the retailer. Furthermore, studies on environmental consciousness can be found in Sengupta [
31], Espínola-Arredondo and Muñoz-García [
32] and Heijinen [
33].
Based on the aforementioned analysis, most of the studies on power structures, government subsidies and channel competition consider a single channel or a dual channel, while few studies have focused on government subsidies under different power structures in a dual exclusive channel with asymmetric relative channel status. Hence, this study extends existing research by considering a dual exclusive channel with asymmetric relative channel status. Moreover, we employ a linear demand based on the utility function of a representative consumer, which has been widely utilized in the economics, marketing, and other related studies (Liu et al. [
18]; Ingene and Parry [
34] ; Cai [
35]). Different from the previous literature, this paper indicates that the leaders always perform better than the followers before emission reduction, while they may not necessarily gain more benefits after emission reduction. Moreover, both retailers and manufacturers will benefit from the implementation of low-carbon strategy when product substitutability and the asymmetric relative channel status are sufficiently low. However, as product substitutability grows, all the channel members will encounter a Prisoner’s dilemma.
The remainder of this paper will proceed as follows. We present assumptions and notations in
Section 2 and depict the model in
Section 3. Then, we analyze the comparison of equilibrium solutions under different power structure in
Section 4. A numerical analysis is presented in
Section 5. Finally, we present conclusions and outlooks in
Section 6. All proofs are presented in
Appendix A.
2. Assumptions and Parameter Notations
Before we introduce our model, some assumptions are provided as follows.
Assumption 1. For the single-channel system, the manufacturer only produces one kind of products, and the demand is linear; for the dual-channel system, each manufacturer distributes its goods through a single exclusive retailer but two goods are substitute, and the demand is also linear. Moreover, the costs of production and operation are normalized to zero under the dual-channel.
Assumption 2. Consumers have low-carbon preference and accordingly will consider the emission reduction level of products. All information is common knowledge to both channel members and the cost for employing low-carbon technologies is assumed to be quadratic functions.
In order to reduce carbon emissions, the manufacturer must invest money to employ low-carbon technologies. Since producing low-carbon products, optimizing production process and saving energy consumption in the production process can be regarded as manufacturer’s emission reduction behaviors. For simplicity, we introduce a respective function to represent the cost of reducing carbon emissions effort, that is, the unit cost function of manufacturer is which conveys diminishing returns, where stands for the cost factor related to eco-friendly production and operations and stands for the eco-friendly level of the product. Similar assumption can be found in Ji, Zhang and Yang (2017). A larger raises the difficulty of reducing carbon emissions so that a higher cost is incurred.
We summarize the decision variables and parameters in
Table 1.
3. The Model and Analysis
This paper focuses on the influence of different power structures, consumers’ price-sensitivity and product substitutability on manufacturers’, retailers’ and the entire supply chain’s pricing and emission reduction strategy in a single channel and a dual exclusive channel. We first examine a traditional single-manufacturer–single-retailer channel (Case 1), which contains four sub-games (Scenario MC, MN, RC, and RN): manufacturer acts as the Stackelberg leader and produces green products (MC), manufacturer acts as the Stackelberg leader but produces normal products (MN), retailer acts as the leader and sells green products (RC), and retailer acts as the leader but sells normal products (RN). Then, we expand the single channel to a dual channel (Case 2), where each manufacturer chooses an exclusive retailer who sells substitutable goods. Similarly, Case 2 also includes four sub-games (Scenario MMC, MMN, RRC, and RRN): both manufacturers act as Stackelberg leaders and produce green products (MMC), and the rest can be deduced by analogy.
To obtain demand functions in different channel structures, we employ a similar utility function established by Ingene and Parry [
33], and the utility function has been widely utilized in marketing, economics, etc.
where
denotes product substitutability, the index
identifies the channel or supply chain or product and b denotes price sensitivity coefficient. In the model, we capture consumers’ low-carbon preference through the parameter t; a larger t means that consumers are more sensitive to low-carbon products.
To avoid confusion in notation, we use superscript C to denote low-carbon products, and N refers to normal products. Maximization of the utility function yields the demand function for low-carbon products as follows,
If
, then the demand function for normal products is defined as,
We assume channel operational costs and production costs to be zero for simplicity and lucidity. Based on the above analysis, the optimal profits of the manufacturers and retailers are defined as,
where
=
or
and L = 0 or 1. L indicates of whether manufacturers choose low-carbon strategy in supply chains. If L = 0, manufacturers will not choose low-carbon strategy, otherwise, they will implement the strategy.
3.1. Case 1: One Manufacturer and One Retailer
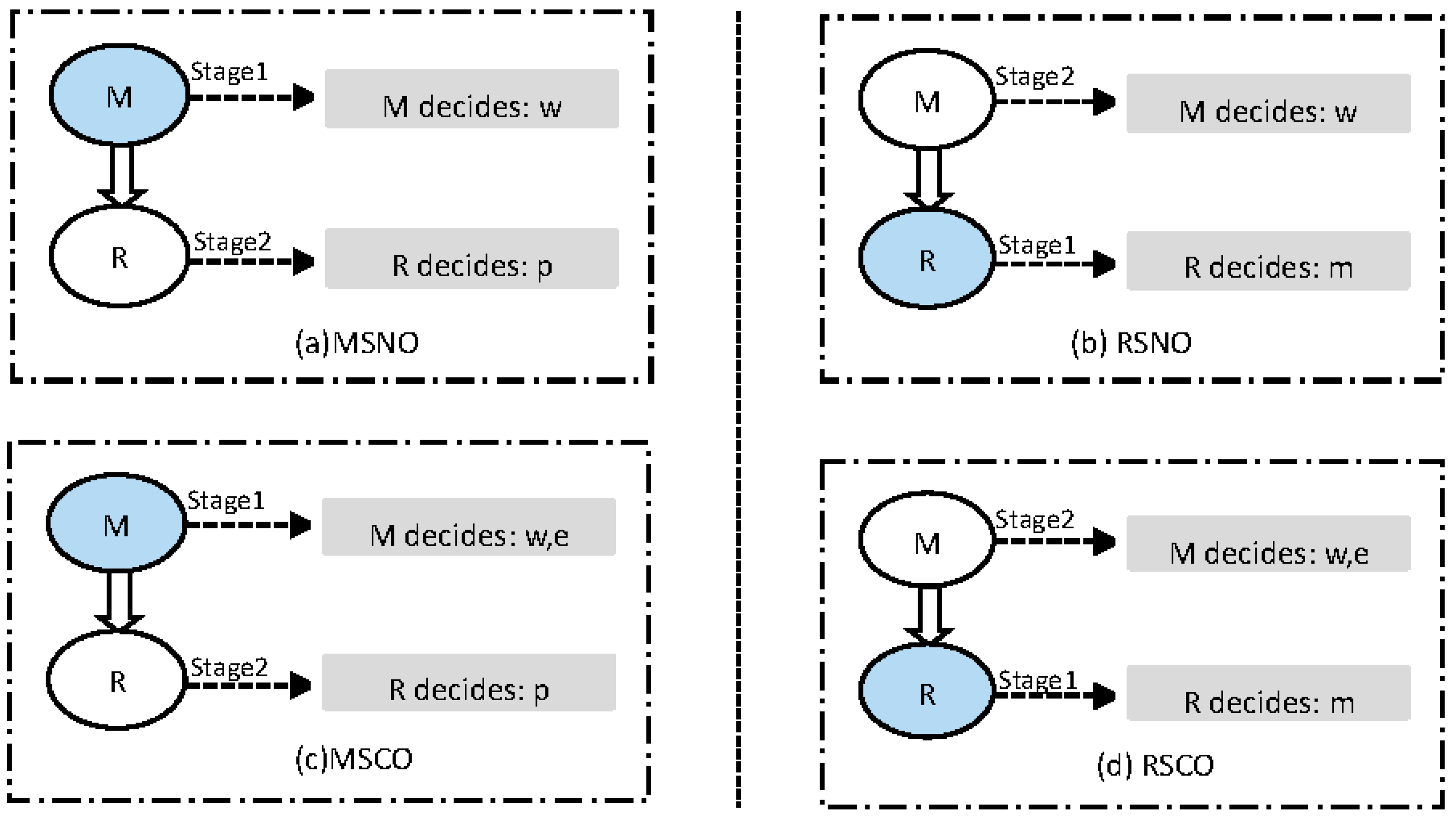
As a benchmark, we start the model with the simple supply chain shown in
Figure 1. It contains four sub-games (MN, MC, RN, and RC), and each proceeds as a two-stage game. For instance, in Scenario RC, the retailer acts as the leader (e.g., Wal-Mart and Home-depot) and the manufacturer acts as the follower. The retailer sets up the sale price using the reaction functions of the manufacturer in the first stage, and the manufacturer determines the wholesale price and emission reduction level in the second stage. It is also worth noting that
,
and
in the single-channel system. Hence, Equations (2) and (3) become
In Scenario MN, the manufacturer acts as the Stackelberg leader and the retailer acts as the Stackelberg follower. The leader in every decision scenario makes his decision to maximize the profit, based on the follower’s response. Accordingly the manufacturer first announces wholesale price , the retailer observes the wholesale price and decides the retail price () later.
According to the inverse order method, solving the two stage optimization problem first, the retailer’s response function can be derived,
We substitute the obtained response function (
) into the manufacturer’s profit function (
), and solve
results into the following wholesale price,
Furthermore, it is easy to get the optimum solutions as follows. From nonnegative demand constraints that , thus, we have .
Similar to Scenario MN, we can obtain the optimal solutions in MC, RN and RC, here we omit the proofs of other scenarios. All of the optimal solutions are summarized in
Table 2.
3.2. Case 2: Two Manufacturers and Two Retailers
This section studies a competing supply chain, and we use product substitutability (
) to represent the degree of substitutability or the intensity of competition between the two channels. A larger
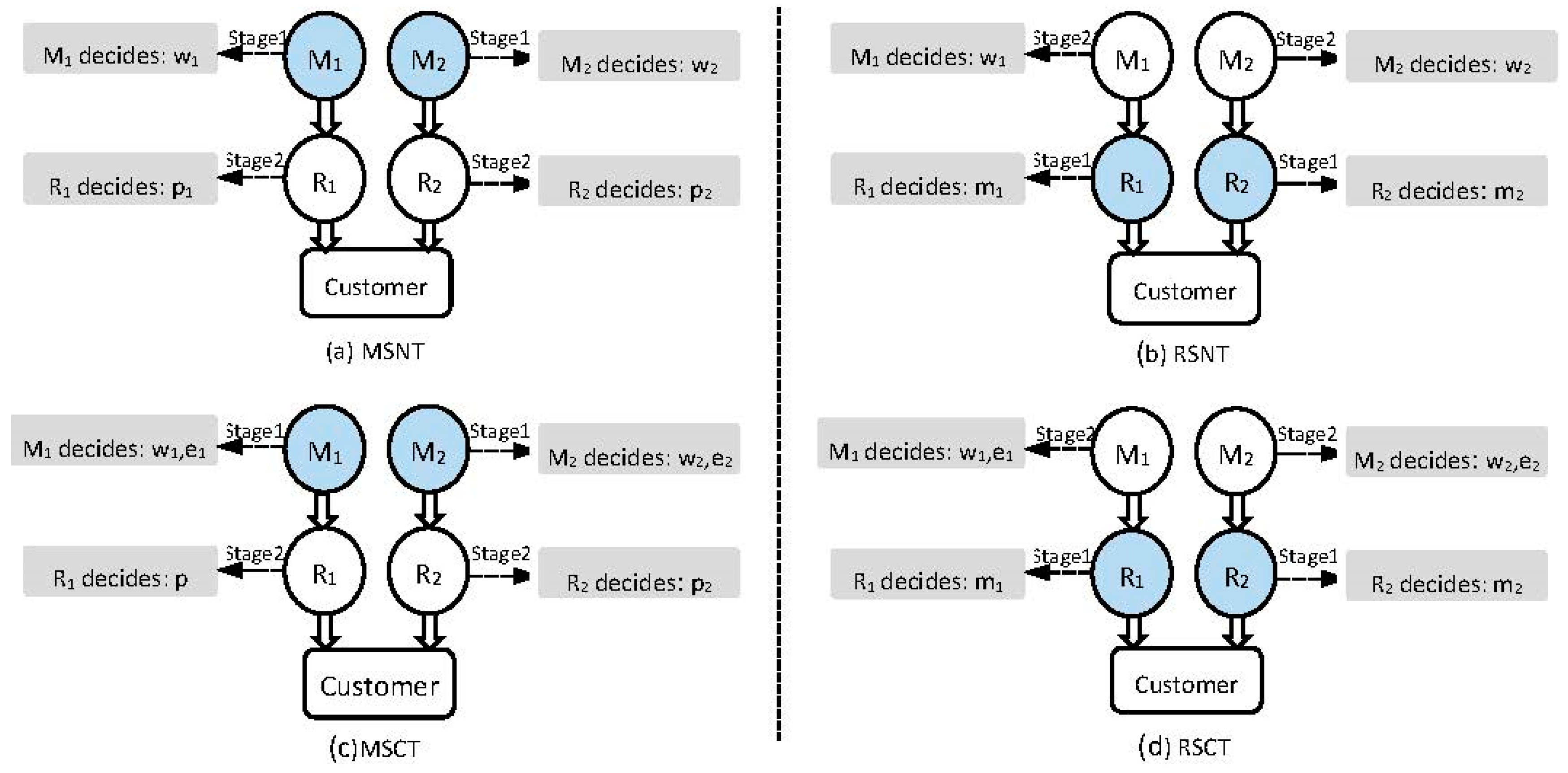
means that the competition is more intense. The supply chain structures and decision processes are depicted in
Figure 2. Similar to Case 1, Case 2 also contains four sub-games (Scenario MMC, MMN, RRC, and RRN), due to symmetry, we only consider the performance of retailer i and manufacturer i. To enable the fair comparison among the various scenarios and for parsimony, we assume parameter
and
are normalized to one, which does not compromise our findings. Hence, the demand functions for low-carbon products and normal products are given by,
(a) MMN
In Scenario MMN, the two manufacturers act as Stackelberg leaders and the two retailers act as the Stackelberg followers. The two manufacturers do not choose low-carbon strategy. Hence, the sequence of the game is as follows, the manufacturers simultaneously determine their respective optimal wholesale prices
in the first stage to maximize their own profit, the retailers determine their respective retail prices
in the second stage when knowing the two manufacturers’ decisions. The profit functions of retailers and manufacturers are given by,
Due to
and Hessian Matrix
,
is concave in
and
. After some algebra work, the best response retail prices are given by,
Having the information about the decisions of the retailers, the two manufacturers would simultaneously use the retailers’ response function to maximize their profits. Substitute
into
, and let the first order condition for manufacturers equal zero. Hence, we can see that the manufacturers’ equilibrium wholesale prices are,
Substitute
into Equation (16) and yield,
According to the above analysis, it is easy to obtain the optimum solutions. From nonnegative demand constraints that
, we have,
(b) RRN
Under Scenario RRN, the retailers become the leaders. Hence, the retailers determine their respective optimal margins
in the first stage, and the manufacturers announce their respective wholesale prices
in the second stage. Similarly, we get the profit functions,
Similar to that in Scenario MMN, we get the manufacturers’ optimal response function,
Substitute
into
, and let the first order condition for retailers equal zero. The optimal retail price can be derived,
Hence, the other optimal solutions can be easily obtained. Likewise, we have,
(c) MMC
Similar to Scenario MMN, we get the decision sequence in Scenario MMC, manufacturers set the wholesale prices
and emission reduction level
first, retailers determine their retail prices
using the response function of the manufacturers later. The profit functions of the retailers and manufacturers are formulated as,
Since the Hessian Matrix is negative definite, retailers’ reaction function can be derived from the first order conditions of Equation (26),
The manufacturers consider the retailers’ reaction function to determine their respective price decisions and emission reduction level, and
where
,
,
,
,
,
,
,
and
.
Thus, we easily get the other optimal solutions.
(d) RRC
Under Scenario RRC, the retailers determine their respective optimal margins
in the first stage, and the manufacturers announce their respective wholesale prices
and emission reduction level
in the second stage. Similar to that in Scenario RRN, the manufacturers’ optimal reaction function can be derived,
Maximize the retailers’ profit with manufacturers’ response function, the optimal retail prices can be reached as follows,
where
,
,
,
,
,
and
.
According to the above analysis, it is easy to obtain the other optimum solutions.
4. Equilibrium Analysis
4.1. Equilibrium Analysis for Case 1
The main goal of this section is to compare the optimal decisions among different power structures and to examine how consumers’ price-sensitivity affects the performance of the supply chain. Based on
Section 2 and
Section 3, we obtain the optimal solutions among MN, MC, RN and RC, which are summarized in
Table 2. For parsimony, this paper uses prefixes C and N to represent equilibrium solutions with and without emission reduction, respectively.
In order to have meaningful comparisons, we first assume
(the details are given in
Appendix A). Then, comparing the optimal profits among MN, MC, RN and RC, we get the following propositions.
Proposition 1. - (i)
, , for ;
- (ii)
, , for ;
- (iii)
, , for ;
- (iv)
for ; and
- (v)
for .
Proposition 1 shows that both manufacturer and retailer are willing to implement low-carbon strategy when consumers’ price-sensitivity is relatively high (). This result is rather intuitive because they can yield more profit after emission reduction. Theoretically, all channel members should choose emission reduction strategies. However, when consumers’ price-sensitivity is sufficiently low (), the retailer tends to choose low-carbon strategy, but the manufacturer has no incentive to implement low-carbon strategy. This is because the retailer performs better than the power manufacturer in MC (e.g., ). Thus, if the retailer wants to cooperate with the manufacturer, it should share a proportion of his profits. We also find that the low-carbon product is more profitable than the normal product in Manufacturer Stackelberg when consumers’ price-sensitivity is sufficiently low. Motivated by this, the manufacturer would like to invest more money to produce more low-carbon products. Which also implies the sale price of low-carbon products is more expensive than normal products, and if customers buy low-carbon products, they will pay more than that of the ordinary products (e.g., for ). Thus, the government should build low-carbon environment and make more citizens develop the preference for low carbon products.
Proposition 1 also indicates that both manufacturer and retailer always benefit from their leadership before emission reduction (e.g., and ). Thus, all supply chain members always want to act as a leader. However, the leadership cannot always insure all members obtain more profits after emission reduction. Moreover, the efficiency of the entire supply chain remains the same under different power structures before emission reduction, while RC ensures the whole supply chain getting a better performance after emission reduction.
Since RC makes the whole supply chain yield benefit more after emission reduction, while the efficiency of the whole supply chain remains the same under different power structures before emission reduction, we are motivated to ask the following research question: Do these findings apply only to a single-channel system? We investigate by next considering a dual exclusive channel system.
4.2. Equilibrium Analysis for Case 2
Now, we consider a dual exclusive channel system to find how the channel power structures (sequence of decisions) and product substitutability affect the manufacturers’, retailers’ and the whole channel’s optimal decisions. To facilitate the discussion, we define as the relative channel status. implies channel system is symmetric, and implies the channel system is asymmetric. In order to have meaningful comparisons among different power structures, we get the common feasible area from nonnegative demand constraints: and .
Based on the above analysis, we obtain the optimum solutions of MMN, MMC, RRN and RRC, and we summarize these optimum solutions in
Table 3 and
Table 4.
To facilitate our discussion, we define , , , , , , , , , , and .
For parsimony, we define , , , , , , , , , , , , and .
Due to the complexity, we just compare the optimum solutions between MMN and RRN, and the other comparisons will be discussed in
Section 5. Comparing the manufacturers’ and retailers’ profits between MMN and RRN under asymmetric relative channel status, we obtain the following propositions (the details are given in
Appendix A),
Proposition 2. - (i)
;
- (ii)
;
- (iii)
;
- (iv)
- (v)
for .
Proposition 2 is rather counter-intuitive. Part (i) and Part (ii) show that manufacturers make the largest profit in MMN and smaller profit in RRN, while retailers’ profits are the reverse order. Moreover, the manufacturers’ pricing power enable them to raise their wholesale prices, their corresponding retailers then have no choice but to increase the retail prices (e.g., ), which leads to lose more demand. Thus, customer will get worst welfare in Scenario MMN. As shown in Part (iii) and Part (iv), the leaders always performer better than their corresponding followers before emission reduction. Unlike the situation in Case 1, which indicates that the efficiency of entire supply chain remains the same before emission reduction under different power structures, Part (v) indicates that the whole channel can be better off in Scenario MMN when the channel status is relatively high, while it can be worse off when the channel status is sufficiently low.
Proposition 2 also indicates that the leadership always guarantees the channel members perform better before emission reduction. However, the leadership is not always profitable for the whole channel. Moreover, the whole channel performs better in RRN than that in MMN when product substitutability is sufficiently low. On the other hand, as the horizontal competition between channels intensify, the whole channel can be better off in MMN.
5. Numerical Analysis
Numerical experiments are conducted in this section to address the impact of product substitutability and asymmetric channel power on the emission reduction strategy in Case 2. In the following, we first compare manufacturer’s and retailer’s profits among different power structures under asymmetric relative channel status. Then, we compare all scenarios in terms of overall supply chain efficiency under symmetric relative channel status. We fix the values of other parameters while choose as the independent variable, and the parameters in common are as follows: and . Due to complexity, we compare these profits with contour plots.
5.1. Comparisons with Asymmetric Channel Power
Given the complexity of the analytical solutions, we define
, then we obtain
. Since the explicit forms of all boundary values (shown in
Figure 3,
Figure 4,
Figure 5,
Figure 6,
Figure 7,
Figure 8,
Figure 9 and
Figure 10), such as the
terms shown in the various figures and analytical results, are very complicated, they are summarized in
Appendix A. We now exhibit the case where
through comparing profits of retailer i and manufacturer i under different power structures. These boundary values and the method for obtaining them are summarized in the
Appendix A.
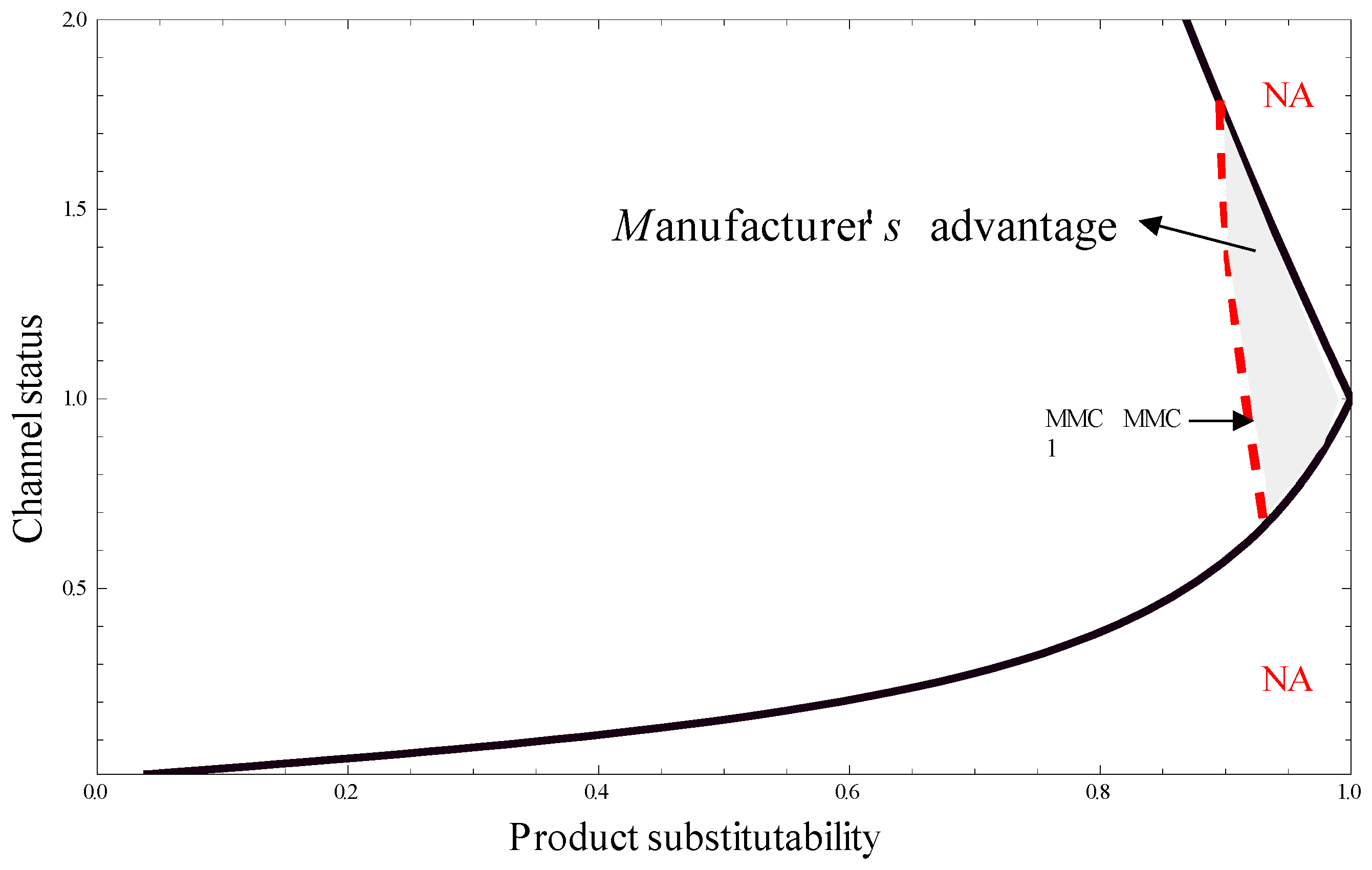
(a) Comparison: MMC versus MMN
Firstly, by comparing the retailers’ and manufacturer’s profits between MMC and MMN with contour plots, we obtain the following results.
- (i)
for and ; and
- (ii)
for and .
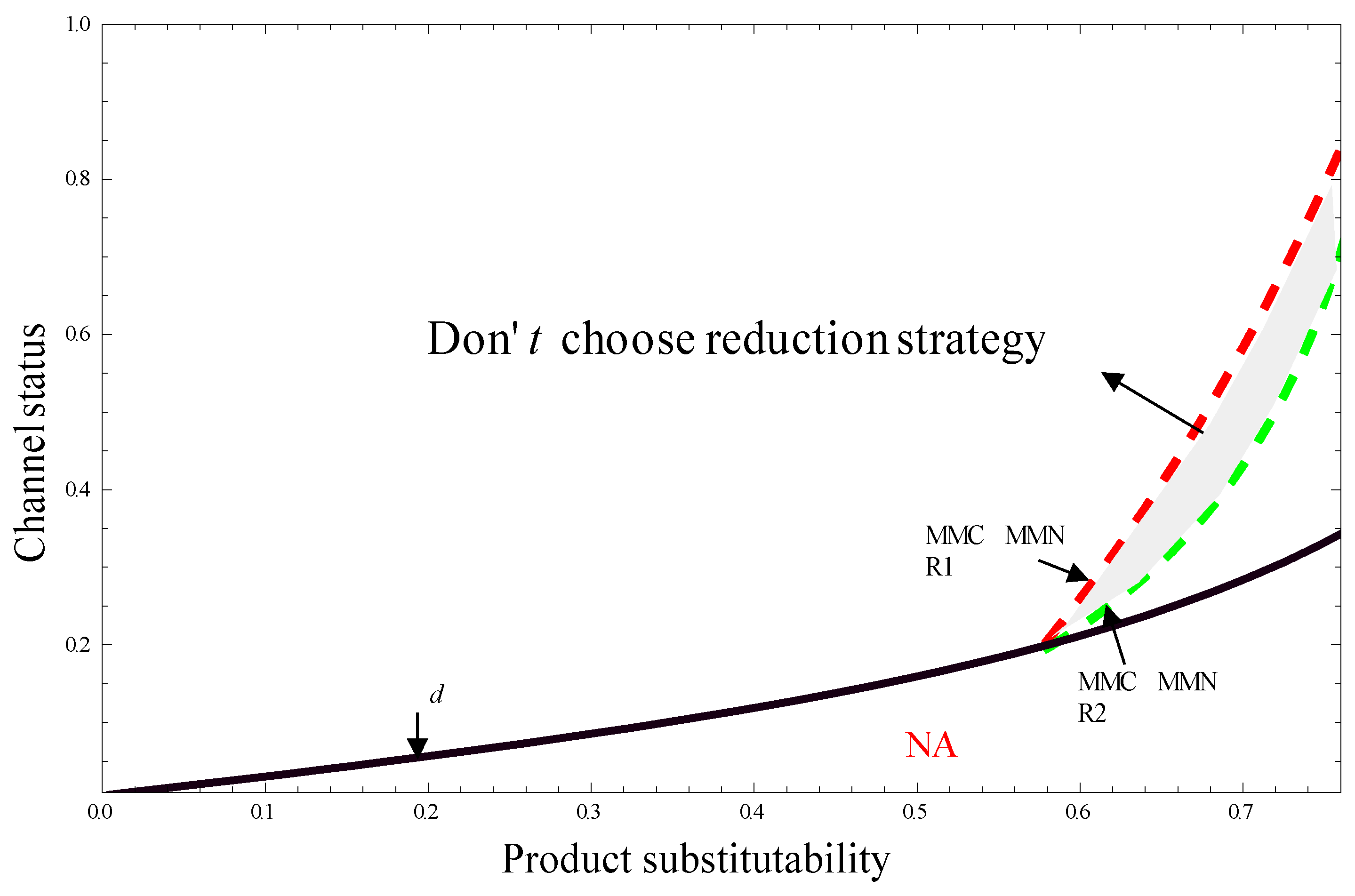
As shown in
Figure 3 and
Figure 4, Scenario MMC is feasible in a larger area than Scenario MMN, which means that all the channel members benefit from emission reduction when product substitutability is small (
for
), hence, they will choose low-carbon strategy. However, emission reduction could make both manufacturers and retailers worse off in MMC than that in MMN if product substitutability is sufficiently intense and the asymmetric relative channel status is relatively high (
for
).
The analysis also points out that the leadership always guarantees the channel members perform better. However, the leadership is not always profitable for the whole channel. Moreover, this seemingly counter-intuitive result reflexes that the whole channel performs better in RS than that in MS when product substitutability is sufficiently low. However, as the horizontal competition between channels intensifies, the whole channel can be better off in MS.
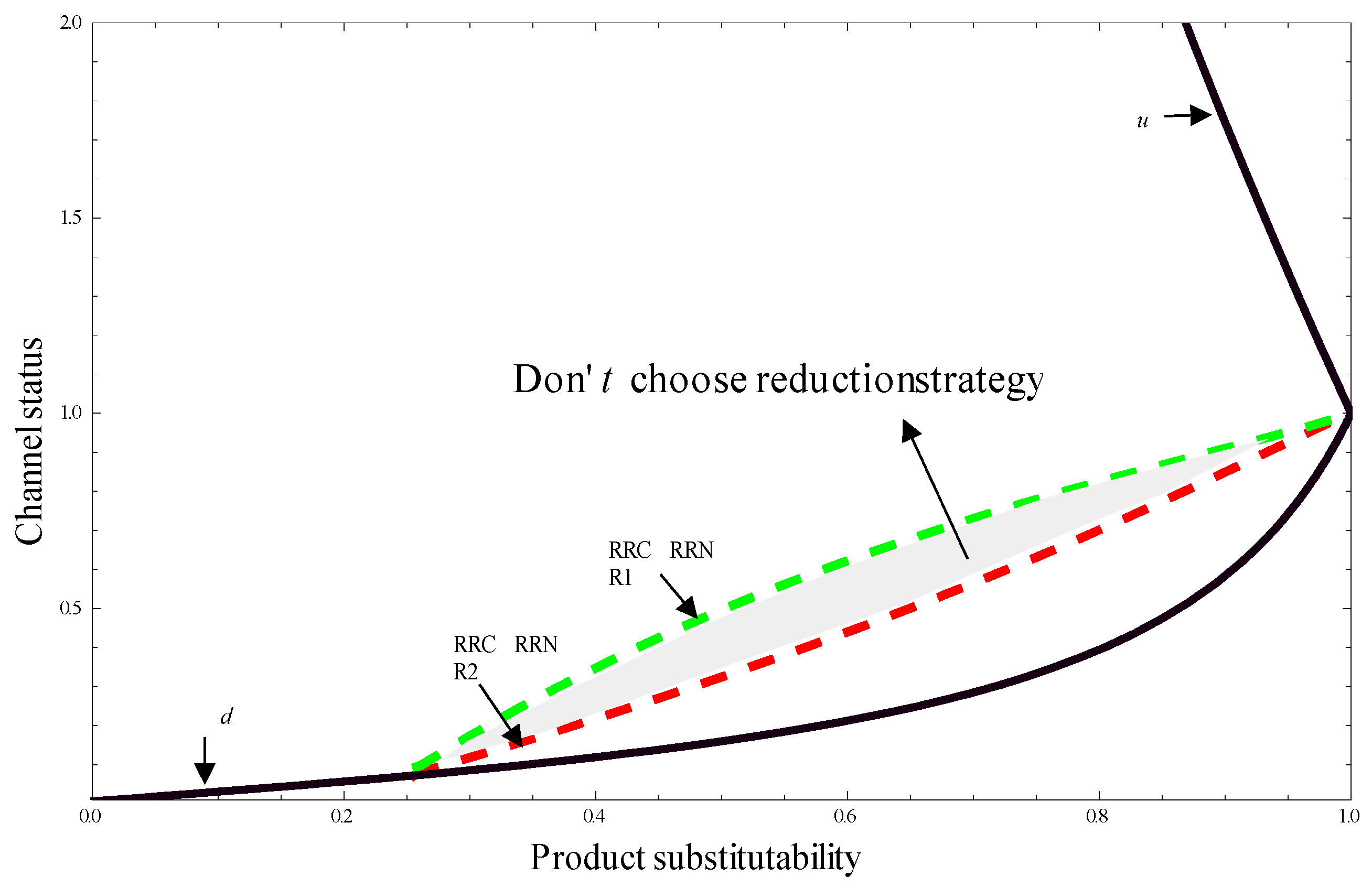
(b) Comparison: RRC versus RRN
Secondly, we compare profits of retailers, manufacturers between RRC and RRN. Correspondingly, we have:
- (i)
for and ; and
- (ii)
for and .
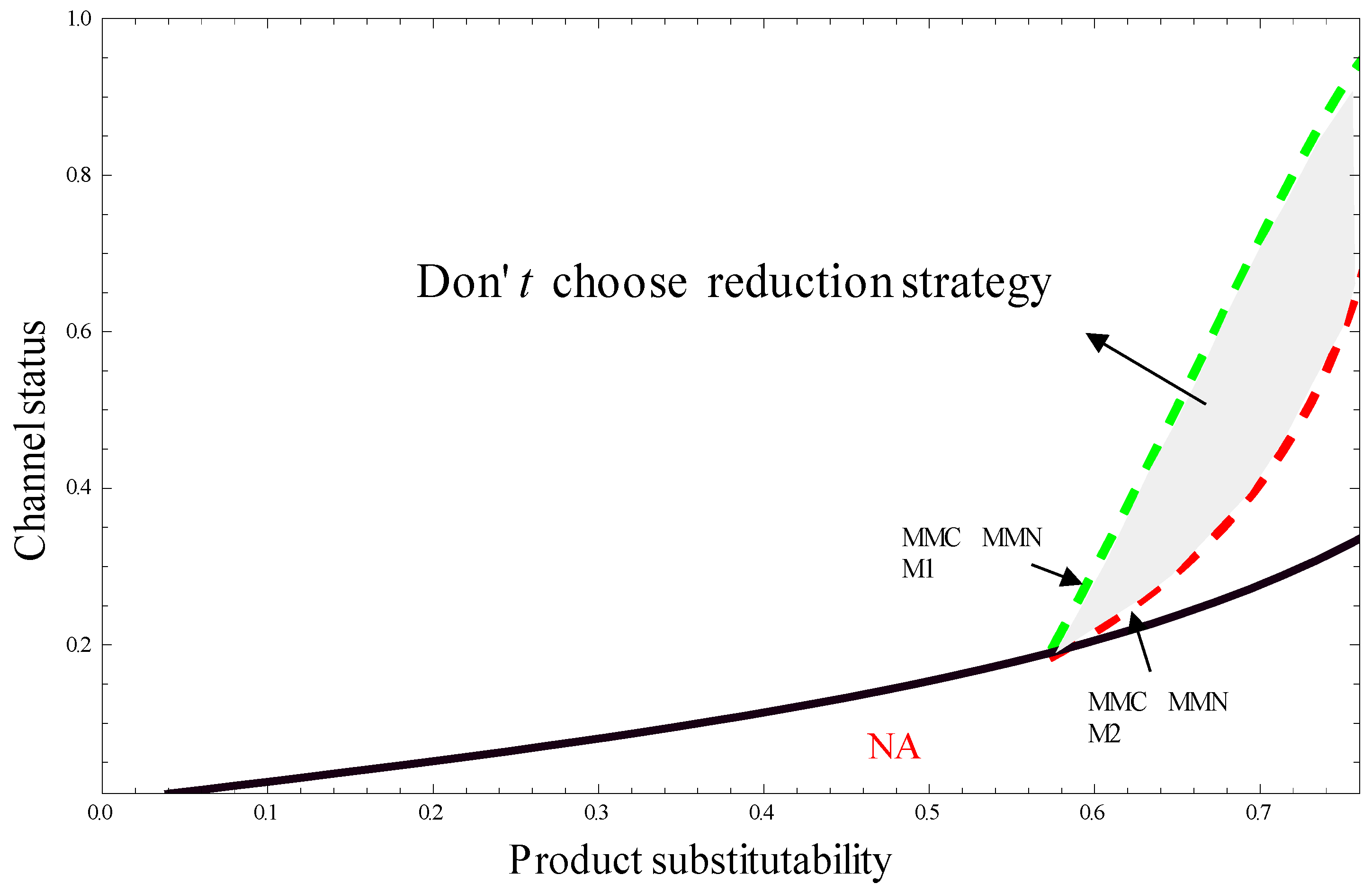
Figure 5 and
Figure 6 exhibit that the profits of retailers and manufacturers in RRC outperform that in RRN when the product substitutability is small. However, as product substitutability grows, emission reduction intensifies the horizontal competition between the two channels, and RRN performs better than RRC (
for
and
). This reflects both manufacturers and retailers will choose low-carbon strategy when the product substitutability is small, while they have no incentive to choose low-carbon strategy if the asymmetric relative channel status and product substitutability are relatively high. The result is similar to that in MMC and MMN.
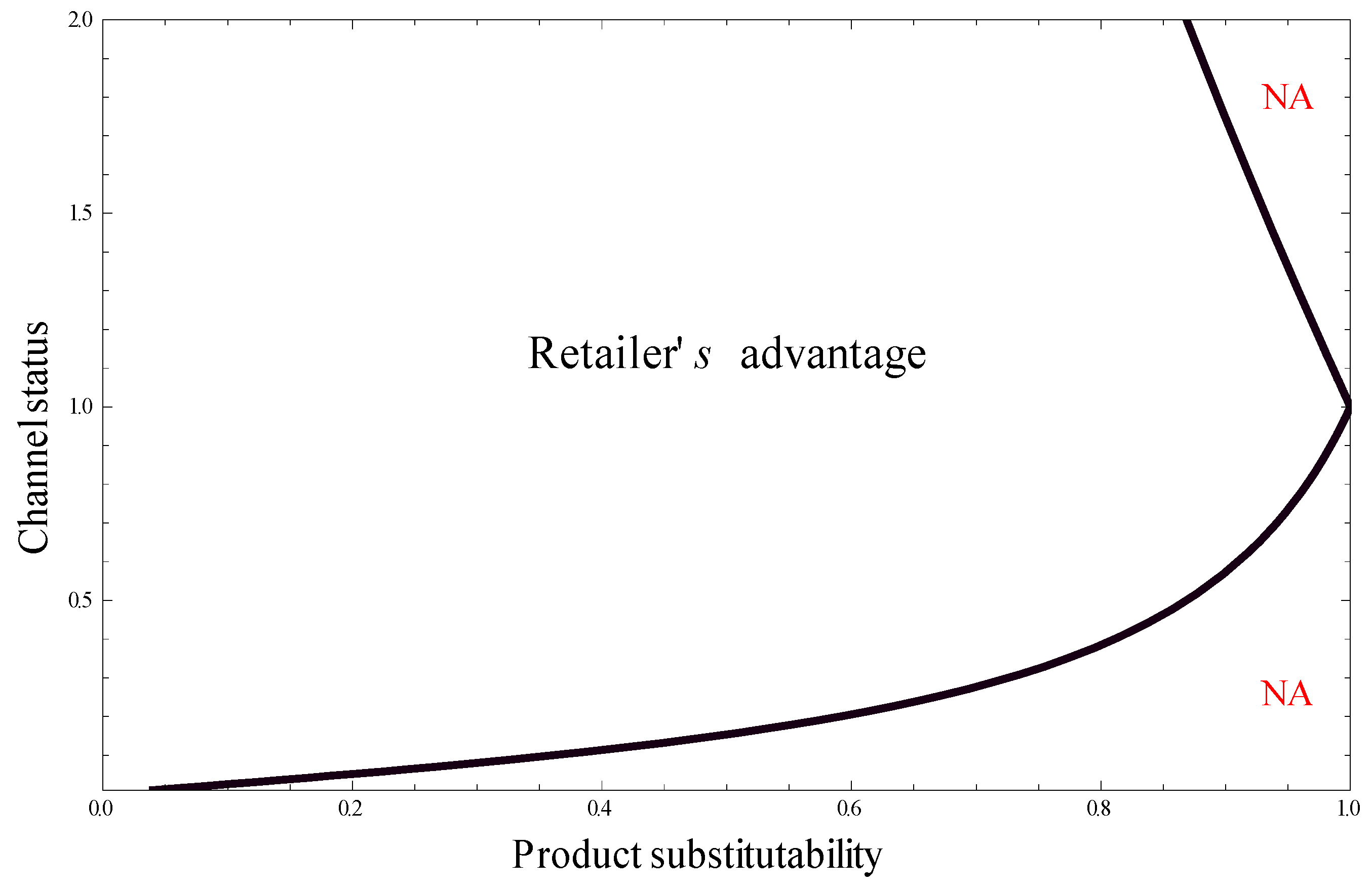
(c) Comparison: Hybrid Scenarios
In this subsection, we present four numerical examples. The first and second examples are used to find whether the leadership (dominant power) can always ensure the channel members getting more benefits. The third and fourth examples show how the profits of the retailers and the manufacturers change as the dominant power shift. Similarly, we have:
- (i)
for and ;
- (ii)
for ; and
- (iii)
for and .
From the previous discussion, the channel members should choose low-carbon strategy when the product substitutability is low. However, this seemingly expected result has never been realized. We observe an interesting result in
Figure 7: manufacturers as a whole benefit from the emission reduction. Nevertheless, retailers gain more profits when the product substitutability is very high in MMC (e.g.,
for
and
), which means that the power manufacturers may not necessarily yield more benefits than the retailers. This observation is seemingly contrary to what one may expect. Thus, manufacturers are reluctant to produce the green products. According to
Figure 8, retailers always get more benefits than manufacturers in RRC, and, unlike MMC, retailers always want to implement low-carbon strategy.
Figure 9 indicates that manufacturers still earn extra profits with dominant power shifting from the manufacturers to the retailers. This is particularly true when product substitutability is high, which implies that manufacturers can be worse off in MMC when the asymmetric relative channel status and product substitutability are relatively high. Similarly, it can be beneficial for retailers with dominant power shifting from the manufacturers to the retailers. The insights gained from the results of the numerical examples above are summarized in Conclusion 1.
Conclusion 1. When the related channel power is asymmetric, both the retailers and manufacturers will be beneficial from the implementation of low-carbon strategy when the product substitutability and the asymmetric relative channel status are sufficiently low. However, as product substitutability grows, all the channel members will encounter a Prisoner’s dilemma. Channel leadership plays an important role in determining the implementation of low-carbon strategy.
Conclusion 1 suggests that the profits of retailers and manufacturers as a whole can be better off after emission reduction, both retailers and manufacturers have a motivation to implement low-carbon strategy. However, emission reduction could make both retailers and manufacturers worse off if product substitutability is sufficiently intense. This is intuitive because emission reduction intensifies the horizontal competition between the two channels; beyond a certain level of substitutability, the channel members face a Prisoner’s Dilemma, which means that neither prefers low-carbon strategy, but, if either party does not then implement a low-carbon strategy, the other has a positive incentive to choose low-carbon strategy. The practical implication for manufacturers is that they should sufficiently differentiate their products.
Conclusion 1 also shows that the asymmetric relative channel status is a key factor that influences the implementation of low-carbon strategy. Comparing the profits of retailers and manufacturers under MMC (RRC), we find that the channel leadership plays an important role in determining the implementation of low-carbon strategy. For instance, in MMC, retailers tend to choose low-carbon strategy, while manufacturers have no incentive to implement low-carbon strategy when the product substitutability is low. This is because retailers perform better than the power manufacturers. In RRC, both retailers and manufacturers will choose low-carbon strategy when the product substitutability is low due to the power retailers are better off than the manufacturers. Moreover, a member with a larger base market is rewarded for its own emission reduction but negatively affected by its competitor’s.
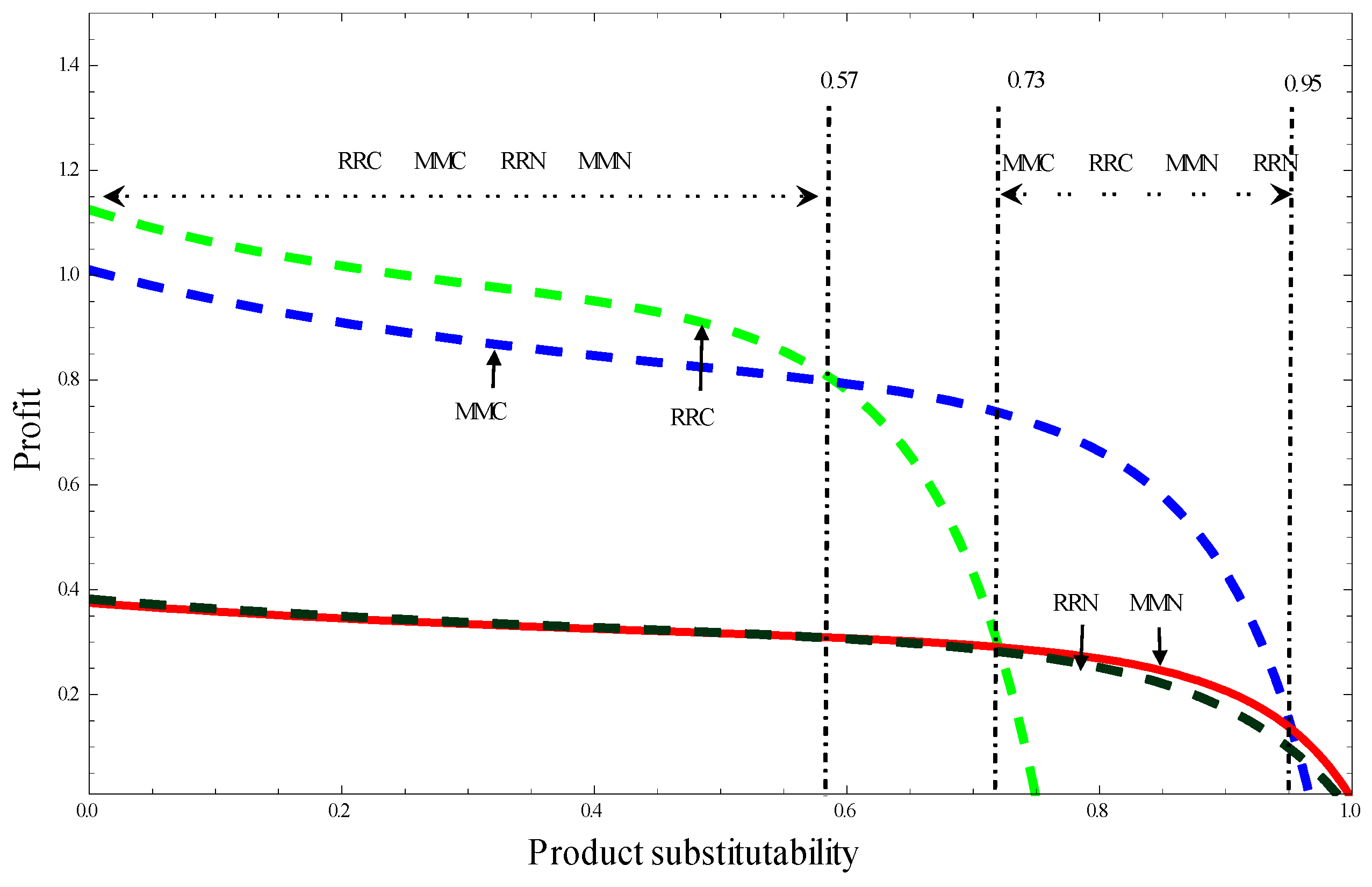
5.2. Comparisons with Symmetric Channel Power
In the above discussion, we have compared manufacturer’s profit and retailer’s profit among different power structures under asymmetric relative channel status. We find that emission reduction brings about more profits to both the manufacturers and retailers as long as product substitutability and the asymmetric relative channel status are sufficiently low. We are now in a position to compare the entire supply chain efficiency among different power structures. Given the symmetric setting (
), that is
, we get the following results from
Figure 10:
- (i)
for ;
- (ii)
for ;
- (iii)
for ; and
- (iv)
for .
Figure 10 depicts the curves of entire supply chain profit in different power structures with respect to
; it is intuitive that the total channel profit decreases with
. The profit gap between cases with emission reduction and without emission reduction becomes greater with the increase of
. Moreover, the profit has a much steeper fall in RRC than that in RRN, which indicates that government subsidies play an important role in increasing the profit of the whole supply chain, but they also intensify the horizontal competition between supply chains. At the same time, according to
Figure 10, Scenario RRC outperforms all other scenarios when product substitutability is lower (e.g.,
for
), which suggests that low-carbon products guarantee success in the market, especially in RS. It also indicates the additional profits are high enough to compensate for the high cost of emission reduction. As the product substitutability increases, Scenario MMC performs better (e.g.,
for
). Part (i) and Part (ii) show that the entire supply chain can be better off after emission reduction regardless of who is operating the channels. However, when the product substitutability is sufficiently intense, MMN outperforms all other scenarios (e.g.,
for
). Thus, it can be concluded that, there is no power structure always ensuring the entire supply chain getting the best performance in the dual channel. Here, the insight is summarized in Conclusion 2.
Conclusion 2. Government subsidies play an important role in increasing the profit of the whole supply chain but intensify the horizontal competition between supply chains. No power structure always ensures the entire supply chain getting the best performance in the dual channel.
6. Conclusions
This paper investigates the impact of consumers’ price-sensitivity, product substitutability and power structures on channel members’ and the entire supply chain’s pricing and emission reduction. Different from previous studies on low-carbon strategy of competing supply chains, we consider two supply chain network structures with different power structures (including a single channel and a exclusive dual channel), and both the single channel and the exclusive dual channel include four sub-games. Our analysis is based on game theory models, and revealed several interesting results by comparing the four different sub-games.
In practice, all supply chain members always want to play the leader’s role, because they get more benefits from playing the leader’s role. However, leadership does not always ensure the leaders getting more benefits than the followers after the emission reduction. We also find that the asymmetric relative channel status is a key factor that influences the implementation of low-carbon strategy, since a member with a larger base market is rewarded for its own emission reduction but negatively affected by its competitor’s. Furthermore, when both product substitutability and the asymmetric relative channel status are sufficiently low, all supply chain members will choose low-carbon strategy in RS game, while only the retailer chooses low-carbon strategy in MS game. In addition, the low-carbon products are more profitable than the normal products in MS when consumers’ price-sensitivity is sufficiently low. It is clear from the results that low-carbon products cost more to produce than the normal products; if manufacturers are going to produce green products, they have to make sure that customers are willing to pay more for these types of products. Moreover, government subsidies play an important role in determining the profit of the whole supply chain but intensify the horizontal competition between supply chains. Finally, we find that no power structure always ensures the entire supply chain getting the best performance in the dual channel.
Our research offers insightful recommendations for enterprises and regulators. On the one hand, our results can help manufacturers and retailers understand that the leadership may not necessarily guarantee more benefits to them, and they should sufficiently differentiate their products to avoid a price war. On the other hand, the results can help policy-makers understand why some policies are successful and others are not, and therefore will be very valuable for future policy-makers. Some policy-makers may believe that the success of implementing low-carbon strategy is only due to government subsidies and improving consumers’ environmental consciousness, however our analysis shows that the leadership also plays an important role in the implementation of low-carbon strategy, and Scenario RS can be more beneficial to promote the emission reduction. Additionally, government subsidies may make both retailers and manufacturers worse off if product substitutability is sufficiently intense. The different result from intuitive thinking will significantly impact the future policy to make appropriate measures to promote the implementation of low-carbon strategy.
While we provide a general framework for future study on the implementation of low-carbon strategy in competing supply chains, there are some limitations in this paper. Firstly, we assume the demand of consumers is linear. Secondly, in our paper, we assume the information is symmetrical between the channels. Finally, only dual channel system and single channel are considered, and other channel systems should likewise be investigated. There are a few directions that we would like to explore in a further step: one interesting extension is to examine how demand uncertainty affects the implementation of low-carbon strategy.