Natural Resource Economics, Planetary Boundaries and Strong Sustainability
Abstract
1. Introduction
2. Materials and Methods
2.1. Key Definitions and Concepts
- Climate change
- Loss of biosphere integrity (e.g., marine and terrestrial biodiversity loss)
- Land-system change
- Freshwater use
- Biochemical flows (e.g., effluents that interfere with nitrogen and phosphorous cycles)
- Ocean acidification
- Atmospheric aerosol loading
- Stratospheric ozone depletion
- Novel entities (e.g., new substances and modified organisms that have undesirable environmental impacts).
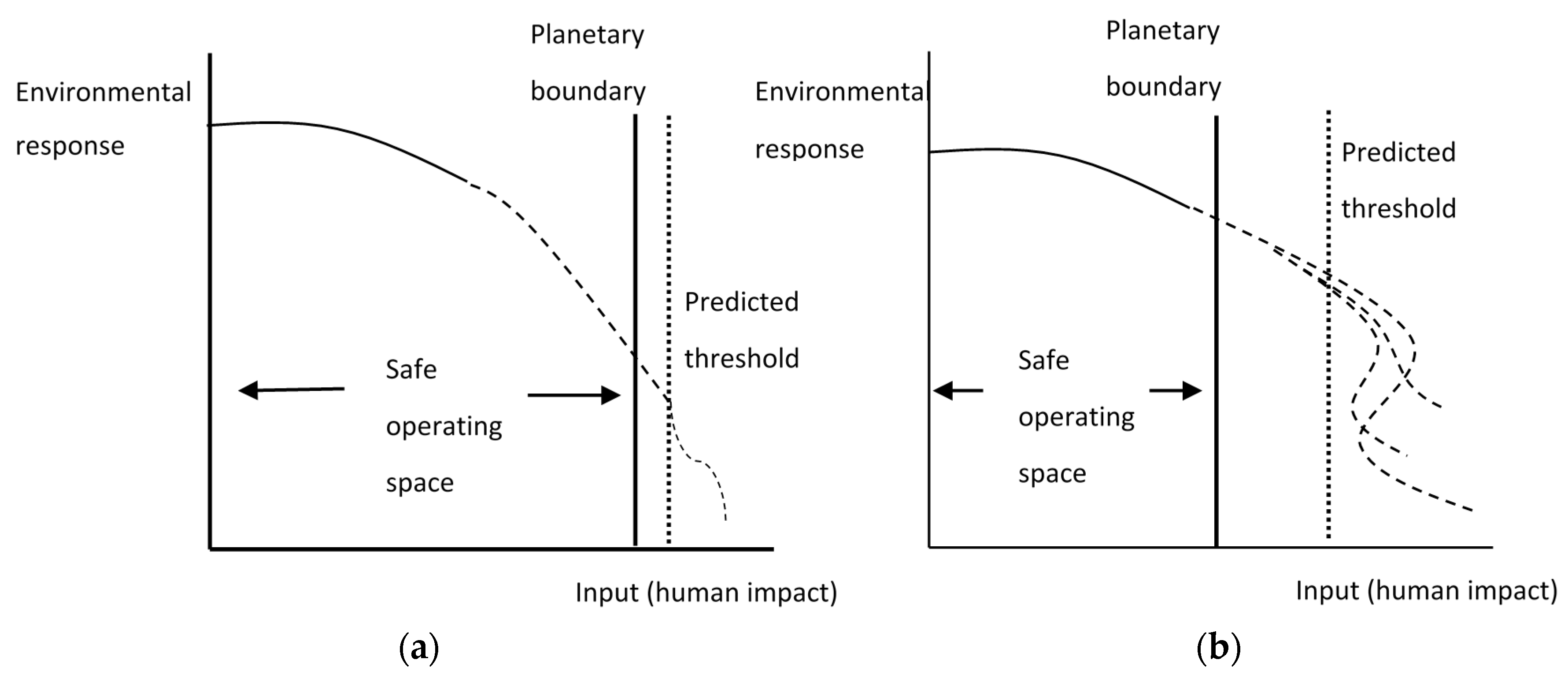
2.2. The Safe Operating Space as an Economic Asset
3. Results
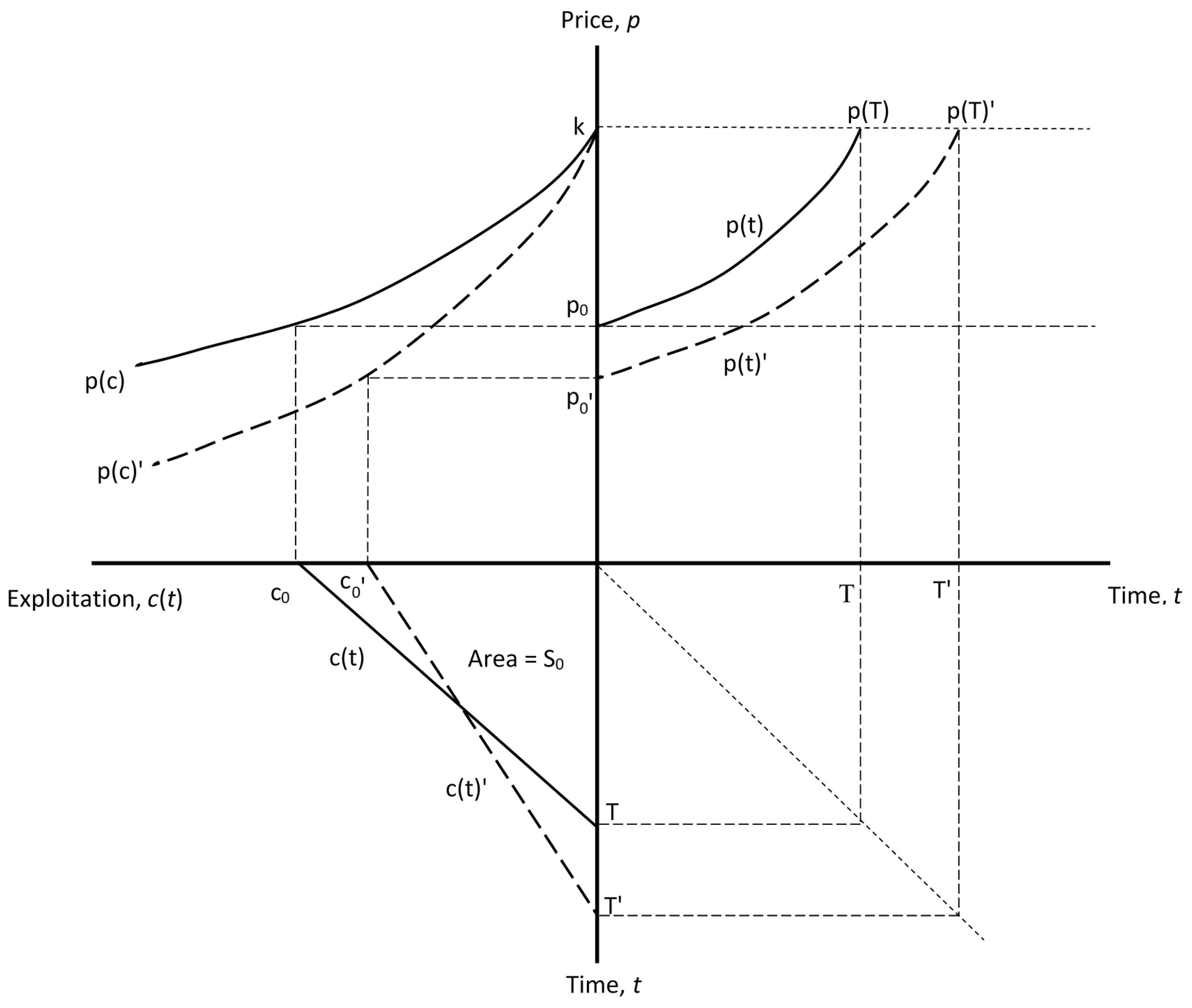
3.1. Optimal Exploitation of the Safe Operating Space
3.2. Technological Innovation
3.3. Stock Externalities
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lenton, T.M.; Held, H.; Kriegler, E.; Hall, J.W.; Lucht, W.; Rahmstorf, S.; Schellnhuber, H.J. Tipping elements in the Earth’s climate system. Proc. Natl. Acad. Sci. USA 2008, 105, 1786–1793. [Google Scholar] [CrossRef] [PubMed]
- Rockström, J.; Steffen, W.; Noone, K.; Persson, A.; Chapin, A.S., III; Lambin, E.F.; Lenton, T.M.; Scheffer, M.; Foke, C.; Schellnhuber, H.J. A safe operating space for humanity. Nature 2009, 461, 472–475. [Google Scholar]
- Running, S.W. A measurable planetary boundary for the biosphere. Science 2012, 337, 1458–1459. [Google Scholar] [CrossRef] [PubMed]
- Steffen, W.; Richardson, K.; Rockström, J.; Cornell, S.E.; Fetzer, I.; Bennett, E.M.; Biggs, R.; Carpenter, S.R.; de Vries, W.; de Wit, E.A. Planetary Boundaries: Guiding Human Development on a Changing Planet. Available online: http://science.sciencemag.org/content/347/6223/1259855 (accessed on 16 October 2017).
- Gerton, D.; Hoff, H.; Rockström, J.; Jägermeyr, J.; Kummu, M.; Pastor, A.V. Towards a revised planetary boundary for consumptive freshwater use: The role of environmental flow requirements. Curr. Opin. Sustain. 2013, 5, 551–558. [Google Scholar] [CrossRef]
- Mace, G.M.; Reyers, B.; Alkemade, R.; Biggs, R.; Chapin, F.S., III; Cornell, S.E.; Díaz, S.; Jennings, S.; Leadley, P.; Mumby, P.J. Approaches to defining a planetary boundary for biodiversity. Glob. Environ. Chang. 2014, 28, 289–297. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2014: Synthesis Report; Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Pachauri, R.K., Meyer, L.A., Eds.; IPCC: Geneva, Switzerland, 2014. [Google Scholar]
- Smith, V.K. Environmental economics and the Anthropocene. Oxf. Res. Encycl. Environ. Sci. 2017. [Google Scholar] [CrossRef]
- Barbier, E.B.; Markandya, A. A New Blueprint for a Green Economy; Routledge/Taylor & Francis: London, UK, 2013. [Google Scholar]
- Barbier, E.B. Nature and Wealth: Overcoming Environmental Scarcity and Inequality; Palgrave MacMillan: London, UK, 2015. [Google Scholar]
- Barbier, E.B. Sustainability and development. Annu. Rev. Resour. Econ. 2016, 8, 261–280. [Google Scholar] [CrossRef]
- Daily, G.C.; Söderqvist, T.; Aniyar, S.; Arrow, K.; Dasgupta, P.; Ehrlich, P.R.; Folke, C.; Jansson, A.; Jansson, B.O.; Kautsky, N. The value of nature and the nature of value. Science 2000, 289, 395–396. [Google Scholar] [CrossRef] [PubMed]
- Crépin, A.S.; Folke, C. The economy, the biosphere and planetary boundaries: Towards biosphere economics. Int. Rev. Environ. Econ. 2014, 8, 57–100. [Google Scholar] [CrossRef]
- Barbier, E.B.; Burgess, J.C. Depletion of the global carbon budget: A user cost approach. Environ. Dev. Econ. 2017, 3, 1–16. [Google Scholar] [CrossRef]
- Van der Ploeg, R. The Safe Carbon Budget; CESifo Working Paper No. 6620; Munich Society for the Promotion of Economic Research—CESifo: Munich, Germany, 2017. [Google Scholar]
- Lambin, E.F.; Meyfroidt, P. Global land use change, economic globalization and the looming land scarcity. Proc. Natl. Acad. Sci. USA 2011, 108, 3465–3472. [Google Scholar] [CrossRef] [PubMed]
- Grainger, A. Is land degradation neutrality feasible in dry areas? J. Arid Environ. 2015, 112, 14–24. [Google Scholar] [CrossRef]
- Barbier, E.B. Capitalizing on Nature: Ecosystems as Natural Assets; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Goulder, L. Induced Technological Change and Climate Policy; Pew Center on Global Climate Change: Arlington, VA, USA, 2004. [Google Scholar]
- Fankhauser, S.; Bowen, A.; Calel, R.; Dechezleprêtre, A.; Grover, D.; Rydge, J.; Sato, M. Who will win the green race? In search of environmental competitiveness and innovation. Glob. Environ. Chang. 2013, 23, 902–913. [Google Scholar] [CrossRef]
- Clift, R.; Sim, S.; King, H.; Chenoweth, J.L.; Christie, I.; Clavreul, J.; Mueller, C.; Posthuma, L.; Boulay, A.M.; Chaplin-Kramer, R. The challenges of applying planetary boundaries as a basis for strategic decision-making in companies with global supply chains. Sustainability 2017, 9, 279. [Google Scholar] [CrossRef]

| Weak Sustainability | Strong Sustainability |
|---|---|
|
|
|
|
|
|
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barbier, E.B.; Burgess, J.C. Natural Resource Economics, Planetary Boundaries and Strong Sustainability. Sustainability 2017, 9, 1858. https://doi.org/10.3390/su9101858
Barbier EB, Burgess JC. Natural Resource Economics, Planetary Boundaries and Strong Sustainability. Sustainability. 2017; 9(10):1858. https://doi.org/10.3390/su9101858
Chicago/Turabian StyleBarbier, Edward B., and Joanne C. Burgess. 2017. "Natural Resource Economics, Planetary Boundaries and Strong Sustainability" Sustainability 9, no. 10: 1858. https://doi.org/10.3390/su9101858
APA StyleBarbier, E. B., & Burgess, J. C. (2017). Natural Resource Economics, Planetary Boundaries and Strong Sustainability. Sustainability, 9(10), 1858. https://doi.org/10.3390/su9101858





