The Multiscale Fluctuations of the Correlation between Oil Price and Wind Energy Stock
Abstract
:1. Introduction
2. Data and Algorithm Description
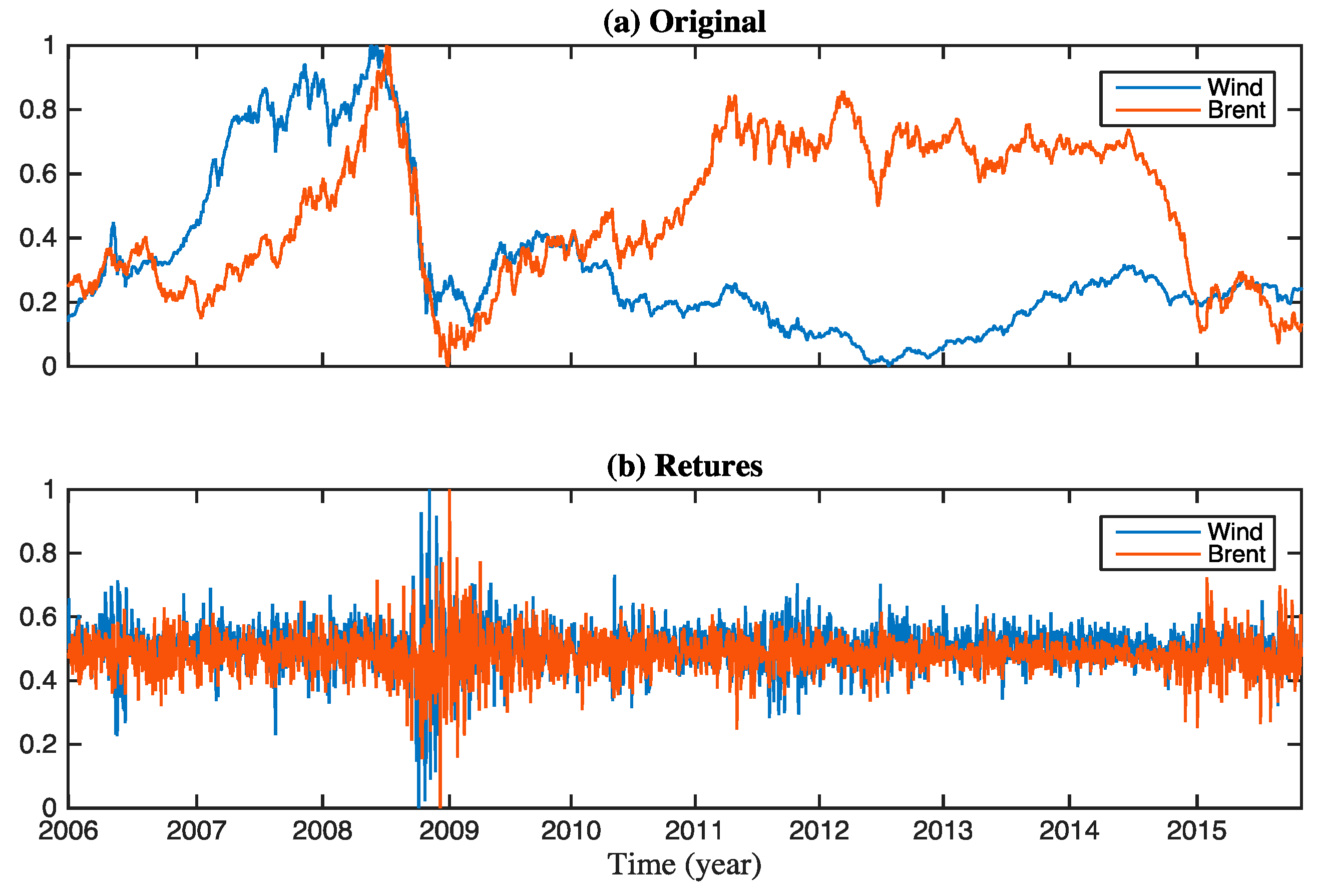
2.1. Data Description
2.2. Algorithms
2.2.1. Co-Movement in Time Domain
2.2.2. Decomposition into the Time–Frequency Domain
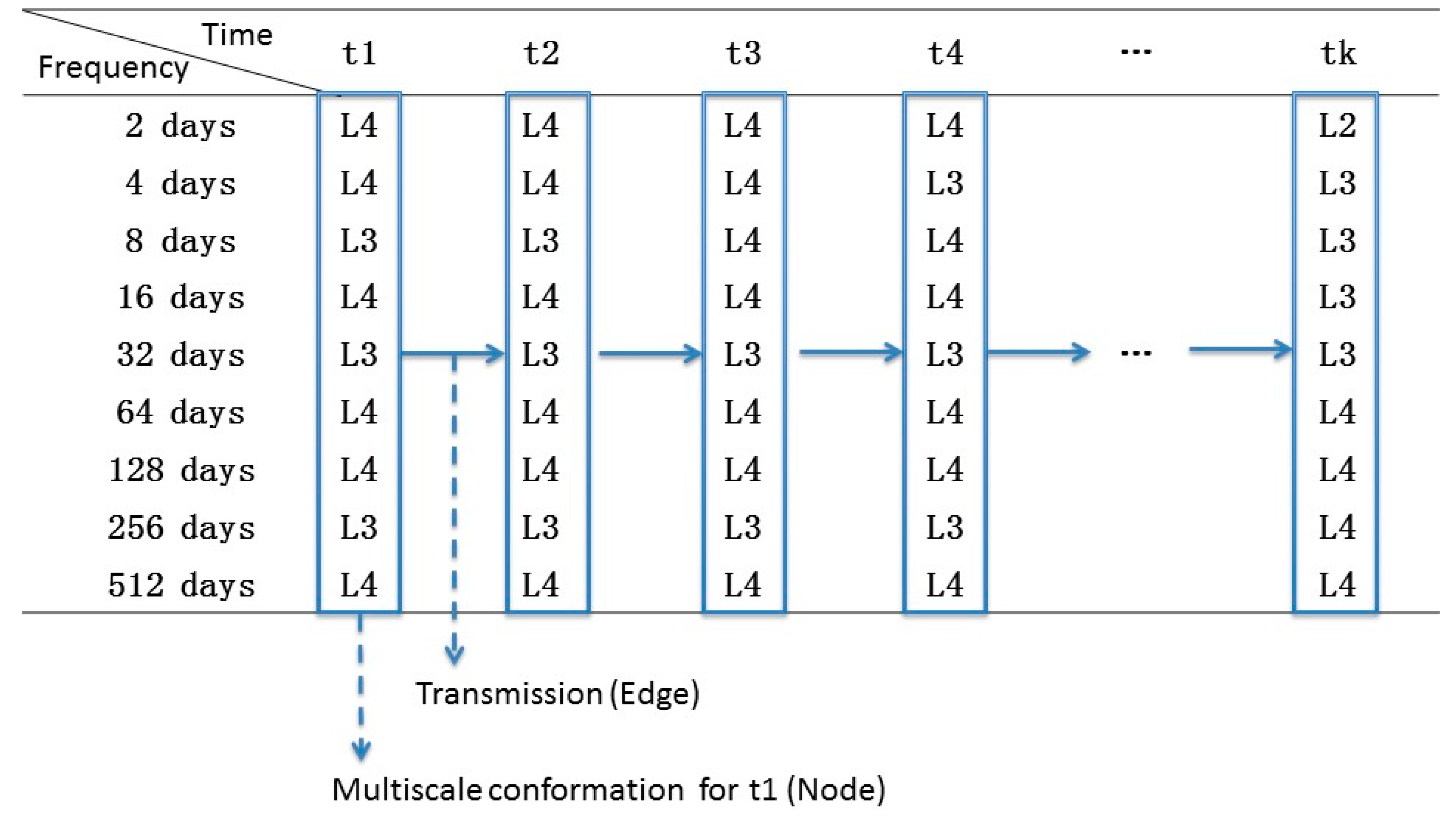
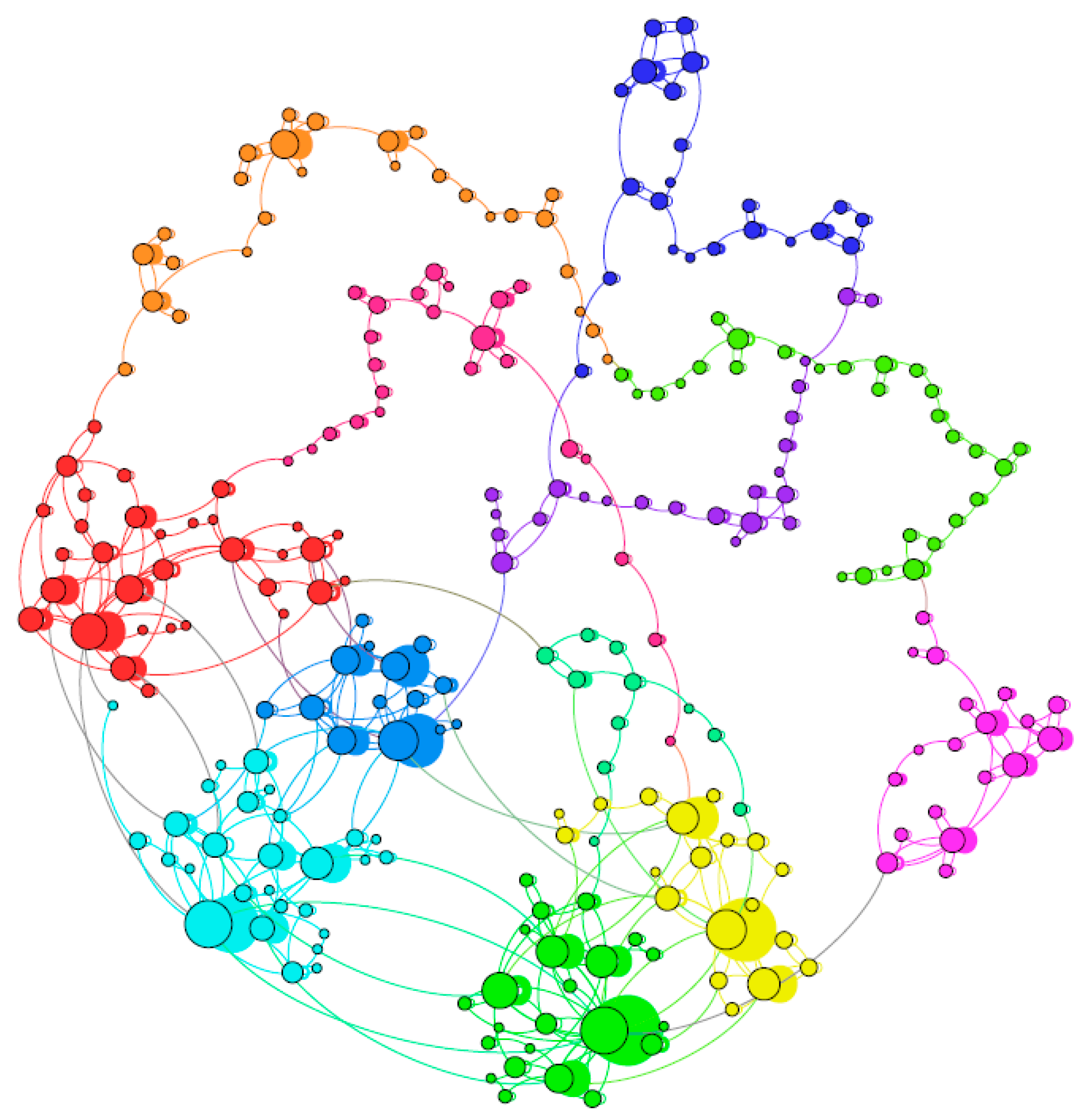
2.2.3. Construction of the Multiscale Conformation Evolution Network
- Step 1.
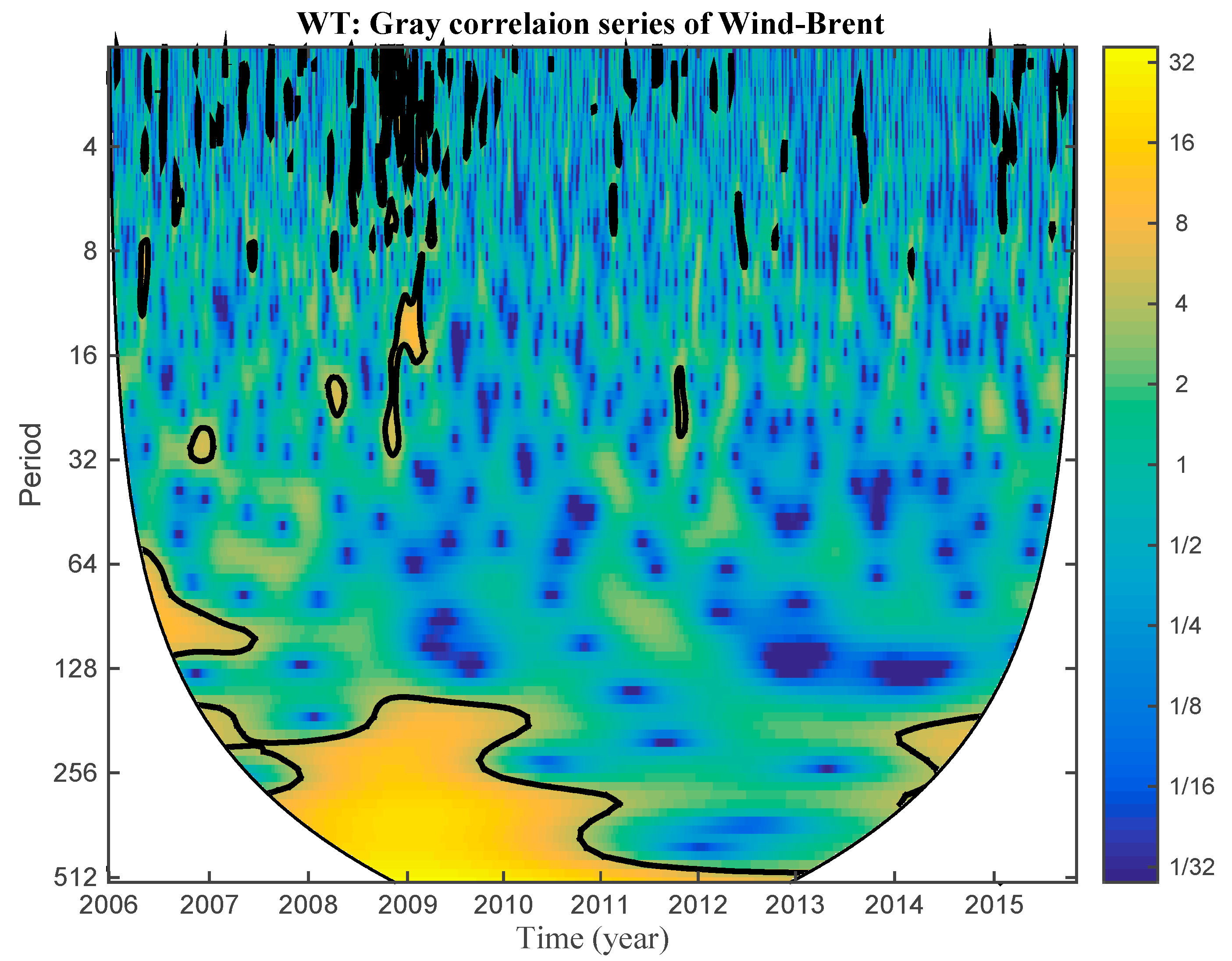
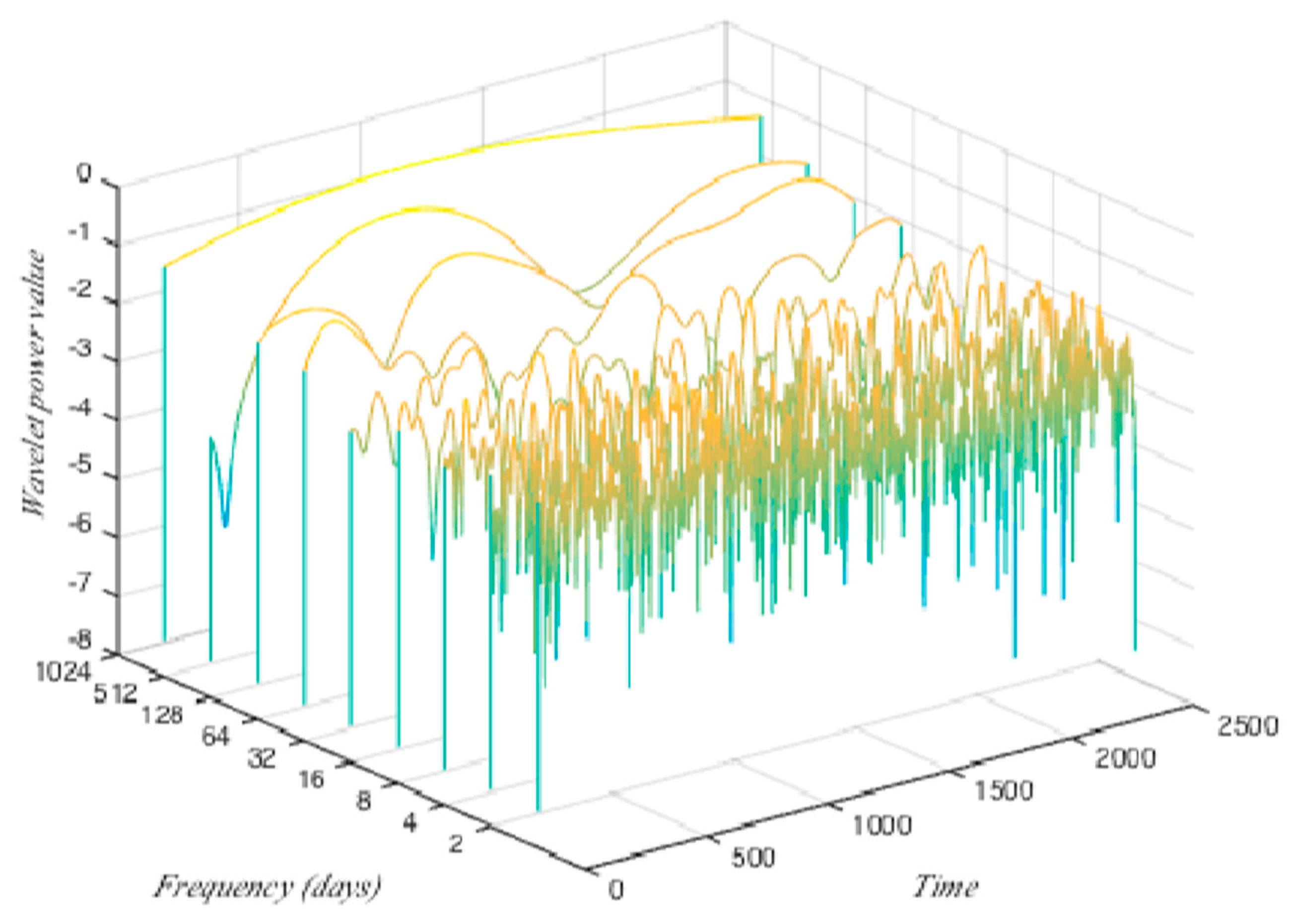
- The discretization of the wavelet power spectrum. The wavelet power spectrum shows a clearer picture of the fluctuation of the correlation of Brent–wind in detail. The frequency band of the wavelet power spectrum is continuous and rings from 2 to 512 days. Here, we choose the frequency band of 2 days, 4 days, 8 days, 16 days, 32 days, 64 days, 128 days, 256 days, and 512 days as the backbone to stand for the entire continuous frequency band according to the discretization method of the discrete wavelet transform. As mentioned, the wavelet power spectrum is a n*m matrix, where n is the number of frequency bands that constitute the continuous frequency band, and m is the number of data points. After the discretization we obtain a new matrix, the size of which is 9*m. We normalize the discretized wavelet power spectrum matrix through the logarithmic transform.
- Step 2.
- The definition of the multiscale conformation. First, we divide the values of the discretized wavelet power spectrum into four levels according to its maximum and minimum and divide the value ranges from the minimum to the maximum into four equal intervals. We also use L1, L2, L3, and L4, which mean the fluctuation is very weak, weak, high, and very high, respectively. For each time point, there are nine components from different time horizons, and the combination of them can determine the status of the original Brent–wind correlation. Here, we define the multiscale combination of nine time scales at one time point as the multiscale conformation.
- Step 3.
- Constructing an evolution network for the multiscale conformations. Taking multiscale conformations as nodes, transmissions among them as edges, we transform the series of multiscale conformations into a network. Details are shown in Figure 2. Among nodes and edges, transmissions between two types of multiscale conformations appear repetitively; therefore, we take the n umber at which these edges appear as its weight.
3. Empirical Results and Discussion
3.1. Fluctuations of Correlations of Brent–wind in the Time Domain
3.2. Decomposition in Time–Frequency Domain
3.3. Construction of the Evolution Network
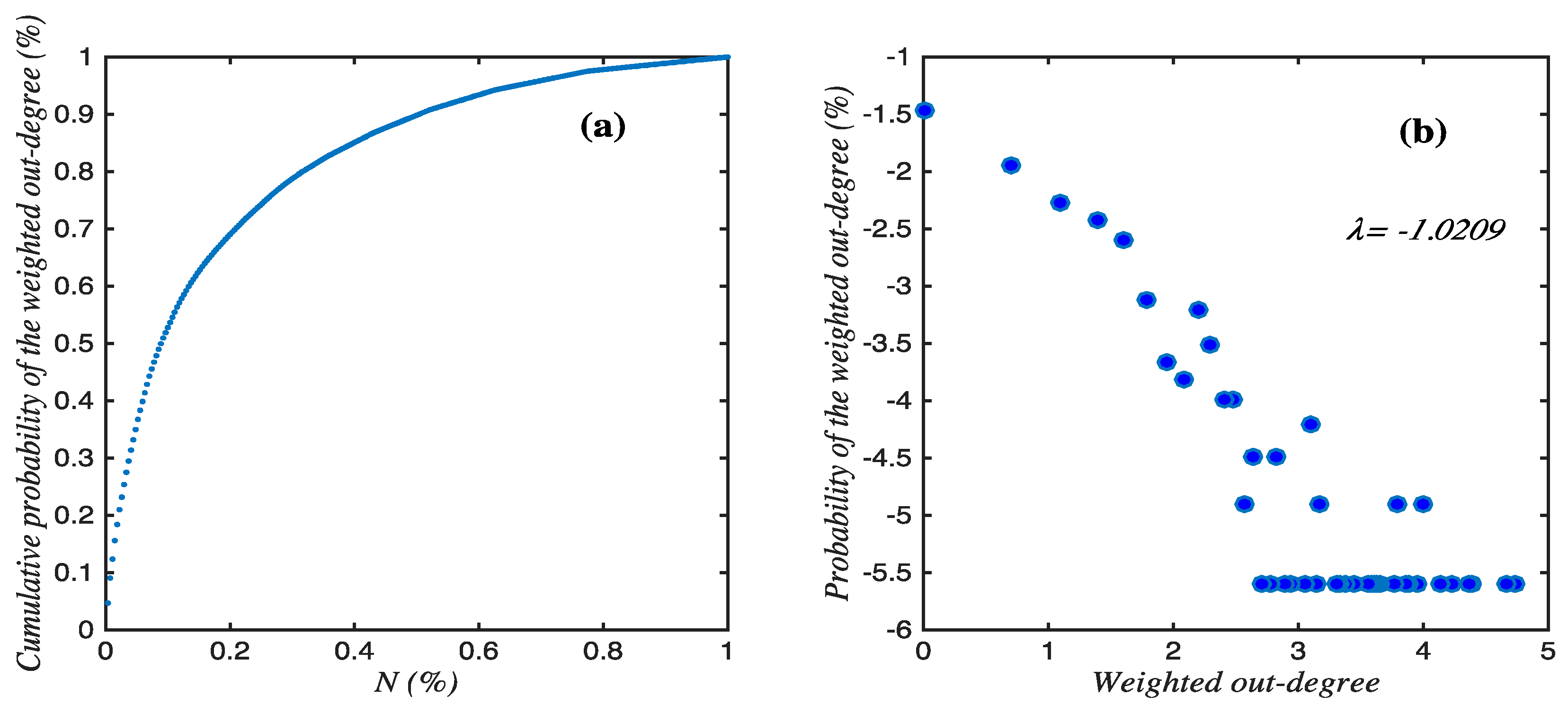
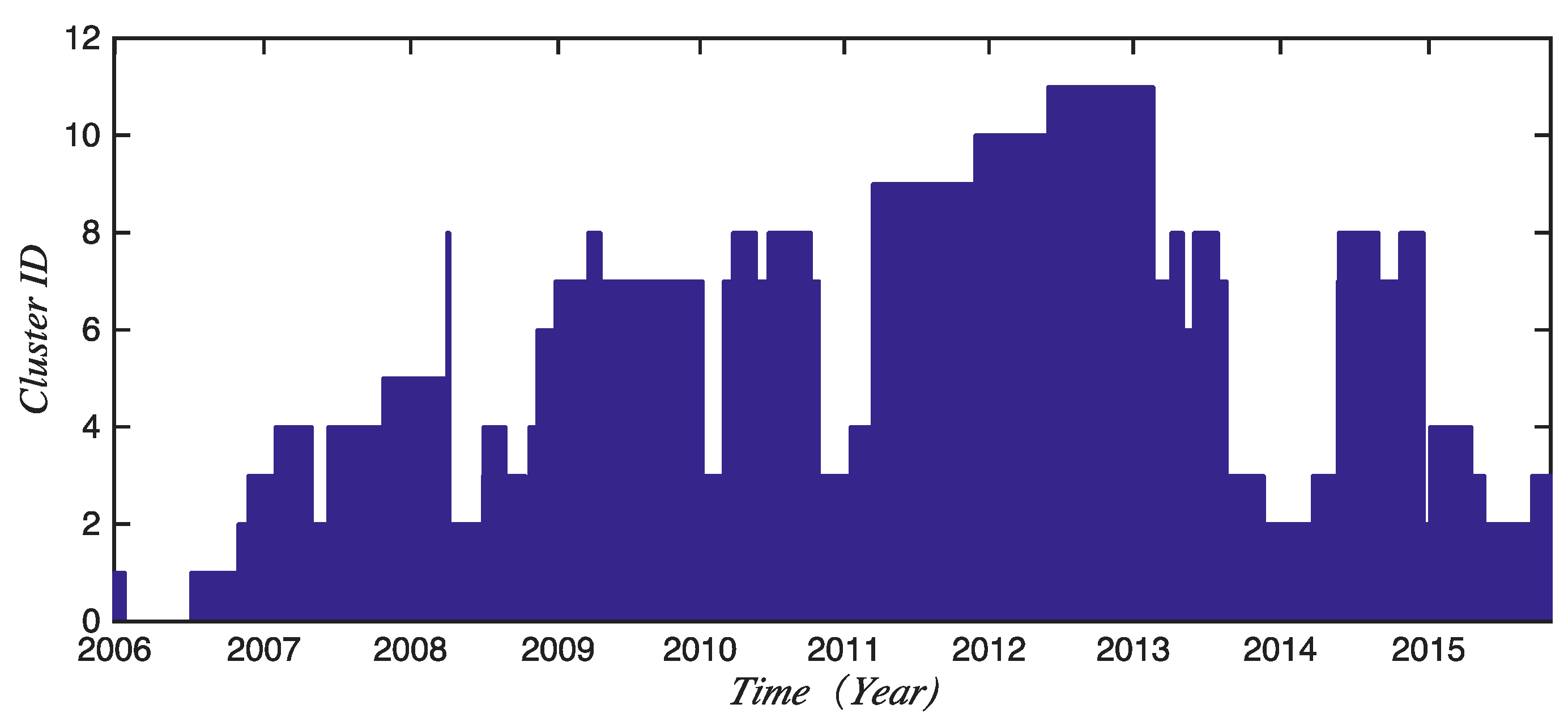
3.4. Evolution Features Analyses
3.4.1. Major Conformations and Transmissions
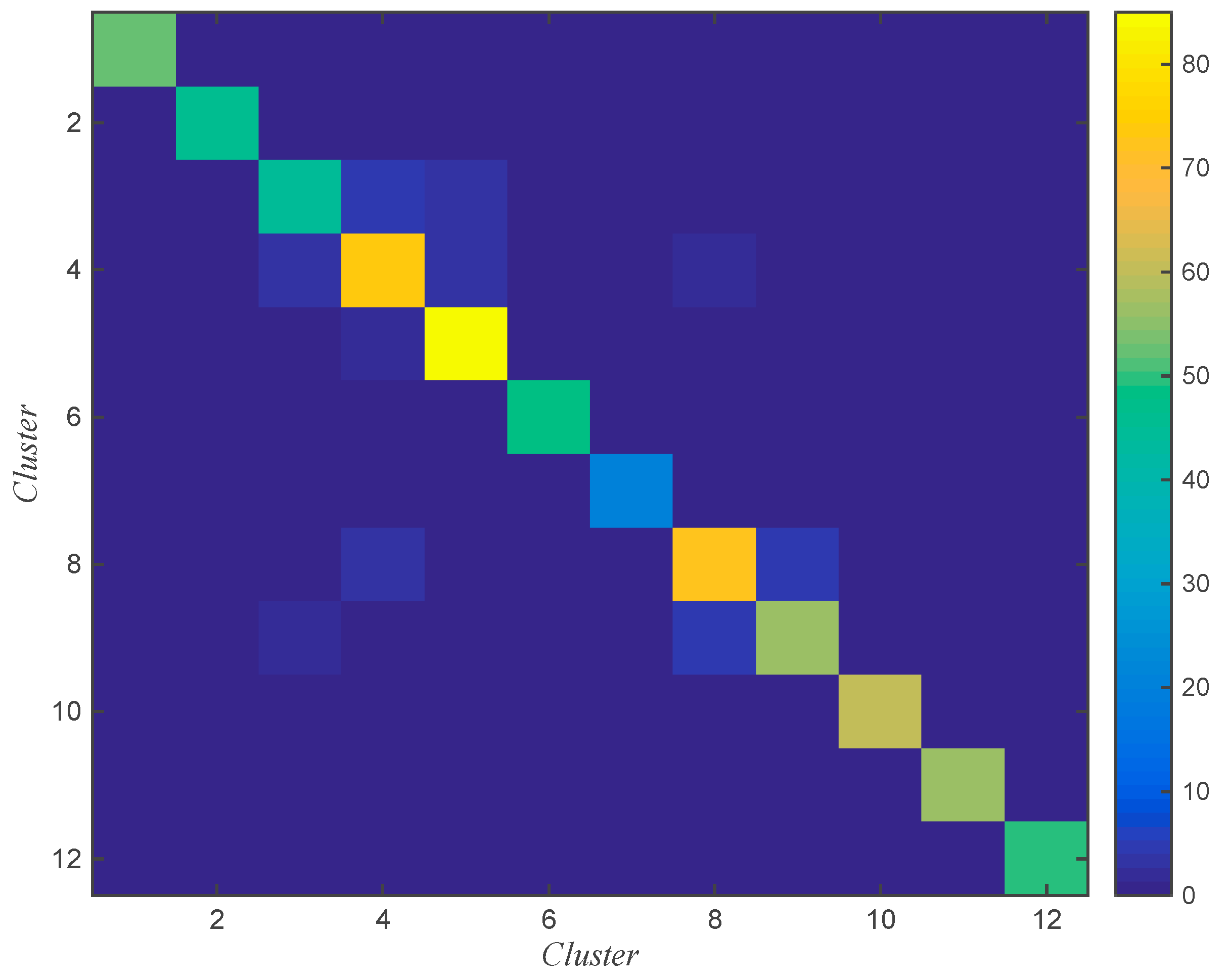
3.4.2. The Clustering Effect
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Buonocore, E.; Vanoli, L.; Carotenuto, A.; Ulgiati, S. Integrating life cycle assessment and emergy synthesis for the evaluation of a dry steam geothermal power plant in italy. Energy 2015, 86, 476–487. [Google Scholar] [CrossRef]
- European Wind Energy Association (EWEA). The Economics of Wind Energy; European Wind Energy Association (EWEA): Brussels, Belgium, 2009. [Google Scholar]
- Reboredo, J.C. Is there dependence and systemic risk between oil and renewable energy stock prices? Energy Econ. 2015, 48, 32–45. [Google Scholar] [CrossRef]
- Henriques, I.; Sadorsky, P. Oil prices and the stock prices of alternative energy companies. Energy Econ. 2008, 30, 998–1010. [Google Scholar] [CrossRef]
- Sadorsky, P. Correlations and volatility spillovers between oil prices and the stock prices of clean energy and technology companies. Energy Econ. 2012, 34, 248–255. [Google Scholar] [CrossRef]
- Sadorsky, P. Modeling renewable energy company risk. Energy Policy 2012, 40, 39–48. [Google Scholar] [CrossRef]
- Wen, X.; Guo, Y.; Wei, Y.; Huang, D. How do the stock prices of new energy and fossil fuel companies correlate? Evidence from China. Energy Econ. 2014, 41, 63–75. [Google Scholar] [CrossRef]
- Kumar, S.; Managi, S.; Matsuda, A. Stock prices of clean energy firms, oil and carbon markets: A vector autoregressive analysis. Energy Econ. 2012, 34, 215–226. [Google Scholar] [CrossRef]
- Gao, Z.K.; Yang, Y.X.; Fang, P.C.; Jin, N.D.; Xia, C.Y.; Hu, L.D. Multi-frequency complex network from time series for uncovering oil-water flow structure. Sci. Rep. 2015, 5. [Google Scholar] [CrossRef] [PubMed]
- Reboredo, J.C.; Rivera-Castro, M.A. Wavelet-based evidence of the impact of oil prices on stock returns. Int. Rev. Econ. Financ. 2014, 29, 145–176. [Google Scholar] [CrossRef]
- Vacha, L.; Barunik, J. Co-movement of energy commodities revisited: Evidence from wavelet coherence analysis. Energy Econ. 2012, 34, 241–247. [Google Scholar] [CrossRef]
- Daubechies, I. Orthonormal bases of compactly supported wavelets. Commun. Pure appl. Math. 1988, 41, 909–996. [Google Scholar] [CrossRef]
- Daubechies, I. Ten Lectures on Wavelets; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 1992; Volume 61. [Google Scholar]
- Huang, S.; An, H.; Gao, X.; Huang, X. Time–frequency featured co-movement between the stock and prices of crude oil and gold. Phys. A Stat. Mech. Appl. 2015, 444, 985–995. [Google Scholar] [CrossRef]
- Huang, S.; An, H.; Gao, X.; Huang, X. Identifying the multiscale impacts of crude oil price shocks on the stock market in china at the sector level. Phys. A Stat. Mech. Appl. 2015, 434, 13–24. [Google Scholar] [CrossRef]
- Huang, X.; An, H.; Gao, X.; Hao, X.; Liu, P. Multiresolution transmission of the correlation modes between bivariate time series based on complex network theory. Phys. Stat. Mech. Appl. 2015, 428, 493–506. [Google Scholar] [CrossRef]
- Aguiar-Conraria, L.; Soares, M.J. The continuous wavelet transform: Moving beyond uni- and bivariate analysis. J. Econ. Surv. 2014, 28, 344–375. [Google Scholar] [CrossRef]
- Crowley, P.M. A guide to wavelets for economists. J. Econ. Surv. 2007, 21, 207–267. [Google Scholar] [CrossRef]
- Jammazi, R. Cross dynamics of oil-stock interactions: A redundant wavelet analysis. Energy 2012, 44, 750–777. [Google Scholar] [CrossRef]
- Jammazi, R.; Aloui, C. Wavelet decomposition and regime shifts: Assessing the effects of crude oil shocks on stock market returns. Energy Policy 2009, 38, 1415–1435. [Google Scholar] [CrossRef]
- Jia, X.; An, H.; Fang, W.; Sun, X.; Huang, X. How do correlations of crude oil prices co-move? A grey correlation-based wavelet perspective. Energy Econ. 2015, 49, 588–598. [Google Scholar] [CrossRef]
- Gallegati, M. Wavelet analysis of stock returns and aggregate economic activity. Comput. Stat. Data Anal. 2008, 52, 3061–3074. [Google Scholar] [CrossRef]
- Gallegati, M. A wavelet-based approach to test for financial market contagion. Comput. Stat. Data Anal. 2012, 56, 3491–3497. [Google Scholar] [CrossRef]
- Huang, S.; An, H.; Gao, X.; Hao, X.; Huang, X. The multiscale conformation evolution of the financial time series. Math. Probl. Eng. 2015, 2015, 563145. [Google Scholar] [CrossRef]
- Gao, X.Y.; An, H.Z.; Fang, W.; Huang, X.; Li, H.J.; Zhong, W.Q. Characteristics of the transmission of autoregressive sub-patterns in financial time series. Sci. Rep. 2014, 4. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.Y.; An, H.Z.; Fang, W.; Huang, X.; Li, H.J.; Zhong, W.Q.; Ding, Y.H. Transmission of linear regression patterns between time series: From relationship in time series to complex networks. Phys. Rev. E 2014, 90. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.-K.; Zhang, X.-W.; Jin, N.-D.; Donner, R.V.; Marwan, N.; Kurths, J. Recurrence networks from multivariate signals for uncovering dynamic transitions of horizontal oil-water stratified flows. EPL 2013, 103. [Google Scholar] [CrossRef]
- Gao, Z.K.; Ding, M.S.; Geng, H.; Jin, N.D. Multivariate multiscale entropy analysis of horizontal oil-water two-phase flow. Phys. Stat. Mech. Appl. 2015, 417, 7–17. [Google Scholar] [CrossRef]
- Gao, Z.K.; Fang, P.C.; Ding, M.S.; Jin, N.D. Multivariate weighted complex network analysis for characterizing nonlinear dynamic behavior in two-phase flow. Exp. Therm. Fluid Sci. 2015, 60, 157–164. [Google Scholar] [CrossRef]
- Lacasa, L.; Luque, B.; Ballesteros, F.; Luque, J.; Nuno, J.C. From time series to complex networks: The visibility graph. Proc. Natl. Acad. Sci. USA 2008, 105, 4972–4975. [Google Scholar] [CrossRef] [PubMed]
- Zanin, M.; Sousa, P.; Papo, D.; Bajo, R.; García-Prieto, J.; Del, P.F.; Menasalvas, E.; Boccaletti, S. Optimizing functional network representation of multivariate time series. Sci. Rep. 2012, 2, 630. [Google Scholar] [CrossRef] [PubMed]
- Marwan, N.; Donges, J.F.; Zou, Y.; Donner, R.V.; Kurths, J. Complex network approach for recurrence analysis of time series. Phys. Lett. A 2009, 373, 4246–4254. [Google Scholar] [CrossRef]
- Donner, R.V.; Small, M.; Donges, J.F.; Marwan, N.; Zou, Y.; Xiang, R.; Kurths, J. Recurrence-based time series analysis by means of complex network methods. Int. J. Bifurc. Chaos 2011, 21, 1019–1046. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, J.; Small, M. Superfamily phenomena and motifs of networks induced from time series. Proc. Natl. Acad. Sci. USA 2008, 105, 19601–19605. [Google Scholar] [CrossRef] [PubMed]
- Kilian, L. The impact of the shale oil revolution on us oil and gasoline prices. Available online: http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2538422 (accessed on 31 May 2016).
- Deng, J. Introduction to grey mathematical resources. J. Grey Syst. 2008, 20, 87–92. [Google Scholar]
- Deng, J.L. Control problems of grey systems. Syst. Control. Lett. 1982, 1, 288–294. [Google Scholar]
- Chang, T.C.; Lin, S.J. Grey relation analysis of carbon dioxide emissions from industrial production and energy uses in taiwan. J. Environ. Manag. 1999, 56, 247–257. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of community hierarchies in large networks. J. Stat. Mech. 2008. [Google Scholar] [CrossRef]

| No. | Conformations | Weighted Out-Degree | Percentage (%) Accounts for Total Weighted Out-Degree |
|---|---|---|---|
| 1 | L3L3L3L3L3L3L4L4L4 | 649 | 4.69 |
| 2 | L3L3L3L4L3L3L4L4L4 | 291 | 4.37 |
| 3 | L3L3L3L3L3L4L4L4L4 | 228 | 3.31 |
| 4 | L3L3L4L4L3L4L4L4L4 | 152 | 3.22 |
| 5 | L3L3L3L4L3L4L4L4L4 | 151 | 2.82 |
| 6 | L3L3L4L4L3L3L4L4L4 | 149 | 2.57 |
| 7 | L3L3L3L3L4L4L4L4L4 | 115 | 2.20 |
| 8 | L3L4L3L3L3L3L4L4L4 | 101 | 2.20 |
| 9 | L3L3L4L3L3L4L4L4L4 | 99 | 2.12 |
| 10 | L3L3L4L3L3L3L4L4L4 | 99 | 1.96 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, S.; An, H.; Gao, X.; Jiang, M. The Multiscale Fluctuations of the Correlation between Oil Price and Wind Energy Stock. Sustainability 2016, 8, 534. https://doi.org/10.3390/su8060534
Huang S, An H, Gao X, Jiang M. The Multiscale Fluctuations of the Correlation between Oil Price and Wind Energy Stock. Sustainability. 2016; 8(6):534. https://doi.org/10.3390/su8060534
Chicago/Turabian StyleHuang, Shupei, Haizhong An, Xiangyun Gao, and Meihui Jiang. 2016. "The Multiscale Fluctuations of the Correlation between Oil Price and Wind Energy Stock" Sustainability 8, no. 6: 534. https://doi.org/10.3390/su8060534
APA StyleHuang, S., An, H., Gao, X., & Jiang, M. (2016). The Multiscale Fluctuations of the Correlation between Oil Price and Wind Energy Stock. Sustainability, 8(6), 534. https://doi.org/10.3390/su8060534







