Optimal Partner Combination for Joint Distribution Alliance using Integrated Fuzzy EW-AHP and TOPSIS for Online Shopping
Abstract
:1. Introduction
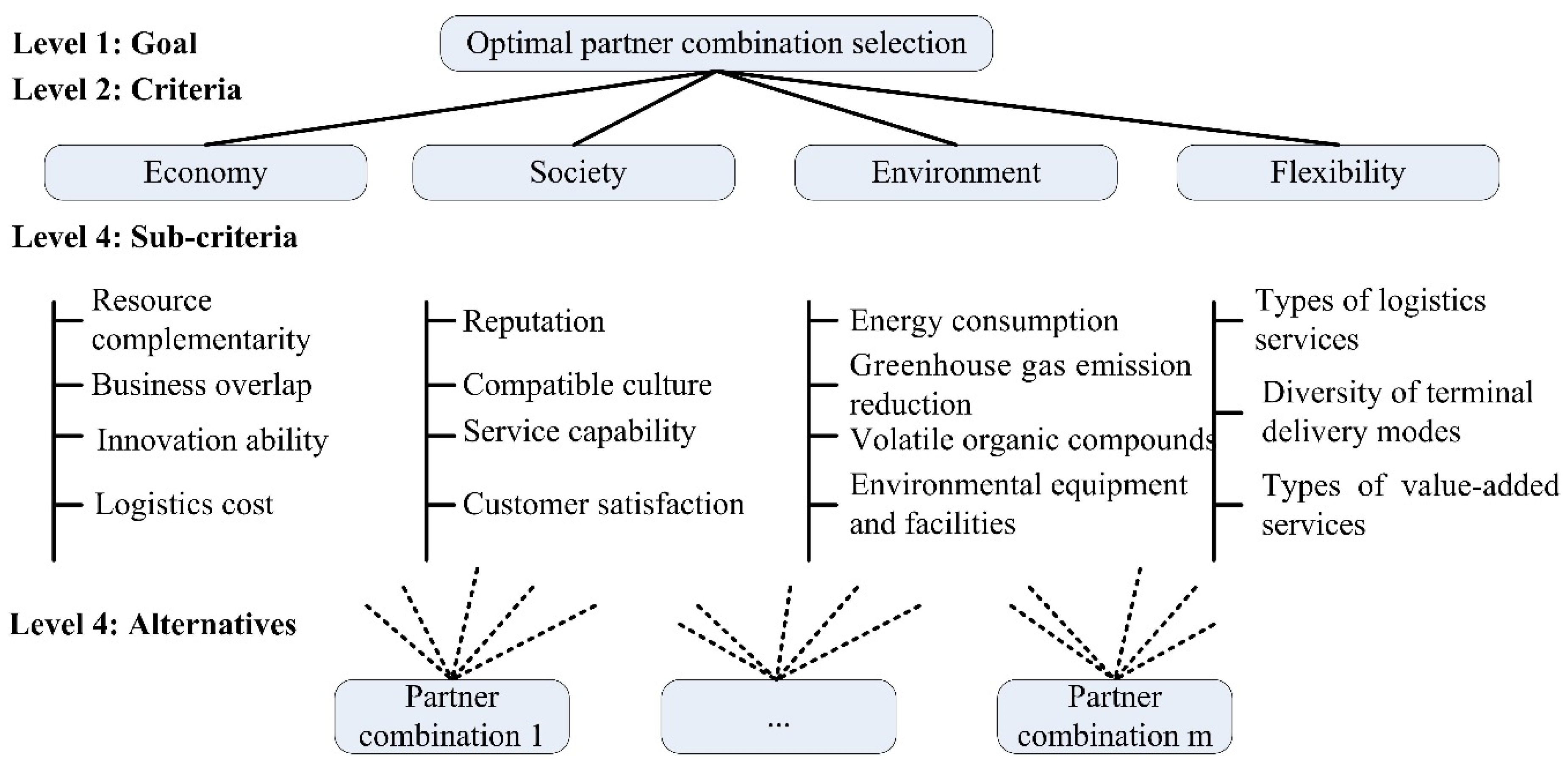
2. Identifying the Evaluation Criteria Based on an ESEF Framework
2.1. Economic Criteria
- (1)
- (2)
- Business overlap (C2): Refers to the degree of similarity in business among these alternatives. The more similar the business is, the fiercer the competition is among partners. Therefore, the large similarity of business among these alternatives can have a negative impact on the sustainability and stability of the alliance.
- (3)
- Innovation ability (C3): Refers to the management of the innovation and technology of enterprises. The alliance that consists of enterprises with strong innovation ability are vastly more competitive [36].
- (4)
- Logistic costs (C4): Includes transportation, warehouse, management and information process costs.
2.2. Societal Criteria
- (1)
- Reputation (C5): Refers to the social assessment of enterprises. Reputation will be one of the key factors for the future stability and successful implementation of an alliance [50].
- (2)
- Compatible culture (C6): Refers to the similarity and openness of enterprise culture. Compatible culture, which has a significant positive effect on the stability and sustainability of an alliance, is viewed as fundamental in the decision-making process [51].
- (3)
- Service capability (C7): Refers to the number of orders that can be completed by partner combinations.
- (4)
- Customer satisfaction (C8): Refers to customer satisfaction levels, one of the most important criteria in the optimal partner combination selection.
2.3. Environmental Criteria
- (1)
- Energy consumption (C9): Measures the energy consumption when completing a certain number of orders.
- (2)
- Greenhouse gas (GHG) emission reduction (C10): The partner combination consisting of these environmental enterprises will emit fewer environmental pollutants (such as CO2 and CH4) in their daily operations [46]. Therefore, the criteria measures the GHG emission reductions of different partner combinations under the same conditions.
- (3)
- Volatile organic compounds (VOCs) (C11): Measures the VOCs emissions from warehouse activities, packing of all mail orders, transportation activities and so on. Since 2015 China has fined enterprises which emit VOCs [52].
- (4)
- Environmental equipment and facilities (C12): Measures the number of orders which are completed by environmental equipment and facilities.
2.4. Flexibility Criteria
- (1)
- Types of logistics services (C13): In general, this refers to the coverage of customer demand for online shopping logistics services. Nowadays, the online shopping logistics mode is shifting from cost-centralized to customer-centralized. The more types of logistics services, the greater coverage of customer demand [6].
- (2)
- (3)
- Types of value-added services (C15): Other than logistics services, some value-added services such as payment collection, product’s package and labeling are offered.
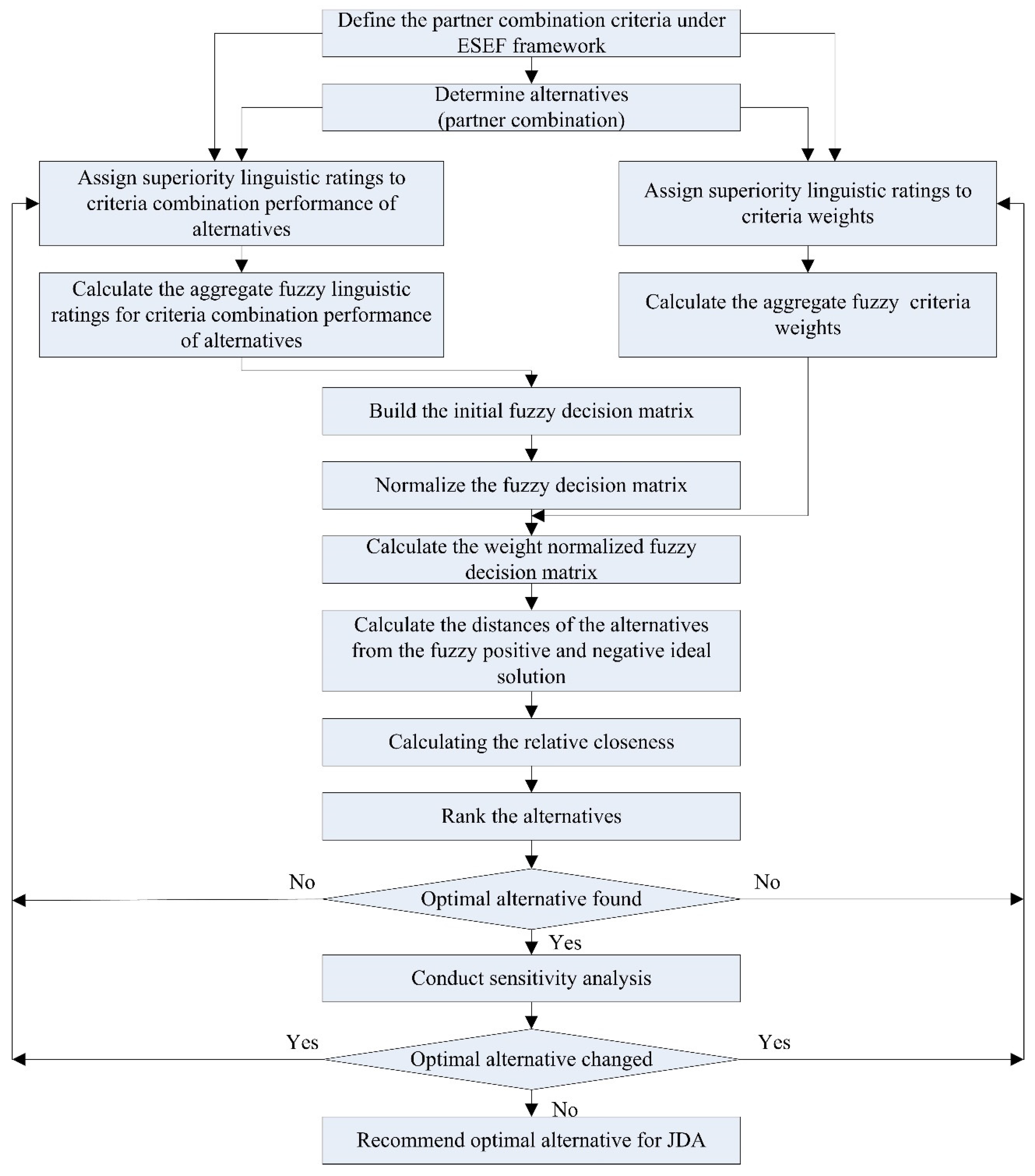
3. The Integrated Fuzzy EW-AHP and TOPSIS Method for Partner Combination Selection
3.1. Fuzzy Set Theory
3.2. Integrated Fuzzy EW-AHP for Determining Criteria Weights
- Step 1:
- Let , , be the superiority linguistic rating on criteria weight assigned to criteria by decision-maker . Assume that is the converted value via . Then the fuzzy entropy can be calculated by:
- Step 2:
- Calculate the fuzzy EW
- Step 3:
- Calculate the criteria weight using the fuzzy AHP considering the subjective factors. Details of calculation process of fuzzy AHP method can be referred to the study of Felix et al. [25].
- Step 4:
- Calculate the final weight by integrating the fuzzy EW and fuzzy AHPwhere .
3.3. Fuzzy TOPSIS Method
- Step 1:
- Calculate the aggregate fuzzy linguistic ratings for combination performance of alternatives.Let us consider a set of alternatives (partner combinations) which are to be evaluated against a set of criteria . The combination performances of criteria are defined in linguistic terms that can be obtained from experts. Let , be combination performance linguistic rating of expert for each alternative with respect to criteria . Then the fuzzy linguistic rating , , , for criteria of alternative can be calculated by:
- Step 2:
- Build the initial fuzzy decision matrix.According to Equation (6), the initial fuzzy decision matrix can be built.
- Step 3:
- Normalize the fuzzy decision matrix.In general, there are two kinds of attributes namely benefit-type and cost-type in the criteria. For the benefit-type criteria, the larger the better, such as resource complementarity; for the cost-type criteria, the smaller the better, such logistics cost. Therefore, the normalization processing on the different kinds of criteria needs to be first performed [18,61].For benefit-type criteria, the normalization processing is expressed as:For cost-type criteria, the normalization processing is expressed as:Then, the normalized fuzzy decision matrix can be obtained as:
- Step 4:
- Determine the integrated fuzzy weights of criteria.The integrated fuzzy weight of criteria can be calculated using Equations (2)–(5).
- Step 5:
- Calculate the weight normalized fuzzy decision matrix.The weight normalized fuzzy decision matrix can be calculated using Equation (11).
- Step 6:
- Calculate the distances of the alternatives from the fuzzy positive and negative ideal solution.
- Step 6.1:
- Determine the fuzzy positive ideal solution and negative ideal solution.Suppose that and respectively represent the benefit-type criteria set and cost-type criteria set. and represent the fuzzy positive ideal solution and negative ideal solution, respectively. Then, and can be calculated bywhere
- Step 6.2:
- Calculate the distances.In this paper, a modified geometrical distance method is employed which can reflect more information of experts with uncertainty than the Euclidean distance [62]. The distance between two triangular fuzzy numbers and can be calculated bywhere and are the uncertainty degree of the two triangular fuzzy numbers and , and , .Therefore, the distance of alternative from the fuzzy positive and negative ideal solution can be calculated by
- Step 7:
- Calculate the relative closeness of alternative to the ideal solution
- Step 8:
- Rank the alternatives on the basis of relative closeness to the ideal solution.According to the calculation results in Step 7, the alternative with the greatest to the ideal solution should be selected as the optimal partner combination.
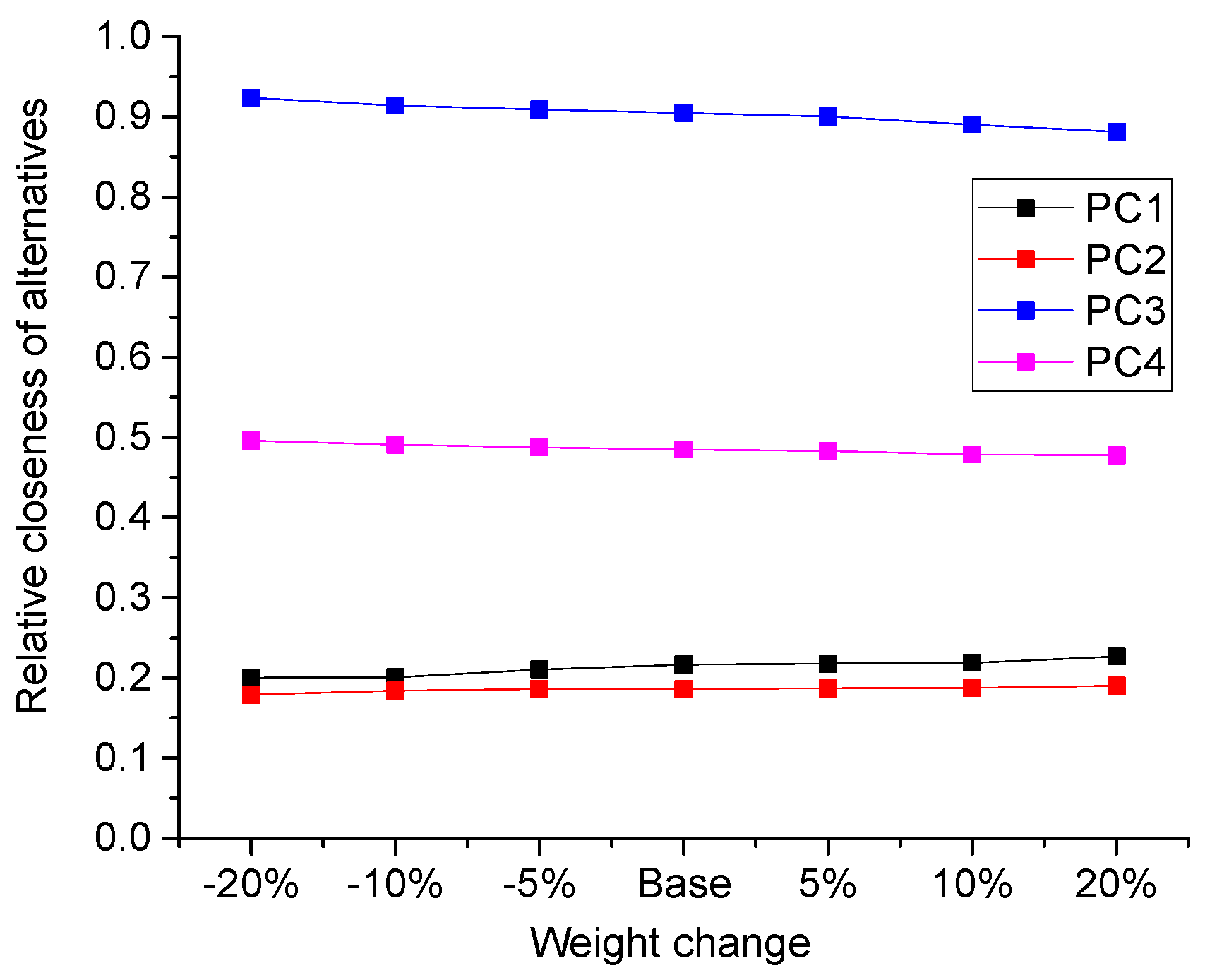
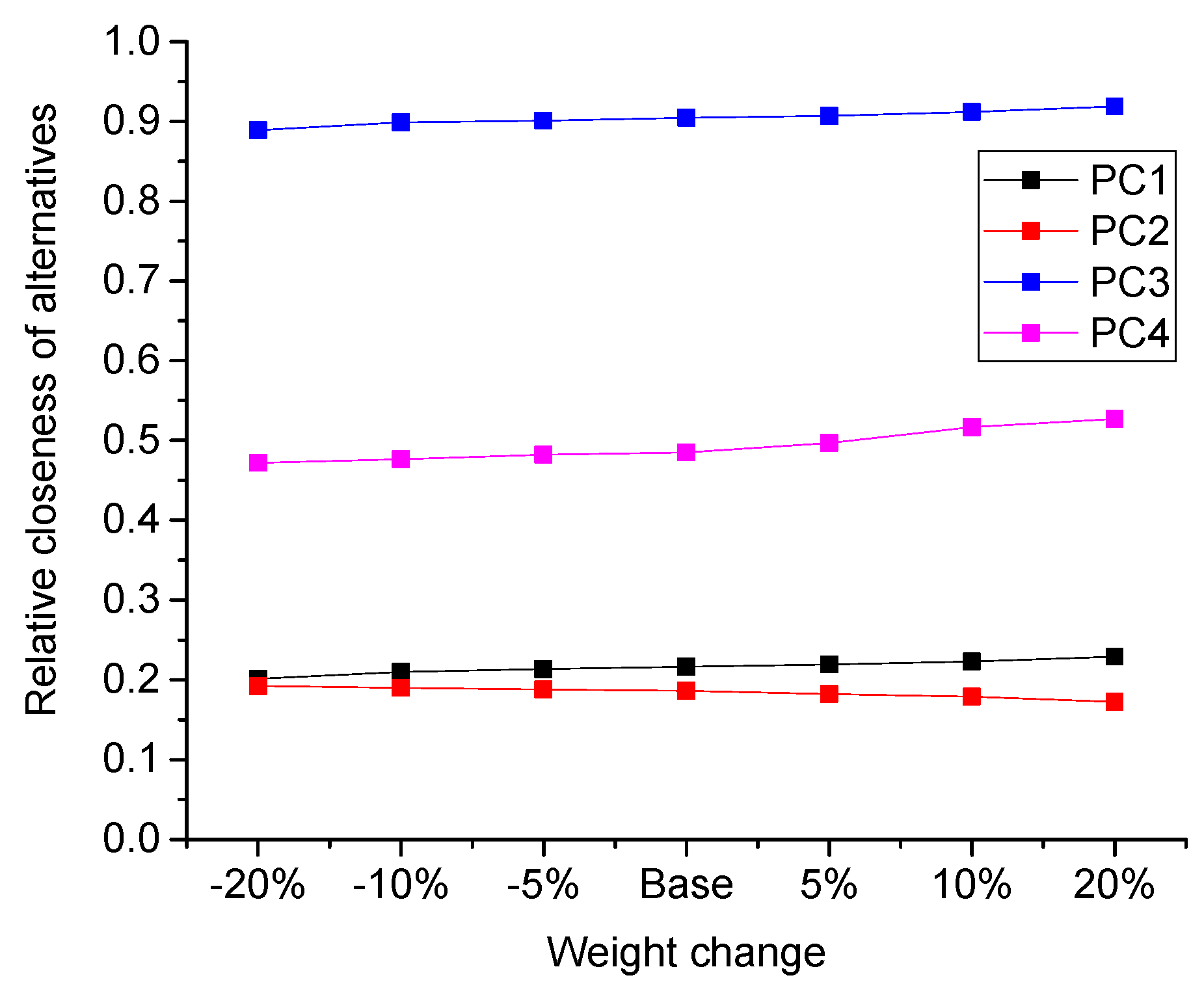
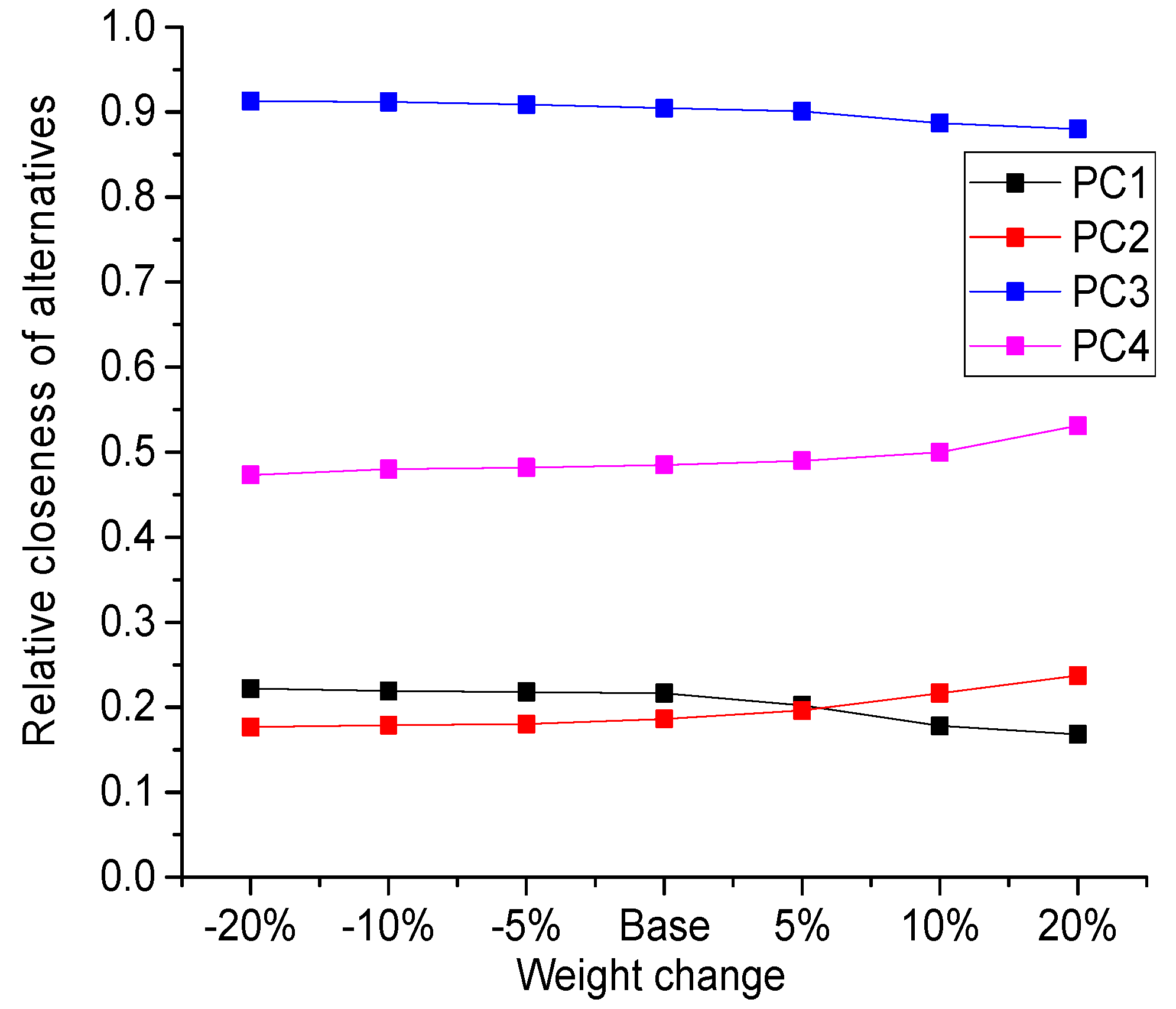
3.4. Sensitivity Analysis
- (1)
- The sub-criteria has 5%, 10%, 20% less weight and 5%, 10%, 20% more weight than the base weight (i.e., the weight obtained in Section 3.2.) in economy criteria.
- (2)
- The sub-criteria has 5%, 10%, 20% less weight and 5%, 10%, 20% more weight than the base weight in society criteria.
- (3)
- The sub-criteria has 5%, 10%, 20% less weight and 5%, 10%, 20% more weight than the base weight in environment criteria.
- (4)
- The sub-criteria has 5%, 10%, 20% less weight and 5%, 10%, 20% more weight than the base weight in flexibility criteria.
4. Numerical Application
- Step 1:
- The linguistic ratings for criteria weights and partner combination performance are obtained according to expert opinion.In order to obtain the linguistic ratings, five groups of expert panels () in the fields of economy, environment, society, logistics, and e-commerce were formed. Each group of expert panel gave the linguistic ratings judgments for the criteria weights and combination performance of each alternative, as can be seen in Table 3 and Table 4.
- Step 2:
- Step 3:
- According to Table 2 and Equations (6) and (7), the initial fuzzy decision matrix can be obtained:
- Step 4:
- The weighted normalized fuzzy decision matrix is calculated using Equations (8)–(11).Among the fifteen criteria, C1, C3, C5, C6, C7, C8, C10, C12, C13, C14 and C15 are benefit-type criteria; C2, C4, C9 and C11 are cost-type criteria. To obtain the normalized fuzzy decision matrix and weighted normalized fuzzy decision matrix , we use Equations (8)–(11). For example, the benefit-type criteria C1 is normalized using Equation (8) as follows:.Then = (0.667,0.667,1). Applying Equation (11) for criteria C1, we get = (0.020,0.025,0.045). Here, refers to the combination performance of alternative 1 with respect to criteria 1 in the normalized fuzzy decision matrix, and refers to the combination performance of alternative 1 with respect to criteria 1 in the weight normalized fuzzy decision matrix.Other elements in weighted normalized fuzzy decision matrix can be calculated in the same way. Therefore, the weighted normalized fuzzy decision matrix is obtained as below:
- Step 5:
- The distances of the alternatives from the fuzzy positive and negative ideal solution are calculated.The fuzzy positive and negative ideal solution can be calculated using Equations (12) and (13), and the distances and of alternative from the fuzzy positive and negative ideal solution can be calculated using Equations (14)–(16), i.e.,
- Step 6:
- The relative closeness of alternatives to the ideal solution is calculated.Finally, the relative closeness of alternative to the ideal solution can be calculated using Equation (17):
- Step 7:
- On the basis of relative closeness, the four alternatives are ranked as follows:It is seen above that the partner combination ranks first, so , namely the partner combination CQ, RK and ML, should be selected as the optimal alternative.
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Qin, K. Study on consumption trends of 11.11 under Internet in China. Electron. Commer. 2016, 1, 1–2. [Google Scholar]
- Yu, B.; Wu, S.; Du, G. Branch Model Simulation for Express Logistics Service System Evaluation under Online Shopping. Chin. J. Manag. Sci. 2014, 22, 72–78. [Google Scholar]
- Ramanathan, R. The moderating roles of risk and efficiency on the relationship between logistics performance and customer loyalty in e-commerce. Transp. Res. Part E 2010, 46, 950–962. [Google Scholar] [CrossRef]
- Xu, S.X.; Cheng, M.; Huang, G.Q. Efficient intermodal transportation auctions for B2B e-commerce logistics with transaction costs. Transp. Res. Part B Methodol. 2015, 80, 322–337. [Google Scholar] [CrossRef]
- Daly, S.P.; Cui, L.X. E-logistics in China: Basic problems, manageable concerns and intractable solutions. Ind. Mark. Manag. 2003, 3, 235–242. [Google Scholar] [CrossRef]
- Wang, X.; Zhan, L.; Ruan, J.; Zhang, J. How to Choose “Last Mile” Delivery Modes for E-Fulfillment. Math. Probl. Eng. 2014, 1, 1–11. [Google Scholar] [CrossRef]
- National Urban Distribution Development Guidelines. Available online: http://paper.ce.cn/jjrb/html/2013–10/28/content_175334.htm (accessed on 28 October 2013).
- Medium and Long Term Development Plan for Logistics. Available online: http://www.gov.cn/zhengce/content/2014–10/04/content_9120.htm (accessed on 4 October 2014).
- Zhang, X. Joint Distribution Patterns and Decision-Making Paths for Terminal Logistics: Based on Supply and Demand Analysis of Electric Business Logistics and Community Service. Res. Financ. Econ. Issues 2013, 3, 123–129. [Google Scholar]
- Ge, X.; Wang, X.; Deng, L. Research on Open and Dynamic Vehicle Routing Problems Based on Joint Distribution. J. Ind. Eng. Eng. Manag. 2013, 27, 60–68. [Google Scholar]
- Zhou, J.; Zhong, X. TAOBAO Logistics Model Based on Joint Distribution// LISS 2014; Springer: Berlin/Heidelberg, Germany, 2015; pp. 29–33. [Google Scholar]
- Adetiloye, T.O. Collaboration Planning of Stakeholders for Sustainable City Logistics Operations; Concordia University: Montreal, Canada, 2012. [Google Scholar]
- Wei, Z.L.; Sun, J.Q. A City-based Joint Distribution Model for Small and Medium-Sized Electronic Enterprises. J. Beijing Jiaotong Univ. 2015, 14, 104–110. [Google Scholar]
- Yang, P.J.; Hao, H.U.; Wang, J.J.; An, F. Location Model for Terminals of Urban Distribution under E-commerce Environment. Ind. Eng. Manag. 2014, 19, 35–40. [Google Scholar]
- Zhang, Q. Research on Optimizing Scheme for City Logistics Based on Joint Distribution. China Soft Sci. 2009, S1, 290–295. [Google Scholar]
- Zhang, X.; Yuan, Z. The Platform and Collaborative Operating Model of “Wisdom Cloud Logistics” in Online Shopping Era. Forum Sci. Technol. China. 2013, 7, 99–104. [Google Scholar]
- Zhou, L.; Lin, Y.; Wang, X.; Zhao, Q.W. Research on capacitated multiclass terminal location-heterogeneous vehicle routing for urban distribution under online shopping. Comput. Integr. Manuf. Syst. 2016, in press. [Google Scholar]
- Awasthi, A.; Adetiloye, T.; Crainic, T.G. Collaboration partner selection for city logistics planning under municipal freight regulations. Appl. Math. Model. 2015, 40, 510–525. [Google Scholar] [CrossRef]
- Cruijssen, F.; Cools, M.; Dullaert, W. Horizontal cooperation in logistics: Opportunities and impediments. Transp. Res. Part E Logist. Transp. Rev. 2007, 43, 129–142. [Google Scholar] [CrossRef]
- Castro, I.; Casanueva, C.; Galán, J.L. Dynamic evolution of alliance portfolios. Eur. Manag. J. 2014, 32, 423–433. [Google Scholar] [CrossRef]
- Kahraman, C.; Onar, S.C.; Oztaysi, B. Fuzzy Multicriteria Decision-Making: A Literature Review. Int. J. Comput. Intell. Syst. 2015, 8, 637–666. [Google Scholar] [CrossRef]
- Mardani, A.; Jusoh, A.; Zavadskas, E.K. Fuzzy multiple criteria decision-making techniques and applications—Two decades review from 1994 to 2014. Expert Syst. Appl. 2015, 42, 4126–4148. [Google Scholar] [CrossRef]
- Mardani, A.; Jusoh, A.; MD Nor, K.; Khalifah, Z.; Zakwan, N.; Valipour, A. Multiple criteria decision-making techniques and their applications–a review of the literature from 2000 to 2014. Econ. Res. Ekonomska Istraživanja 2015, 28, 516–571. [Google Scholar] [CrossRef]
- Chan, F.T.S.; Kumar, N.; Tiwari, M.K.; Lau, H.C.W.; Choy, K.L. Global supplier selection: A fuzzy-AHP approach. Int. J. Prod. Res. 2008, 46, 3825–3857. [Google Scholar] [CrossRef]
- Behzadian, M.; Kazemzadeh, R.B.; Albadvi, A.; Aghdasi, M. PROMETHEE: A comprehensive literature review on methodologies and applications. Eur. J. Oper. Res. 2010, 200, 198–215. [Google Scholar] [CrossRef]
- Behzadian, M.; Khanmohammadi Otaghsara, S.; Yazdani, M.; Ignatius, J. A state-of the-art survey of TOPSIS applications. Expert Syst. Appl. 2012, 39, 13051–13069. [Google Scholar] [CrossRef]
- Mardani, A.; Zavadskas, E.K.; Govindan, K.; Amat Senin, A.; Jusoh, A. VIKOR Technique: A Systematic Review of the State of the Art Literature on Methodologies and Applications. Sustainability 2016, 8, 37. [Google Scholar] [CrossRef]
- Govindan, K.; Jepsen, M.B. ELECTRE: A comprehensive literature review on methodologies and applications. Eur. J. Oper. Res. 2016, 250, 1–29. [Google Scholar] [CrossRef]
- Chen, S.H.; Wang, P.W.; Chen, C.M.; Lee, H.T. An analytic hierarchy process approach with linguistic variables for selection of an R&D strategic alliance partner. Comput. Ind. Eng. 2010, 58, 278–287. [Google Scholar]
- Liao, H.; Xu, Z.; Zeng, X.J. Hesitant fuzzy linguistic VIKOR method and its application in qualitative multiple criteria decision making. IEEE Trans. Fuzzy Syst. 2015, 23, 1343–1355. [Google Scholar] [CrossRef]
- Feng, B.; Fan, Z.P.; Ma, J. A method for partner selection of codevelopment alliances using individual and collaborative utilities. Int. J. Prod. Econ. 2010, 124, 159–170. [Google Scholar] [CrossRef]
- Govindan, K.; Rajendran, S.; Sarkis, J.; Murugesan, P. Multi criteria decision making approaches for green supplier evaluation and selection: A literature review. J. Clean. Prod. 2015, 98, 66–83. [Google Scholar] [CrossRef]
- Govindan, K.; Soleimani, H.; Kannan, D. Reverse logistics and closed-loop supply chain: A comprehensive review to explore the future. Eur. J. Oper. Res. 2015, 240, 603–626. [Google Scholar] [CrossRef]
- Pidduck, A.B. Issues in supplier partner selection. J. Enterp. Inf. Manag. 2004, 19, 262–276. [Google Scholar]
- Cui, X.; Gong, L.; Chen, Y. Determining Factors in TNCs’ University R&D Partner Selection: An Empirical Study Based on China’s Data. Trans. Corp. Rev. 2009, 1, 24–35. [Google Scholar]
- Karlson, B.; Callagher, L. Which university to partner with: An investigation into partner selection motives among small innovative firms. Int. J. Innov. Manag. 2012, 16. [Google Scholar] [CrossRef]
- Amida, A.; Ghodsypourb, S.H.; O’Brienc, C. A weighted additive fuzzy multiobjective model for the supplier selection problem under price breaks in a supply Chain. Int. J. Prod. Econ. 2009, 121, 323–332. [Google Scholar] [CrossRef]
- Yeh, W.C.; Chuang, M.C. Using multi-objective genetic algorithm for partner selection in green supply chain problems. Expert Syst. Appl. 2011, 38, 4244–4253. [Google Scholar] [CrossRef]
- Niu, S.H.; Ong, S.K.; Nee, A.Y.C. An enhanced ant colony optimiser for multi-attribute partner selection in virtual enterprises. Int. J. Prod. Res. 2012, 50, 1–18. [Google Scholar] [CrossRef]
- Dao, S.D.; Abhary, K.; Marian, R. Optimisation of partner selection and collaborative transportation scheduling in Virtual Enterprises using GA. Expert Syst. Appl. 2014, 41, 6701–6717. [Google Scholar] [CrossRef]
- Wan, S.P.; Wang, F.; Lin, L.-L.; Dong, J.-Y. An intuitionistic fuzzy linear programming method for logistics outsourcing provider selection. Knowl. Based Syst. 2015, 82, 80–94. [Google Scholar] [CrossRef]
- Erkayman, B.; Gundogar, E.; Yılmaz, A. An integrated fuzzy approach for strategic alliance partner selection in third-party logistics. Sci. World J. 2012, 2012, 269–276. [Google Scholar] [CrossRef] [PubMed]
- Su, J.; Chen, J. Multilevel Grey Evaluation Method for Logistics Partner Selection. Oper. Res. Manag. Sci. 2006, 3, 66–70. [Google Scholar]
- Büyüközkan, G.; Feyzioğlu, O.; Nebol, E. Selection of the strategic alliance partner in logistics value chain. Int. J. Prod. Econ. 2008, 113, 148–158. [Google Scholar] [CrossRef]
- Li, L.; Liu, F.; Li, C. Customer satisfaction evaluation method for customized product development using Entropy weight and Analytic Hierarchy Process. Comput. Ind. Eng. 2014, 77, 80–87. [Google Scholar] [CrossRef]
- Guo, S.; Zhao, H. Optimal site selection of electric vehicle charging station by using fuzzy TOPSIS based on sustainability perspective. Appl. Energy 2015, 158, 390–402. [Google Scholar] [CrossRef]
- Hayel, Y.; Quadri, D.; Jimenez, T.; Brotcorne, L. Decentralized optimization of last-mile delivery services with non-cooperative bounded rational customers. Ann. Oper. Res. 2014, 1–19. [Google Scholar] [CrossRef]
- Soda, G.; Furlotti, M. Bringing Tasks Back In: An Organizational Theory of Resource Complementarity and Partner Selection. J. Manag. 2014. [Google Scholar] [CrossRef]
- Xu, L.; Shi, J.J. Dynamic Stability for Alliance: Theory Based on Interdependence Balance. China Ind. Econ. 2010, 30, 97–107. [Google Scholar]
- Jiang, X.; Li, Y.; Gao, S. The stability of strategic alliances: Characteristics, factors and stages. J. Int. Manag. 2008, 14, 173–189. [Google Scholar] [CrossRef]
- Carter, J.R.; Maltz, A.; Maltz, E.; Goh, M.; Yan, T. Impact of culture on supplier selection decision making. Int. J. Logist. Manag. 2010, 21, 353–374. [Google Scholar] [CrossRef]
- Pilot Measures for the Discharge of Volatile Organic Compounds. Available online: http://www.envir.gov.cn/info/2015/12/1221-029.htm (accessed on 18 June 2015).
- Zadeh, L.A. Fuzzy sets. Inform. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, X. Research on the supplier selection of supply chain based on entropy weight and improved ELECTRE-III method. Int. J. Prod. Res. 2011, 49, 637–646. [Google Scholar] [CrossRef]
- Tavana, M.; Caprio, D.D.; Santos-Arteaga, F.J.; O’Connor, A. A Novel Entropy-Based Decision Support Framework for Uncertainty Resolution in the Initial Subjective Evaluations of Experts: The NATO Enlargement Problem. Decis. Support Syst. 2015, 74, 135–149. [Google Scholar] [CrossRef]
- Tavana, M. A Priority Assessment Multi-criteria Decision Model for Human Spaceflight Mission Planning at NASA. J. Oper. Res. Soc. 2006, 57, 1197–1215. [Google Scholar] [CrossRef]
- Hwang, C.L.; Lai, Y.J.; Liu, T.Y. A new approach for multiple objective decision making. Comput. Oper. Res. 1993, 20, 889–899. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Mardani, A.; Jusoh, A.; Zavadskas, E.K.; Cavallaro, F.; Khalifah, Z. Sustainable and Renewable Energy: An Overview of the Application of Multiple Criteria Decision Making Techniques and Approaches. Sustainability 2015, 7, 13947–13984. [Google Scholar] [CrossRef]
- Khalili-Damghani, K.; Sadi-Nezhad, S.; Tavana, M. Solving Multi-Period Project Selection Problems with Fuzzy Goal Programming Based on TOPSIS and a Fuzzy Preference Relation. Inf. Sci. 2013, 252, 42–61. [Google Scholar] [CrossRef]
- Junior, F.R.L.; Osiro, L.; Carpinetti, L.C.R. A comparison between Fuzzy AHP and Fuzzy TOPSIS methods to supplier selection. Appl. Soft Comput. 2014, 21, 194–209. [Google Scholar] [CrossRef]
- Lan, R.; Fan, J.L. TOPSIS Decision-Making Method for Three Parameters Interval-Valued Fuzzy Sets. Syst. Eng. Theory Pract. 2009, 29, 129–136. [Google Scholar] [CrossRef]

| Linguistic Term | Fuzzy Number |
|---|---|
| Of little important (LI) | (1,1,3) |
| Moderately important (MI) | (1,3,5) |
| Important (I) | (3,5,7) |
| Very important (VI) | (5,7,9) |
| Absolutely important (AI) | (7,9,9) |
| Linguistic Term | Fuzzy Number |
|---|---|
| Very low (VL) | (1,1,3) |
| Low (L) | (1,3,5) |
| Medium (M) | (3,5,7) |
| High (H) | (5,7,9) |
| Very high (VH) | (7,9,9) |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | C13 | C14 | C15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EP1 | AI | VI | AI | VI | I | AI | I | AI | AI | AI | AI | AI | AI | AI | AI |
| EP2 | AI | I | VI | I | VI | VI | MI | AI | VI | VI | AI | VI | AI | AI | VI |
| EP3 | VI | I | VI | I | I | VI | VI | AI | AI | VI | VI | AI | AI | VI | I |
| EP4 | VI | MI | AI | MI | I | AI | I | VI | AI | I | V | VI | AI | AI | I |
| EP5 | AI | I | VI | MI | VI | AI | I | I | VI | I | VI | AI | VI | VI | VI |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | C13 | C14 | C15 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EP1 | PC1 | VH | VH | H | H | H | M | M | M | L | M | VH | H | M | H | M |
| PC2 | H | VH | H | M | H | M | M | M | VL | L | L | M | H | M | H | |
| PC3 | H | VH | M | H | VH | VH | H | VH | VH | VH | VH | H | VH | VH | VH | |
| PC4 | VH | H | M | H | H | M | M | VH | VH | H | H | M | M | H | H | |
| EP2 | PC1 | H | H | VH | H | H | M | M | M | L | M | H | M | M | H | H |
| PC2 | H | M | M | H | H | M | M | L | L | M | L | M | H | M | H | |
| PC3 | VH | H | H | VH | H | VH | VH | VH | H | VH | H | VH | VH | M | VH | |
| PC4 | H | H | M | H | H | M | H | VH | H | VH | H | H | M | M | H | |
| EP3 | PC1 | H | VH | H | M | M | H | L | M | M | L | H | H | M | H | VH |
| PC2 | M | H | H | M | H | M | H | L | M | M | M | M | L | H | M | |
| PC3 | VH | VH | H | H | VH | H | H | VH | VH | H | VH | VH | VH | VH | H | |
| PC4 | H | M | H | H | H | H | M | H | VH | VH | H | M | H | H | H | |
| EP4 | PC1 | H | H | VH | M | M | L | M | M | L | M | VH | H | H | H | M |
| PC2 | M | H | M | M | H | H | VH | L | M | L | M | M | H | H | M | |
| PC3 | H | VH | VH | VH | VH | VH | VH | H | H | VH | VH | H | VH | H | VH | |
| PC4 | H | VH | M | M | H | H | H | VH | H | H | H | H | M | M | H | |
| EP5 | PC1 | H | M | H | H | H | M | M | M | L | VL | VH | H | M | M | H |
| PC2 | M | H | H | VH | H | VH | M | L | H | M | M | H | M | H | VH | |
| PC3 | VH | VH | H | H | H | VH | VH | VH | H | VH | H | VH | VH | H | VH | |
| PC4 | H | H | M | H | H | VH | H | VH | VH | H | H | M | H | M | M | |
| Fuzzy-EW | C1 | C2 | C3 | C4 | C5 |
| [0.023,0.025,0.032] | [0.116,0.144,0.146] | [0.025,0.025,0.036] | [0.178,0.211,0.250] | [0.052,0.056,0.082] | |
| C6 | C7 | C8 | C9 | C10 | |
| [0.023,0.025,0.036] | [0.116,0.144,0.0148] | [0.058,0.066,0.083] | [0.023,0.026,0.034] | [0.078,0.080,0.092] | |
| C11 | C12 | C13 | C14 | C15 | |
| [0.025,0.026,0.036] | [0.021,0.024,0.037] | [0.016,0.025,0.025] | [0.024,0.025,0.034] | [0.079,0.080,0.091] | |
| Fuzzy-AHP | C1 | C2 | C3 | C4 | C5 |
| [0.073,0.078,0.082] | [0.040,0.048,0.057] | [0.073,0.074,0.077] | [0.034,0.044,0.053] | [0.050,0.055,0.063] | |
| C6 | C7 | C8 | C9 | C10 | |
| [0.074,0.079,0.082] | [0.040,0.047,0.058] | [0.070,0.075,0.076] | [0.073,0.080,0.082] | [0.060,0.063,0.066] | |
| C11 | C12 | C13 | C14 | C15 | |
| [0.058,0.061,0.063] | [0.073,0.078,0.082] | [0.072,0.082,0.087] | [0.073,0.078;0.082] | [0.062,0.063,0.066] | |
| Integrated weights | C1 | C2 | C3 | C4 | C5 |
| [0.030,0.037,0.045] | [0.092,0.110,0.134] | [0.030,0.037,0.044] | [0.130,0.165,0.182] | [0.050,0.051,0.084] | |
| C6 | C7 | C8 | C9 | C10 | |
| [0.030,0.033,0.045] | [0.092,0.113,0.133] | [0.066,0.097,0.103] | [0.030,0.036,0.045] | [0.084,0.094,0.096] | |
| C11 | C12 | C13 | C14 | C15 | |
| [0.024,0.031,0.036] | [0.030,0.036,0.044] | [0.027,0.030,0.035] | [0.031,0.038,0.046] | [0.084,0.094,0.096] |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; Wang, X.; Lin, Y.; Zhou, F. Optimal Partner Combination for Joint Distribution Alliance using Integrated Fuzzy EW-AHP and TOPSIS for Online Shopping. Sustainability 2016, 8, 341. https://doi.org/10.3390/su8040341
He Y, Wang X, Lin Y, Zhou F. Optimal Partner Combination for Joint Distribution Alliance using Integrated Fuzzy EW-AHP and TOPSIS for Online Shopping. Sustainability. 2016; 8(4):341. https://doi.org/10.3390/su8040341
Chicago/Turabian StyleHe, Yandong, Xu Wang, Yun Lin, and Fuli Zhou. 2016. "Optimal Partner Combination for Joint Distribution Alliance using Integrated Fuzzy EW-AHP and TOPSIS for Online Shopping" Sustainability 8, no. 4: 341. https://doi.org/10.3390/su8040341
APA StyleHe, Y., Wang, X., Lin, Y., & Zhou, F. (2016). Optimal Partner Combination for Joint Distribution Alliance using Integrated Fuzzy EW-AHP and TOPSIS for Online Shopping. Sustainability, 8(4), 341. https://doi.org/10.3390/su8040341







