Optimal Path for Controlling Sectoral CO₂ Emissions Among China’s Regions: A Centralized DEA Approach

Abstract

This paper proposes a centralized data envelopment analysis (DEA) model for industrial optimization based on several different production technologies among several regions. We developed this model based on improved Kuosmanen environmental DEA technology, which avoids positive shadow price on undesirable outputs. We also designed a dual model for our centralized DEA model, and used it to analyze shadow prices on CO₂ emissions. We further employed the proposed model to determine the optimal path for controlling CO₂ emissions at the sector level for each province in China. At sectoral level, manufacturing showed the highest potential emissions reduction, and transportation was the largest accepter of emission quotas. At regional level, western and northeastern areas faced the largest adjustments in allowable emissions, while central and eastern areas required the least amount of adjustment. Because our model represents increase or decrease in emissions bidirectionally in terms of shadow price analysis, this setting makes the shadow price on CO₂ emissions lower than strong regulation (decreasing CO₂ emissions along with increasing value added) used by directional distance function (DDF).

1. Introduction

Climate change caused by greenhouse gas (GHG) emitted by human activity is one of the most urgent global issues of our time. According to Stern [1], if no action is taken to reduce GHG emissions, the overall cost of climate change will be equivalent to the loss of at least 5% of the world’s GDP per year. Numerous countries have taken action to reduce their greenhouse gas emissions by enforcing market-oriented or administration-oriented regulations, including energy/carbon taxation, cap and trade systems, energy efficiency standards, and subsidies for new and renewable energy. China, the world’s largest developing country and possessor currently of the most dynamic economy, has seen a dramatic increase in energy consumption and CO₂ emissions over the past three decades. According to International Energy Agency (IEA) report, Mainland China (excluding Hong Kong) emitted 8205.9 million tons of CO₂ in 2012, making it the world’s largest CO₂ emitter at 25.9% of the world’s total. China’s CO₂ emissions sources were mainly fossil fuel combustion (90%) and cement production (10%); coal consumption accounted for about 70% of CO₂ emissions from fossil fuel combustion. As for sector shares of China’s CO₂ emissions, manufacturing and power generation are the largest contributors, accounting for more than 70% of China’s total CO₂ emissions. Transportation and household sectors contributed only about 10% [2]. These phenomena are particularly notable when comparing China to developed countries, where CO₂ emissions come mostly from transportation and household sectors. Controlling CO₂ emissions in the production sector and enforcing dramatic, but proven-feasible, adjustments to industrial structure is highly necessary to ensure rational distribution of CO₂ emissions among transport, consumption, production, and processing industries, and to decrease China’s overall carbon footprint.

In order to control the country’s excessive energy consumption and resulting CO₂ emission problem, China’s central government has established a series of energy conservation and emissions reduction regulations. Specifically, China has committed to reducing its CO₂ emissions by 40%–45% from 2005 levels per unit of GDP by 2020. Considering the sizeable differences in natural environment, resources, and economic development across different provinces, the government decomposed the national emissions reduction target to the province level, as outlined in the 11th and 12th Five Year Plans (FYPs) (in the 12th FYP, China outlined policies to decrease energy consumption and cut CO₂ emissions 16% and 17%, respectively, in 2015 compared to the end of the 11th FYP). In an effort to most effectively share the burden of carbon emissions, emissions reduction plans at both provincial and sectoral levels require further research.

Previous studies have examined CO₂ allocation according to well-established environmental production technology [3]. For example, Färe et al. [4] developed a generalized DEA framework for determining the optimal inter-temporal CO₂ allocation for 28 OECD countries. They found that OECD countries should be with weak regulations during 1991–1998 and strong regulations during 2000–2006 on CO₂ emissions, which is different to immediate CO₂ emissions reduction regulations advocated by Stern. The same research team further extended this model to multi-undesirable outputs (e.g., CO₂, NO_x, and SO₂) and proposed methods of allocating undesirable outputs for U.S. electric power plants under command-and-control and tradable permit regulations [5]. The results indicate that tradable permit regulation yields more potential gains than command-and-control regulation and in most cases good output increases more when three or more bad outputs are traded. Zhou et al. [6] transformed the CO₂ allocation problem into an optimal path for controlling CO₂ emissions under specific spatial, temporal, and spatial-temporal allocation strategies in China’s 30 provinces. It is found that the spatial-temporal allocation strategy can achieve optimal CO₂ emissions distribution.

We established the model proposed here according to our own research and a careful review of the literature. First, we transformed the existing model from a constant returns to scale (CRS) to variable returns to scale (VRS) assumption, in terms of desirable and undesirable output joint-production framework, which better represents the real-world production in industry. Next, we improved the method of representing “environmental production technology”, avoiding the emergence of positive shadow price on undesirable outputs. Of course, the traditional approach to manage weak disposability in the DEA model is to set undesirable output constraints as equal, resulting in positive shadow price, which does not reflect real-world production conditions. We set undesirable constraints as less than or equal to each other (Färe (2014) introduced an inequality for undesirable outputs to avoid any condition when less desirable output can be yielded by producing more undesirable output; he also indicated that the inequality can yield unbounded output sets, which can be avoided by setting the right-hand side of output sets equal to a bound such as the largest observed undesirable output value), which avoids positive shadow price but still meets weak disposability and null-jointness assumptions [5,7,8]. Finally, we conducted an empirical study from the provincial level to the sector level in different provinces and regions, allowing us to examine production technology homogeneously in sectors among provinces rather than heterogeneously in provinces across the entire nation, exploring China’s optimal CO₂ emissions path with new and valuable information.

The remainder of this paper is organized as follows. Section 2 provides a literature review focusing on allocation methods based on DEA techniques. In Section 3, we propose new environmental DEA technology and space-temporal centralized DEA model, plus strategies for controlling emissions at various levels (sectoral and regional) in China. Section 4 presents the data and variable descriptions for China, and the results obtained using the proposed model. Section 5 makes conclusions and policy recommendations based on our findings.

2. Literature Review

CO₂ emission is closely related to industrial production, and especially the combustion of fuel necessary for production processes. For the sake of analysis, it is an “undesirable output” that is produced simultaneously with “desirable outputs”. If we consider the environmental capacity for CO₂ emissions to be limited, CO₂ emissions are an exhaustible resource. The optimal utilization of CO₂ emission is both temporal and spatial, and achieves the maximum economic outputs with limited impact on the environment.

DEA is a specific method of using non-parametric mathematical programming to approximate production technology [9]. The principle of DEA is to allow data to speak for itself, rather than forcing any rigid, arbitrarily specified functional form [10]. This principle was originated by activity analysis [11,12,13,14,15] and non-parametric production analysis [16,17,18,19,20]. According to established DEA methodology, it can be implemented to solve resource allocation among peer decision making units (DMUs). Some researchers assume that there is a powerful, centralized decision-making environment for allocating resources to DMUs so as to maximize the summarized benefits or minimize the summarized costs. Golany and Tamir [21], for example, integrated efficiency, cost-benefit, and equality into an aggregated non-radial oriented DEA allocation model. Lozano and Villa [22] proposed a centralized reallocation DEA model, implementing step-by-step optimization according to the productive efficiency of a group of DMUs [23]; this model set unique shadow prices of inputs and outputs, as opposed to Golany and Tamir. Asmild et al. [24] extended the centralized reallocation DEA model to the BCC model, which only adjusts any previously inefficient DMUs. Mar-Molinero et al. [25] simplified the BCC centralized model using common intensity variables, which made measuring the productive efficiency of DMU groups as easy as measuring the single productive efficiency of average inputs and outputs of the DMUs. Fang [26] explored several centralized reallocation DEA models and proposed a generalized model that incorporates several advantages.

In addition to the series of Lozano models, researchers have used other optimization models based on DEA for resource allocation. Korhonen and Syrjänen [27] developed a multiple-objective linear programming model based on production technology for allocating resources. Hadi-Vencheh et al. [28] proposed a strongly efficient resource allocation model based on inverse DEA which maintains DMU efficiency levels after allocation. Amirteimoori and Tabar [29] provided a DEA-based fixed-resource allocation model that considers lower and upper goals achieved by individual DMUs. Athanassopoulos [30] developed the goal programming and data envelopment analysis (GoDEA) model, which combines the centralized target-based planning model and data envelopment analysis.

A wealth of previous researchers have used the DEA model to investigate CO₂ allocation, specifically. Gomes [31] developed the zero-sum game DEA (ZSG-DEA) model, taking CO₂ as the input variable allocated among Kyoto Protocol Contracting Parties—ZSG-DEA was proven to realize technical efficiency for all DMUs after optimization by multiplying an allocation coefficient. Other researchers applied ZSG-DEA, including Serro [32], Wang et al. [33], Pang et al. [34], and Chiu et al. [35], and provided valuable findings; Lozano et al. [36] used the centralized reallocation DEA model for emissions allocation. Notable studies on the centralized DEA model were conducted by Wu et al. [37], Singh and Majumdar [38], Sun et al. [39], Homayounfar et al. [40], and Feng et al. [41].

As reviewed above, prior research on allocation models and methods based on DEA has mostly concentrated on weight restrictions with user-specified preference structure [42]. Decision maker preference information can also be incorporated into DEA by employing the multiple criteria decision-making concept [43,44]. A well-known drawback of weight restrictions is the fact that their use in the multiplier model implicitly changes the model of production technology in the envelopment form [45], and that they inappropriately represent the demands of real-world productive activities [46]; in other words, their use makes the traditional meanings of “technical efficiency” and “technologically feasible improvement” become unsubstantiated [47,48]. Comparing to the other research up to now, this paper considers the weights of the outputs and inputs will only be restricted by the constraints used to form environmental production technology, without any user-specified preference restriction on weights. In that way, we can ensure the optimized activities will be projected on the facet of environmental production technology, then allocates CO₂ emissions in effort to maximize the aggregated desirable outputs.

3. Methodology

3.1. Environmental DEA Technology

The joint production of desirable and undesirable outputs can be described as “environmental production technology”. It depicts the process of converting input vectors ($x$) to desirable output vectors ($y$) and undesirable output vectors ($b$) [3]:

$$T=\{(x,y,b):x\text{ can produce }(y,b\left)\right\}$$

(1)

The production technology set ($T$) is assumed to satisfy the following assumptions:

(1)

If $(x,y,b)\in T$ and $0\le \theta \le 1$, then $(x,\mathsf{\theta }y,\mathsf{\theta }b)\in T$ (weak disposability for desirable and undesirable outputs).

(2)

If $(x,y,b)\in T$ and $b=0$, then $y=0$ (null-jointness of desirable and undesirable outputs).

The conceptual definition of environmental production technology can be approximated by piecewise linear combinations of the observed data, which is similar theoretically to DEA form; as such, it can also be called “environmental DEA technology” [49,50]. Under CRS assumption, environmental production technology $T$ can be approximately formulated as follows:

$$\begin{array}{ll}{\widehat{T}}_{\text{W}}=\{(x,y,b):& {\displaystyle \sum _{k=1}^K{z}_k{x}_{mk}\le x_m},m=1,2,\cdots ,M\\ & {\displaystyle \sum _{k=1}^K{z}_k{y}_{nk}\ge y_n,n=1,2,\cdots ,N}\\ & {\displaystyle \sum _{k=1}^K{z}_k{b}_{jk}=b_j},j=1,2,\cdots ,J\\ & z_k\ge 0,k=1,2,\cdots ,K\}\end{array}$$

(2)

Under VRS assumption, environmental production technology $T$ can be approximately characterized as Shephard environmental DEA technology [51] and Kuosmanen environmental DEA technology [52].

The formulation of Shephard environmental DEA technology is as follows:

$$\begin{array}{ll}{\widehat{T}}_{\text{S}}=\{(x,y,b):& {\displaystyle \sum _{k=1}^K{z}_k{x}_{nk}\le x_n},n=1,2,\cdots ,N\\ & \mathsf{\theta }{\displaystyle \sum _{k=1}^K{z}_k{y}_{mk}\ge y_m},m=1,2,\cdots ,M\\ & \mathsf{\theta }{\displaystyle \sum _{k=1}^K{z}_k{b}_{jk}=b_j},j=1,2,\cdots ,J\\ & 0\le \mathsf{\theta }\le 1,{\displaystyle \sum _{k=1}^K{z}_k=1}\\ & z_k\ge 0,k=1,2,\cdots ,K\}\end{array}$$

(3)

where $\mathsf{\theta }$ is the abatement factor, which ensures that ${\widehat{T}}_{\text{s}}$ satisfies the two assumptions above. The second and third constraints in Model (3) are non-linear, and must be converted to linear form. We defined a new variable, ${\tilde{z}}_k$, then let ${\tilde{z}}_k=\mathsf{\theta }{z}_k$ replace the old variable. The converted model can be expressed as follows:

$$\begin{array}{ll}{\widehat{T}}_{\text{S}}=\{(x,y,b):& {\displaystyle \sum _{k=1}^K{\tilde{z}}_k{x}_{nk}\le \mathsf{\theta }{x}_n},n=1,2,\cdots ,N\\ & {\displaystyle \sum _{k=1}^K{\tilde{z}}_k{y}_{mk}\ge y_m},m=1,2,\cdots ,M\\ & {\displaystyle \sum _{k=1}^K{\tilde{z}}_k{b}_{jk}=b_j},j=1,2,\cdots ,J\\ & 0\le \mathsf{\theta }\le 1,{\displaystyle \sum _{k=1}^K{\tilde{z}}_k=\mathsf{\theta }}\\ & {\tilde{z}}_k\ge 0,k=1,2,\cdots ,K\\ & x_n\ge \min \left\{x_{nk}\right\}\}\end{array}$$

(4)

It is worth noting that we added constraint $x_n\ge \min \left\{x_{nk}\right\}$, which prevents the condition $\mathsf{\theta }=0$ causing ${\tilde{z}}_k=0$ so that any activity $(x,0,0)$ will be feasible. This is because according to the first constraint in Model (3), input vectors $x$ cannot be smaller than the observed practical value.

An improvement upon Shephard environmental DEA technology, Kuosmanen environmental DEA technology can be expressed as follows:

$$\begin{array}{ll}{\widehat{T}}_{\text{K}}=\{(x,y,b):& {\displaystyle \sum _{k=1}^K{z}_k{x}_{nk}\le x_n},n=1,2,\cdots ,N\\ & {\displaystyle \sum _{k=1}^K{\mathsf{\theta }}_k{z}_k{y}_{mk}\ge y_m},m=1,2,\cdots ,M\\ & {\displaystyle \sum _{k=1}^K{\mathsf{\theta }}_k{z}_k{b}_{jk}=b_j},j=1,2,\cdots ,J\\ & 0\le {\mathsf{\theta }}_k\le 1,{\displaystyle \sum _{k=1}^K{z}_k=1}\\ & z_k\ge 0,k=1,2,\cdots ,K\}\end{array}$$

(5)

The difference between Models (3) and (5) is that Model (5) takes multiple abatement factors with desirable and undesirable outputs [53]. The strength of Model (5) is that it allows for each observed activity to abate by a different abatement factor before the convex combination is formed, opening the possibility that a target DMU with less abatement cost reduces more. Model (5) also includes non-linear constraints, so it must be converted to solvable form with linear constraints. The converted model is as follows:

$$\begin{array}{ll}{\widehat{T}}_{\text{K}}=\{(x,y,b):& {\displaystyle \sum _{k=1}^K(z_k+{\lambda }_k)x_{nk}\le x_n},n=1,2,\cdots ,N\\ & {\displaystyle \sum _{k=1}^K{z}_k{y}_{mk}\ge y_m},m=1,2,\cdots ,M\\ & {\displaystyle \sum _{k=1}^K{z}_k{b}_{jk}=b_j},j=1,2,\cdots ,J\\ & {\displaystyle \sum _{k=1}^K(z_k+{\lambda }_k)}=1\\ & z_k\ge 0,{\lambda }_k\ge 0,k=1,2,\cdots ,K\}\end{array}$$

(6)

Because Kuosmanen environmental DEA technology sets equal undesirable output constraints, positive shadow price may emerge on undesirable outputs (as also discussed by Kuosmanen and Kazemi Matin [54]). To avoid this, we adopted a suggestion by Leleu [55] and set an $\le$ on undesirable output constraints (the same work done under CRS assumptions can be found in a study by Färe et al. (2014) [5]). Our proposed environmental DEA technology can be expressed as follows:

$$\begin{array}{ll}{\widehat{T}}_{\text{New}}=\{(x,y,b):& {\displaystyle \sum _{k=1}^K{z}_k{x}_{nk}\le x_n},n=1,2,\cdots ,N\\ & {\displaystyle \sum _{k=1}^K{\mathsf{\theta }}_k{z}_k{y}_{mk}\ge y_m},m=1,2,\cdots ,M\\ & {\displaystyle \sum _{k=1}^K{\mathsf{\theta }}_k{z}_k{b}_{jk}\le b_j},j=1,2,\cdots ,J\\ & 0\le {\mathsf{\theta }}_k\le 1,{\displaystyle \sum _{k=1}^K{z}_k=1}\\ & z_k\ge 0,k=1,2,\cdots ,K\}\end{array}$$

(7)

We created a numerical example comparing ${\widehat{T}}_{\text{W}}$, ${\widehat{T}}_{\text{S}}$, ${\widehat{T}}_{\text{K}}$, and ${\widehat{T}}_{\text{New}}$ by output sets ${\widehat{P}}_{\text{W}}(x)$, ${\widehat{P}}_{\text{S}}(x)$, ${\widehat{P}}_{\text{K}}(x)$ and ${\widehat{P}}_{\text{New}}(x)$. Considering the production activity with one input, one desirable output, and one undesirable output, four observed DMUs and constructed output sets were analyzed as presented in Table 1 and Figure 1.

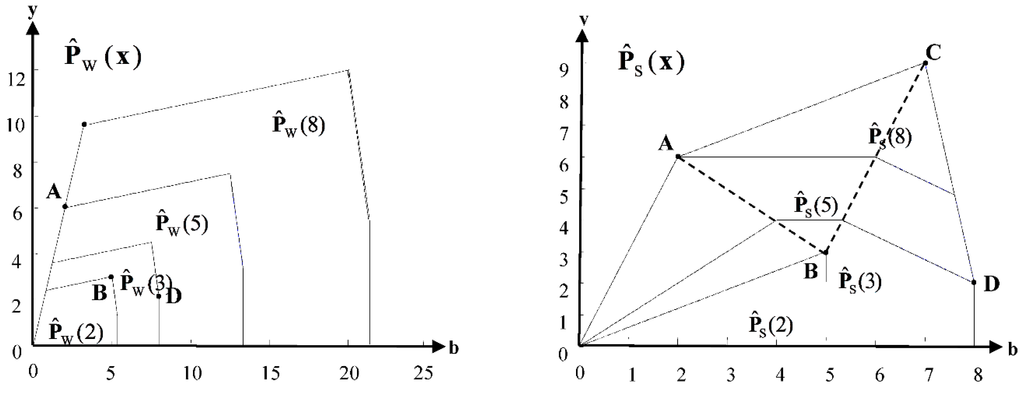
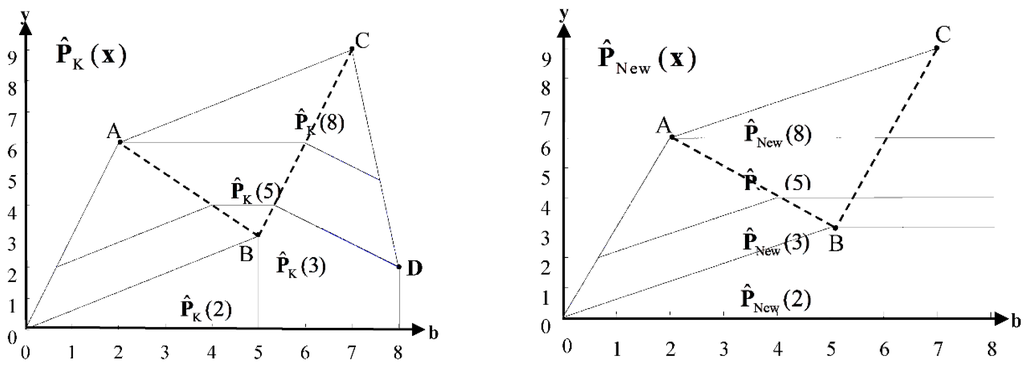
Figure 1. ${\widehat{P}}_{\text{W}}(x)$, ${\widehat{P}}_{\text{S}}(x)$, ${\widehat{P}}_{\text{K}}(x)$ and ${\widehat{P}}_{\text{New}}(x)$ induced by observed DMUs.

Figure 1. ${\widehat{P}}_{\text{W}}(x)$, ${\widehat{P}}_{\text{S}}(x)$, ${\widehat{P}}_{\text{K}}(x)$ and ${\widehat{P}}_{\text{New}}(x)$ induced by observed DMUs.

Table 1. Comparison between ${\widehat{P}}_{\text{W}}(x)$, ${\widehat{P}}_{\text{S}}(x)$, ${\widehat{P}}_{\text{K}}(x)$ and ${\widehat{P}}_{\text{New}}(x)$.

DMU	A	B	C	D
b	2	5	7	8
x	5	2	8	3
y	6	3	9	2

Table 1. Comparison between ${\widehat{P}}_{\text{W}}(x)$, ${\widehat{P}}_{\text{S}}(x)$, ${\widehat{P}}_{\text{K}}(x)$ and ${\widehat{P}}_{\text{New}}(x)$.

DMU	A	B	C	D
b	2	5	7	8
x	5	2	8	3
y	6	3	9	2

As shown in Figure 1, all the output sets satisfy Assumptions (1) and (2). Meanwhile, all the output sets above are the compact sets, but ${\widehat{P}}_{\text{New}}(x)$ is not a bounded and closed set due to the strong disposability set on input. Because ${\widehat{P}}_{\text{K}}(x)$ possesses multi abatement factors and ${\widehat{P}}_{\text{S}}(x)$ possesses a single abatement factor, which makes ${\widehat{P}}_{\text{K}}(x)$ larger than ${\widehat{P}}_{\text{S}}(x)$ (see ${\widehat{P}}_{\text{K}}(3)$ is larger than ${\widehat{P}}_{\text{K}}(3)$). Therefore, the DMU in ${\widehat{P}}_{\text{K}}(x)$ has more choices to conduct undesirable output abatement. However, we often observe a negative slope in the frontier of ${\widehat{P}}_{\text{K}}(x)$ (see piecewise lines are located on the right side of line BC in ${\widehat{P}}_{\text{K}}(x)$), on which the shadow price of undesirable output is positive (e.g., $-\partial y/\partial c>0$)and the marginal abatement cost is negative (e.g., $\partial y/\partial c<0$). Hence, this anti-fact situation must be improved. We improved ${\widehat{P}}_{\text{K}}(x)$ to ${\widehat{P}}_{\text{New}}(x)$ according to a suggestion made by Leleu [55], and set strong disposability on undesirable output, making ${\widehat{P}}_{\text{New}}(x)$ satisfies two necessary assumptions. The success of doing so is evidenced by piecewise horizontal lines on the right side of line BC in ${\widehat{P}}_{\text{New}}(x)$, which can avoid the positive shadow price emerging on undesirable output.

3.2. Centralized Model for New Environmental DEA Technology

The centralized model based on new environmental DEA technology was designed to reallocate undesirable outputs to allow the substitution of CO₂ emissions between DMUs in order to maximize total desirable outputs. After centralized optimization, all DMU activities are as efficient as possible under the potential desirable outputs and allocated undesirable outputs set by the model. All DMU activities in the time period t are marked with a subscript t. There is an emissions control coefficient $\mathsf{\delta }$ for period t, which implies that the total emissions permitted is equal to $\mathsf{\delta }$ multiplied by the aggregate baseline emissions for all the DMUs. Then, the centralized DEA model for reallocation of CO₂ emissions can be formulated as follows:

Total control strategy (Primal):

$$\begin{array}{ll}& \max {\displaystyle \sum _{t=1}^T{\displaystyle \sum _{s=1}^S{\displaystyle \sum _{l=1}^K{\widehat{y}}_{s,l}^t}}}\\ \text{s.t.\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}}& {\displaystyle \sum _{k=1}^K(z_{s,k,l}^t+{\mathsf{\lambda }}_{s,k,l}^t)x_{s,m,k}^t\le x_{s,m,l}^t},m=1,\cdots ,M\\ & {\displaystyle \sum _{k=1}^K{z}_{s,k,l}^t{y}_{s,k}^t\ge {\widehat{y}}_{s,l}^t}\\ & {\displaystyle \sum _{k=1}^K{z}_{s,k,l}^t{b}_{s,k}^t\le {\widehat{b}}_{s,l}^t}\\ & {\displaystyle \sum _{k=1}^K(z_{s,k,l}^t+{\mathsf{\lambda }}_{s,k,l}^t)}=1\\ & {\displaystyle \sum _{t=1}^T{\displaystyle \sum _{s=1}^S{\displaystyle \sum _{l=1}^K{\widehat{b}}_{s,l}^t}}}=\mathsf{\delta }\cdot {\displaystyle \sum _{t=1}^T{\displaystyle \sum _{s=1}^S{\displaystyle \sum _{l=1}^K{b}_{s,l}^t}}}\\ & z_{s,k,l}^t\ge 0,{\mathsf{\lambda }}_{s,k,l}^t\ge 0,{\widehat{y}}_{s,l}^t\ge \mathsf{\epsilon },{\widehat{b}}_{s,l}^t\ge \mathsf{\epsilon }\\ & t=1,\cdots ,T;s=1,\cdots ,S;l=1,\cdots ,K;\end{array}$$

(8)

Sectoral control strategy (Primal):

$$\begin{array}{ll}& \max {\displaystyle \sum _{t=1}^T{\displaystyle \sum _{s=1}^S{\displaystyle \sum _{l=1}^K{\widehat{y}}_{s,l}^t}}}\\ \text{s.t.\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}}& {\displaystyle \sum _{k=1}^K(z_{s,k,l}^t+{\lambda }_{s,k,l}^t)x_{s,m,k}^t\le x_{s,m,l}^t},m=1,\cdots ,M\\ & {\displaystyle \sum _{k=1}^K{z}_{s,k,l}^t{y}_{s,k}^t\ge {\widehat{y}}_{s,l}^t}\\ & {\displaystyle \sum _{k=1}^K{z}_{s,k,l}^t{b}_{s,k}^t\le {\widehat{b}}_{s,l}^t}\\ & {\displaystyle \sum _{k=1}^K(z_{s,k,l}^t+{\mathsf{\lambda }}_{s,k,l}^t)}=1\\ & {\displaystyle \sum _{t=1}^T{\displaystyle \sum _{l=1}^K{\widehat{b}}_{s,l}^t}=}{\mathsf{\delta }}_s\cdot {\displaystyle \sum _{t=1}^T{\displaystyle \sum _{l=1}^K{b}_{s,l}^t}}\\ & z_{s,k,l}^t\ge 0,{\mathsf{\lambda }}_{s,k,l}^t\ge 0,{\widehat{y}}_{s,l}^t\ge \mathsf{\epsilon },{\widehat{b}}_{s,l}^t\ge \mathsf{\epsilon }\\ & t=1,\cdots ,T;s=1,\cdots ,S;l=1,\cdots ,K;\end{array}$$

(9)

In Models (8) and (9), the number of time periods, environmental production technology and observed activity are T, S and K. We used the piecewise linear programming constraints to form Kuosmanen environmental production technology. The first and second constraints represent the strong disposability of M inputs and one desirable output, respectively. The third constraint represents the strong disposability of one undesirable output. $z_{s,k,l}^t$ and ${\lambda }_{s,k,l}^t$ are the intensity variables valued according to Kuosmanen environmental production technology. The fourth constraint denotes variable returns to scale. All the possible combinations of desirable and undesirable outputs ${\left({\widehat{y}}_{s,l}^t,{\widehat{b}}_{s,l}^t\right)}^T$ with fixed input $x_{s,l}^t$ will be optimized by maximizing the aggregated $T\times S\times K$ activities’ desirable outputs. ${\widehat{y}}_{s,l}^t\ge \mathsf{\epsilon }$ and ${\widehat{b}}_{s,l}^t\ge \mathsf{\epsilon }$ ensure that the optimized desirable output and undesirable output take the value greater than zero. In order to control the undesirable outputs, we designed two models to denote sectoral and total undesirable outputs control strategies in Models (8) and (9), respectively:

(1)

${\displaystyle \sum _{t=1}^T{\displaystyle \sum _{s=1}^S{\displaystyle \sum _{l=1}^K{\widehat{b}}_{s,l}^t}}}=\mathsf{\delta }\cdot {\displaystyle \sum _{t=1}^T{\displaystyle \sum _{s=1}^S{\displaystyle \sum _{l=1}^K{b}_{s,l}^t}}}$, can be defined as total control strategy, which implies that the total undesirable outputs permitted is equal to $\mathsf{\delta }$ multiplied by the aggregate baseline undesirable outputs from all DMU.

(2)

${\displaystyle \sum _{t=1}^T{\displaystyle \sum _{l=1}^K{\widehat{b}}_{s,l}^t}=}{\mathsf{\delta }}_s\cdot {\displaystyle \sum _{t=1}^T{\displaystyle \sum _{l=1}^K{b}_{s,l}^t}}$, we define it as sectoral control strategy, which denotes the optimized sum of aggregated undesirable outputs produced by $T\times K$ activities refer to environmental production technology s, which will be equal to ${\mathsf{\delta }}_s$ times from observed aggregated undesirable outputs produced by $T\times K$ activities.

We can deduce the dual forms of Models (8) and (9) with the aim to explore the shadow price of inputs, desirable and undesirable output, and the formulations can be induced as follows:

Total control strategy (Dual):

$$\begin{array}{ll}\min & {\displaystyle \sum _{s=1}^S{\displaystyle \sum _{t=1}^T{\displaystyle \sum _{l=1}^K{\displaystyle \sum _{m=1}^M{v}_{s,m,l}^t{x}_{s,m,l}^t}}}}+\mathsf{\delta }\cdot {\displaystyle \sum _{s=1}^S{\displaystyle \sum _{t=1}^T{\displaystyle \sum _{l=1}^K{b}_{s,l}^t}}}\cdot \mathsf{\sigma }+{\displaystyle \sum _{s=1}^S{\displaystyle \sum _{t=1}^T{\displaystyle \sum _{l=1}^K{\mathsf{\phi }}_{s,l}^t}}}\\ \text{s.t.\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}}& {\displaystyle \sum _{m=1}^M{v}_{s,m,l}^t{x}_{s,m,l}^t}-{\mathsf{\mu }}_{s,l}^t{y}_{s,l}^t+{\mathsf{\omega }}_{s,l}^t{b}_{s,l}^t+{\mathsf{\phi }}_{s,l}^t\ge 0\\ & {\displaystyle \sum _{m=1}^M{v}_{s,m,l}^t{x}_{s,m,l}^t}+{\mathsf{\phi }}_{s,l}^t\ge 0\\ & {\mathsf{\mu }}_{s,l}^t\ge 1,\\ & \mathsf{\sigma }+{\mathsf{\omega }}_{s,l}^t\ge 0,\\ & v_{s,m,l}^t\ge 0,{\mathsf{\mu }}_{s,l}^t\ge 0,{\mathsf{\omega }}_{s,l}^t\ge 0,\mathsf{\sigma }:URS,{\mathsf{\phi }}_{s,l}^t:URS\\ & m=1,\cdots ,M;t=1,\cdots ,T;s=1,\cdots ,S;l=1,\cdots ,K\end{array}$$

(10)

Sectoral control strategy (Dual):

$$\begin{array}{ll}\min & {\displaystyle \sum _{s=1}^S{\displaystyle \sum _{t=1}^T{\displaystyle \sum _{l=1}^K{\displaystyle \sum _{m=1}^M{v}_{s,m,l}^t{x}_{s,m,l}^t}}}}+{\displaystyle \sum _{s=1}^S({\mathsf{\delta }}_s\cdot {\displaystyle \sum _{t=1}^T{\displaystyle \sum _{l=1}^K{b}_{s,l}^t}}\cdot {\mathsf{\sigma }}_s)}+{\displaystyle \sum _{s=1}^S{\displaystyle \sum _{t=1}^T{\displaystyle \sum _{l=1}^K{\mathsf{\phi }}_{s,l}^t}}}\\ \text{s.t.\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}\hspace{0.05em}}& {\displaystyle \sum _{m=1}^M{v}_{s,m,l}^t{x}_{s,m,l}^t}-{\mathsf{\mu }}_{s,l}^t{y}_{s,l}^t+{\mathsf{\omega }}_{s,l}^t{b}_{s,l}^t+{\mathsf{\phi }}_{s,l}^t\ge 0\\ & {\displaystyle \sum _{m=1}^M{v}_{s,m,l}^t{x}_{s,m,l}^t}+{\mathsf{\phi }}_{s,l}^t\ge 0\\ & {\mathsf{\mu }}_{s,l}^t\ge 1,\\ & {\mathsf{\sigma }}_s+{\mathsf{\omega }}_{s,l}^t\ge 0,\\ & v_{s,m,l}^t\ge 0,{\mathsf{\mu }}_{s,l}^t\ge 0,{\mathsf{\omega }}_{s,l}^t\ge 0,{\mathsf{\sigma }}_s:URS,{\mathsf{\phi }}_{s,l}^t:URS\\ & m=1,\cdots ,M;t=1,\cdots ,T;s=1,\cdots ,S;l=1,\cdots ,K\end{array}$$

(11)

In Models (10) and (11), $v_{s,m,l}^t$, ${\mathsf{\mu }}_{s,l}^t$ and ${\mathsf{\omega }}_{s,l}^t$ are the dual variables of first three constraints of primal model. They interpret the marginal contributions for aggregated $T\times S\times K$ desirable outputs from inputs, desirable output and undesirable output, so we name them shadow prices. ${\mathsf{\phi }}_{s,l}^t$ is the dual variable of the convexity constraint of primal model.

4. Empirical Study

4.1. Data

The mathematical model provided above was instantiated using Chinese production data at the sectoral level for several provinces. We set the time period t from 1995 to 2011 (In general, reference base year sets are 1990, 1995, 2000, 2005. The Kyoto Protocol set the reduction target for industrial countries, in which average CO₂ emission from 2008 to 2012 reached 95% by 1990. Because China established its market-based economic institution in 1992, and its economy is yet transitioning, we set the base year as 1995 [56]. Chinese CO₂ emissions from fuel combustion in 1995–2010 accounted for 64.3% of the total emissions from 1971–2010 [57]. We collected as much recent data as possible.), constructed environmental DEA technologies S = {agriculture, manufacturing, construction, transportation, service} at provincial, multi-sectoral level, and the observed DMUs K = {Beijing, Tianjin, Hebei, Shanxi, Inner Mongolia, Liaoning, Jilin, Heilongjiang, Shanghai, Jiangsu, Zhejiang, Anhui, Fujian, Jiangxi, Shandong, Henan, Hubei, Hunan, Guangdong, Guangxi, Hainan, Chongqing+Sichuan (since Chongqing was a part of Sichuan before 1997, the data for Chongqing in 1995–1996 is inseparable from Sichuan; therefore, we combined them together from 1997–2011), Guizhou, Yunnan, Shaanxi, Gansu, Qinghai, Ningxia, Xinjiang}. The number of activities collected was $T(17)\times S(5)\times K(29)=2465$.

We described activities as capital stock (K) and labor force (L) as inputs, and sectoral value added (Y) as desirable outputs and CO₂ emissions (C) as undesirable outputs. We collected energy data for all provinces in each sector, but did not use them as inputs, because CO₂ emission is the transformation form of energy inputs considering the energy mix weighted with CO₂ emission coefficients. As shown in Model (8), we gave strong disposability to the undesirable output, making it similar to the common input; that way, when we added energy and CO₂ emission simultaneously as inputs, a substitutional relationship formed. However, there is a positive correlation between CO₂ and energy. Given this, we leave out energy input. The similar processing can be referred to [4,58].

While estimating capital stock at sectoral level, it is easy to obtain the provincial-level capital stock according to the method developed by Zhang [59], but there is no support specifically for obtaining sectoral capital stock data by province. We implemented an approach suggested by Guo [60], Gan and Zheng [61] and Lv and Zhou [62]: first, we collected the new fixed assets at province/sector level from 1981 to 2011. We then took the five-year moving average of the province/sector time series (the new fixed asset data for years before 1985 took the moving average from 1981, and our methods were developed in effort to eliminate interference between these data, price indices, and investment depreciation rate), then used it to aggregate the new fixed assets from 1981 to each year province/sector level. We then computed the sectoral new fixed asset proportions province-by-province, then used the proportions to allocate the provincial-level capital stock to the province/sectoral level. The new fixed asset data 1981–1985, 1996–1998, and 2002–2011 we used came from the Statistical Yearbooks of China’s Investment in Fixed Assets [63]. The data from1986–1995 and 1999–2001 came from the China Statistical Yearbook [64], and the provincial-level capital stock was estimated by perpetual inventory approach taking 1952 as the base year. In order to estimate provincial capital stock, we took gross fixed capital formation as the annual investment data, then converted it to a 2000 constant price using the investment price index. We estimated the labor force at province/sector level according to 1995–2011 employment data by sector and region from the 1996–2012 China Labor Statistical Yearbook [65].

We estimated value added at province/sector level according to 1995–2011 data from the 1996–2012 China Statistical Yearbook, and converted the data to 2000 constant price according to the value added index [66]. Energy consumption at province/sector level was estimated according to end-use energy consumption, with basic data collected from the energy balance table in the 1996–2012 China Energy Statistical Yearbook [67]. We used the standard coal conversion coefficient to convert these data to standard coal equivalent, and the portion of energy consumption of raw material in the manufacturing sector was removed from the energy balance table.

Table 2. Descriptive statistics of inputs and outputs for province/sector level over 1995–2011.

Index	Sector	Unit	Dimension	Quantity	Mean	Standard Deviation	Minimum	Maximum
Capital Stock (2000 constant price)	Agriculture	100 million RMB	provincial sector	29×17	379.46	417.68	25.61	2843.24
	Manufacturing	100 million RMB	provincial sector	29×17	6182.51	6558.73	274.76	48,577.60
	Construction	100 million RMB	provincial sector	29×17	186.14	219.64	9.30	2134.61
	Transportation	100 million RMB	provincial sector	29×17	1905.75	1687.42	61.25	9526.33
	Service	100 million RMB	provincial sector	29×17	6370.96	7042.74	145.72	39,632.95
Labor Force	Agriculture	10 thousand persons	provincial sector	29×17	1099.34	853.02	37.09	3996.00
	Manufacturing	10 thousand persons	provincial sector	29×17	426.05	399.76	19.60	2283.46
	Construction	10 thousand persons	provincial sector	29×17	146.53	141.98	9.80	715.10
	Transportation	10 thousand persons	provincial sector	29×17	87.86	84.37	8.40	792.02
	Service	10 thousand persons	provincial sector	29×17	594.30	396.37	40.70	1915.42
Energy (standard coal equivalent)	Agriculture	10 thousand tons	provincial sector	29×17	179.18	122.51	7.96	691.64
	Manufacturing	10 thousand tons	provincial sector	29×17	3702.02	3135.19	76.72	17,649.98
	Construction	10 thousand tons	provincial sector	29×17	74.77	82.01	1.12	605.01
	Transportation	10 thousand tons	provincial sector	29×17	493.44	477.83	13.73	2716.30
	Service	10 thousand tons	provincial sector	29×17	318.02	297.73	3.13	1969.78
Value Added (2000 constant price)	Agriculture	100 million RMB	provincial sector	29×17	600.36	450.00	33.51	2065.31
	Manufacturing	100 million RMB	provincial sector	29×17	2567.06	3115.48	42.99	19,950.01
	Construction	100 million RMB	provincial sector	29×17	343.27	299.55	14.45	1760.92
	Transportation	100 million RMB	provincial sector	29×17	399.12	409.84	8.44	2916.87
	Service	100 million RMB	provincial sector	29×17	1671.10	1735.37	50.31	10,590.03
CO2	Agriculture	10 thousand tons	provincial sector	29×17	565.88	374.80	22.43	1948.69
	Manufacturing	10 thousand tons	provincial sector	29×17	12,408.36	10,493.94	265.52	58,033.89
	Construction	10 thousand tons	provincial sector	29×17	220.54	220.70	8.03	1598.10
	Transportation	10 thousand tons	provincial sector	29×17	1148.49	1064.41	33.30	6123.26
	Service	10 thousand tons	provincial sector	29×17	1082.89	1004.35	17.84	6034.86

Table 2. Descriptive statistics of inputs and outputs for province/sector level over 1995–2011.

Index	Sector	Unit	Dimension	Quantity	Mean	Standard Deviation	Minimum	Maximum
Capital Stock (2000 constant price)	Agriculture	100 million RMB	provincial sector	29×17	379.46	417.68	25.61	2843.24
	Manufacturing	100 million RMB	provincial sector	29×17	6182.51	6558.73	274.76	48,577.60
	Construction	100 million RMB	provincial sector	29×17	186.14	219.64	9.30	2134.61
	Transportation	100 million RMB	provincial sector	29×17	1905.75	1687.42	61.25	9526.33
	Service	100 million RMB	provincial sector	29×17	6370.96	7042.74	145.72	39,632.95
Labor Force	Agriculture	10 thousand persons	provincial sector	29×17	1099.34	853.02	37.09	3996.00
	Manufacturing	10 thousand persons	provincial sector	29×17	426.05	399.76	19.60	2283.46
	Construction	10 thousand persons	provincial sector	29×17	146.53	141.98	9.80	715.10
	Transportation	10 thousand persons	provincial sector	29×17	87.86	84.37	8.40	792.02
	Service	10 thousand persons	provincial sector	29×17	594.30	396.37	40.70	1915.42
Energy (standard coal equivalent)	Agriculture	10 thousand tons	provincial sector	29×17	179.18	122.51	7.96	691.64
	Manufacturing	10 thousand tons	provincial sector	29×17	3702.02	3135.19	76.72	17,649.98
	Construction	10 thousand tons	provincial sector	29×17	74.77	82.01	1.12	605.01
	Transportation	10 thousand tons	provincial sector	29×17	493.44	477.83	13.73	2716.30
	Service	10 thousand tons	provincial sector	29×17	318.02	297.73	3.13	1969.78
Value Added (2000 constant price)	Agriculture	100 million RMB	provincial sector	29×17	600.36	450.00	33.51	2065.31
	Manufacturing	100 million RMB	provincial sector	29×17	2567.06	3115.48	42.99	19,950.01
	Construction	100 million RMB	provincial sector	29×17	343.27	299.55	14.45	1760.92
	Transportation	100 million RMB	provincial sector	29×17	399.12	409.84	8.44	2916.87
	Service	100 million RMB	provincial sector	29×17	1671.10	1735.37	50.31	10,590.03
CO2	Agriculture	10 thousand tons	provincial sector	29×17	565.88	374.80	22.43	1948.69
	Manufacturing	10 thousand tons	provincial sector	29×17	12,408.36	10,493.94	265.52	58,033.89
	Construction	10 thousand tons	provincial sector	29×17	220.54	220.70	8.03	1598.10
	Transportation	10 thousand tons	provincial sector	29×17	1148.49	1064.41	33.30	6123.26
	Service	10 thousand tons	provincial sector	29×17	1082.89	1004.35	17.84	6034.86

To estimate CO₂ emissions at province/sector level, we considered 20 distinct types of end-use energies as the sources of carbon emission. The emission coefficients were taken from 2006 IPCC guidelines for national greenhouse gas inventories. To calculate the emission coefficients of electricity and heat generation, we computed the total CO₂ emissions from energy mix inputs for generating electricity and heat nationally, then converted these energy mix inputs to standard coal equivalent as the denominator, and plugged in the total CO₂ emissions to be divided by this denominator to obtain the emission coefficients of electricity and heat.

To obtain enough activities to construct the environmental DEA technology, we instantiated the proposed model using the province/sector level data gathered as discussed above (as shown in Table 2). We further aggregated the sector-level data by province into sectoral data by region, which provided more convenient analysis (with less influence due to administrative divisions). We followed the technique proposed by the China State Council Development Research Center and divided the 29 provinces into four areas: east, central, west and northeast. The four areas were then further divided into eight economic regions, as shown in Table 3.

Table 3. Compositions of four areas and eight economic regions in China.

Area	Economic Region	Provinces
East	Northern Coastal	Beijing, Tianjin, Hebei, Shandong
	Eastern Coastal	Shanghai, Jiangsu, Zhejiang
	Southern Coastal	Fujian, Guangdong, Hainan
Central	Middle Yellow River	Shanxi, Inner Mongolia, Henan, Shaanxi
	Middle Yangtze River	Anhui, Jiangxi, Hubei, Hunan
West	Southwest	Guangxi, Chongqing+Sichuan, Guizhou, Yunan
	Northwest	Gansu, Qinghai, Ningxia, Xinjiang
Northeast	Northeast	Liaoning, Jilin, Heilongjiang

Table 3. Compositions of four areas and eight economic regions in China.

Area	Economic Region	Provinces
East	Northern Coastal	Beijing, Tianjin, Hebei, Shandong
	Eastern Coastal	Shanghai, Jiangsu, Zhejiang
	Southern Coastal	Fujian, Guangdong, Hainan
Central	Middle Yellow River	Shanxi, Inner Mongolia, Henan, Shaanxi
	Middle Yangtze River	Anhui, Jiangxi, Hubei, Hunan
West	Southwest	Guangxi, Chongqing+Sichuan, Guizhou, Yunan
	Northwest	Gansu, Qinghai, Ningxia, Xinjiang
Northeast	Northeast	Liaoning, Jilin, Heilongjiang

4.2. Main Results

We take CO₂ emissions at province/sector level as the research objective, using Models (8) and (9) with the data in Table 2 to research optimal CO₂ emissions allocations in different sectors within different provinces between 1995 and 2011. To appropriately set the emission control coefficient $\mathsf{\delta }$, we employed two patterns of restriction. First, we set $\mathsf{\delta }=1$ corresponding to Model (8), made the aggregated CO₂ emissions for five sectors from all provinces mixed equally to their gross emissions from 1995–2011. Second, we set ${\delta }_s=1$ following Model (9), controlled the aggregated sectoral CO₂ emissions including all provincial sub-sectors equal to its actual emissions from 1995–2011. Then, the annually optimal allocation of CO₂ emissions was solvable using above models, for all eight economic regions.

In the regional agriculture sectors, as shown in Figure 2, under sectoral emissions control strategy, compared to actual emissions, middle Yangtze River and southwest regions were allocated more emission quotas than middle Yellow River, northwest, or northeast regions. More CO₂ emissions allocated to middle Yangtze River and southwest regions would then produce more value-added yield than the other regions. This can be attributed to different agricultural mechanization levels and water resources endowment in northern and southern China. Mechanized production processes in southern China are more difficult than in northern China due to the abundance of mountains and hills in the south. Mechanization is carbon-intensive. At the same time, however, the natural supply of water in southern China saves costs that would otherwise accrue for irrigation, also saving energy input. As far as grain production overall, rice in southern China can be harvested 2–4 times more often than the wheat in northern China. To this effect, southern China has overall low energy input and high grain output compared to northern China. Additionally, under total emissions control strategy, the agriculture sector showed low emissions overall and as such should accept emission quotas from other sectors.

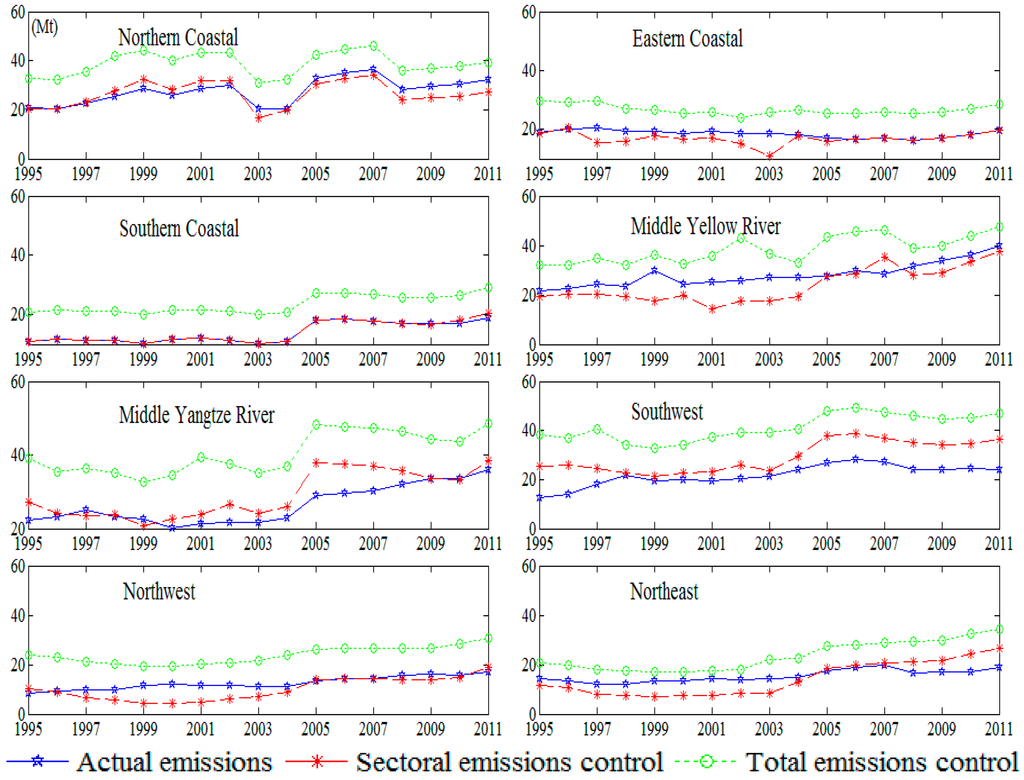
Figure 2. Optimal emission paths for regional agriculture sectors.

Figure 2. Optimal emission paths for regional agriculture sectors.

Figure 3. Optimal emission paths for regional manufacturing sectors.

Figure 3. Optimal emission paths for regional manufacturing sectors.

Figure 3 shows the optimal emission paths for regional manufacturing sectors under sectoral emissions control and total emissions control strategies with their actual emissions. Under sectoral emissions control strategies, eastern coastal and southern coastal regions (i.e., more developed parts of the country) showed high energy use efficiency and the potential to produce more value-added yield. To this effect, eastern and southern coastal regions were given more emission quotas in 1995–2011. Other regions, conversely, were limited by emissions reduction regulations of varying degree. Northern coastal, middle Yellow River, and southwest regions began dramatically overproducing CO₂ emissions, so those regions must improve energy use efficiency as soon as possible. Under total emissions control strategy, the manufacturing sector in each region obtained lower emission quotas than the control sectoral emissions allowance, suggesting that policies should be implemented to ensure that manufacturing emission quotas are extended to other sectors.

Given that the aggregated emissions from 29 provinces is equal to the actual emissions aggregated at the province level for regional construction sectors. As marked by red lines in Figure 4, construction in the northern coastal region must be strongly regulated. Northern coastal region inputs excessive energy into building infrastructure and housing, and absolutely must significantly improve energy use efficiency. Northwest and northeast regions obtained emission quotas greater than their actual emissions from 2003 to stay financially viable. The eastern coastal region faced similar emissions reduction regulations as the northern coastal region. The middle Yellow River, middle Yangtze River, and southwest regions should reduce their emissions in early periods and increase emissions in latter periods, indicating that the energy efficiency of the construction sector in these regions improved rapidly. Suppose that emission quotas are transferable across sectors and regions, as marked by green lines in Figure 4, the construction sector in each region obtained more emission quotas than their actual emissions, suggesting that construction should accept emission quotas from other sectors and does not require any major emissions reduction policies be enacted.

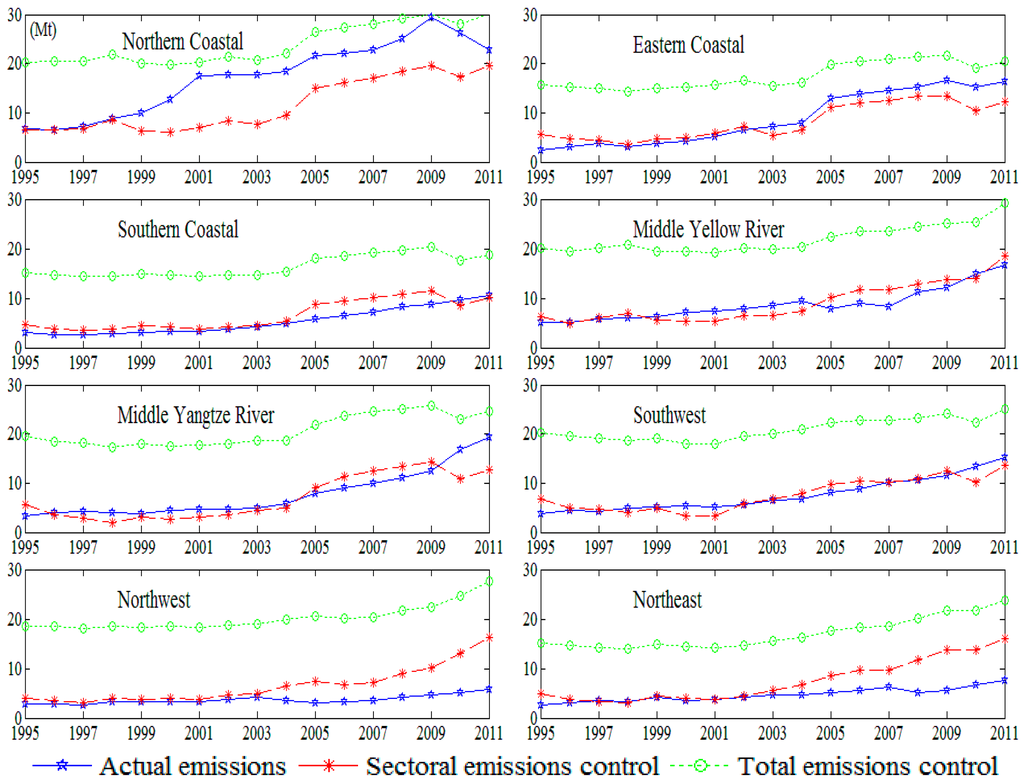
Figure 4. Optimal emission paths for regional construction sectors.

Figure 4. Optimal emission paths for regional construction sectors.

As shown by red lines in Figure 5, for regional transportation sector, goods transported most commonly in northwest and northeast regions are coal, industrial equipment, and production materials, which have low value-added yield compared to agriculture products and tourism. To this effect, northwest and northeast regions received emissions reduction regulations in 1995–2011. Southwest region was allowed to increase its emissions from 2003 to 2011 even though its actual emissions dramatically increased, which can be attributed to energy efficiency for the transportation sector in southwest region improved rapidly in 2003–2011. The energy efficiency of the transportation sector was higher in southern coastal region than other regions, so it obtained emission quotas from other regions in 2005–2010. Northern coastal, eastern coastal, middle Yellow River, and middle Yangtze River regions were required to reduce emissions in 1995–2003, but still received more emission quotas in 2003–2011. These results altogether suggest that strategies where emissions are reduced first and increased later are suitable for these regions, evidenced by their enhanced energy efficiency over time. Results also suggested that the transportation sector should accept emission quotas from other sectors, because it is not a major producer of emissions.

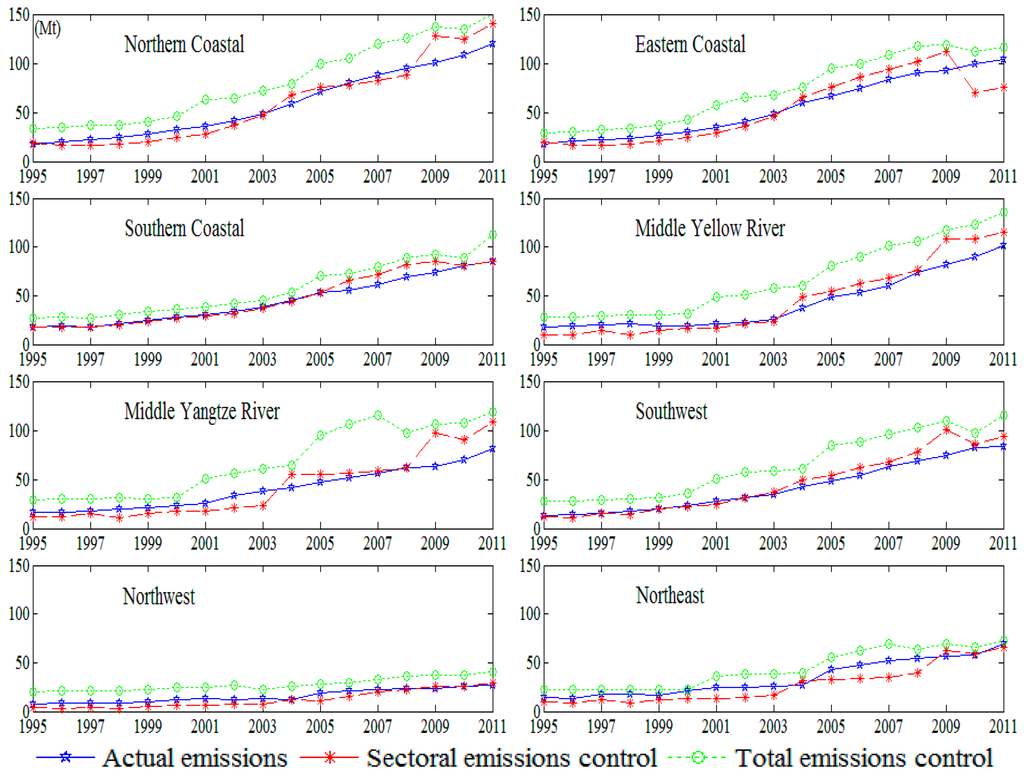
Figure 5. Optimal emission paths for regional transportation sector.

Figure 5. Optimal emission paths for regional transportation sector.

As marked by red lines in Figure 6, under sectoral emissions control strategy, northern coastal regions received strict emissions reduction regulations. The energy input for the service sector in the northern coastal region was excessive, and efficiency of energy utilization should be improved immediately. The northeast region also received emissions reduction regulation, as it employs extensive heating equipment (which is carbon-intensive) to cope with its cold climate. Middle Yangtze River and southwest regions obtained their emission quotas continuously in 1995–2011, suggesting that these regions should increase emissions to release value-added potential in observed time series. Eastern coastal and southern coastal regions, as mentioned above, are China’s most developed areas and showed high energy efficiency and value-added yield in the service sector, so they do not particularly require emissions reduction regulations. Under total emissions control strategy, as marked by green lines in Figure 6, the service sector in almost all regions received more emissions than actual—the only exception was the northern coastal region, which received strict emissions reduction regulations in 2006–2011. Northern coastal region, to this effect, is urgently tasked with improving its service sector’s energy efficiency. In general, the service sector should obtain emission quotas from other sectors as it does not require any major reduction in emissions.

In order to compare the differences between optimal emission paths and actual emission paths according to controlled sectoral and total emissions, we defined the degree of cumulative deviation as follows:

$$d{(s)}_l={\displaystyle \sum _{t=1}^T\left|\frac{\overline{b}{(s)}_l^t-b_l^t}{b_l^t}\right|}/T$$

(12)

Figure 6. Optimal emission paths for regional service sectors.

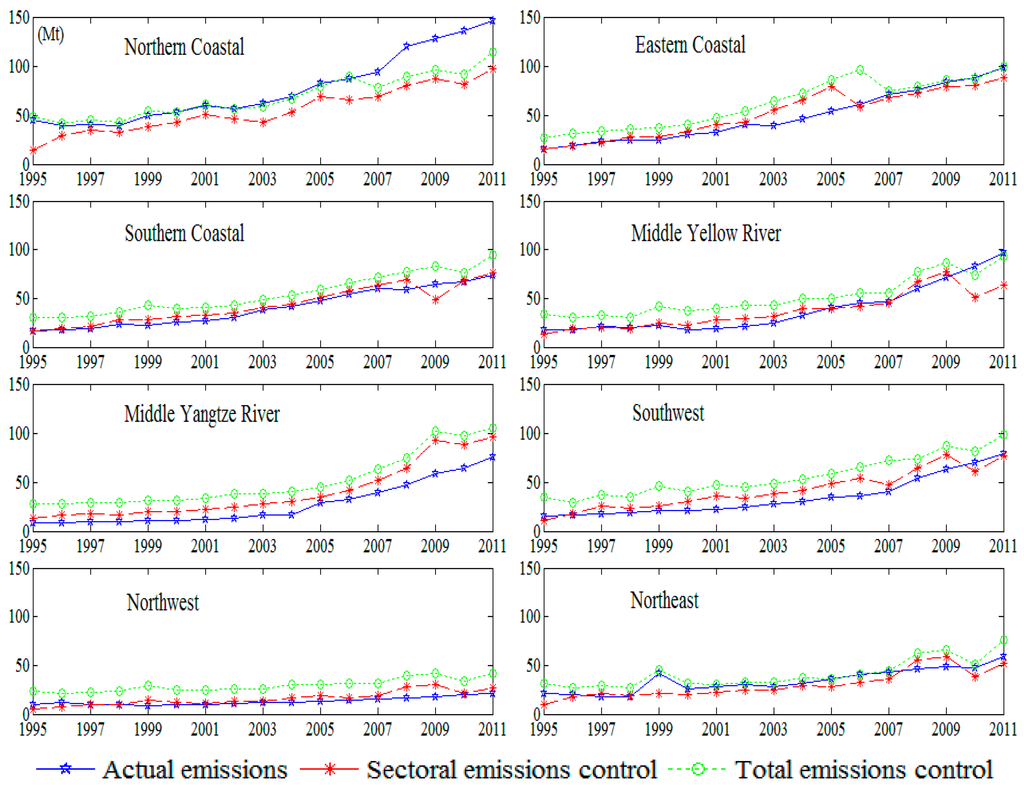
Figure 6. Optimal emission paths for regional service sectors.

Similarly, we defined the following absolute quantity of cumulative deviation for optimal emission path and actual emission path:

$$d{(s)}_l^t=\left|\overline{b}{(s)}_l^t-b_l^t\right|$$

(13)

In Models (12) and (13), $s\in \left\{\mathrm{sectoral emissions control, total emissions control}\right\}$, $t=\{1995-2011\}$, $l\in \left\{\text{agriculture, manufacturing, constructing, transportation, service}\right\}$. $\overline{b}{(s)}_l^t$ denotes optimal emissions from emissions control strategy s in sector l at period t, and $b_l^t$ denotes actual emissions from sector l at period t.

As shown in Table 4, under sectoral emissions control strategy, the degree of deviation was largest in the construction sector and smallest in manufacturing. In effect, there were significant differences in construction emissions efficiency between provinces, and the manufacturing sector needs tightly controlled energy inputs overall. Under total emissions control strategy, the degree of deviation was largest in the transportation sector (attributed to receiving the largest emissions quota, 259.38 million tons, from the manufacturing sector, as transportation networks expanded).The second largest accepter of emission quotas was the agriculture sector, which required mechanization (and related energy input) to substitute for labor force input. The service sector also has rigid energy demands to maintain operation, but its energy input is not the important production factor—instead, most of its energy consumption was due to mechanical heating and refrigeration.

As shown in Table 5, western and northeastern areas had the largest degree of deviation under sectoral emissions control, indicating that western and northeastern China utilize energy very differently between their respective provinces and sectors. Eastern area had the smallest degree of deviation under sectoral emissions control, indicating that the gaps in emissions efficiency between provinces in eastern China are fairly narrow. Under total emissions control strategy, the degrees of deviation are similar to those under sectoral emissions control strategy. Central, western, and northeastern areas show low emission efficiency overall, so these areas should provide emission quotas to eastern areas, which have higher emission efficiency.

We used Models (10) and (11) to measure the shadow price on CO₂ emissions under sectoral and total emissions control strategies. We also measured the shadow price under variable returns to scale, based on the directional distance function. The directional distance function serves to increase desirable outputs and reducing undesirable outputs with the directional vector $(g^y,g^c)=(1,-1)$ and the same scaling factor $\mathsf{\beta }$. The specific expression can be found in a previous study [68].

The average shadow price for all province/sectors over 1995–2011 from strategies of sectoral emissions control (SEC), total emissions control (TEC), and directional distance function (DDF) can be calculated.

Table 4. Cumulative deviations between optimal and actual emission paths at sector level.

Sector	Deviation Under Sectoral Emissions Control		Deviation Under Total Emissions Control
	Degree	Quantity (Unit: 10 Thousand Tons)	Degree	Quantity (Unit: 10 Thousand Tons)
Agriculture	0.635	0	0.091	173655
Manufacturing	0.128	0	0.072	-784174
Construction	1.984	0	0.141	173426
Transportation	0.539	0	0.183	259380
Service	0.439	0	0.081	177712

Table 4. Cumulative deviations between optimal and actual emission paths at sector level.

Sector	Deviation Under Sectoral Emissions Control		Deviation Under Total Emissions Control
	Degree	Quantity (Unit: 10 Thousand Tons)	Degree	Quantity (Unit: 10 Thousand Tons)
Agriculture	0.635	0	0.091	173655
Manufacturing	0.128	0	0.072	-784174
Construction	1.984	0	0.141	173426
Transportation	0.539	0	0.183	259380
Service	0.439	0	0.081	177712

Table 5. Cumulative deviations between optimal and actual emission paths at area level.

Area	Deviation Under Sectoral Emissions Control		Deviation Under Total Emissions control
	Degree	Quantity (Unit: 10 Thousand Tons)	Degree	Quantity (Unit: 10 Thousand Tons)
East	0.951	117,672	0.908	123,870.9
Central	1.146	−47,519.2	1.123	−28,893.7
West	1.758	1932.418	1.939	−28,708.4
Northeast	1.794	−72,085.3	1.905	−66,268.8

Table 5. Cumulative deviations between optimal and actual emission paths at area level.

Area	Deviation Under Sectoral Emissions Control		Deviation Under Total Emissions control
	Degree	Quantity (Unit: 10 Thousand Tons)	Degree	Quantity (Unit: 10 Thousand Tons)
East	0.951	117,672	0.908	123,870.9
Central	1.146	−47,519.2	1.123	−28,893.7
West	1.758	1932.418	1.939	−28,708.4
Northeast	1.794	−72,085.3	1.905	−66,268.8

As shown in Table 6, under sectoral emissions control strategy, the shadow price of manufacturing and construction sectors were both zero. To this effect, these sectors can obtain maximum value-added yield by allocating CO₂ emission quotas appropriately within each sector. Agriculture, transportation, and service sectors showed negative values after optimization, indicating that these sectors should receive more emission quotas from other sectors to increase their value-added yield. The transportation sector had the largest negative value, suggesting that it needs more emission quotas to reach its value-added potential. The shadow prices for all sectors were zero under total emissions control strategy, indicating that all productive activities obtained maximum value-added yield by allocating CO₂ emission quotas across all sectors.

Table 6. Average values of provincial CO₂ emission shadow prices for each sector.

Year (1995–2011)	Agriculture			Manufacturing			Construction			Transportation			Service
	DDF	SEC	TEC	DDF	SEC	TEC	DDF	SEC	TEC	DDF	SEC	TEC	DDF	SEC	TEC
Average	−0.504	−0.050	0	−0.090	0	0	−1.471	0	0	−0.152	−0.109	0	−0.921	−0.057	0

Table 6. Average values of provincial CO₂ emission shadow prices for each sector.

Year (1995–2011)	Agriculture			Manufacturing			Construction			Transportation			Service
	DDF	SEC	TEC	DDF	SEC	TEC	DDF	SEC	TEC	DDF	SEC	TEC	DDF	SEC	TEC
Average	−0.504	−0.050	0	−0.090	0	0	−1.471	0	0	−0.152	−0.109	0	−0.921	−0.057	0

The directional distance function optimization model aims to establish policies that target CO₂ emissions while increasing value-added yield for all productive activities. Our proposed model aims to optimize allocation of fixed, undesirable output quantity to maximize the desirable output. The shadow price generated through our model is smaller than that of the directional distance function model due to the lack of necessity for severe regulations to decrease undesirable output when increasing desirable output simultaneously.

5. Conclusions

The optimal path for controlling CO₂ emissions, classified by both sector and region, represents a cross-analytical foundation for sectoral and regional emissions reduction policies. Many previous studies have explored the DEA approach to allocate emissions allowances at different levels, but in this study, we developed a new environmental DEA technology based on Kuosmanen environmental DEA technology which changes weak disposability to strong disposability on undesirable outputs, and ensures non-positive shadow price on undesirable outputs. We proposed a centralized DEA model based on multi-sector and multi-region data over time to explore efficiency maximization in China. The model was applied to study the optimal allocation of CO₂ emissions for each province and its sectors in China from 1995 to 2011, specifically, and the optimal paths for controlling CO₂ emissions at sectoral and regional levels under sectoral emissions control and total emissions control strategies were derived. We also designed a dual model for our centralized DEA model, and used it to analyze the shadow price on CO₂ emissions.

We conducted an empirical analysis on a sample of province/sector level data from 1995–2011. The results indicate that the manufacturing sector showed the most dramatic reduction in emissions, and emissions in the agriculture, construction, transportation, and service sectors all increased. The transportation sector was the largest accepter of emission quotas. Under sectoral emission control regulation, the construction sector must significantly increase its energy use efficiency, as its allowable emissions must undergo the most dramatic adjustment. Under total emission control regulation, the emission quotas should be removed from the manufacturing sector.

Agriculture, construction, transportation, and service sectors should receive more emission quotas to release their value-added potential. At the region level, western and northeastern areas require the most drastic adjustment to allowable emissions, which can be attributed to differences in emission efficiency among regions (as described in detail above). Eastern area has high energy use efficiency, so it can obtain more emission quotas from other areas. Based on our shadow price analysis, total emission control regulation policies can indeed enhance value-added potentials for all sectors. If optimization of CO₂ emissions is centralized, emissions increase or decrease bidirectionally, ensuring that the shadow price on CO₂ emissions is lower than the directional distance function regulation, decreasing CO₂ emissions and increasing value-added yield.

Despite the merits of this study, it did encounter limitations. First, we only considered agriculture, manufacturing, construction, transportation, and service sectors. The manufacturing sector, in particular, is divisible into more detailed sub-sectors. Second, our centralized model aims to realize the optimal allocation of CO₂ emission quotas while maximizing desirable output, which keeps capital and labor force input fixed, and fails to account for the price level of other production factors. In future, we plan to include the price of production factors into the dual model of our centralized model and research their influence on the allocation of CO₂ emission quotas. Third, our model mainly depicts environmental production technology and focuses on desirable output potentials while allocating undesirable outputs, but selecting detailed technology to improve emission efficiency is the next necessary step. We plan to discover how to integrate our centralized DEA model into energy technology system optimization platforms, such as TIMES (The Integrated MARKAL-EFOM System) (http://www.iea-etsap.org/web/Times.asp), LEAP (Long range Energy Alternatives Planning System) (http://www.energycommunity.org/default.asp?action=47), and AIM (The Asian Pacific Integrated Model) (http://www-iam.nies.go.jp/aim/datalibrary.htm) in future studies.