Water Scarcity Footprints by Considering the Differences in Water Sources
Abstract
:1. Introduction
2. Methods
2.1. Characterization Model
| Dataset | Version | Resolution | Period | Terrestrial (mm/year) | Ocean (mm/year) | Global (mm/year) |
|---|---|---|---|---|---|---|
| CMAP [32] | 0203 | 2.5 × 2.5 degrees, monthly | 1979–2001 | 689 | 1093 | 975 |
| GPCP [33] | 2.2 | 2.5 × 2.5 degrees, monthly | 1979–2010 | 845 | 1021 | 975 |
| GPCP [34] | 1DD | 1 × 1 degrees, daily | 1997–2000 | 785 | 1006 | 949 |
| Baumgartner and Reichel [35] | - | - | - | 830 | 1007 | 970 |
| Korzun et al. [36] | - | - | - | 800 | 1270 | 1130 |
| GPCC [37] | v6_1.0 | 1 × 1 degrees, monthly | 1901–2010 | 781 | - | - |
| GSWP2 [38,39] | B1 | 1 × 1 degrees, 3 hourly | 1986–1995 | 699 | - | - |
| WFD [40] | - | 0.5 × 0.5 degrees, 6 hourly | 1960–2000 | 867 | - | - |
| Lvovitch [41] | - | - | - | 834 | - | - |
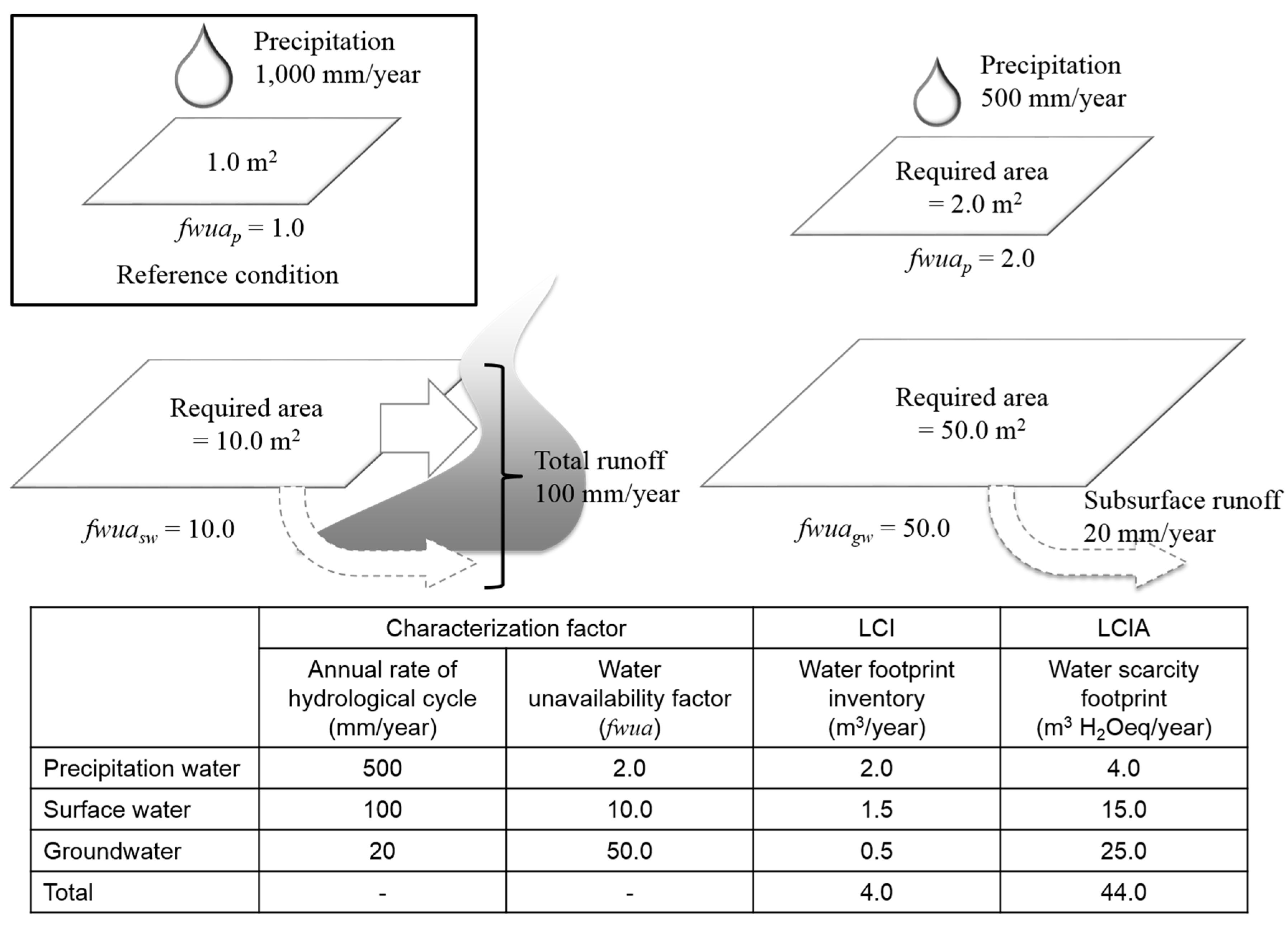
2.2. Estimating Characterization Factors
2.3. LCIA of the Global Virtual Water Trade
3. Results
3.1. Global Distribution

3.2. Country-Average Values
| Continent | Country | Entire country | Rainfed Cropland | Irrigated Cropland | ||||
|---|---|---|---|---|---|---|---|---|
| fwuap | fwuasw | fwuagw | fwuap | fwuap | fwuasw | fwuagw | ||
| Asia | China | 1.6 | 4.6 | 10.0 | 1.4 | 1.2 | 3.2 | 7.4 |
| India | 0.8 | 1.4 | 6.8 | 0.8 | 0.8 | 1.4 | 6.8 | |
| Russia | 2.0 | 4.7 | 6.5 | 1.7 | 1.8 | 4.8 | 6.1 | |
| Indonesia | 0.4 | 0.6 | 2.8 | 0.4 | 0.4 | 0.7 | 3.0 | |
| Bangladesh | 0.5 | 0.7 | 4.1 | 0.5 | 0.5 | 0.7 | 4.1 | |
| Vietnam | 0.5 | 0.9 | 4.0 | 0.5 | 0.5 | 0.9 | 4.0 | |
| Turkey | 1.7 | 4.0 | 6.0 | 1.7 | 1.7 | 4.0 | 6.0 | |
| Thailand | 0.6 | 1.2 | 4.2 | 0.6 | 0.7 | 1.3 | 4.3 | |
| Pakistan | 3.3 | 7.2 | 15.0 | 2.9 | 3.1 | 6.2 | 12.9 | |
| Myanmar | 0.5 | 0.6 | 3.9 | 0.5 | 0.5 | 0.7 | 4.0 | |
| Malaysia | 0.3 | 0.6 | 2.5 | 0.3 | 0.4 | 0.6 | 2.6 | |
| Europe | France | 1.0 | 1.8 | 3.4 | 1.0 | 1.0 | 1.8 | 3.4 |
| Germany | 1.2 | 2.2 | 3.4 | 1.2 | 1.2 | 2.3 | 3.5 | |
| Spain | 1.5 | 3.5 | 6.3 | 1.6 | 1.5 | 3.5 | 6.3 | |
| United Kingdom | 0.9 | 1.6 | 3.4 | 0.9 | 1.1 | 2.1 | 3.8 | |
| Ukraine | 1.7 | 4.6 | 5.1 | 1.7 | 1.7 | 4.7 | 5.2 | |
| Poland | 1.5 | 3.3 | 4.0 | 1.5 | 1.5 | 3.3 | 4.0 | |
| Italy | 1.2 | 2.3 | 4.2 | 1.1 | 1.2 | 2.3 | 4.2 | |
| Netherlands | 1.1 | 2.1 | 3.4 | 1.1 | 1.1 | 2.1 | 3.4 | |
| North America | United States | 1.2 | 3.4 | 6.5 | 1.1 | 1.2 | 3.8 | 6.7 |
| Canada | 1.7 | 3.6 | 5.8 | 1.3 | 1.3 | 3.0 | 5.3 | |
| Mexico | 1.2 | 3.6 | 10.9 | 1.2 | 1.3 | 4.0 | 11.6 | |
| South America | Brazil | 0.6 | 1.2 | 4.0 | 0.6 | 0.6 | 1.5 | 4.7 |
| Argentina | 1.4 | 5.8 | 10.7 | 1.1 | 1.2 | 4.9 | 9.2 | |
| Africa | Nigeria | 0.8 | 1.6 | 5.7 | 0.8 | 0.8 | 1.5 | 5.7 |
| Egypt | 47.7 | 41.0 | 79.1 | 1985.4 | 23.6 | 12.7 | 24.3 | |
| Oceania | Australia | 1.8 | 8.8 | 23.3 | 1.5 | 1.5 | 6.5 | 16.2 |
3.3. Flow of Water Footprint Inventory and Water Scarcity Footprint
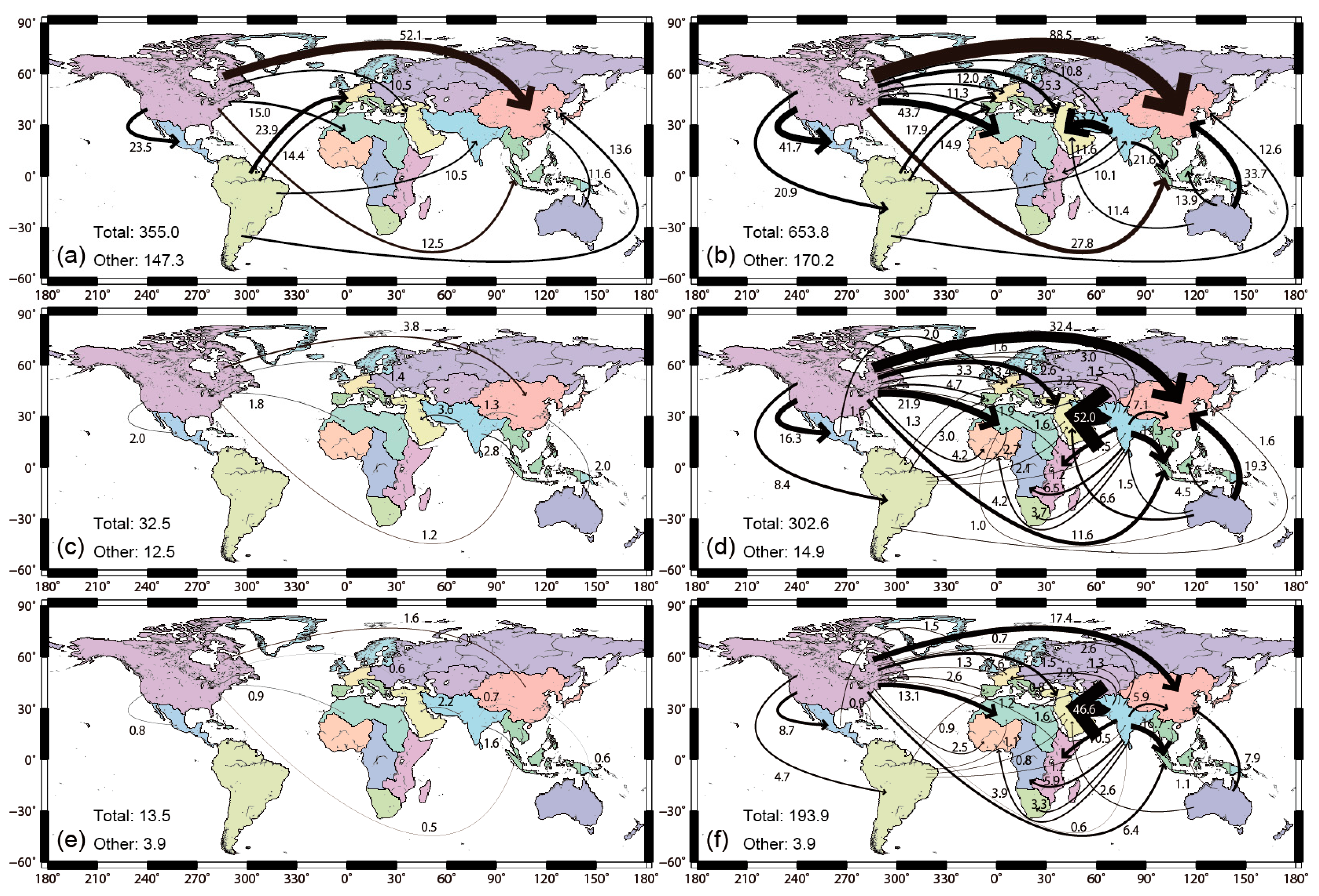
4. Discussion
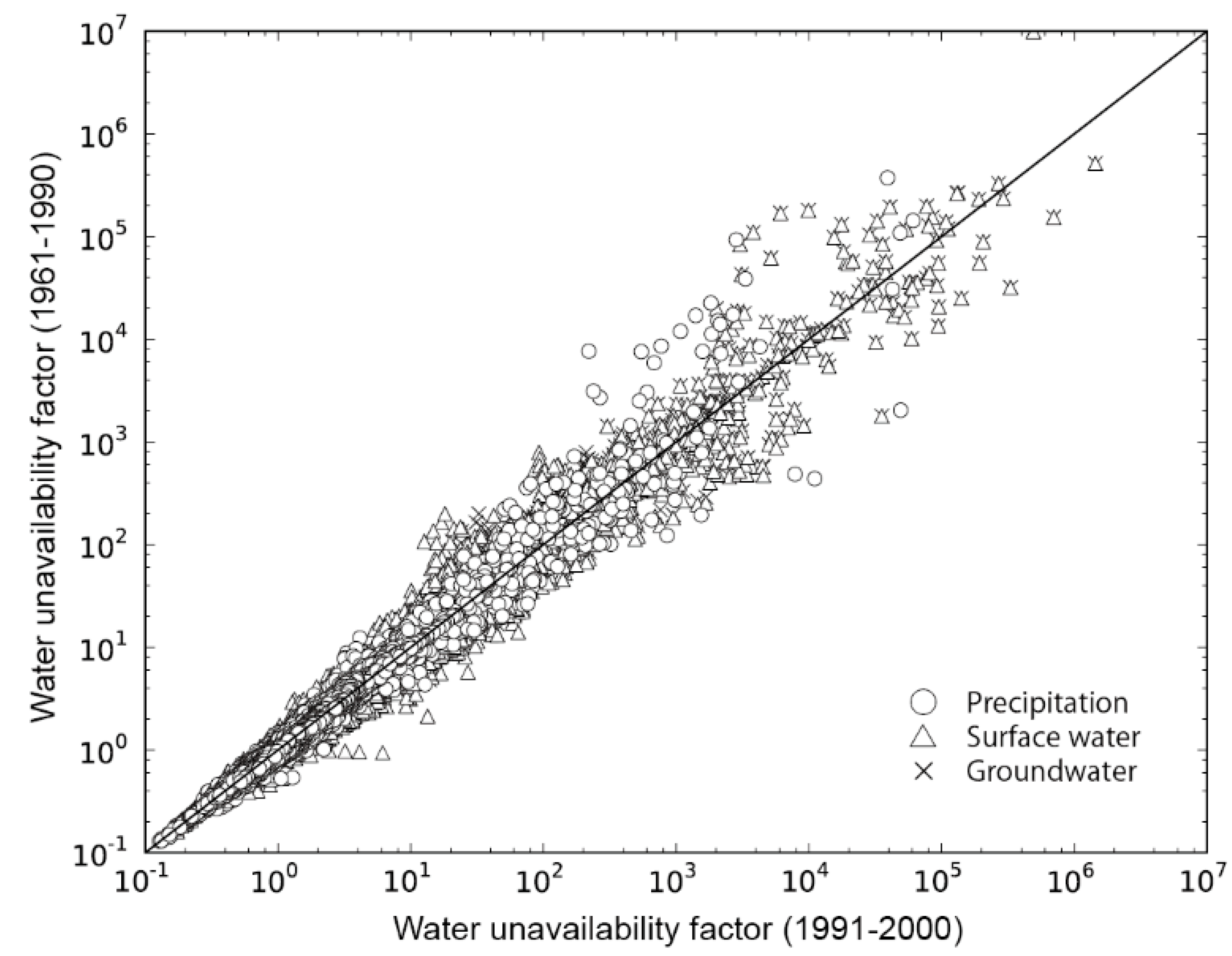
4.1. Uncertainty of Characterization Factors


4.2. Applications in LCIAs
| Method | Reference | Weighting by Place | Weighting by Time | Weighting by Source | Reflecting Effects of Conservation |
|---|---|---|---|---|---|
| Water availability factor (fwua) | This study | Y | Y | Y | Y |
| Water Stress Index (WSI) | Pfister et al. [20] | Y | Y | N | Y |
| Groundwater Footprint (GF) | Gleeson et al. [23] | Y | N | N | Y |
| Water footprint (WFN) | Hoekstra et al. [4] | N | N | N | N |
5. Conclusions
Supplementary Files
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shiklomanov, I.A.; Rodda, J.C. World Water Resources at the Beginning of the 21st Century; International Hydrology Series; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- FAO. The State of the World’s Land and Water Resources for Food and Agriculture (SOLAW)—Managing Systems at Risk; Food and Agriculture Organization of the United Nations: Rome, Italy, 2011. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998. [Google Scholar]
- Hoekstra, A.Y.; Chapagain, A.K.; Aldaya, M.M.; Mekonnen, M.M. The Water Footprint Assessment Manual: Setting the Global Standard; Earthscan: London, UK, 2011. [Google Scholar]
- Ercin, A.E.; Aldaya, M.M.; Hoekstra, A.Y. Corporate water footprint accounting and impact assessment: The case of the water footprint of a sugar-containing carbonated beverage. Water Resour. Manag. 2011, 25, 721–741. [Google Scholar] [CrossRef]
- Mekonnen, M.M.; Hoekstra, A.Y. The green, blue and grey water footprint of crops and derived crop products. Hydrol. Earth Syst. Sci. 2011, 15, 1577–1600. [Google Scholar] [CrossRef]
- Wu, M.; Chiu, Y.; Demissie, Y. Quantifying the regional water footprint of biofuel production by incorporating hydrologic modeling. Water Resour. Res. 2012, 48, W10518. [Google Scholar] [CrossRef]
- Gerbens-Leenes, P.W.; Xu, L.; de Vries, G.J.; Hoekstra, A.Y. The blue water footprint and land use of biofuels from algae. Water Resour. Res. 2014, 50, 8549–8563. [Google Scholar] [CrossRef]
- Hoekstra, A.Y.; Chapagain, A.K.; Aldaya, M.M.; Mekonnen, M.M. Water Footprint Manual, State of the Art 2009; Water Footprint Network: Enschede, The Netherlands, 2009. [Google Scholar]
- Heijungs, R.; Guinée, J.B.; Huppes, G.; Lankreijer, R.M.; Udo de Haes, H.A.; Wegener Sleeswijk, A.; Ansems, A.M.M.; Eggels, P.G.; van Duin, R.; de Goede, H.P. Environmental Life Cycle Assessment of Products I: Guide—October; B&G Leiden University: Leiden, The Netherlands, 1992. [Google Scholar]
- Zhang, L.; Dawes, W.R.; Walker, G.R. Response of mean annual evapotranspiration to vegetation changes at catchment scale. Water Resour. Res. 2001, 37, 701–708. [Google Scholar] [CrossRef]
- Berger, M.; Finkbeiner, M. Methodological challenges in volumetric and impact-oriented water footprints. J. Ind. Ecol. 2013, 17, 79–89. [Google Scholar] [CrossRef]
- Bayart, J.B.; Bulle, C.; Deschênes, L.; Margni, M.; Pfister, S.; Vince, F.; Koehler, A. A framework for assessing off-stream freshwater use in LCA. Int. J. LCA 2010, 15, 439–453. [Google Scholar] [CrossRef]
- ISO. ISO 14046 Environmental Management, Water Footprint—Principles, Requirements and Guidelines; International Organization for Standardization: Geneva, Switzerland, 2014. [Google Scholar]
- ISO. ISO 14040 Environmental Management—Life Cycle Assessment—Principles and Framework; International Organization for Standardization: Geneva, Switzerland, 2006. [Google Scholar]
- Frischknecht, R.; Jungbluth, N.; Althaus, H.; Doka, G.; Dones, R.; Heck, T.; Hellweg, S.; Hischier, R.; Nemecek, T.; Rebitzer, G.; et al. The ecoinvent database: Overview and methodological framework. Int. J. LCA 2005, 10, 3–9. [Google Scholar] [CrossRef]
- Hanasaki, N.; Inuzuka, T.; Kanae, S.; Oki, T. An estimation of global virtual water flow and sources of water withdrawal for major crops and livestock products using a global hydrological model. J. Hydrol. 2010, 384, 232–244. [Google Scholar] [CrossRef]
- Pfister, S.; Bayer, P.; Koehler, A.; Hellweg, S. Environmental impacts of water use in global crop production: Hotspots and trade-offs with land use. Environ. Sci. Technol. 2011, 45, 5761–5768. [Google Scholar] [CrossRef] [PubMed]
- ISO. ISO 14044 Environmental Management—Life Cycle Assessment—Requirements and Guidelines; International Organization for Standardization: Geneva, Switzerland, 2006. [Google Scholar]
- Pfister, S.; Koehler, A.; Hellweg, S. Assessing the environmental impacts of freshwater consumption in LCA. Environ. Sci. Technol. 2009, 43, 4098–4104. [Google Scholar] [CrossRef] [PubMed]
- Alcamo, J.; Henrichs, T. Critical regions: A model-based estimation of world water resources sensitive to global changes. Aquat. Sci. 2002, 64, 352–362. [Google Scholar] [CrossRef]
- Alcamo, J.; Doll, P.; Henrichs, T.; Kaspar, F.; Lehner, B.; Rosch, T.; Siebert, S. Development and testing of the WaterGAP 2 global model of water use and availability. Hydrol. Sci. J. 2003, 48, 317–337. [Google Scholar] [CrossRef]
- Gleeson, T.; Wada, Y.; Bierkens, M.F.P.; van Beek, L.P.H. Water balance of global aquifers revealed by groundwater footprint. Nature 2012, 488, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Jefferies, D.; Muñoz, I.; Hodges, J.; King, V.J.; Aldaya, M.M.; Ercin, A.E.; Milà i Canals, L.; Hoekstra, A.Y. Water Footprint and Life Cycle Assessment as approaches to assess potential impacts of products on water consumption. Key learning points from pilot studies on tea and margarine. J. Clean. Prod. 2012, 33, 155–166. [Google Scholar] [CrossRef]
- Milà i Canals, L.; Chenoweth, J.; Chapagain, A.; Orr, S.; Antón, A.; Clift, R. Assessing freshwater use impacts in LCA: Part I—Inventory modelling and characterisation factors for the main impact pathways. Int. J. LCA 2009, 14, 28–42. [Google Scholar] [CrossRef]
- Guinée, J.B.; Heijungs, R. A proposal for the definition of resource equivalency factors for use in product life-cycle assessment. Environ. Toxicol. Chem. 1995, 14, 917–925. [Google Scholar] [CrossRef]
- Pfister, S.; Baumann, J. Monthly characterization factors for water consumption and applica-tion to temporally explicit cereals inventory. In Proceedings of the 8th International Conference on LCA in the Agri-Food Sector, Rennes, France, 2–4 October 2012.
- Allan, J.A. Virtual water: A strategic resource global solutions to regional deficits. Groundwater 1998, 36, 545–546. [Google Scholar] [CrossRef]
- Oki, T.; Kanae, S. Global hydrological cycles and world water resources. Science 2006, 313, 1068–1072. [Google Scholar] [CrossRef] [PubMed]
- Yano, S.; Hanasaki, N.; Itsubo, N.; Oki, T. Characterization factors for water availability footprint considering the difference of water sources based on a global water resource model. J. LCA Jpn. 2014, 10, 327–339. [Google Scholar] [CrossRef]
- European Commission. Joint Research Centre—Institute for Environment and Sustainability International Reference Life Cycle Data System (ILCD) Handbook—General Guide for Life Cycle Assessment—Detailed Guidance; Publications Office of the European Union: Luxembourg, 2010. [Google Scholar]
- Xie, P.; Arkin, P.A. Global precipitation: A 17-year monthly analysis based on gauge observations, satellite estimates, and numerical model outputs. Bull. Am. Meteorol. Soc. 1997, 78, 2539–2558. [Google Scholar] [CrossRef]
- Adler, R.F.; Huffman, G.J.; Chang, A.; Ferraro, R.; Xie, P.; Janowiak, J.; Rudolf, B.; Schneider, U.; Curtis, S.; Bolvin, D.; et al. The version-2 global precipitation climatology project (GPCP) monthly precipitation analysis (1979–present). J. Hydrometeorol. 2003, 4, 1147–1167. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Morrissey, M.; Bolvin, D.T.; Curtis, S.; Joyce, R.; McGavock, B.; Susskind, J. Global precipitation at one-degree daily resolution from multisatellite observations. J. Hydrometeorol. 2001, 2, 36–50. [Google Scholar] [CrossRef]
- Baumgartner, A.; Reichel, E. The World Water Balance: Mean Annual Global, Continental and Maritime Precipitation, Evaporation and Run-Off; Elsevier Scientific Publishing Company: Amsterdam, The Netherlands; New York, NY, USA, 1975. [Google Scholar]
- Korzun, V.I.; Sokolov, A.A.; Budyko, M.I.; Voskresensky, K.P.; Kalinin, G.P. World Water Balance and Water Resources of the Earth, Studies and Reports in Hydrology; Studies and Reports in Hydrology (UNESCO), no. 25; United Nations Educational, Scientific and Cultural Organization: Paris, France, 1978. [Google Scholar]
- Rudolf, B.; Beck, C.; Grieser, J.; Schneider, U. Global Precipitation Analysis Products of the GPCC; Global Precipitation Climatology Centre (GPCC); Deutscher Wetterdienst: Offenbach am Main, Germany, 2005. [Google Scholar]
- Dirmeyer, P.A.; Gao, X.A.; Zhao, M.; Guo, Z.C.; Oki, T.; Hanasaki, N. GSWP-2—Multimodel analysis and implications for our perception of the land surface. Bull. Am. Meteorol. Soc. 2006, 87, 1381–1397. [Google Scholar] [CrossRef]
- Hanasaki, N.; Kanae, S.; Oki, T.; Masuda, K.; Motoya, K.; Shirakawa, N.; Shen, Y.; Tanaka, K. An integrated model for the assessment of global water resources—Part 1: Model description and input meteorological forcing. Hydrol. Earth Syst. Sci. 2008, 12, 1007–1025. [Google Scholar] [CrossRef]
- Weedon, G.P.; Gomes, S.; Viterbo, P.; Shuttleworth, W.J.; Blyth, E.; Österle, H.; Adam, J.C.; Bellouin, N.; Boucher, O.; Best, M. Creation of the WATCH forcing data and Its use to assess global and regional reference crop evaporation over land during the twentieth century. J. Hydrometeorol. 2011, 12, 823–848. [Google Scholar] [CrossRef]
- Lvovitch, M.I. The global water balance. US IHD Bull. 1973, 23, 28–53. [Google Scholar] [CrossRef]
- Feng, K.; Chapagain, A.; Suh, S.; Pfister, S.; Hubacek, K. Comparison of bottom-up and top-down approaches to calculating the water footprints of nations. Econ. Syst. Res. 2011, 23, 371–385. [Google Scholar] [CrossRef]
- CIESIN. Gridded Population of the World Version 3 (GPWv3) Data Collection, Columbia University. Available online: http://sedac.ciesin.columbia.edu/data/collection/gpw-v3 (accessed on 1 August 2013).
- Ramankutty, N.; Evan, A.; Monfreda, C.; Foley, J.A. Farming the planet: 1. Geographic distribution of global agricultural lands in the year 2000. Glob. Biogeochem. Cycles 2008, 22, GB1003. [Google Scholar] [CrossRef]
- Siebert, S.; Doll, P.; Hoogeveen, J.; Faures, J.M.; Frenken, K.; Feick, S. Development and validation of the global map of irrigation areas. Hydrol. Earth Syst. Sci. 2005, 9, 535–547. [Google Scholar] [CrossRef]
- FAOSTAT. Available online: http://faostat.fao.org/ (accessed on 5 August 2014).
- Tang, Q.; Lettenmaier, D.P. 21st century runoff sensitivities of major global river basins. Geophys. Res. Lett. 2012, 39, L06403. [Google Scholar] [CrossRef]
- Kounina, A.; Margni, M.; Bayart, J.B.; Boulay, A.M.; Berger, M.; Bulle, C.; Frischknecht, R.; Koehler, A.; Milà i Canals, L.; Motoshita, M.; et al. Review of methods addressing freshwater use in life cycle inventory and impact assessment. Int. J. LCA 2013, 18, 707–721. [Google Scholar] [CrossRef]
- Boulay, A.M.; Bulle, C.; Bayart, J.B.; Deschenes, L.; Margni, M. Regional characterization of freshwater use in LCA: Modeling direct impacts on human health. Environ. Sci. Technol. 2011, 45, 8948–8957. [Google Scholar] [CrossRef] [PubMed]
- Bösch, M.E.; Hellweg, S.; Huijbregts, M.A.J.; Frischknecht, R. Applying cumulative exergy demand (CExD) indicators to the ecoinvent database. Int. J. LCA 2007, 12, 181–190. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yano, S.; Hanasaki, N.; Itsubo, N.; Oki, T. Water Scarcity Footprints by Considering the Differences in Water Sources. Sustainability 2015, 7, 9753-9772. https://doi.org/10.3390/su7089753
Yano S, Hanasaki N, Itsubo N, Oki T. Water Scarcity Footprints by Considering the Differences in Water Sources. Sustainability. 2015; 7(8):9753-9772. https://doi.org/10.3390/su7089753
Chicago/Turabian StyleYano, Shinjiro, Naota Hanasaki, Norihiro Itsubo, and Taikan Oki. 2015. "Water Scarcity Footprints by Considering the Differences in Water Sources" Sustainability 7, no. 8: 9753-9772. https://doi.org/10.3390/su7089753
APA StyleYano, S., Hanasaki, N., Itsubo, N., & Oki, T. (2015). Water Scarcity Footprints by Considering the Differences in Water Sources. Sustainability, 7(8), 9753-9772. https://doi.org/10.3390/su7089753







