2. Materials and Methods
2.1. Indicator Selection and Data Source
Research for a vegetable prices’ early-warning system is focused on defining an alert, looking for the alert source, analyzing alertness, determining the alert degree and absolving the alert, and early-warning indicators include alert indicators and warning-sign indicators. An alert stems from an imbalance in the market supply and demand, whose external performance is measured by fluctuations of the vegetable prices, and we use the vegetable price index as the alert indicator in this paper. For the early warning for vegetable prices, the alert source mainly comes from four aspects: supplying alert source, demanding alert source, economic and policy environment alert source and the natural environment alert source. Hence, in the paper, we will consider the corresponding warning-sign indicators from the above four aspects, which are listed in
Table 1. The early-warning system for vegetable prices includes 29 warning-sign indicators, and the sample data comes from the “China Statistical Yearbook”, “China Rural Statistical Yearbook”, “National Agricultural Costs and Returns Compilation”, “China Customs Statistics Yearbook” and “The People’s Republic of China Yearbook”. The time span of each indicator is from 1995–2010, a total of 16 years of annual data. Taking into consideration the seasonal pattern of agricultural production, the time period for vegetable planting is at least one season every year. Hence, annual data are sufficient for a warning system.
It is noteworthy that, in the above-mentioned indicators, the material expense investment is represented by the total amount of annual investment into the material expenses per mu; the labor investment is represented by the annual investment of standard working days per mu; the marketization level is represented by the average per-capita annual social retailing amount of consumer goods; the urbanization level is represented by the proportion of urban population to the national population; the traffic condition is represented by the average per-capita annual freight volume; the average years of receiving education equals: the ratio of illiterate or literate people with very few words × 1 + the ratio of primary school × 6 + ratio of junior high school × 9 + ratio of senior high school × 12 + ratio of technical secondary school × 12 + ratio of junior college or above × 15.); for the relevant alternative price index, we use the retailing price index of national meat and poultry to denote it; rural residents’ consumption for vegetables equals: number of rural population × average per-capita consumption of vegetables in rural households; urban residents’ consumption for vegetables equals: number of urban population × average per-capita consumption of vegetables in urban households; vegetable disaster area equals: vegetable sown acreage × (disaster area/agricultural products sown acreage).
Table 1.
The warning-sign indicators of the vegetable prices’ early-warning system.
Table 1.
The warning-sign indicators of the vegetable prices’ early-warning system.
| Symbol | Indicator | Unit | Symbol | Indicator | Unit |
|---|
| Y | Vegetable price index | * | X15 | Engel’s coefficient of urban households | % |
| X1 | Material expenses investment | yuan/mu | X16 | Gross domestic product (GDP) | Hundred million Yuan |
| X2 | Labor investment | day/mu | X17 | Rural population | Ten thousand people |
| X3 | Cost-profit ratio | % | X18 | Net income per rural capita | yuan |
| X4 | Marketization level | yuan/person | X19 | Engel’s coefficient of rural households | % |
| X5 | Urbanization level | % | X20 | Relevant alternative price index | * |
| X6 | Traffic condition | ton/person | X21 | Vegetable exports | Ten thousand tons |
| X7 | Education level of rural labor | year | X22 | Rural residents’ consumption of vegetables | Ten thousand tons |
| X8 | Vegetable production | Ten thousand tons | X23 | Urban residents’ consumption of vegetables | Ten thousand tons |
| X9 | vegetable sown acreage | thousand hectares | X24 | Agricultural investment in fixed assets | Hundred million Yuan |
| X10 | Vegetable imports | Ten thousand tons | X25 | National agriculture expenditure | Hundred million Yuan |
| X11 | Crude oil price | U.S. dollar/barrel | X26 | Money supply | Hundred million Yuan |
| X12 | Agricultural machinery total power | gigawatts | X27 | Consumer price index (CPI) | * |
| X13 | Urban population | ten thousand people | X28 | RMB exchange rate | yuan/U.S. dollar |
| X14 | Disposable income per urban capita | yuan | X29 | Vegetable disaster area | thousand hectares |
2.2. Support Vector Regression
Estimation of a real-valued function from a finite number of samples is the central problem in regression. Similar to the well-known support vector machine, a regression model is also trained by certain training data. Support vector regression (SVR) is an effective supervised learning model armed with associated learning algorithms that recognize regression patterns [
19]. It applies the support vector method to the case of regression and maintains the fundamental features that reflect the maximal margin algorithm. Here, a non-linear function with parameters is learned by a learning machine, so as to meet the best regression effect. The method does not depend on the dimensionality of the space, nor the background of the data, which is not specific with respect to vegetable prices.
First, we denote training data by
, where
is the input sample with a corresponding value
,
I = 1,
…,
l. The idea of the support vector regression is to predict future values accurately by determining an approximation function:
where
,
and
denotes a non-linear transformation from
to a high dimensional space. The value of
and
should be found, so that values of
can be determined by minimizing the regression risk:
where
is a cost function,
is a constant and:
By substituting Equation (3) into Equation (1), we obtain:
Once the Mercer condition is meted, the dot product in Equation (4) can be replaced with kernel function
, enabling the dot product to be performed in a high-dimensional feature space with inputs in the low dimensional space. Among all of the known kernel functions, the radial basis function (RBF) is commonly used, which also satisfies Mercer’s condition:
In the meantime, the
-insensitive loss function is the most widely used cost function,
This loss function amounts to simultaneous minimization of
-insensitive loss and minimization of the norm of linear parameters (
). Theorems in computational mathematics show that the regression risk in Equation (2) and the
-insensitive loss function in Equation (6) can be minimized by solving the quadratic optimization problem in Equation (7):
subject to:
Only the non-zero values of the Lagrange multipliers,
and , in Equation (7) are useful in predicting the regression line. The constant C introduced in Equation (2) determines penalties to estimation errors. Meanwhile, C is important for a good tradeoff of penalty and accuracy. A larger C means less error, while a least C means the SVR will tolerate a larger amount of errors and that the model would be less complex.
On the other hand, for the variable
, it is computed by applying Karush–Kuhn–Tucker (KKT) conditions. This shows that the product of the Lagrange multipliers and constraints has to equal zero:
where
and
are slack variables used to measure errors outside the
-tube. Since
and
for
can be computed as follows:
Till now, the construction of the SVR is achieved.
2.3. Evaluation Algorithm of Important Features
In order to evaluate the importance of features, a numerical importance score (NIS) of each feature is obtained by analyzing the performance of the predictor with different kinds of feature combinations. In the following algorithm, the NIS of each feature is computed.
Step 1. Categorize features into n feature classes, according to certain criteria.
Step 2. For all kinds of feature combinations, run the classifying test. The total chance is N = 2n − 1. The F-score is recorded in each experiment.
Step 3. Sort N combinations with the feature list based on the value of F-score.
Step 4. Loop i from 1 to n, j from 1 to N initialize Oi and cij as zero.
Step 5. Loop j from 1 to N, loop i from 1 to n, if the i-th feature occurred in the j-th feature combination, Oi++; cij = Oi/j.
Step 6. Loop i from 1 to n, and compute the numerical importance score NIS (i) = ∑cij.
2.4. Algorithm of ICAVP and Experiment Procedure
In order to effectively extract the characteristic indicators in the vegetable price early-warning system, we propose the algorithm of the index contribution analysis for vegetable prices (ICAVP).
The explicit steps for the implementation are below:
Step 1: For consistency, the indicators are normalized firstly for the purpose of eliminating heteroscedasticity with the normalization form: .
Step 2: Many indicators have no obvious effect on the vegetable price index, and also, there may exist interference between indicators. By eliminating redundant indicators, so as to identify vital and reliable indicators, 10 indicators are randomly selected as the input set, and we use SVR to forecast the vegetable prices, including the training samples from 1995–2002, the test samples from 2003–2006 and the prediction samples from 2007–2010. The optimal SVR parameters are obtained through the PSO algorithm, which is used to calculate MSE (mean square error). The formula is the criteria to measure the prediction results, where is the predicted value, is the regression value and n is the amount of samples.
Step 3: The 10 indicators are randomly selected from 29 indicators, including 20 million training samples. Due to limitations in computing power and computing time, we employ the grouping section sampling method, i.e., dividing data into three random sampling groups, with each group consisting of 5000 samples. In order to fully express the important indicators, we add some important indicators to the samples. Through expert analysis, the most important indicators of the vegetable price index are X1, X8 and X9, and the least important indicators are X11, X13, X14, X17, X18, X20, X22, X23, X26, X27 and X29. Besides, the specific groups for random sampling are: (1) Randomly select 10 indicators from 29 indicators. The method is to use the Rand function in MATLAB to generate 29 corresponding random numbers that represent the 29 indicators, which are then sorted by descending order, with the corresponding indicators of the first 10 random numbers chosen for experiments. We have 5000 samples; (2) Directly put the most important indicators X1, X8 and X9 into the samples, and then, randomly choose seven indicators from the remaining 26 indicators. The method uses the 29 numbers sorted in Step 1, then deletes the corresponding numbers of indicators X1, X8 and X9 and, finally, takes the corresponding indicators of the first seven numbers from the remaining 26. We also sampled 5000 times; (3) When selecting seven indicators from the remaining 26 indicators, the probability of the occurrence of less important indicators, including X11, X13, X14, X17, X18, X20, X22, X23, X26, X27 and X29, should be increased. The method uses the 29 numbers mentioned above, and the random numbers of the less important corresponding indicators should double. Then, these random numbers are sorted by descending order, and the corresponding numbers of X1, X8 and X9, are deleted. We then take the corresponding indicators of the first seven numbers for our experiment. We run the sample 5000 times. The 10 indicators of 15,000 samples and their corresponding MSEs are recorded, with a two-dimensional table of 15,000 × 11 generated.
Step 4: Re-order the MSE values by ascending order in the above two-dimensional table, and obtain a new table. To facilitate the study, we only count the numbers of occurrence of each indicator in the first 100 rows of the new two-dimensional table. Denote Cij as the number of occurrences of the indicator at the i-th row and j-th column, where i = 1, 2 … 100, j = 1, 2 … 29. The lesser the MSE value is, the more important the indicator is. In order to quantify the importance of indicators, we introduce the indicator contribution degree Mj, which represents the contribution degree of indicator j, the calculation formula is . Then, we sort the indicators according to Mj values to get the sorted indicator sequence Ni.
Step 5: According to the indicator sequence Ni, we add the indicators into the input one by one, that is add the first indicator into the input when the indicator dimension is 1; add the first two indicators into the input when the dimension is 2; and the like; all of the 29 indicators will be added into the input when the dimension size is 29. Specifically, we use SVR to compute the MSEj values in different dimensions, where MSEj represents the MSE value when the dimension equals j. Then, MSEj values are plotted in a graph, and the necessary indicators will be finally selected according to the values and variation trend of MSE.
Step 6: Treat extracted indicators and all indicators as inputs, respectively; then obtain the vegetable price index prediction results and, finally, compare the results for analysis.
3. Results and Discussion
Using the above experimental procedure, we finally obtain the contribution degree values of the 29 indicators, as shown in
Table 2.
Table 2.
Contribution degree of warning-sign indicators.
Table 2.
Contribution degree of warning-sign indicators.
| Indicators | Contribution Degree | Indicators | Contribution Degree | Indicators | Contribution Degree |
|---|
| X1 | 1742.81 | X11 | 1256.76 | X21 | 281.91 |
| X2 | 333.57 | X12 | 449.83 | X22 | 1391.18 |
| X3 | 1017.08 | X13 | 687.05 | X23 | 987.79 |
| X4 | 448.76 | X14 | 637.01 | X24 | 856.31 |
| X5 | 489.43 | X15 | 773.41 | X25 | 518.59 |
| X6 | 181.43 | X16 | 538.74 | X26 | 1194.85 |
| X7 | 639.38 | X17 | 1081.16 | X27 | 1533.77 |
| X8 | 1611.66 | X18 | 1188.54 | X28 | 182.37 |
| X9 | 1764.75 | X19 | 579.76 | X29 | 324.37 |
| X10 | 190.87 | X20 | 1133.75 | | |
The table shows that there are big differences between different indicator contribution degree values, and then, according to the sorting sequence of the degree values, we obtain the indicator sorting sequence Ni = {X9, X1, X8, X27, X22, X11, X26, X18, X20, X17, X3, X23, X24, X15, X13, X7, X14, X19, X16, X25, X5, X12, X4, X2, X29, X21, X10, X28, X6}.
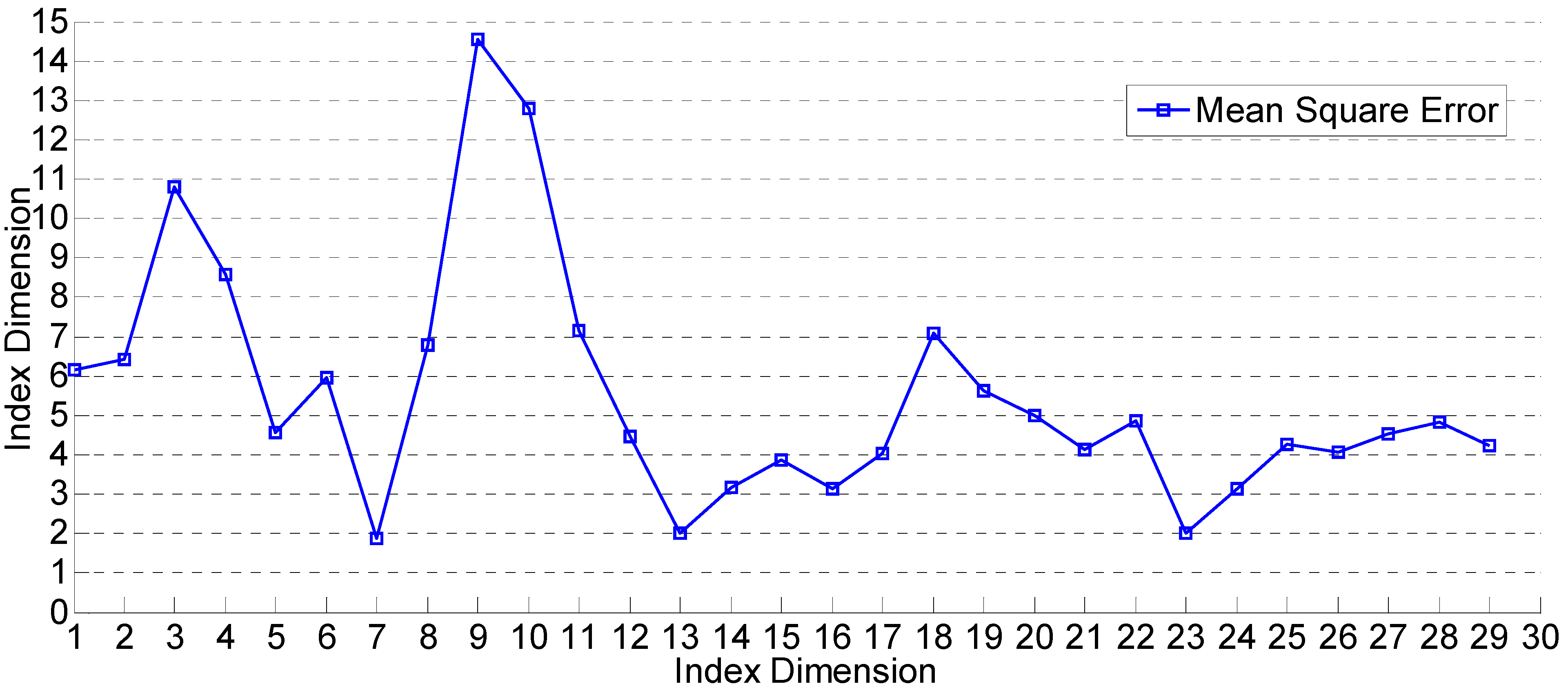
Figure 1 describes the MSE values in different indicator dimensions. It can be seen from the figure that MSE reaches the minimum when the indicator dimension is seven; as the indicator dimension increases, MSE will fluctuate heavily and then tend towards stability. Therefore, we have selected the first seven indicators, including vegetable sown acreage (X
9), material expenses’ investment (X
1), vegetable production (X
8), consumer price index (CPI) (X
27), rural residents’ consumption for vegetables (X
22), crude oil price (X
11) and money supply (X
26).
Figure 1.
Mean square error (MSE) in different dimensions.
Figure 1.
Mean square error (MSE) in different dimensions.
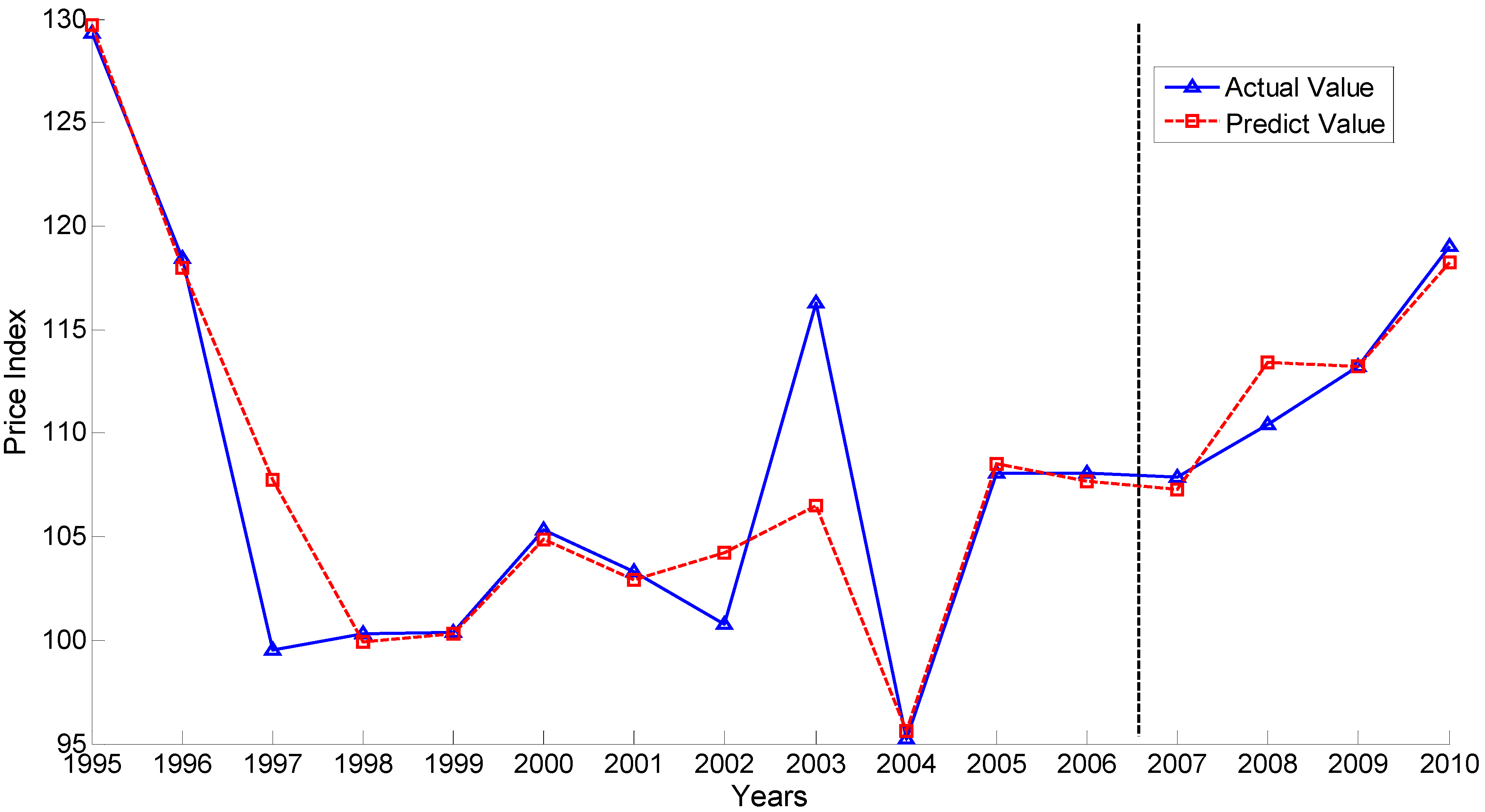
Figure 2 describes the forecasting results based on the seven indicators as the input.
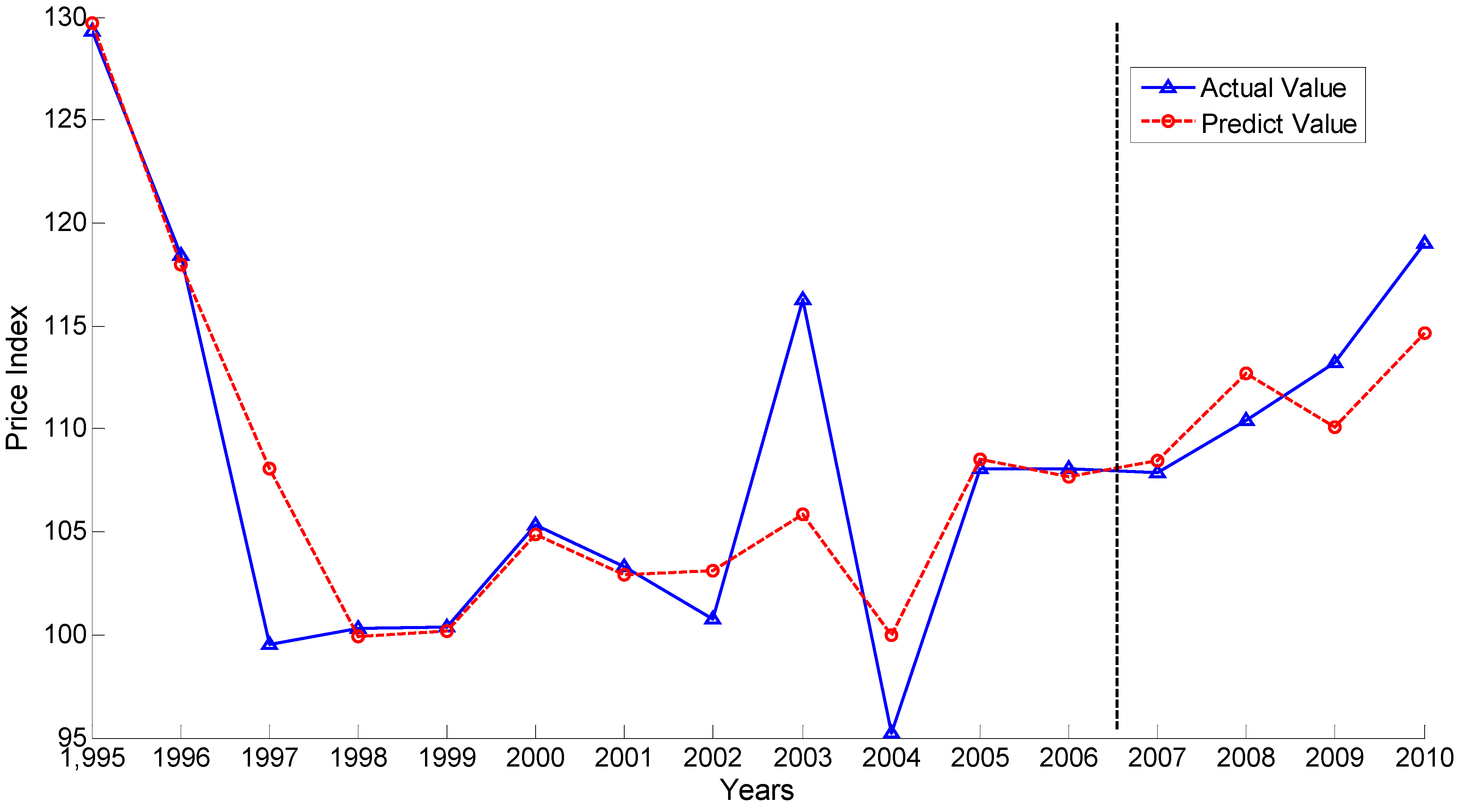
Figure 3 depicts the forecasting results based on the 29 indicators as the input. Through comparison of the two figures, it can be obviously found that the forecasting results of selected indicators based on the ICAVP algorithm perform better.
Figure 2.
Forecasting results from selected indicators based on the index contribution analysis for vegetable prices (ICAVP).
Figure 2.
Forecasting results from selected indicators based on the index contribution analysis for vegetable prices (ICAVP).
Because the other 22 indicators seldom influence the results of the early-warning system, we choose the above seven indicators (X9, X1, X8, X27, X22, X11, X26) to discuss the economic rationale. From the view of economic analysis, the seven feature indicators extracted through the ICAVP algorithm have obvious relevance to the vegetable price index.
Figure 3.
Forecasting results from 29 indicators as the input.
Figure 3.
Forecasting results from 29 indicators as the input.
In order to fully understand the effectiveness of ICAVP, BP network methods are carried out on the same data. The result is shown in
Figure 4. It is clear to show that ICAVP performs better than BP networks. Thus, the features we extracted via ICAVP contribute to the accuracy of regression and have reasonable relevance to the vegetable price index.
Figure 4.
Comparative experiment design by using BP networks.
Figure 4.
Comparative experiment design by using BP networks.
Vegetable sown acreage is an important factor affecting the supply of vegetables, and how large the vegetable supply is will directly affect the price of vegetables. There is a high correlation between vegetable sown acreage and vegetable production, and it can be shown that China’s vegetable sown acreage and vegetable production continues to grow year after year. The vegetable sown acreage and vegetable production in 2010 are, respectively, 3.10-times and 3.4-times those in 1990. The annual vegetable production will have accompanying changes with the volatility of vegetable sown acreage, which means the annual vegetable production will change corresponding to heavy fluctuations in the vegetable sown acreage in the next year. Overall, there exists a lagged correlation between the changes of annual vegetable production and vegetable sown acreage.
Material expenses’ investment, including seeds, pesticides, fertilizers, irrigation, machinery, tools, materials, marketing and other expenses, is an essential element supporting the growth of vegetables. The material expenses’ investment is represented by the total amount of material expenses per acre and per year. From data analysis of 1995–2010, there is a significant, increasing trend for this indicator. The material expenses’ investment has a positive relationship with vegetable production, which directly affects the production cost of vegetables, thus affecting the vegetable price.
Vegetable production changes will affect the market supply of vegetables, resulting in fluctuations in the price of vegetables. Over the years, with the rapid development of China’s vegetable industry, annual vegetable production grows year after year. China’s vegetable production increased rapidly in the 1990s, and up until 2010, the production amount increased by more than three times that in the early 1990s.
The Consumer Price Index (CPI) measures the relative ratio of residents’ consumer goods and service price level with time changes, which comprehensively reflects the changes between the living consumer goods purchased by residents and the service price levels. The vegetable prices and CPI influence each other, and there is a dialectical relationship between the two, which means, from the contribution analysis of the main agricultural products prices on CPI, the retail price index of meat, poultry and eggs and also the retail price index of fresh vegetables have the greatest impact on the Consumer Price Index.
Next is the rural residents’ demand for vegetables. China is a large agricultural country, where the number of rural residents makes up a high proportion of the population, and so, rural residents’ demand for vegetables has a significant impact on vegetable prices. Since the 1980s, rural residents’ consumption first increased, then decreased and, finally, has tended towards stability. The vegetable consumption of rural residents in 2010 was 62.62 million tons, so this huge demand has a major influence on vegetable prices.
The crude oil price has played an instrumental role in the increase of vegetable prices. According to estimates, as the crude oil price increases four percent, the vegetable sown cost will grow by three percent. In addition to increased planting costs, transportation costs also increase significantly.
The fluctuation of vegetable prices has a close relationship with domestic money supply. In the early period when the prices of China’s agricultural products rose sharply, correspondingly, there often existed a rapid growth in money supply. Money supply in circulation promotes the growth of vegetable prices. Some Chinese scholars have done research showing that when the amount of currency in circulation is increased by one trillion yuan, the prices of cabbage, cucumbers, tomatoes, green pepper and green beans will also be increased by 0.43 yuan, 0.76 yuan, 0.83 yuan, 1 yuan and 1.2 yuan per kilogram, respectively [
20].