Opportunity Costs of Carbon Emissions Stemming from Changes in Land Use
Abstract
:1. Introduction
- (I)
- Local/micro-level empirical data estimates: these are based on empirical data, are region specific, and reflect local conditions and costs.
- (II)
- Generic or average production cost estimates: are calculated using data from other countries.
- (III)
- Land price estimates: reflect the discounted stream of returns from the most productive use of land.
- (IV)
- Global partial equilibrium model estimates: simulate relevant parts of the world economy (including the forest, agriculture, and energy sectors) to estimate supply curves for emissions reductions.
| Research Area | Average | High | Low | Source |
|---|---|---|---|---|
| Global | 12.32 | 17.86 | 6.77 | Boucher [16] |
| Global | 5.52 | 8.28 | 2.76 | Stern [17] |
| Tanzania | 10.5 | 12 | 9 | Tom Blomley and Timm Tennigkeit [18] |
| Indonesia | 21.65 | 33.44 | 9.85 | Venter et al. [19] |
| Indonesia | 3.15 | 4.66 | 1.63 | Venter et al. [19] |
| Indonesia | 13.45 | 19.24 | 7.66 | Butler et al. [20] |
| Brazil | 9.1 | 11.5 | 6.7 | IIED [21] |
2. Methods
2.1. Baseline Modeling
- (1)
- State of each cell as represented by spatial variables (e.g., the various land use types).
- (2)
- Probability of land conversion.
- (3)
- Physical suitability, which describes the degree to which the cell was suitable for use as a plantation based on its elevation, slope, aspect, and soil type.
- (4)
- Spatial constraints that prohibit the cell from being converted to certain land use types, which assures that deforestation does not occur in certain prohibited areas.
- (5)
- Accessibility, which describes the ease with which a plantation can fulfill the cell’s needs for transportation and mobility given the underlying transportation system (e.g., distances to rivers, roads, and villages).
- (6)
- Each cell’s neighborhood, which represents the impact of land use from all cells surrounding the focal cell. The Moore neighborhood was adopted in this study and eight neighbors were used.
2.2. Opportunity Costs
| Parameter | Description | Value | Source |
|---|---|---|---|
| V1 | One-time net revenue from logging per hectare | 830 US$ | Yamamoto et al. [43] |
| Vg | Net revenue from rubber plantations per hectare | 75.1 US$ | Yamamoto et al. [43] |
| Vp | Net revenue from oil palm plantations per hectare | 258.27 US$ | Fairhurst and McLaughlin [44] |
| θs | Percentage of rice cultivation in the total area of expanding agricultural land | 16.3% | Field survey |
| θg | Percentage of rubber plantations in the total area of expanding agricultural land | 32.7% | Field survey |
| θp | Percentage of oil palm plantations in the total area of expanding agricultural land | 51% | Field survey |
| P3 | Price of rice | 0.32 US$/kg | Yamamoto et al. [43] |
| Pg | Price of rubber | 0.87 US$/kg | Yamamoto et al. [43] |
| W | Minimum wage | 0.68 | Yamamoto et al. [43] |
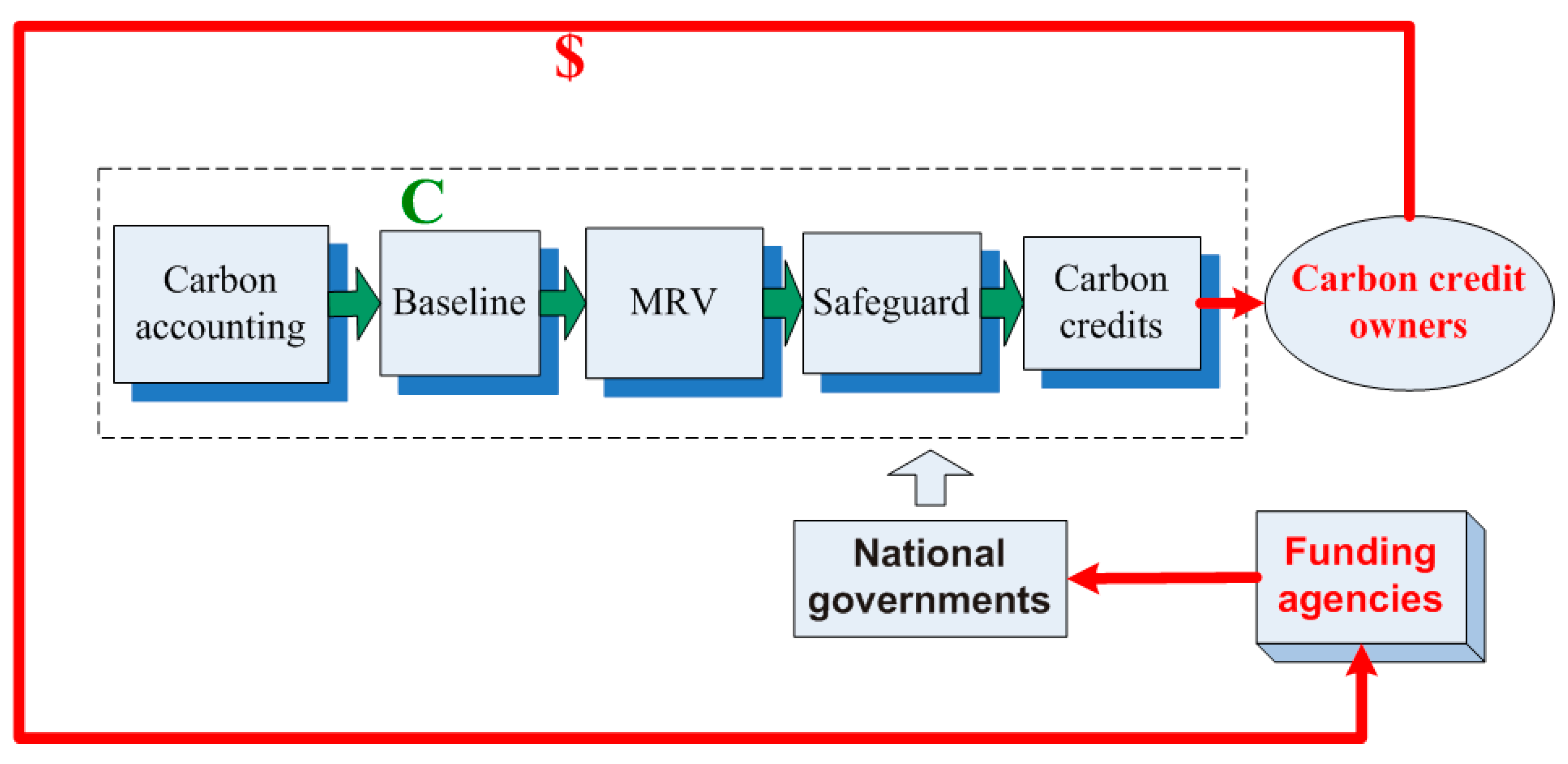
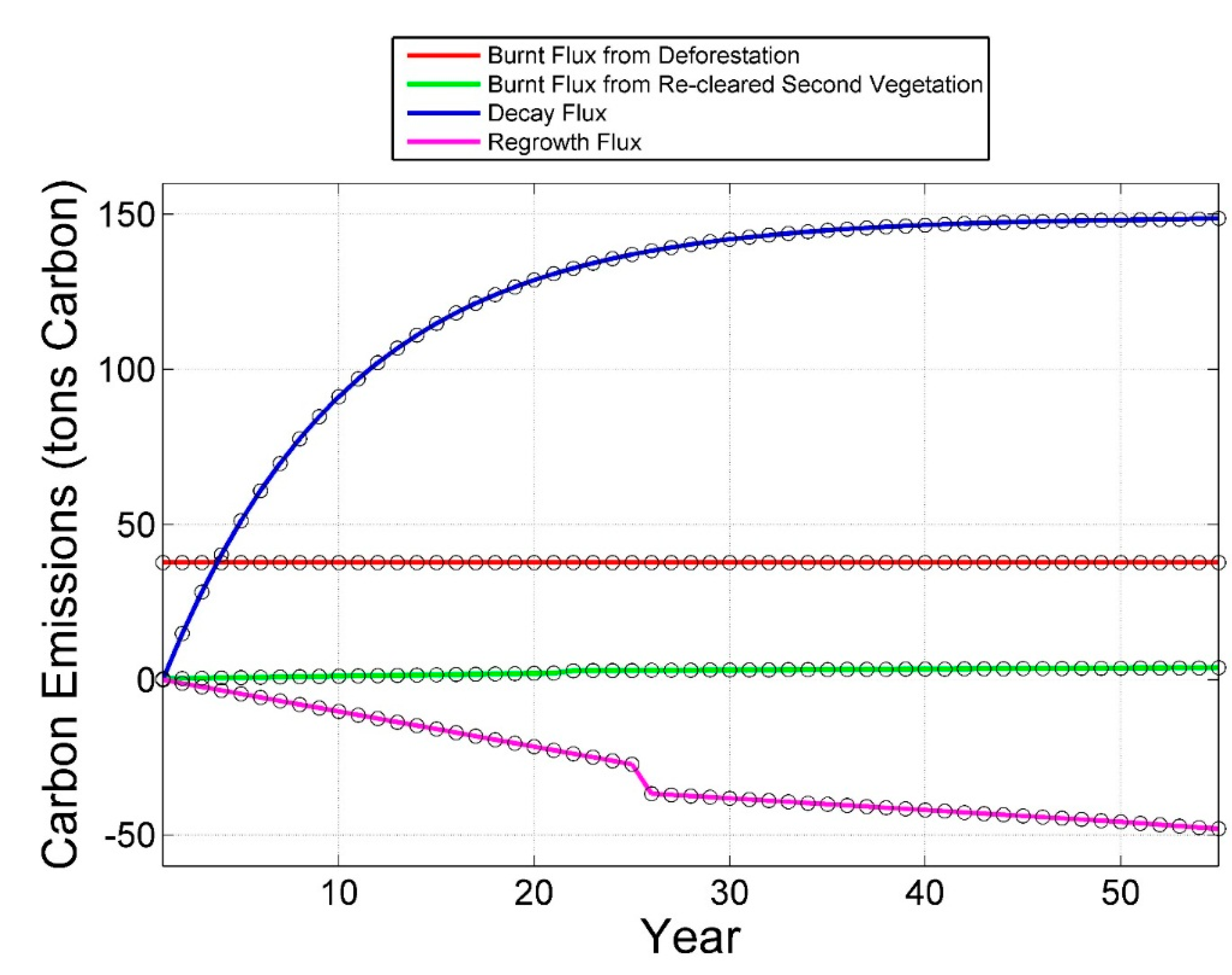
2.3. Accounting Methodology
2.4. Market Price of Carbon
3. Results
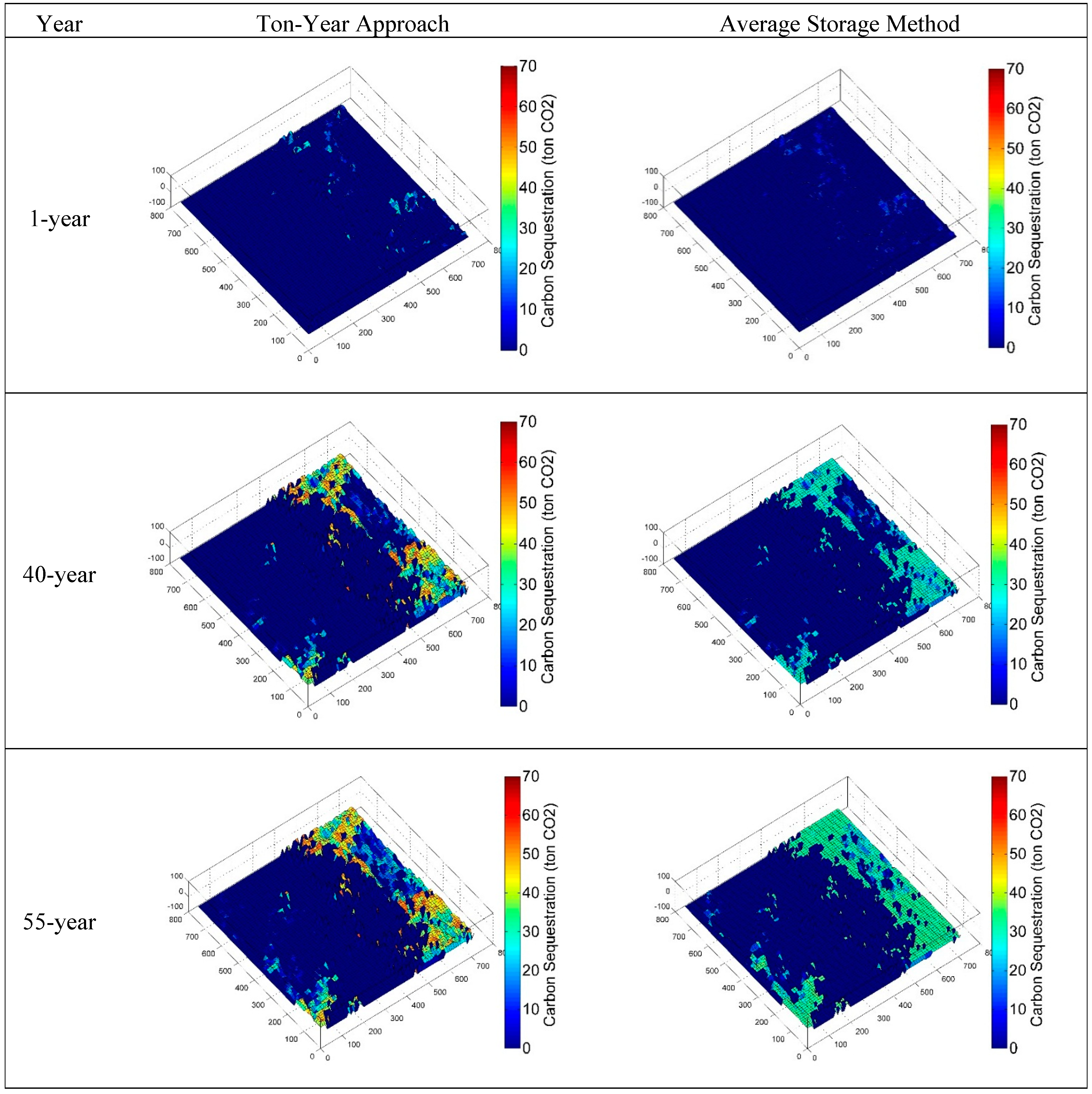
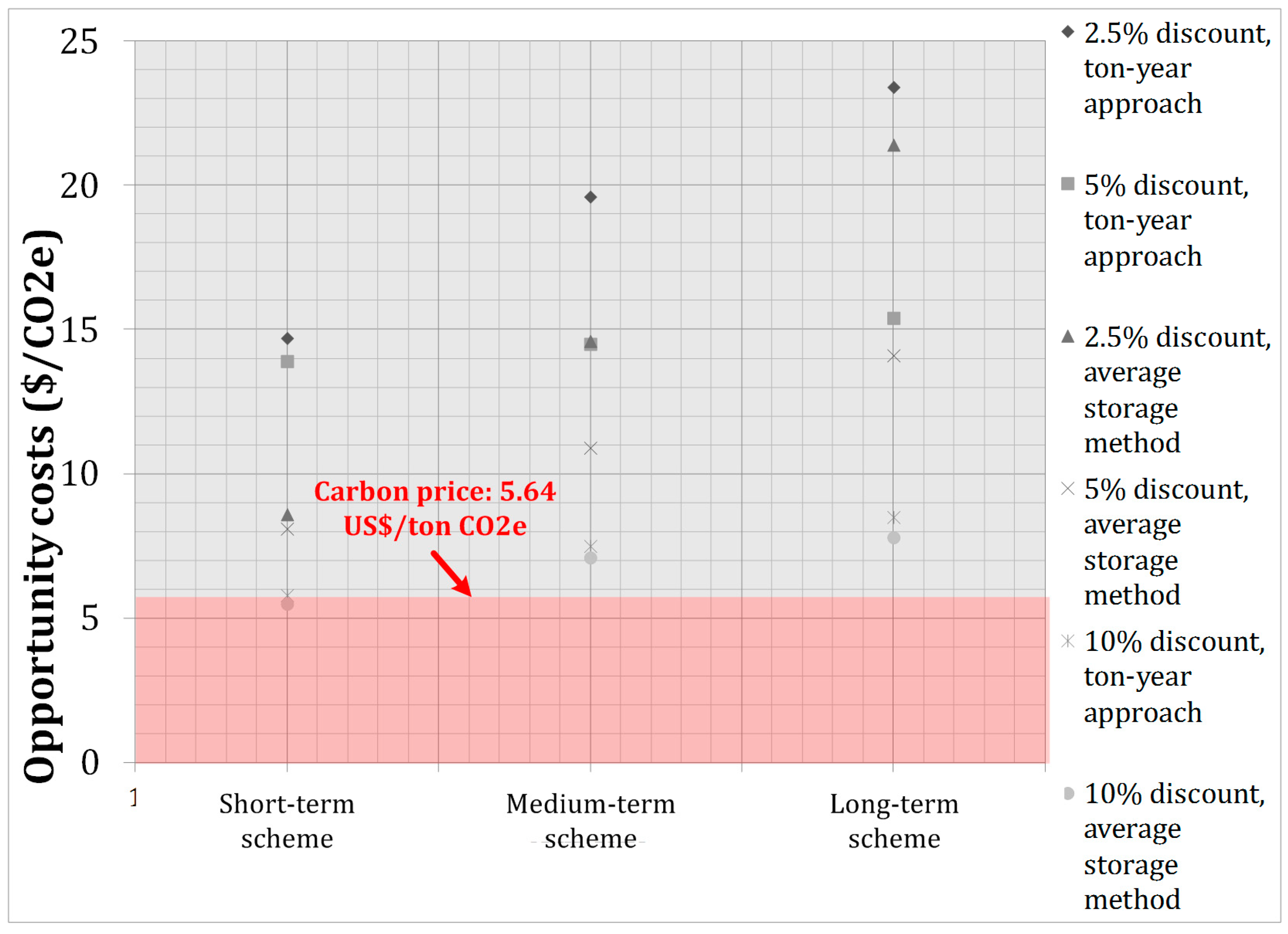
| Accounting Method | Scenario | Opportunity costs (US$/ton CO2e) | ||
|---|---|---|---|---|
| 2.5% Discount | 5% discount | 10% discount | ||
| Ton-year approach | Short-term scheme: 15-year | 14.7 | 13.9 | 5.8 |
| Medium-term scheme: 25-year | 19.6 | 14.5 | 7.5 | |
| Long-term scheme: 55-year | 23.4 | 15.4 | 8.5 | |
| Average storage method | Short-term scheme: 15-year | 8.6 | 8.1 | 5.5 |
| Medium-term scheme: 25-year | 14.6 | 10.9 | 7.1 | |
| Long-term scheme: 55-year | 21.4 | 14.1 | 7.8 | |
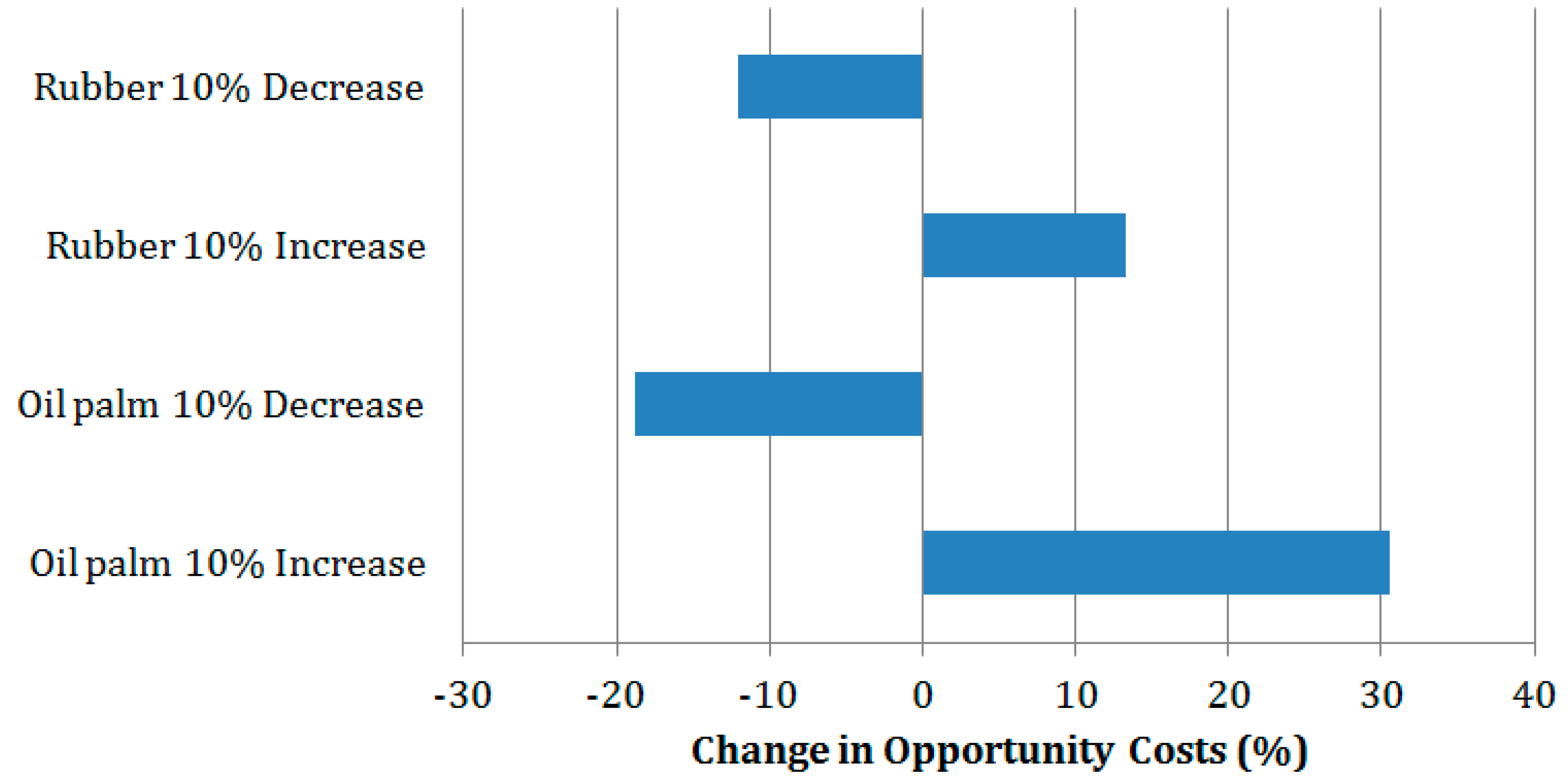
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Melillo, J.M.; McGuire, A.D.; Kicklighter, D.W.; Moore, B.; Vorosmarty, C.J.; Schloss, A.L. Global climate change and terrestrial net primary production. Nature 1993, 363, 234–240. [Google Scholar] [CrossRef]
- Dixon, R.K.; Brown, S.; Houghton, R.A.; Solomon, A.M.; Trexler, M.C.; Wisniewski, J. Carbon pools and flux of global forest ecosystems. Science 1994, 263, 185–190. [Google Scholar] [CrossRef] [PubMed]
- Field, C.B.; Behrenfeld, M.J.; Randerson, J.T.; Falkowski, P. Primary production of the biosphere: integrating terrestrial and oceanic components. Science 1998, 281, 237–240. [Google Scholar] [CrossRef] [PubMed]
- Intergovernmental Panel on Climate Change (IPCC). IPCC Fifth Assessment Report—Climate Change 2013: Agriculture, Forestry and Other Land Use (AFOLU); Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). IPCC Fourth Assessment Report—Climate Change 2007: The Physical Science Basis Summary for Policymakers; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- World Resources Institute (WRI). Navigating the Numbers: Greenhouse Gas Data, 2005; World Resources Institute: Washington, DC, USA, 2005. [Google Scholar]
- Houghton, R.A. Emissions (and Sinks) of Carbon from Land-Use Change. Report to the World Resources Institute from the Woods Hole Research Center; Woods Hole Research Center: Falmouth, MA, USA, 2003. [Google Scholar]
- Angelsen, A. (Ed.) Moving Ahead with REDD: Issues, Options and Implications; CIFOR: Bogor, Indonesia, 2008.
- Lu, H.; Liu, G. Distributed land use modeling and sensitivity analysis for REDD+. Land Use Policy 2013, 33, 54–60. [Google Scholar] [CrossRef]
- Introductory course on reducing emissions from deforestation and forest degradation (REDD): A participant resource manual. Available online: https://unfccc.int/files/land_use_and_climate_change/redd/submissions/application/pdf/redd_20090617_tnc_participantmanual.pdf (accessed on 25 March 2015).
- Pagiola, S.; Bosquet, B. Estimating the costs of REDD at the Country Level. Available online: http://mpra.ub.uni-muenchen.de/18062/1/MPRA_paper_18062.pdf (accessed on 25 March 2015).
- Gregersen, H.; El Lakany, H.; Karsenty, H.; White, A. Does the Opportunity Cost Approach Indicate the Real Cost of REDD+? Rights and Realities for Paying for REDD+; Rights and Resources Initiative: Washington, DC, USA, 2010. [Google Scholar]
- Wertz-Kanounnikoff, S. Estimating the Costs of Reducing Forest Emissions: A Review of Methods; CIFOR: Bogor, Indonesia, 2010. [Google Scholar]
- World Bank. Estimating the Opportunity Costs of REDD+: A Training Manual; World Bank: Washington, DC, USA, 2011. [Google Scholar]
- Grieg-Gran, M. The Cost of Avoiding Deforestation: Report Prepared for the Stern Review of the Economics of Climate Change; IIED: London, UK, 2008. [Google Scholar]
- Boucher, D. Out of the Woods: A Realistic Role for Tropical Forests in Curbing Global Warming; Union of Concerned Scientists: Cambridge, MA, USA, 2008. [Google Scholar]
- Stern, N. Stern Review: The Economics of Climate Change; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Tom Blomley, T.; Tennigkeit, T. Estimating the costs of REDD+ in Tanzania. Available online: http://www.eldis.org/go/home&id=62907&type=Document#.VRIjDOEsLAQ (accessed on 25 March 2015).
- Venter, O.; Meijaard, E.; Possingham, H.; Dennis, R.; Sheil, D.; Wich, S.; Hovani, L.; Wilson, K. Carbon payments as a safeguard for threatened tropical mammals. Conserv. Lett. 2009, 2, 123–129. [Google Scholar] [CrossRef]
- Butler, R.A.; Koh, L.P.; Ghazoul, J. REDD in the red: Palm oil could undermine carbon payment schemes. Conserv. Lett. 2009, 2, 67–73. [Google Scholar] [CrossRef]
- IIED. The Costs of REDD: Lessons from Amazonas. Available online: http://www.iied.org (accessed on 25 March 2015).
- Schlamadinger, B.; Marland, G. Land Use and Global Climate Change: Forests, Land Management, and the Kyoto Protocol; Pew Center on Global Climate Change: Arlington, VA, USA, 2000. [Google Scholar]
- Chomitz, K.M. Evaluating Carbon Offsets from Forestry and Energy Projects: How Do They Compare? World Bank: Washington, DC, USA, 2000. [Google Scholar]
- Fearnside, P.M.; Lashof, D.A.; Moura-Costa, P. Accounting for time in mitigating global warming through land-use change and forestry. Mitig. Adapt. Strat. Glob. Chang. 2000, 5, 239–270. [Google Scholar] [CrossRef]
- Dutschke, M. Fractions of permanence: squaring the cycle of sink carbon accounting. Mitig. Adapt. Strat. Glob. Chang. 2002, 7, 381–402. [Google Scholar] [CrossRef]
- Sedjo, R.A.; Marland, G. Inter-trading permanent emissions credits and rented temporary carbon emissions offsets: Some issues and alternatives. Clim. Policy 2003, 3, 435–444. [Google Scholar] [CrossRef]
- Moura-Costa, P. Carbon Accounting, Trading and the Temporary Nature of Carbon Storage. 2000. Available online: http://pdf.usaid.gov/pdf_docs/PNACY491.pdf (accessed on 24 March 2015). [Google Scholar]
- Sedjo, R.A. Forest Carbon Sequestration: Some Issues for Forest Investments; RFF Discussion Paper 01–34; Resources for the Future: Washington, DC, USA, 2001. [Google Scholar]
- Griscom, B.; Shoch, D.; Stanley, B.; Cortez, R.; Virgilio, N. Implications of REDD Baseline Methods for Different Country Circumstances during an Initial Performance Period; The Nature Conservancy: Arlington, VA, USA, 2009. [Google Scholar]
- Huettner, M.; Leemans, R.; Kok, K.; Ebeling, J. A comparison of baseline methodologies for Reducing Emissions from Deforestation and Degradation. Carbon Balance Manag. 2009, 4. [Google Scholar] [CrossRef]
- Von Neumann, J. Theory of Self-Reproducing Automata; University of Illinois Press: Urbana, IL, USA, 1996. [Google Scholar]
- Wolfram, S. Cellular automata as models of complexity. Nature 1984, 311, 419–424. [Google Scholar] [CrossRef]
- White, R.; Engelen, G.; Uljee, I. The use of constrained cellular automata for high-resolution modeling of urban land use dynamics. Environ. Plann. B 1997, 24, 323–343. [Google Scholar] [CrossRef]
- Barredo, J.I.; Kasanko, M.; McCormick, N.; Lavalle, C. Modeling dynamic spatial processes: Simulation of urban future scenarios through cellular automata. Landsc. Urban Plan 2003, 64, 145–160. [Google Scholar] [CrossRef]
- Barredo, J.I.; Engelen, G. Land Use Scenario Modeling for Flood Risk Mitigation. Sustainability 2010, 2, 1327–1344. [Google Scholar] [CrossRef]
- Eggleston, S.; Buendia, L.; Miwa, K.; Ngara, T.; Tanabe, K. IPCC Guidelines for National Greenhouse Gas Inventories, Agriculture, Forestry and other Land Use. 2006. Available online: http://www.ipccnggip.iges.or.jp/public/2006gl/vol4.html (accessed on 24 March 2015).
- Moore, B.; Boone, R.; Hobbie, J.; Houghton, R.; Melillo, J. A simple model for analysis of the role of terrestrial ecosystems in the global carbon budget. In Modelling the Global Carbon Cycle; Bolin, B., Ed.; Wiley: New York, NY, USA, 1981. [Google Scholar]
- Houghton, R.A.; Hobbie, J.E.; Melillo, J.M.; Moore, B.; Peterson, B.J.; Shaver, G.R.; Woodwell, G.M. Changes in the carbon content of terrestrial biota and soils between 1860 and 1980: A net release of CO2 to the atmosphere. Ecol. Monogr. 1983, 53, 236–262. [Google Scholar]
- Houghton, R.A.; Hackler, J.L. Carbon flux to the atmosphere from land-use changes: 1850 to 1990. Available online: http://cdiac.ornl.gov/epubs/ndp/ndp050/ndp050.html (accessed on 24 March 2015).
- Ramankutty, N.; Gibbs, H.K.; Achard, F.; DeFries, R.; Foley, J.A.; Houghton, R.A. Challenges to estimating carbon emissions from tropical deforestation. Glob. Chang. Biol. 2007, 13, 51–66. [Google Scholar] [CrossRef]
- Rahajoe, J. ARCP2009–06CMY-Braimoh, Managing Ecosystems Services in Asia: A Critical Review of Experiences in Montane Upper Tributary Watersheds. Available online: http://www.apn-gcr.org/resources/items/show/1557 (accessed on 25 March 2015).
- Bellassen, V.; Gitz, V. Reducing emissions from deforestation and degradation in Cameroon: Assessing costs and benefits. Ecol. Econ. 2008, 68, 336–344. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Takeuchi, K. Estimating the break-even price for forest protection in Central Kalimantan. Environ. Econ. Policy Stud. 2012, 14, 289–301. [Google Scholar] [CrossRef]
- Fairhurst, T.; McLaughlin, D. Sustainable Oil Palm Development. 2009. Available online: http://www.worldwildlife.org/what/globalmarkets/agriculture/ (accessed on 1 June 2011).
- Smith, K. Discounting, risk and uncertainty in economic appraisals of climate change policy: Comparing Nordhaus, Garnaut and Stern, Commissioned work. Available online: http://www.garnautreview.org.au/update-2011/commissioned-work/discounting-risk-uncertainty-ecomonic-appraisals-climate-change-policy.html (accessed on 26 March 2015).
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2001: Working Group III: Mitigation. 2001. Available online: http://www.IPCC.org (accessed on 26 March 2015).
- Sathaye, J.M.W.; Dale, L.; Chan, P.; Andrasko, K. GHG mitigation potential, costs and benefits in global forests: A dynamic partial equilibrium approach. Available online: https://escholarship.org/uc/item/92d5m16v (accessed on 26 March 2015).
- Hunt, C. Local and global benefits of subsidizing tropical forest conservation. Environ. Dev. Econ. 2002, 7, 325–340. [Google Scholar] [CrossRef]
- Camino, R.V.; Alfaro, D.M.; Sage, L.F.M. Teak (Tectona grandis) in Central America. Available online: http://www.fao.org/docrep/005/y7205e/y7205e00.htm (accessed on 25 March 2015).
- Schroeder, P. Carbon storage potential of short rotation tropical tree plantations. For. Ecol. Manag. 1992, 50, 31–41. [Google Scholar] [CrossRef]
- MacLaren, J.P. Trees in the Greenhouse: The Role of Forestry in Mitigating the Enhanced Greenhouse Effect; Forest Research Bulletin No. 219; Forest Research: Rotorua, New Zealand, 2000. [Google Scholar]
- Marshall, L.; Kelly, A. The Time Value of Carbon and Carbon Storage: Clarifying the Terms and the Policy Implications of the Debate; WRI Working Paper; World Resources Institute: Washington, DC, USA, 2010. [Google Scholar]
- Dobes, L.; Enting, I.; Mitchell, C. Accounting for carbon sinks: The problem of time. In Trading Greenhouse Emissions: Some Australian Perspectives; Occasional Papers No 115; Dobes, L., Ed.; Bureau of Transport Economics: Canberra, Australia, 1998. [Google Scholar]
- Moura-Costa, P.; Wilson, C. An equivalence factor between CO2 avoided emissions and sequestration: Description and applications in forestry. Mitig. Adapt. Strateg. Glob. Chang. 2000, 5, 51–60. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 1994: Radiative Forcing of Climate Change; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Houghton, J.T.; Jenkins, G.J.; Ephramus, J.J. (Eds.) Climate Change: the IPCC Scientific Assessment; Cambridge University Press: Cambridge, UK, 1990.
- Nordhaus, W. A Question of Balance: Weighing the Options on Global Warming Policies; Yale University Press: New Haven, CT, USA, 2008. [Google Scholar]
- Forest Trends’ Ecosystem Marketplace. Maneuvering the Mosaic: State of the Voluntary Carbon Markets. 2013. Available online: http://www.forest-trends.org/vcm2014.php (accessed on 25 March 2015).
- Forestwatch. Available online: http://www.forestwatch.org (accessed on 25 March 2015).
- Kanninen, M.; Murdiyarso, D.; Seymour, F.; Angelsen, A.; Wunder, S.; German-Bogor, L. Do trees grow on money? In The Implications of Deforestation Research for Policies to Promote REDD; Center for International Forestry Research (CIFOR): Bogor, Indonesia, 2007. [Google Scholar]
- Ring, I.; Drechsler, M.; van Teeffelen, A.J.A.; Irawan, S.; Venter, O. Biodiversity conservation and climate mitigation: what role can economic instruments play? Curr. Opin. Environ. Sustain. 2010, 2, 50–58. [Google Scholar] [CrossRef]
- Cattaneo, A. How to Distribute REDD funds Across Countries? In A Stock-Flow Mechanism; Woods Hole Research Center: Falmouth, UK, 2008. [Google Scholar]
- Strassburg, B.; Turner, R.K.; Fisher, B.; Schaeffer, R.; Lovett, A. Reducing emissions from deforestation—The “combined incentives” mechanism and empirical simulations. Glob. Environ. Chang. 2009, 19, 265–278. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, H.; Liu, G. Opportunity Costs of Carbon Emissions Stemming from Changes in Land Use. Sustainability 2015, 7, 3665-3682. https://doi.org/10.3390/su7043665
Lu H, Liu G. Opportunity Costs of Carbon Emissions Stemming from Changes in Land Use. Sustainability. 2015; 7(4):3665-3682. https://doi.org/10.3390/su7043665
Chicago/Turabian StyleLu, Heli, and Guifang Liu. 2015. "Opportunity Costs of Carbon Emissions Stemming from Changes in Land Use" Sustainability 7, no. 4: 3665-3682. https://doi.org/10.3390/su7043665
APA StyleLu, H., & Liu, G. (2015). Opportunity Costs of Carbon Emissions Stemming from Changes in Land Use. Sustainability, 7(4), 3665-3682. https://doi.org/10.3390/su7043665





