1. Introduction
Groundwater demand has increased because groundwater is one of the most important natural resources, supporting human health, economic development, and ecological diversity. Moreover, it is readily obtainable anywhere, provides excellent water quality, and has low development costs [
1]. Surface water accounts for only 0.3% of the freshwater that exists on Earth and groundwater can be recharged each year by rainfall. However, the rapid increase in human population has increased the use and demand for groundwater resources for drinking, agricultural, and industrial purposes. Therefore, to ensure that a secure amount of water is available, systematic development and management planning should be established. In Korea, the occupancy rate of groundwater is 11% [
2], and public water supplies (e.g., water supplies of towns) of groundwater are only 5% of total water use. Considering that the amount of groundwater used in Korea increased by more than 210% [
3] between 1994 and 2008, development and utilization at the national level currently do not meet people’s growing needs. Hence, the development of reliable analytical methods and models for predicting locations that have GPP is urgently needed for systematic development, efficient management, and sustainable use of groundwater resources.
GIS and other technologies have great potential for use in studies of groundwater hydrology, and thus many researches have used GIS and remote sensing techniques along with thematic layers such as geomorphology, drainage pattern, lineament, lithology, and soil for that purpose. Some studies have applied probabilistic models such as multi-criteria decision analysis and weights-of-evidence modeling for groundwater-potential mapping [
4]. The other approaches have conducted numerical modeling, decision trees, fuzzy logic, and analytic hierarchical process analyses [
5]. Some researchers have also integrated GIS, remote sensing, and geophysical surveys to derive additional thematic layers of surface parameters such as resistivity, aquifer thickness, or fault maps [
6]. However, such studies had limitations because they used indirect indicators such as yield, groundwater depth, resistivity, and spring location, rather than hydraulic constants such as SPC and transmissivity (T). Furthermore, past studies have not validated the results by comparison with other datasets.
The decision tree is a decision support method that uses a tree-like model of decisions. It is a hierarchical model composed of decision rules that recursively splits independent variables into homogeneous zones [
7]. They split to favorable and non-favorable for groundwater productivity based on the relationship between SPC and each hydrogeological factor. The SPC is related to groundwater productivity and the SPC was measured and calculated. Moreover, an exhaustive search tends to select variables that afford more splits. Also, unlike other statistical models, a decision tree makes no statistical assumptions, can handle data represented on different measurement scales, and is computationally fast [
8]. Therefore, in this study, a data-driven application of the decision tree methodology was provided to obtain more accurate and reliable estimates. More specifically, the main novelty of the study was to apply the decision tree model to make a better GPP map using the SPC value for the criterion variable in the Boryeong and Pohang cites, Korea.
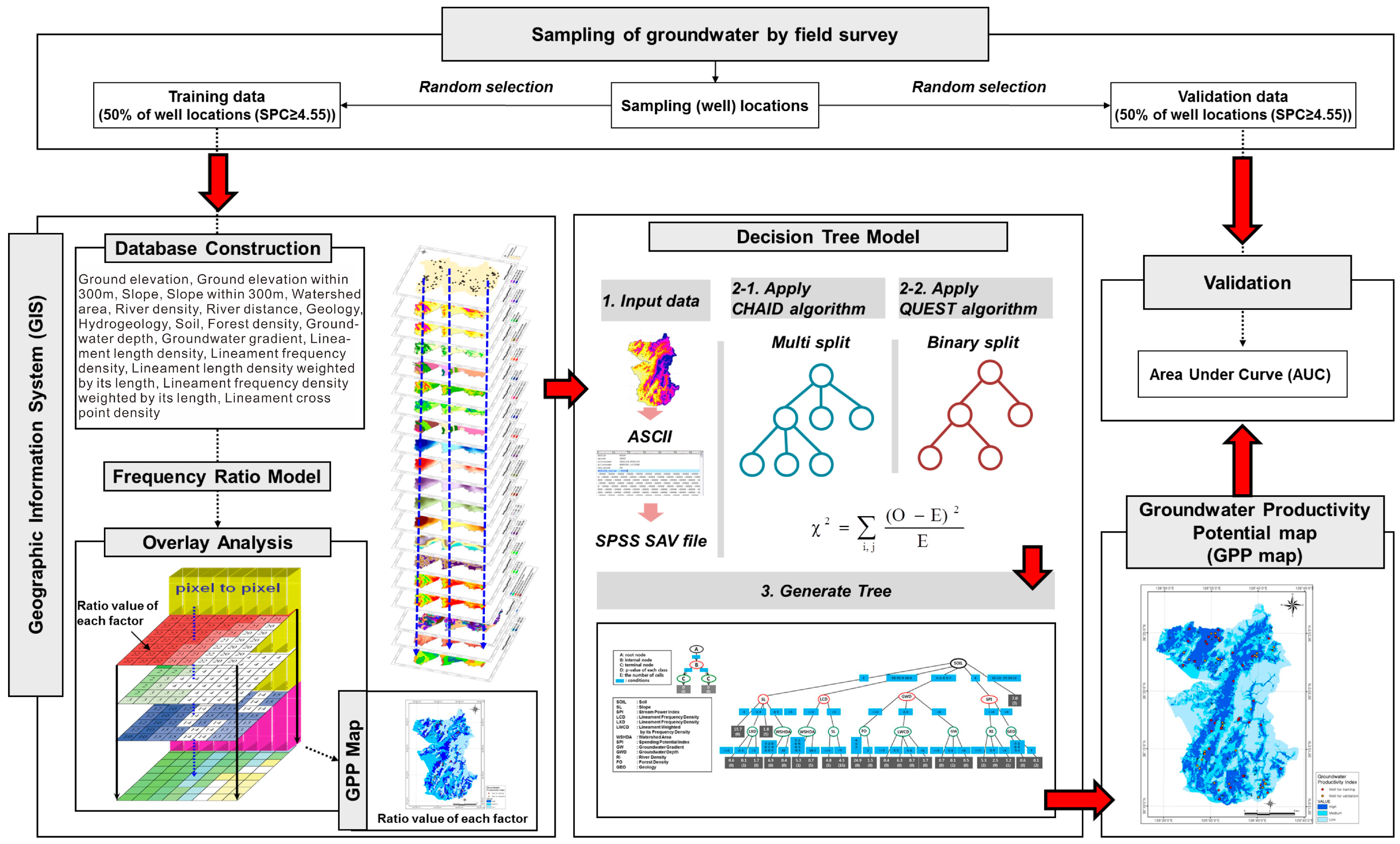
The study flow, shown in
Figure 1 is as follows: (1) Assembly of a spatial database. A total of 124 SPC data points (Boryeong) and 83 SPC data (Pohang) points were used to create a spatial database using GIS. Topography, hydrogeology, lineament, and soil data were collected and input into a spatial database. (2) The SPC data of ≥ 4.55 m
3/day/m (Boryeong) and ≥ 6.25 m
3/day/m (Pohang) were randomly divided into training data (50% of well locations) and validation data (50% of well locations). (3) Topography, lineament, hydrogeology, and soil datasets were compiled in a spatial database. Then, 19 factors in Boryeong city and 15 factors in Pohang city were extracted from the spatial database as potential contributing factors. (4) Using the decision tree model and the well locations selected for training, the probability of the groundwater potential were calculated and GPP maps were made. (5) The GPP maps were validated using the well locations that were not used for training.
Figure 1.
Study flow for groundwater productivity potential mapping.
Figure 1.
Study flow for groundwater productivity potential mapping.
2. Study Area
The study areas, Boryeong and Pohang cities, Korea, have experienced rapid population growth and increased demand for groundwater reserves, and thus is appropriate for evaluating groundwater potential.
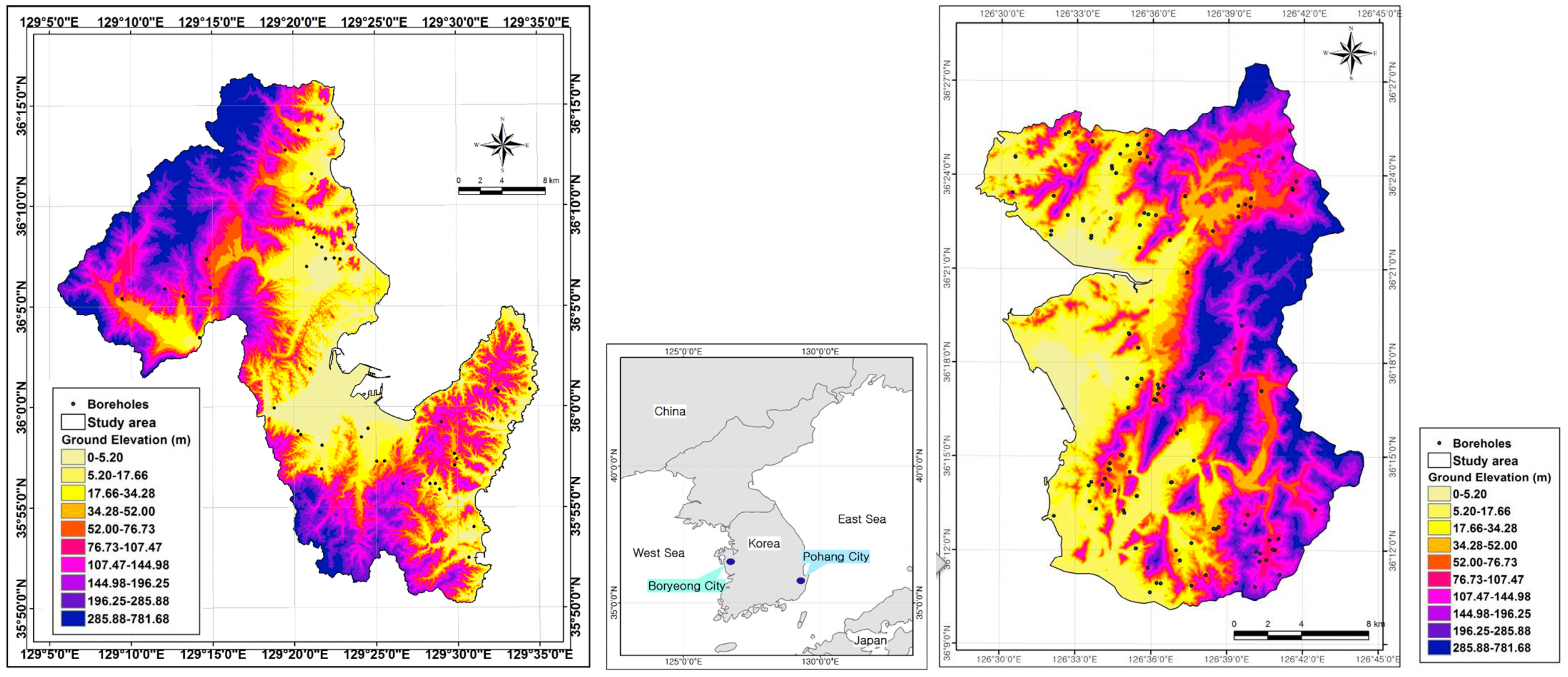
The study area of Boryeong city lies between 36°10′15″ N and 36°31′20″ N latitude and 126°28′21″ E and 126°43′54″ E longitude and covers an area of 567.92 km
2. The other study area, Pohang city lies between 35°50′07″ N and 36°16′34″ N latitude and 129°05′31″ E and 129°34′57″ E longitude and covers 891.44 km (
Figure 2). The bedrock geology of the Boryeong city consists mainly of Cretaceous granitic rocks; Jurassic sediment rocks; Precambrian sediment and granitic rocks; and Quaternary alluvium rocks (
Figure 3a) [
9]. Also, the bedrock geology of the Pohang city consists mainly of Cretaceous sedimentary, granitic, and volcanic rocks; Tertiary granitic, volcanic, and sedimentary rocks; and Quaternary basalt (
Figure 3b) [
10,
11]. As the groundwater productivity data, the statistics of SPC in the study area is shown in
Table 1.
Figure 2.
Study areas with topographic map.
Figure 2.
Study areas with topographic map.
Figure 3.
(a) Geological map of Boryeong city; (b) Geological map of Pohang city.
Figure 3.
(a) Geological map of Boryeong city; (b) Geological map of Pohang city.
Table 1.
Statistics of groundwater productivity data of study area.
Table 1.
Statistics of groundwater productivity data of study area.
| Type | No. | Min. | Max. | Avg. | Median |
|---|
| Boryeong city SPC (m3/day/m) | 124 | 1.08 | 393.33 | 11.46 | 5.54 |
| Pohang city SPC (m3/day/m) | 83 | 1.42 | 111.14 | 16.54 | 6.73 |
3. Data
To calculate groundwater productivity, the SPC are set as dependent variable, and various hydrogeological factors, which are known to influence groundwater productivity, are set as independent valuables. The SPC is a quantity which a water well can produce per unit of drawdown. It is normally obtained from a step drawdown test. SPC is expressed as:
where
Sc is the specific capacity ([L2 T−1]; m³/day/m)
Q is the pumping rate ([L3 T−1]; m³/day), and
h−h0 is the drawdown ([L]; m)
The SPC of a well is also a function of the pumping rate it is determined at. The SPC of a well is simply the pumping rate (yield) divided by the drawdown. It can be used to identify potential well, pump, or aquifer problems, and accordingly to develop a proper well maintenance schedule. It can also be used to estimate the T of the aquifer(s) tapped by the well’s perforations. T is the rate water is transmitted through an aquifer under a unit width and a unit hydraulic gradient. It equals the aquifer's hydraulic conductivity (permeability) times the aquifer thickness. The higher the T, the more prolific the aquifer and the less drawdown observed in the well. In the study, the T was not used. Instead of the T, the SPC was used because of the limited number of the T data [
1,
12].
Groundwater productivity is governed by many hydrogeological factors, such as surface and bedrock lithology, structure, slope steepness and morphology, stream evolution, climate, soil, vegetation cover, land use, and human activity, but for the study area these relationships have not been verified statistically and quantitatively. In this study, the 27 hydrogeological factors expected to be related to groundwater potential were reviewed with SPC. Finally, 19 hydrogeological factors for Boryeong city and 15 hydrogeological factors for Pohang city were selected according to the opinion of a groundwater expert and applied to the decision tree model (
Table 2). The detail influences of the hydrogeological factors for groundwater productivity were analyzed by previous research [
13,
14,
15].
To predict ground control problems in underground structures [
16], lineament is strongly related to discontinuities such as joints, faults, and folds. For these reasons, lineament was used for structural analysis, analysis of the relationship with geology, and assessment of groundwater productivity. In this study, lineament was detected through interpretation of Landsat TM (Thematic Mapper) imagery and hillshade maps from a DEM (Digital Elevation Model) made by a structural geologist with much experience in such interpretations. Lineament density is useful for understanding the local distribution of lineaments. Lineament density analysis was considered to be the lineament length, frequency and cross points, and the density of frequency and length were also analyzed using the weight of lineament length in the study area.
A TIN (triangulated irregular network) was made using the elevation value, and a DEM was made with 30 m × 30 m resolution. One input factor, the ground elevation within 300 m, was given a mean value at each grid cell based on the value of neighboring cells within a 300 m radius. Using the DEM, the slope and SPI (stream power index) were calculated. Mean ground elevation and slope within watershed area were obtained after watershed delineation. River density and distance from the river were considered as the indicators for selection of groundwater potential sites because they indirectly indicate the permeability and porosity of the terrain.
As land surface data, the soil was used as a factor related to groundwater potential. Soil texture invariably controls the penetration of surface water into an aquifer system. The soil texture of the study area was generated by a 1:25,000 scale soil map published by National Institute of Agricultural Science and Technology. 38 different categories of soil were extracted from the soil map: forest, grassland, gravel, gravelly sandy loam, fine gravelly sandy loam, sandy loam, loamy fine sand, fine sandy, loam, gravelly loam, silt loam, gravelly silt loam, clay silty loam, and silty clay loam.
The spatial database was constructed with a resolution of 30 m × 30 m on the basis of Landsat TM. The 19 hydrogeological factors were converted to ArcGIS grid format, and the GRID set comprised 767 rows by 1078 columns. In the study area, the total number of cells was known 502,456 and SPC in 124 cells (88 cells (including the SPC data of < 4.55 m3/day/m) for training and 36 cells for validation). Also, in the Pohang city, the total number of cells was known 990,495 and SPC in 83 cells (61 cells (including The SPC data of < 6.25 m3/day/m) for training and 22 cells for validation).
Groundwater productivity data (
Table 1) such as T, SPC, yield, well depth, well diameter, and water table were collected from the national groundwater survey in the Boryeong [
9] and Pohang cities [
17], the national groundwater monitoring network construction report [
18], and the rural groundwater survey report [
19].
Table 2.
Hydrogeological factors related to groundwater productivity in the study.
Table 2.
Hydrogeological factors related to groundwater productivity in the study.
| Category | Factors | Data Type | Scale |
|---|
| Boryeong City | Pohang City |
|---|
| Topography a | Ground Elevation
Ground Elevation within 300m
Ground Slope
Ground Slope within 300 m
Stream Power Index
Watershed Area | Ground Elevation
Ground Elevation within 300 m
Ground Slope
Ground Elevation Difference within 300 m
Mean Ground Elevation within watershed Area
Mean Ground Slope within watershed Area
Ground Curvature
Topographic Wetness Index
Cumulative watershed area | Grid | 1:5000 |
| River a | River Density
Distance from River | River Density
Distance from River | Line | 1:5000 |
| Geology b | Geology Bedrock
Hydrogeology | Hydrogeology | Polygon | 1:50,000 |
| Lineament c | Lineament Length Density
Lineament Frequency
Density
Lineament Length Density
Weighted by its Length
Lineament Frequency
Density Weighted by its Length
Density for Lineament
Cross Points | Lineament Length Density
Lineament Length Density Weighted by its Length
Lineament Frequency Density Weighted by its Length | Line | |
| Soil d | Soil | Soil | Polygon | R:30 m |
| Forest e | Forest Density | - | Polygon | 1:25,000 |
| Groundwater | Groundwater Depth
Groundwater Gradient | - | Point | |
4. Methods
The general progression of GPP mapping is illustrated in
Figure 1. The groundwater potential related factors were used as the input data. The GPP-likely locations and the GPP-unlikely locations were selected as training sites. In the decision tree model, the selection of the training site is important, and the areas deemed likely and not likely were carefully considered for training in this study. So, to select the training sites based on scientific and objective criteria, the SPC criterion 4.55 m
3/day/m (Boryeong) and 6.25 m
3/day/m (Pohang) were used. In the Boryeong city, for example, the average yield of well data is 225 m
3/day, mean depth of wells is 114 m and 10 m water table from ground. The SPC = 4.55 m
3/day/m was taken as the criterion for division purposes. The criteria, 4.55 m
3/day/m, are equivalent to well yield 300 m
3/day, with supposed drawdown of 2/3 of the total well depth. The value was calculated from the relationship between mean depth of wells and yield SPC = yield/{2/3(mean depth of wells)−(water table from ground)}. The mean SPC was 11.46 m
3/day/m (median 5.54 m
3/day/m) with a maximum of 393.33 m
3/day/m and a minimum of 1.08 m
3/day/m. The SPC data that were not fewer than 4.55 m
3/day/m were classified as GPP-likely training dataset, and the SPC data less than 4.55 m
3/day/m were classified as GPP-unlikely dataset. Then, 50% of the SPC values that were classified as GPP-likely training dataset were randomly selected and used for training. The remaining 50% of the GPP-likely dataset were used for validation.
Using decision-tree model, the relationships between GPP-likely training dataset and each factor were calculated quantitatively and GPP maps were created based on these relationships. The decision trees were constructed using the CHAID and the QUEST algorithms. Because the QUEST algorithm supports only nominal categorical data, related factors used for analysis of GPP were classified by the value of the frequency ratio.
The decision tree is a hierarchical model composed of decision rules that recursively splits independent variables into homogeneous zones [
24,
25,
26]. It is a decision support method that uses a tree-like model of decisions and their possible consequences. The decision tree combines the features in a hierarchical fashion such that the most important feature is located at the root of the tree. Each node in the tree refers to one of the features, and each leaf is assigned to one class (productive/non-productive area) representing the most frequent class value. Additionally, the leaf holds a probability vector indicating the probability of the feature's indicating a groundwater-productive area. New points are classified by navigating from the root of the tree to a leaf according to the outcome of tests along the path [
27].
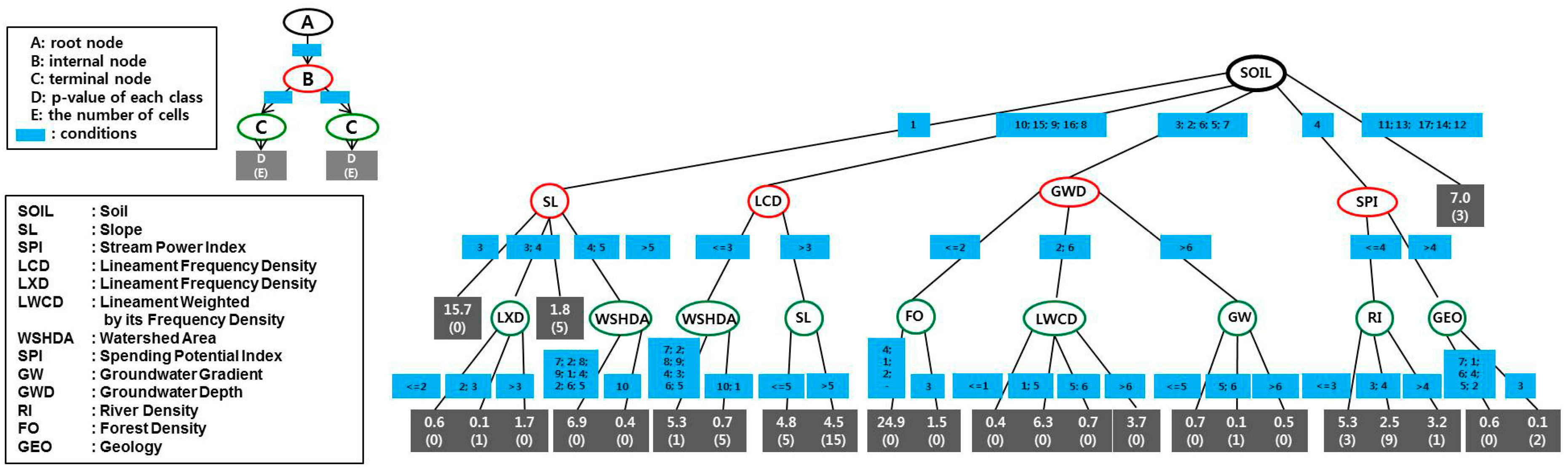
Figure 4 shows the general structure of a decision tree, which consists of three elements: node, condition, and production. Moreover, there are three types of node, namely decision, chance, and end nodes. In
Figure 4, A is a decision node, B is chance (internal) nodes, and C is an end (leaf or terminal) node. Because of its advantages, the decision tree is a popular classification model. There are many algorithms for constructing decision tree models, such as the Classification and Regression Tree (CART) [
28], the CHAID [
29], the Iterative Dichotomiser 3 (ID3) [
30], the QUEST [
7], and the C4.5 algorithm [
31].
In this study, the CHAID and QUEST decision tree algorithms were applied to GPP mapping. A CHAID decision tree is constructed by repeatedly splitting subsets of the space into two or more child nodes (multiway split), beginning with the entire dataset [
29,
32]. The CHAID algorithm, which is applied widely in many fields, uses a recursive partitioning method and allows multiple splits of a node [
33]. The CHAID algorithm consists of three steps: merging, splitting, and stopping. To determine the best split at any node, any allowable pair of categories of the predictor variables is merged until there is no statistically significant difference within the pair with respect to the target variable. The final nodes identify subgroups defined by different sets of independent variables. The result of these processes is a decision tree structure. The QUEST algorithm developed by Loh and Shih (1997) is a quick, unbiased, and efficient statistical tree. It is a tree-structured classification algorithm that yields a growing binary decision tree. The QUEST tree-growing process consists of selecting a split predictor, selecting a split point for the selected predictor, and stopping. The QUEST algorithm uses an unbiased or linear variable selection technique and employs imputation instead of surrogate splits to deal with missing values [
34]. It can easily handle categorical predictor variables with many categories [
7].
To apply the CHAID algorithm to develop decision trees, all the continuous factors except geology, hydrogeology, and soil were reclassified into 10 classes using frequency ratio values. The frequency ratio is the ratio of the area where SPC data existed to the total area. Factors were initially reclassified into 10 classes, each with a similar number of cells in total area. Thus, the range of each class was determined automatically based on equal area. Reclassification is a generalization technique used to reassign values, such as the ratio from the frequency ratio model, in an input theme to create a new input theme. Using the frequency ratio values, the 10 classes were then reclassified into three classes for applying the CHAID and QUEST algorithms.
SPSS software [
35] was used to implement the CHAID and QUEST algorithms. At the first step of the decision tree analysis, the frequency ratio data of factors, which were saved as ASCII files, were converted and loaded into SPSS data files. The SPSS decision trees algorithm offers a pruning mechanism in the tree induction stage for controlling the growth of the tree. At the next step, the values of the output attribute denoting groundwater productivity potential were listed via a model analysis tool. Finally, the observed and predicted values were saved in an ASCII file. An example of a decision tree derived from the CHAID algorithm is presented in
Figure 4.
Figure 4.
Architecture of the decision-tree model. A decision tree consists of the following three elements: node, condition, and production (p-value). Moreover, there are three types of node, the root (A), internal (B), and terminal nodes (C).
Figure 4.
Architecture of the decision-tree model. A decision tree consists of the following three elements: node, condition, and production (p-value). Moreover, there are three types of node, the root (A), internal (B), and terminal nodes (C).
5. Results
The decision trees constructed using the two algorithms were applied to each grid cell of the study area. For GPP mapping, predictors as factors and the probability (
p-value) in the leaf node can be considered as the GPP. After the tree-construction process, leaf nodes were calculated. Then, the probability in the leaf node was considered as the groundwater productivity potential index (GPPI). To obtain a GPP map, the GPPI values were reclassified into different productivity potential classes. The index was classified into three classes based on area for easy visual interpretation: high, medium, and low index ranges considering distribution area, respectively. GPP maps made using the GPPI are shown in
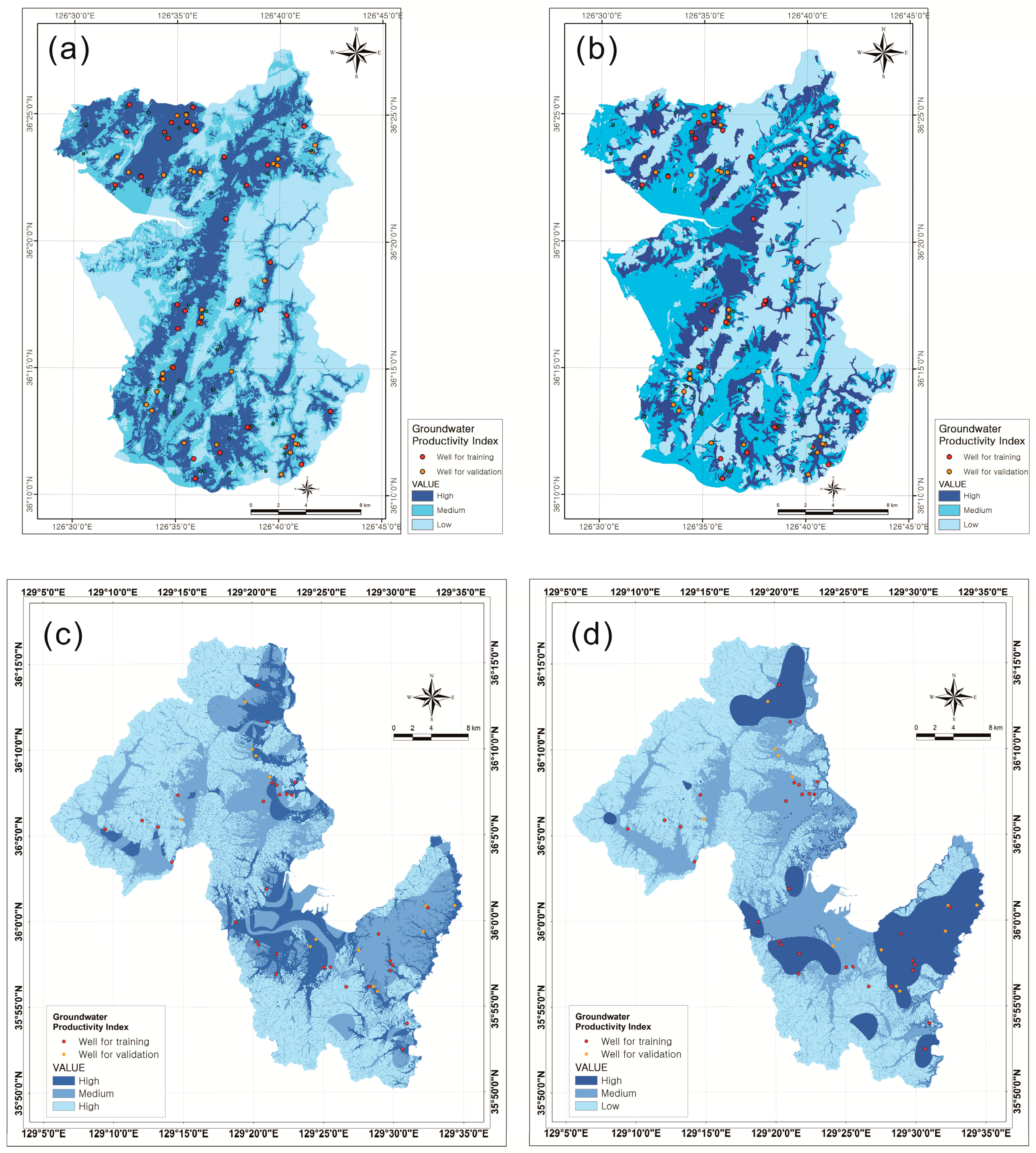
Figure 5. The classification is useful for estimating GPP in each class and for visually delineating predicted GPP areas.
Figure 5.
Groundwater productivity potential map created using decision-tree model. The index was classified into three classes based on area for easy and visual interpretation: high, medium, and low index ranges of the study area, respectively. (a) CHAID algorithm for Boryeong city; (b) QUEST algorithm for Pohang city; (c) CHAID algorithm for Boryeong city; and (d) QUEST algorithm for Pohang city.
Figure 5.
Groundwater productivity potential map created using decision-tree model. The index was classified into three classes based on area for easy and visual interpretation: high, medium, and low index ranges of the study area, respectively. (a) CHAID algorithm for Boryeong city; (b) QUEST algorithm for Pohang city; (c) CHAID algorithm for Boryeong city; and (d) QUEST algorithm for Pohang city.
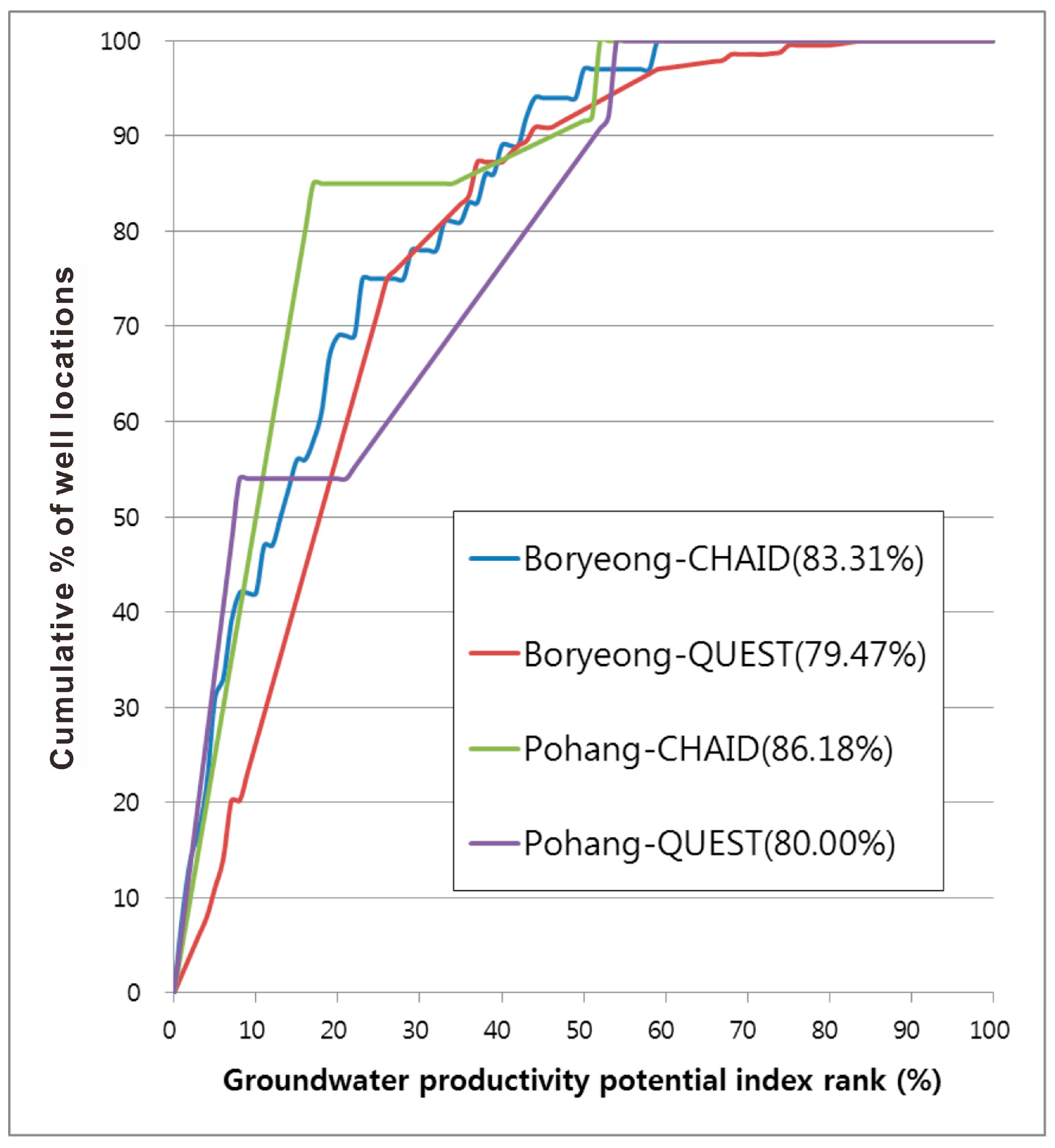
A GPP map should effectively predict GPP areas and can be validated by incorporating data from new GPP-likely datasets as they occur. Here, the result of the GPP analysis was validated using a test GPP-likely dataset (50% of the total GPP-likely dataset) that was not used for the analysis. To validate the GPP map, the calculated GPPI values of all cells were sorted in descending order. Then, the ordered cell values were divided into 100 classes at 1% cumulative intervals. The above procedure was also adapted for the GPP-likely dataset cells by comparing the 100 classes obtained with the distribution in the study area. Then, a graph was made by connecting the two classified values. For example, in the case of the CHAID algorithm, the 90%–100% (10%) class of the Boryeong city where the GPPI had a higher rank could explain 51% of the entire productivity potential. Furthermore, the 80%–100% (20%) class of the study area where the GPPI had a higher rank could explain 68% of the productivity potential. To compare the results quantitatively, the areas under the curve (AUC) were re-calculated as the total area [
36,
37]. Hence, the area under a curve can be used to assess the prediction accuracy qualitatively.
From the validation of the GPP maps, the decision tree (CHAID and QUEST algorithms) approaches produced AUC values of 83.31 and 79.47, respectively, meaning that the GPP maps had accuracies of 83.31% (CHAID) and 79.47% (QUEST) (
Figure 6) in the case of Boryeong city. In the case of Pohang city, the decision tree (CHAID and QUEST algorithms) approaches produced AUC values of 86.18 and 80.00, respectively, meaning that the GPP maps had accuracies of 86.18% (CHAID) and 80.00% (QUEST) (
Figure 6).
Figure 6.
Cumulative frequency diagram showing the groundwater-productivity-potential (GPP) index rank (x axis) occurring in the cumulative percent of well (SPC>4.55 m3/day/m (Boryeong) and 6.25 m3/day/m (Pohang)) (y axis). From the validation of the GPP maps using decision tree (CHAID and QUEST algorithms) approaches produced AUC values.
Figure 6.
Cumulative frequency diagram showing the groundwater-productivity-potential (GPP) index rank (x axis) occurring in the cumulative percent of well (SPC>4.55 m3/day/m (Boryeong) and 6.25 m3/day/m (Pohang)) (y axis). From the validation of the GPP maps using decision tree (CHAID and QUEST algorithms) approaches produced AUC values.
The other validation is performed by comparing the GPP map with borehole SPC data. The 72 wells in Boryeong city and 44 wells in Pohang city were used to validate the accuracy of the predicted map. The actual SPC value in each wells were compared with GPP maps and the Agreement/Disagreement between the expected/actual SPC data are shown in
Table 3. The values which are greater than 4.55 m
3/day/m in Boryeong city and are greater than 6.25 m
3/day/m in Pohang city were used as actually high SPC value. So, the Equation (2) was used to calculate to accuracy.
Table 3.
Validation table for the prediction map in Boryeong and Pohang city.
Table 3.
Validation table for the prediction map in Boryeong and Pohang city.
| ID | Location | SPC | CHA ID | Remarks | QUEST | Remarks | ID | Location | SPC | CHA ID | Remarks | QUEST | Remarks |
|---|
| 1 | BR(PH) | 18.65(26.38) | H(H) | A(A) | H(H) | A(A) | 37 | BR(PH) | 46.14(16.10) | M(H) | - (A) | M(M) | - (-) |
| 2 | BR(PH) | 5.91(27.11) | H(L) | A(D) | H(H) | A(A) | 38 | BR(PH) | 60.93(6.50) | H(H) | A(A) | H(M) | A(-) |
| 3 | BR(PH) | 10.69(16.67) | H(H) | A(A) | M(H) | - (A) | 39 | BR(PH) | 47.95(7.08) | M(M) | - (-) | H(M) | A(-) |
| 4 | BR(PH) | 8.11(39.84) | H(L) | A(D) | M(L) | - (D) | 40 | BR(PH) | 20.80(10.47) | H(H) | A(A) | H(M) | A(-) |
| 5 | BR(PH) | 6.34(111.14) | H(H) | A(A) | H(H) | A(A) | 41 | BR(PH) | 9.51(26.09) | M(M) | - (-) | H(M) | A(-) |
| 6 | BR(PH) | 6.40(85.54) | H(H) | A(A) | H(H) | A(A) | 42 | BR(PH) | 24.45(31.29) | H(M) | A(-) | H(M) | A(A) |
| 7 | BR(PH) | 8.37(80.00) | H(H) | A(A) | H(M) | A(-) | 43 | BR(PH) | 11.72(8.81) | H(H) | A(A) | H(H) | A(A) |
| 8 | BR(PH) | 19.55(69.17) | H(H) | A(A) | H(H) | A(A) | 44 | BR(PH) | 7.77(8.33) | H(H) | A(A) | H(H) | A |
| 9 | BR(PH) | 16.75(6.73) | M(H) | - (A) | H(M) | A(-) | 45 | BR | 10.97 | H | A | H | A |
| 10 | BR(PH) | 11.29(6.38) | H(M) | A(-) | H(M) | A(-) | 46 | BR | 5.68 | H | A | H | A |
| 11 | BR(PH) | 54.83(10.26) | M(H) | - (A) | H(H) | A(A) | 47 | BR | 20.71 | H | A | H | A |
| 12 | BR(PH) | 4.83(53.66) | H(H) | A(A) | M(H) | - (A) | 48 | BR | 7.65 | H | A | H | A |
| 13 | BR(PH) | 14.71(12.06) | H(H) | A(A) | H(H) | A(A) | 49 | BR | 5.06 | L | D | M | - |
| 14 | BR(PH) | 13.43(9.02) | H(H) | A(A) | H(H) | A(A) | 50 | BR | 20.85 | H | A | M | - |
| 15 | BR(PH) | 6.93(23.08) | M(H) | - (A) | M(M) | - (-) | 51 | BR | 8.35 | M | - | M | - |
| 16 | BR(PH) | 8.13(14.96) | H(H) | A(A) | H(H) | A(A) | 52 | BR | 14.02 | H | A | H | A |
| 17 | BR(PH) | 8.33(16.13) | M(H) | - (A) | H(H) | A(A) | 53 | BR | 4.96 | H | A | M | - |
| 18 | BR(PH) | 9.96(25.59) | H(H) | A(A) | H(M) | A(-) | 54 | BR | 10.84 | H | A | H | A |
| 19 | BR(PH) | 5.26(46.30) | H(H) | A(A) | L(H) | D(A) | 55 | BR | 6.10 | H | A | H | A |
| 20 | BR(PH) | 12.10(22.99) | H(H) | A(A) | H(H) | A(A) | 56 | BR | 10.54 | M | - | H | A |
| 21 | BR(PH) | 7.35(40.00) | H(H) | A(A) | M(H) | - (A) | 57 | BR | 6.70 | M | - | H | A |
| 22 | BR(PH) | 4.94(12.17) | H(H) | A(A) | H(H) | A(A) | 58 | BR | 5.54 | H | A | H | A |
| 23 | BR(PH) | 6.84(8.95) | H(H) | A(A) | H(H) | A(A) | 59 | BR | 9.96 | H | A | H | A |
| 24 | BR(PH) | 5.88(7.20) | H(H) | A(A) | H(H) | A(A) | 60 | BR | 5.60 | H | A | M | - |
| 25 | BR(PH) | 6.35(36.90) | H(H) | A(A) | H(H) | A(A) | 61 | BR | 6.49 | H | A | H | A |
| 26 | BR(PH) | 5.48(23.35) | H(M) | A(-) | H(M) | A(-) | 62 | BR | 7.18 | M | - | H | A |
| 27 | BR(PH) | 9.96(44.03) | H(M) | A(-) | H(M) | A(-) | 63 | BR | 6.06 | M | - | H | A |
| 28 | BR(PH) | 6.99(31.88) | H(M) | A(-) | H(M) | A(D) | 64 | BR | 4.98 | H | A | H | A |
| 29 | BR(PH) | 5.77(8.60) | H(L) | A(D) | H(L) | A(D) | 65 | BR | 5.16 | M | - | L | D |
| 30 | BR(PH) | 14.73(20.34) | M(L) | - (D) | H(L) | A(-) | 66 | BR | 8.78 | H | A | H | A |
| 31 | BR(PH) | 18.00(7.81) | H(M) | A(-) | H(M) | A(-) | 67 | BR | 6.39 | H | A | H | A |
| 32 | BR(PH) | 9.88(8.59) | H(M) | A(-) | H(M) | A(-) | 68 | BR | 10.28 | H | A | H | A |
| 33 | BR(PH) | 6.33(15.39) | H(H) | A(A) | H(M) | A(-) | 69 | BR | 4.66 | H | A | H | A |
| 34 | BR(PH) | 5.49(66.80) | H(M) | A(-) | H(M) | A(-) | 70 | BR | 16.00 | L | D | L | D |
| 35 | BR(PH) | 19.85(64.02) | H(H) | A(A) | H(M) | A(-) | 71 | BR | 9.11 | H | A | M | - |
| 36 | BR(PH) | 10.33(24.90) | H(M) | A(-) | M(M) | - (-) | 72 | BR | 393.33 | H | A | H | A |
For example, the accuracy of the prediction in Boryeong city (CHAID and QUEST) is estimated as follows:
Number of boreholes where there is agreement between the expected (High potential) and the actual SPC = 56/56
Number of boreholes where there is disagreement between the expected (Low potential) and the actual yield = 2/3
The accuracy of the prediction of CHAID = 56 / (56 + 2) × 100 = 96.55%
The accuracy of the prediction of QUEST = 56 / (56 + 3) × 100 = 94.92%
Also, the accuracy of the prediction in Pohang city (CHAID and QUEST) is estimated as 87.88% and 87.50%, respectively.
6. Conclusions and Discussion
This study used the decision tree model to predict GPP areas in the Boryeong and Pohang cites, where groundwater production is expected to continue into the future. Two tree-constructing algorithms, CHAID and QUEST, were applied to map GPP and the GPP maps were validated. Generally, with respect to spatial distribution, the maps produced using the decision tree (CHAID and QUEST algorithms) approaches showed similar patterns, but patterns in some areas were different. The high potential areas are lowlands and either residential or agricultural areas. These areas of high and very high potential should be a priority concern for new development sites during groundwater development planning. The validation results showed satisfactory agreement between the GPP map and the existing well location data. In Boryeong city, the map produced using the CHAID and QUEST algorithms had high accuracies of 83.31% and 79.47% by the AUC method. In Pohang city, the accuracies were 86.18% (CHAID) and 80.00% (QUEST). The other validation method by comparing the GPP map with borehole SPC data showed accuracies of 96.55% and 94.92% (CHAID and QUEST) in Boryeong city and 87.88% and 87.50% (CHAID and QUEST) in Pohang city. The prediction accuracy obtained showed that the method applied for this study produced very reliable and accurate results. Generally, the CHAID algorithm showed better accuracy than the QUEST algorithm. The decision tree model can be used efficiently for GPP analysis and may be used widely for prediction of various spatial events. However, for generalizing the approach, more case studies including validations should be performed. For this, a hydrogeological database covering many areas should be prepared and the decision tree model should be applied to create a GPP map. To improve accuracy, not only applications and validation models but also accurate (large scale) and various input data should be considered.
The main advantage of classification trees is the insight that their split points are believed to provide. Loh and Shih (1997) demonstrated that an exhaustive search tends to result in the selection of variables that afford more splits. Therefore, such trees should be interpreted with caution. In terms of classification accuracy, the variability in split points, and tree size, there is no clear best choice among most algorithms when univariate splits are used. However, the QUEST algorithm based on linear combination splits is usually shorter and more accurate than the same trees based on univariate splits [
7]. Also, unlike other statistical models, a decision tree makes no statistical assumptions, can handle data represented on different measurement scales, and is computationally fast [
8].
The model proposed in this paper and the resultant GPP maps can be applied to the establishment of development and management plans for the use of groundwater resources, such as for regional groundwater-development planning, decisions about promising areas for groundwater development, and control over the water supply system, based on a systematic, objective, and scientific decision model. The resulting maps also can help planners choose locations suitable for implementing further detailed explorations. Moreover, the use of the same analysis in other districts with similar topographic and geological conditions could result in time and cost savings in predicting groundwater productivity. If applied in other areas, the GPP mapping method developed in this study could become a widespread and useful analysis model for groundwater productivity. However, care should be taken in using the model for the development of specific sites as the scale of the analysis should be considered. Therefore, the model used in the study is valid only for generalized planning and assessment purposes.