Biomass Power Generation Industry Efficiency Evaluation in China
Abstract
:1. Introduction
2. Literature Review and Emerged Concerns
3. Industrial Characteristics of Biomass Power Generation in China
3.1. Conservative Rising Development Tendency
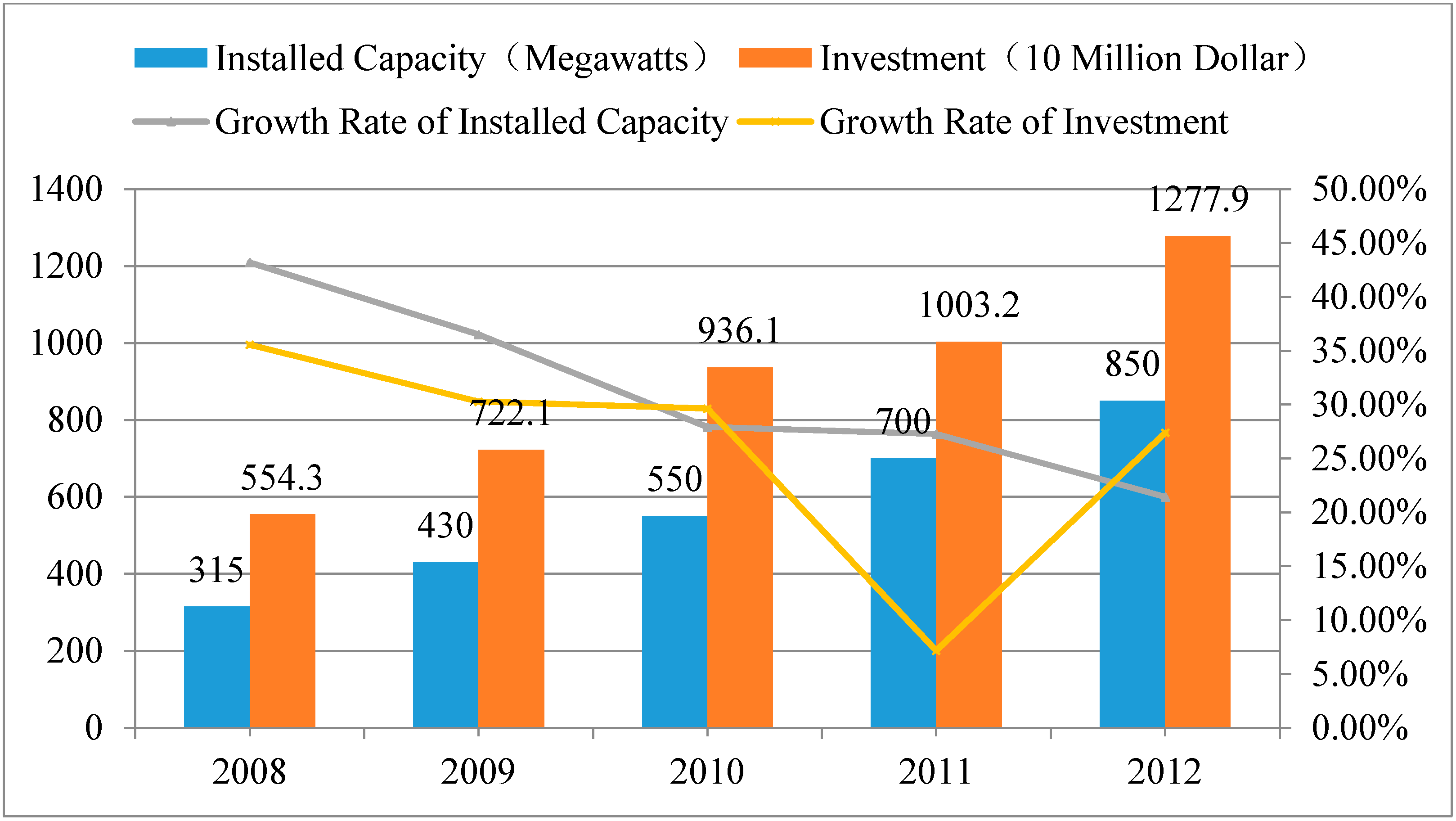
3.2. Simple Impacts from the Industry Chain
| Year | 2010 | 2020 | 2030 | 2050 | |
|---|---|---|---|---|---|
| Biomass resource type | Present biomass resource | 2.8 | 2.8 | 2.8 | 2.8 |
| Newly-added organic waste | 0.6 | 1.7 | 2.2 | 2.7 | |
| Present woodland growth | 0.05 | 0.3 | 0.7 | 1.37 | |
| New ground marginal product | 0.05 | 0.3 | 1 | 2 | |
| Total potential | 3.5 | 5.1 | 6.7 | 8.9 |
3.3. Distinct Regional Difference
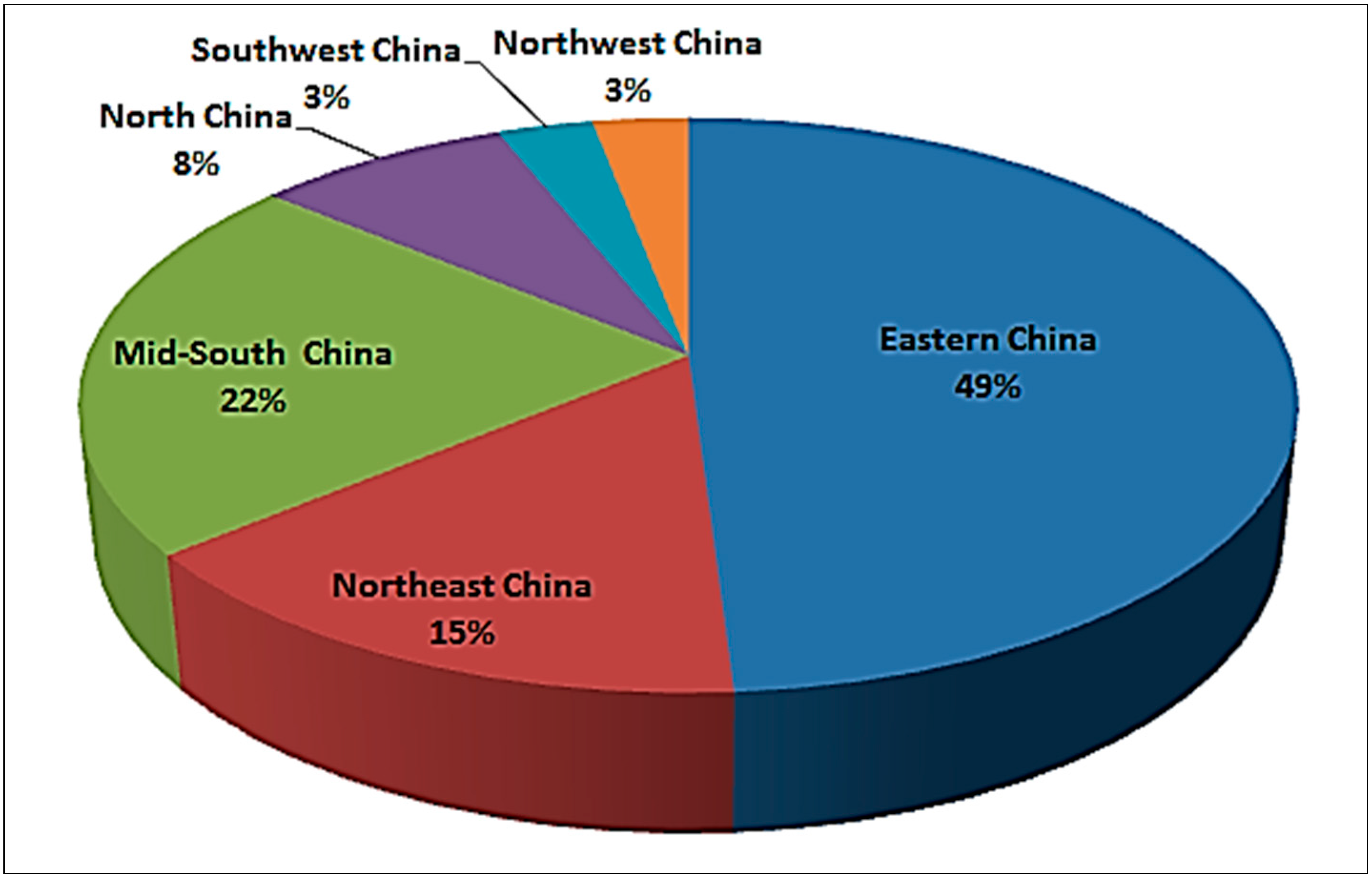
4. Methodology
4.1. Drawbacks of Traditional DEA Models
4.2. Additive-Based DEA Models
- (P1)
- The optima is between 0 and 1;
- (P2)
- The optima is 0 when DMUo is fully inefficient, while the optima is 1 when DMUo is fully efficient;
- (P3)
- The optima is well defined and unit invariant;
- (P4)
- The optima is strongly monotonic;
- (P5)
- The optima is translation invariant.
| Model | P1 | P2 | P3 | P4 | P5 |
|---|---|---|---|---|---|
| CCR | Yes | Yes | Partially Units Invariance | Monotonic | NO |
| Normalized weighted CCR | Yes | Yes | Units Invariance | Monotonic | NO |
| BCC | Yes | Yes | Partially Units Invariance | Monotonic | Partially Translation Invariance |
| Normalized weighted BCC | Yes | Yes | Units Invariance | Monotonic | Partially Translation Invariance |
| Additive model | No | No | No | Monotonic | Yes |
| Normalized weighted Additive Model | No | No | Units Invariance | Monotonic | Yes |
| SBM | Yes | Yes | Yes | Monotonic | Yes |
| RAM | Yes | Yes | Yes | Strongly Monotonic | Yes |
| BAM | Yes | Yes | Yes | Monotonic | Yes |
4.3. Generalized Additive-Based DEA Model-BMA Model
4.4. BMAS Model
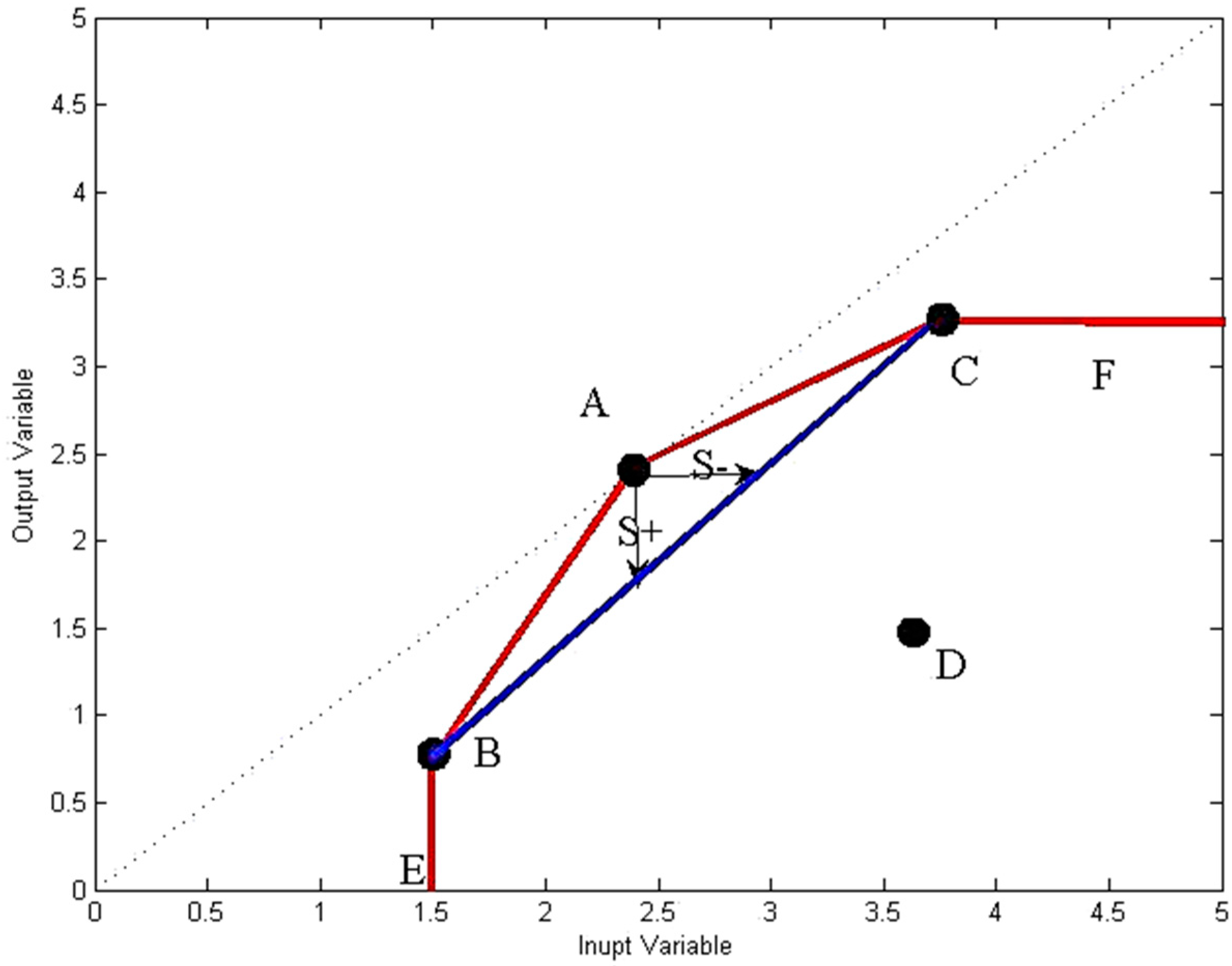
5. Empirical Analysis
5.1. Efficiency Analysis
| Inputs/Outputs | Unit | Average | Std | Max | Min |
|---|---|---|---|---|---|
| Greenhouse Gas Emissions (I) | tCO2/GWh | −203.961 | 542.0662 | 600 | −1223 |
| O&M + CC Costs (I) | RMB/MWh | 14.69 | 25.4917 | 62.53 | −26.52 |
| Investment Costs (I) | RMB/MWh | 38.15727 | 18.70269 | 76 | 14.96 |
| Potential Job Creation (O) | Job/TWh | 7811.348 | 11,466.02 | 35,347.69 | 1.88 |
| Potential Distributed Power Generation (O) | GWH/year | 54,870.36 | 35,121.65 | 133,296 | 6833 |
| Biomass Power Plants | BCC Efficiency | BMA Efficiency | BMAS Efficiency | BCC Rank | BMA Rank | Location |
|---|---|---|---|---|---|---|
| Shangdong Pingyuan | 1.00 | 0.882389 | 7 | 9 | South | |
| Hebei Wuqiao | 1.00 | 0.984928 | 9 | 8 | North | |
| Hebei Yuanshi | 1.00 | 0.981673 | 10 | 10 | North | |
| Anhui Shouxian | 1.00 | 0.859524 | 11 | 11 | South | |
| Jilin Changling | 1.00 | 1.000000 | 1.010540 | 6 | 3 | North |
| Neimeng Zhaoxin | 1.00 | 1.000000 | 1.012733 | 3 | 2 | North |
| Hengshui Taida | 1.00 | 0.988927 | 2 | 5 | North | |
| Jilin Gongzhuling | 1.00 | 1.000000 | 1.033233 | 1 | 1 | North |
| Dongping Guangyuan | 1.00 | 0.887661 | 5 | 6 | South | |
| Shandong Pingquan | 1.00 | 0.886453 | 8 | 7 | South | |
| Jiangxi Ganxian | 0.331 | 0.888768 | 4 | 4 | South |
5.2. Group Analysis
| Group | Mean | Std | Max | Min |
|---|---|---|---|---|
| North | 0.9923 | 0.0079 | 1.0000 | 0.9814 |
| South | 0.8009 | 0.0421 | 0.8888 | 0.7595 |
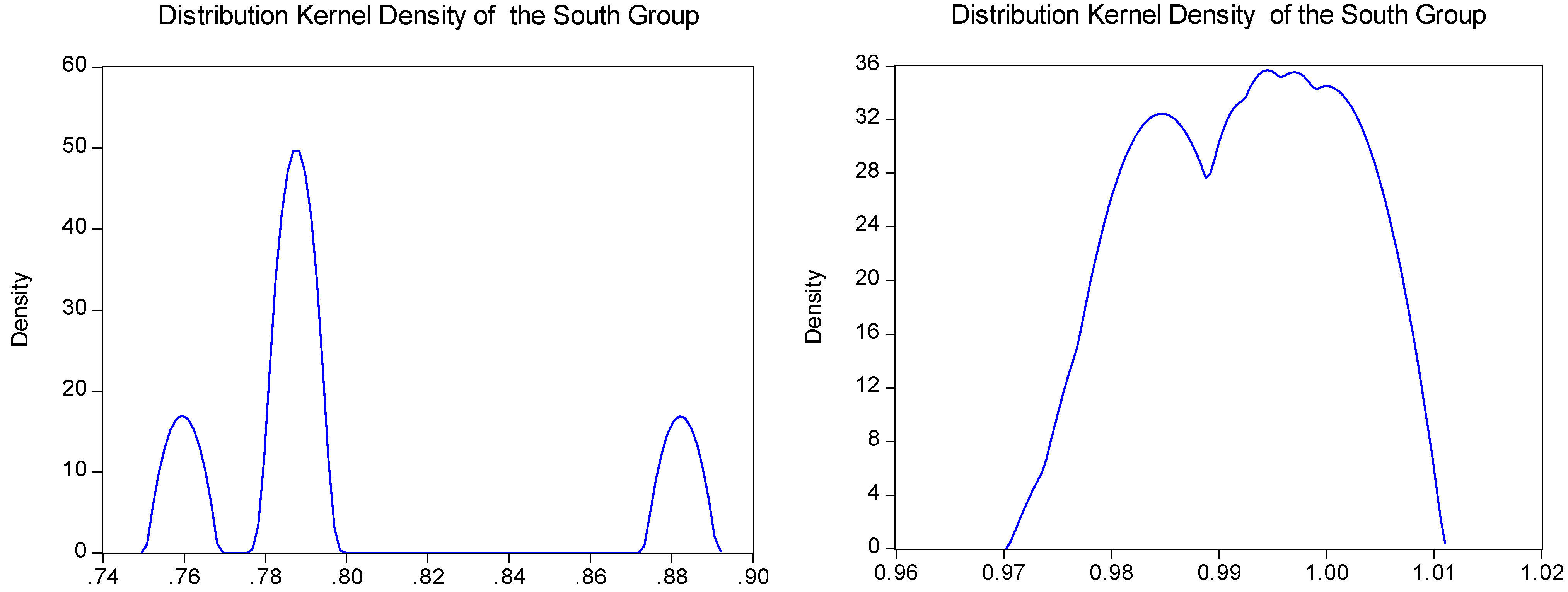
| Variable | Mann–Whitney U | Prob | K-S | Prob |
|---|---|---|---|---|
| efficiency | 15 | 0.006 | 1.651 | 0.009 |
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hooper, R.; Li, J. Summary of the factors critical to the commercial application of bioenergy technologies. Biomass Bioenerg. 1996, 11, 469–474. [Google Scholar] [CrossRef]
- Weber, C.; Perrels, A. Modelling lifestyle effects on energy demand and related emissions. Energ. Policy 2000, 28, 549–566. [Google Scholar] [CrossRef]
- Klevas, V.; Streimikiene, D.; Grikstaite, R. Sustainable energy in Baltic States. Energ. Policy 2007, 35, 76–90. [Google Scholar] [CrossRef]
- St. Denis, G.; Parker, P. Community energy planning in Canada: The role of renewable energy. Renew. Sustain. Energ. Rev. 2009, 13, 2088–2095. [Google Scholar] [CrossRef]
- Zhou, P.; Ang, B.W.; Wang, H. Energy and CO2 emission performance in electricity generation: A non-radial directional distance function approach. Eur. J. Oper. Res. 2012, 221, 625–635. [Google Scholar] [CrossRef]
- Zhao, Z.Y.; Yan, H. Assessment of the biomass power generation industry in China. Renew. Energ. 2012, 37, 53–60. [Google Scholar] [CrossRef]
- Kautto, N.; Peck, P. Regional biomass planning—Helping to realise national renewable energy goals? Renew. Energ. 2012, 46, 23–30. [Google Scholar] [CrossRef]
- San Cristóbal, J.R. A multi criteria data envelopment analysis model to evaluate the efficiency of the Renewable Energy technologies. Renew. Energ. 2011, 36, 2742–2746. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Zheng, F. Unified Efficiency Measurement of Electric Power Supply Companies in China. Sustainability 2014, 6, 779–793. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Ali, A.I.; Seiford, L.M. The Mathematical Programming Approach to Efficiency Analysis. In The Measurement of Productive Efficiency: Techniques and Applications; Fried, H.O., Schmidt, S.S., Eds.; Oxford University Press: London, UK, 1993; pp. 120–159. [Google Scholar]
- Du, J.; Liang, L.; Zhu, J. A slacks-based measure of super-efficiency in data envelopment analysis: A comment. Eur. J. Oper. Res. 2010, 204, 694–697. [Google Scholar] [CrossRef]
- Tone, K. A slacks-based measure of efficiency in data envelopment analysis. Eur. J. Oper. Res. 2001, 130, 498–509. [Google Scholar] [CrossRef]
- Oral, M.; Kettani, O.; Lang, P. A methodology for collective evaluation and selection of industrial R&D projects. Manag. Sci. 1991, 37, 871–885. [Google Scholar] [CrossRef]
- Thompson, R.G.; Langemeier, L.N.; Lee, C.T.; Lee, E. The role of multiplier bounds in efficiency analysis with application to Kansas farming. J. Econom. 1990, 46, 93–108. [Google Scholar] [CrossRef]
- Liu, J.S.; Lu, L.Y.Y.; Lu, W.M.; Lin, B.Y.J. A survey of DEA applications. Omega 2013, 41, 893–902. [Google Scholar] [CrossRef]
- Xingang, Z.; Zhongfu, T.; Pingkuo, L. Development goal of 30 GW for China’s biomass power generation: Will it be achieved? Renew. Sustain. Energ. Rev. 2013, 25, 310–317. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef]
- Lins, M.E.; Oliveira, L.B.; Da Silva, A.C.M.; Rosa, L.P. Performance assessment of Alternative Energy Resources in Brazilian power sector using Data Envelopment Analysis. Renew. Sustain. Energ. Rev. 2012, 16, 898–903. [Google Scholar] [CrossRef]
- Lovell, C.A.K.; Pastor, J.T. Units invariant and translation invariant DEA models. Oper. Res. Lett. 1995, 18, 147–151. [Google Scholar] [CrossRef]
- Cooper, W.; Park, K.; Pastor, J. RAM: A Range Adjusted Measure of Inefficiency for Use with Additive Models, and Relations to Other Models and Measures in DEA. J. Product. Anal. 1999, 11, 5–42. [Google Scholar] [CrossRef]
- Cooper, W.W.; Pastor, J.T.; Borras, F.; Aparicio, J. BAM: A bounded adjusted measure of efficiency for use with bounded additive models. J. Product. Anal. 2011, 35, 85–94. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Q.; Tao, J. Biomass Power Generation Industry Efficiency Evaluation in China. Sustainability 2014, 6, 8720-8735. https://doi.org/10.3390/su6128720
Yan Q, Tao J. Biomass Power Generation Industry Efficiency Evaluation in China. Sustainability. 2014; 6(12):8720-8735. https://doi.org/10.3390/su6128720
Chicago/Turabian StyleYan, Qingyou, and Jie Tao. 2014. "Biomass Power Generation Industry Efficiency Evaluation in China" Sustainability 6, no. 12: 8720-8735. https://doi.org/10.3390/su6128720
APA StyleYan, Q., & Tao, J. (2014). Biomass Power Generation Industry Efficiency Evaluation in China. Sustainability, 6(12), 8720-8735. https://doi.org/10.3390/su6128720




