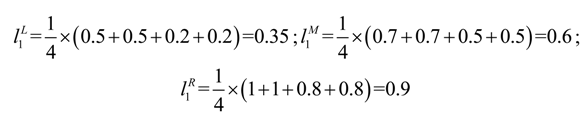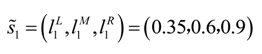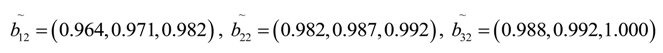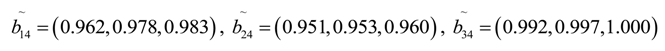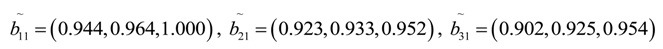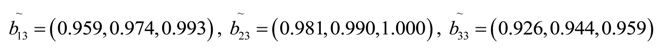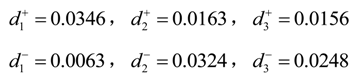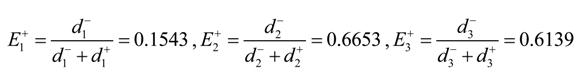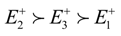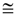1. Introduction
Since China’s move towards reform and opening up, a large number of power plant projects have been constructed in order to meet the demands of social and economic development for electricity. In order to meet this development requirement, the public bidding and tendering system has been applied to the procurement of thermal power equipment since the year 1985. The selection of thermal power equipment suppliers is a very important part of the thermal power equipment bidding and tendering management, which is also essential to the smooth and sustainable construction of thermal power plants.
With the significant increase of fossil energy consumption and the ever-worsening pollution of our environment, ‘green development’ and ‘sustainable development’ have become the focus of global attention [
1,
2]. Green supply chain management (GSCM) is a modern sustainable management mode considering resources efficiency and environmental impact, which contains all processes of product life cycle from designing to recycling [
3]. GSCM has been implemented by many companies for their own sustainable development. Thermal power is the main power generation form in China, and the green supplier selection of thermal power equipment is essential to the smooth and sustainable construction of thermal power plants. Therefore, within an environment of advocating the sustainable development of energy conservation and emissions reduction, selecting the proper green supplier of thermal power equipment with green production consciousness is of great importance to the company’s sustainable development and the sustainability of China’s electric power industry.
The selection of green suppliers is a multi-criteria decision making (MCDM) problem [
4]. MCDM technique ranks the potential alternatives and selects the best alternative by using certain approaches based on the existing decision-making information arising from the multiple criteria, which has gradually been a research focus in the field of decision science, system science, and management science. The green supplier selection is a MCDM issue, which need consider many criteria comprehensively, such as cost, delivery time, environment, and so on.
Nowadays, there are many approaches to be used for the supplier selection. However, the approaches that are proposed to apply in the selection of green suppliers are rather limited. Kannan,
et al. [
5] combined the fuzzy-AHP and multi-objective linear programming approach to select the green supplier in the field of automobile manufacturing. Shen,
et al. [
6] used the fuzzy TOPSIS to combine linguistic preferences to generate an overall performance score for each supplier. Buyukozkan and Cifci [
7] proposed a novel hybrid fuzzy multiple criteria decision making (MCDM) model that combines the fuzzy Decision Making Trial and Evaluation Laboratory Model (DEMATEL), ANP, and TOPSIS, to perform the green supplier evaluation for Ford Otosan Company. Buyukozkan [
8] adopted a fuzzy group decision-making approach to evaluate green supplier alternatives, of which a fuzzy AHP was applied to determine the criteria weights and an axiomatic design (AD)-based fuzzy group decision-making approach was employed to rank the alternatives. Cifci and Buyukozkan [
9] presented a decision framework for evaluating and selecting the green suppliers based on the fuzzy analytic hierarchy process (FAHP) and group decision making (GDM) method. Kuo,
et al. [
10] integrated the artificial neural network and two multi-attribute decision analysis methods including data envelopment analysis and analytic network process, namely ANN-MADA hybrid method, to perform the green supplier selection by taking the international well-known camera manufacturer as an example. Bai and Sarkis [
11] used the rough set theory to analyze the relationships between supplier development program involvement attributes, organizational attributes, and performance outcomes, which fill the research gap in the green supplier selection. Lee,
et al. [
12] applied the Delphi method to differentiate the criteria and fuzzy extended analytic hierarchy process to rank the green supplier alternatives, and then selected the most suitable green supplier for cooperation.
In this paper, a new hybrid multi-criteria decision making approach is proposed to select the proper green supplier of thermal power equipment, namely the fuzzy entropy-TOPSIS approach. Due to the ambiguity and intangibility arising from human qualitative judgment as well as the vagueness and uncertainty arising from the lack of complete information, the fuzzy set theory [
13], which uses linguistic terms to represent decision makers’ preferences, is employed to overcome these drawbacks. The decision makers provide linguistic ratings to the evaluation criteria and to the green suppliers (alternatives). A combination of subjective weight determination and objective weight determination for evaluation criteria is employed. The subjective weight determination by using superiority linguistic ratings can reflect the experts’ thoughts and opinions, while the objective weight determination by using fuzzy-entropy method can measure the average essence of information quantity of criteria data as well as grasp the actual conditions of evaluation criteria. The fuzzy TOPSIS, which distinguishes between Benefit and Cost category criteria and selects the best solution close to the positive ideal ones and far from negative ideal ones, is employed to generate an overall performance score for each green supplier. The green supplier of thermal power equipment with the highest performance score is finally selected.
The rest of the paper is organized as follows.
Section 2 briefly describes the fuzzy set theory, which includes triangular fuzzy number and linguistic variable. The fuzzy-entropy weighting method is introduced in
Section 3. In
Section 4, the basic theory of fuzzy-TOPSIS is presented. The framework of proposed hybrid fuzzy entropy-TOPSIS for prioritize the green supplier of thermal power equipment is described in
Section 5. The empirical case study is conducted in
Section 6. Finally, the conclusions are presented in
Section 7.
3. Fuzzy-Entropy Weighting Method
The entropy method, firstly appeared in thermodynamics, is used to describe the matter status, and then was introduced into information theory by Shannon [
21]. Entropy weighting method is an objective method for criteria weight determination, which can effectively reflect the information essence and measure the useful information of the provided data [
22]. If the difference of the same criteria value among the evaluated alternatives is large, the information entropy is small, and there is more useful information provided by the criteria data, so the weight of this criterion should be set high correspondingly [
23]. In this paper, the entropy weighting method is employed to determinate the weights of objective criteria.
The procedure of the weight determination of objective criteria by using the entropy weighting method characterized by triangular fuzzy numbers is as follows.
Step 1: Suppose
ãik be the triangular fuzzy number evaluation value of alternative
Ai in terms of objective criterion
Ck . Let
m and
p represent the numbers of alternatives and objective criteria, respectively. Let
hik =
R(
ãik),
i = 1,2, … ,
m,
k = 1,2, … ,
p, be the graded mean integration representation value of
ãik , which can be calculated according to Equation (2), 0 ≤
hik ≤ 1. Define
Step 2: Calculate the entropy value of objective criterion
Ck
where
ek ≥ 0.
Step 3: Calculate the weight of objective criterion
Ck
where 0 ≤
λk ≤ 1,
![Sustainability 06 00217 i011]()
.
4. Fuzzy-TOPSIS
TOPSIS (Technique for Order Preference by Similarity to an Ideal Solution) is a classic multi-criteria decision making (MCDM) method proposed by Hwang and Yoon (1981) [
24]. TOPSIS is a frequently-used decision-making technique, which is easy to understand and large in scope to apply [
25,
26,
27]. For the traditional TOPSIS approach, the elements in the initial judgment matrix normalize decision matrix and weighted normalized matrix are represented with crisp values. However, using the linguistic value rather than crisp value to measure things in real life is a better way in some cases [
28,
29,
30]. Therefore, the fuzzy TOPSIS method which combines the traditional TOPSIS approach and fuzzy set theory presenting the linguistic value is much more suitable for solving the problems under a fuzzy environment in real life.
The specific steps of fuzzy TOPSIS approach are presented as follows.
4.1. Calculate the Aggregate Fuzzy Linguistic Ratings for the Alternatives with Respect to Subjective Criteria
Suppose that there are m possible alternatives called A = {A1, A2, … Am} which are to be evaluated against n criteria consisting of objective criteria and subjective criteria. Considering the specific requirements of the problem, the criteria are classified into objective criteria and subjective criteria in this paper. The objective criteria have quantitative/monetary definition and the subjective criteria are defined in qualitative/linguistic terms. The subjective criteria are termed as qualitative criteria which required subjective decisions to be made during their evaluation.
Let
![Sustainability 06 00217 i012]()
,
![Sustainability 06 00217 i013]()
,
i = 1,2, … ,
m,
k =
p + 1,
p + 2, … ,
n,
j = 1,2, … ,
r be the superiority linguistic ratings assigned to alternative
Ai by decision-maker
Dj for subjective criteria
Ck, and the scale used for linguistic rating is given in
Table 2. Then, the aggregate fuzzy linguistic rating
![Sustainability 06 00217 i059]()
for the alternative
Ai with respect to subjective criteria
Ck can be calculated by
where
![Sustainability 06 00217 i015]()
,
![Sustainability 06 00217 i016]()
,
![Sustainability 06 00217 i017]()
.
4.2. Determine the Weights of all Criteria
The determination of criteria weight is quite important, which has a big impact on the final evaluation and selection result. The subjective criteria weight determination methods can embody the consciousness tendency of decision-makers, while the objective criteria weight determination methods can reflect the information essence and measure the useful information of the provided data. Many articles assign the criteria weight subjectively, which may lead to the inaccuracy of green supplier selection based on company requirements [
31]. Therefore, a combination of subjective and objective criteria weight determination method is employed in this paper,
i.e. the weights of subjective criteria are assigned by the superiority linguistic ratings of decision-makers, and the objective criteria weights are determined via the superiority linguistic ratings of decision-makers and fuzzy entropy weighting method.
Let
![Sustainability 06 00217 i018]()
,
![Sustainability 06 00217 i019]()
,
k = 1,2, … ,
p, … ,
n ,
j = 1,2, … ,
r be the superiority linguistic ratings assigned to criteria
Ck by decision-maker
Dj, and the scale used for linguistic rating is given in
Table 1. Then, the aggregated fuzzy weights
![Sustainability 06 00217 i060]()
for the criteria
Ck can be calculated by
where
![Sustainability 06 00217 i021]()
,
![Sustainability 06 00217 i022]()
,
![Sustainability 06 00217 i023]()
.
Allow ãik be the triangular fuzzy number evaluation value of alternative Ai in terms of objective criterion Ck (k = 1,2, … , p). Then the objective weight λk of objective criterion Ck can be calculated by using fuzzy entropy weighting method according to Equation (3) and Equation (4).
The normalized subjective weight
uk of all criteria can be calculated according to Equation (6)
In this paper, there are
p (
p ≤
n) objective criteria. Define
Then, the integrated weight
zk of the objective criterion
Ck can be obtained:
Based on the above analysis, the integration weights
wk of all criteria can be obtained by
4.3. Build the Initial Fuzzy Decision Matrix
In this paper, the criteria are classified into objective criteria and subjective criteria. The objective criteria evaluation values of each alternative is given in the form of triangular fuzzy number according to the actual objective conditions, while the subjective criteria evaluation values of each alternative is given in the form of triangular fuzzy number by the decision-makers’ superiority linguistic ratings. Then, the initial fuzzy decision matrix
A can be obtained
4.4. Normalize the Initial Fuzzy Decision Matrix
Considering the different dimensions and units of objective criteria, the raw data of objective criteria are needed to be converted to dimensionless scales in order to ensure the compatibility between fuzzy evaluation value of objective criteria and linguistic rating of subjective criteria [
17].
Let
![Sustainability 06 00217 i029]() i
i = 1,2, … ,
m,
k = 1,2, … ,
p be the fuzzy evaluation value of objective criterion
Ck, and the dimensionless processing procedure is as follows.
For benefit criterion
where
The subjective criteria have no need for dimensionless processing. Let
![Sustainability 06 00217 i034]()
,
i = 1,2, … ,
m;
k =
p + 1,
p + 2, … ,
n. Then, the normalized fuzzy decision matrix
B is given by
4.5. Construct the Weighted Normalized Fuzzy Decision Matrix
The weighted normalized fuzzy decision matrix
C can be calculated by multiplying the weights (
wk) of the criteria with the normalized fuzzy decision matrix
B. 4.6. Determine the Fuzzy Positive Ideal Solution and Fuzzy Negative Ideal Solution
Let and represent the fuzzy positive ideal solution and fuzzy negative ideal solution, respectively, both of which can be computed by
where
where
J1 and
J2 represent the benefit criteria set and cost criteria set, respectively.
4.7. Calculate the Distance of Each Alternative from Fuzzy Positive Ideal Solution and Fuzzy Negative Ideal Solution
There are many methods that can be applied to calculate the distance between two triangular fuzzy numbers. A modified geometrical distance with the advantages of easy implementation and powerful concept is employed in this paper [
16,
17]. The distance
d(
ãi,
ãj) between triangular fuzzy number
ãi and
ãj can be computed by
Then, the distance
![Sustainability 06 00217 i040]()
of each alternative
i (
i = 1,2, … ,
m) from the fuzzy positive ideal solution and fuzzy negative ideal solution can be calculated as follows:
4.8. Compute the Closeness Coefficient (CCi) of Each Alternative
The closeness coefficient represents the distances closet to the fuzzy positive ideal solution
C+ and far from the fuzzy negative ideal solution
C− simultaneously. The closeness coefficient of each alternative can be computed by:
4.9. Rank the Alternatives
According to the closeness coefficient CCi in decreasing order, all the alternatives can be ranked. The alternative with the maximum value of closeness coefficient CCi is selected as the best alternative.
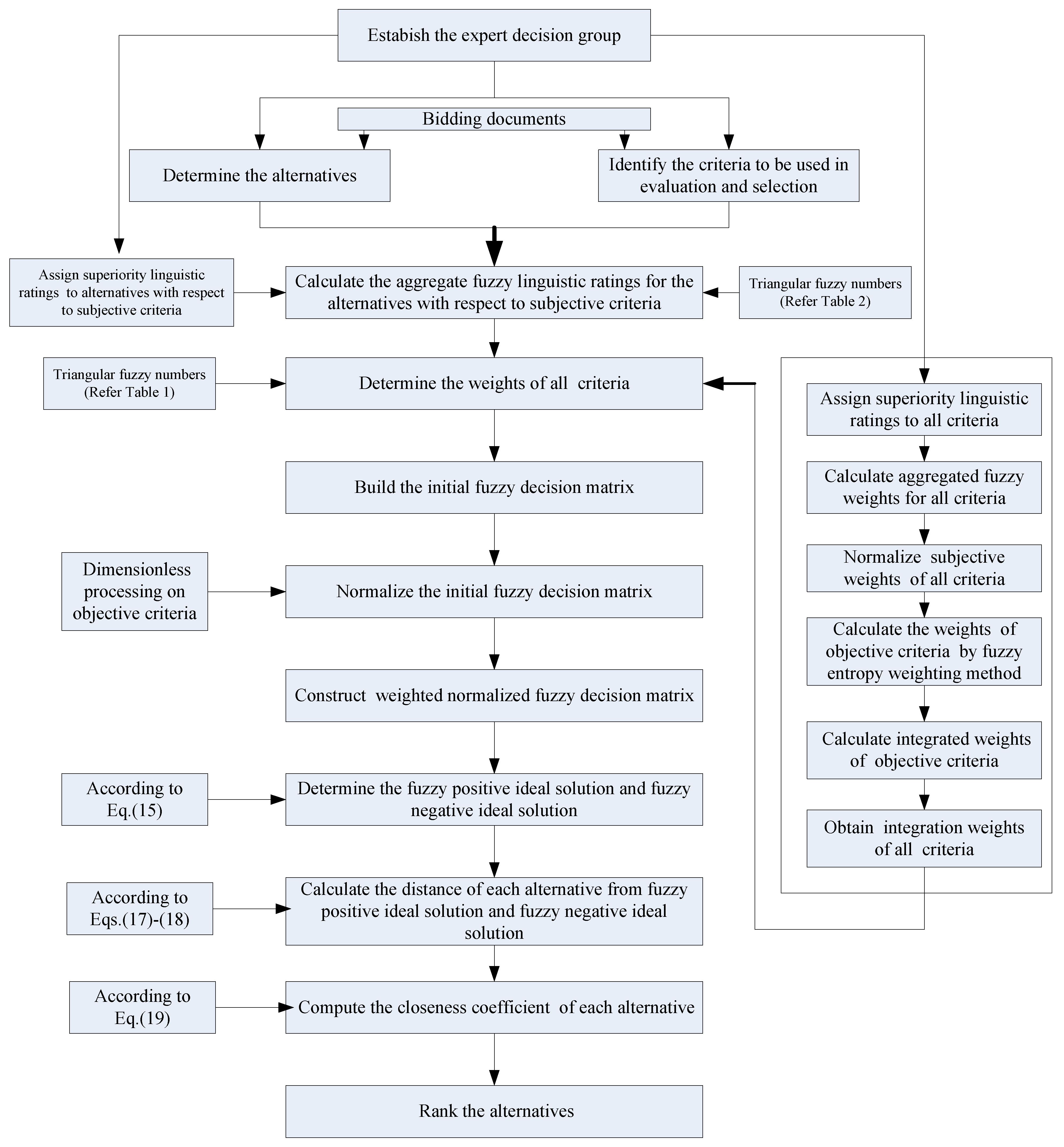
5. The Framework of Proposed Hybrid Fuzzy Entropy-TOPSIS Approach
The proposed fuzzy entropy-TOPSIS approach for green supplier selection of thermal power equipment has following two phases, which is shown in
Figure 2.
Phase 1: Determine the alternatives and identify the evaluation criteria. In the first phase, an expert decision group which is composed of electricity senior executives, bidding project managers, supply chain experts, and environmental experts is formed for the green supplier selection of thermal power equipment. After reviewing the bidding documents of all the bidders, these executives, managers and experts select the potential alternatives for supplying the thermal power equipment. Then, according to the experts’ opinion and company characteristics as well as industry background, the determination of evaluation criteria for green supplier selection of thermal power equipment is performed.
Phase 2: Evaluation of the green suppliers of thermal power equipment and determines final rank by fuzzy entropy-TOPSIS approach. In this step, the linguistic ratings are firstly allocated to the criteria and to the potential alternatives with respect to subjective criteria. Four selected decision makers perform the linguistic ratings by using rating scales given in
Table 1 to the five criteria and scales given in
Table 2 to the three alternatives, and then are transformed to triangular fuzzy numbers. Secondly, all criteria which include the objective and subjective criteria are weighted by using subjective superiority linguistic ratings and objective entropy weighting method. The subjective criteria weights are determined by using decision makers’ superiority linguistic ratings and the objective ones are determined by combining the superiority linguistic ratings and fuzzy-entropy weighting method. Finally, the fuzzy TOPSIS method is applied to aggregate the ratings of criteria and alternatives to compute the evaluation scores of the potential alternatives (green suppliers of thermal power equipment). Ranking of the green suppliers is finalized according to
CCi values in descending order. The alternative with the highest
CCi value is preferable and should be recommended as the best green suppliers of thermal power equipment.
This proposed fuzzy entropy-TOPSIS approach has the ability to evaluate and select the green suppliers of thermal power equipment under partial or lack of quantitative information. Using the triangular fuzzy numbers and linguistic values can overcome the uncertainty due to human qualitative judgment. The fuzzy-entropy weighting method can measure the average essence of information quantity of criteria data as well as grasp the actual conditions of evaluation criteria, and the superiority linguistic ratings can reflect the experts’ thoughts and opinions. The fuzzy TOPSIS method which uses the linguistic value rather than crisp value is much more suitable for solving the problems under a fuzzy environment in real life.
Figure 2.
The framework of proposed hybrid fuzzy entropy-TOPSIS approach for green supplier selection of thermal power equipment.
Figure 2.
The framework of proposed hybrid fuzzy entropy-TOPSIS approach for green supplier selection of thermal power equipment.
6. Numerical Illustration
In this section, the green suppliers of thermal power equipment are evaluated and selected by applying the proposed fuzzy entropy-TOPSIS approach, and the computational procedure of this proposed approach is demonstrated.
A thermal power plant owned by China Datang Corporation is under construction and need purchase thermal power equipment. After the 10 biding documents are reviewed by the expert decision group, three alternatives (green suppliers of thermal power equipment, GS1, GS2 and GS3) are chosen for the final selection.
The criteria determination of green supplier selection largely depends on the individual companies and industry background, such as enterprise culture, management strategy and organizational structure [
4]. In this paper, the final list contains five criteria, which are equipment quotation (I1), delivery accuracy rate (I2), equipment operational costs (I3), equipment efficiency (I4), and environmental consciousness (I5), respectively. Among these five criteria, I1 and I3 are the cost criteria that are the lower the value, the more preferable the alternative is; I2, I4, and I5 are the benefit criteria that are the higher the value, the more preferable the alternative is. I1, I2, I3 and I4 are the objective criteria, and I5 is the subjective criteria. Meanwhile, we select four decision-makers (DM1, DM2, DM3 and DM4) from the initial expert decision group to perform the linguistic preference ratings for the criteria and the alternatives according to
Table 1 and
Table 2.
6.1. Calculate the Aggregate Fuzzy Linguistic Ratings for the Alternatives with Respect to Subjective Criteria
Four decision makers provide the linguistic ratings to the alternatives with respect to subjective criteria using
Table 2, and the results are given in
Table 3. Then, the aggregate fuzzy linguistic ratings for the alternatives with respect to subjective criteria (I5) can be calculated according to Equation (5). For example, the aggregate fuzzy rating of green supplier GS1 in term of criteria I5 is computed as follows:
So,
![Sustainability 06 00217 i045]()
Table 3.
Linguistic ratings for the three alternatives with respect to subjective criteria (I5).
Table 3.
Linguistic ratings for the three alternatives with respect to subjective criteria (I5).
| (I5) | DM1 | DM2 | DM3 | DM4 |
|---|
| TS1 | F | G | P | G |
| TS2 | G | G | G | F |
| TS3 | F | G | F | G |
Likewise, the aggregate fuzzy ratings of another two green supplier (GS2 and GS3) in term of criteria I5 are computed. The aggregate fuzzy ratings of the alternatives are presented in
Table 4. Also, according to the biding documents and practical situation, the triangular fuzzy number values of objective criteria (I1, I2, I3 and I4) are determined, which are list in
Table 4.
Table 4.
Aggregate fuzzy decision matrix for alternatives.
Table 4.
Aggregate fuzzy decision matrix for alternatives.
| Criteria | Equipment Quotation (106 RMB) (I1) | Delivery Accuracy Rate (%) (I2) | Equipment Operational Costs (104 RMB) (I3) | Equipment Efficiency (%) (I4) | Environmental Consciousness (I5) |
|---|
| Alternatives | |
|---|
| TS1 | Approximately 576 | Approximately 95 | Approximately 310 | Approximately 92.5 | (0.375,0.575,0.775) |
| (555,576,588) | (94.3,95,96) | (304,310,315) | (91,92.5,93) |
| TS2 | Approximately 595 | Approximately 96.5 | Approximately 305 | Approximately 90.2 | (0.525,0.725,0.925) |
| (583,595,601.5) | (96,96.5,97) | (302,305,308) | (90,90.2,90.8) |
| TS3 | Approximately 600 | Approximately 97 | Approximately 320 | Approximately 94.3 | (0.450,0.650,0.850) |
| (582,600,615) | (96.6,97,97.8) | (315,320,326) | (93.8,94.3,94.6) |
6.2. Determine the Weights of All Criteria
- (1)
Calculate the aggregated fuzzy weights of all criteria
Four decision makers provide the linguistic ratings to all criteria using
Table 1, and the results are given in
Table 5. Then, the aggregate fuzzy linguistic ratings for all criteria can be calculated according to Equation (6). For example, the aggregated fuzzy weight
![Sustainability 06 00217 i061]()
of criteria I1 is computed as follows:
So,
![Sustainability 06 00217 i047]()
Table 5.
Linguistic ratings for all criteria.
Table 5.
Linguistic ratings for all criteria.
| | DM1 | DM2 | DM3 | DM4 |
|---|
| I1 | H | H | M | M |
| I2 | L | H | M | L |
| I3 | M | L | H | H |
| I4 | M | L | H | M |
| I5 | L | M | H | H |
Likewise, the aggregate weights of the remaining four criteria can be computed. The aggregated fuzzy weights of all criteria are list in
Table 6.
Table 6.
Aggregate fuzzy criteria weights.
Table 6.
Aggregate fuzzy criteria weights.
| Criteria | Decision Makers | Aggregated Fuzzy Weight |
|---|
| DM1 | DM2 | DM3 | DM4 |
|---|
| I1 | (0.5,0.7,1) | (0.5,0.7,1) | (0.2,0.5,0.8) | (0.2,0.5,0.8) | (0.350,0.600,0.900) |
| I2 | (0,0.3,0.5) | (0.5,0.7,1) | (0.2,0.5,0.8) | (0,0.3,0.5) | (0.175,0.450,0.700) |
| I3 | (0.2,0.5,0.8) | (0,0.3,0.5) | (0.5,0.7,1) | (0.5,0.7,1) | (0.300,0.550,0.825) |
| I4 | (0.2,0.5,0.8) | (0,0.3,0.5) | (0.5,0.7,1) | (0.2,0.5,0.8) | (0.225,0.500,0.775) |
| I5 | (0,0.3,0.5) | (0.2,0.5,0.8) | (0.5,0.7,1) | (0.5,0.7,1) | (0.300,0.550,0.825) |
Then, the normalized subjective weights
uk of all criteria can be calculated according to Equation (7), which are
- (2)
Calculate the weights of objective criteria by using fuzzy-entropy weighting method
For the objective criteria I1, I2, I3 and I4, the graded mean integration representation value
hik of these four criteria can be computed according to Equation (2).
Then, the entropy values and weights of objective criteria can be computed according to Equation (3) and Equation (4), and the results are list in
Table 7.
Table 7.
Objective weights of objective criteria by using fuzzy-entropy weighting method.
Table 7.
Objective weights of objective criteria by using fuzzy-entropy weighting method.
| Criteria | I1 | I2 | I3 | I4 |
|---|
| Entropy value ek | 0.999848 | 0.999964 | 0.999813 | 0.999857 |
| Objective weight | 0.2934 | 0.0687 | 0.3619 | 0.2759 |
- (3)
Calculate the integrated weight of all criteria
The integrated weight
zk (
k = 1,2,3,4) of objective criteria (I1, I2, I3 and I4) can be computed according to Equation (8) and Equation (9),
i.e.,
Then, the integration weights of all criteria can be obtained according to Equation (10),
i.e.,
6.3. Build the Initial Fuzzy Decision Matrix
According to
Table 4, the initial fuzzy decision matrix
A can be obtained, namely
6.4. Normalize the Initial Fuzzy Decision Matrix
6.4.1. For the objective criteria (I1, I2, I3 and I4)
- (1)
For benefit criteria (I2 and I4)
- (i)
For I2 (Delivery accuracy rate)
According to Equation (11) and Equation (12), we can get
t2 = max {96,97,97.8}, and then
- (ii)
For I4 (Equipment efficiency)
According to Equation (11) and Equation (12), we can get
t4 = max {93,90.8,94.6} = 94.6, and then
- (2)
For cost criteria (I1 and I3)
- (i)
For I1 (Equipment quotation)
According to Equation (13) and Equation (14), we can get
t1 = min {55500,58300,58200} = 55500, and then
- (ii)
For I3 (Equipment operational costs)
According to Equation (13) and Equation (14), we can get
t1 = min {304,302,315} = 302, and then
6.4.2. For the subjective criteria (I5)
The subjective criteria have no need for dimensionless processing.
Then, the normalized fuzzy decision matrix
B can be obtained:
6.5. Construct the Weighted Normalized Fuzzy Decision Matrix
The weighted normalized fuzzy decision matrix
C for 3 alternatives can be constructed by multiplying the weights (
wk) of the criteria with the normalized fuzzy decision matrix
B, namely
6.6. Determine the Fuzzy Positive Ideal Solution and Fuzzy Negative Ideal Solution.
According to Equation (15), the fuzzy positive ideal solution
C+ and fuzzy negative ideal solution
C− can be computed:
6.7. Calculate the Distance of Each Alternative from Fuzzy Positive Ideal Solution and Fuzzy Negative Ideal Solution
According to Equation (17) and Equation (18), the distance of each alternative from fuzzy positive ideal solution and fuzzy negative ideal solution can be computed:
6.8. Compute the Closeness Coefficient (CCi) of Each Alternative
According to Equation (19), the closeness coefficient (
CCi) of each alternative can be computed:
6.9. Rank the Alternatives
According to the closeness coefficient
CCi in decreasing order, we obtain
Therefore, alternative GS2, namely green supplier #2 of thermal power equipment, is the best alternative and should be selected.
7. Conclusions
With the ever-worsening pollution of the environment, the worldwide awareness of environmental protection and sustainable development are growing, and green purchasing has become an important issue for companies to gain environmental sustainability and will determine their sustainability in the long term. The environmental performance of a company is not only related to its inner environmental efforts, but also affected by the suppliers’ environmental performances. Therefore, a performance evaluation on green suppliers is necessary to select the proper supplier to cooperate with the company. Selecting green suppliers is a strategic decision for a company, which can promote its sustainable development and be more competitive in today’s global market. In this paper, a new multi-criteria decision making approach based on incorporated fuzzy set theory, entropy, and TOPSIS is proposed to evaluate and select the green suppliers of thermal power equipment under fuzzy environment. The proposed fuzzy entropy-TOPSIS approach comprises of two steps. In the first step, the alternatives are determined and the evaluation criteria for green supplier selection of thermal power equipment are identified. These criteria are equipment quotation, delivery accuracy rate, equipment operational costs, equipment efficiency, and environmental consciousness. In the second step, the decision makers provide linguistic ratings to the criteria and to the alternatives with respect to subjective criteria, and all criteria which include the objective and subjective criteria are weighted by using subjective superiority linguistic ratings and objective fuzzy entropy weighting method, and then the fuzzy-TOPSIS is employed to aggregate the ratings and rank all the green suppliers of thermal power equipment. The alternative with the highest performance score is selected. The evaluation result shows the alternative GS2 is the best green supplier of thermal power equipment.
Our proposed approach has the ability to evaluate and select the green suppliers of thermal power equipment with partial or a lack of quantitative information, and using the triangular fuzzy numbers and linguistic values can overcome the uncertainty due to human qualitative judgment. A combination of subjective weight determination and objective weight determination for evaluation criteria is employed. The fuzzy-entropy weighting method can measure the average essence of information quantity of criteria data as well as grasp the actual conditions of evaluation criteria, and the superiority linguistic ratings can reflect the experts’ thoughts and opinions. This proposed method can facilitate its implementation as a computer-based decision support system for tackling the MCDM problems in a fuzzy environment, and it can also be applied to other MCDM issues. For further research, this proposed fuzzy entropy-TOPSIS evaluation result can be compared with other fuzzy MCDM techniques like fuzzy PROMETHEE [
32], fuzzy matter-element extension method [
33], and fuzzy VIKOR [
34].
The obtained results can help companies perform the green supplier selection of thermal power equipment, which can promote its own sustainable development and the sustainability of China’s electric power industry to some extent.
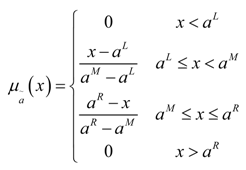
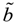 = [bL, bM, bR] be two triangular fuzzy numbers. The main operations between ã,
= [bL, bM, bR] be two triangular fuzzy numbers. The main operations between ã, 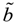 and real number λ are expressed as follows:
and real number λ are expressed as follows:
= (aL + bL, aM + bM, aR + bR)
= (aL − bL, aM − bM, aR − bR)
(aL × bL, aM × bM, aR × bR), aL ≥ 0, bL ≥ 0
(aL / bR, aM / bM, aR / bL), aL ≥ 0, bL ≥ 0)
ã = (λaL, λaM, λaR), λ ≥ 0
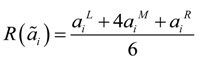
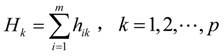
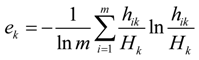
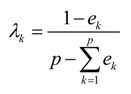
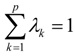 .
.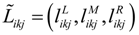 ,
, 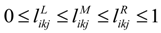 , i = 1,2, … , m, k = p + 1, p + 2, … , n, j = 1,2, … , r be the superiority linguistic ratings assigned to alternative Ai by decision-maker Dj for subjective criteria Ck, and the scale used for linguistic rating is given in Table 2. Then, the aggregate fuzzy linguistic rating
, i = 1,2, … , m, k = p + 1, p + 2, … , n, j = 1,2, … , r be the superiority linguistic ratings assigned to alternative Ai by decision-maker Dj for subjective criteria Ck, and the scale used for linguistic rating is given in Table 2. Then, the aggregate fuzzy linguistic rating 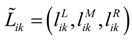 for the alternative Ai with respect to subjective criteria Ck can be calculated by
for the alternative Ai with respect to subjective criteria Ck can be calculated by
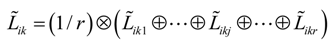
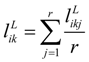 ,
, 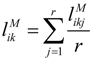 ,
, 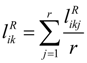 .
.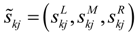 ,
, 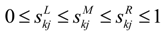 , k = 1,2, … , p, … , n , j = 1,2, … , r be the superiority linguistic ratings assigned to criteria Ck by decision-maker Dj, and the scale used for linguistic rating is given in Table 1. Then, the aggregated fuzzy weights
, k = 1,2, … , p, … , n , j = 1,2, … , r be the superiority linguistic ratings assigned to criteria Ck by decision-maker Dj, and the scale used for linguistic rating is given in Table 1. Then, the aggregated fuzzy weights 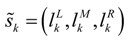 for the criteria Ck can be calculated by
for the criteria Ck can be calculated by

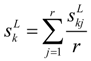 ,
, 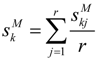 ,
, 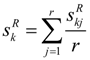 .
.
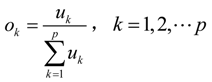
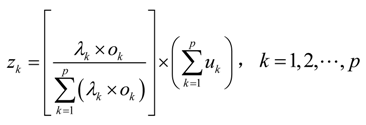
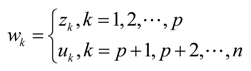
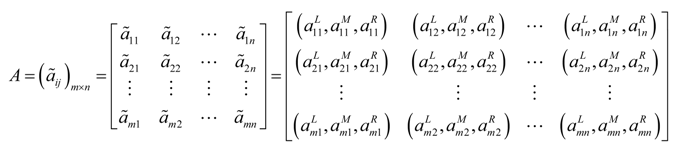
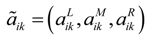 i = 1,2, … , m, k = 1,2, … , p be the fuzzy evaluation value of objective criterion Ck, and the dimensionless processing procedure is as follows.
i = 1,2, … , m, k = 1,2, … , p be the fuzzy evaluation value of objective criterion Ck, and the dimensionless processing procedure is as follows.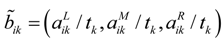
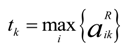

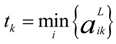
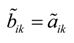 , i = 1,2, … , m; k = p + 1, p + 2, … , n. Then, the normalized fuzzy decision matrix B is given by
, i = 1,2, … , m; k = p + 1, p + 2, … , n. Then, the normalized fuzzy decision matrix B is given by
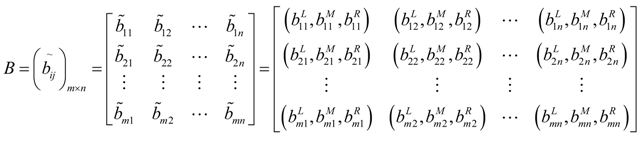
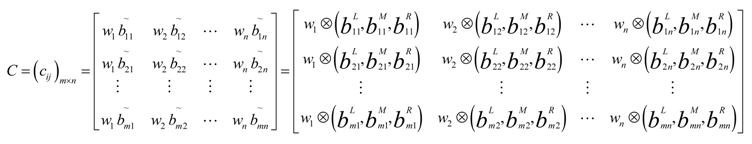
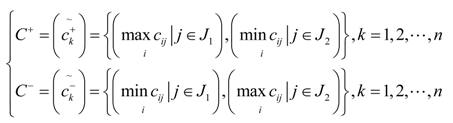
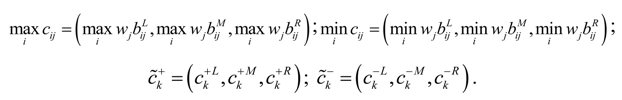
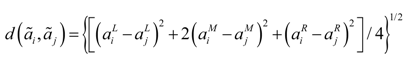
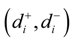 of each alternative i (i = 1,2, … , m) from the fuzzy positive ideal solution and fuzzy negative ideal solution can be calculated as follows:
of each alternative i (i = 1,2, … , m) from the fuzzy positive ideal solution and fuzzy negative ideal solution can be calculated as follows:
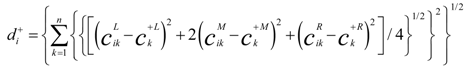
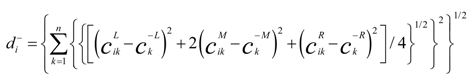
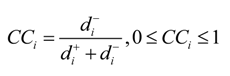
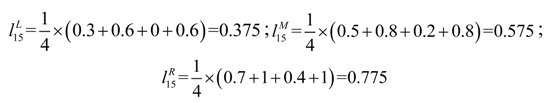
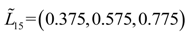
 of criteria I1 is computed as follows:
of criteria I1 is computed as follows: