A Review of the Modelling of Thermally Interacting Multiple Boreholes
Abstract
:1. Introduction
2. Objectives of GHE Modeling
2.1. Environmental Impacts
2.2. Sustainability
2.3. Thermal Interaction
3. Modeling Ground Heat Exchangers
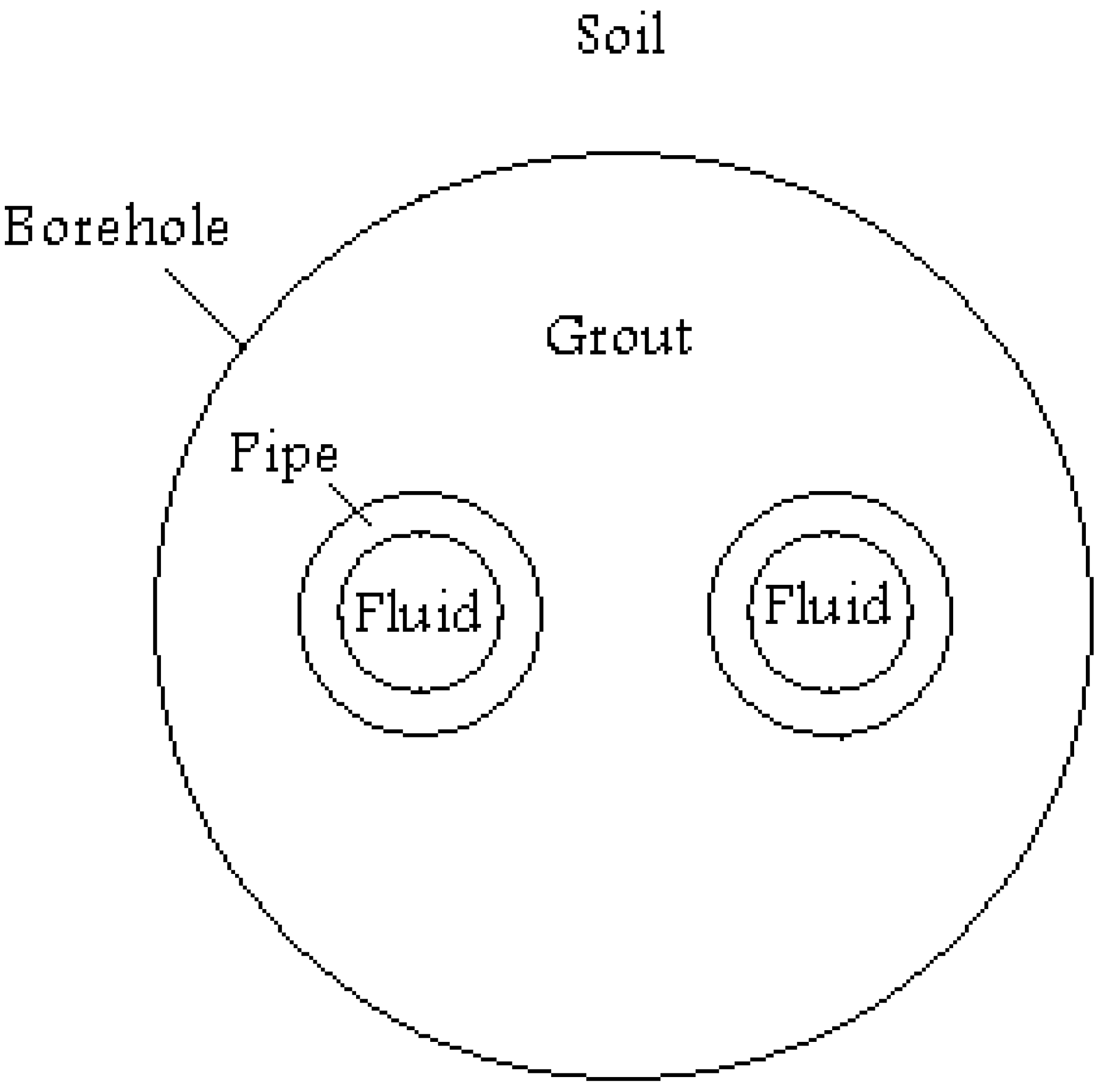
3.1. Analytical Approach
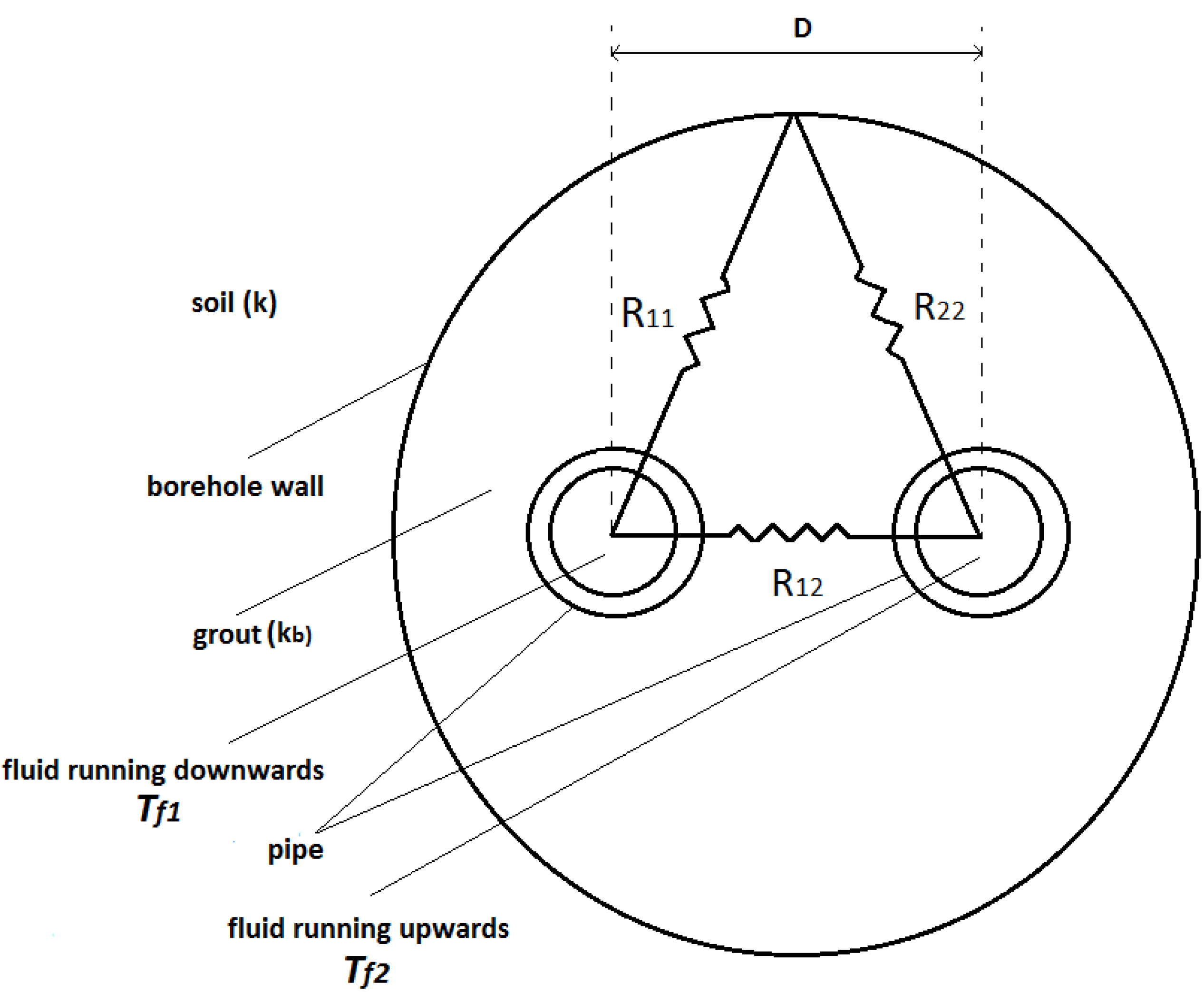
3.1.1. Heat Transfer inside the Borehole
 ), and the impact of thermal capacity of objects inside the borehole can be neglected [11]. Such simplification has been proved approximate and convenient for most engineering analyses dealing with responses of more than a few hours [12].
), and the impact of thermal capacity of objects inside the borehole can be neglected [11]. Such simplification has been proved approximate and convenient for most engineering analyses dealing with responses of more than a few hours [12].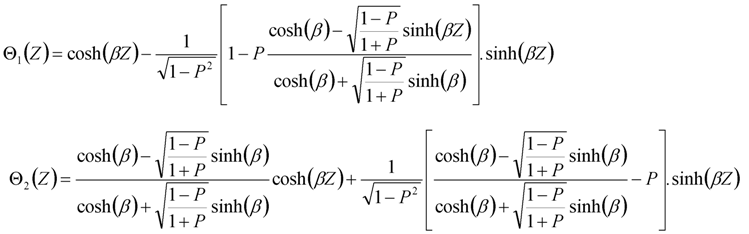
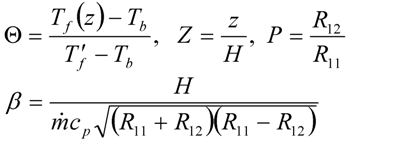
| 1D (Equivalent diameter) [14] | 1D (Shape factor) [17] | 2D [18] | Quasi 3D [20] | |
|---|---|---|---|---|
| U-tube disposal | N | Y | Y | Y |
| Quantitative expressions of the thermal resistance in the cross-section | N | N | Y | Y |
| Thermal interference | N | N | N | Y |
| Extinction between the entering and exiting pipes | N | N | N | Y |
| Axial convection by fluid flow | N | N | N | Y |
| Axial conduction in grout | N | N | N | N |
3.1.2. Heat Transfer outside the Borehole
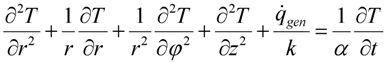
- -
- The ground is homogeneous in its thermal properties and initial temperature.
- -
- Moisture migration is negligible.
- -
- Thermal contact resistance is negligible between the pipe and grout and between the grout and soil.
- -
- The effect of ground surface is negligible for the initial 5–10 years (depending on the borehole depth).
 ) is:
) is:
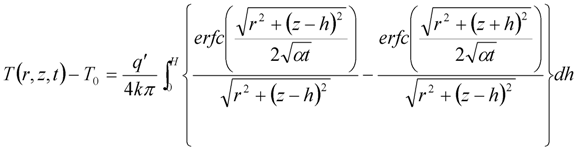
3.2. Numerical Models
3.3. Some Modeling Limitations
3.4. Other Modeling Aspects
4. Conclusions
Acknowledgments
Conflict of Interest
References
- Geothermal Heat Pump Consortium. Available online: http://energy.nstl.gov.cn/MirrorResources/902/index.html/ (accessed on 1 November 2011).
- Fisheries and Oceans Canada, Ontario-Great Lakes Area (DFO-OGLA). Fish Habitat and Fluctuating Water Levels on the Great Lakes. Available online: http://www.dfo-mpo.gc.ca/regions/central/pub/factsheets-feuilletsinfos-on/t2-eng.htm (accessed on 1 November 2011).
- Markle, J.M.; Schincariol, R.A. Thermal plume transport from sand and gravel pits: Potential thermal impacts on cool water streams. Hydrology 2007, 338, 174–195. [Google Scholar]
- York, K.P.; Sarwar Jahangir, Z.M.G.; Solomon, T.; Stafford, L. Effects of a Large Scale Geothermal Heat Pump Installation on Aquifer Microbiota. In Proceedings of the Second International Conference on Geothermal Heat Pump systems at Richard Stockton College, Pomona, NJ, USA, 16–17 March 1998.
- Ferguson, G.; Woodbury, A.D. Thermal sustainability of groundwater-source cooling in Winnipeg, Manitoba. Can. Geothechnical J. 2005, 42, 1290–1301. [Google Scholar]
- Ferguson, G.; Woodbury, A.D. Observed thermal pollution and and post-development simulations of low-temperature geothermal systems in Winnipeg, Canada. Hydrogeology 2006, 14, 1206–1215. [Google Scholar]
- Younger, P.L. Ground-coupled heating-cooling systems in urban areas: How sustainable are they? Bull. Sci. Technol. Soc. 2008, 28, 174–182. [Google Scholar]
- Andrushuk, R.; Merkel, P. Performance of ground source heat pumps in Manitoba. Available online: http://www.hydro.mb.ca/regulatory_affairs/electric/gra_2012_2013/Appendix_38.pdf (accessed on 1 November 2011).
- Ferguson, G. Unfinished business in geothermal energy. Ground Water 2009, 47, 167–167. [Google Scholar]
- Eskilson, P.; Claesson, J. Simulation model for thermally interacting heat extraction boreholes. Numer. Heat Transf. 1988, 13, 149–165. [Google Scholar]
- Jun, L.; Xu, Z.; Jun, G.; Jie, Y. Evaluation of heat exchange rate of GHE in geothermal heat pump systems. Renew. Energy 2009, 34, 2898–2904. [Google Scholar]
- Yavuzturk, C. Modeling of vertical ground loop heat exchangers for ground source heat pump systems. Ph.D. thesis, Oklahoma State University, Oklahoma, OK, USA, 1999. [Google Scholar]
- Bose, J.E.; Parker, J.D.; McQuiston, F.C. Design/Data Manual for Closed-Loop Ground Coupled Heat Pump Systems; Oklahoma State University for ASHRAE: Stillwater, OK, USA, 1985. [Google Scholar]
- Claesson, J.; Dunand, A. Heat Extraction from the Ground by Horizontal Pipes: A Mathematical Analysis; Swedish Council for Building Research: Stockholm, Sweden, 1983. [Google Scholar]
- Gu, Y.; O’Neal, D.L. Development of an equivalent diameter expression for vertical U-tube used in ground-coupled heat pumps. ASHRAE Trans. 1998, 104, 347–355. [Google Scholar]
- Gu, Y.; O’Neal, D.L. Modeling the effect of backfills on U-tube ground coil performance. ASHRAE Trans. 1998, 104, 356–365. [Google Scholar]
- Paul, N.D. The effect of grout conductivity on vertical heat exchanger design and performance. Master Thesis, South Dakota State University, Madison, SD, USA, 1996. [Google Scholar]
- Hellström, G. Ground heat storage: Thermal analyses of duct storage systems. Ph.D. thesis, Department of Mathematical Physics, University of Lund, Lund, Sweden, 1991. [Google Scholar]
- Zeng, H.Y.; Diao, N.R.; Fang, Z. Efficiency of vertical geothermal heat exchangers in ground source heat pump systems. J. Therm. Sci. 2003, 12, 77–81. [Google Scholar] [CrossRef]
- Zeng, H.Y.; Diao, N.R.; Fang, Z. Heat transfer analysis of boreholes in vertical ground heat exchangers. Int. J. Heat Mass Transf. 2003, 46, 4467–4481. [Google Scholar]
- Claesson, J.; Hellström, G. Multipole method to calculate borehole thermal resistances in a borehole heat exchanger. HVAC&R Res. 2011, 17, 895–911. [Google Scholar]
- Bauer, D.; Heidemann, W.; Muller-Steinhagen, H.; Diersch, H.-J.G. Thermal resistance and capacity models for borehole heat exchangers. Int. J. Energy Res. 2011, 35, 312–320. [Google Scholar]
- Al-Khoury, R.; Bonnier, P.G.; Brinkgreve, R.B.J. Efficient finite element formulation for geothermal heating systems, Part I: Steady state. Int. J. Numer. Methods Eng. 2005, 63, 988–1013. [Google Scholar] [CrossRef]
- Al-Khoury, R.; Bonnier, P.G. Efficient finite element formulation for geothermal heating systems, Part II: Transient. Int. J. Numer. Methods Eng. 2006, 67, 725–745. [Google Scholar]
- Chiasson, A.D.; Rees, S.J.; Spitler, J.D. A preliminary assessment of the effects of groundwater flow on closed-loop ground-source heat pump systems. ASHRAE Trans. 2000, 106, 380–393. [Google Scholar]
- Ingersoll, L.R.; Zobel, O.J.; Ingersoll, A.C. Heat Conduction with Engineering, Geological, and other Applications, rev. ed.; University of Wisconsin Press: Madison, WI, USA, 1954. [Google Scholar]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Claremore Press: Oxford, UK, 1946. [Google Scholar]
- Marcotte, D.; Pasquier, P. Fast fluid and ground temperature computation for geothermal ground-loop heat exchanger systems. Geothermics 2008, 37, 651–665. [Google Scholar]
- Ingersoll, L.R.; Plass, H.J. Theory of the ground pipe heat source for the heat pump. ASHVE Trans. 1948, 47, 339–348. [Google Scholar]
- Hart, D.P.; Couvillion, R. Earth Coupled Heat Transfer; National Water Well Association: Dublin, OH, USA, 1986. [Google Scholar]
- Lamarche, L.; Beauchamp, B. A new contribution to the finite line source model for geothermal boreholes. Energy Build. 2007, 39, 188–198. [Google Scholar]
- Cui, P.; Yang, H.; Fang, Z.H. Heat transfer analysis of ground heat exchangers with inclined boreholes. Appl. Therm. Eng. 2006, 26, 1169–1175. [Google Scholar]
- Kavanaugh, S.P. A design method for commercial ground-coupled heat pumps. ASHRAE Trans. 1995, 101, 1088–1094. [Google Scholar]
- Bernier, M.; Pinel, A.; Labib, P.; Paillot, R. A multiple load aggregation algorithm for annual hourly simulations of GCHP systems. HVAC&R Res. 2004, 10, 471–487. [Google Scholar]
- Hikari, F.; Ryuichi, I.; Takashi, I. Improvements on analytical modeling for vertical U-tube ground heat exchangers. Geotherm. Resour. Counc. Trans. 2004, 28, 73–77. [Google Scholar]
- Eskilson, P. Thermal analysis of heat extraction boreholes. Doctoral thesis, Department of Mathematical Physics, University of Lund, Lund, Sweden, 1987. [Google Scholar]
- Zeng, H.Y.; Diao, N.R.; Fang, Z. A finite line-source model for boreholes in geothermal heat exchangers. Heat Transf. Asian Res. 2002, 31, 558–567. [Google Scholar] [CrossRef]
- Diao, N.R.; Zeng, H.Y.; Fang, Z.H. Improvement in modeling of heat transfer in vertical ground heat exchangers. HVAC&R Res. 2004, 10, 459–470. [Google Scholar]
- Yavuzturk, C.; Spitler, J. A short time step response factor model for vertical ground loop heat exchangers. ASHRAE Trans. 1999, 105, 475–485. [Google Scholar]
- Mei, V.C.; Baxter, V.D. Performance of a ground-coupled heat pump with multiple dissimilar U-tube coils in series. ASHRAE Trans. 1986, 92, 22–25. [Google Scholar]
- Yavuzturk, C.; Spitler, J.D.; Rees, S.J. A transient two-dimensional finite volume model for the simulation of vertical U-tube ground heat exchangers. ASHRAE Trans. 1999, 105, 465–474. [Google Scholar]
- Yavuzturk, C.; Spitler, J.D. Field validation of a short time step model for vertical ground-loop heat exchangers. ASHRAE Trans. 2001, 107, 617–625. [Google Scholar]
- Muraya, N.K. Numerical modeling of the transient thermal interference of vertical U-tube heat exchangers. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 1995. [Google Scholar]
- Kavanaugh, S.P. Simulation and experimental verification of vertical ground coupled heat pump systems. Ph.D. Thesis, Oklahoma State University, Oklahoma, OK, USA, 1985. [Google Scholar]
- Rottmayer, S.P.; Beckman, W.A.; Mitchell, J.W. Simulation of a single vertical U-tube ground heat exchanger in an infinite medium. ASHRAE Trans. 1997, 103, 651–658. [Google Scholar]
- Lee, C.K.; Lam, H.N. Computer simulation of borehole ground heat exchangers for geothermal heat pump systems. Renew. Energy 2008, 33, 1286–1296. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, M. Development of a numerical model for the simulation of vertical U-tube ground heat exchangers. Appl. Therm. Eng. 2009, 29, 920–924. [Google Scholar] [CrossRef]
- He, M.; Rees, S.; Shao, L. Simulation of a Domestic Ground Source Heat Pump System Using a Transient Numerical Borehole Heat Exchanger Model. In Proceedings of 11th International Building Performance Simulation Association Conference, Glasgow, Scotland, 27–30 July 2009; pp. 607–614.
- Fang, Z.H.; Diao, N.R.; Cui, P. Discontinuous operation of geothermal heat exchangers. Tsinghua Sci. Technol. 2002, 7, 194–197. [Google Scholar]
- Austin, W.A.; Yavuzturk, C.; Spitler, J.D. Development of an in situ system for measuring ground thermal properties. ASHRAE Trans. 2000, 106, 356–379. [Google Scholar]
- Bauer, D.; Heidemann, W.; Diersch, H.-J.G. Transient 3D analysis of borehole heat exchanger modeling. Geothermics 2011, 40, 250–260. [Google Scholar] [CrossRef]
- Koohi-Fayegh, S.; Rosen, M.A. Long-term Study of Thermal Interaction of Vertical Ground Heat Exchangers with Seasonal Heat Flux Variation. In Proceedings of 11th International Conference on Sustainable Technologies, Vancouver, BC, Canada, 2–5 September 2012.
- Koohi-Fayegh, S.; Rosen, M.A. Thermally Interacting Multiple Boreholes with Variable Heating Strength. In Proceedings of eSim Conference, Halifax, NS, Canada, 2–3 May 2012.
- Koohi-Fayegh, S.; Rosen, M.A. A Numerical Approach to Assessing Thermally Interacting Multiple Boreholes with Variable Heating Strength. In Proceedings of 1st World Sustainability Forum, 1–30 November 2011.
- Koohi-Fayegh, S.; Rosen, M.A. On thermally interacting multiple boreholes with variable heating strength: Comparison between analytical and numerical approaches. Sustainability 2012, 4, 1848–1866. [Google Scholar] [CrossRef]
- Yang, W.; Shi, M.; Liu, G.; Chen, Z. A two-region simulation model of vertical U-tube ground heat exchanger and its experimental verification. Appl. Energy 2009, 86, 2005–2012. [Google Scholar] [CrossRef]
- Salah El-Din, M.M. On the heat flow into the ground. Renew. Energy 1999, 18, 473–490. [Google Scholar] [CrossRef]
- Mihalakakou, G. On estimating ground surface temperature profiles. Energy Build. 2002, 34, 251–259. [Google Scholar] [CrossRef]
- Mihalakakou, G.; Lewis, J.O. The influence of different ground covers on the heating potential of the earth-to-air heat exchangers. Renew. Energy 1996, 7, 33–46. [Google Scholar] [CrossRef]
- Jacovides, C.P.; Mihalakakou, G.; Santamouris, M.; Lewis, J.O. On the ground temperature profile for passive cooling applications in buildings. Solar Energy 1996, 57, 167–175. [Google Scholar] [CrossRef]
- Leong, W.H.; Tarnawski, V.R. Effects of Simultaneous Heat and Moisture Transfer in Soils on the Performance of a Ground Source Heat Pump System. In Proceedings of ASME-ATI-UIT Conference on Thermal and Environmental Issues in Energy Systems, Sorrento, Italy, 16–19 May 2010.
- Piechowski, M. Heat and mass transfer model of a ground heat exchanger: Theoretical development. Int. J. Energy Res. 1999, 23, 571–588. [Google Scholar] [CrossRef]
- Sutton, M.; Nutter, D.; Couvillion, R. A ground resistance for vertical bore heat exchangers with groundwater flow. J. Energy Resour. Technol. 2003, 125, 183–189. [Google Scholar] [CrossRef]
- Gehlin, S.E.A.; Hellström, G. Influence on thermal response test by groundwater flow in vertical fractures in hard rock. Renew. Energy 2003, 28, 2221–2238. [Google Scholar] [CrossRef]
- Nam, Y.; Ooka, R.; Hwang, S. Development of a numerical model to predict heat exchange rates for a ground-source heat pump system. Energy Build. 2008, 40, 2133–2140. [Google Scholar] [CrossRef]
- Hecht-Mendez, J.; Molina-Giraldo, N.; Blum, P.; Bayer, P. Evaluating MT3DMS for heat transport simulation of closed geothermal systems. Ground Water 2010, 48, 741–756. [Google Scholar] [CrossRef]
- Diao, N.R.; Li, Q.; Fang, Z.H. Heat transfer in ground heat exchangers with groundwater advection. Int. J. Therm. Sci. 2004, 43, 1203–1211. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Koohi-Fayegh, S.; Rosen, M.A. A Review of the Modelling of Thermally Interacting Multiple Boreholes. Sustainability 2013, 5, 2519-2536. https://doi.org/10.3390/su5062519
Koohi-Fayegh S, Rosen MA. A Review of the Modelling of Thermally Interacting Multiple Boreholes. Sustainability. 2013; 5(6):2519-2536. https://doi.org/10.3390/su5062519
Chicago/Turabian StyleKoohi-Fayegh, Seama, and Marc A. Rosen. 2013. "A Review of the Modelling of Thermally Interacting Multiple Boreholes" Sustainability 5, no. 6: 2519-2536. https://doi.org/10.3390/su5062519
APA StyleKoohi-Fayegh, S., & Rosen, M. A. (2013). A Review of the Modelling of Thermally Interacting Multiple Boreholes. Sustainability, 5(6), 2519-2536. https://doi.org/10.3390/su5062519






