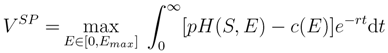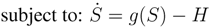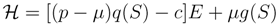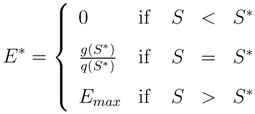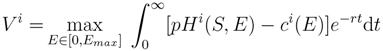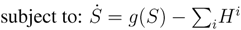2. Game Theory and Common Property
How do non-cooperative games play out in situations where a good is shared by all? Let me start out by quoting the original passage in Hardin’s article that is the basis of his metaphor. It is a situation where a group of herdsmen put cows on a common pasture:
As a rationale being, each herdsman seeks to maximize his gain. Explicitly or implicitly, more or less consciously, he asks, “what is the utility to me of adding one more animal to my herd?” This utility has a negative and a positive component.
(1) The positive component is a function of the increment of one animal. Since the herdsman receives all the proceeds from the sale of the additional animal, the positive utility is nearly +1.
(2) The negative component is a function of the additional overgrazing created by one more animal. Since, however, the effects of overgrazing are shared by all [...], the negative utility for any particular decision-making herdsman is only a fraction of −1.
Adding together the component particular utilities, the rational herdsman concludes that the only sensible course for him to pursue is to add another animal to his herd. And another; and another... But this is the conclusion reached by each and every rational herdsman sharing a commons. Therein is the tragedy. Each man is locked into a system that compels him to increase his herd without limit—in a world that is limited. Ruin is the destination towards which all men rush, each pursuing his own best interest in a society that believes in the freedom of the commons. Freedom in a commons brings ruin to all. [
1, p. 1244]
Partha Dasgupta [
4, p. 13] writes about this passage that “it is difficult to locate a passage of comparable length and fame that contains as many errors as the one above.” What should one think of this criticism? To answer this question, consider
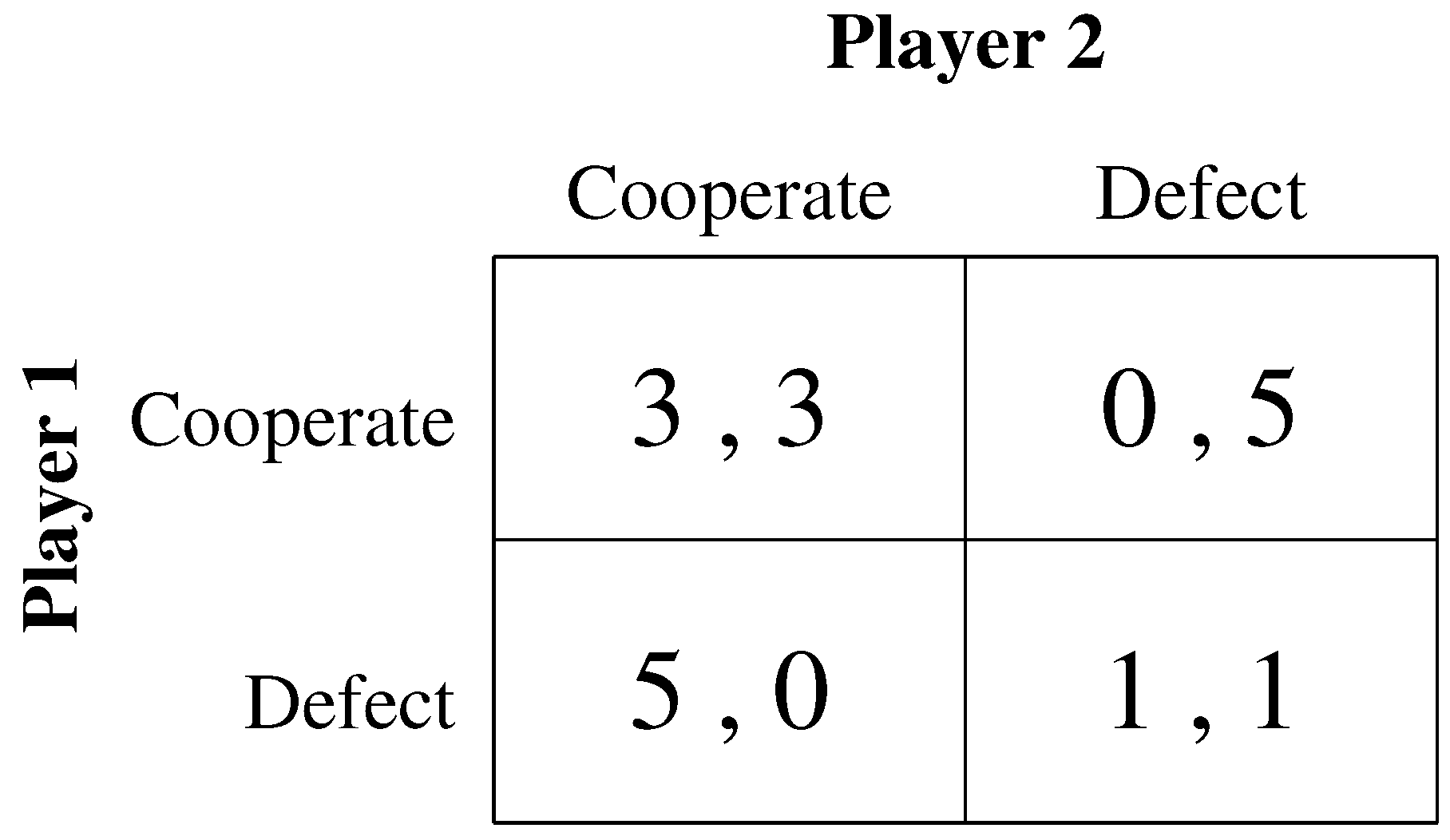
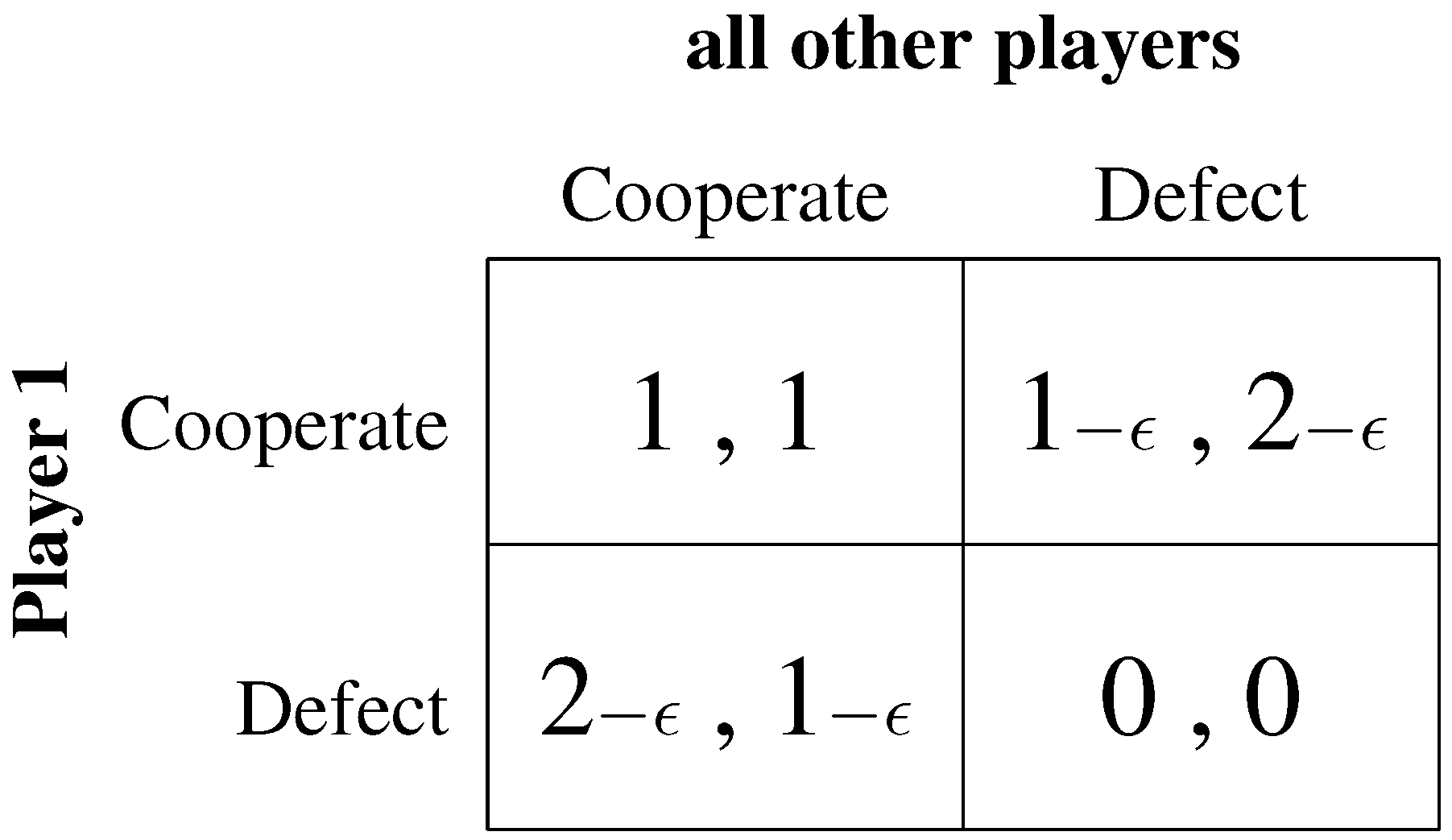
Figure 3 which captures Hardin’s game in a payoff-matrix: If all players cooperate and have one cow each on the pasture, everybody receives a payoff of 1. (Note that
Figure 3 depicts the payoff for any one of all the other players that are presumed to behave identically.) However, player 1 can increase his payoff by putting another cow on the pasture. This player would then receive a payoff of almost two (2 − c, since putting another cow on the pasture causes some costs which are shared by all, including himself). All other players would receive a payoff of slightly less than one. They only carry the cost of the additional animal but derive no benefit from it. Since the situation is the same for all, Hardin says, everyone will defect and the result is a payoff of zero for everyone. Investigating the payoff-matrix, one realizes that everybody defecting is actually not a Nash-equilibrium. Rather it seems that we face a coordination problem (as in the “Bach or Stravinsky” example of
Figure 1). But this is obviously not what Hardin had in mind.
Figure 3.
An essay to capture Hardin’s game in normal form.
Figure 3.
An essay to capture Hardin’s game in normal form.
There are several issues with Hardin’s metaphor. First, it is not clear who is “all”. Commonly, “all” is interpreted as “open-access”, meaning that there are no barriers to enter the pasture and that the number of players is in fact indeterminate. Under open access, effort will enter until all rents/profits are dissipated. There are two things to say about this argument: First, common property is not nobody’s property. Quite to the opposite, common property belongs to an often well-defined group of people and in many cases institutions and social norms exist that regulate the harvesting/extraction of the communally owned property, so that it is managed in a more or less sustainable way. Second, if the characterization of open-access is correct, then the individual actor plays such a small part that his actions have only a negligible effect on the other players. In this case, Game Theory plays no role.
Furthermore, Hardin’s metaphor is criticized on the grounds that it contains a dynamic dimension which should be treated explicitly. For example, Brekke
et al. [
5] discuss how the tragedy might lead to destabilized ecosystems when temporal dynamics are added to the analysis. Moreover, it is not necessarily the case that all rents are dissipated when the numbers of players are fixed and they play a non-cooperative game.
In order to discuss the effect of non-cooperative harvesting, one needs a benchmark of optimal dynamic resource management. Consider therefore the canonical model of renewable resource use [
6], which has most often been applied in the context of fisheries:
Equation (1) says that the objective of a social planner is to maximize the Net-Present-Value from harvesting the resource by choosing the appropriate level of effort E between zero and some maximum effort level Emax. Effort causes cost according to some function c(E) and produces, for a given resource stock S, an amount H of harvest that can be sold at price p. Current profits (the term in the squared brackets) are exponentially discounted at rate r. The stock of the resource is governed by the dynamic Equation (2), where g(S) is the “natural” growth function of the resource. So, when growth is larger than harvest, the stock will increase, and when growth is smaller than harvest, the stock will decline. When re-growth and harvest are equal, the stock will not change over time. The Net-Present-Value is the discounted sum of profits: revenue (the harvest multiplied by its price per unit) minus the cost of effort that is required for harvesting. To keep things very simple it is common to assume that cost and harvest are proportional to effort and that the latter depends on the existing state of the resource according to some function q(S), so that H(S, E) = q(S)E. The Hamiltonian of this problem can then be written as:
We can see that it is linear in the control variable E so that whenever the term in the squared brackets is negative, it is best to set effort to zero, and whenever the term in the squared brackets is positive, it is best to set effort to its maximum level (technically, the optimal strategy is of the bang/bang type):
In other words, when the initial stock level is low, it is optimal to let the stock grow until it has reached the optimal level and then just take out what is re-growing in equilibrium. In contrast, with a high initial stock size, the stock is “harvested down” to the optimal level as fast as possible.
Turning to a dynamic game, one sees that the problem for player i looks very much like the social planner’s problem, only that the stock development depends on the harvest of all players (Equations 3 and 4). This is of course exactly where the tragedy comes in. The benefits from harvesting are private, but the cost—in terms of a reduced stock size—are borne by all.
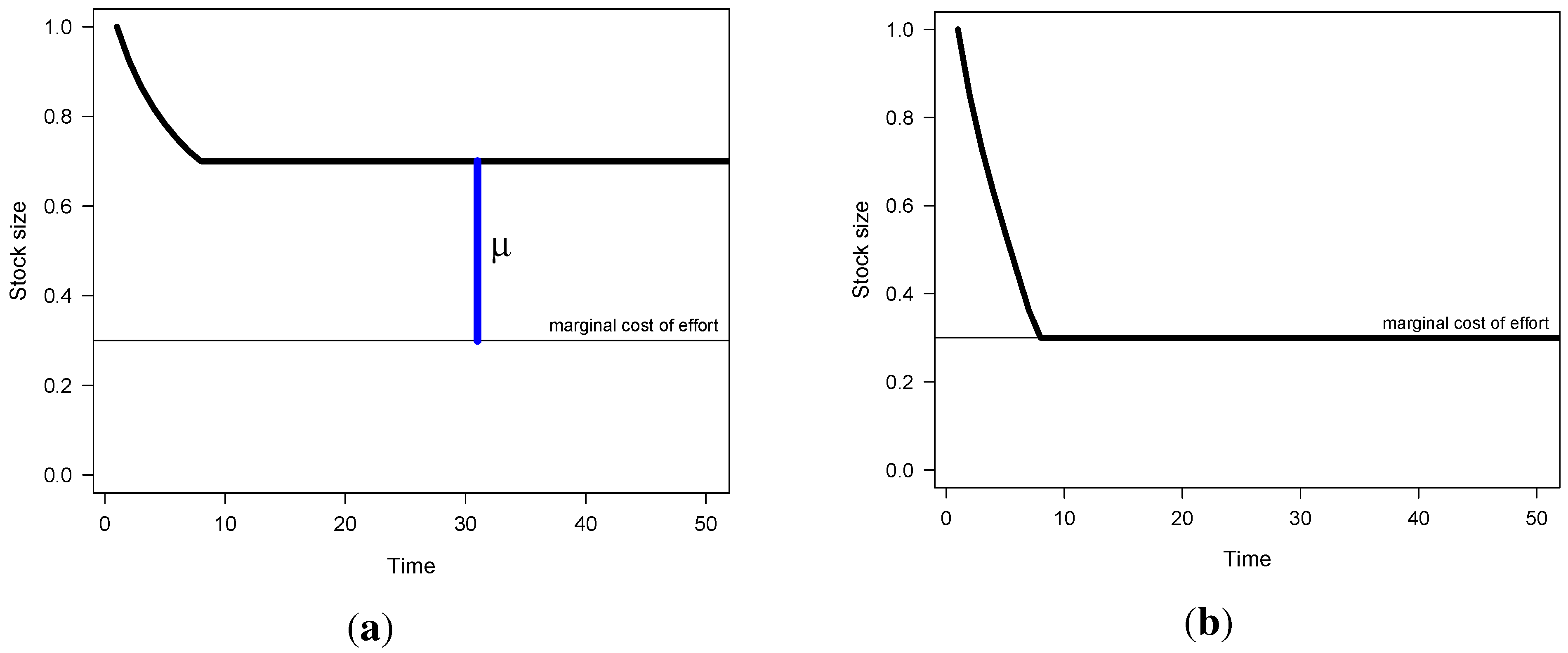
Let me illustrate the outcome of a game with two symmetric players (see, for example [
6, ch.5.4], by symmetric I mean that they have the same marginal cost of effort
c, apply the same discount rate
r, and face the same price
p). If the two players now start at a very high stock level and harvest the stock down to the optimal level, can they then agree to keep the stock at the optimal level? The players might agree, but without the possibility to make and enforce a binding agreement, each player has an incentive to deviate: Given that the opponent restrains his harvesting effort, it is in each player’s individual interest to expand effort, benefiting from a high stock size. Since this is true for both players, the stock will be depleted to a level where no player makes any profit. Hence, in this simple model, two symmetric players are sufficient to dissipate all rents. This situation, as depicted in
Figure 4b, stands in stark contrast to the optimal management (
Figure 4a, where µ is the shadow value of the stock,
i.e., the difference between marginal revenue and cost which is attributable to the stock size).
Figure 4.
Stock development under optimal and non-cooperative management. (a) Social planner; (b) Two symmetric players.
Figure 4.
Stock development under optimal and non-cooperative management. (a) Social planner; (b) Two symmetric players.
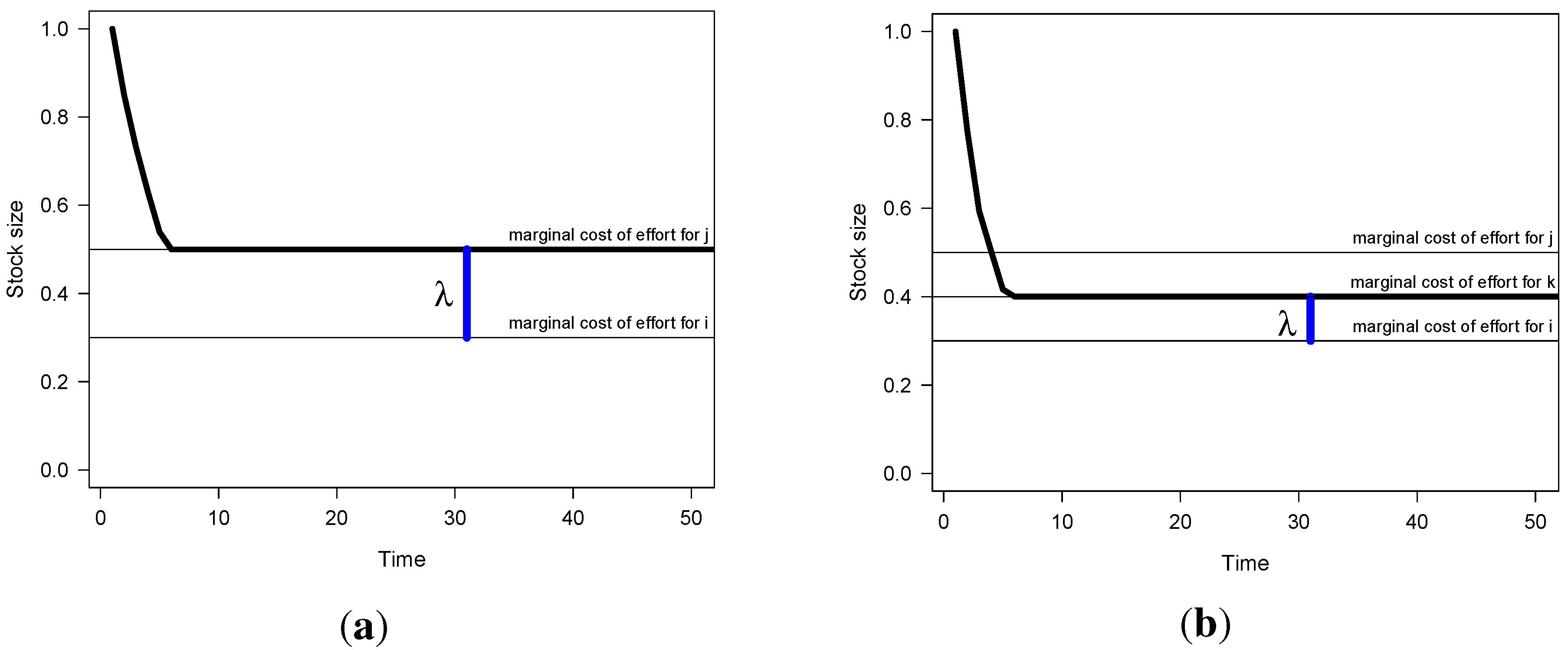
Now let me turn to a game where the players are asymmetric in the sense that player
i is more efficient than player
j. That is, the cost of using one additional unit of effort are lower for one player than for the other (in symbols:
ci <cj). Suppose the game starts and the players harvest the stock down to a level where the less efficient player makes no more profits. He or she would then leave the fishery. Would the other player then want to deplete the stock further? No, of course not; but player
i cannot let the stock increase either because then the less efficient player would want to enter again. So in effect, when the players are asymmetric in this simple game, some rents remain in equilibrium (but less than in the social optimum). The situation is illustrated in
Figure 5a, where
λ refers to the marginal profit of the most efficient player.
Figure 5.
Stock development under non-cooperative management. (a) Two asymmetric players; (b) Three asymmetric players.
Figure 5.
Stock development under non-cooperative management. (a) Two asymmetric players; (b) Three asymmetric players.
Considering a situation where there are three or more asymmetric players, the stock will be reduced until the first (least efficient) player leaves the fishery. But the two remaining players can also not cooperate on keeping the stock at that level. The situation will be just as before and only the most efficient player will remain in the fishery. He or she obtains some rents, but these are limited by the threat of re-entry of the second-most efficient player. It is plain to see that as the number of players with unique marginal effort cost increases, rents will be dissipated, but all rents will only be dissipated as this number tends to infinity.
To sum up, although Hardin’s simile of the pasture’s problem does not lend itself to a formal model while maintaining the same properties that Hardin claimed, formal dynamic models can be constructed that lead to the total dissipation of rents.
3. Cooperation in the Commons
Among the most prominent scholars who have criticized Hardin’s essay and its dismal implications is the Nobel laureate Elinor Ostrom. She highlights that Hardin’s essay is overly pessimistic and warns that those who blindly advocate formal property rights solutions might do more harm than good. There are many empirical examples of successful community management and introducing formal property rights and other external laws in these regimes might crowd out existing informal arrangements. There is by now also ample evidence from lab-experiments that people are not only rational, narrowly self-interested maximizers. In many lab-games, where self-interest would dictate zero contributions to a public good, many people actually do contribute significant sums. Thus, there are not only “rational maximizers” but also “conditional cooperators” and “willing punishers”. To quote Ostrom [
7, p. 138]: “In all known self-organized governance regimes that have survived for multiple generations, participants invest resources in monitoring and sanctioning the actions of each other so as to reduce the probability of free-riding.”
In her work, Ostrom identifies a series of factors that are crucial for success, which can be paraphrased as follows (for an original elaboration see [
8]): (1) membership can be controlled; (2) social networks exist; (3) actions are observable; (4) graduated sanctions are feasible; and (5) the resource is not too variable. Here, I will focus on the ability to sanction behavior,
i.e., the ability to promote cooperative actions and in particular to punish non-cooperative behavior. Cooperation can be made self-enforcing by threatening defectors with punishment.
To illustrate, imagine that a prisoner’s dilemma game (
Section 1.1) would be played many times. Then cooperation could be obtained if the players start out by playing “cooperate” and threat to respond to any defection by retaliating and playing defection forever. A deviator would then have to weigh the current gains from defection against the future losses from playing “defect/defect” instead of “cooperate/cooperate” forever. Clearly, if the players are not too impatient, they would abstain from defecting. This strategy—aptly called “grim trigger”—has one shortcoming: the threat is not credible. As all parents learn very quickly, any threat of punishment has to be credible to be effective. (As an aside, the evolution of cooperation in the context of repeated Prisoner’s Dilemma games is an extensively studied field. The original science paper from Axelrod and Hamilton [
9] acquires more than 20,000 citations on google scholar, some 2000 more than “The tragedy of the commons”.) A paper which proposes a credible, renegotiation-proof (a dynamic Nash equilibrium is said to be renegotiation-proof when no player, or group of players, has an incentive to deviate from its path of actions at a later point in time) threat strategy in the dynamic game that was discussed above is from Polasky
et al. [
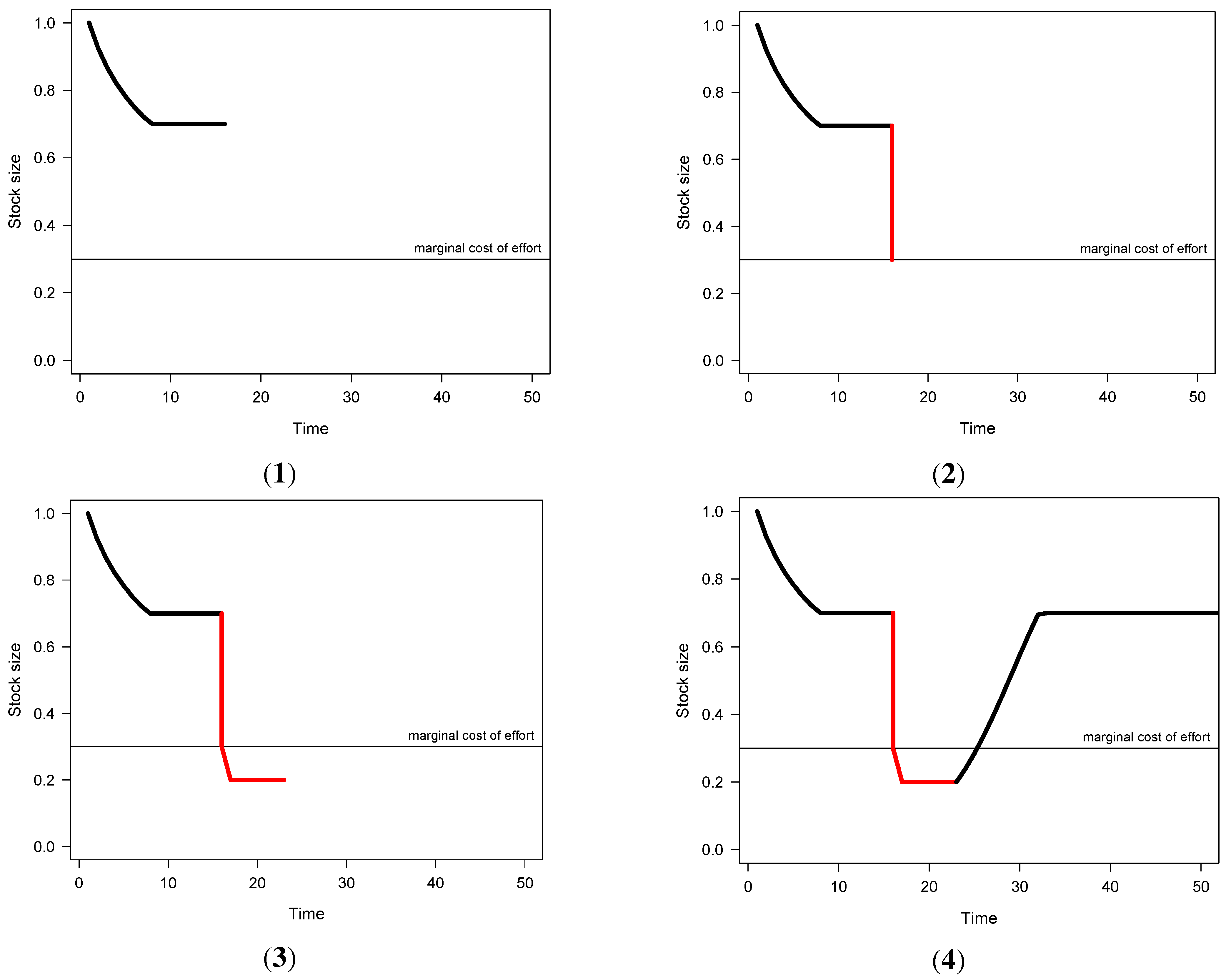
10]. The idea is the following (see
Figure 6): The players start the game and harvest cooperatively at the socially optimal stock level, equally sharing the ensuing surplus. If now, for some reason, some player defects and grabs all the surplus rents for himself, a two-phase punishment regime is enacted. The players agree on the following procedure: First, the defecting player has to make a loss by harvesting with high effort for some time. The punishment period is so long that the defector loses exactly the same amount that he has previously gained by defecting. After this punishment phase, the resource stock is not harvested so that it recovers and eventually all players return to harvesting cooperatively.
Figure 6.
Illustration of two-phase punishment scheme in [
10]. (
1) cooperation; (
2) defection; (
3) punishment; (
4) cooperation.
Figure 6.
Illustration of two-phase punishment scheme in [
10]. (
1) cooperation; (
2) defection; (
3) punishment; (
4) cooperation.
When all players follow this two-phase punishment scheme, no player has an incentive to stray from the path of cooperation, but also note that—and this is important—a deviating player has no incentive to not accept the punishment and all other players have no incentive to not punish. This two-phase punishment strategy ensures cooperation as long as the rents from cooperating are large enough, there are not too many players, and the future is not discounted too heavily.
4. Game Theory, Cooperation, and Climate Change
In many ways, the climate problem is the “tragedy of the commons” in inverse: Here the benefits (avoidance of dangerous climate change) are public but the costs (of abatement) are private. Hence every country has an incentive to free-ride on the abatement effort of the others. As the local commons analyzed in the previous section, the climate problem is essentially a dynamic stock problem. That is, the strategic interactions play out over the level of the stock variable that is shared by all players. However, cooperation in the climate commons is extremely difficult to establish and enforce. It fails on almost all aspects that Ostrom found to be critical for successful management. In particular, the climate system differs from the local commons discussed above, namely, it is a global commons. This implies that the damages from climate change are potentially unbounded, whereas in a local commons the players could always secure themselves a payoff of zero. They could simply leave the fishery, but one cannot leave this planet (at least not today).
In the following, I will discuss three recent papers that deal with different aspects of establishing cooperation in the commons. In the first paper, Heitzig
et al. [
11] propose a “relative punishment scheme”, which they call
linC. This punishment scheme works in the following way: At the beginning the players coordinate on a given target and the shares that each player has to contribute. If some player falls short of his contribution, he has to repay in the next period by taking some share of the other player’s contributions on his shoulder so that the overall contributions stay the same. In the third period, cooperation is re-established and the game continues as before the defection of the player. The authors argue that their proposed strategy can implement any allocation of target contributions in a renegotiation-proof way. However, the model is a “repeated game” where the benefits from reduced emissions are the same every period. In other words, actions of one player have no consequence for the total payoff in the next period.
In contrast, Mason
et al. [
12] (basically the same authors as in [
10]) model a truly dynamic game where the benefits from reduced emissions depend on the stock of pollution which accumulates over time. As in the renewable-resource game, they propose a two-phase scheme with a harsh punishment (which is arbitrarily set at some constant level). This allows for sustainable cooperation, but only in some cases. These cases depend on the parameters in a non-stationary way. For example, cooperation is only self-enforcing when the discount rate is neither too high nor too low.
The last paper I want to mention on this topic is a working paper from Scott Barrett [
13]. He analyses, in a static framework, the effect of catastrophes on the ability to establish cooperation in the climate commons. The basic idea is that there is a threshold and a catastrophe happens upon crossing it (think of walking over a cliff). Now when the location of this threshold is known, the static climate game changes its structure fundamentally. Instead of a cooperation problem like in the Prisoner’s Dilemma (
Figure 2) one now only has a coordination problem (like in the Bach-or-Stravinsky game,
Figure 1). It is clear that if the players want to avoid the catastrophe, they only have to share the burden of doing so. Once the burden sharing agreement is in place, no agent has an incentive to over-emit, as this would cause a discontinuous jump in the damages. In a way, “nature herself enforces the agreement [13, p.1].”
However, when the location of the threshold is uncertain, then coordination is ineffective. Technically speaking, the expected damage function is continuous again. Figuratively speaking, the players are walking towards the edge of a cliff, but it is so foggy that they do not see anything and do not know where exactly to stop. Then each individual has an incentive to just take one more tiny step. We are back again in a situation where cooperation is necessary, but very difficult to enforce.