Optimal and Sustainable Groundwater Extraction

Abstract

With climate change exacerbating over-exploitation, groundwater scarcity looms as an increasingly critical issue worldwide. Minimizing the adverse effects of scarcity requires optimal as well as sustainable patterns of groundwater management. We review the many sustainable paths for groundwater extraction from a coastal aquifer and show how to find the particular sustainable path that is welfare maximizing. In some cases the optimal path converges to the maximum sustainable yield. For sufficiently convex extraction costs, the extraction path converges to an internal steady state above the level of maximum sustainable yield. We describe the challenges facing groundwater managers faced with multiple aquifers, the prospect of using recycled water, and the interdependence with watershed management. The integrated water management thus described results in less water scarcity and higher total welfare gains from groundwater use. The framework also can be applied to climate-change specifications about the frequency, duration, and intensity of precipitation by comparing before and after optimal management. For the case of South Oahu in Hawaii, the prospect of climate change increases the gains of integratedgroundwater management.

1. Introduction

Water scarcity has long been an important issue in many regions worldwide, and the threat of climate change has brought it further to the forefront of policy discussions. The United Nations [1] recommends a multidisciplinary approach to managing water scarcity, since it “affects all social and economic sectors and threatens the sustainability of the natural resources base”. (For consistency with sustainability science, substitute “transdisciplinary” for “multidisciplinary”, such that scientific research is organized around a specific set of resource management and/or policy questions [2].) As demand for water continues to grow, a variety of both demand- and supply-side management strategies are being developed and considered. A true systems approach to the problem requires incorporating a portfolio of instruments into a resource management plan. Such instruments might include expansion of reservoirs, investment in watershed conservation, more efficient conjunctive use of ground and surface water, improved pricing structures, quality restrictions, and implementation of wastewater recycling and desalination. In this paper we discuss three management tools: (i) efficient use of multiple groundwater sources, (ii) watershed conservation, and (iii) implementation of wastewater recycling. We illustrate that rule of thumb groundwater management strategies such as always-extract-MSY are inefficient, and the magnitude of the inefficiency is increased when any of the instruments are incorporated into a standard groundwater economics optimization model. For every case considered, the optimal management plan is both sustainable and welfare-maximizing.

2. Groundwater as a Renewable Resource

Groundwater is commonly treated as a non-renewable resource in resource economics, the management of which involves determining how to mine the stock in every period [3,4,5,6]. In the case of a coastal aquifer, however, leakage (submarine groundwater discharge into the sea) is a function of the groundwater stock. The larger the freshwater lens, the greater the surface area along which freshwater can leak and the greater the pressure at the saltwater-freshwater interface. Therefore leakage, and hence the net growth function, are stock-dependent, and coastal groundwater should be characterized as a renewable resource [7,8,9]. 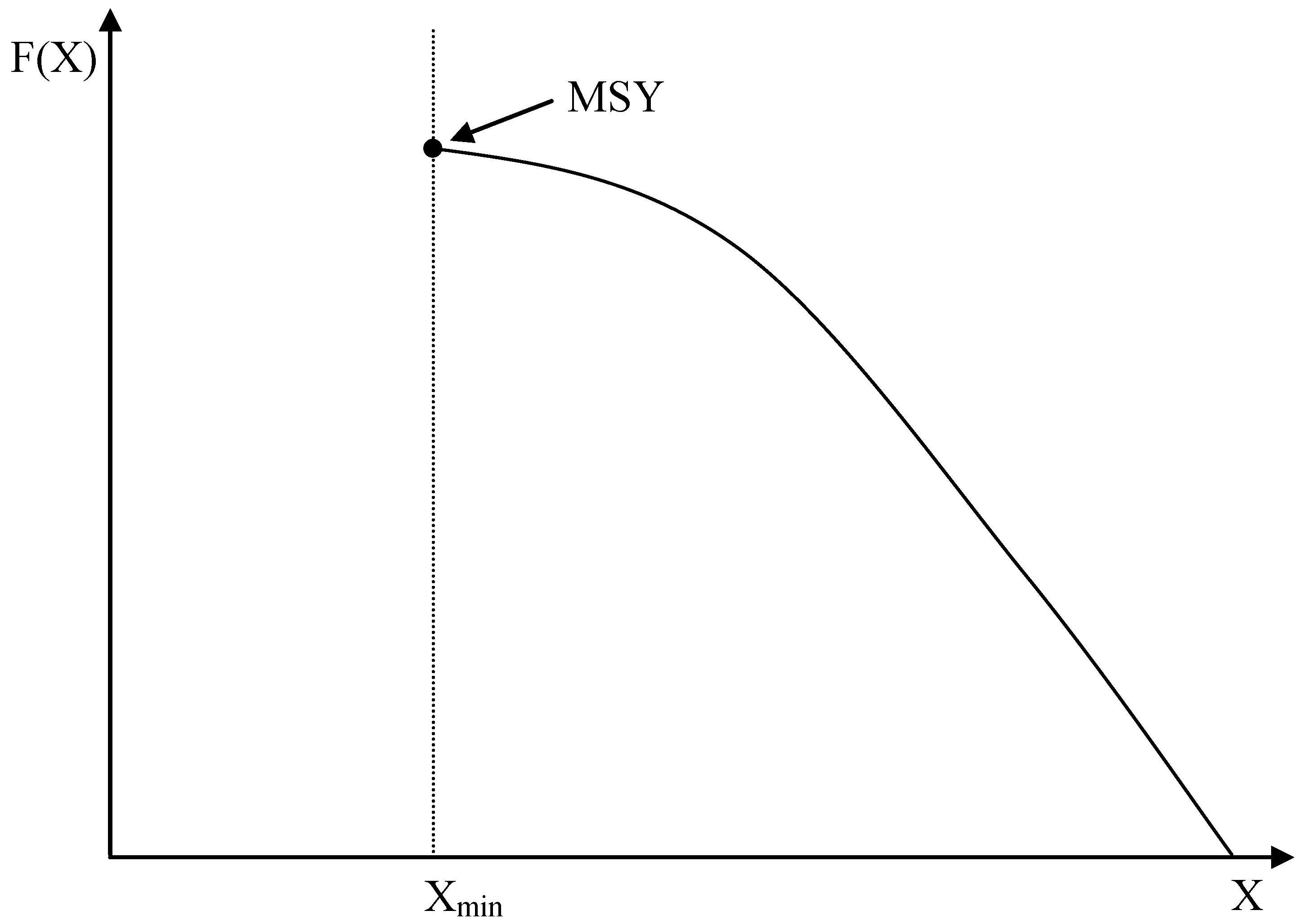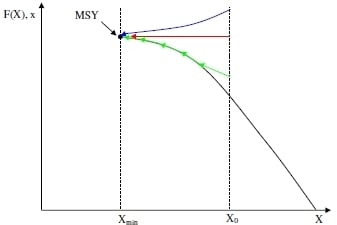As Figure 1 illustrates, the net growth function for groundwater (F) follows the standard shape for a renewable resource, albeit without the upward sloping portion. Growth of an ordinary renewable resource is typically an increasing function of stock for levels less than the stock that delivers maximum sustainable yield (MSY). The stock constraint X_min characterizes the minimum stock level, below which saltwater intrusion occurs. The constraint is analogous to a stock/concentration/pollution threshold in other resource management problems.

Figure 1. Groundwater growth curve.

Figure 1. Groundwater growth curve.

3. Sustainable Yield as a Management Strategy Is at Best Incomplete

In resource economics, sustainable yield is generally understood to be the rate of extraction or harvest that maintains a particular population or stock level X [10]. Thus, any point on the F(X) curve in Figure 1 is a sustainable yield. In the groundwater literature, sustainable yield is understood to be “the allowable net draft at steady state for a selected equilibrium head” [11], or the “forced withdrawal (draft) of groundwater at a rate that could be sustained indefinitely without affecting either the quality of the pumped water or the volume rate of pumping” [12]. In groundwater studies, “head” is typically used as an index of stock, where head is the vertical distance between mean sea level and the top of the freshwater lens. Although the lens is technically parabolic, the relationship between groundwater stock and head level can be reasonably approximated assuming a triangular shape [13,14]. In that case, volume can be converted to head with a constant factor, ${(41 \theta WL/2)}^{-1}$, where $\theta$ is the aquifer porosity, W is the aquifer width, and L is the aquifer length. But which target head level should the water manager select? A natural candidate is the head level corresponding to maximum sustainable yield (MSY), the highest rate of extraction that can be sustained indefinitely. Any harvest rate larger than MSY will lead to the depletion of the population for a typical renewable resource or saltwater intrusion in the case of a coastal groundwater aquifer.

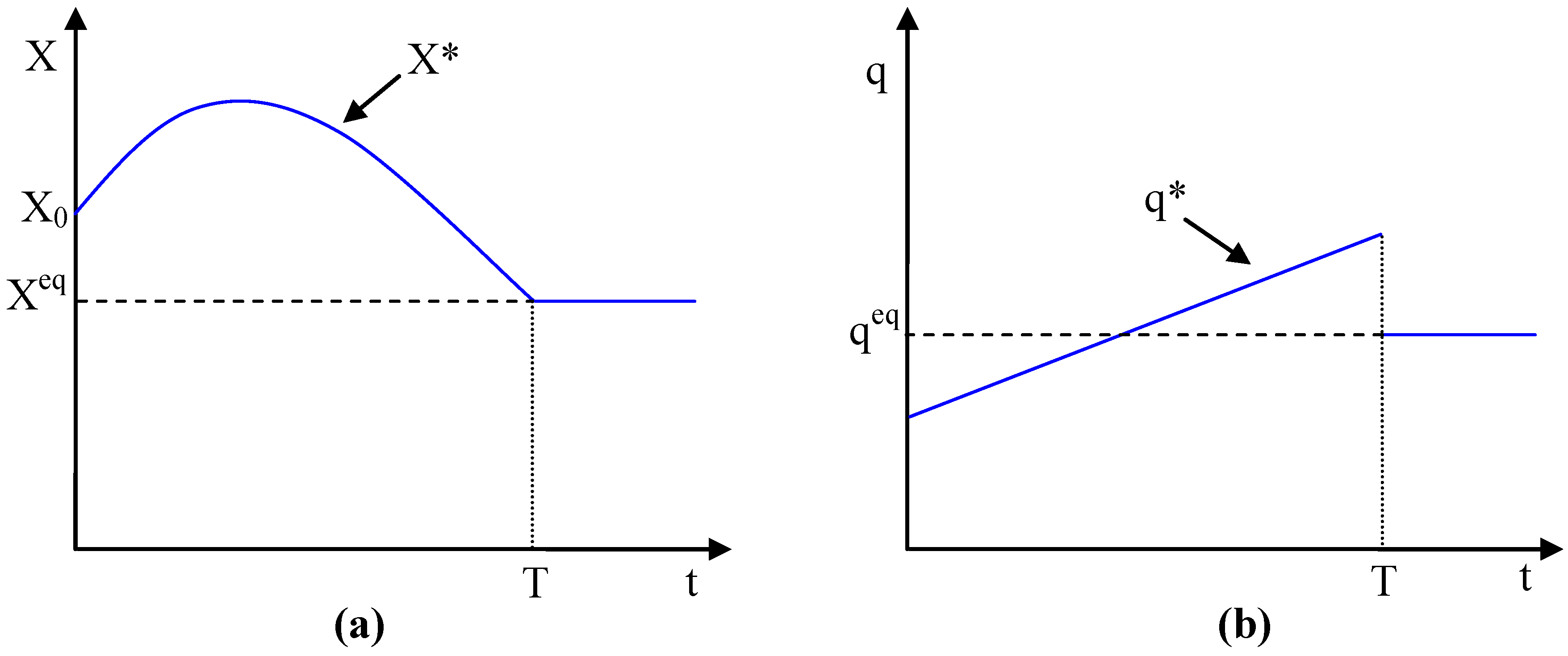
The management of renewable resources is often based on the concept of MSY, even though it is nearly impossible that MSY is ever entirely consistent with an economic optimum. In fact, the optimal rate of extraction may never coincide with MSY in any period. Even the long-run equilibrium or steady state extraction rate, may fall to the right of MSY on the aquifer growth curve (or on either side of MSY for a renewable resource in general) [10]. (A steady state is defined as a situation in which all state variables remain constant. The meaning of this concept in the context of resource economics will be made clearer in the following section.) Inasmuch as the sole purpose of MSY is to maximize the growth rate, and hence, the yield of the resource, the concept clearly fails to consider extraction and other opportunity costs and may promote waste in intertemporal management. Nonetheless, in cases where the unit extraction costs varies only slightly within the ranges of head being considered, MSY often turns out to be economically optimal in the long run, i.e., eventually optimal. However, even if the combination of X_min and MSY is a suitable target, we still have the open question of how to get there, i.e., how to transition from an initial stock level to X_min. 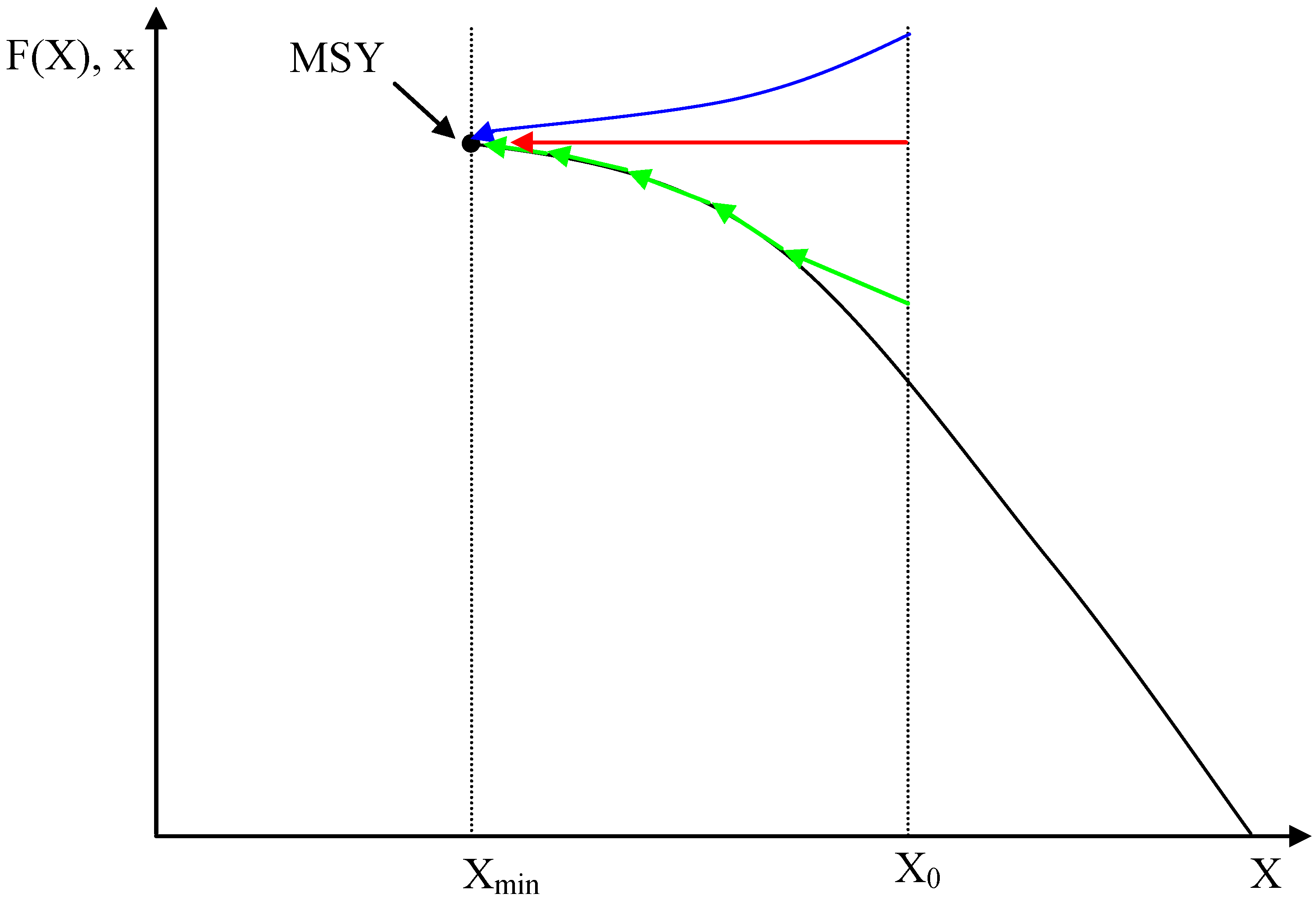Figure 2 illustrates a few of the infinitely possible extraction paths that can ultimately lead to the MSY steady state. Starting from an initial stock level X₀, extraction (x) can approach from above or below MSY, or be maintained at MSY indefinitely.

Figure 2. Various feasible extraction paths leading to MSY.

Figure 2. Various feasible extraction paths leading to MSY.

4. Optimal Extraction Is Sustainable, but “MSY Always” Is Not Optimal

If one takes the definition of maximum sustainable yield quite literally as “MSY always”, the selected transition path is given by the flat, red line in Figure 2. Following the declining blue path instead confers greater benefits in the near term but at the cost of hastening the drawdown to the MSY steady state. The rising green path provides much reduced yields during the transition, but prolongs the transition time. Which is better? In this section, we more formally show that the optimal steady state stock is endogenously determined by a resource economics model, and thus not generally equal to the MSY stock level. We characterize an optimality condition that, in combination with the equation of motion describing the dynamics of the aquifer, determines the transition to the steady state. In addition, through the use of a real-world application, we illustrate how “MSY always” management is incapable of generating optimal non-monotonic stock trajectories. Moreover, MSY may not even be the optimal long run target.

In what follows, we use the term “optimal” to characterize management strategies and outcomes obtained from the criterion of maximizing the present value (PV) of net social benefits. Supposing that an abundant but costly alternative to groundwater exists (e.g., desalinated seawater), a groundwater manager faces the problem of choosing water extraction (q) and desalination (b) in every period to maximize PV as follows:

$$\underset{q_t,b_t}{Max}{\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-rt}[B(q_t+b_t)-c(X_t)q_t}-c_b{b}_t]dt$$

(1)

subject to

$$\dot{X}=F(X_t)-q_t$$

(2)

$$X_t\ge X_{\text{min}}$$

(3)

and standard non-negativity constraints on the control variables. The benefit function (B) is dependent on the total quantity of water consumed, regardless of the source, measured for example by the area under the inverse demand curve for water. Although the unit cost of desalination ($c_b)$ is constant (supposing capital costs are amortized), the unit extraction cost of groundwater is stock-dependent. As the volume of coastal groundwater is reduced, the freshwater lens shrinks, which means more energy is required to pump the water a longer distance to the ground surface. The flow of net benefits is discounted to the present period at discount rate $r\in (0,1)$. Equation (2) describes the change in the groundwater stock over time. Growth from net recharge (F) adds to the stock, while extraction subtracts from it. The minimum stock constraint (3) ensures that the quality of the pumped water is maintained, i.e., it prevents saltwater intrusion of the aquifer.

Upon solving the dynamic resource management problem (1), one can derive the following optimality condition for resource extraction:

$$p_t=c(X_t)+\underset{MU{C}_t}{\underbrace{\frac{{\dot{p}}_t-F(X_t)c^{´}(X_t)}{r-F^{´}(X_t)}}}$$

(4)

where the efficiency price (p) is chosen to induce the level of consumption that equates marginal benefit with marginal opportunity cost (MOC), or the right hand side of Equation (4). MOC is comprised of marginal extraction cost and marginal user cost (MUC), the latter of which is defined as the cost of using the resource now in terms of forgone future benefits. Intuitively, extracting a unit of groundwater for consumption today increases stock-dependent extraction costs in all future periods and forgoes capital gains that could be obtained by leaving the resource in situ.

In the steady state, $\dot{p}=0$ in Equation (4). Provided that demand is growing over time, the backstop is optimally used in the steady state, and the efficiency price must rise to the unit cost of desalination. The equimarginality condition (4) can then be solved for a unique steady state stock level. (For a convex extraction cost function and a concave net recharge function, it can be shown that the right hand side of Equation (4) is monotonically decreasing in X and therefore admits an inverse and unique solution for X.) Under certain circumstances (e.g., for a fairly flat extraction cost function), the optimal steady-state stock level is in fact X_min [15]. If so, optimal extraction is sustainable in the long run, and moreover, the optimal steady state rate of extraction coincides with MSY. The optimal path of extraction is characterized by MSY in no more than a single period prior to arrival at the steady state, however. For rapidly increasing extraction cost, or more formally if the extraction cost function is very convex, the steady state stock is likely to be above the MSY stock level [8]. Intuitively, the potential gains from extracting MSY at the steady state are more than offset by higher extraction costs sustained into the future.

Figure 3 qualitatively illustrates the optimal trajectories of extraction and stock for a coastal aquifer on the island of Oahu, Hawaii [8,15]. Imposing rules of thumb such as always-extract-MSY can never be optimal if the stock path optimally rises from X₀ before declining to the steady state equilibrium level X^eq at year T. Extracting MSY from the outset would result in the stock declining monotonically. Even when the optimal steady state rate of extraction q^eq coincides with MSY, MSY is on the optimal extraction path (q*) for only a single instant of time prior to the steady state. Before that period, MSY is too high, and afterward MSY is too low (Figure 3b).

Figure 3. (a) Optimal stock can approach the steady state non-monotonically. (b) Optimal extraction is not constant over time.

Figure 3. (a) Optimal stock can approach the steady state non-monotonically. (b) Optimal extraction is not constant over time.

5. Managing Multiple Aquifers

When multiple sources of groundwater are managed simultaneously, optimal extraction remains sustainable [15], and moreover increases welfare relative to independent optimization [15]. Imposing management rules of thumb such as always-extract-MSY becomes even more inefficient when one takes the proper systems approach, even with only two aquifers. It may be optimal, for example, to not extract from one aquifer at all for a period of time. With two sources available, optimality requires drawing from the source for which the equimarginality condition (4) is satisfied. In other words, if the MB of consumption from source k is less than the aquifer’s MOC, then it is not optimal to extract from source k in that particular period of time. If MB=MOC, then positive extraction is optimal, as in the single aquifer case. More formally, this result is summarized as:

$$\begin{array}{l}{B}^{´}(q_t^1+q_t^2+b_t)\le c_1(X_t^1)+MU{C}_1(X_t^1) if <\text{ then }{q}_t^1=0\\ B^{´}(q_t^1+q_t^2+b_t)\le c_2(X_t^2)+MU{C}_2(X_t^2) if <\text{ then }{q}_t^2=0.\end{array}$$

(5)

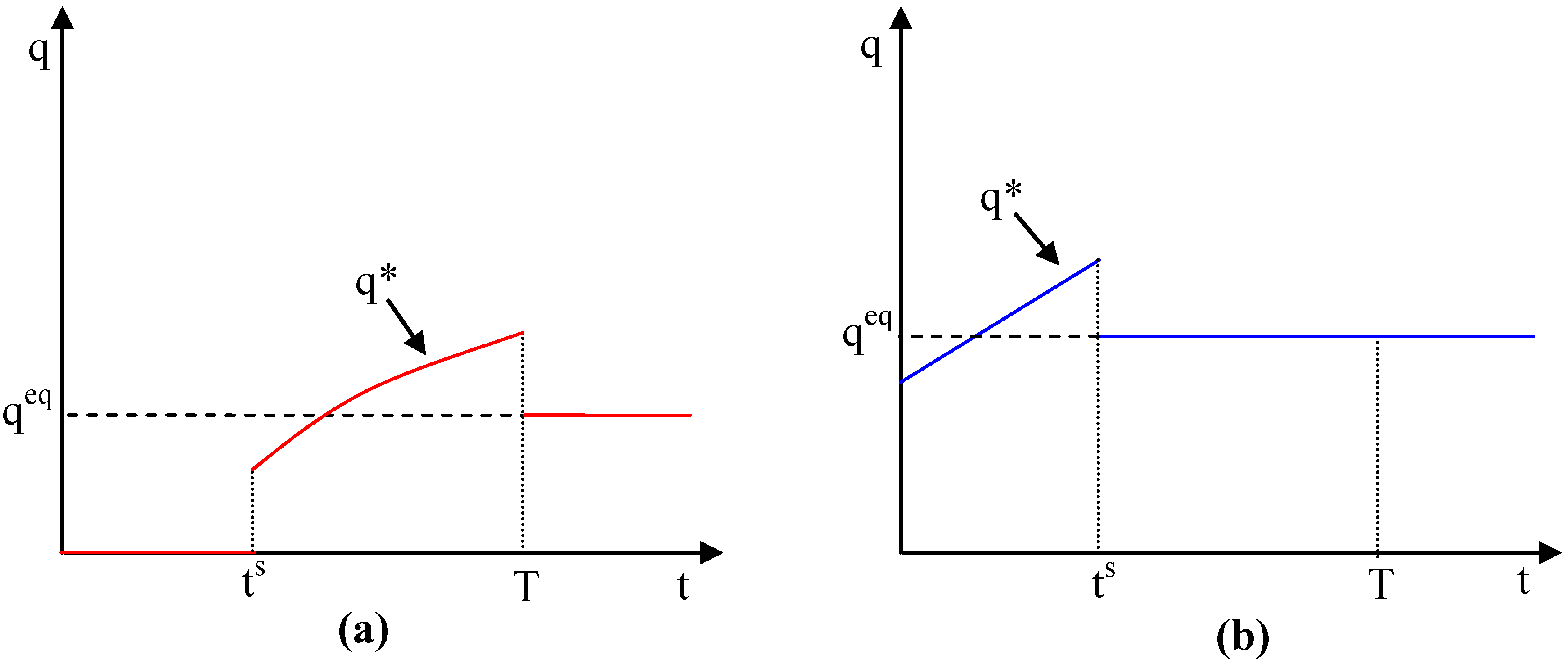
If an extraction moratorium for one or more of the resources is part of the optimal management plan, then extracting MSY indefinitely is even more welfare reducing in PV terms. For the aquifer that should be optimally allowed to replenish, MSY is far too high (Figure 4a). The year t^s denotes the period after which extraction optimally becomes positive for both aquifers.

Figure 4. (a) Inefficiency increases if optimality calls for zero extraction for a period of time. (b) Extracting MSY from the second aquifer is still inefficient.

Figure 4. (a) Inefficiency increases if optimality calls for zero extraction for a period of time. (b) Extracting MSY from the second aquifer is still inefficient.

6. Sustaining the Watershed

The quality of watersheds in many regions around the world is in decline due to urban development, invasive species, logging, or other activities that use the watershed, and climate change may exacerbate (or ameliorate) the problem [16,17]. Consequently, groundwater recharge has been declining and will continue to do so in the absence of corrective measures. Optimal groundwater management should therefore incorporate investment in watershed conservation capital in order to enhance the recharge capacity of the aquifer. Capital expenditures might include investment in fencing for feral animals, removal of invasive plants, reforestation of native flora, or construction of engineering structures designed to increase infiltration [18].

Unless the watershed is in pristine condition and/or the cost of conservation capital is prohibitively high, the optimal rate of investment is likely to be positive in every period in transition to the long-run equilibrium. Sustaining the watershed at some point is optimal precisely because optimal groundwater extraction is sustainable. In order to maintain MSY (or some other rate of extraction) in the steady state, recharge to the aquifer must also be maintained. Solving the integrated optimization problem yields rather intuitive results [15]. First, investing in recharge reduces the scarcity value or MOC of groundwater. Recalling that optimal extraction is determined where MB = MOC (condition 4), the quantity of groundwater extracted and consumed is consequently higher over time. Second, while the steady state is unchanged, the drawdown period of the aquifer (before desalination is optimally implemented) is extended. Lastly, if recharge is declining over time even with investment (because of climate change), the excess burden of not properly managing the watershed is higher. The intuition is that as water scarcity increases, so does the value of the marginal groundwater unit. Thus, it is optimal to actually maintain a higher conservation capital stock with climate change, even though the resulting recharge rate is lower than in the absence of climate change.

7. Optimal Wastewater Recycling

For demand sectors that do not require potable water (e.g., industry, certain types of agriculture), lower quality water can serve as a substitute for extracted groundwater. Recycled wastewater is a natural substitute, especially in areas where residential consumption meets or exceeds withdrawals for non-potable water users. In regions where the scarcity value of groundwater is very high, some substitution is already occurring, but perhaps not as much as the casual observer might expect. One explanation is that non-potable water requires its own set of infrastructure, which adds a non-negligible cost to treatment and distribution costs. Implicitly, the unit cost of recycled wastewater is then an increasing function of distance to the treatment facility. If one imagines that users can be ordered by that distance, then the unit cost can be characterized as an increasing function of quantity rather than distance.

If wastewater recycling is incorporated into an optimal groundwater management plan, then the use of recycled water grows over time as the scarcity value of groundwater increases. As the aquifer stock is drawn down, i.e., groundwater becomes scarcer, the MOC of groundwater shifts upward. Given the choice between groundwater and recycled water, the source with the lowest MOC is used first. Initially, groundwater may be sufficiently abundant, such that optimality entails groundwater use exclusively in both sectors. Eventually, the MOC of groundwater rises to the cost of the first unit of recycled water. In the following periods, water is recycled until the MOCs of the two resources are equal, and the remainder of the quantity demanded by the industrial and/or agricultural sector is met by groundwater extraction. The network of recycled water users continues to endogenously expand in that manner until eventually the system reaches an internal steady state or expansion ceases and recycling infrastructure is sustained, while the remainder of consumption is met by desalination.

Using recycled water in the industrial and/or agricultural sector lowers groundwater extraction costs by conserving on freshwater. The lower extraction path allows for an extended period of drawdown before the desalination steady state and a higher steady state stock (assuming the stock constraint is not binding). Analogous to investment in watershed conservation capital, water recycling reduces the scarcity of groundwater. MSY-type extraction rules lead to unnecessarily high drawdown in initial periods, thus reducing much of the welfare gain provided by the integrated groundwater management program.

8. Conclusions

Water scarcity is a complex systems problem, yet an important problem for nearly all regions across the globe. In order to proceed, we need a solid methodological framework rooted in sustainability science. Fundamental principles of resource and environmental economics must be combined with concepts from a variety of fields (e.g., hydrogeology, engineering, climatology, ecology) to answer specific policy questions related to water management.

The concept of sustainable yield is incomplete as a management strategy because it fails to specify which ultimate head level the water manager should target and how to get there (transition path). Application of economic analysis is a means of formalizing the problem and providing operational management strategies designed to maximize a specific objective. Economically optimal resource management typically implies eventually sustainable management, but rules-of-thumb, such as “always withdraw according to MSY”, are likely suboptimal. We conclude that rule-of-thumb sustainability rules are either redundant or wasteful of intertemporal welfare. Even if the stock corresponding to MSY happens to be the correct steady state target, extracting MSY in every period leading up to the steady state is very unlikely to maximize PV. Instead, in transition to the steady state, the resource should be extracted so that its marginal benefit is equal to its marginal opportunity cost in every period.

Generally, the optimal transition path cannot be determined independently of other management strategies, such as extraction from adjacent aquifers, watershed conservation, or wastewater recycling. The availability of another groundwater source can substantially change the optimal transition. In the extreme case, an extraction moratorium from one source may be optimal for a finite period. Instruments that augment the resource growth capacity directly, such as watershed conservation, reduce scarcity and increase welfare by extending the drawdown period of the aquifer before the steady state. Similarly, optimally implementing wastewater recycling extends the drawdown period by replacing groundwater for non-potable users.