Dynamic Estimation of Travel Time Reliability for Road Network Using Trajectory Data
Abstract
1. Introduction
2. Brief Review of Previous Research
2.1. Estimation of Travel Time Reliability
2.2. Trajectory Data
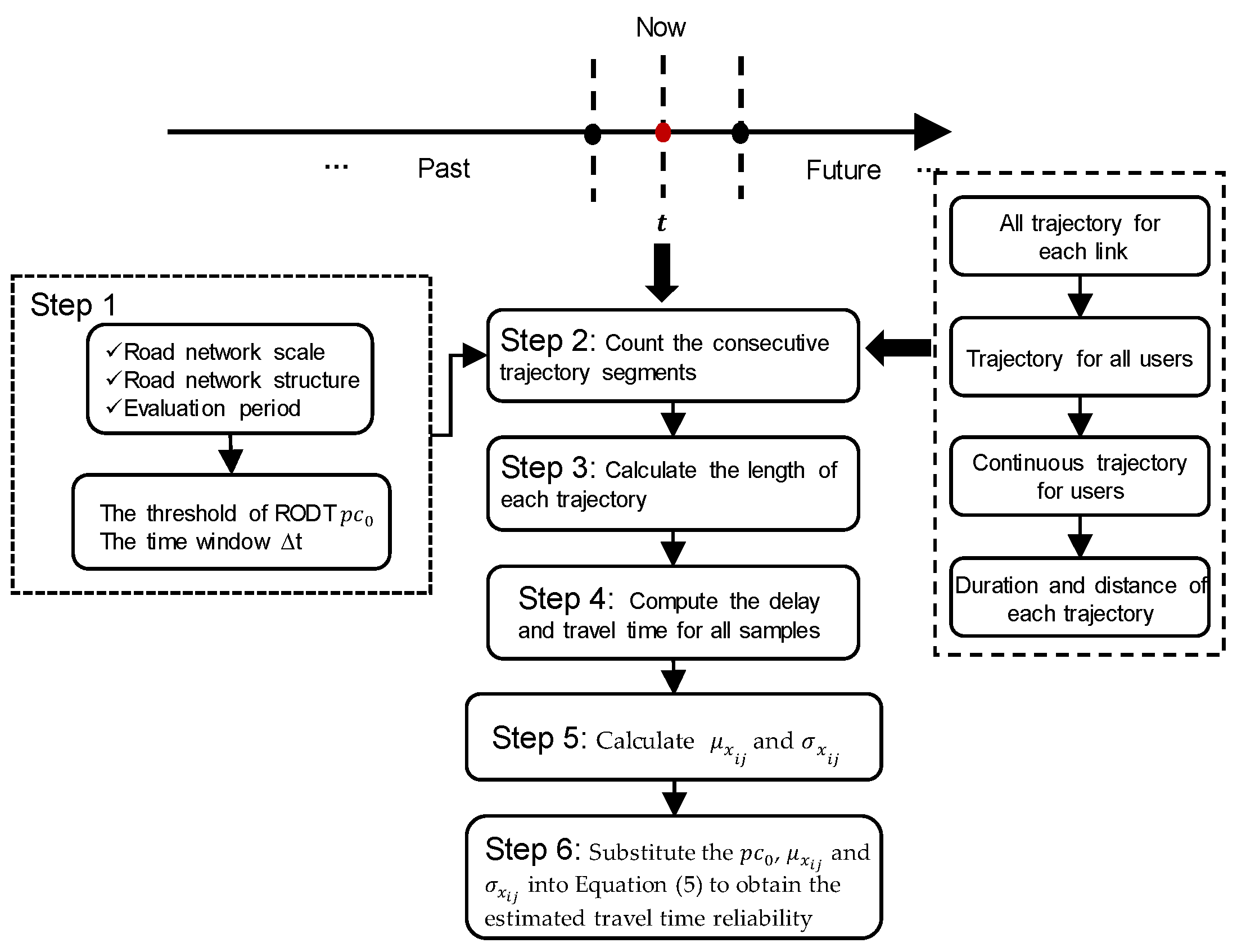
3. Dynamic Estimation Method of Travel Time Reliability by Trajectory Data
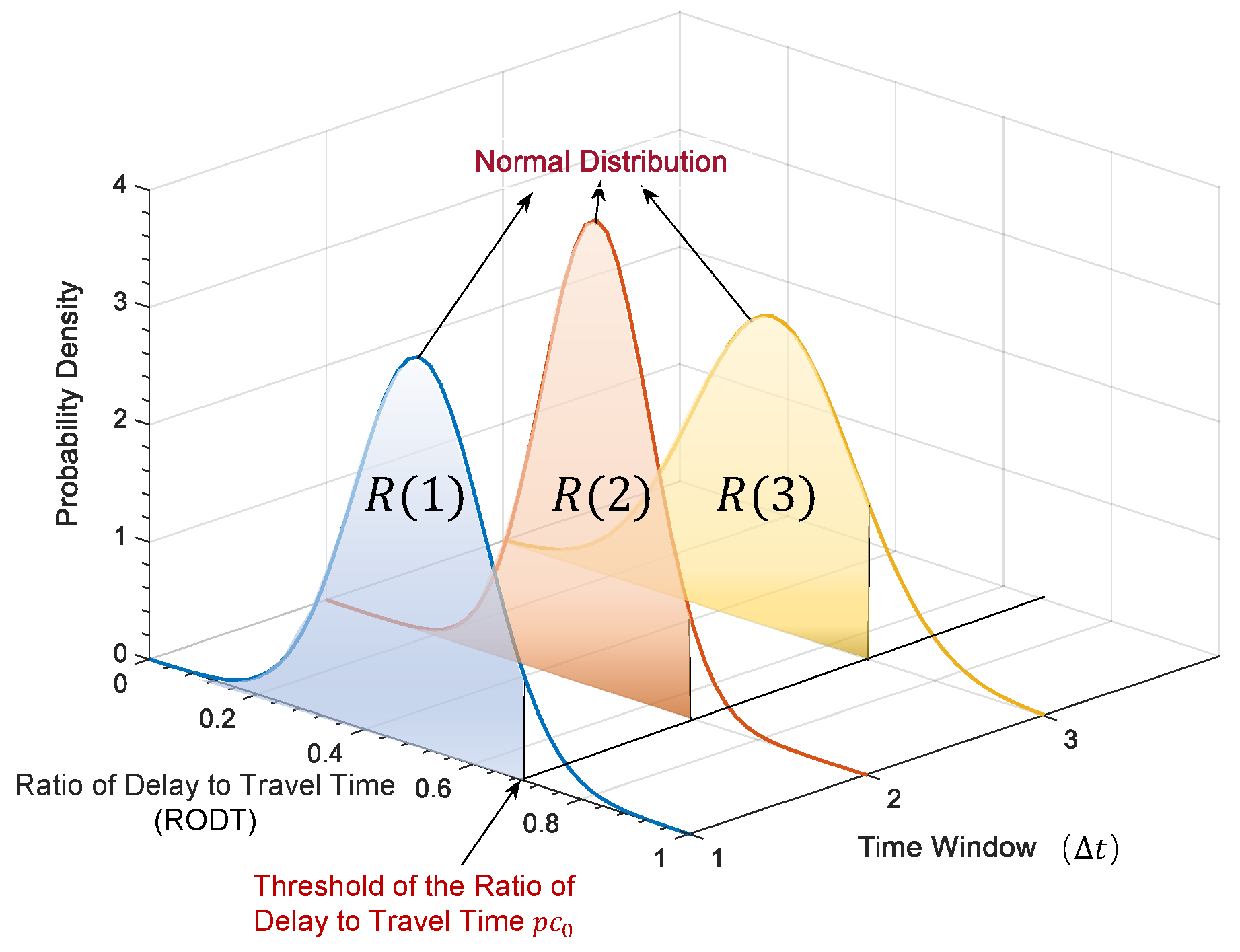
3.1. Parameter Description
3.2. Travel Time Reliability Estimation
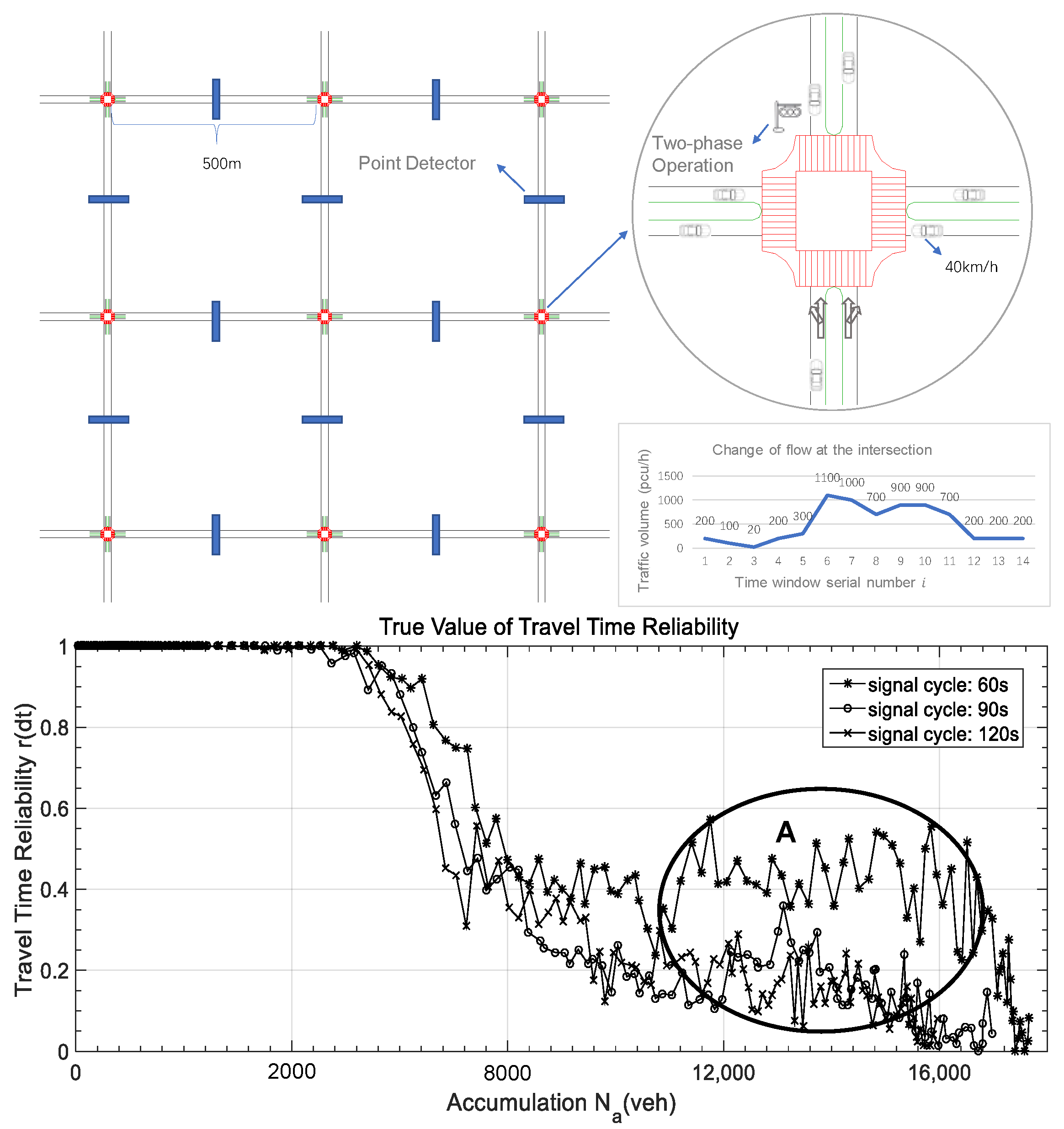
4. Result and Discussion
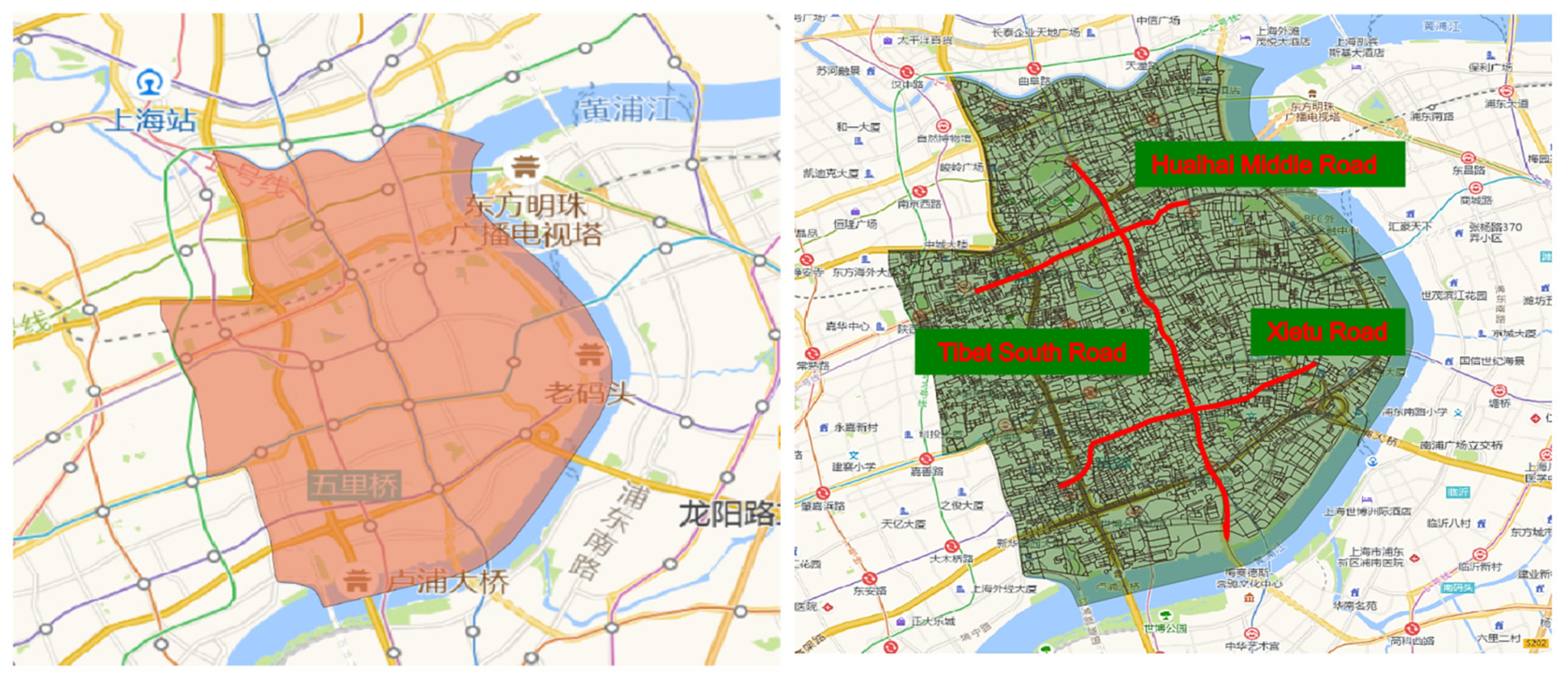
4.1. Data Source
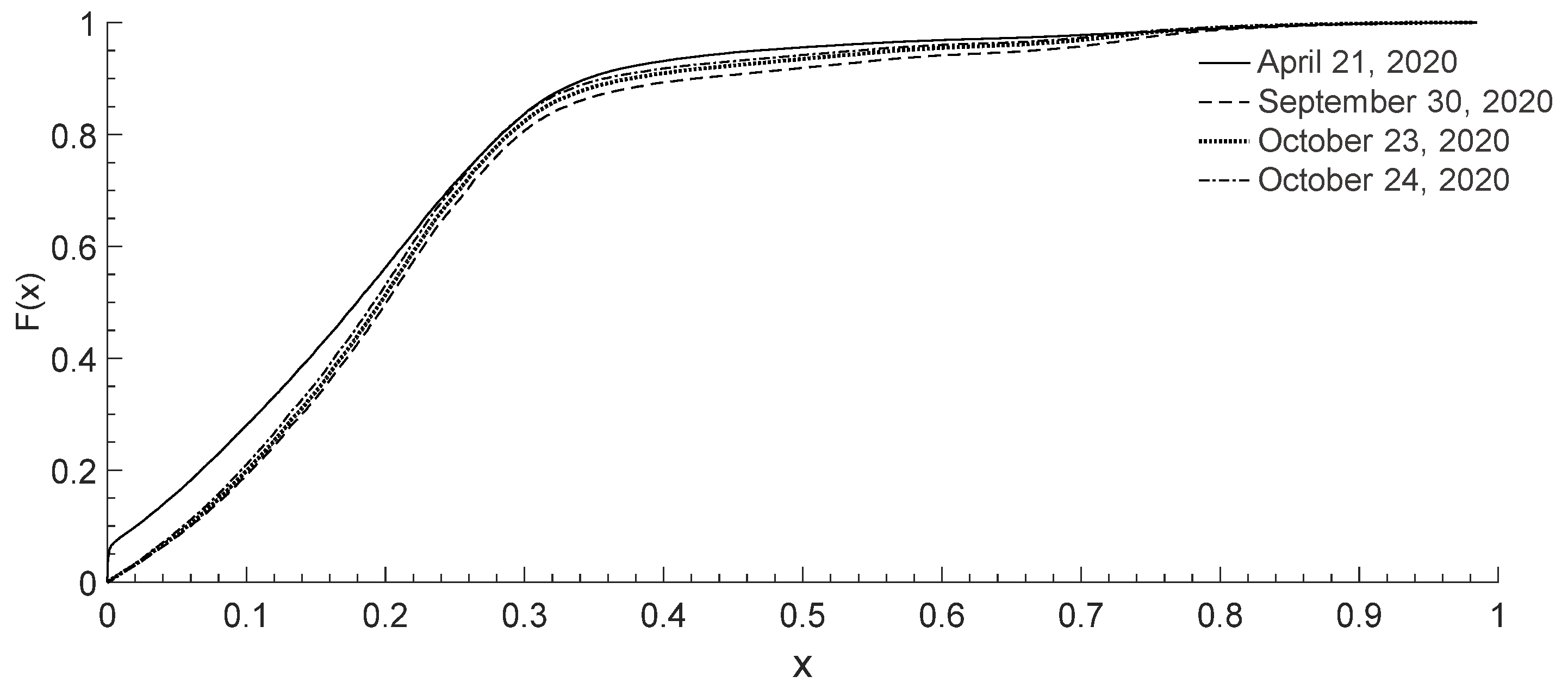
4.2. Hypothesis Verification
4.3. Applicability Analysis of the Proposed Method
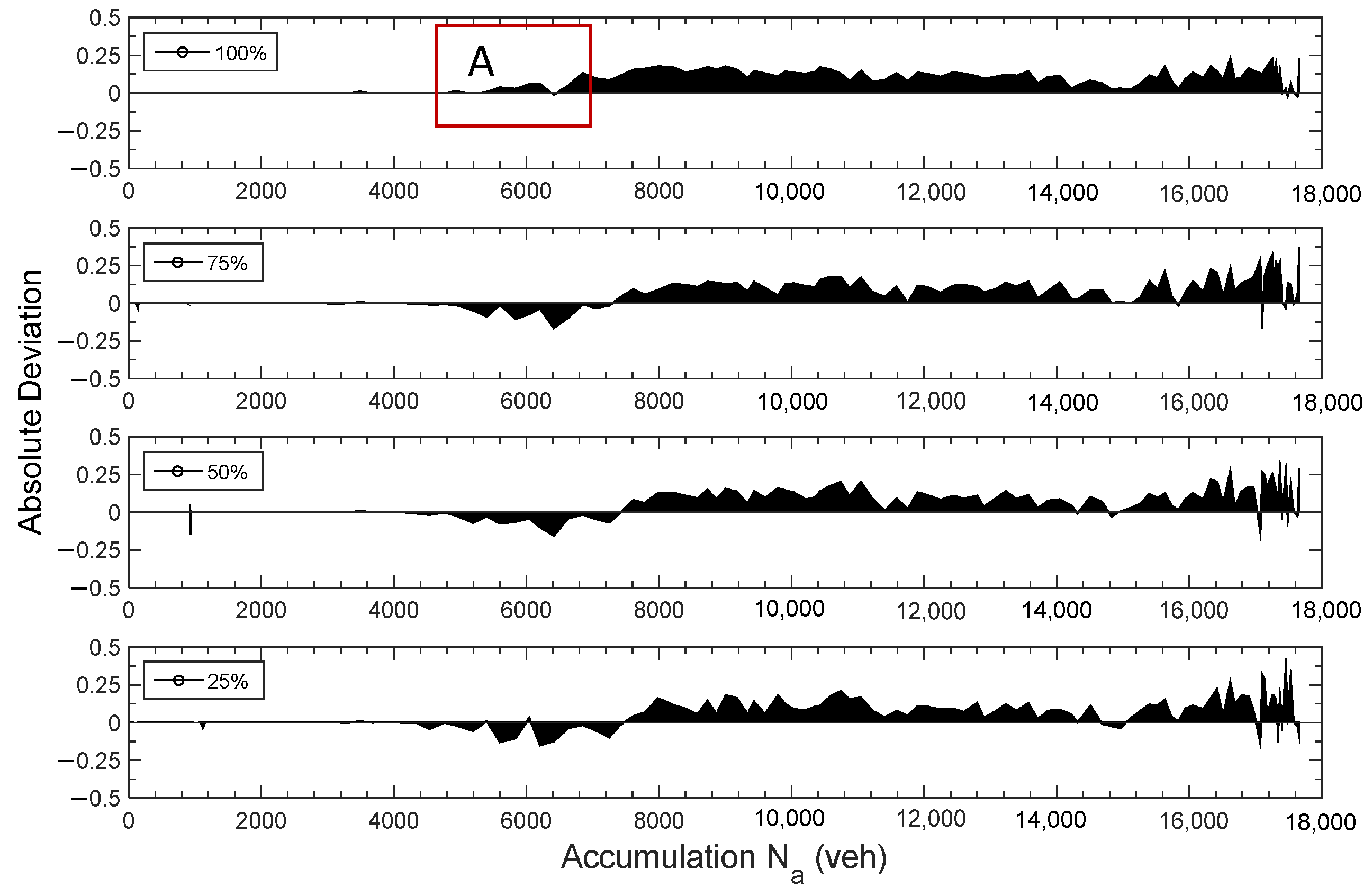
4.3.1. True Value of Travel Time Reliability Under Different Road Network Capacities
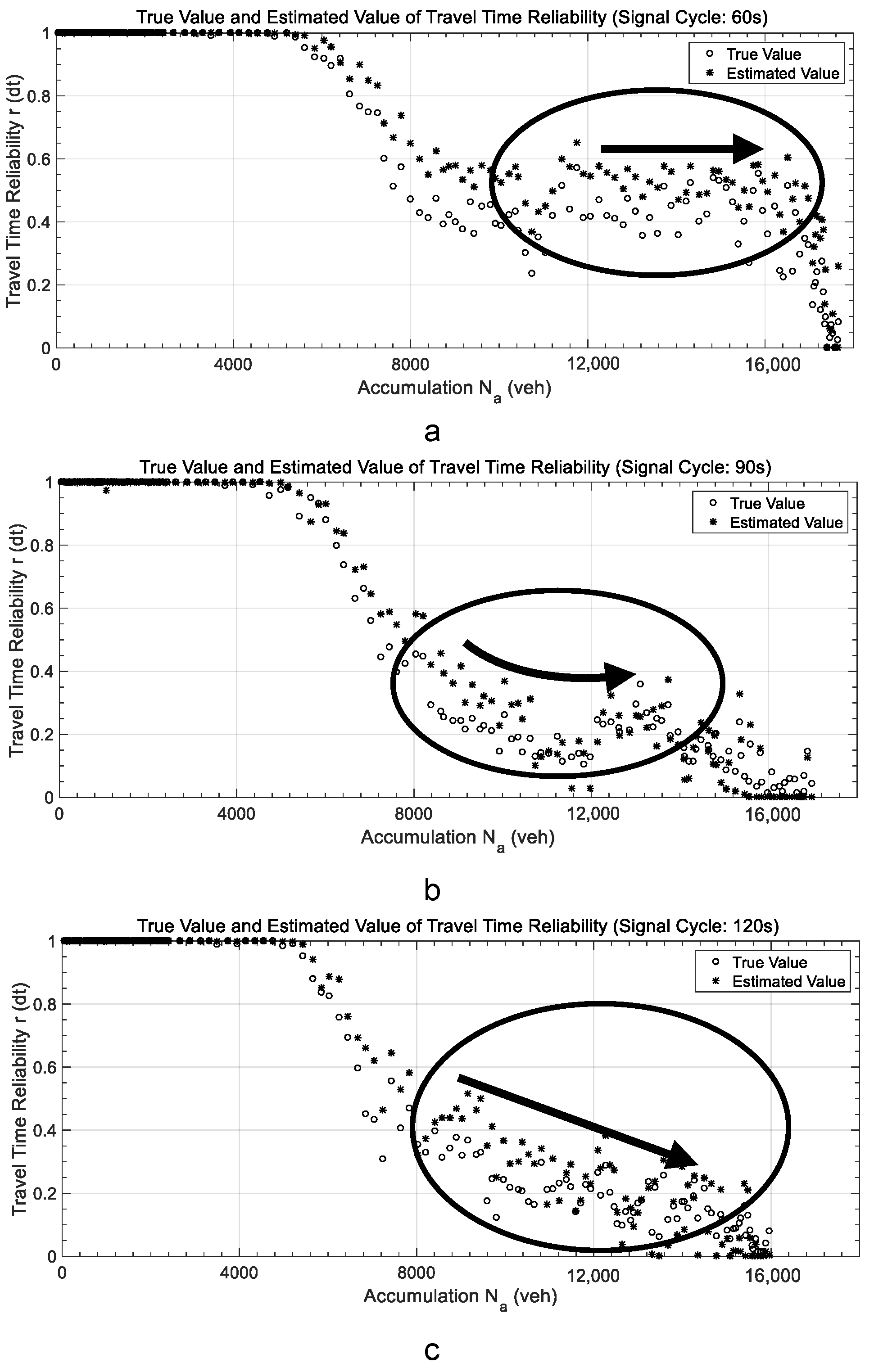
4.3.2. Estimated Value of Travel Time Reliability Under Different Road Network Capacities
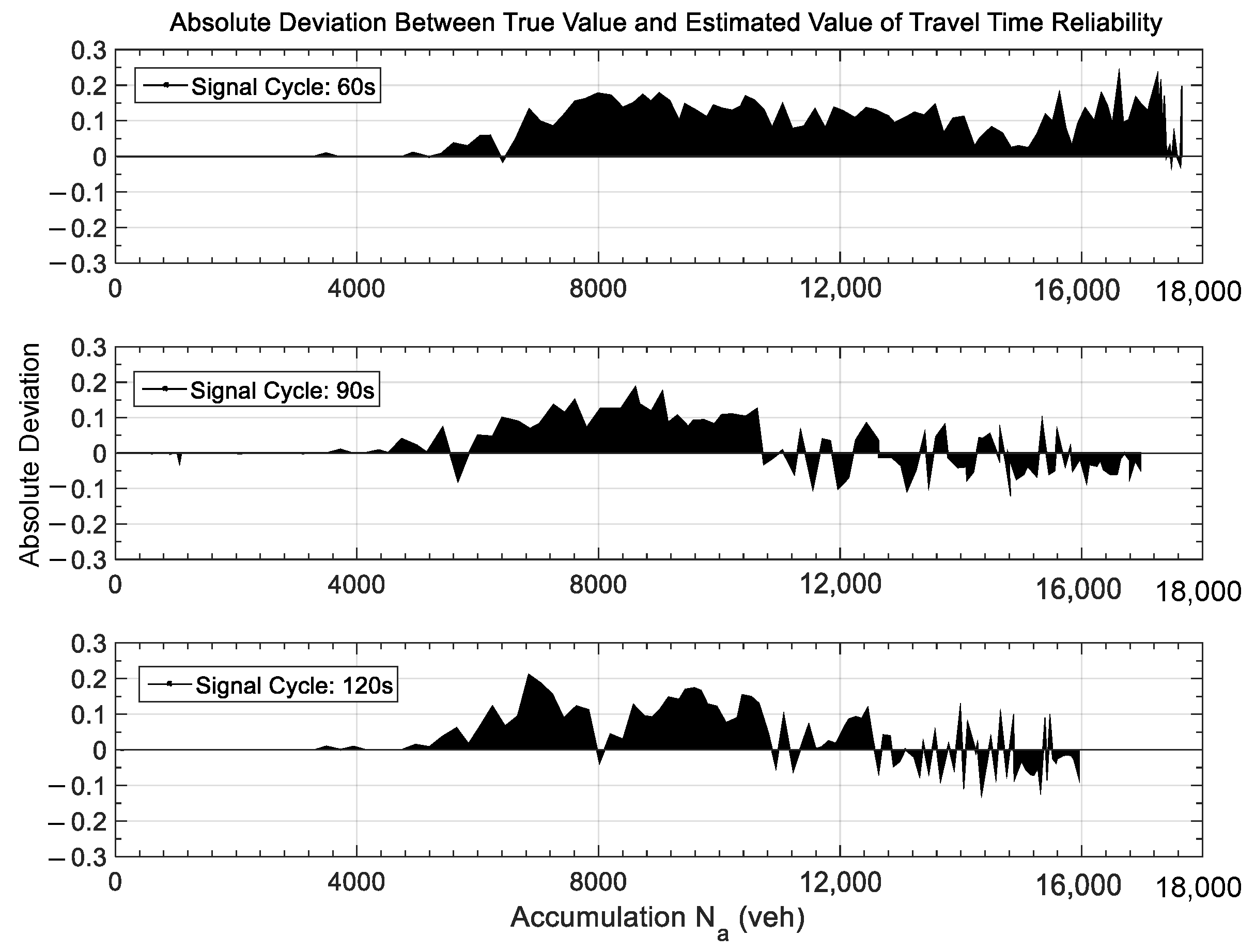
4.3.3. Error Analysis Between Estimated Value and True Value of Travel Time Reliability
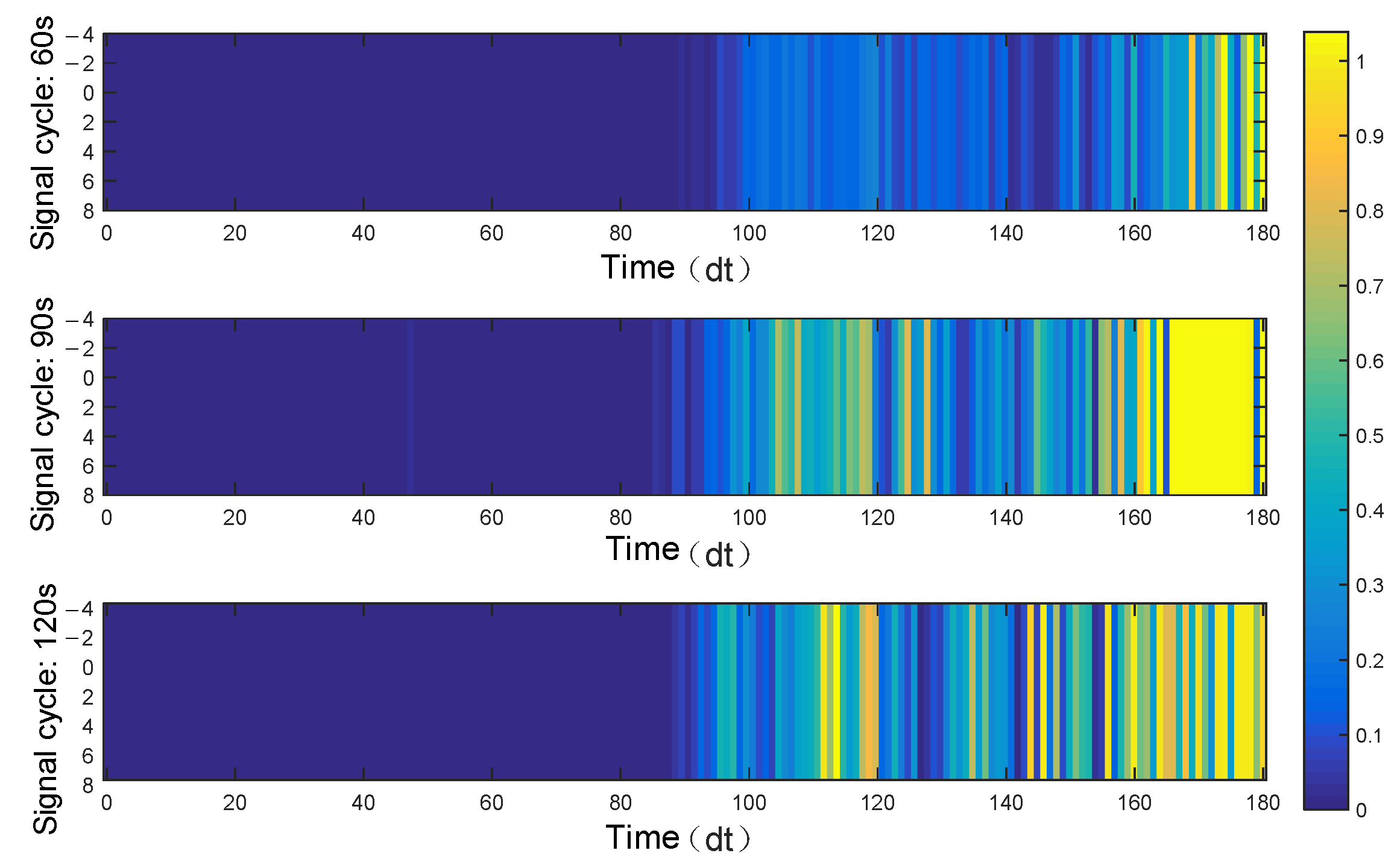
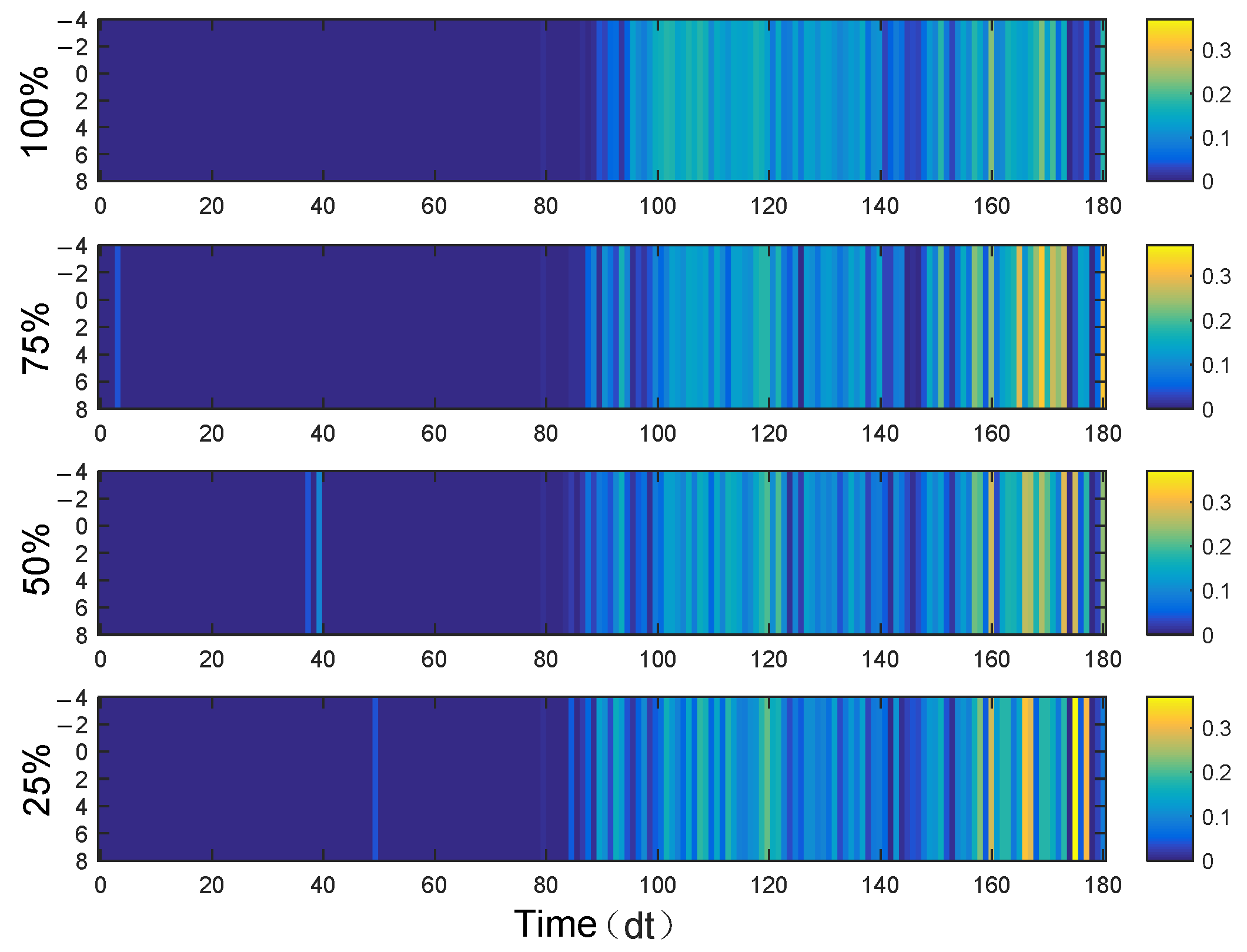
4.3.4. Estimated Value of Travel Time Reliability Under Different Trajectory Data Penetration Rates
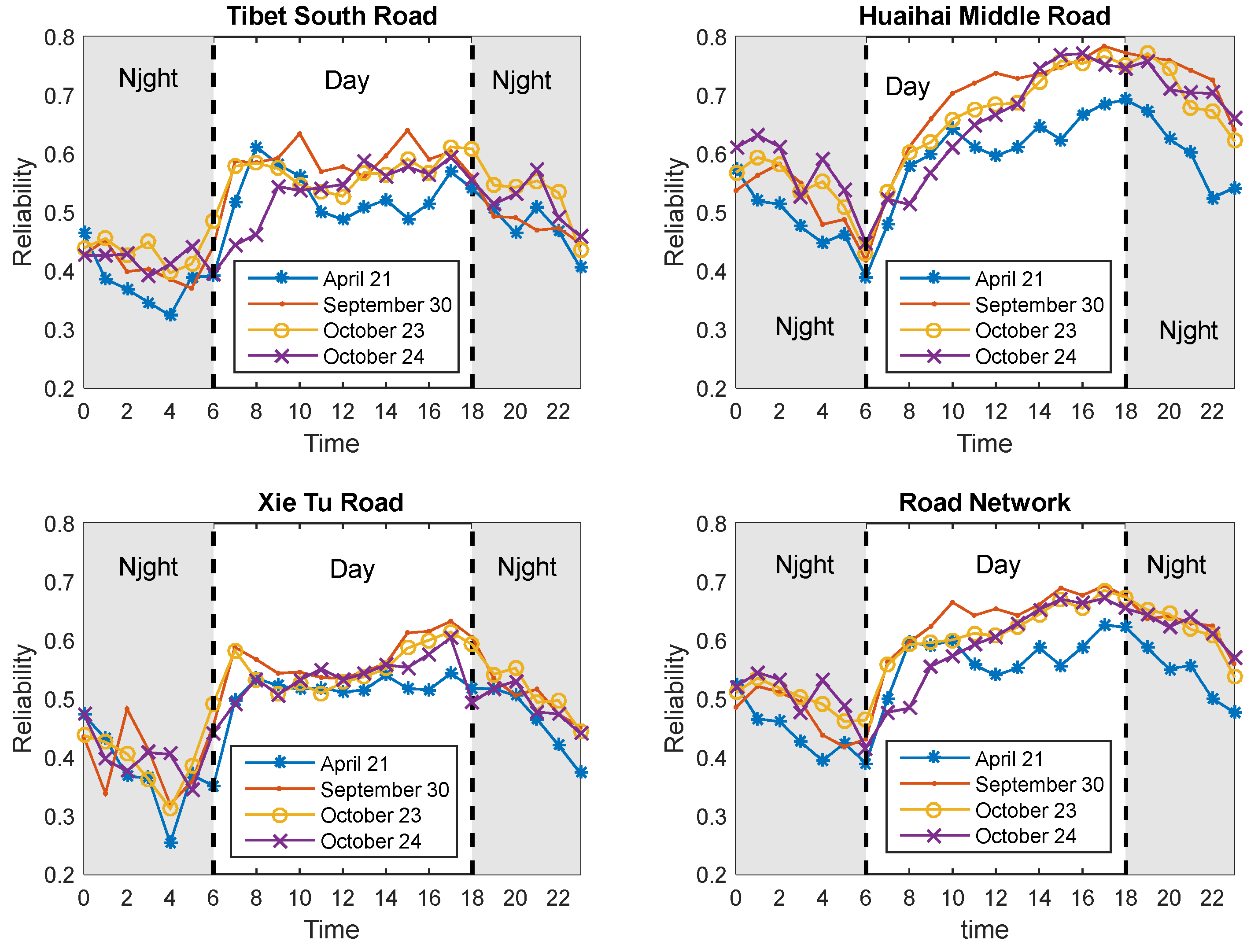
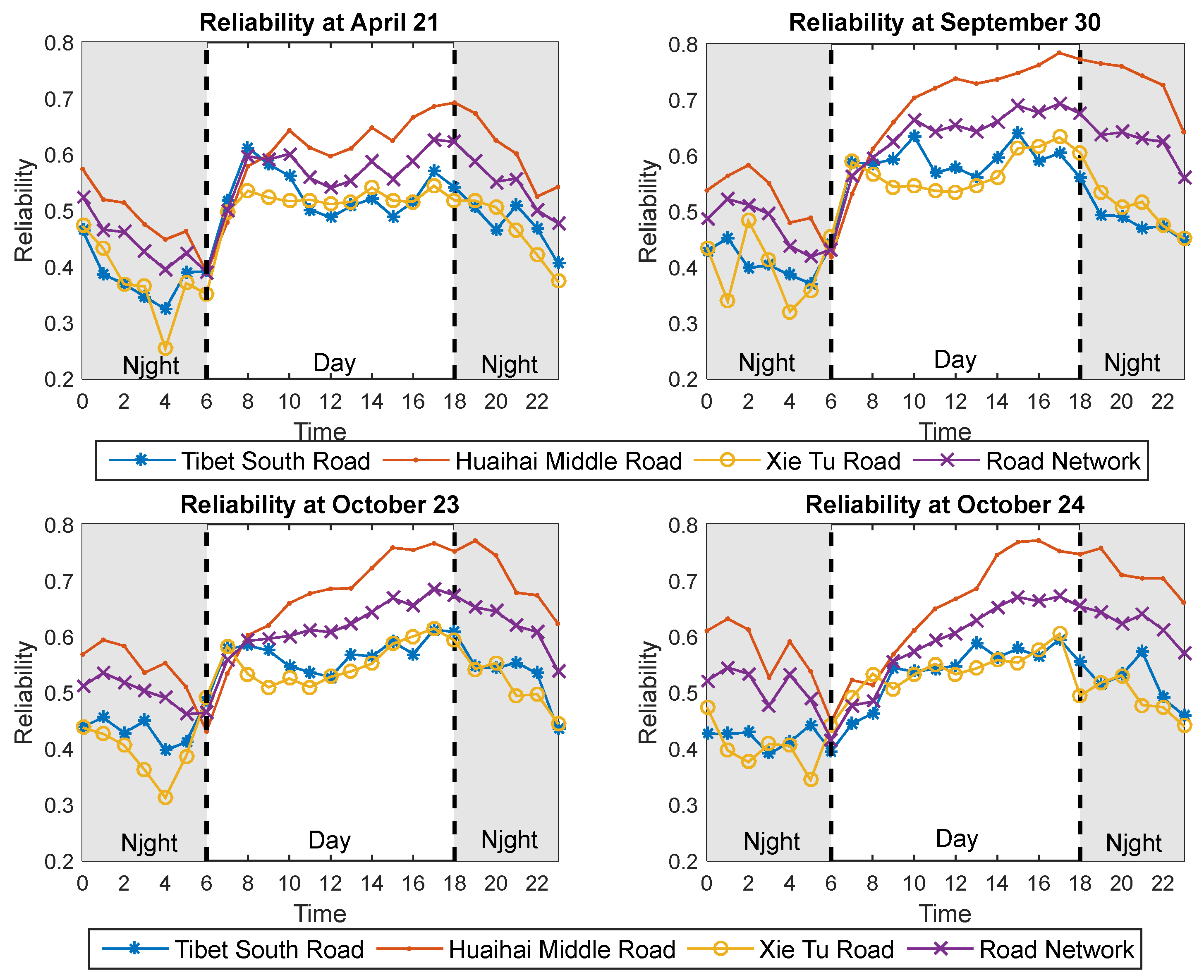
4.4. Travel Time Reliability of Real-World Road Network
5. Conclusions
- (1)
- The RODT (Ratio of Delay to Travel Time) of vehicles follows a normal distribution, as verified using real-world data from a homogeneous road network in Huangpu District, Shanghai, collected over four normal days. The analysis shows that travel time reliability for the real-world road network is generally higher during the day than at night. Additionally, reliability during the severe stage of the COVID-19 pandemic was lower compared to the remission stage.
- (2)
- The estimated RODT values obtained through the proposed method were generally consistent with the observed trends of the true values. The absolute error under the three tested signal cycles was less than 0.23, demonstrating that the travel time reliability estimated by the proposed method is representative for evaluating road network performance.
- (3)
- Error analysis indicates that the dynamic estimation method achieves higher accuracy when vehicle accumulation in the road network is low. Enhancing the accuracy of reliability estimation under conditions of high vehicle accumulation remains a key area for future research.
- (4)
- From the error analysis of travel time reliability estimates under varying data penetration rates, the absolute errors were found to be less than 0.3. This confirms that the dynamic estimation of travel time reliability for road networks based on trajectory data is both reasonable and reliable.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qu, K.; Fan, X.; Xu, X.; Hanasusanto, G.A.; Chen, A. Improving transportation network redundancy under uncertain disruptions via retrofitting critical components. Transp. Res. Part B Methodol. 2025, 194, 103174. [Google Scholar] [CrossRef]
- Wang, J.; You, L.; Hang, J. Pre-trip reservation enabled route guidance and signal control cooperative method for improving network throughput. Physica A 2023, 609, 128405. [Google Scholar] [CrossRef]
- Zang, Z.; Batley, R.; Xu, X.; Wang, D.Z. On the value of distribution tail in the valuation of travel time variability. Transp. Res. Part E Logist. Transp. Rev. 2024, 190, 103695. [Google Scholar] [CrossRef]
- Zang, Z.; Xu, X.; Qu, K.; Chen, R.; Chen, A. Travel time reliability in transportation networks: A review of methodological developments. Transp. Res. Part C Emerg. Technol. 2022, 143, 103866. [Google Scholar] [CrossRef]
- Yue, W.; Li, C.; Wang, S.; Xue, N.; Wu, J. Cooperative incident management in mixed traffic of CAVs and human-driven vehicles. IEEE Trans. ITS 2023, 24, 12462–12476. [Google Scholar] [CrossRef]
- Song, M.; Cheng, L. Incorporating travel time means and standard deviations into transportation network design problem: A hybrid method based on column generation and Lagrangian relaxation. Transp. Lett. 2023, 16, 131–143. [Google Scholar] [CrossRef]
- Moylan, E.K.; Bliemer, M.C.; Hossein Rashidi, T. Travellers’ perceptions of travel time reliability in the presence of rare events. Transportation 2022, 49, 1–25. [Google Scholar] [CrossRef]
- Teng, W.; Chen, B.Y. Reliable lifelong planning A*: Technique for re-optimizing reliable shortest paths when travel time distribution updating. Transp. Res. Part E Logist. Transp. Rev. 2024, 188, 103635. [Google Scholar] [CrossRef]
- Li, H.; Wang, Z.; Li, X.; Wang, H.; Man, Y.; Shi, J. Travel time probability prediction based on constrained LSTM quantile regression. J. Adv. Transp. 2023, 2023, 9910142. [Google Scholar] [CrossRef]
- Qian, Y.; Ding, H.; Meng, Y.; Zheng, N.; Di, Y.; Zheng, X. Combination of H∞ perimeter control and route guidance for heterogeneous urban road networks. Transp. Met. B Transp. Dyn. 2024, 12, 2359025. [Google Scholar] [CrossRef]
- Ma, Z.; Yang, X.; Shang, W.; Wu, J.; Sun, H. Resilience analysis of an urban rail transit for the passenger travel service. Transp. Res. Part D Transp. Environ. 2024, 128, 104085. [Google Scholar] [CrossRef]
- Saedi, R.; Saeedmanesh, M.; Zockaie, A.; Saberi, M.; Geroliminis, N.; Mahmassani, H.S. Estimating Network Travel Time Reliability with Network Partitioning. Transp. Res. Part C Emerg. Technol. 2020, 112, 46–61. [Google Scholar] [CrossRef]
- Tian, H.; Wang, T.; Xu, L.; Sha, M.; Chen, S.; Yang, Z.; Tian, X. Research and development of prevention and control measures on the transmission of pathogens in compartments of passenger transport. Transp. Saf. Environ. 2024, 6, tdad011. [Google Scholar] [CrossRef]
- Cheng, Q.; Liu, Z.; Lu, J.; List, G.; Liu, P.; Zhou, X.S. Using frequency domain analysis to elucidate travel time reliability along congested freeway corridors. Transp. Res. Part B Methodol. 2024, 184, 102961. [Google Scholar] [CrossRef]
- Liu, Y.; Francis, A.; Hollauer, C.; Lawson, M.C.; Shaikh, O.; Cotsman, A.; Asensio, O.I. Reliability of electric vehicle charging infrastructure: A cross-lingual deep learning approach. Commun. Transp. Res. 2023, 3, 100095. [Google Scholar] [CrossRef]
- Li, F.; Cheng, J.; Mao, Z.; Wang, Y.; Feng, P. Enhancing safety and efficiency in automated container terminals: Route planning for hazardous material AGV using LSTM neural network and Deep Q-Network. J. Intell. Connect. Veh. 2024, 7, 64–77. [Google Scholar] [CrossRef]
- Kato, T.; Uchida, K.; Lam, W.H.; Sumalee, A. Estimation of the value of travel time and of travel time reliability for heterogeneous drivers in a road network. Transportation 2021, 48, 1639–1670. [Google Scholar] [CrossRef]
- Cheok, C.C.; Khoo, W.C.; Khoo, H.L. Bus travel time variability modelling using Burr type XII regression: A case study of Klang Valley. KSCE J. Civ. Eng. 2024, 28, 3998–4009. [Google Scholar] [CrossRef]
- Zhai, C.; Wu, W.; Xiao, Y. Modeling continuous traffic flow with the average velocity effect of multiple vehicles ahead on gyroidal roads. Digit. Transp. Saf. 2023, 2, 124–138. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Yang, J.; Zhang, Z.; Wang, C.; Qian, B.; Tian, X.; Wang, T. Airborne transmission of virus-laden droplets in an aircraft cabin. Transp. Saf. Environ. 2023, 5, tdac079. [Google Scholar] [CrossRef]
- Wang, J.; He, X.; Peeta, S. Feedback perimeter control with online estimation of maximum throughput for an incident-affected road network. J. Intell. Transp. Syst. 2021, 26, 81–99. [Google Scholar] [CrossRef]
- Jian, Z.H.; Xu, X.D.; Zang, Z.Q. Estimating a route travel time distribution function with segment correlations Using segment-level travel time data only: A moment-based method. IEEE Trans. Intell. Transp. Syst. 2024, 25, 18815–18830. [Google Scholar] [CrossRef]
- Saw, K.; Katti, B.K.; Joshi, G.J.; Kedia, A. Travel time reliability evaluation using fuzzy-possibility approach: A case study of an Indian city. Transp. Plann. Technol. 2024, 47, 1092–1110. [Google Scholar] [CrossRef]
- Costa, T.G.D.; Isler, C.A.; Bessa Júnior, J.E. Method for Identifying Homogeneous Periods to Evaluate Urban Travel Time Reliability. Transp. Res. Rec. 2025, 03611981241306753. [Google Scholar] [CrossRef]
- Zhao, M.; Zhang, X.; Appiah, J.; Fontaine, M.D. Travel time reliability prediction using random forests. Transp. Res. Rec. 2024, 2678, 531–545. [Google Scholar] [CrossRef]
- Sun, Y.X.; Chen, Y. Travel time variability in urban mobility: Exploring transportation system reliability performance using ridesharing data. Sustainability 2024, 16, 8103. [Google Scholar] [CrossRef]
- Meng, Y.; Zhao, X.; Xu, X.; Ma, W. Vulnerability assessment of large-scale urban road network under emerging disinformation attacks. Transportmetrica A 2025, 1–25. [Google Scholar] [CrossRef]
- Chen, L.; Xie, C.; Ma, D.; Yang, Y.; Li, Y. A short-term traffic flow prediction model for road networks using inverse isochrones to determine dynamic spatiotemporal correlation ranges. Physica A 2025, 657, 130244. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, Y.; Shi, C.; Li, Q.; Yang, B.; Hao, W. Identifying vehicle types from trajectory data based on spatial-semantic information. Geo-Spat. Inf. Sci. 2024, 1–17. [Google Scholar] [CrossRef]
- Mizzi, C.; Baroncini, A.; Fabbri, A.; Micheli, D.; Vannelli, A.; Criminisi, C.; Bazzani, A. Individual mobility deep insight using mobile phones data. EPJ Data Sci. 2023, 12, 56. [Google Scholar] [CrossRef]
- Sekar, N.K.; Malaghan, V.; Pawar, D.S. Micro-simulation insights into the safety and operational benefits of autonomous vehicles. J. Intell. Connect. Veh. 2023, 6, 202–210. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, X.; Hu, R.; Huang, W.; Li, L.; Xie, J.; Yao, D. Vehicle trajectory reconstruction with sparse automatic license plate recognition data for urban road networks. Transportmetrica A 2025, 1–24. [Google Scholar] [CrossRef]
- Deng, J.; Gao, L.; Chen, X.; Yuan, Q. Taking the same route every day? An empirical investigation of commuting route stability using personal electric vehicle trajectory data. Transportation 2024, 51, 1547–1573. [Google Scholar] [CrossRef]
- Mathivanan, S.K.; Rajadurai, H.; Cho, J.; Easwaramoorthy, S.V. A multi-modal geospatial–temporal LSTM based deep learning framework for predictive modeling of urban mobility patterns. Sci. Rep. 2024, 14, 31579. [Google Scholar]
- Jin, J.; Wang, Y.; Chen, A.; Dimitrijevic, B.; Lee, J. Dynamic nonrecurrent congestion event detection and tracking method with DBSCAN on speed watersheds. J. Adv. Transp. 2024, 2024, 8404251. [Google Scholar] [CrossRef]
- Saffari, E.; Yildirimoglu, M.; Hickman, M. Estimation of macroscopic fundamental diagram solely from probe vehicle trajectories with an unknown penetration rate. IEEE Trans. Intell. Transp. Syst. 2023, 24, 1214970–1214981. [Google Scholar] [CrossRef]
- Gao, H.; Zhou, L.; Dong, Y.; Wang, X.; Sun, Q.; Wang, S.; Yuan, L. Identifying critical road sections using the weighted periodicity mined from trajectory data for efficient urban transportation. GISci. Remote Sens. 2025, 62, 2448251. [Google Scholar] [CrossRef]
- Raju, N.; Arkatkar, S.; Joshi, G. Modeling following behavior of vehicles using trajectory data under mixed traffic conditions: An Indian viewpoint. Transp. Lett. 2021, 13, 649–663. [Google Scholar] [CrossRef]
- Sun, J.; Kim, J. Joint Prediction of Next Location and Travel Time from Urban Vehicle Trajectories using Long Short-term Memory Neural Networks. Transp. Res. Part C Emerg. Technol. 2021, 128, 103114. [Google Scholar] [CrossRef]
- Dokuz, A.S. Weighted spatio-temporal taxi trajectory big data mining for regional traffic estimation. Physica A 2022, 589, 126645. [Google Scholar] [CrossRef]
- Akopov, A.S.; Beklaryan, L.A. Evolutionary Synthesis of High-Capacity Reconfigurable Multilayer Road Networks Using a Multiagent Hybrid Clustering-Assisted Genetic Algorithm. IEEE Access 2025, 13, 53448–53474. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, M. Finding paths with least expected time in stochastic time-varying networks considering uncertainty of prediction information. IEEE Trans. Intell. Transp. Syst. 2023, 24, 14362–14377. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, Z.; Guo, X.; Li, G.; Zhang, C.; Tang, L. Three-dimensional road network empowered traffic emission estimation via trajectory data. J. Clean. Prod. 2023, 475, 143669. [Google Scholar] [CrossRef]
- Shin, Y.; Yoon, Y. Incorporating Dynamicity of Transportation Network with Multi-weight Traffic Graph Convolutional Network for Traffic Forecasting. IEEE Trans. Intell. Transp. Syst. 2022, 23, 2082–2092. [Google Scholar] [CrossRef]
- Matin, A.; Dia, H. Public perception of connected and automated vehicles: Benefits, concerns, and barriers from an Australian perspective. J. Intell. Connect. Veh. 2024, 7, 108–128. [Google Scholar] [CrossRef]
- Hang, J.Y.; Zhou, X.Z.; Wang, J.W. Modeling Traffic Function Reliability of Signalized Intersections with Control Delay. Adv. Civ. Eng. 2020, 1–13. [Google Scholar] [CrossRef]
- Chen, P.; Sun, J.; Qi, H. Estimation of delay variability at signalized intersections for urban arterial performance evaluation. J. Intell. Transp. Syst. 2017, 21, 94–110. [Google Scholar] [CrossRef]
- Lin, Y.T.; Cheng, Y.; Chang, G.L. Integration of progression maximization and delay minimization controls for commuting arterials accommodating highly asymmetric directional traffic flows. J. Intell. Transp. Syst. 2024, 1–17. [Google Scholar] [CrossRef]
| Symbol | Description |
|---|---|
| Input | |
| : | |
| : | |
| : | is unreliable |
| : | |
| : | -th time window |
| : | The number of samples |
| : | |
| : | Cumulative number of vehicles |
| : | The number of vehicles leaving the road |
| Output | |
| : | |
| : | -th time window, pcu |
| : | -th time window, pcu |
| : | |
| : | |
| : | Travel time reliability of road network during time window |
| Data Source | Attributes | Data Usage |
|---|---|---|
| Data of an approximately homogeneous road network area in Shanghai | 1. Time: the update frequency is 120 s. 2. Road link ID, which matches the basic road network data. 3. Average speed of the road link, km/h. 4. Travel time, s. 5. Actual travel time divided by free-flow travel time. 6. Road name. | Verify hypothesis |
| Individual driving trajectory data | 1. Trajectory ID. 2. Time; update frequency at 5 s. 3. User ID, identification of user ID. 4. Longitude, latitude, real time location. 5. Link ID, matching with basic road data. 6. Link name; the Chinese name of the link. | Empirical research |
| Vehicle trajectory data from micro-simulation | 1. Vehicle records Vehicle number; vehicle type; headway; travel distance (total); time in the road network (total); speed; simulation seconds; delay. 2. Vehicle travel time Time interval; simulation number; vehicle; vehicle type; travel time. 3. Delay Time interval; simulation number; stop time (average); vehicle delay (average); number of vehicles. | Applicability research |
| April 21 | September 30 | October 23 | October 24 | |
|---|---|---|---|---|
| Distribution | Normal | |||
| Log likelihood | 1.22 × 106 | 1.06 × 106 | 1.27 × 106 | 1.36 × 106 |
| Range | –Inf < y < Inf | –Inf < y < Inf | –Inf < y < Inf | –Inf < y < Inf |
| Mean | 0.195553 | 0.229745 | 0.219377 | 0.212252 |
| Variance | 0.0239349 | 0.0289365 | 0.0248536 | 0.0233159 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hang, J.; Tang, T.; Wang, J. Dynamic Estimation of Travel Time Reliability for Road Network Using Trajectory Data. Sustainability 2025, 17, 4244. https://doi.org/10.3390/su17094244
Hang J, Tang T, Wang J. Dynamic Estimation of Travel Time Reliability for Road Network Using Trajectory Data. Sustainability. 2025; 17(9):4244. https://doi.org/10.3390/su17094244
Chicago/Turabian StyleHang, Jiayu, Tianpei Tang, and Jiawen Wang. 2025. "Dynamic Estimation of Travel Time Reliability for Road Network Using Trajectory Data" Sustainability 17, no. 9: 4244. https://doi.org/10.3390/su17094244
APA StyleHang, J., Tang, T., & Wang, J. (2025). Dynamic Estimation of Travel Time Reliability for Road Network Using Trajectory Data. Sustainability, 17(9), 4244. https://doi.org/10.3390/su17094244






