Enhanced Landslide Risk Assessment Through Non-Probabilistic Stability Analysis: A Hybrid Framework Integrating Space–Time Distribution and Vulnerability Models
Abstract
1. Introduction
2. Methods
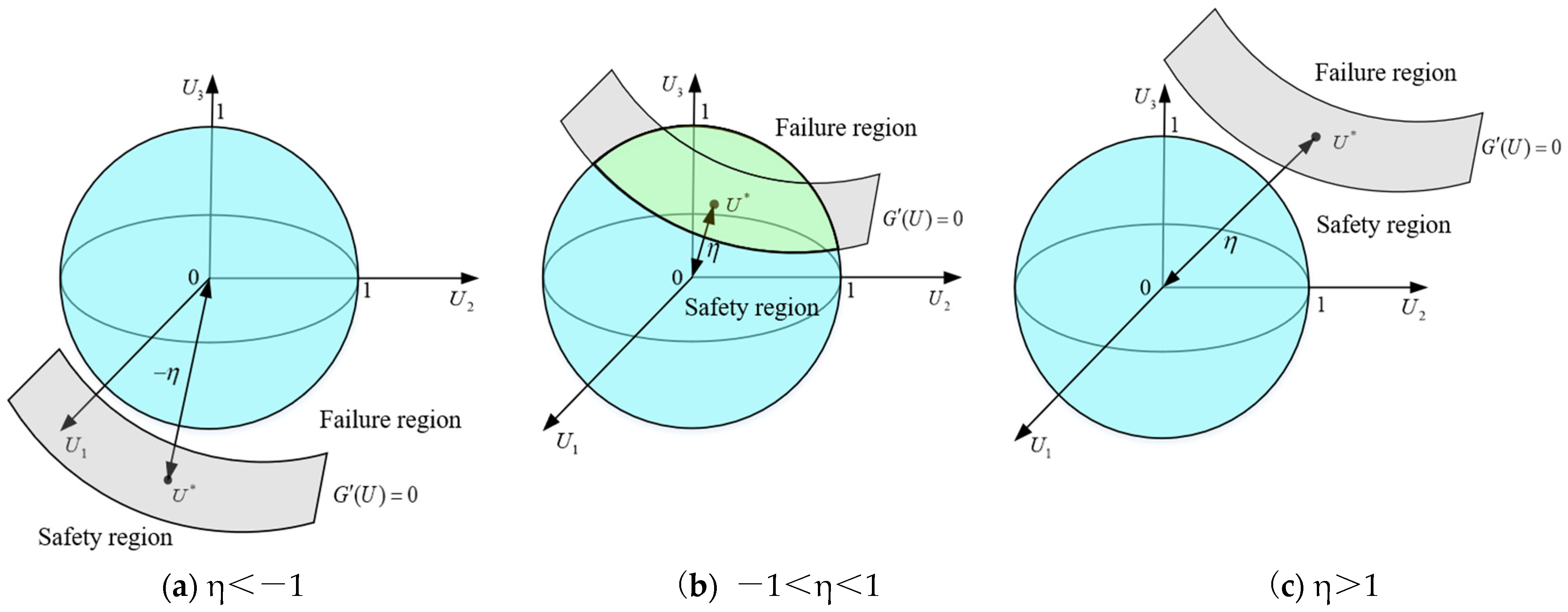
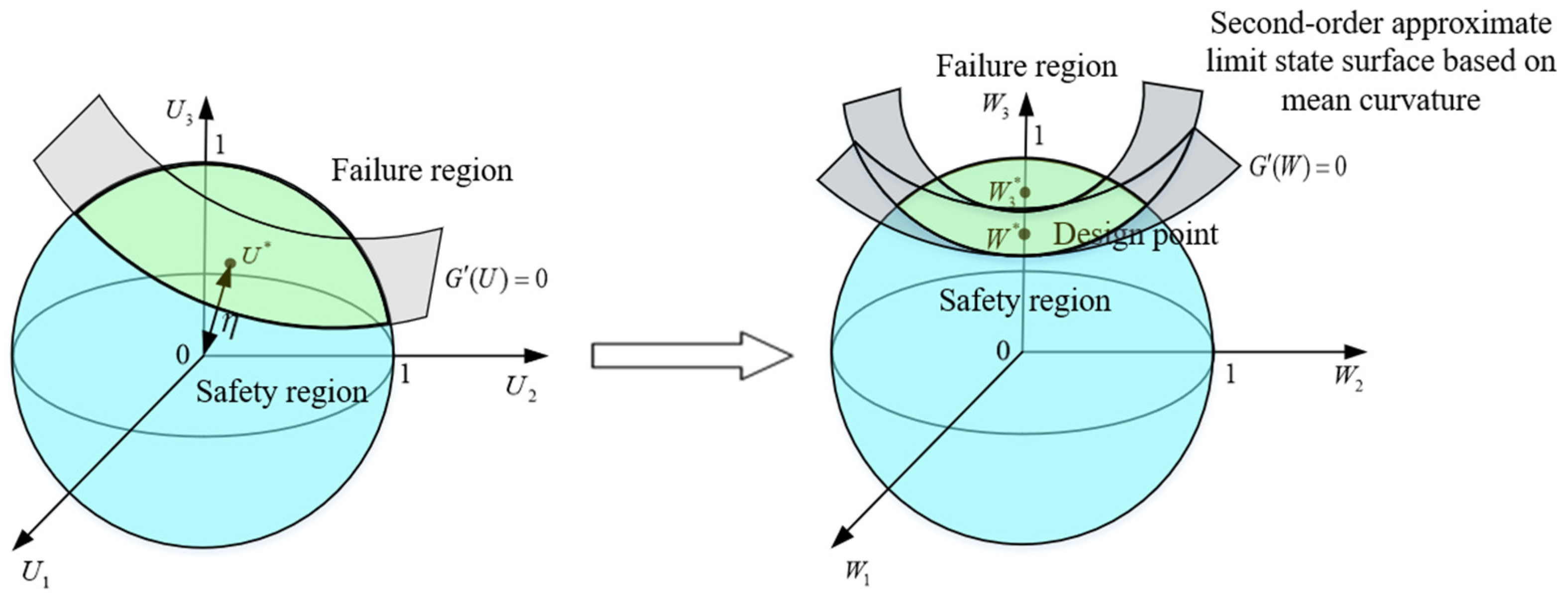
2.1. Possibility of Landslide Occurrence
2.2. Space–Time Distribution Probability of Disaster-Bearing Bodies
2.3. Vulnerability of Disaster-Bearing Bodies
2.4. Calculation of Landslide Risk
2.5. Risk Judgment of Landslide
3. Example Analysis
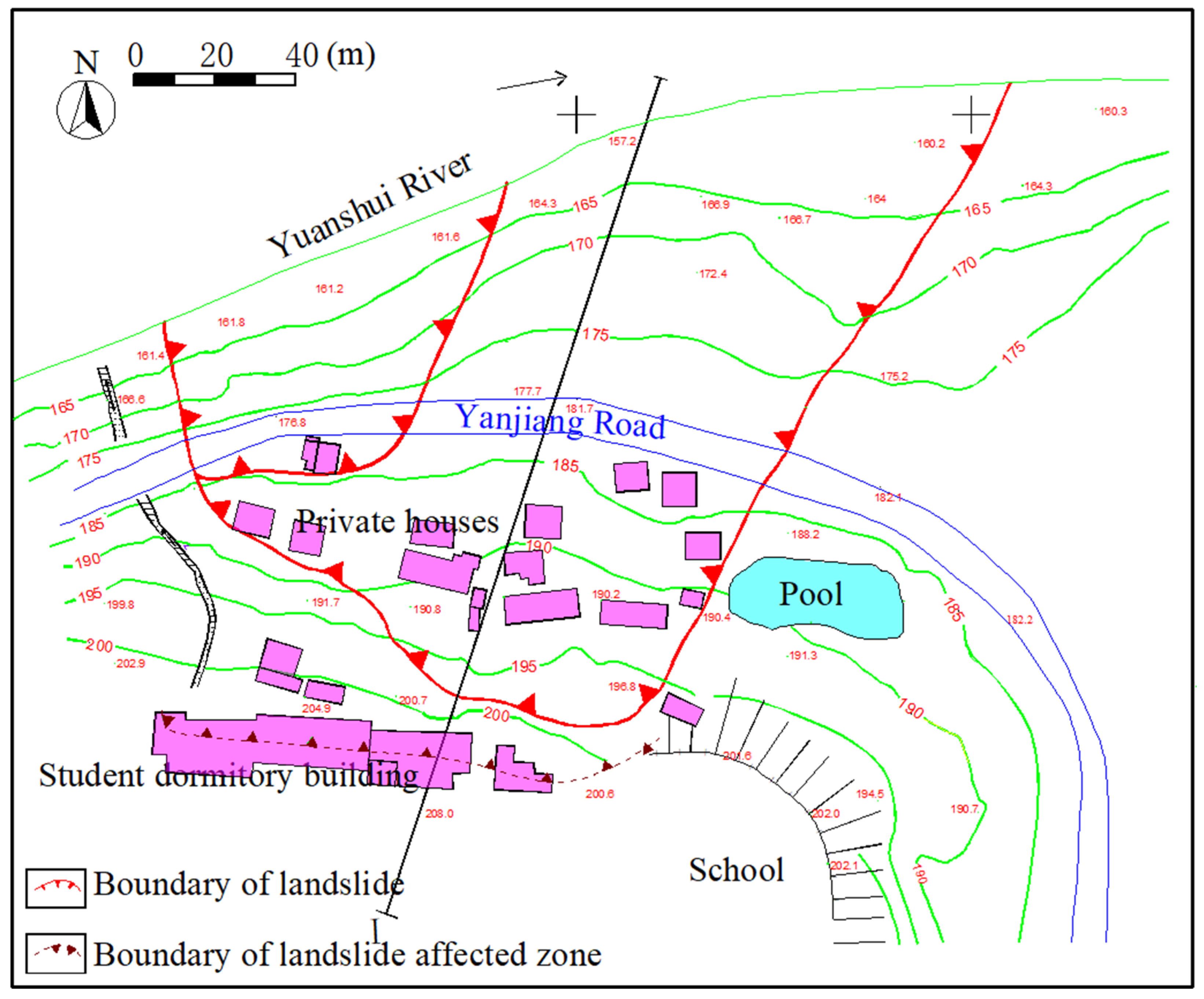
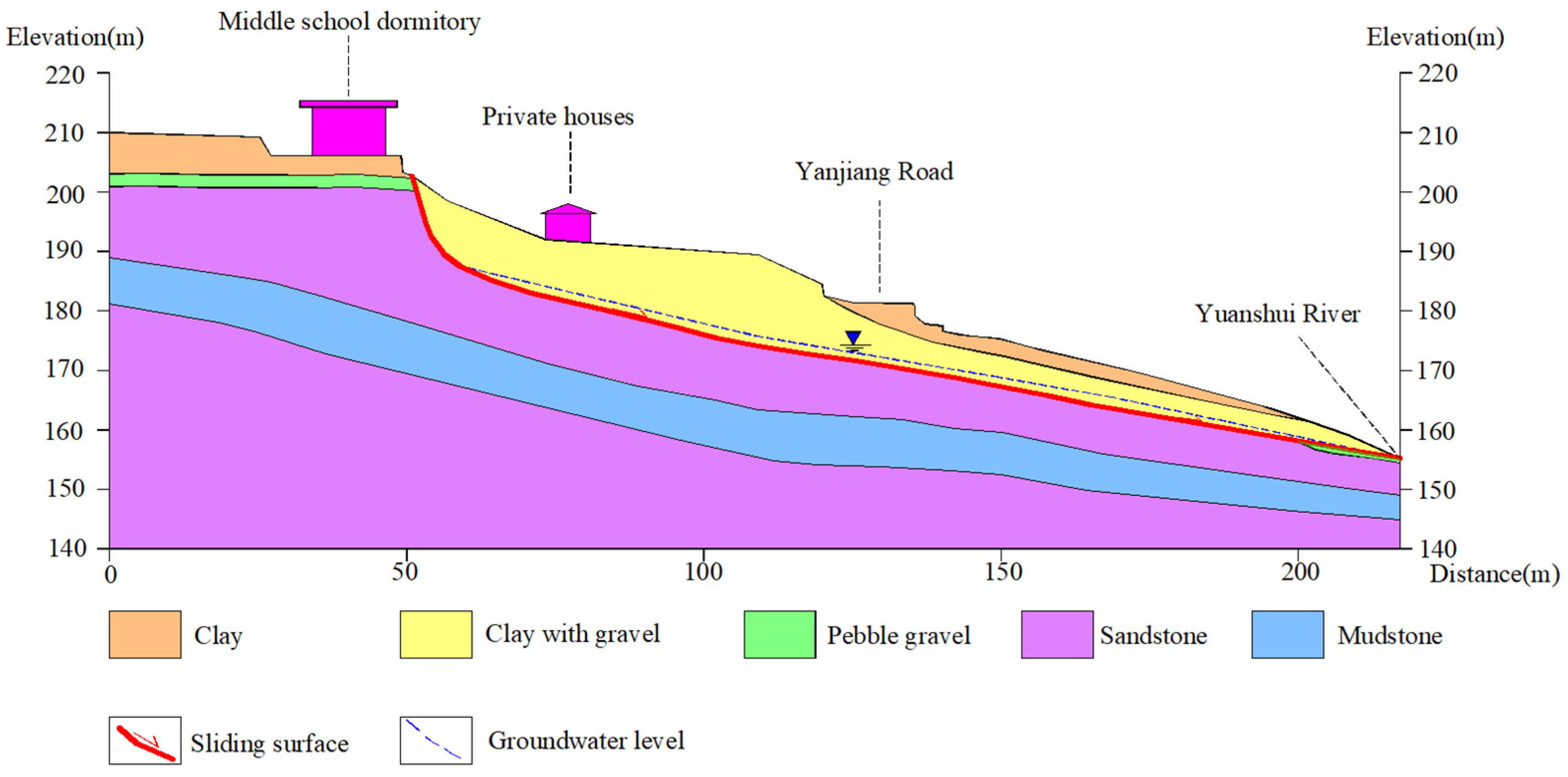
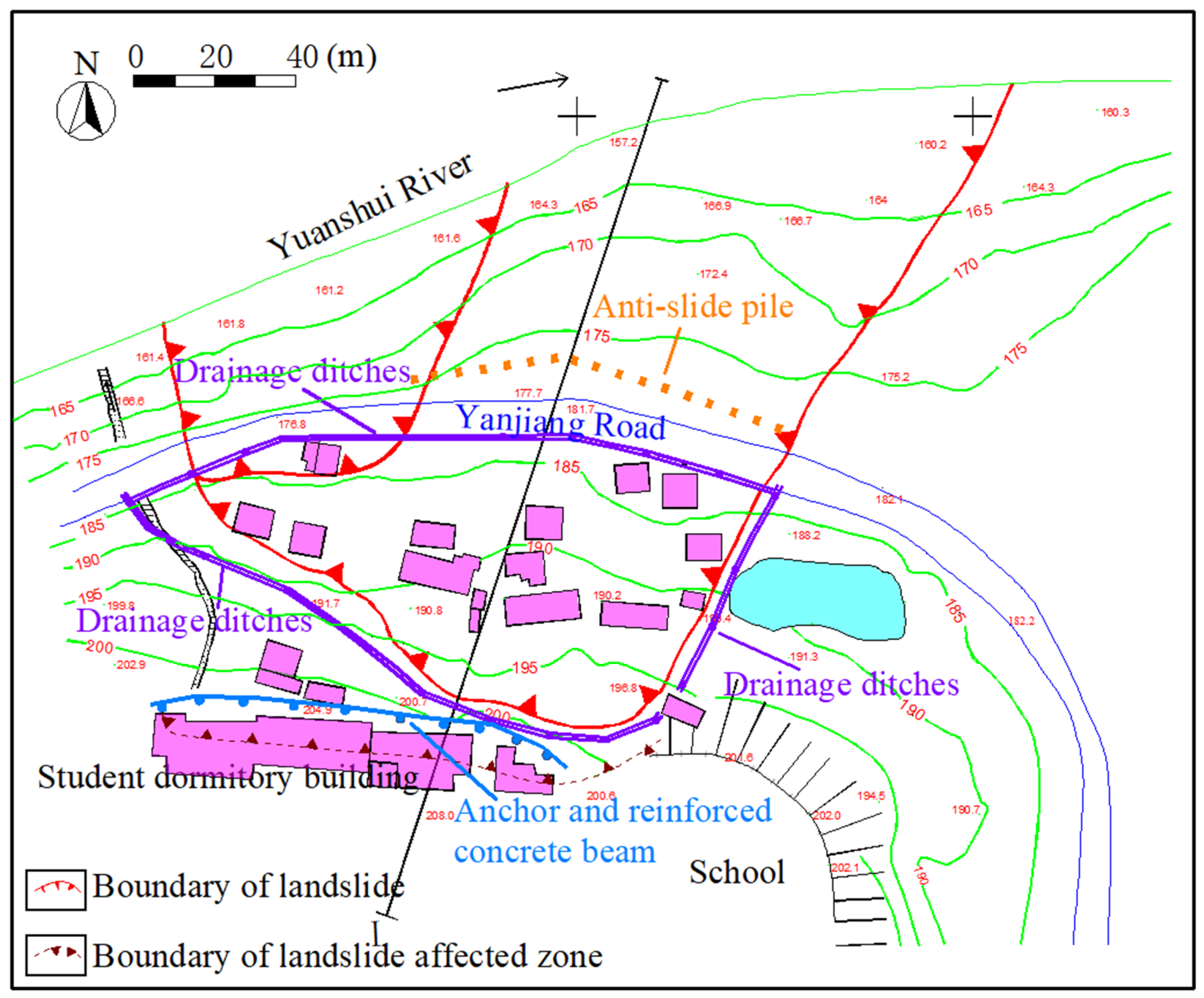
3.1. Study Area and Data
3.2. Risk Assessment
3.3. Landslide Treatment
4. Results and Discussion
5. Future Work and Limitations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hu, R.; Fan, L.; Wang, S.; Wang, L.; Wang, X. Theory and method for landslide risk assessment-current status and future development. J. Eng. Geol. 2013, 21, 76–84. [Google Scholar]
- Xu, J.; Zhang, M.; Fan, W. An overview of geological disaster risk assessment. J. Catastrophol. 2015, 30, 130–134. [Google Scholar]
- Ahmed, B. Landslide susceptibility mapping using multi-criteria evaluation techniques in Chittagong Metropolitan Area, Bangladesh. Landslides 2015, 12, 1077–1095. [Google Scholar] [CrossRef]
- Chang, M.; Cui, P.; Dou, X.; Su, F. Quantitative risk assessment of landslides over the China-Pakistan economic corridor. Int. J. Disaster Risk Reduct. 2021, 63, 102441. [Google Scholar] [CrossRef]
- Varnes, D.J. Landslide Hazard Zonation: A Review of Principles and Practice; Unesco: Paris, France, 1984. [Google Scholar]
- Fell, R. Landslide risk assessment and acceptable risk. Can. Geotech. J. 1994, 31, 261–272. [Google Scholar] [CrossRef]
- Van Westen, C.; Van Asch, T.W.; Soeters, R. Landslide hazard and risk zonation—Why is it still so difficult? Bull. Eng. Geol. Environ. 2006, 65, 167–184. [Google Scholar] [CrossRef]
- Zhou, G.; Pei, Y.; Wu, C. Regional landslide risk assessment of Muchuan county as s case based on contributing weight model and GIS. Met. Mine 2013, 11, 130–134. [Google Scholar]
- Saleem, J.; Ahmad, S.S.; Butt, A. Hazard risk assessment of landslide-prone sub-Himalayan region by employing geospatial modeling approach. Nat. Hazards 2020, 102, 1497–1514. [Google Scholar] [CrossRef]
- Liu, X.; Shao, S.; Shao, S. Landslide susceptibility zonation using the analytical hierarchy process (AHP) in the Great Xi’an Region, China. Sci. Rep. 2024, 14, 2941. [Google Scholar] [CrossRef]
- Han, S.; Liu, M.; Wu, J.; Zhang, S.; Sun, Q.; Zhang, T. Risk assessment of slope disasters induced by typhoon-rainfall in the southeast coastal area, China: A case study of the Shiyang north slope. J. Geomech. 2022, 28, 583–595. [Google Scholar]
- Huang, J.; Lyamin, A.V.; Griffiths, D.V.; Krabbenhoft, K.; Sloan, S.W. Quantitative risk assessment of landslide by limit analysis and random fields. Comput. Geotech. 2013, 53, 60–67. [Google Scholar] [CrossRef]
- Ali, A.; Huang, J.; Lyamin, A.V.; Sloan, S.W.; Griffiths, D.V.; Cassidy, M.J.; Li, J.H. Simplified quantitative risk assessment of rainfall-induced landslides modelled by infinite slopes. Eng. Geol. 2014, 179, 102–116. [Google Scholar] [CrossRef]
- Guettouche, M.S. Modeling and risk assessment of landslides using fuzzy logic. Application on the slopes of the Algerian Tell (Algeria). Arab. J. Geosci. 2013, 6, 3163–3173. [Google Scholar] [CrossRef]
- Pan, Y.; Zheng, Y.; Li, K.; Liao, J. Framework for the preliminary risk classification of slopes prone to large failure. Eng. Geol. 2021, 287, 106124. [Google Scholar] [CrossRef]
- Bentivenga, M.; Gizzi, F.T.; Palladino, G.; Piccarreta, M.; Potenza, M.R.; Perrone, A.; Bellanova, J.; Calamita, G.; Piscitelli, S. Multisource and multilevel investigations on a historical landslide: The 1907 Servigliano earth flow in Montemurro (Basilicata, Southern Italy). Land 2022, 11, 408. [Google Scholar] [CrossRef]
- Marr, P.; Donato, Y.A.J.; Carraro, E.; Kanta, R.; Glade, T. The role of historical data to investigate slow-moving landslides by long-term monitoring systems in Lower Austria. Land 2023, 12, 659. [Google Scholar] [CrossRef]
- Kanwal, S.; Atif, S.; Shafiq, M. GIS based landslide susceptibility mapping of northern areas of Pakistan, a case study of Shigar and Shyok Basins. Geomat. Nat. Hazards Risk 2017, 8, 348–366. [Google Scholar] [CrossRef]
- Jennifer, J.J.; Saravanan, S.; Abijith, D. Application of Frequency Ratio and Logistic Regression Model in the Assessment of Landslide Susceptibility Mapping for Nilgiris District, Tamilnadu, India. Indian Geotech. J. 2021, 51, 773–787. [Google Scholar] [CrossRef]
- Xue, Q.; Zhang, M.; Li, L. Loess landslide susceptibility evaluation based on slope unit and information value method in Baota District, Yan’an. Geol. Bull. China 2015, 34, 2108–2115. [Google Scholar]
- Cheng, J.; Wang, X.; Du, W.; Shi, H. Application of Janbu method in slope stability analysis of Baiyunebo west iron mine. Coal Technol. 2015, 34, 130–132. [Google Scholar]
- Chen, Z. Soil Slope Stability Analysis—Theory Methods and Programs; China Water & Power Press: Beijing, China, 2003. [Google Scholar]
- Zheng, Y.; Zhao, S. Application of strength reduction FEM in soil and rock slope. Chin. J. Rock Mech. Eng. 2004, 19, 3381–3388. [Google Scholar]
- Zhao, Z.; Zhu, Y.; Hou, H.; Li, L. Stability analysis of loess fill slope supported by frame prestressed anchors considering tensile strength cut-off. Sci. Rep. 2024, 14, 3007. [Google Scholar] [CrossRef]
- Wang, Y. Uncertain parameter sensitivity in Monte Carlo simulation by sample reassembling. Comput. Geotech. 2012, 46, 39–47. [Google Scholar] [CrossRef]
- Guo, Z.; Chen, L.; Yin, K.; Shrestha, D.P.; Zhang, L. Quantitative risk assessment of slow-moving landslides from the viewpoint of decision making: A case study of the Three Gorges Reservoir in China. Eng. Geol. 2020, 273, 105667. [Google Scholar] [CrossRef]
- Huang, C.; Yin, K.; Liang, X.; Gui, L.; Zhao, B.; Liu, Y. Study of direct and indirect risk assessment of landslide impacts on ultrahigh-voltage electricity transmission lines. Sci. Rep. 2024, 14, 25719. [Google Scholar] [CrossRef] [PubMed]
- Dong, L.; Sun, D.; Li, X.; Zhou, Z. Interval non-probabilistic reliability of a surrounding jointed rockmass in underground engineering: A case study. IEEE Access 2017, 5, 18804–18817. [Google Scholar] [CrossRef]
- Zheng, Z.; Li, Y.; Wen, L.; Zhang, Y.; Wang, T. Reliability analysis of an embankment dam slope based on an ellipsoid model and PSO-ELM. Structures 2023, 55, 2419–2432. [Google Scholar] [CrossRef]
- Bi, R.; Han, X.; Jiang, C.; Bai, Y.; Liu, J. Uncertain buckling and reliability analysis of the piezoelectric functionally graded cylindrical shells based on the nonprobabilistic convex model. Int. J. Comput. Methods 2013, 11, 1350080. [Google Scholar] [CrossRef]
- Gao, L.; Liang, B.; Wu, Z. Nonprobabilistic reliability solution method of slope convex set model. J. High. Transp. Res. Dev. 2022, 16, 51–59. [Google Scholar] [CrossRef]
- Liao, X.; Huang, R.; Yang, L.; Li, Y.; Wang, Y.; Wang, B.; Li, Y. Risk analysis and evaluation of a landslide in Shiyan city. Resour. Environ. Eng. 2020, 34, 388–395. [Google Scholar]
- Wei, Q. Risk Assessment of Rain-Induced Unstable Slope in Danjia. Master’s Thesis, Southwest University of Science and Technology, Mianyang, China, 2023. [Google Scholar]
- Sui, H.; Su, T.; Hu, R.; Wang, D.; Zheng, Z. Study on the risk assessment method of rainfall landslide. Water 2022, 14, 3678. [Google Scholar] [CrossRef]
- Corominas, J.; Van Westen, C.; Frattini, P.; Cascini, L.; Malet, J.P.; Fotopoulou, S.; Catani, F.; Van Den Eeckhaut, M.; Mavrouli, O.; Agliardi, F.; et al. Recommendations for the quantitative analysis of landslide risk. Bull. Eng. Geol. Environ. 2014, 73, 209–263. [Google Scholar] [CrossRef]
- Wong, F.S. Slope reliability and response surface method. J. Geotech. Eng. 1985, 111, 32–53. [Google Scholar] [CrossRef]
- Zhou, D.; Mei, Y.; Yang, T. Research on stability of high slope of sandy loess road cutting based on response surface method. J. Saf. Sci. Technol. 2024, 20, 139–147. [Google Scholar]
- Jiang, C.; Han, X.; Lu, G.; Liu, J.; Zhang, Z.; Bai, Y. Correlation analysis of non-probabilistic convex model and corresponding structural reliability technique. Comput. Methods Appl. Mech. Eng. 2011, 200, 2528–2546. [Google Scholar] [CrossRef]
- Kang, Z.; Luo, Y.; Li, A. On non-probabilistic reliability-based design optimization of structures with uncertain-but-bounded parameters. Struct. Saf. 2011, 33, 196–205. [Google Scholar] [CrossRef]
- Jiang, C.; Bi, R.; Lu, G.; Han, X. Structural reliability analysis using non-probabilistic convex model. Comput. Methods Appl. Mech. Eng. 2013, 254, 83–98. [Google Scholar] [CrossRef]
- Shu, S.; Qian, J.; Gong, W.; Pi, K.; Yang, Z. Non-probabilistic reliability analysis of slopes based on fuzzy set theory. Appl. Sci. 2023, 13, 7024. [Google Scholar] [CrossRef]
- Liu, G.; Xi, J.; Dai, E.; Wu, W. Loss risk assessment of the hazard-affectted body of landslides in China. J. Nat. Disasters 2014, 23, 39–46. [Google Scholar]
- Han, Y. Risk Assessment of Hua-Yen Temple Landslide. Master’s Thesis, Chang’an University, Xi’an, China, 2017. [Google Scholar]
- Sui, H.; Hu, R.; Gao, W.; Gao, W.; Luo, G. Risk assessment of individual landslide based on the risk acceptable model: A case study of the Shiyantan landslide in Mayang County, China. HERA 2020, 26, 2500–2519. [Google Scholar] [CrossRef]
- Uzielli, M.; Nadim, F.; Lacasse, S.; Kaynia, A.M. A conceptual framework for quantitative estimation of physical vulnerability to landslides. Eng. Geol. 2008, 102, 251–256. [Google Scholar] [CrossRef]
- Li, Z.; Nadim, F.; Huang, H.; Uzielli, M.; Lacasse, S. Quantitative vulnerability estimation for scenario-based landslide hazards. Landslides 2010, 7, 125–134. [Google Scholar] [CrossRef]
- Nguyen, T.T.N.; Liu, C.C. A new approach using AHP to generate landslide susceptibility maps in the Chen-Yu-Lan Watershed, Taiwan. Sensors 2019, 19, 505. [Google Scholar] [CrossRef]
- Fahad, S.; Hossain, M.S.; Huong, N.T.L.; Nassani, A.A.; Haffar, M.; Naeem, M.R. An assessment of rural household vulnerability and resilience in natural hazards: Evidence from flood prone areas. Environ. Dev. Sustain. 2023, 25, 5561–5577. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, D.; Lu, X.; Song, Q. Vulnerability assessment model for hazard bearing body and landslide risk index. Rock Soil Mech. 2011, 32, 2487–2492+2499. [Google Scholar]
- Yin, Z. Prediction Method of Earthquake Disaster and Loss; Seismological Press: Beijing, China, 1995. [Google Scholar]
- Du, J. Risk Assessment of Individual Landslide. Ph.D. Thesis, China University of Geosciences, Wuhan, China, 2012. [Google Scholar]
- Fell, R.; Ho, K.K.S.; Lacasse, S.; Leroi, E. A frame work for landslide risk assessment and management. In Landslide Risk Management; CRC Press: London, UK, 2005. [Google Scholar]
- Song, Y.; Fan, W.; Li, J.; Du, X. Risk assessment of property loss caused by unstable slopes under different rainfall conditions—A case study of Xinglong town of Zhenba county. J. Eng. Geol. 2020, 28, 401–411. [Google Scholar]
- Wu, Y.; Yin, K.; Li, S. Stability analysis and treatment engineering design of Xiatudiling landslide. In Proceedings of the National Geotechnical and Engineering Academic Conference, Beijing, China, 22 December 2003. [Google Scholar]
- Dai, Y.; Yin, K.; Wang, Y. Discussion on method of landslide velocity calculation and surge prediction. Rock Soil Mech. 2008, 29, 407–411. [Google Scholar]
- Wen, H.; Zhang, Y.; Fu, H.; Xie, P.; Hu, J. Research status of instability mechanism of rainfall-induced landslide and stability evaluation methods. China J. Highw. Transp. 2018, 31, 15–29+96. [Google Scholar]
- Geological Disaster Prevention Headquarters of the Three Gorges Reservoir Area. Geological Disaster Prevention Engineering of the Three Gorges Reservoir Area Phase III. Technical Requirements for Geological Investigation; Geological Disaster Prevention Headquarters of the Three Gorges Reservoir Area: Yichang, China, 2004. [Google Scholar]
- Morgenstern, N.R.; Price, V.E. The analysis of the stability of general slip surface. Geotechnique. 1965, 15, 79–93. [Google Scholar] [CrossRef]
- Gong, W.; Zhang, S.; Juang, C.H.; Tang, H.; Pudasaini, S.P. Displacement prediction of landslides at slope-scale: Review of physics-based and data-driven approaches. Earth-Sci. Rev. 2024, 258, 104948. [Google Scholar] [CrossRef]
- Kuan, X. Geomorphologic prediction of landslide movement distance. Translated by Wang NQ. Railw. Geol. Subgrade 1989, 3, 42–47. [Google Scholar]
- Liu, C. Landslide Risk Assessment at Wanzhou Urban area in the Three Gorges Reservoir. Ph.D. Thesis, China University of Geosciences, Wuhan, China, 2014. [Google Scholar]
- Wang, J. Landslide Risk Assessment in Wanzhou County, Three Gorges Reservoir. Ph.D. Thesis, China University of Geosciences, Wuhan, China, 2015. [Google Scholar]
- Jiang, J. Risk Assessment of Fengxi Villa Slope in Feng County. Master’s Thesis, Chang’an University, Xi’an, China, 2018. [Google Scholar]
- Pan, J. Analysis of Anti-Sliding Stability of Buildings and Landslides; China Water & Power Press: Beijing, China, 1980. [Google Scholar]
- Peng, L. Landslide Risk Assessment in the Three Gorges Reservoir. Ph.D. Thesis, China University of Geosciences, Wuhan, China, 2014. [Google Scholar]


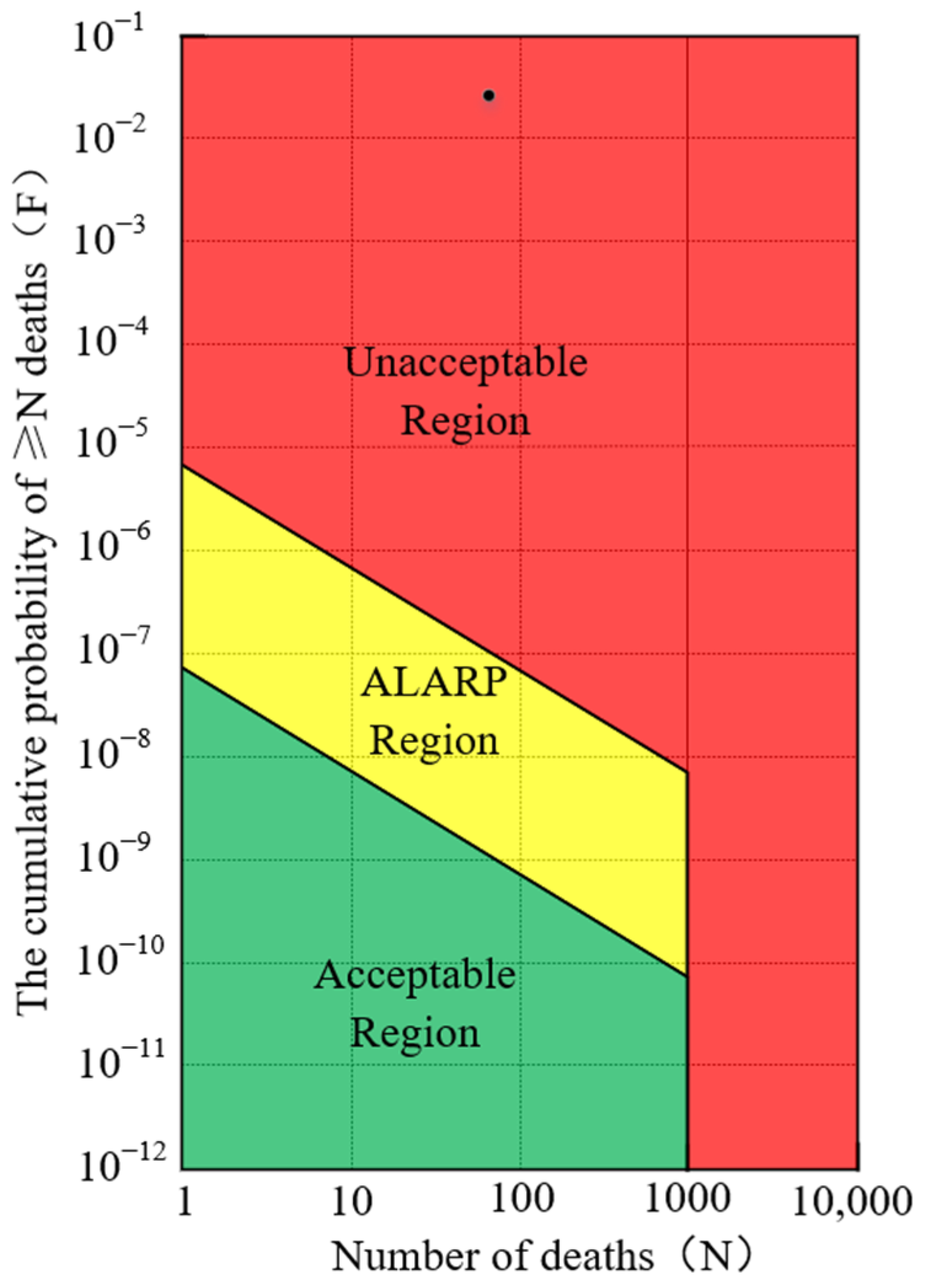
| Landslide impact depth index (m) | <0.1 | 0.1–0.3 | 0.3–0.6 | 0.6–0.8 | ≥0.8 |
| 0.1 | 0.3 | 0.7 | 0.9 | 1.0 |
| Landslide impact width index (m) | <50 | 50–200 | 200–400 | 400–700 | ≥700 |
| 0.1 | 0.3 | 0.5 | 0.8 | 1.0 |
| Health status | Good | Less functional | Deformity |
| 0.1 | 0.1–0.8 | 0.8–1.0 |
| Local disaster warning level | Perfection | Moderation | Plain | No early warning system |
| 0–0.2 | 0.2–0.6 | 0.6–1.0 | 1.0 |
| Natural Density (kN/m3) | Saturated Density (kN/m3) | Cohesion (kPa) | Internal Friction Angle (°) | |
|---|---|---|---|---|
| Landslide body | 21.5 | 23.5 | 30.0 | 24.0 |
| Sliding zone | 19.2 | 19.7 | 14.0 | 15.8 |
| Underlying sandstone | 300.0 | 40.0 | ||
| Underlying mudstone | 200.0 | 22.0 |
| Working Condition | Load Combination | Stability Factor |
|---|---|---|
| 1 | Weight + 145 m water level | 1.404 |
| 2 | Weight + 162 m water level | 1.409 |
| 3 | Weight + 162 m water level + Rainfall with a return period of 1 year | 1.013 |
| 4 | Weight + 162 m water level + Rainfall with a return period of 10 years | 0.984 |
| 5 | Weight + 175 m water level | 1.418 |
| 6 | Weight + 175 m water level + Rainfall with a return period of 1 year | 1.126 |
| 7 | Weight + 175 m water level + Rainfall with a return period of 10 years | 1.093 |
| Personnel Category | Number | Time Distribution Probability of the Personnel Indoors | Time Distribution Probability of the Personnel Outdoors |
|---|---|---|---|
| Students | 5 | 0.52 | 0.21 |
| Workers | 25 | 0.50 | 0.14 |
| Other residents | 35 | 0.64 | 0.36 |
| Personnel Category | Risk Value of the Personnel Indoors (Persons/year) | Risk Value of the Personnel Outdoors (Persons/year) | Total Risk Value (Persons/year) |
|---|---|---|---|
| Students | 0.0636 | 0.0571 | 1.8499 |
| Workers | 0.3058 | 0.1903 | |
| Other residents | 0.5480 | 0.6851 |
| Disaster-Bearing Bodies | Value (CNY) | Risk Value (CNY/year) | Total Risk Value (CNY/year) |
|---|---|---|---|
| Yanjiang Road | 400,000 | 21,748 | 184,858 |
| Houses | 1,200,000 | 65,244 | |
| Land and fruit trees | 2,000,000 | 97,866 |
| This Study | Similar Article | |
|---|---|---|
| Method | The non-probability reliability method is used to calculate the stability of the landslide, and the classification of the disaster-bearing bodies is divided in detail. The vulnerability analysis is carried out by different methods. | The probabilistic reliability method is used to calculate the stability of the landslide, and the disaster-bearing bodies are analyzed simply. Only two methods are used to analyze the vulnerability. |
| Calculation process | Simple | Complex |
| Results accuracy | Accurate | Generally accurate |
| Applicability | Highly applicable | Generally applicable |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shu, S.; Pi, K.; Gong, W.; Zhou, C.; Qian, J.; Yang, Z. Enhanced Landslide Risk Assessment Through Non-Probabilistic Stability Analysis: A Hybrid Framework Integrating Space–Time Distribution and Vulnerability Models. Sustainability 2025, 17, 4146. https://doi.org/10.3390/su17094146
Shu S, Pi K, Gong W, Zhou C, Qian J, Yang Z. Enhanced Landslide Risk Assessment Through Non-Probabilistic Stability Analysis: A Hybrid Framework Integrating Space–Time Distribution and Vulnerability Models. Sustainability. 2025; 17(9):4146. https://doi.org/10.3390/su17094146
Chicago/Turabian StyleShu, Suxun, Kang Pi, Wenhui Gong, Chunmei Zhou, Jiajun Qian, and Zhiquan Yang. 2025. "Enhanced Landslide Risk Assessment Through Non-Probabilistic Stability Analysis: A Hybrid Framework Integrating Space–Time Distribution and Vulnerability Models" Sustainability 17, no. 9: 4146. https://doi.org/10.3390/su17094146
APA StyleShu, S., Pi, K., Gong, W., Zhou, C., Qian, J., & Yang, Z. (2025). Enhanced Landslide Risk Assessment Through Non-Probabilistic Stability Analysis: A Hybrid Framework Integrating Space–Time Distribution and Vulnerability Models. Sustainability, 17(9), 4146. https://doi.org/10.3390/su17094146





