Impact of Window Size Modification on Energy Consumption in UK Residential Buildings: A Feasibility and Simulation Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Explanation and Introduction of Research Methods
2.1.1. Windows Energy Consumption
Total Heat Gain Through Windows
2.1.2. Window Modification of This Project
2.1.3. Change Window Size
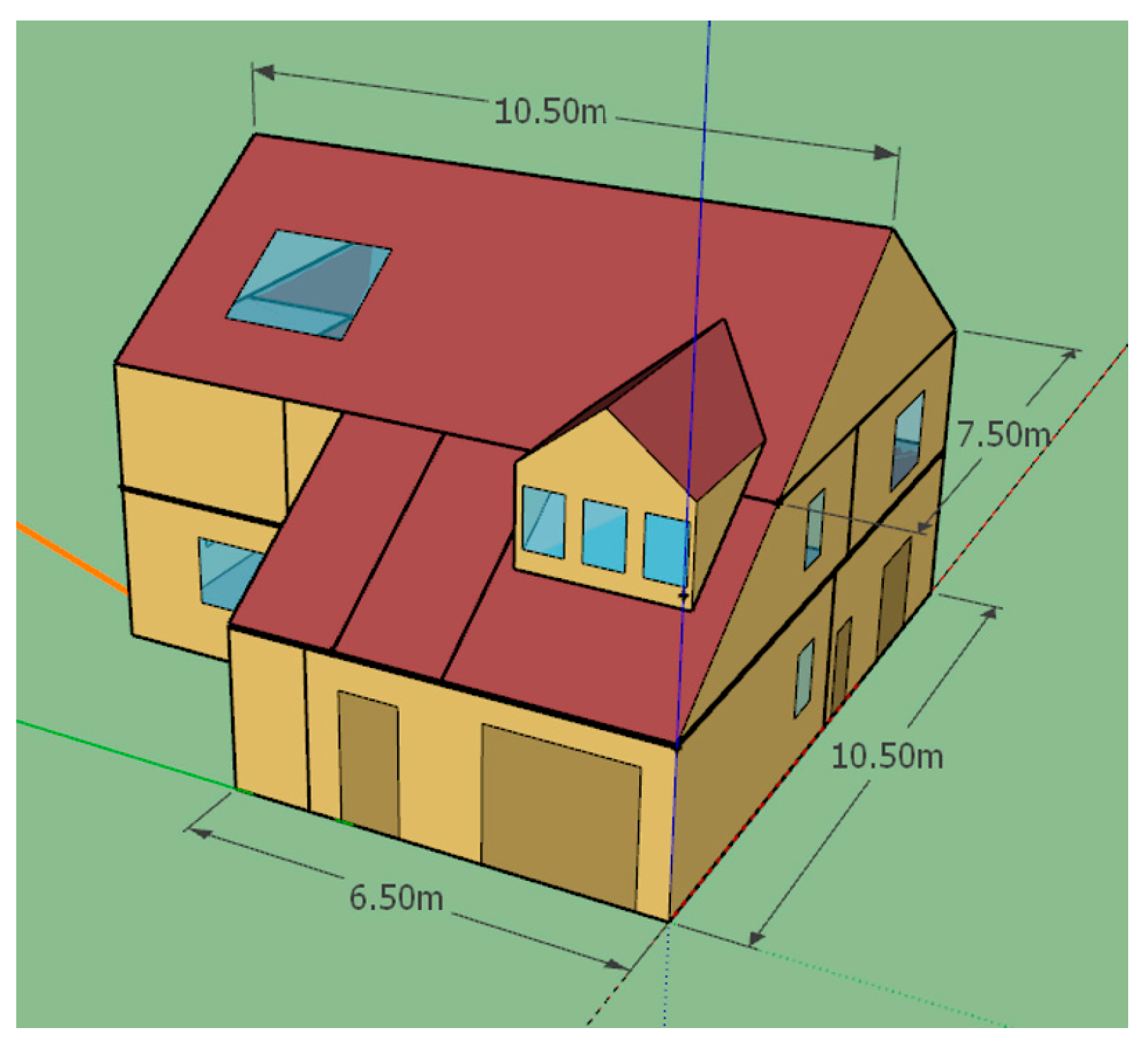
2.2. Description of the Base Case Building
- Weather File
- Occupancy and Load Scheduling
- Tested Scenarios
3. Results
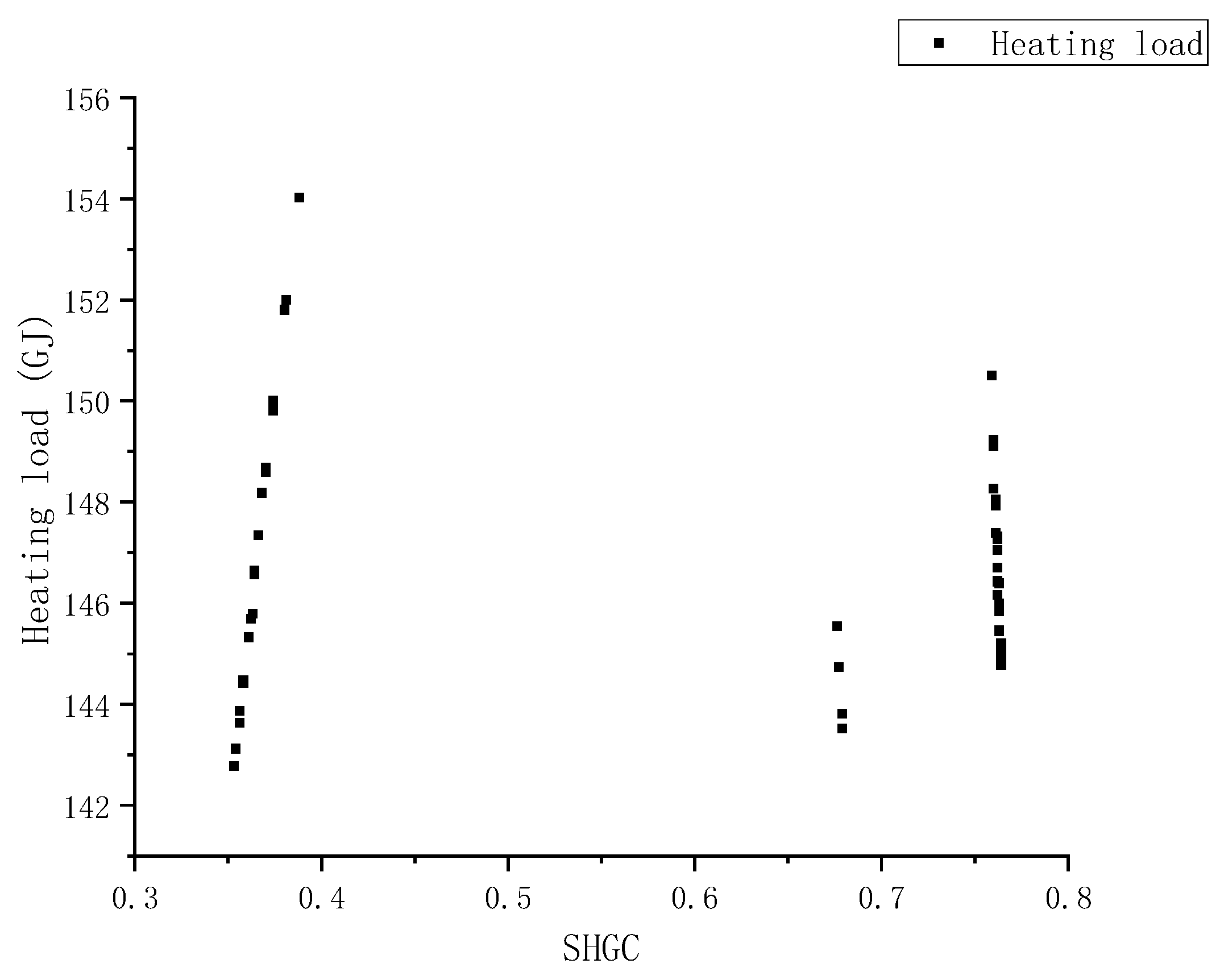
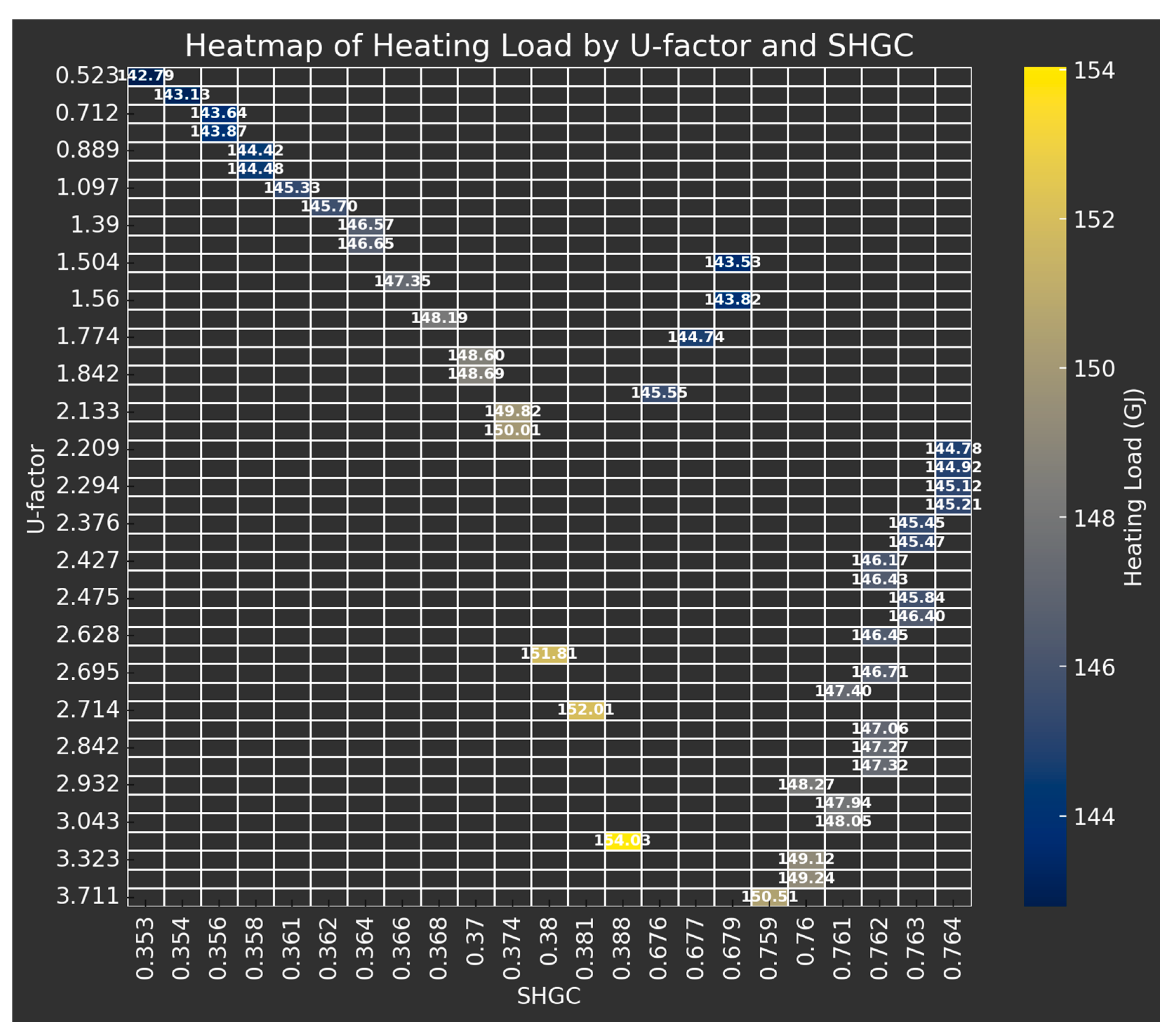
3.1. Windows Energy Consumption Analysis
3.2. Summary of Window Size Modification
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| WWR | window-to-wall ratio |
| SHGC | Solar Heat Gain Coefficient |
| VT | visible transmittance |
References
- Collins, L.C.; Natarajan, S.; Levermore, G. Climate change and future energy consumption in UK housing stock. Build. Serv. Eng. 2010, 31, 75–90. [Google Scholar] [CrossRef]
- Kolokotroni, M.; Ren, X.; Davies, M.; Mavrogianni, A. London’s urban heat island: Impact on current and future energy consumption in office buildings. Energy Build. 2012, 47, 302–311. [Google Scholar] [CrossRef]
- Office, M. Climate Summaries. Available online: https://www.metoffice.gov.uk/research/climate/maps-and-data/summaries/index (accessed on 8 October 2024).
- Tummala, S.; Kumar, D.R.V.; Narsimha, K.; Kosaraju, S.; Bobba, P.; Singh, S. Spatial Day Light Autonomy and Energy Analysis of a Residential Building for Different Climatic Conditions and Window-to-Wall Ratios. E3S Web Conf. 2020, 184, 01117. [Google Scholar] [CrossRef]
- Liu, J.; Liu, X.; Fan, H.; Zhang, Z.; Mao, P. Study on the Optimal Window and Wall Ratio of Village and Town Housing Based on Energy Consumption. Earth Environ. Sci. 2019, 219, 012021. [Google Scholar] [CrossRef]
- Lahmar, I.; Cannavale, A.; Martellotta, F.; Zemmouri, N. The Impact of Building Orientation and Window-to-Wall Ratio on the Performance of Electrochromic Glazing in Hot Arid Climates: A Parametric Assessment. Buildings 2022, 12, 724. [Google Scholar] [CrossRef]
- Albatayneh, A.; Atieh, H.; Jaradat, M.; Al-Omary, M.; Zaquot, M.; Juaidi, A.; Abdallah, R.; Manzano-Agugliaro, F. The Impact of Modern Artificial Lighting on the Optimum Window-to-Wall Ratio of Residential Buildings in Jordan. Appl. Sci. 2021, 11, 5888. [Google Scholar] [CrossRef]
- Shaeri, J.; Habibi, A.; Yaghoubi, M.; Chokhachian, A. The Optimum Window-to-Wall Ratio in Office Buildings for Hot–Humid, Hot–Dry, and Cold Climates in Iran. Environments 2019, 6, 45. [Google Scholar] [CrossRef]
- Dewi, O.C.; Rahmasari, K.; Hanjani, T.A.; Ismoyo, A.D.; Dugar, A.M. Window-to-Wall Ratio as a Mode of Daylight Optimization for an Educational Building with Opaque Double-Skin Façade. J. Sustain. Archit. Civ. Eng. 2022, 30, 142–152. [Google Scholar] [CrossRef]
- Ma, P.; Wang, L.-S.; Guo, N. Maximum window-to-wall ratio of a thermally autonomous building as a function of envelope U -value and ambient temperature amplitude. Appl. Energy 2015, 146, 84–91. [Google Scholar] [CrossRef]
- Fathi, S.; Kavoosi, A. Optimal Window to Wall Ratio Ranges of Photovoltachromic Windows in High-Rise Office Buildings of Iran. J. Daylighting 2021, 8, 134–148. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Z.; Ma, X.; Lu, W.; Li, D.; Kojima, S. Optimization Analysis of the Residential Window-to-Wall Ratio Based on Numerical Calculation of Energy Consumption in the Hot-Summer and Cold-Winter Zone of China. Sustainability 2021, 13, 6138. [Google Scholar] [CrossRef]
- Xue, P.; Li, Q.; Xie, J.; Zhao, M.; Liu, J. Optimization of window-to-wall ratio with sunshades in China low latitude region considering daylighting and energy saving requirements. Appl. Energy 2019, 233–234, 62–70. [Google Scholar] [CrossRef]
- Li, A.; Cheng, L.; Tao, Q.; Tang, Y.; Olofsson, T.; Kosonen, R. Optimized design and energy consumption simulation of window-wall ratio in Yanqui Library, Jimei University. E3S Web Conf. 2022, 356, 01056. [Google Scholar] [CrossRef]
- Chiesa, G.; Acquaviva, A.; Grosso, M.; Bottaccioli, L.; Floridia, M.; Pristeri, E.; Sanna, E. Parametric Optimization of Window-to-Wall Ratio for Passive Buildings Adopting A Scripting Methodology to Dynamic-Energy Simulation. Sustainability 2019, 11, 3078. [Google Scholar] [CrossRef]
- Mahdavi Adeli, M.; Sarhaddi, F.; Farahat, S. Parametric Study of the Impact of Windows to Wall Ratio on Reduction of Energy Consumption and Environmental Impact of a Zero-Energy Building in Different Orientations. J. Comput. Appl. Mech. 2019, 50, 295–302. [Google Scholar] [CrossRef]
- Li, J.; Zheng, B.; Chen, X.; Zhou, Y.; Rao, J.; Bedra, K.B. Research on Annual Thermal Environment of Non-Hvac Building Regulated by Window-to-Wall Ratio in a Chinese City (Chenzhou). Sustainability 2020, 12, 6637. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, M.; Shu, C.; Mmereki, D.; Uzzal Hossain, M.; Zhan, X. Impact Analysis of Window-Wall Ratio on Heating and Cooling Energy Consumption of Residential Buildings in Hot Summer and Cold Winter Zone in China. J. Eng. 2015, 2015, 548254. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, W.L.; Fang, T.Y. Impact of Building Orientation and Window-Wall Ratio on the Office Building Energy Consumption. Appl. Mech. Mater. 2013, 409–410, 606–611. [Google Scholar] [CrossRef]
- Lago, T.G.S.; Ismail, K.A.R.; Lino, F.A.M. Ventilated double glass window with reflective film: Modeling and assessment of performance. Sol. Energy 2019, 185, 72–88. [Google Scholar] [CrossRef]
- Fang, Y.; Eames, P. The effect of glass coating emittance and frame rebate on heat transfer through vacuum and electrochromic vacuum glazed windows. Sol. Energy Mater. Sol. Cells 2006, 90, 2683–2695. [Google Scholar] [CrossRef]
- Fang, Y.; Eames, P.C.; Norton, B.; Hyde, T.J.; Zhao, J.; Wang, J.; Huang, Y. Low emittance coatings and the thermal performance of vacuum glazing. Sol. Energy 2007, 81, 8–12. [Google Scholar] [CrossRef]
- Ismail, K.A.R.; Salinas, C.T.; Henriquez, J.R. A comparative study of naturally ventilated and gas filled windows for hot climates. Energy Convers. Manag. 2009, 50, 1691–1703. [Google Scholar] [CrossRef]
- Onatayo, D.; Aggarwal, R.; Srinivasan, R.S.; Shah, B. A data-driven approach to thermal transmittance (U-factor) calculation of double-glazed windows with or without inert gases between the panes. Energy Build. 2024, 305, 113907. [Google Scholar] [CrossRef]
- Gasparella, A.; Pernigotto, G.; Cappelletti, F.; Romagnoni, P.; Baggio, P. Analysis and modelling of window and glazing systems energy performance for a well insulated residential building. Energy Build. 2011, 43, 1030–1037. [Google Scholar] [CrossRef]
- Urbikain, M.K.; Sala, J.M. Analysis of different models to estimate energy savings related to windows in residential buildings. Energy Build. 2009, 41, 687–695. [Google Scholar] [CrossRef]
- Tsikaloudaki, K.; Theodosiou, T.; Laskos, K.; Bikas, D. Assessing cooling energy performance of windows for residential buildings in the Mediterranean zone. Energy Convers. Manag. 2012, 64, 335–343. [Google Scholar] [CrossRef]
- Li, H.S.; Gao, Y.; Zhao, G.J.; Jing, Y.Z. Impact of Window-Wall Ratio on Air Conditioning Energy Consumption under Different Residential Using Modes in Guangzhou. Appl. Mech. Mater. 2013, 316–317, 1123–1127. [Google Scholar] [CrossRef]
- Ma, R.; Ma, R.; Long, E. Analysis of the rule of window-to-wall ratio on energy demand of residential buildings in different locations in China. Heliyon 2023, 9, e12803. [Google Scholar] [CrossRef]
- Troup, L.; Phillips, R.; Eckelman, M.J.; Fannon, D. Effect of window-to-wall ratio on measured energy consumption in US office buildings. Energy Build. 2019, 203, 109434. [Google Scholar] [CrossRef]
- Ozel, M.; Ozel, C. Effect of window-to-wall-area ratio on thermal performance of building wall materials in Elazig, Turkey. PLoS ONE 2020, 15, e0237797. [Google Scholar] [CrossRef]
- Veillette, D.; Rouleau, J.; Gosselin, L. Impact of Window-to-Wall Ratio on Heating Demand and Thermal Comfort When Considering a Variety of Occupant Behavior Profiles. Front. Sustain. Cities 2021, 3, 700794. [Google Scholar] [CrossRef]
- Goia, F. Search for the optimal window-to-wall ratio in office buildings in different European climates and the implications on total energy saving potential. Sol. Energy 2016, 132, 467–492. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Hu, S.; Du, T. Study on Determination of Best Window-Wall Ratio of Office Building in Cold Area. Appl. Mech. Mater. 2012, 260–261, 209–216. [Google Scholar] [CrossRef]
- Budhiyanto, A. The Effect of the Window-to-Wall Ratio on Cooling Energy Usage and Comfort Temperature. DIMENSI J. Archit. Built Environ. 2017, 44, 189–194. [Google Scholar] [CrossRef]
- Caggiano, A.; Junlin, Z.; Longwei, Z. Multi objective optimization of window to wall ratio of University Gymnasium in severe cold area by coupling natural lighting and energy consumption. E3S Web Conf. 2021, 293, 02044. [Google Scholar] [CrossRef]
- Alibaba, H. Determination of Optimum Window to External Wall Ratio for Offices in a Hot and Humid Climate. Sustainability 2016, 8, 187. [Google Scholar] [CrossRef]
- Mangkuto, R.A.; Rohmah, M.; Asri, A.D. Design optimisation for window size, orientation, and wall reflectance with regard to various daylight metrics and lighting energy demand: A case study of buildings in the tropics. Appl. Energy 2016, 164, 211–219. [Google Scholar] [CrossRef]
- Bueno, B.; Cejudo-López, J.M.; Katsifaraki, A.; Wilson, H.R. A systematic workflow for retrofitting office façades with large window-to-wall ratios based on automatic control and building simulations. Build. Environ. 2018, 132, 104–113. [Google Scholar] [CrossRef]
- Altun, A.F. Determination of Optimum Building Envelope Parameters of a Room concerning Window-to-Wall Ratio, Orientation, Insulation Thickness and Window Type. Buildings 2022, 12, 383. [Google Scholar] [CrossRef]
- Szcześniak, J.T.; Ang, Y.Q.; Letellier-Duchesne, S.; Reinhart, C.F. A method for using street view imagery to auto-extract window-to-wall ratios and its relevance for urban-level daylighting and energy simulations. Build. Environ. 2022, 207, 108108. [Google Scholar] [CrossRef]
- Vukadinović, A.; Radosavljević, J.; Đorđević, A.; Protić, M. Influence of Facade Structure, Glazing Type, and Window-to-Wall Ratio on the Energy Performance of a Detached Residential Building with a Sunspace. J. Energy Eng. 2023, 149, 04022046. [Google Scholar] [CrossRef]
- Li, S.; Zou, K.; Sun, G.; Zhang, X. Simulation research on the dynamic thermal performance of a novel triple-glazed window filled with PCM. Sustain. Cities Soc. 2018, 40, 266–273. [Google Scholar] [CrossRef]
- Urbikain, M.K. Energy efficient solutions for retrofitting a residential multi-storey building with vacuum insulation panels and low-E windows in two European climates. J. Clean. Prod. 2020, 269, 121459. [Google Scholar] [CrossRef]
- Cho, S.; Kim, S.-H. Analysis of the Performance of Vacuum Glazing in Office Buildings in Korea: Simulation and Experimental Studies. Sustainability 2017, 9, 936. [Google Scholar] [CrossRef]
- Lee, W.; Kang, J.; Cho, S.W. A New Structure of Vacuum Insulation Glazing for Edge Effect Reduction: A Parametric Study. Int. J. Precis. Eng. Manuf. 2018, 19, 447–452. [Google Scholar] [CrossRef]
- Myroniuk, K.; Furdas, Y.; Zhelykh, V.; Adamski, M.; Gumen, O.; Savin, V.; Mitoulis, S.-A. Passive Ventilation of Residential Buildings Using the Trombe Wall. Buildings 2024, 14, 3154. [Google Scholar] [CrossRef]
- Amirat, Y.; Idouanaou, A.; Cherqi, O.; Malha, M.; Bah, A. Impact of Shading and Glazing Types of Trombe Walls on the Carbon Footprint of Residential Buildings in Morocco. E3S Web Conf. 2024, 572, 03002. [Google Scholar] [CrossRef]



| Gas Type | Unit | Air | Argon | Krypton | Xenon |
|---|---|---|---|---|---|
| Thickness | m | 0.008 | 0.008 | 0.008 | 0.008 |
| Conductivity Coefficient A | W/mK | 0.002873 | 0.002285 | 0.0009443 | 0.0004538 |
| Conductivity Coefficient B | W/mK2 | 0.0000776 | 0.00005149 | 0.00002826 | 0.00001723 |
| Conductivity Coefficient C | W/mK3 | 0 | 0 | 0 | 0 |
| Viscosity Coefficient A | Kg/ms | 0.00000372 | 0.00000338 | 0.00000221 | 0.00000107 |
| Viscosity Coefficient B | Kg/msK | 0.00000005 | 0.00000006 | 0.00000008 | 0.00000007 |
| Viscosity Coefficient C | Kg/msK2 | 0 | 0 | 0 | 0 |
| Specific Heat Coefficient A | J/kgK | 1002.737 | 521.9285278 | 248.0906982 | 158.3397064 |
| Specific Heat Coefficient B | J/kgK2 | 0.012324 | 0 | 0 | 0 |
| Specific Heat Coefficient C | J/kgK3 | 0 | 0 | 0 | 0 |
| Molecular Weight | g/mol | 28.97 | 39.948 | 83.8 | 131.3 |
| Thickness | m | Air | Argon | Krypton | Xenon |
| Conductivity Coefficient A | W/mK | 0.008 | 0.008 | 0.008 | 0.008 |
| Conductivity Coefficient B | W/mK2 | 0.002873 | 0.002285 | 0.0009443 | 0.0004538 |
| Conductivity Coefficient C | W/mK3 | 0.0000776 | 0.00005149 | 0.00002826 | 0.00001723 |
| Viscosity Coefficient A | Kg/ms | 0 | 0 | 0 | 0 |
| Viscosity Coefficient B | Kg/msK | 0.00000372 | 0.00000338 | 0.00000221 | 0.00000107 |
| Spacing | U-Factor | SHGC | VT | |
|---|---|---|---|---|
| (mm) | (W/m2·K) | |||
| Vacuum Radius 1.5 mm | 20 | 3.711 | 0.759 | 0.814 |
| 25 | 3.323 | 0.76 | 0.814 | |
| 30 | 3.043 | 0.761 | 0.814 | |
| 35 | 2.842 | 0.762 | 0.814 | |
| 40 | 2.695 | 0.762 | 0.814 | |
| Vacuum Radius 1.0 mm | 20 | 3.356 | 0.76 | 0.814 |
| 25 | 3.015 | 0.761 | 0.814 | |
| 30 | 2.786 | 0.762 | 0.814 | |
| 35 | 2.628 | 0.762 | 0.814 | |
| 40 | 2.517 | 0.763 | 0.814 | |
| Vacuum Radius 0.5 mm | 20 | 2.855 | 0.762 | 0.814 |
| 25 | 2.619 | 0.763 | 0.814 | |
| 30 | 2.475 | 0.763 | 0.814 | |
| 35 | 2.381 | 0.763 | 0.814 | |
| 40 | 2.318 | 0.764 | 0.814 | |
| Vacuum Radius 0.25 mm | 20 | 2.517 | 0.763 | 0.814 |
| 25 | 2.376 | 0.763 | 0.814 | |
| 30 | 2.294 | 0.764 | 0.814 | |
| 35 | 2.243 | 0.764 | 0.814 | |
| 40 | 2.209 | 0.764 | 0.814 | |
| Vacuum low-e Radius 1.5 mm | 20 | 3.268 | 0.388 | 0.69 |
| 25 | 2.659 | 0.38 | 0.69 | |
| 30 | 2.183 | 0.374 | 0.69 | |
| 35 | 1.819 | 0.37 | 0.69 | |
| 40 | 1.539 | 0.366 | 0.69 | |
| Vacuum low-e Radius 1.0 mm | 20 | 2.714 | 0.381 | 0.69 |
| 25 | 2.133 | 0.374 | 0.69 | |
| 30 | 1.713 | 0.368 | 0.69 | |
| 35 | 1.408 | 0.364 | 0.69 | |
| 40 | 1.184 | 0.362 | 0.69 | |
| Vacuum low-e Radius 0.5 mm | 20 | 1.842 | 0.37 | 0.69 |
| 25 | 1.39 | 0.364 | 0.69 | |
| 30 | 1.097 | 0.361 | 0.69 | |
| 35 | 0.901 | 0.358 | 0.69 | |
| 40 | 0.764 | 0.356 | 0.69 | |
| Vacuum low-e Radius 0.25 mm | 20 | 1.184 | 0.362 | 0.69 |
| 25 | 0.889 | 0.358 | 0.69 | |
| 30 | 0.712 | 0.356 | 0.69 | |
| 35 | 0.599 | 0.354 | 0.69 | |
| 40 | 0.523 | 0.353 | 0.69 |
| Buildings | Gas Consumption (GJ) | Electricity Consumption (GJ) |
|---|---|---|
| Original Wall Building 1 | 65.96 | 6.27 |
| Actual Values (Average) 2 | 72.56 | 7.52 |
| Common Cavity Wall Building 3 | 148.27 | 12.77 |
| Spacing | SHGC/(Uwindow − Uwall) | Heating Load 1 1 (2) 2 | Difference Value | |
|---|---|---|---|---|
| (mm) | (GJ) | (GJ) | ||
| Double air | 0.65 | 148.27 (147.31) | 0.96 | |
| Triple air | 3.23 | 145.55 (144.25) | 1.3 | |
| Double argon | 0.82 | 147.4 (146.33) | 1.07 | |
| Triple argon | 84.62 | 144.74 (143.32) | 1.42 | |
| Double Krypton | 1.10 | 146.43 (145.21) | 1.22 | |
| Triple Krypton | −3.30 | 143.82 (142.28) | 1.54 | |
| Double Xenon | 1.15 | 146.17 (144.89) | 1.28 | |
| Triple Xenon | −2.59 | 143.53 (141.92) | 1.61 | |
| Vacuum Radius 1.5 mm | 20 | 0.39 | 150.51 (149.86) | 0.65 |
| 25 | 0.49 | 149.12 (148.28) | 0.84 | |
| 30 | 0.60 | 148.05 (147.06) | 0.99 | |
| 35 | 0.71 | 147.27 (146.17) | 1.1 | |
| 40 | 0.82 | 146.71 (145.53) | 1.18 | |
| Vacuum Radius 1.0 mm | 20 | 0.48 | 149.24 (148.42) | 0.82 |
| 25 | 0.61 | 147.94 (146.94) | 1 | |
| 30 | 0.75 | 147.06 (145.93) | 1.13 | |
| 35 | 0.88 | 146.45 (145.24) | 1.21 | |
| 40 | 1.02 | 146 (144.73) | 1.27 | |
| Vacuum Radius 0.5 mm | 20 | 0.70 | 147.32 (146.23) | 1.09 |
| 25 | 0.89 | 146.4 (145.18) | 1.22 | |
| 30 | 1.08 | 145.84 (144.54) | 1.3 | |
| 35 | 1.24 | 145.47 (144.12) | 1.35 | |
| 40 | 1.38 | 145.21 (143.82) | 1.39 | |
| Vacuum Radius 0.25 mm | 20 | 1.02 | 146 (144.73) | 1.27 |
| 25 | 1.25 | 145.45 (144.1) | 1.35 | |
| 30 | 1.45 | 145.12 (143.72) | 1.4 | |
| 35 | 1.60 | 144.92 (143.49) | 1.43 | |
| 40 | 1.72 | 144.78 (143.33) | 1.45 | |
| Vacuum low-e Radius 1.5 mm | 20 | 0.26 | 154.03 (154.12) | −0.09 |
| 25 | 0.43 | 151.81 (151.59) | 0.22 | |
| 30 | 0.90 | 150.01 (149.54) | 0.47 | |
| 35 | 6.98 | 148.6 (147.92) | 0.68 | |
| 40 | −1.61 | 147.35 (146.5) | 0.85 | |
| Vacuum low-e Radius 1.0 mm | 20 | 0.40 | 152.01 (151.82) | 0.19 |
| 25 | 1.02 | 149.82 (149.31) | 0.51 | |
| 30 | −6.94 | 148.19 (147.46) | 0.73 | |
| 35 | −1.02 | 146.65 (145.69) | 0.96 | |
| 40 | −0.62 | 145.8 (144.6) | 1.1 | |
| Vacuum low-e Radius 0.5 mm | 20 | 4.87 | 148.69 (148.03) | 0.66 |
| 25 | −0.97 | 146.57 (145.6) | 0.97 | |
| 30 | −0.54 | 145.33 (144.17) | 1.16 | |
| 35 | −0.41 | 144.48 (143.2) | 1.28 | |
| 40 | −0.36 | 143.87 (142.51) | 1.36 | |
| Vacuum low-e Radius 0.25 mm | 20 | −0.62 | 145.7 (144.6) | 1.1 |
| 25 | −0.41 | 144.42 (143.14) | 1.28 | |
| 30 | −0.34 | 143.64 (142.24) | 1.4 | |
| 35 | −0.30 | 143.13 (141.66) | 1.47 | |
| 40 | −0.28 | 142.79 (141.26) | 1.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Omer, S.; Hu, R. Impact of Window Size Modification on Energy Consumption in UK Residential Buildings: A Feasibility and Simulation Study. Sustainability 2025, 17, 3258. https://doi.org/10.3390/su17073258
Zhang Y, Omer S, Hu R. Impact of Window Size Modification on Energy Consumption in UK Residential Buildings: A Feasibility and Simulation Study. Sustainability. 2025; 17(7):3258. https://doi.org/10.3390/su17073258
Chicago/Turabian StyleZhang, Yue, Siddig Omer, and Ruichang Hu. 2025. "Impact of Window Size Modification on Energy Consumption in UK Residential Buildings: A Feasibility and Simulation Study" Sustainability 17, no. 7: 3258. https://doi.org/10.3390/su17073258
APA StyleZhang, Y., Omer, S., & Hu, R. (2025). Impact of Window Size Modification on Energy Consumption in UK Residential Buildings: A Feasibility and Simulation Study. Sustainability, 17(7), 3258. https://doi.org/10.3390/su17073258







