Controlling Factors Affecting NAPL Residuals in Aquifers Containing Low-Permeability Lens Bodies
Abstract
1. Introduction
2. Materials and Methods
2.1. Soil Column Simulation Experiment
2.1.1. Experimental Materials
2.1.2. Experimental Apparatus
2.1.3. Soil Column Experiment
2.2. Mercury Intrusion Porosimetry Test
2.2.1. Equipment and Materials of Mercury Intrusion Porosimetry Test
2.2.2. Mercury Intrusion Porosimetry Procedure
2.3. Particle Size Analysis
2.3.1. Equipment and Materials of Particle Size Analysis
2.3.2. Particle Size Measurement
2.4. NAPL Concentration Measurement
2.4.1. Equipment and Materials of NAPL Concentration Measurement
2.4.2. Standard Curve Development
3. Results
3.1. Soil Column Experiment Results
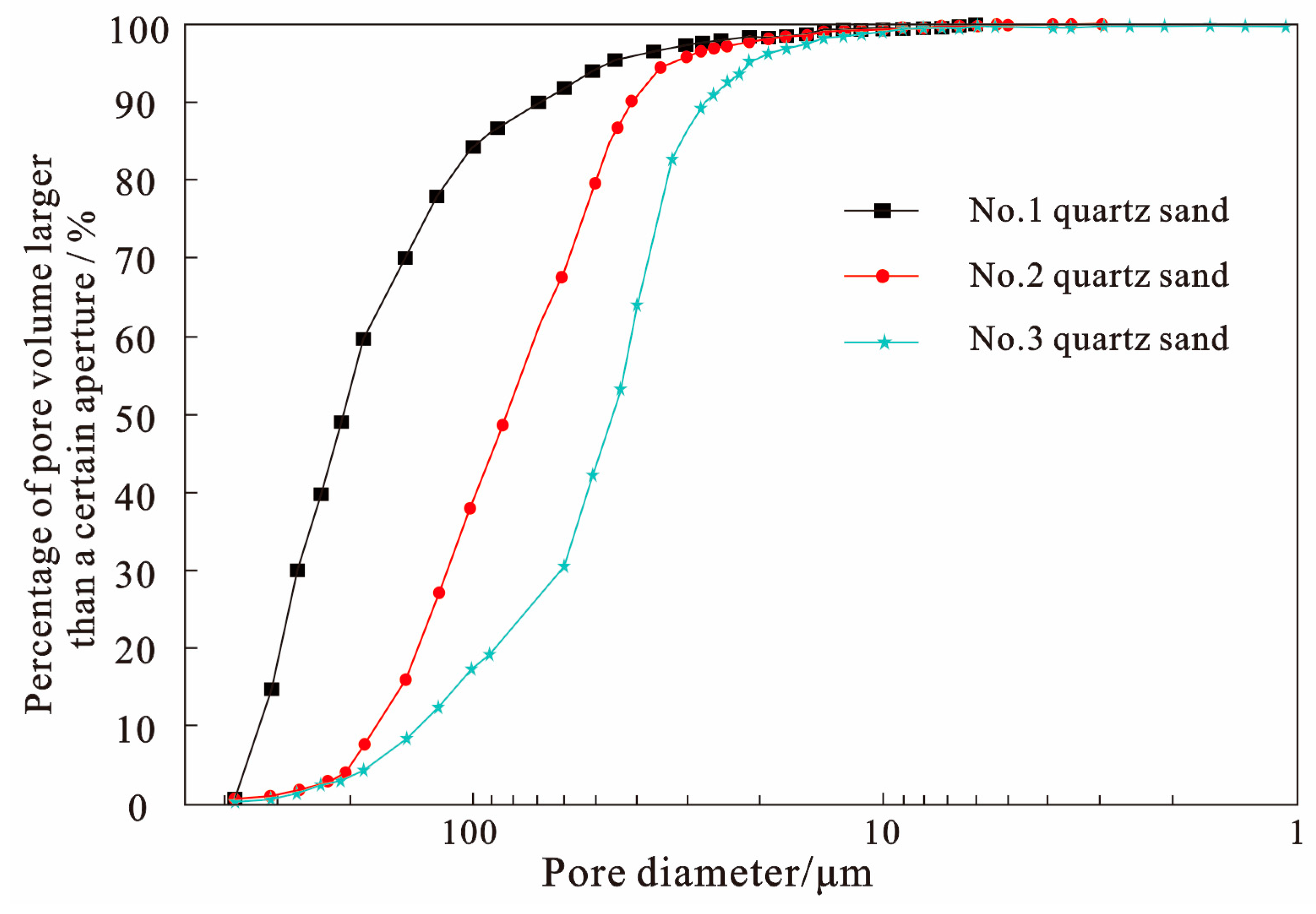
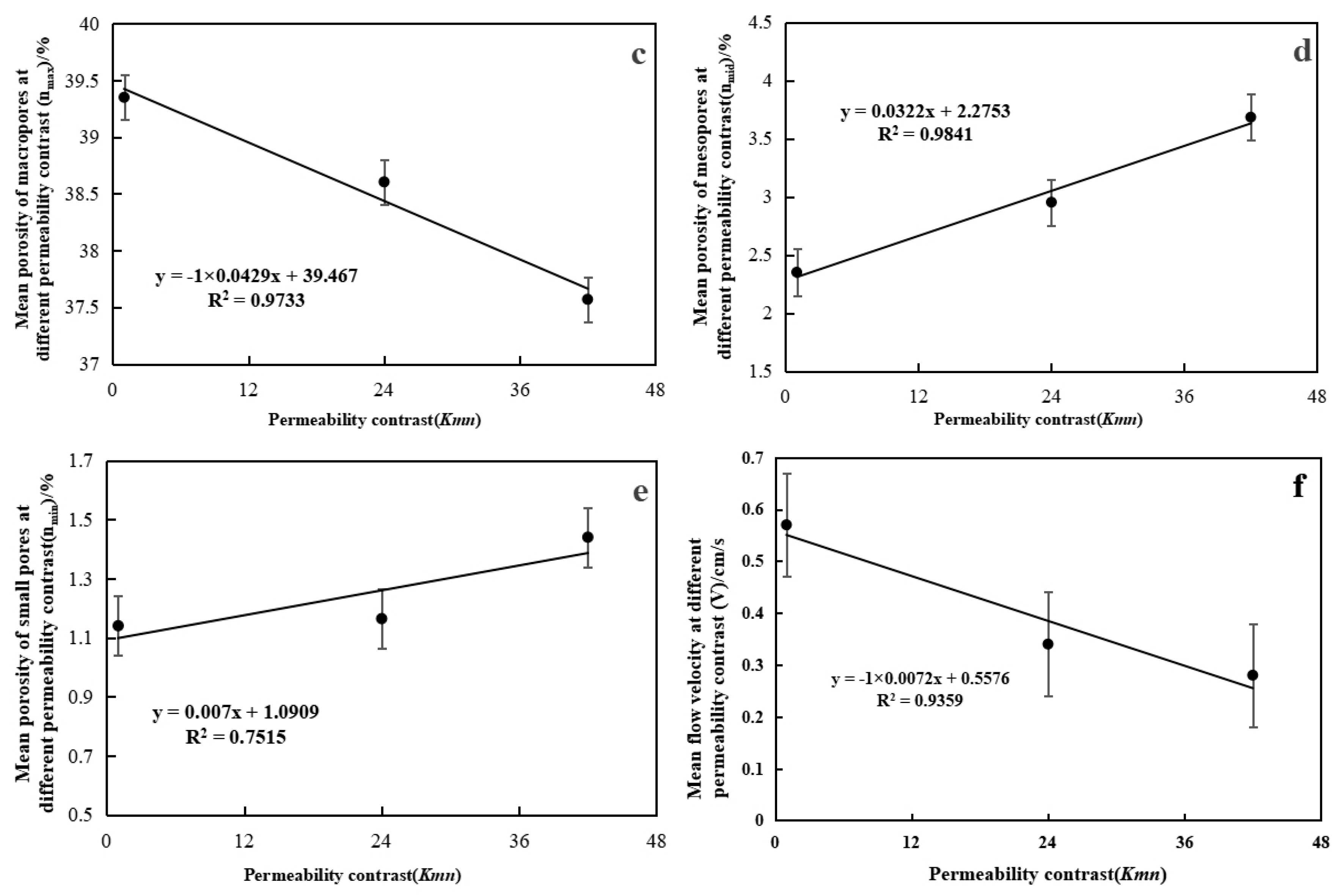
3.2. Mercury Intrusion Porosimetry Results
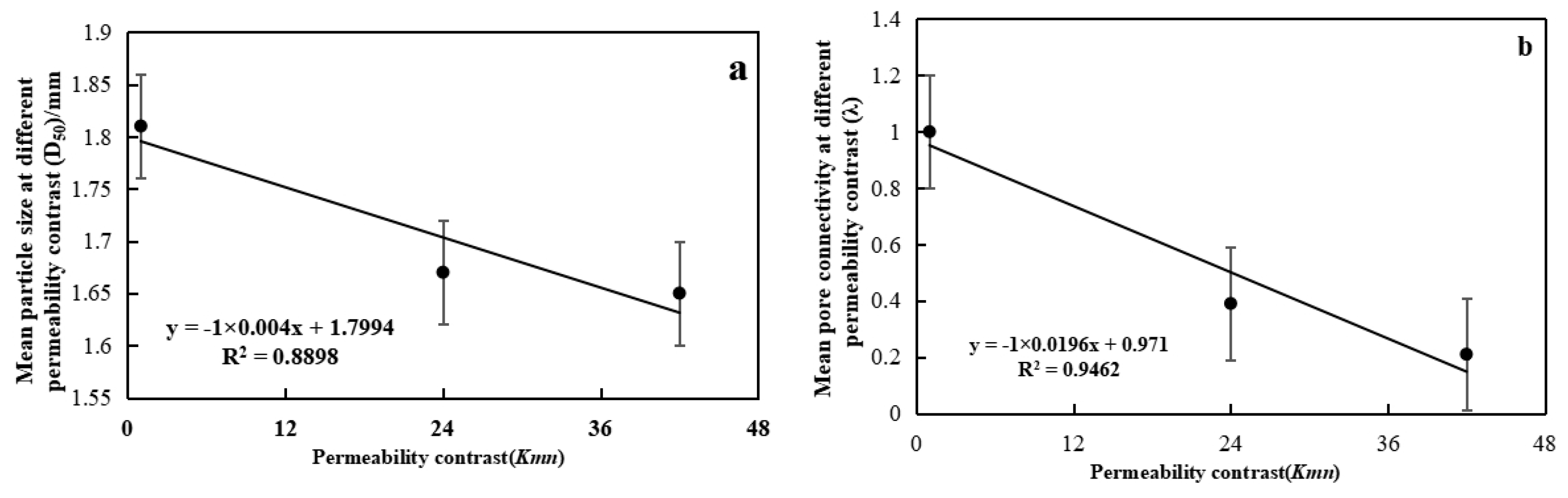
3.3. Particle Size Distribution Results
4. Discussion
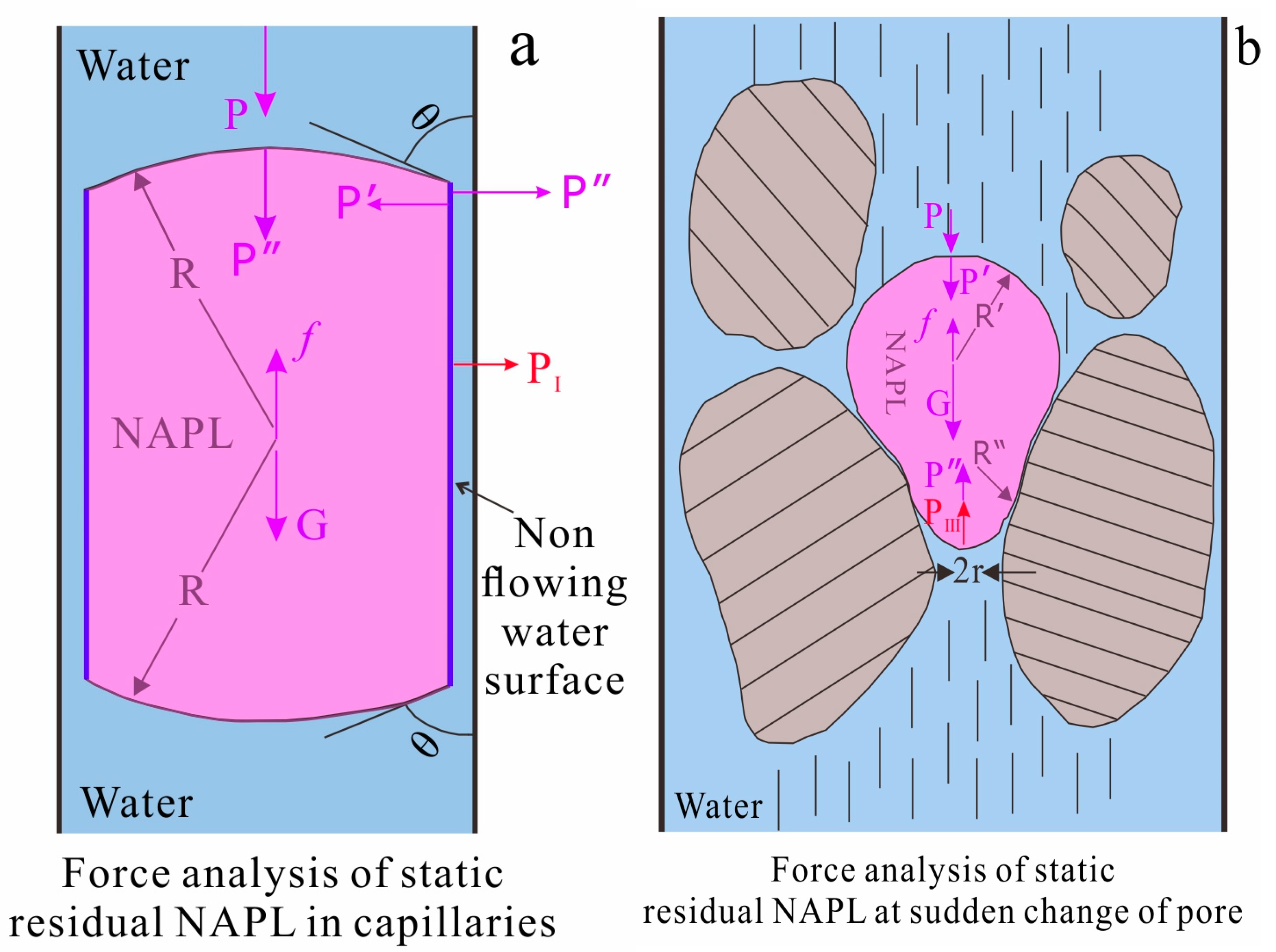
4.1. NAPL Residuals Mechanism
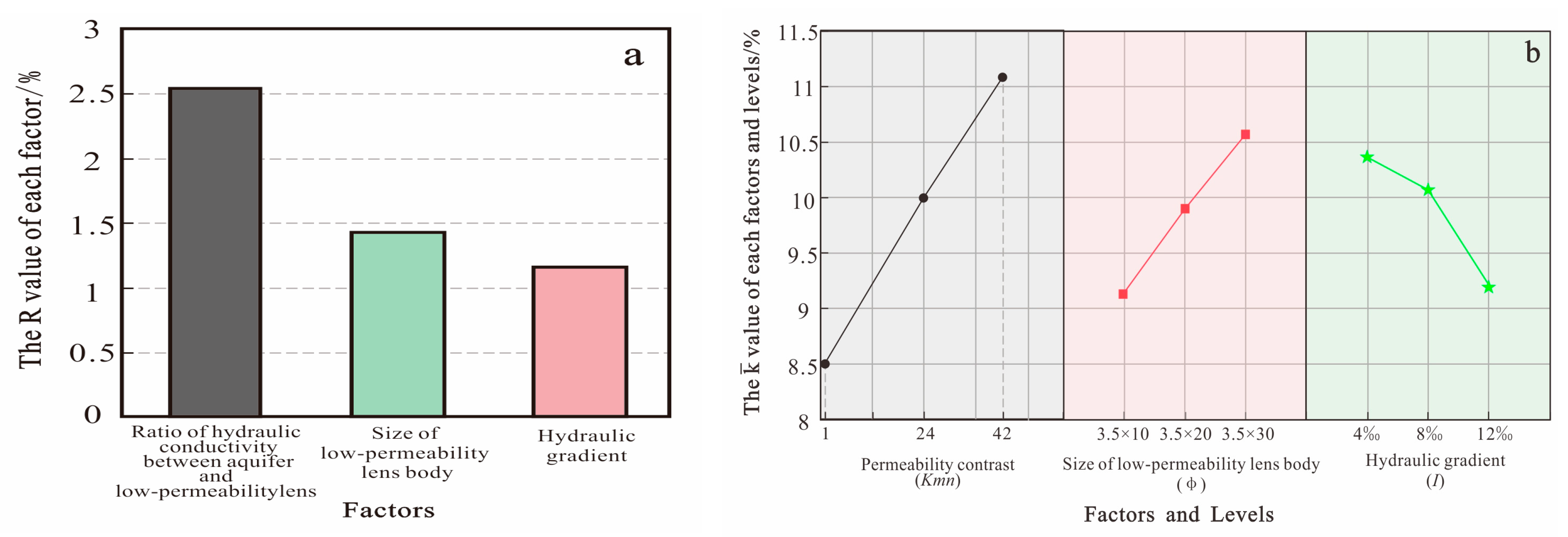
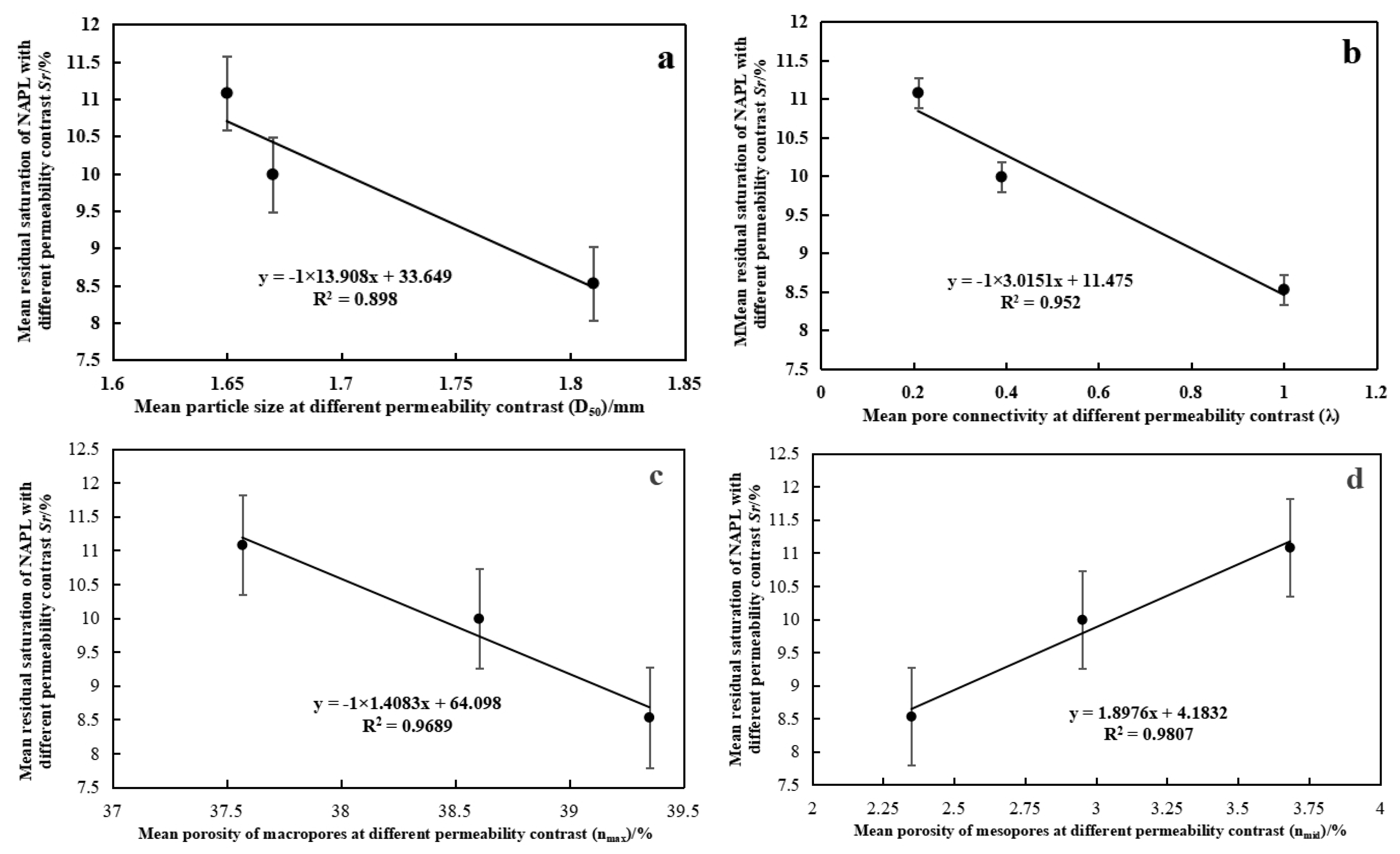
4.2. Effect of Permeability Coefficient Range on NAPL Residuals
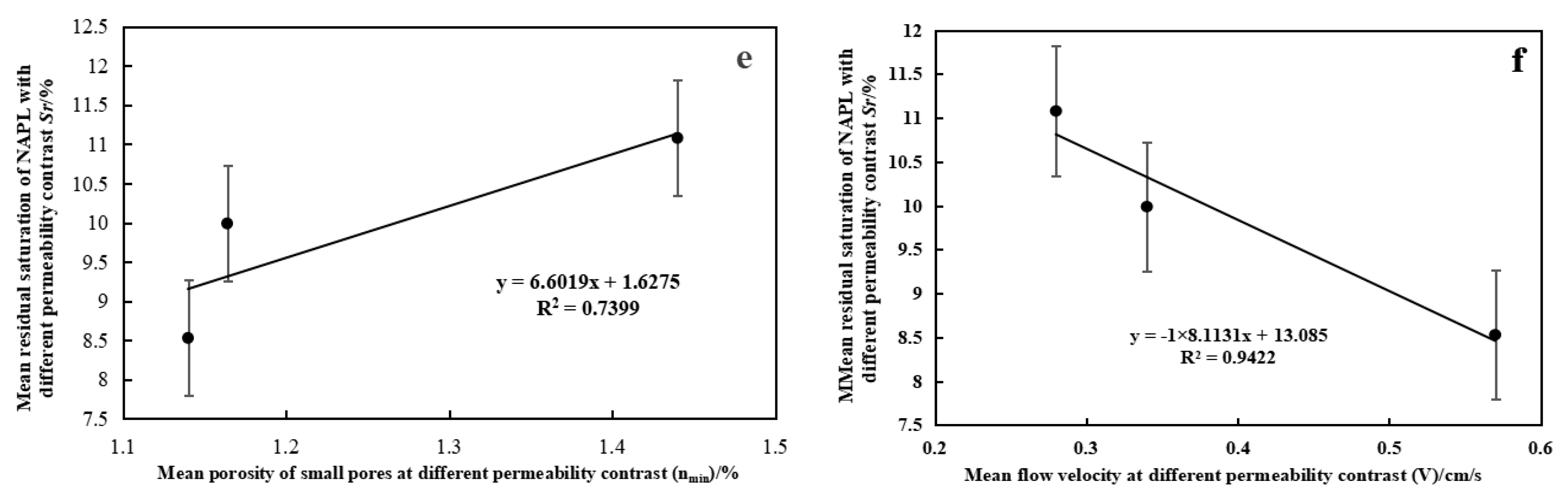
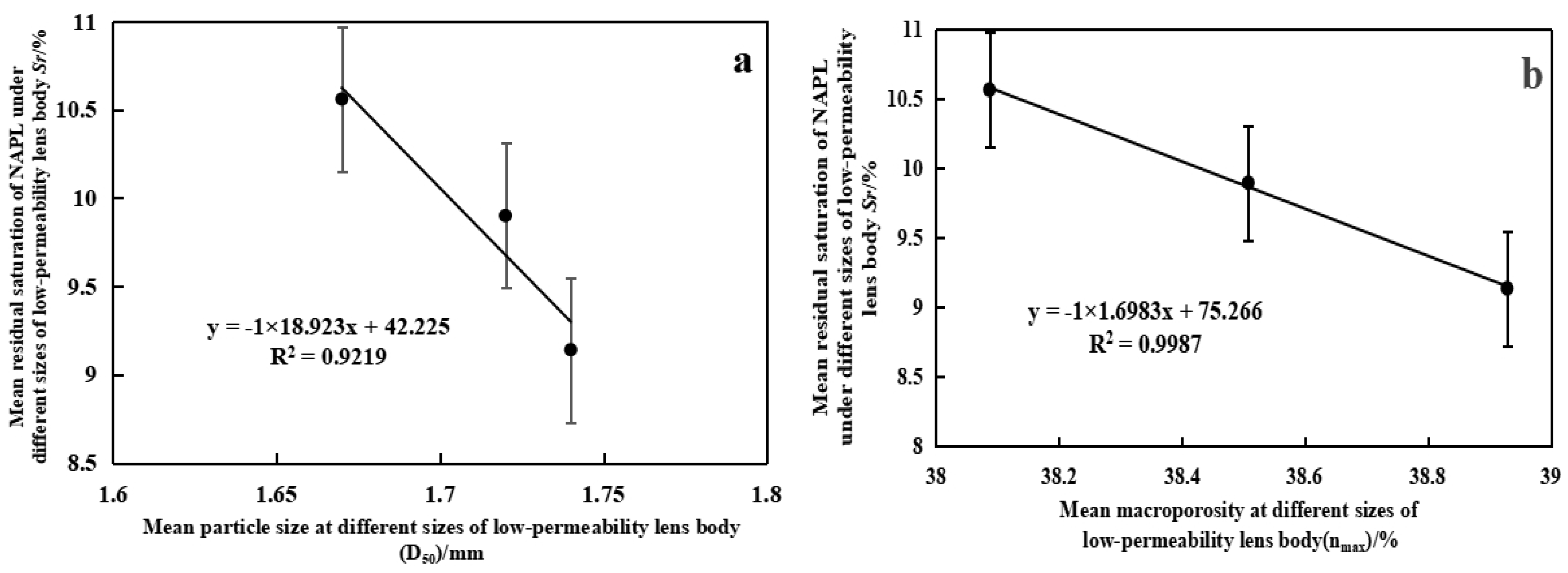
4.3. Mechanism Affecting ϕ on NAPL Residuals
4.4. Mechanism Affecting I on NAPL Residuals
5. Conclusions and Outlook
5.1. Conclusions
5.2. Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, H.; Li, Y.; Li, C.; Zhu, H.; Li, Z.; Wang, L.; Medina-Rodriguez, B.X. Unveil the controls on CO2 diffusivity in saline brines for geological carbon storage. Geoenergy Sci. Eng. 2025, 244, 213483. [Google Scholar] [CrossRef]
- Gong, J.; Tang, K.; Wang, H. Zone-division of water crisis and corresponding strategies in China. Resour. Sci. 2015, 37, 1314–1321. [Google Scholar]
- Lin, K.S.; Mdlovu, N.V.; Chen, C.Y.; Chiang, C.L.; Dehvari, K. Degradation of TCE, PCE, and 1, 2–DCE DNAPLs in contaminated groundwater using polyethylenimine-modified zero-valent iron nanoparticles. J. Clean. Prod. 2018, 175, 456–466. [Google Scholar]
- Li, S.; Liu, F.; Li, W.; Li, C.; Huang, F.; Jin, S.; Liu, J.; Yang, L.; Piao, H.; Zhang, Y.; et al. Prioritization of organic contaminants in China’s groundwater based on national-scale monitoring data and their persistence, bioaccumulation, and toxicity. Sci. Total Environ. 2024, 929, 172656. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Han, B.; Yin, E. Research Progress on Groundwater Contamination by DNAPLs. Sichuan Environ. 2005, 24, 65–70. [Google Scholar]
- Wang, H.; Xin, Y.; Kou, Z.; He, C.; Li, Y.; Wang, T. Unveil the role of engineering parameters on hydrogen recovery in deep saline aquifer, Rock Springs Uplift, Wyoming. Renew. Energy 2024, 255, 120261. [Google Scholar]
- Wang, H.; Kou, Z.; Ji, Z.; Wang, S.; Li, Y.; Jiao, Z.; Johnson, M.; McLaughlin, J.F. Fred McLaughlin. Investigation of enhanced CO2 storage in deep saline aquifers by WAG and brine extraction in the Minnelusa sandstone, Wyoming. Energy 2023, 265, 126379. [Google Scholar] [CrossRef]
- Rao, P.C.; Annable, M.D.; Kim, H. NAPL source zone characterization and remediation technology performance assessment: Recent developments and applications of tracer techniques. J. Contam. Hydrol. 2000, 45, 63–78. [Google Scholar]
- Zheng, F.; Gao, Y.; Shi, X.; Wu, J. Influence of groundwater flow velocity and geological heterogeneity on DNAPL migration in saturated porous media. J. Hydraul. Eng. 2015, 46, 925–933. [Google Scholar]
- Shi, Y. Fate and Transport of Typical Organic Pollutants in Saturated Porous Media. Ph.D. Thesis, Nanjing University, Nanjing, China, 2019. [Google Scholar]
- Chapman, S.W.; Parker, B.L. Plume persistence due to aquitard back diffusion following dense nonaqueous phase liquid source removal or isolation. Water Resour. Res. 2005, 41, W12411. [Google Scholar]
- Pan, Y.; Yang, J.; Jia, Y.; Xu, Z. Experimental study on non-aqueous phase liquid multiphase flow characteristics and controlling factors in heterogeneous porous media. Environ. Earth Sci. 2016, 75, 1–13. [Google Scholar] [CrossRef]
- Song, Y.A.; Hou, D.Y.; Zhao, Y.S.; Zhu, J.; Zhang, Q.; Qin, C.Y.; Wang, W.F. Remediation strategies for contanminated groundwater at chemical industrial sites in the Bejing-Tianjin-Hebei region. Res. Environ. Sci. 2020, 33, 1345–1356. [Google Scholar]
- Mateas, D.J.; Tick, G.R.; Carroll, K.C. In situ stabilization of NAPL contaminant source-zones as a remediation technique to reduce mass discharge and flux to groundwater. J. Contam. Hydrol. 2017, 204, 40–56. [Google Scholar] [CrossRef]
- Shu, S.; Liang, H.; Yuan, Y. Numerical analysis of transportation and distribution of light non-aqueous phase liquids in partially saturated heterogeneous soils. J. Hydraul. Eng. 2002, 11, 31–37. [Google Scholar]
- Cheng, Z.; Wu, J.; Xu, H.; Wang, J.; Gao, Y.; Li, J.; Dong, S. Investigation of the migration characteristic of DNAPL in aquifer with lenses and under the action of surfactant. China Environ. Sci. 2014, 34, 2888–2896. [Google Scholar]
- Wang, L. Experimental Study on Multiphase Flow in Soil Contaminated with Light Non-Aqueous Phase Liquid (LNAPL). Master’s Thesis, Chang’an University, Xi’an, China, 2009. [Google Scholar]
- Panter, S.E. The Hidden Potential of Mass-based Treatment: A Method for Preventing Rebound. Remediat. J. Environ. Cleanup Costs Technol. Tech. 2015, 25, 99–109. [Google Scholar] [CrossRef]
- Tao, J.; Shi, X.; Kang, X.; Xu, H.; Wu, J. Numerical analyses of factors affecting the LNAPL source-zone architecture. Hydrogeol. Eng. Geol. 2018, 45, 132–140. [Google Scholar]
- Kamon, M.; Endo, K.; Kawabata, J.; Inui, T.; Katsumi, T. Two-dimensional DNAPL migration affected by groundwater flow in unconfined aquifer. J. Hazard. Mater. 2004, 110, 1–12. [Google Scholar] [CrossRef]
- Luciano, A.; Viotti, P.; Papini, M.P. Laboratory investigation of DNAPL migration in porous media. J. Hazard. Mater. 2010, 176, 1006–1017. [Google Scholar] [CrossRef]
- Erning, K.; Grandel, S.; Dahmke, A.; Schäfer, D. Simulation of DNAPL infiltration and spreading behavior in the saturated zone at varying flow velocities and alternating subsurface geometries. Environ. Earth Sci. 2012, 65, 1119–1131. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; He, T.; Li, Y.; Hou, L. The mechanism of NAPL layer formation in a microfluidic device with dual-permeability: Experiments and numerical simulation. IOP Conf. Ser. Earth Environ. Sci. 2021, 675, 012175. [Google Scholar]
- Kueper, B.H.; Abbott, W.; Farquhar, G. Experimental observations of multiphase flow in heterogeneous porous media. J. Contam. Hydrol. 1989, 5, 83–95. [Google Scholar] [CrossRef]
- Liu, H.L.; Zhou, Q.Y.; Xu, S. An experimental investigation of LNAPL migration and redistribution in unsaturated heterogeneous porous media. Hydrogeol. Eng. Geol. 2006, 52–57. [Google Scholar]
- Zhang, Y.; Zhu, S.; Xiao, R.; Wang, J.; Li, F. Vertical transport of polycyclic aromatic hydrocarbons in different particle-size fractions of sandy soils. Environ. Geol. 2008, 53, 1165–1172. [Google Scholar]
- Shi, X.Q.; Wu, J.C.; Liu, D.P.; Jiang, S.; Sun, Y.; Xu, H. Numerical simulation of transportation of dense non-aqueous phase liquids in the subsurface environment. J. Nanjing Univ. 2011, 47, 299–307. [Google Scholar]
- Al-Raoush Riyadh, I. Experimental investigation of the influence of grain geometry on residual NAPL using synchrotron microtomography. J. Contam. Hydrol. 2014, 159, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Liu, Z.; Liu, S.; Wei, Q.; Wang, Y.; Lu, L. Study on Influence of Geological Heterogeneity on Migration of LNAPL in Contaminated Site Through Numerical Analysis; Springer: Singapore, 2019; pp. 834–841. [Google Scholar]
- Wang, B.; Xia, Y.; Qu, Z.; Zhao, Y. Natural attenuation of diesel in aquifers. Hydrogeol. Eng. Geol. 2014, 41, 138–143. [Google Scholar]
- Ning, Z.; Sheng, Y.; Gan, S.; Guo, C.; Wang, S.; Cai, P.; Zhang, M. Experimental and numerical study of pollution process in an aquifer in relation to a garbage dump field. Environ. Geol. 2005, 48, 1107–1115. [Google Scholar]
- Ning, Z.; Sheng, Y.; Gan, S.; Guo, C.; Wang, S.; Cai, P.; Zhang, M. Metagenomic and Isotopic Insights into Carbon Fixation by Autotrophic Microorganisms in a Petroleum Hydrocarbon Impacted Red Clay Aquifer. Environ. Pollut. 2024, 361, 124824. [Google Scholar]
- Zhou, J.; Shen, R. Dictionary of Soil Science; Science Press: Beijing, China, 2013. [Google Scholar]
- Heidari, P.; Li, L. Solute transport in low-heterogeneity sandboxes: The role of correlation length and permeability variance. Water Resour. Res. 2015, 50, 8240–8264. [Google Scholar] [CrossRef]
- Mackay, D.M.; Cherry, J.A. Groundwater contamination: Pump-and-treat remediation. Environ. Sci. Technol. 1989, 23, 630–636. [Google Scholar] [CrossRef]
- Hunt, J.R.; Sitar, N.; Udell, K.S. Nonaqueous phase liquid transport and cleanup: 1. Analysis of mechanisms. Water Resour. Res. 1988, 24, 1247–1258. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Zhang, L.; Hou, J. Characterization on pore structure of tectonic coals based on the method of mercury intrusion, carbon dioxide adsorption and nitrogen adsorption. J. China Coal Soc. 2019, 44, 1188–1196. [Google Scholar]
- Zhang, X.; Kong, L.; Guo, A.; Tuo, Y. Experiment study of pore distribution of strong structural clay under different consolidation pressures. Rock Soil Mech. 2014, 35, 2794–2800. [Google Scholar]
- Sun, L.; Wang, S.W.; Guo, C.J.; Shi, C.; Su, W. Using pore-solid fractal dimension to estimate residual LNAPLs saturation in sandy aquifers: A column experiment. J. Groundw. Sci. Eng. 2022, 10, 87–98. [Google Scholar]
- Zhang, X. Research of Coal-Like Materials Development and Drilling Test. Master’s Thesis, China University of Mining and Technology, Beijing, China, 2021. [Google Scholar]
- Huang, C.; Xu, J. Soil Science; China Agricultural Press: Beijing, China, 2010. [Google Scholar]
- Thomasson, A.J. Towards an objective classification of soil structure. Eur. J. Soil Sci. 1978, 29, 38–46. [Google Scholar] [CrossRef]
- Qian, N.; Wang, Z. Mechanics of Sediment Transport; Science Press: Beijing, China, 1986; pp. 28–32. [Google Scholar]
- Becher, P. Emulsions: Theory and Practice; Reinhold Pub. Corp: Washington, DC, USA, 1965. [Google Scholar]
- Zhao, G. Physical Chemistry of Surfactants; Peking University Press: Beijing, China, 1991; pp. 65–127. [Google Scholar]
- Xiao, Y.; Lu, Q.; Cheng, H.; Zhu, X.; Tang, H. Surface properties of sediments and its effect on phosphorus adsorption. J. Sediment Res. 2011, 6, 64–68. [Google Scholar]
- Xiao, Y.; Han, K.; Cheng, H.; Li, Q. Surface Properties of Sediments in the Waterway of Poyang Lake to Yangtze River and the Nanjing Reach of Yangtze River. South-North Water Transf. Water Scence Technol. 2014, 12, 47–50. [Google Scholar]
- Wu, J.W.; Zheng, X.L.; Li, L.L.; Sun, J. Adsorption of Aqueous Oil on Sands and Its Studies of Effective Factors. Environ. Sci. 2006, 27, 2019–2023. [Google Scholar]
- Liu, H.; Gao, S.; Lv, X. Reservoir Physics; Petroleum Industry Press: Beijing, China, 2016. [Google Scholar]
- Fetter, C.W. Contaminant Hydrogeology, 2nd ed.; Zhou, N.; Huang, Y., Translators; Higher Education Press: Beijing, China, 2011. [Google Scholar]
- Luo, Y.; Wen, T.; Lin, X.; Chen, X.; Shao, L. Quantitative analysis of pore-size influence on granite residual soil permeability using CT scanning. J. Hydrol. 2024, 645, 132133. [Google Scholar] [CrossRef]
- Wen, T.; Luo, Y.; Tang, M.; Chen, X.; Shao, L. Effects of representative elementary volume size on three-dimensional pore characteristics for modified granite residual soil. J. Hydrol. 2024, 643, 132006. [Google Scholar] [CrossRef]
- Bedient, P.B.; Rifai, H.S.; Newell, C.J. Groundwater Contamination Transport and Remediation; China Architecture & Building Press: Beijing, China, 2010. [Google Scholar]







| Viscosity (mPa·s) | Surface Tension (mN·m) | Liquefied Density (g/mL) | Boiling Point (°C) | Octane Number |
|---|---|---|---|---|
| 287 | 2.68 | 0.83 | 180–360 | 40–55 |
| Medium Identification Number | Medium Particle Size D (mm) | Bulk Density ρ (g/cm3) | Permeability Coefficient K (m/day) | Porosity n (%) |
|---|---|---|---|---|
| Quartz Sand No. 1 (Simulated Aquifer Medium) | 0.25–4.00 | 1.53 | 267.84 | 42.85 |
| Quartz Sand No. 2 (Simulated Lens Medium) | 0.08–2.00 | 1.61 | 11.15 | 41.07 |
| Quartz Sand No. 3 (Simulated Lens Medium) | 0.05–1.00 | 1.69 | 6.39 | 40.67 |
| Experiment ID | Aquifer Medium Particle Size (mm) | Low-Permeability Medium Particle Size (mm) | Permeability Contrast (Kmn) | Lens Size (ϕ) | Hydraulic Gradient (I) | Groundwater Velocity V (cm/s) |
|---|---|---|---|---|---|---|
| 1 | 0.75–2.25 | 0.75–2.25 | 1 | 3.5 × 10 | 4‰ | 0.28 |
| 2 | 0.75–2.25 | 0.75–2.25 | 1 | 3.5 × 20 | 8‰ | 0.58 |
| 3 | 0.75–2.25 | 0.75–2.25 | 1 | 3.5 × 30 | 12‰ | 0.86 |
| 4 | 0.75–2.25 | 0.125–0.25 | 24 | 3.5 × 10 | 8‰ | 0.43 |
| 5 | 0.75–2.25 | 0.125–0.25 | 24 | 3.5 × 20 | 12‰ | 0.48 |
| 6 | 0.75–2.25 | 0.125–0.25 | 24 | 3.5 × 30 | 4‰ | 0.11 |
| 7 | 0.75–2.25 | 0.086–0.18 | 42 | 3.5 × 10 | 12‰ | 0.61 |
| 8 | 0.75–2.25 | 0.086–0.18 | 42 | 3.5 × 20 | 4‰ | 0.1 |
| 9 | 0.75–2.25 | 0.086–0.18 | 42 | 3.5 × 30 | 8‰ | 0.14 |
| Experiment ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Residual NAPL Saturation Sr (%) | 8.61 | 8.59 | 8.39 | 9.30 | 9.67 | 11.01 | 9.50 | 11.43 | 12.30 |
| Source | Sum of Squares (Type III) | Degrees of Freedom | Mean Square | F-Value | p-Value | Significance |
|---|---|---|---|---|---|---|
| Kmn | 9.816 | 2 | 4.908 | 20.255 | 0.047 | * |
| ϕ | 3.056 | 2 | 1.528 | 6.307 | 0.137 | |
| I | 2.198 | 2 | 1.099 | 4.535 | 0.181 | |
| Error | 0.485 | 2 | 0.242 | / | / | / |
| Total | 891.57 | 9 | / | / | / | / |
| Medium Number | Average Particle Diameter D50 (mm) | Uniformity Coefficient Cu | Curvature Coefficient Cs |
|---|---|---|---|
| Quartz Sand 1 | 1.80 | 3.77 | 1.03 |
| Quartz Sand 2 | 0.44 | 3.75 | 1.22 |
| Quartz Sand 3 | 0.19 | 3.07 | 1.11 |
| Experiment ID | Permeability Contrast (Kmn) | Lens Size (φ) | Hydraulic Gradient (I) | Average Particle Diameter D50/mm | Porosity of Macropores nmax/% | Porosity of Mesopores nmid/% | Porosity of Small Pores nmin/% | Pore Connectivity λ |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 3.5 × 10 | 4‰ | 1.81 | 39.33 | 2.45 | 1.05 | 1 |
| 2 | 1 | 3.5 × 20 | 8‰ | 1.81 | 39.33 | 2.45 | 1.05 | 1 |
| 3 | 1 | 3.5 × 30 | 12‰ | 1.81 | 39.33 | 2.45 | 1.05 | 1 |
| 4 | 24 | 3.5 × 10 | 8‰ | 1.71 | 38.94 | 2.70 | 1.07 | 0.39 |
| 5 | 24 | 3.5 × 20 | 12‰ | 1.69 | 38.57 | 2.96 | 1.09 | 0.39 |
| 6 | 24 | 3.5 × 30 | 4‰ | 1.61 | 38.18 | 3.21 | 1.11 | 0.39 |
| 7 | 42 | 3.5 × 10 | 12‰ | 1.7 | 38.43 | 3.02 | 1.21 | 0.21 |
| 8 | 42 | 3.5 × 20 | 4‰ | 1.67 | 37.51 | 3.59 | 1.38 | 0.21 |
| 9 | 42 | 3.5 × 30 | 8‰ | 1.58 | 36.60 | 4.17 | 1.54 | 0.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Wang, S.; Sun, L. Controlling Factors Affecting NAPL Residuals in Aquifers Containing Low-Permeability Lens Bodies. Sustainability 2025, 17, 3205. https://doi.org/10.3390/su17073205
Sun W, Wang S, Sun L. Controlling Factors Affecting NAPL Residuals in Aquifers Containing Low-Permeability Lens Bodies. Sustainability. 2025; 17(7):3205. https://doi.org/10.3390/su17073205
Chicago/Turabian StyleSun, Weichao, Shuaiwei Wang, and Lin Sun. 2025. "Controlling Factors Affecting NAPL Residuals in Aquifers Containing Low-Permeability Lens Bodies" Sustainability 17, no. 7: 3205. https://doi.org/10.3390/su17073205
APA StyleSun, W., Wang, S., & Sun, L. (2025). Controlling Factors Affecting NAPL Residuals in Aquifers Containing Low-Permeability Lens Bodies. Sustainability, 17(7), 3205. https://doi.org/10.3390/su17073205








