Flue Gas Oxygen Content Model Based on Bayesian Optimization Main–Compensation Ensemble Algorithm in Municipal Solid Waste Incineration Process
Abstract
1. Introduction
2. Materials and Method
2.1. Flue Gas Oxygen Content Description
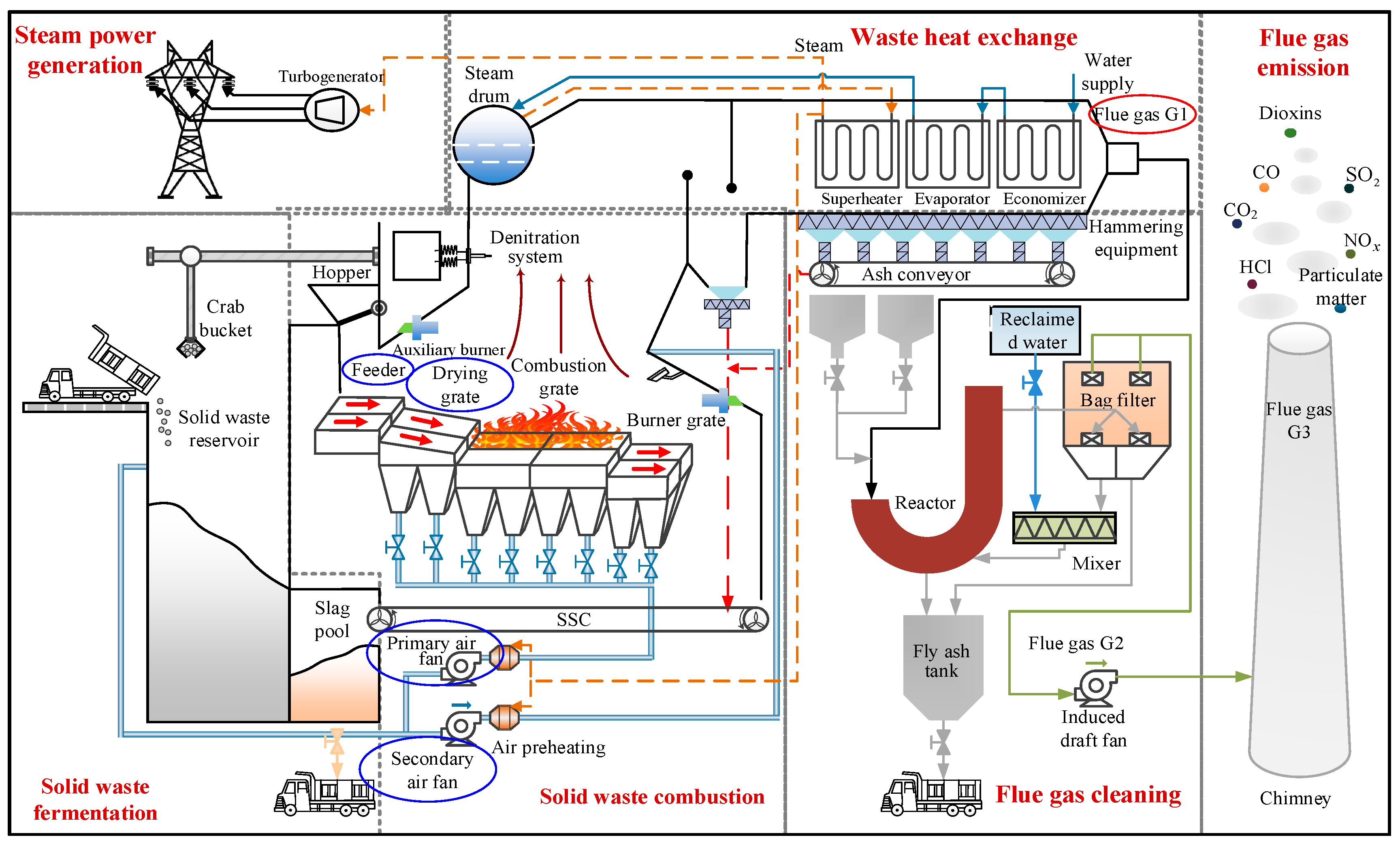
2.1.1. Municipal Solid Waste Incineration (MSWI) Process for Key Controlled Variables
- Solid waste fermentation stage. The original MSW contains a significant amount of moisture, which hinders combustion. Therefore, it undergoes bio-fermentation in a solid waste reservoir. This process typically takes 5–7 days and increases the calorific value of the solid portion by approximately 30%. After fermentation, the MSW is transferred to the hopper and then pushed into the incinerator by the feeder, signaling the transition to the solid waste combustion stage.
- Solid waste combustion stage. This stage involves converting MSW into high temperatures through the coupling interaction of multiple phases (solid, gas, liquid) and fields (heat, flow, force). It can be divided into three phases: drying, combustion, and burnout. The drying phase is achieved through the furnace’s heat radiation and the preheated primary air’s drying function. During the combustion phase, MSW is ignited, producing flue gas. After approximately 1.5 h of high-temperature combustion, the combustible components are fully burned, transitioning into the burnout phase. In this phase, non-combustible ash is pushed out of the furnace by the burnout grate.
- Waste heat exchange stage. First, the high-temperature flue gas is initially cooled by the water wall. Next, heat energy is transferred to the boiler through radiation and convection via equipment such as superheaters, evaporators, and economizers. The water in the boiler is then converted into high-pressure superheated steam, entering the steam generation stage. Finally, the outlet flue gas temperature of the boiler is reduced to 200 °C. During this stage, it is crucial to strictly control the cooling rate to prevent the reformation of trace pollutants.
- Steam power generation stage. This stage uses the high-temperature steam generated by the waste heat boiler to convert mechanical energy into electrical energy. This process achieves self-sufficiency in power consumption at the plant level and allows for the external supply of surplus power. In doing so, it facilitates resource utilization and generates economic benefits.
- Flue gas cleaning stage. First, the denitrification system is employed to remove NOx. Next, the acid gases are neutralized using the semi-dry deacidification process. Then, activated carbon is used to adsorb DXN and heavy metals from the flue gas. Finally, the particles, neutralizing reactants, and activated carbon adsorbates in the flue gas are removed by the bag filter.
- Flue gas emission stage. The flue gas that meets national emission standards is discharged into the atmosphere through the chimney, assisted by the induced draft fan.
2.1.2. Detection Description of Flue Gas Oxygen Content
2.1.3. Importance of Flue Gas Oxygen Content Control in MSWI Process
- Case 1: When the flue gas oxygen content is too low and the excess air coefficient is insufficient, it can lead to the production of a large amount of toxic and harmful gases. In addition, this condition results in increased heat loss and a decrease in combustion efficiency [14].
- Case 2: When the flue gas oxygen content is too high and the excess air coefficient is too large, it indicates that the amount of air supplied is excessive. This excess air can carry away a significant amount of heat and dust. Additionally, high flue gas oxygen content can lead to an increase in the emission of NOx pollutants [14].
2.2. Modeling Data Descripiton
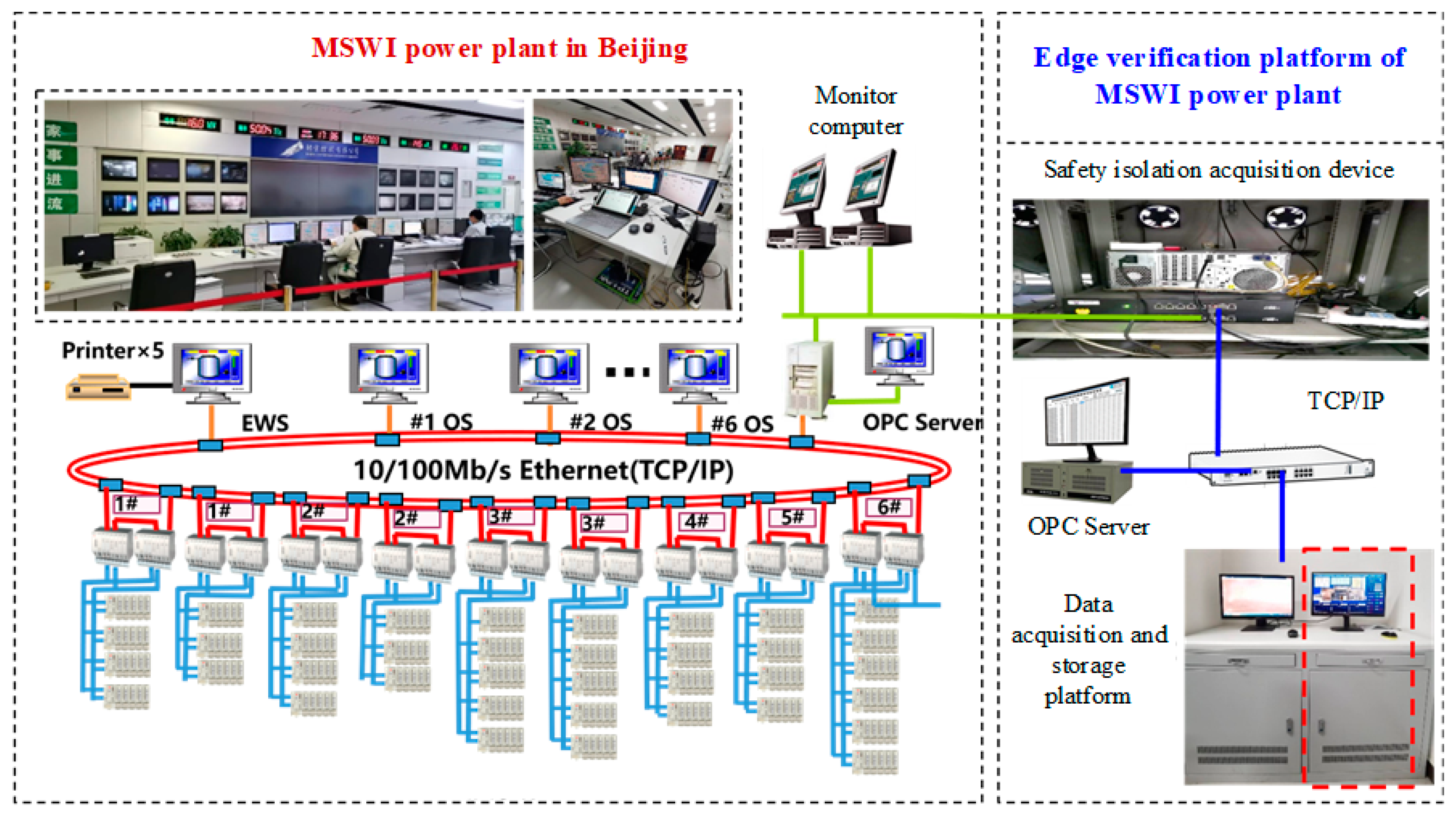
2.2.1. Data Acquisition Devices Description
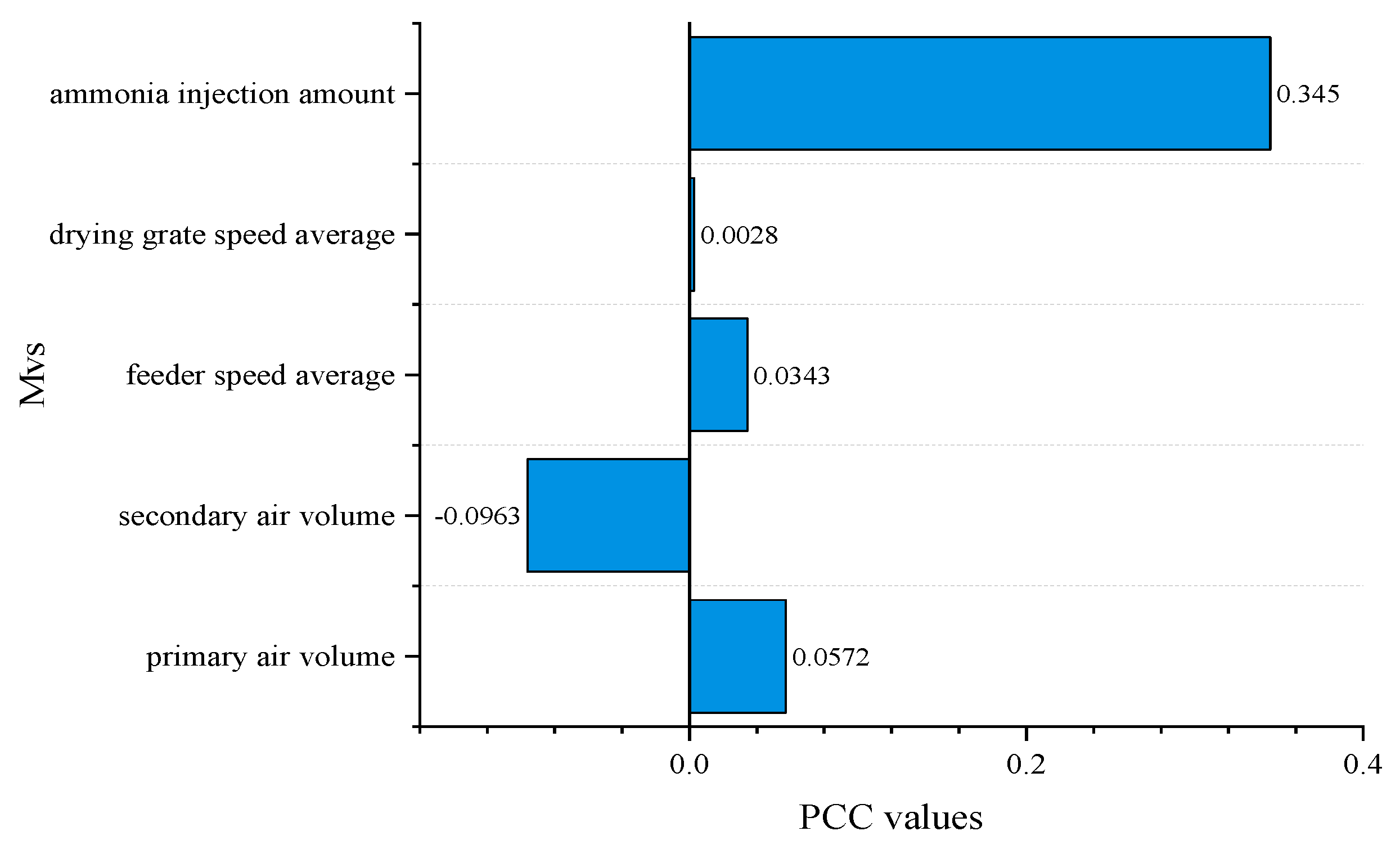
2.2.2. Experimental Data Analysis
2.3. Method
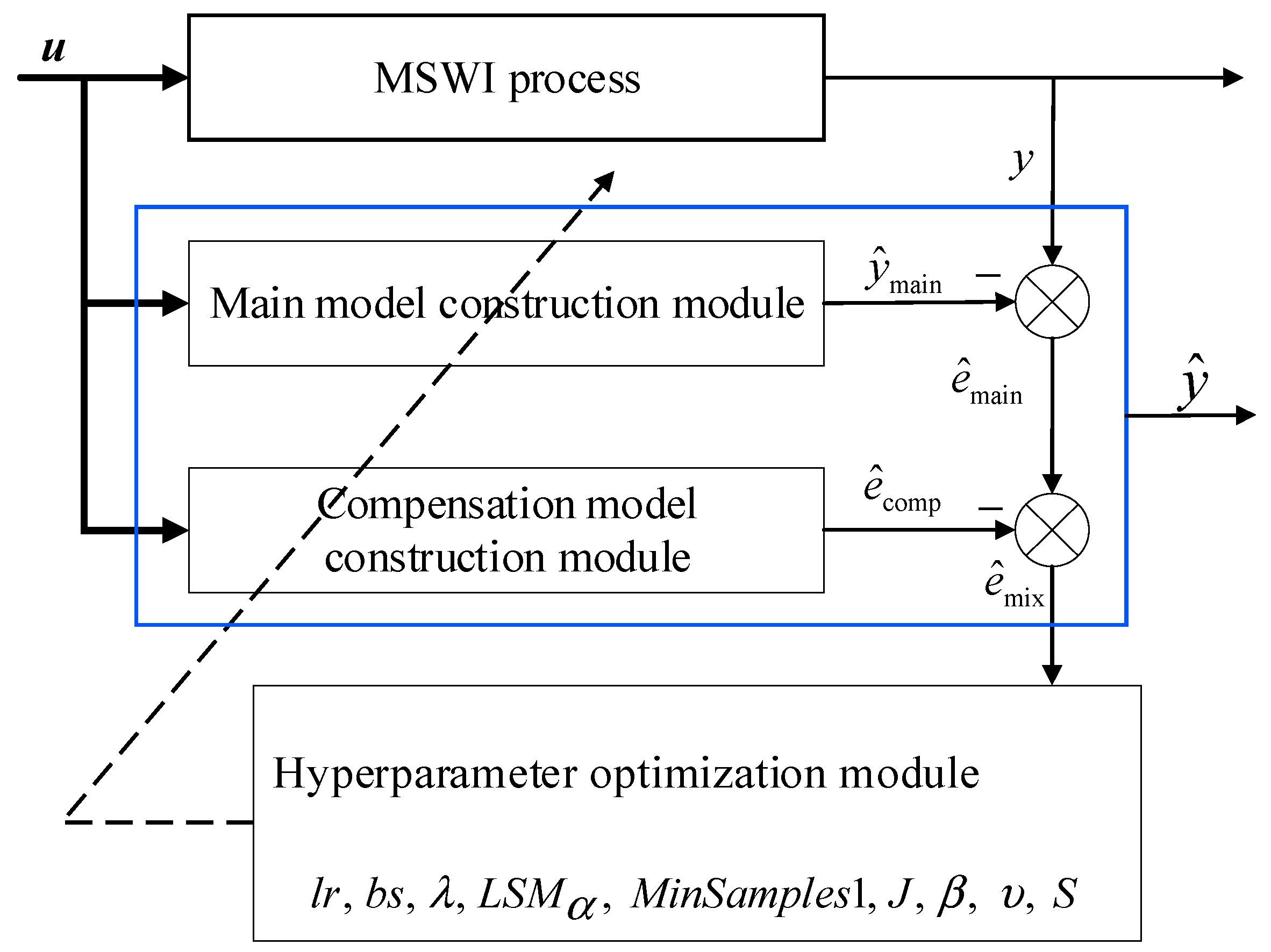
2.3.1. Main–Compensation Ensemble Modeling Strategy
2.3.2. Modeling Algorithm Implementation
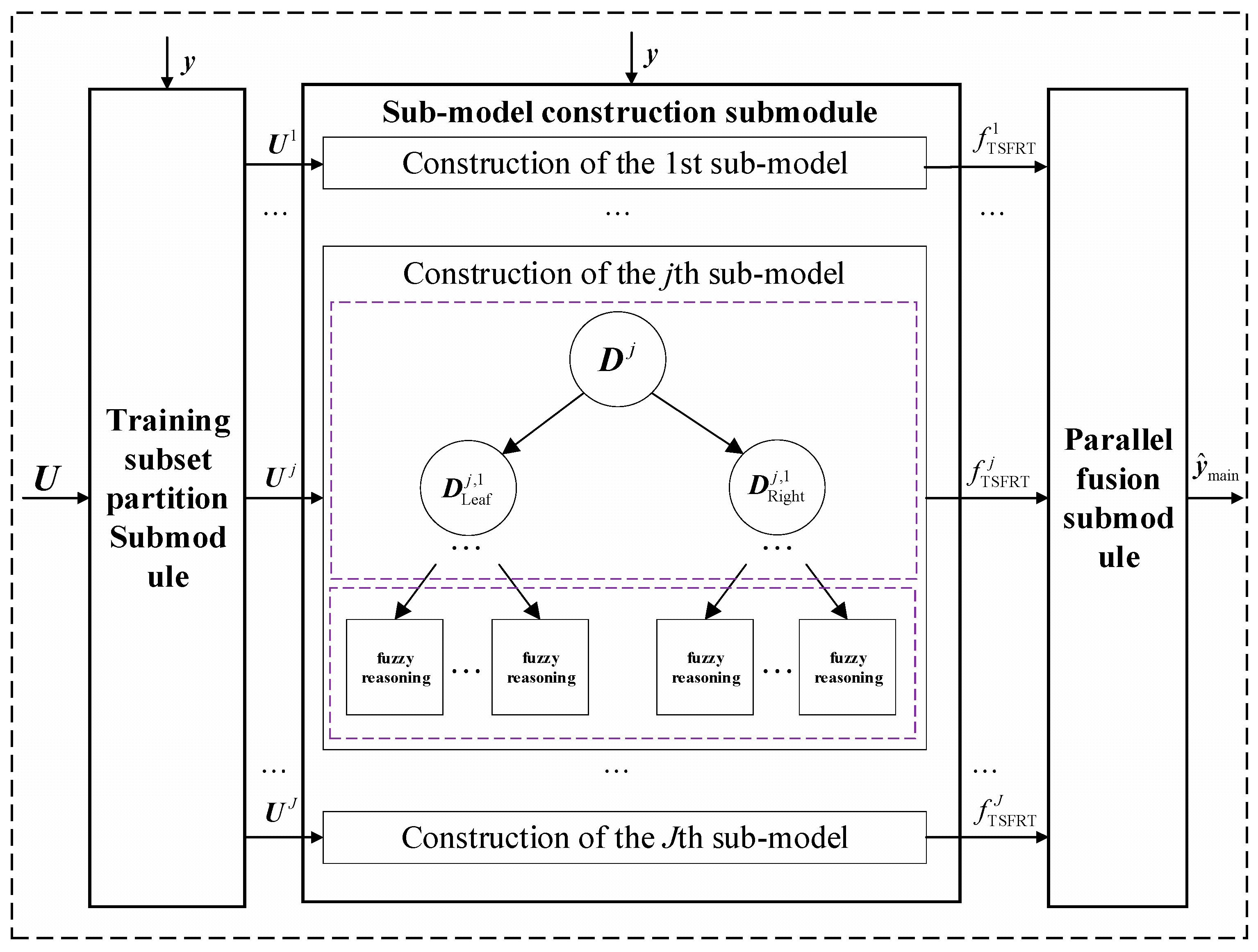
Main Model Construction Module
- (1)
- Training subsets’ partition sub-module.
- (2)
- Sub-model construction sub-module.
- (3)
- Parallel fusion sub-module
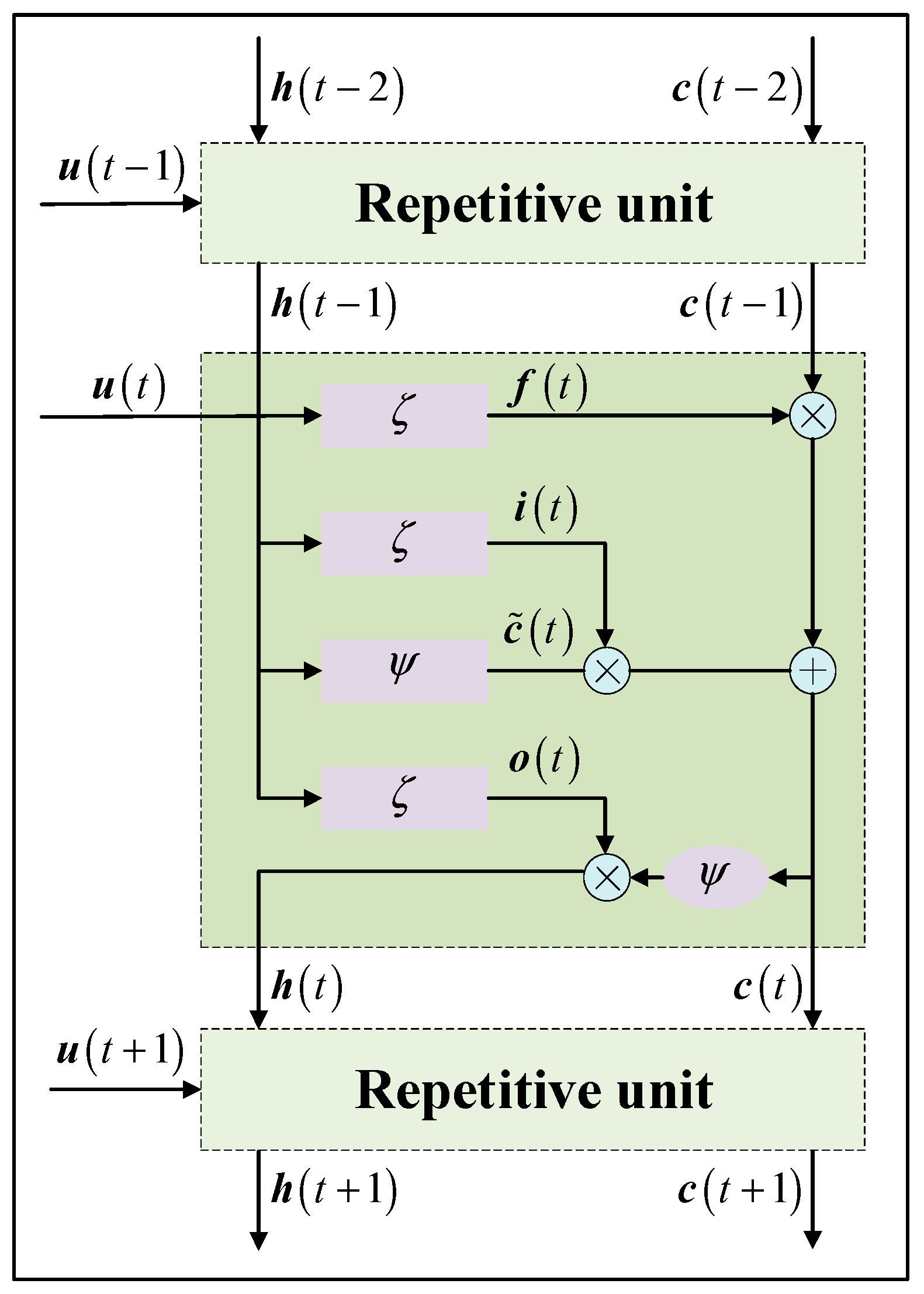
Compensation Model Construction Module
- (1)
- Forward calculation process
- (2)
- Backpropagation process
Hyperparameter Optimization Module
- (1)
- Set the boundary space.
- (2)
- Construct the initial data set.
- (3)
- Construct/train the GPR model.
- (4)
- Estimate the parameters of the GPR model.
- (5)
- Sampling.
- (6)
- Update the data set.
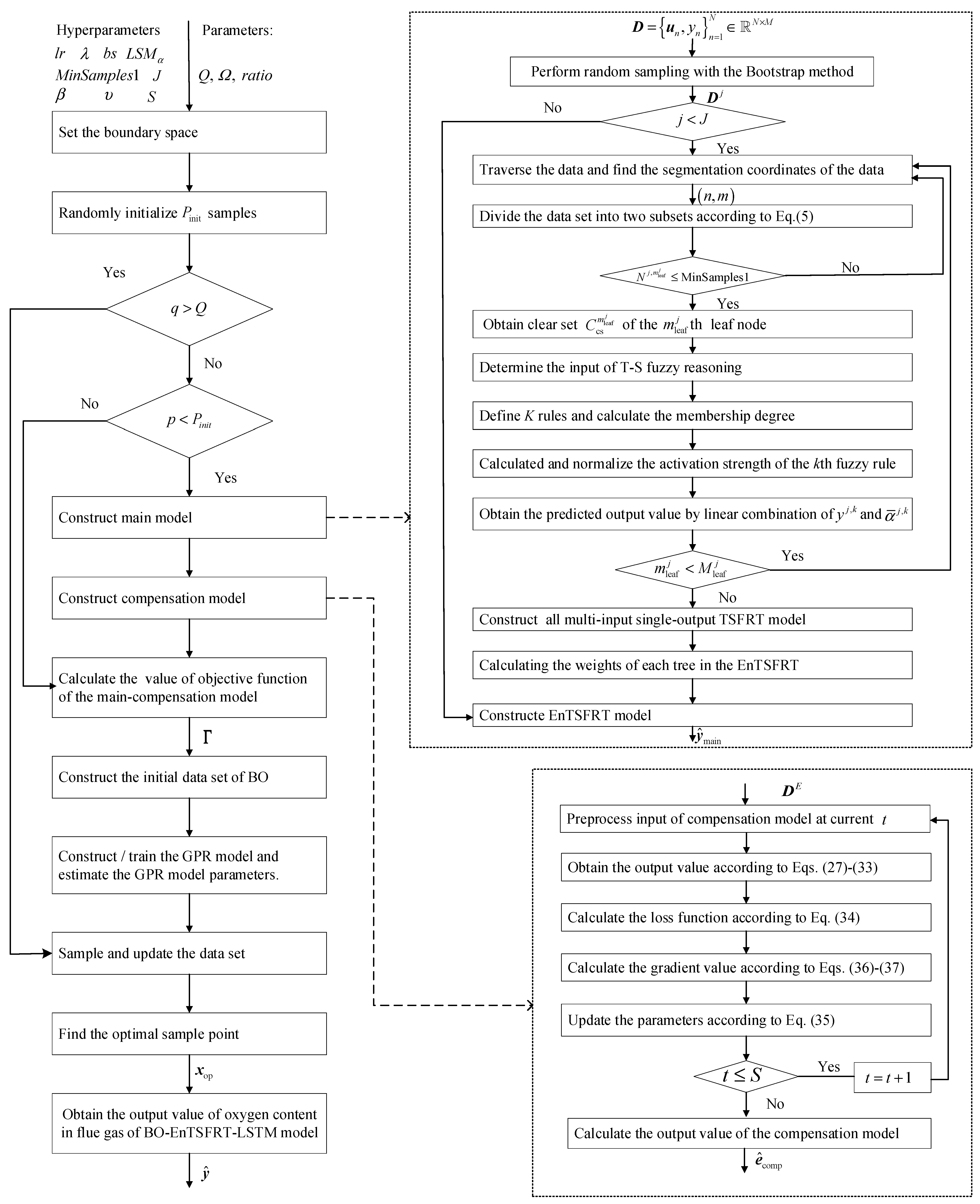
2.3.3. Pseudocode and Flow Chart
Pseudocode
| Algorithm 1. Pseudocode of the BO-EnTSFRT-LSTM algorithm. | |
| 1 | Data set ; Parameters of BO: , , ; Hyperparameters of EnTSFRT: , , , , and ; Hyperparameters of LSTM: , and Output: Predicted value |
| 2 | Read the data, set the boundary space, and randomly initialize samples; |
| 3 | If |
| 4 | If |
| 5 | Take as the input of the EnTSFRT model; |
| 6 | If |
| 7 | If |
| 8 | If |
| 9 | Traverse the data and determine the optimal segmentation point by minimizing the MSE; |
| 10 | Divide the data into two subsets, and ; |
| 11 | end |
| 12 | Obtain subsets , and the clear set of the leaf node; |
| 13 | Obain the input of the fuzzy reasoning layer corresponding to the leaf node ; |
| 14 | Define K rules to represent the local linear relationship between the input variable and the output; |
| 15 | Calculate the membership degree of to ; |
| 16 | Calculate the activation intensity of the kth fuzzy rule and carry out the normalization operation to obtain ; |
| 17 | Obtain the predicted output value by linear combination of and ; |
| 18 | end |
| 19 | Construct a multi-input single-output TSFRT sub-model ; |
| 20 | Update the weights of consequent. |
| 21 | end |
| 22 | Construct EnTSFRT by ensemble multiple TSFRT sub-models; |
| 23 | Calculate the error value of the EnTSFRT model; |
| 24 | Use as the input of LSTM model; |
| 25 | Initialize the parameters; |
| 26 | If |
| 27 | Calculation the outputs according to Equations (26)–(32); |
| 28 | Calculate the loss function according to Equation (33); |
| 29 | Calculate the gradient value according to Equations (35) and (36); |
| 30 | Update the parameters according to Equation (34); |
| 31 | end |
| 32 | end |
| 33 | Construct BO initial data set; |
| 34 | Construct GPR model; |
| 35 | Sample and update the data set; |
| 36 | Find the optimal sample point; |
| 37 | end |
| 38 | Obtain the predicted value . |
Flow Chart
3. Results and Discussion
3.1. Evaluation Indices
3.2. Experimental Results
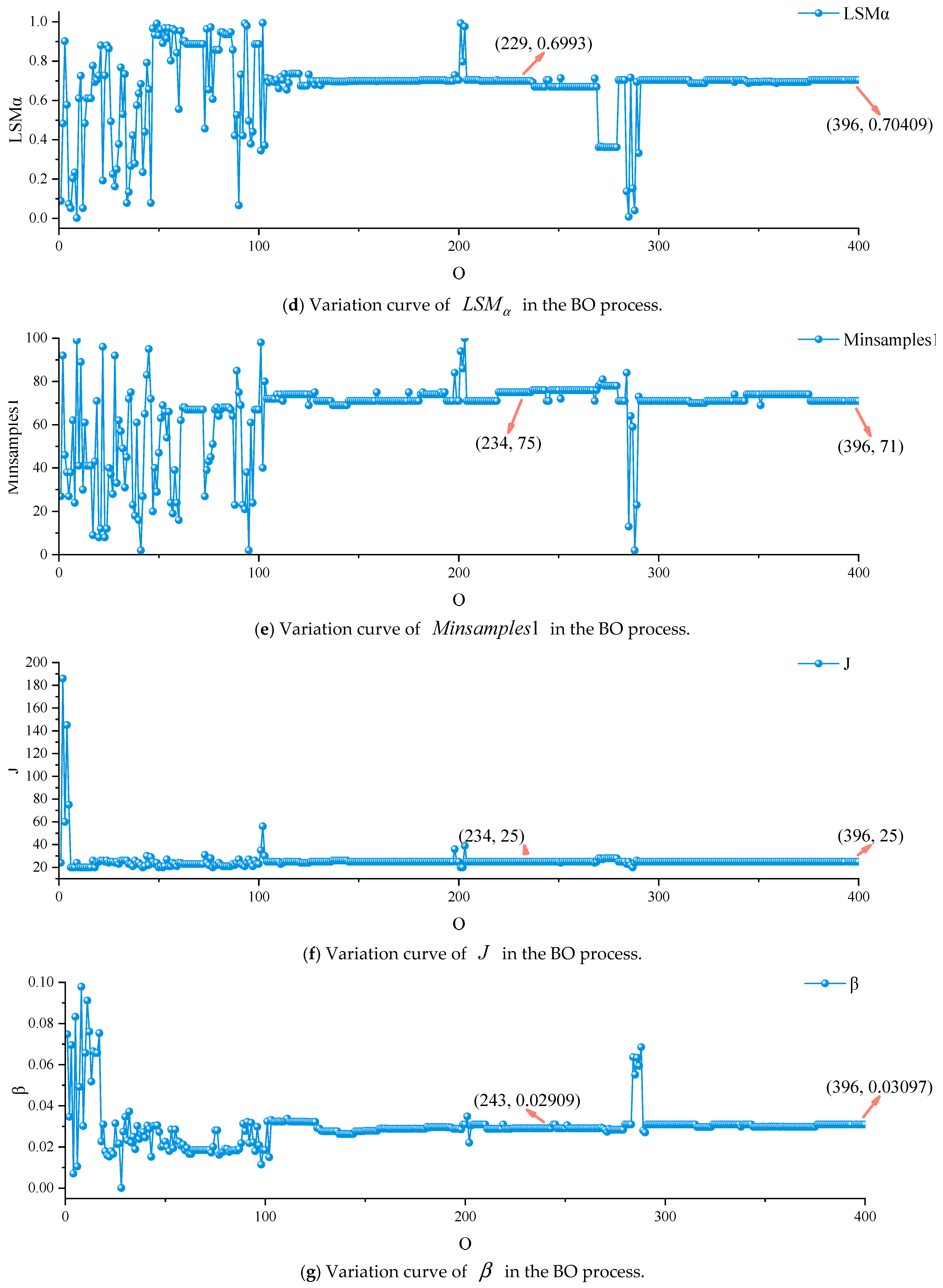
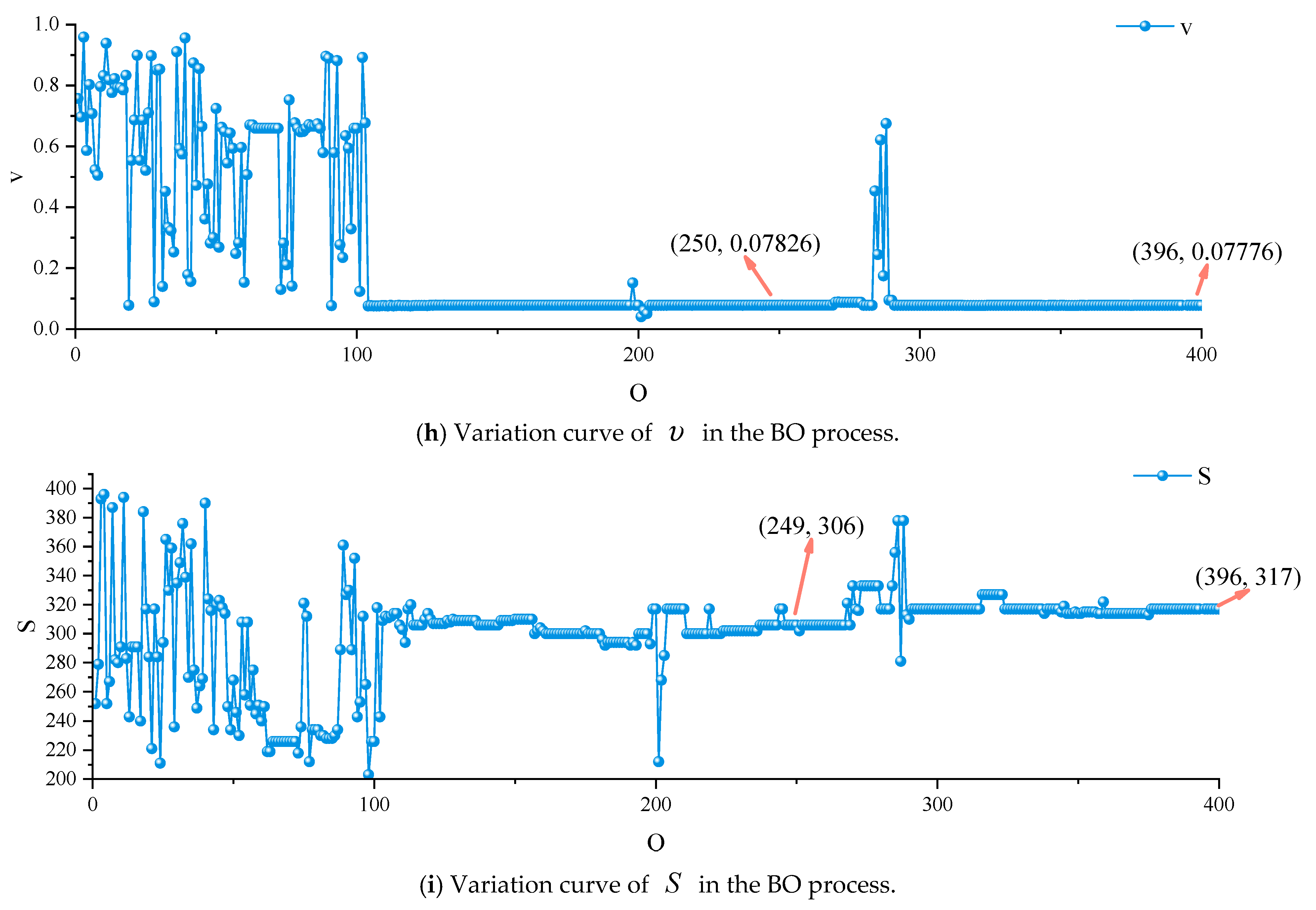
3.2.1. BO Parameters Based on the Grid Search
3.2.2. Main–Compensation Ensemble Modeling Results
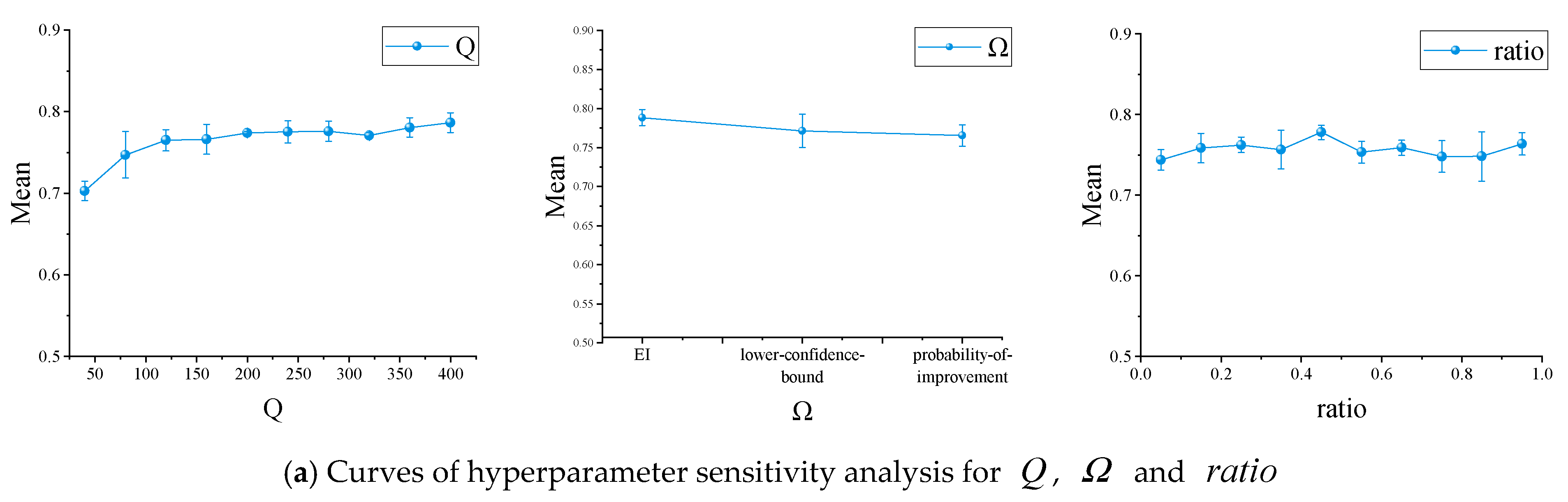
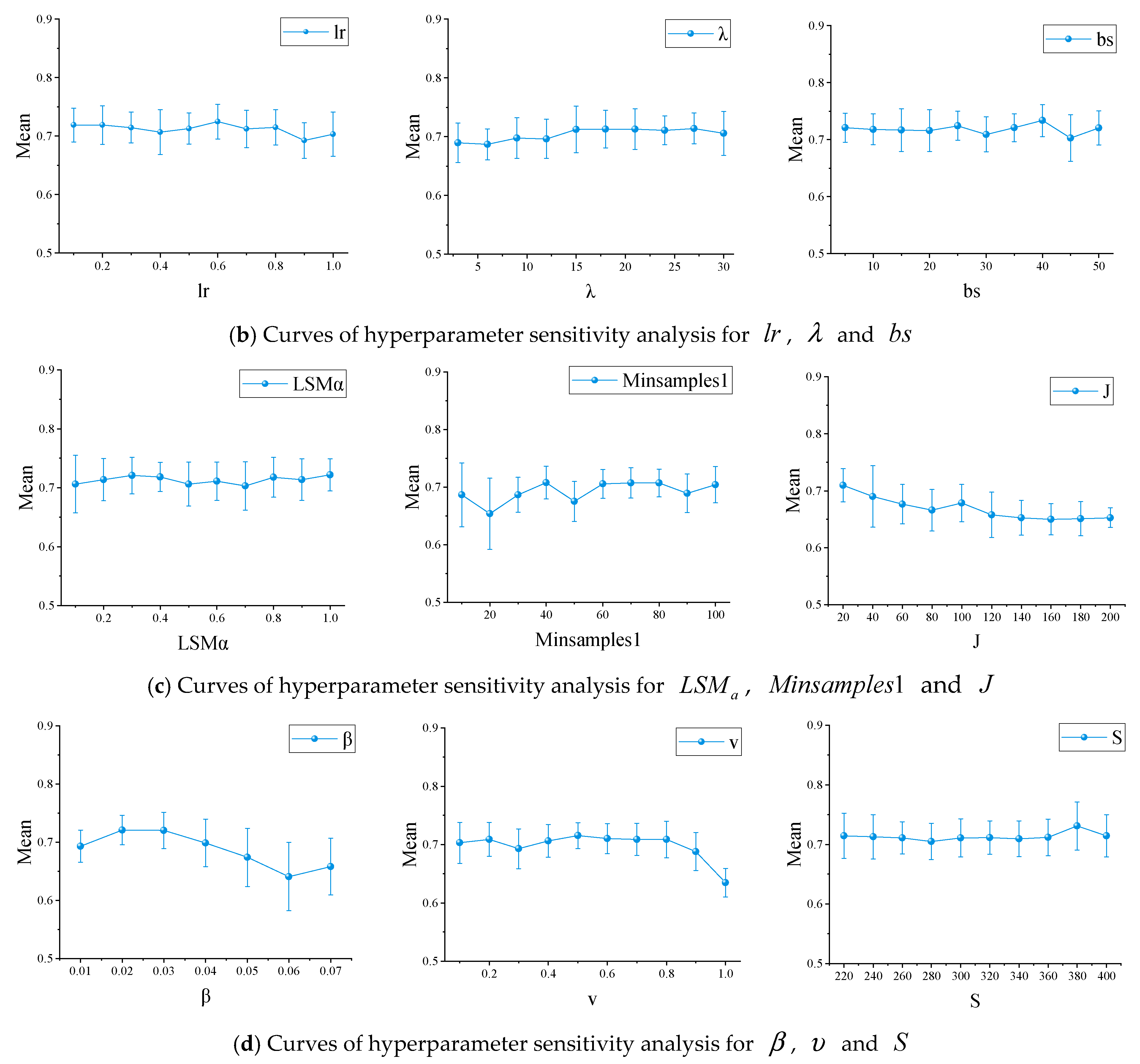
3.2.3. Hyperparameter Variation Results Based on BO
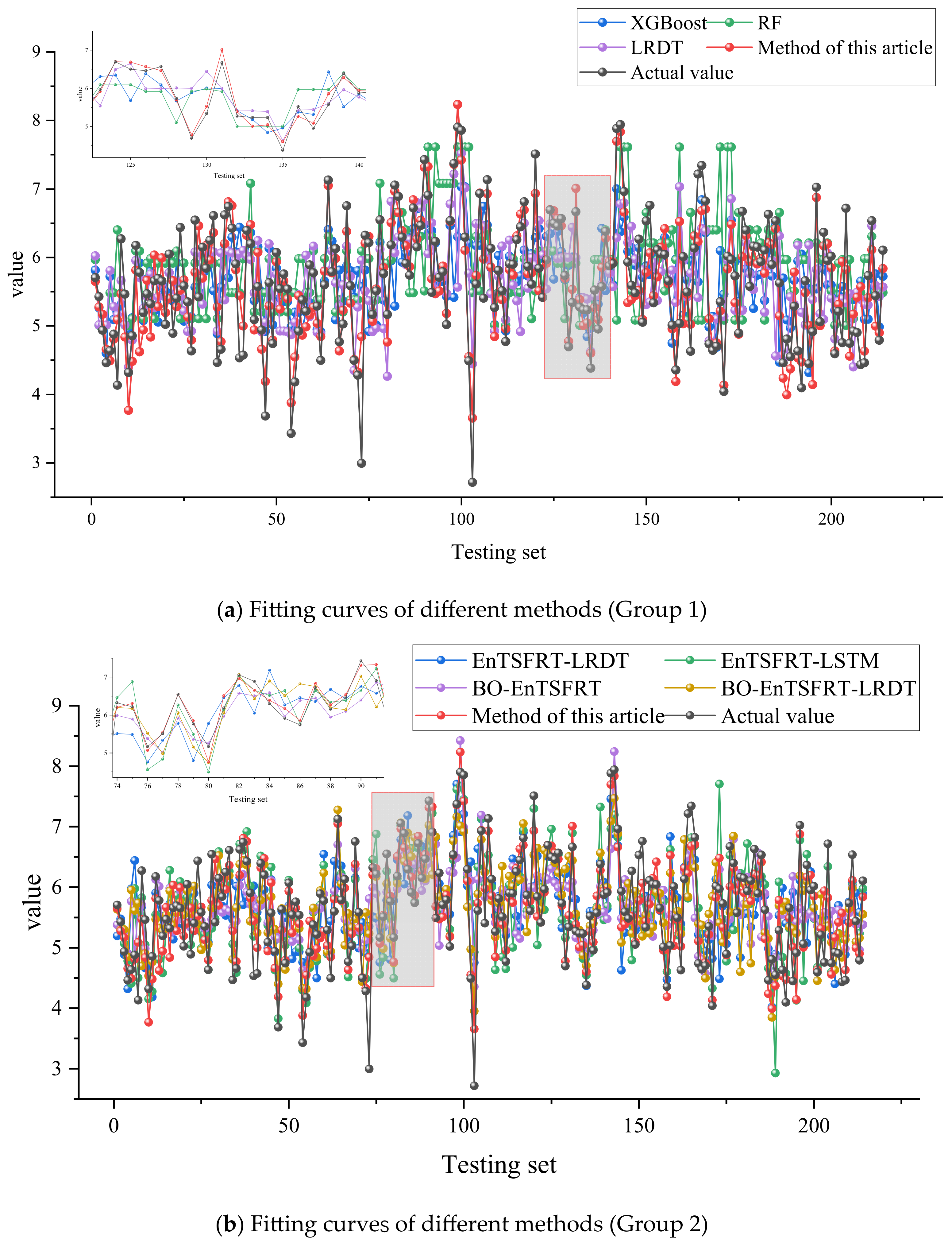
3.3. Method Comparison
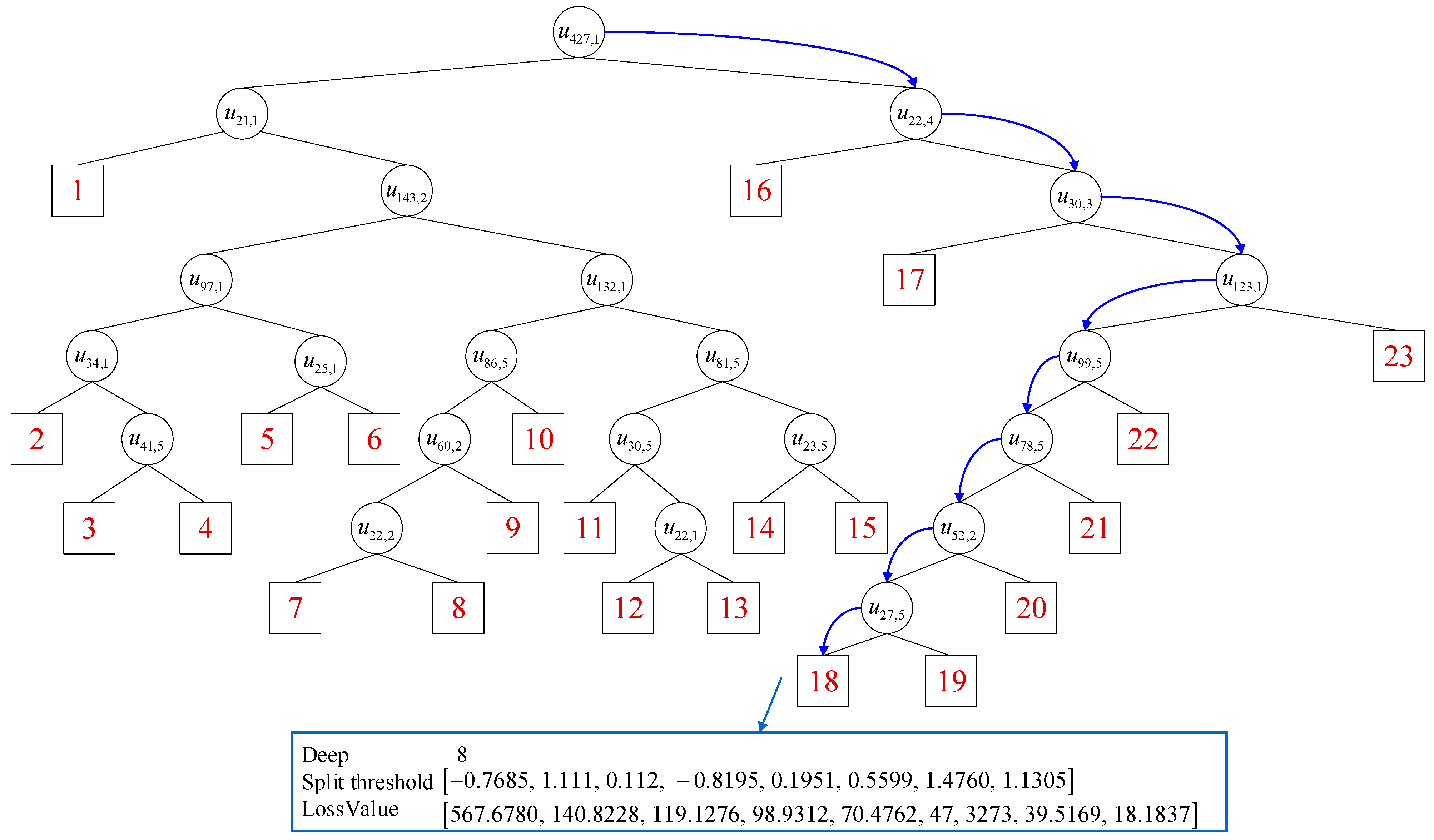
3.4. Interpretability Analysis
3.5. Hyperparameter Discussion
3.6. Comprehensive Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Order | Stage | Elements | Descriptions |
|---|---|---|---|
| 1 | Solid waste fermentation | Crab bucket | It is primarily used to grab MSW and transport it from the waste reservoir to the feeding inlet of the incinerator. |
| 2 | Solid waste reservoir | It is used for storing and pre-processing MSW that is awaiting incineration. | |
| 3 | Slag pool | It is used for collecting and processing the slag generated after incineration. | |
| 4 | Solid waste combustion | Hopper | It is a device used for the temporary storage and transportation of MSW. |
| 5 | Auxiliary burner | It is a key device used to provide additional heat. | |
| 6 | Feeder | It is a device used to transport MSW from the hopper to the incinerator. | |
| 7 | Drying grate | It is used for the drying and pre-processing of MSW. | |
| 8 | Combustion grate | It is a key device used for the combustion of MSW. | |
| 9 | Burner grate | It is a device used for the burnout of MSW and the handling of slag. | |
| 10 | SSC | It is used to process the slag generated after incineration, achieving the dual goals of resource recovery and environmental protection by separating metals, cooling the slag, and reducing environmental pollution. | |
| 11 | Primary air fan | It is a key device used to supply the primary air required for combustion. | |
| 12 | Secondary air fan | It is a key device used to supply secondary air. | |
| 13 | Air preheating | Through certain equipment or systems, the air temperature is raised to a predetermined level. | |
| 14 | Denitration system | A system that removes nitrogen oxides (NOx) from flue gases through chemical or physical methods. | |
| 15 | Steam power generation | Turbogenerator | Transforming the heat energy generated during the incineration process into electricity. |
| 16 | Waste heat exchange | Steam | The high-temperature, high-pressure gas generated by heating water through a boiler is mainly used for converting and utilizing the thermal energy from waste heat. |
| 17 | Superheater | The already evaporated saturated steam is further heated to raise its temperature, converting it into superheated steam. | |
| 18 | Evaporator | Waste heat or other heat sources are utilized to heat the liquid to its boiling point and evaporate it into steam. | |
| 19 | Economizer | By recovering and utilizing the waste heat from flue gases, this preheats the cold water entering the boiler or other equipment. | |
| 20 | Water supply | Provides the necessary cold water for the waste heat exchange system, which, after waste heat exchange, can absorb heat and circulate within the system. | |
| 21 | Flue gas G1 | It is the flue gas emitted from the outlet of the waste heat boiler, which contains high concentrations of various pollutants and requires cleaning treatment. | |
| 22 | Hammering equipment | Through mechanical vibration or tapping, it helps remove dirt, deposits, or other substances that may accumulate on the surface of the heat exchanger and obstruct heat transfer. | |
| 23 | Ash conveyor | Collects and transports the ash generated during the combustion process from the combustion equipment to the designated processing or storage area. | |
| 24 | Flue gas cleaning | Reclaimed water | It is treated wastewater. |
| 25 | Reactor | Removes or transforms harmful substances in flue gas through chemical or physical processes. | |
| 26 | Bag filter | Used to remove solid particles from flue gas, effectively capturing dust, particulate matter, and other pollutants in the flue gas through physical filtration. | |
| 27 | Mixer | Evenly mixes different gases or liquid components to achieve a more effective cleaning treatment. | |
| 28 | Fly ash tank | Used to collect and store the fly ash removed from the flue gas. | |
| 29 | Flue gas G2 | It is cleaned flue gas that is discharged into the chimney through an induced draft fan. | |
| 30 | Induced draft fan | Discharges flue gas, maintains system pressure, and promotes airflow. | |
| 31 | Flue gas emission | Dioxins | It is generated by the reaction of chlorine and aromatic hydrocarbons under high-temperature conditions, usually as a byproduct of the combustion process. |
| 32 | CO | It is generated by the reaction of carbon and oxygen under incomplete combustion conditions, and is a colorless, odorless, and tasteless gas. | |
| 33 | SO2 | It is a common pollutant generated by the reaction of sulfur and oxygen, and is typically released during the combustion of sulfur-containing fuels. | |
| 34 | CO2 | It is one of the main greenhouse gases produced in the combustion process. | |
| 35 | NOx | It consists of thermal NOx, which is formed by the oxidation of nitrogen (N2) in the air at high temperatures during combustion, and fuel NOx, which is generated from the combustion of nitrogen-containing organic matter in waste. It is one of the major pollutants in incineration flue gas. | |
| 36 | HCl | It is one of the major acidic pollutants in the flue gas, primarily originating from the combustion of chlorine-containing substances in the waste. | |
| 37 | Particulate matter | It is one of the important pollutants in the flue gas, primarily composed of incompletely combusted solid particles, fly ash, heavy metal oxides, and salt particles formed by the reaction of acidic gases with alkaline substances. | |
| 38 | Flue gas G3 | It is the flue gas emitted into the atmosphere through chimneys, and the concentration of pollutants it contains must meet the requirements of the national environmental protection department. | |
| 39 | Chimney | It is the final channel for flue gas emissions from the incineration plant, primarily used to discharge the cleaned flue gas into the atmosphere. |
| Order | English Abbreviation | English Full Name |
|---|---|---|
| 1. | MSW | Municipal solid waste |
| 2. | MSWI | MSW incineration |
| 3. | AI | Artificial intelligence |
| 4. | CV | Controlled variable |
| 5. | DXN | Dioxin |
| 6. | SO2 | Sulfur dioxide |
| 7. | NN | Neural network |
| 8. | LSTM | Long short-term memory |
| 9. | ILSTM | Improved LSTM |
| 10. | TS | Takagi–Sugeno |
| 11. | TSFNN | TS fuzzy neural network |
| 12. | MIMO | Multiple-input multiple-output |
| 13. | EnTSFRT | TS fuzzy regression tree |
| 14. | SCR | Selective catalytic reduction |
| 15. | GBDT | Gradient boosting decision tree |
| 16. | BO | Bayesian optimization |
| 17. | MV | Manipulated variable |
| 18. | PCC | Pearson correlation coefficient |
| 19. | MSE | Mean square error |
| 20. | RNN | Recurrent neural network |
| 21. | EI | Expected improvement |
| 22. | R2 | R-square |
| 23. | UB | Upper boundary |
| 24. | LB | Lower boundary |
| 25. | GPR | Gaussian process regression |
| 26. | MLE | Maximum likelihood estimation |
| 27. | RMSE | Root mean square error |
| 28. | MAE | Mean absolute error |
| 29. | eXtreme gradient boosting | XGBoost |
| 30. | Random forest | RF |
| 31. | Linear regression decision tree | LRDT |
| Order | Symbol | Meaning |
|---|---|---|
| 1. | Manipulated variables | |
| 2. | True value of flue gas oxygen content | |
| 3. | Output value of flue gas oxygen content of the main model | |
| 4. | Error value of the main model | |
| 5. | Output value of the compensation model | |
| 6. | Error value of the compensation model | |
| 7. | Output value of BO-EnTSFRT-LSTM model | |
| 8. | Learning rate | |
| 9. | Number of batches | |
| 10. | Initial value of intermediate variable in the recursive calculation process | |
| 11. | Regularization coefficient of the main model | |
| 12. | Minimum number of samples of the main model | |
| 13. | Number of sub-models that constitute the EnTSFRT model | |
| 14. | Learning rate of the compensation model | |
| 15. | Regularization coefficient of the compensation model | |
| 16. | Maximum number of iterations of the compensation model | |
| 17. | Input of EnTSFRT | |
| 18. | Index of the sample | |
| 19. | Total number of input samples | |
| 20. | Dimension of the input feature | |
| 21. | Index of the input feature | |
| 22. | input sample in | |
| 23. | True value of the sample in | |
| 24. | Index of the training subset | |
| 25. | training subset | |
| 26. | training subset obtained by performing random sampling with the Bootstrap method on | |
| 27. | Left subset obtained by splitting the first non-leaf node | |
| 28. | Right subset obtained by splitting the first non-leaf node | |
| 29. | True value vector of flue gas oxygen content | |
| 30. | TSFRT sub-model | |
| 31. | Number of non-leaf nodes in the TSFRT sub-model | |
| 32. | Index of the non-leaf nodes in the TSFRT sub-model | |
| 33. | Number of leaf nodes in the TSFRT sub-model | |
| 34. | Index of the leaf nodes in the TSFRT sub-model | |
| 35. | ||
| 36. | TSFRT sub-model | |
| 37. | TSFRT sub-model | |
| 38. | MSE value of the left subset (or right subset ) | |
| 39. | ||
| 40. | ||
| 41. | non-leaf node | |
| 42. | ||
| 43. | ||
| 44. | Number of samples in the (or ) | |
| 45. | non-leaf node | |
| 46. | leaf node | |
| 47. | ||
| 48. | leaf node | |
| 49. | ||
| 50. | ||
| 51. | leaf node | |
| 52. | Fuzzy reasoning layer corresponding to the leaf node | |
| 53. | input vector of the fuzzy reasoning layer | |
| 54. | feature of input vector of the fuzzy reasoning layer | |
| 55. | Number of samples in the leaf node | |
| 56. | Total number of fuzzy rules | |
| 57. | Index of the fuzzy rule | |
| 58. | Membership degree of belonging to | |
| 59. | fuzzy rule | |
| 60. | Nonlinear function between and | |
| 61. | rule | |
| 62. | ||
| 63. | ||
| 64. | ||
| 65. | fuzzy rule | |
| 66. | Cartesian product | |
| 67. | ||
| 68. | non-leaf nodes are split | |
| 69. | Weight of the initial time | |
| 70. | value in | |
| 71. | Intermediate variable in the recursive process | |
| 72. | ||
| 73. | A large positive value | |
| 74. | Unit matrix | |
| 75. | sub-model | |
| 76. | samples | |
| 77. | Weight matrix of TSFRT sub-models when EnTSFRT model is contrusted | |
| 78. | Current moment (iteration time) | |
| 79. | Hidden state | |
| 80. | Cell state | |
| 81. | Candidate cell state | |
| 82. | Sigmoid function | |
| 83. | Tanh function | |
| 84. | Value of the forget gate | |
| 85. | Value of the input gate | |
| 86. | Value of the output gate | |
| 87. | Element-by-element multiplication | |
| 88. | Input of the compensation model | |
| 89. | Weight matrix | |
| 90. | Bias matrix | |
| 91. | Output weight matrix | |
| 92. | Loss function in the training process of LSTM | |
| 93. | Hyperparameters set for BO | |
| 94. | Optimization number of BO iterations | |
| 95. | EI sampling function | |
| 96. | Exploration ratio | |
| 97. | Number of sample features | |
| 98. | Number of iterations of the optimization | |
| 99. | Number of data set samples at the current time | |
| 100. | Number of initial inputs for the BO algorithm | |
| 101. | Objective function value corresponding to the observation sample | |
| 102. | ||
| 103. | Mean function | |
| 104. | Covariance matrix | |
| 105. | Variance of noise | |
| 106. | Kernel function between and sample points | |
| 107. | sample | |
| 108. | Kernel amplitude of kernel function | |
| 109. | dimension of the sample | |
| 110. | Training testing set covariance | |
| 111. | Posterior mean value | |
| 112. | Posterior variance | |
| 113. | New samples obtained by updating the data set in BO process | |
| 114. | Minimum number of samples of LRDT model |
References
- Gómez-Sanabria, A.; Kiesewetter, G.; Klimont, Z.; Schoepp, W.; Haberl, H. Potential for future reductions of global GHG and air pollutants from circular waste management systems. Nat. Commun. 2022, 13, 106. [Google Scholar] [PubMed]
- Ali, K.; Kausar, N.; Amir, M. Impact of pollution prevention strategies on environment sustainability: Role of environmental management accounting and environmental proactivity. Environ. Sci. Pollut. Res. 2023, 30, 88891–88904. [Google Scholar]
- Song, Y.; Xian, X.; Zhang, C.; Zhu, F.; Yu, B.; Liu, J. Residual municipal solid waste to energy under carbon neutrality: Challenges and perspectives for China. Resour. Conserv. Recycl. 2023, 198, 107177. [Google Scholar]
- Tang, J.; Xia, H.; Yu, W.; Qiao, J. Research status and prospect of intelligent optimization control of municipal solid waste incineration process. Acta Autom. Sin. 2023, 49, 2019–2059. [Google Scholar]
- Chen, A.; Chen, J.; Cui, J.; Fan, C.; Han, W. Research on risks and countermeasures of “cities besieged by waste” in China-an empirical analysis based on DIIS. Bull. Chin. Acad. Sci. 2019, 34, 797–806. [Google Scholar]
- Efforts to Promote the Realization of Carbon Peak Carbon Neutral Target. Available online: https://www.ndrc.gov.cn/wsdwhfz/202111/t20211111_1303691.html (accessed on 15 January 2025).
- Walser, T.; Limbach, L.K.; Brogioli, R.; Erismann, E.; Flamigni, L.; Hattendorf, B.; Juchli, M.; Krumeich, F.; Ludwig, C.; Prikopsky, K.; et al. Persistence of engineered nanoparticles in a municipal solid-waste incineration plant. Nat. Nanotechnol. 2012, 7, 520–524. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, L.; Chen, L.; Ma, B.; Zhang, Y.; Ni, W.; Tsang, D. Treatment of municipal solid waste incineration fly ash: State-of-the-art technologies and future perspectives. J. Hazard. Mater. 2021, 411, 125132. [Google Scholar]
- Lu, J.-W.; Zhang, S.; Hai, J.; Lei, M. Status and perspectives of municipal solid waste incineration in China: A comparison with developed regions. Waste Manag. 2017, 69, 170–186. [Google Scholar]
- Zhang, M.; Wei, J.; Li, H.; Chen, Y.; Liu, J. Comparing and optimizing municipal solid waste (MSW) management focused on air pollution reduction from MSW incineration in China. Sci. Total. Environ. 2024, 907, 167952. [Google Scholar]
- Chen, Z.; Wang, L.; Huang, Z.; Zhuang, P.; Shi, Y.; Evrendilek, F.; Huang, S.; He, Y.; Liu, J. Dynamic and optimal ash-to-gas responses of oxy-fuel and air combustions of soil remediation biomass. Renew. Energy 2024, 225, 120229. [Google Scholar]
- Zhao, P.; Gao, Y.; Sun, X. The impact of artificial intelligence on pollution emission intensity—evidence from China. Environ. Sci. Pollut. Res. 2023, 30, 91173–91188. [Google Scholar] [CrossRef]
- Ding, Y.; Zhao, J.; Liu, J.-W.; Zhou, J.; Cheng, L.; Zhao, J.; Shao, Z.; Iris, Ç.; Pan, B.; Li, X.; et al. A review of China’s municipal solid waste (MSW) and comparison with international regions: Management and technologies in treatment and resource utilization. J. Clean. Prod. 2021, 293, 126144. [Google Scholar] [CrossRef]
- Qiao, J.; Sun, J.; Meng, X. Event-triggered adaptive model predictive control of oxygen content for municipal solid waste incineration process. IEEE Trans. Autom. Sci. Eng. 2022, 21, 463–474. [Google Scholar] [CrossRef]
- Sun, J.; Meng, X.; Qiao, J. Data-driven predictive control of flue gas oxygen content in municipal solid waste incineration process. Control. Theory Appl. 2024, 41, 484–495. [Google Scholar]
- Huang, W.; Ding, H.; Qiao, J. Adaptive multi-objective competitive swarm optimization algorithm based on kinematic analysis for municipal solid waste incineration. Appl. Soft Comput. 2023, 149, 110925. [Google Scholar] [CrossRef]
- Sun, J.; Meng, X.; Qiao, J. Event-based data-driven adaptive model predictive control for nonlinear dynamic processes. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 1982–1994. [Google Scholar] [CrossRef]
- Li, L.; Ding, S.; Yang, Y.; Peng, K.; Qiu, J. A fault detection approach for nonlinear systems based on data-driven realizations of fuzzy kernel representations. IEEE Trans. Fuzzy Syst. 2017, 26, 1800–1812. [Google Scholar] [CrossRef]
- Cho, S.; Kim, Y.; Kim, M.; Cho, H.; Moon, I.; Kim, J. Multi-objective optimization of an explosive waste incineration process considering nitrogen oxides emission and process cost by using artificial neural network surrogate models. Process. Saf. Environ. Prot. 2022, 162, 813–824. [Google Scholar] [CrossRef]
- Sildir, H.; Sarrafi, S.; Aydin, E. Optimal artificial neural network architecture design for modeling an industrial ethylene oxide plant. Comput. Chem. Eng. 2022, 163, 107850. [Google Scholar]
- Rahimieh, A.; Mehriar, M.; Zamir, S.M.; Nosrati, M. Fuzzy-decision tree modeling for H2S production management in an industrial-scale anaerobic digestion process. Biochem. Eng. J. 2024, 208, 109380. [Google Scholar] [CrossRef]
- Samek, W.; Montavon, G.; Lapuschkin, S.; Anders, C.J.; Muller, K.-R. Explaining deep neural networks and beyond: A review of methods and applications. Proc. IEEE 2021, 109, 247–278. [Google Scholar]
- Xia, H.; Tang, J.; Yu, W.; Cui, C.; Qiao, J. Takagi–Sugeno Fuzzy Regression Trees With Application to Complex Industrial Modeling. IEEE Trans. Fuzzy Syst. 2023, 31, 2210–2224. [Google Scholar]
- Ma, Y.; Zhou, Y.; Peng, J.; Chen, R.; Dai, H.; Hao, M.; Hu, G.; Xie, Y. Prediction of flue gas oxygen content of power plant with stacked target-enhanced autoencoder and attention-based LSTM. Measurement 2024, 235, 115036. [Google Scholar] [CrossRef]
- Lin, C.; Lee, C. Neural-network-based fuzzy logic control and decision system. IEEE Trans. Comput. 1991, 40, 1320–1336. [Google Scholar] [CrossRef]
- Wu, D.; Peng, R.; Mendel, J. Type-1 and interval type-2 fuzzy systems. IEEE Comput. Intell. Mag. 2023, 18, 81–83. [Google Scholar]
- Takalo-Mattila, J.; Heiskanen, M.; Kyllonen, V.; Maatta, L.; Bogdanoff, A. Explainable steel quality prediction system based on gradient boosting decision trees. IEEE Access 2022, 10, 68099–68110. [Google Scholar]
- Alrbai, M.; Al-Dahidi, S.; Alahmer, H.; Al-Ghussain, L.; Hayajneh, H.; Shboul, B.; Abusorra, M.; Alahmer, A. Utilizing waste heat in wastewater treatment plants for water desalination: Modeling and Multi-Objective optimization of a Multi-Effect desalination system using Decision Tree Regression and Pelican optimization algorithm. Therm. Sci. Eng. Prog. 2024, 54, 102784. [Google Scholar]
- Meng, T.; Zhang, W.; Huang, J.; Chen, Y.-H.; Chew, C.-M.; Yang, D.; Zhong, Z. Fuzzy reasoning based on truth-value progression: A control-theoretic design approach. Int. J. Fuzzy Syst. 2023, 25, 1559–1578. [Google Scholar] [CrossRef]
- Yang, T.; Ma, K.; Lv, Y.; Fang, F.; Chang, T. Hybrid dynamic model of SCR denitrification system for coal-fired power plant. In Proceedings of the 2019 IEEE 28th International Symposium on Industrial Electronics (ISIE), Vancouver, BC, Canada, 12–14 June 2019; pp. 106–111. [Google Scholar]
- Luo, A.; Liu, B. Temperature prediction of roller kiln based on mechanism and SSA-ELM data-driven integrated model. In Proceedings of the 2022 China Automation Congress (CAC), Xiamen, China, 25–27 November 2022; pp. 5598–5603. [Google Scholar]
- Dong, S.; Zhang, Y.; Liu, J.; Zhou, X.; Wang, X. Intelligent compensation prediction of leaching process based on GRU neural network. In Proceedings of the 2022 China Automation Congress (CAC), Xiamen, China, 25–27 November 2022; pp. 1663–1668. [Google Scholar]
- Li, B.; Tian, W.; Zhang, C.; Hua, F.; Cui, G.; Li, Y. Positioning error compensation of an industrial robot using neural networks and experimental study. Chin. J. Aeronaut. 2022, 35, 346–360. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Wang, W.; Deng, C.; Zhao, L. Research on the application of ellipsoid bound algorithm in hybrid modeling. Acta Autom. Sin. 2014, 40, 1875–1881. [Google Scholar]
- Zhang, R.; Tang, J.; Xia, H.; Chen, J.; Yu, W.; Qiao, J. Heterogeneous ensemble prediction model of CO emission concentration in municipal solid waste incineration process using virtual data and real data hybrid-driven. J. Clean. Prod. 2024, 445, 141313. [Google Scholar] [CrossRef]
- Ma, S.; Chen, Z.; Zhang, D.; Du, Y.; Zhang, X.; Liu, Q. Interpretable multi-task neural network modeling and particle swarm optimization of process parameters in laser welding. Knowl. Based Syst. 2024, 300, 112116. [Google Scholar]
- Deng, J.; Liu, G.; Wang, L.; Liu, G.; Wu, X. Intelligent optimization design of squeeze casting process parameters based on neural network and improved sparrow search algorithm. J. Ind. Inf. Integr. 2024, 39, 100600. [Google Scholar]
- Zhou, X.; Tan, J.; Yu, J.; Gu, X.; Jiang, T. Online robust parameter design using sequential support vector regression based Bayesian optimization. J. Math. Anal. Appl. 2024, 540, 128649. [Google Scholar]
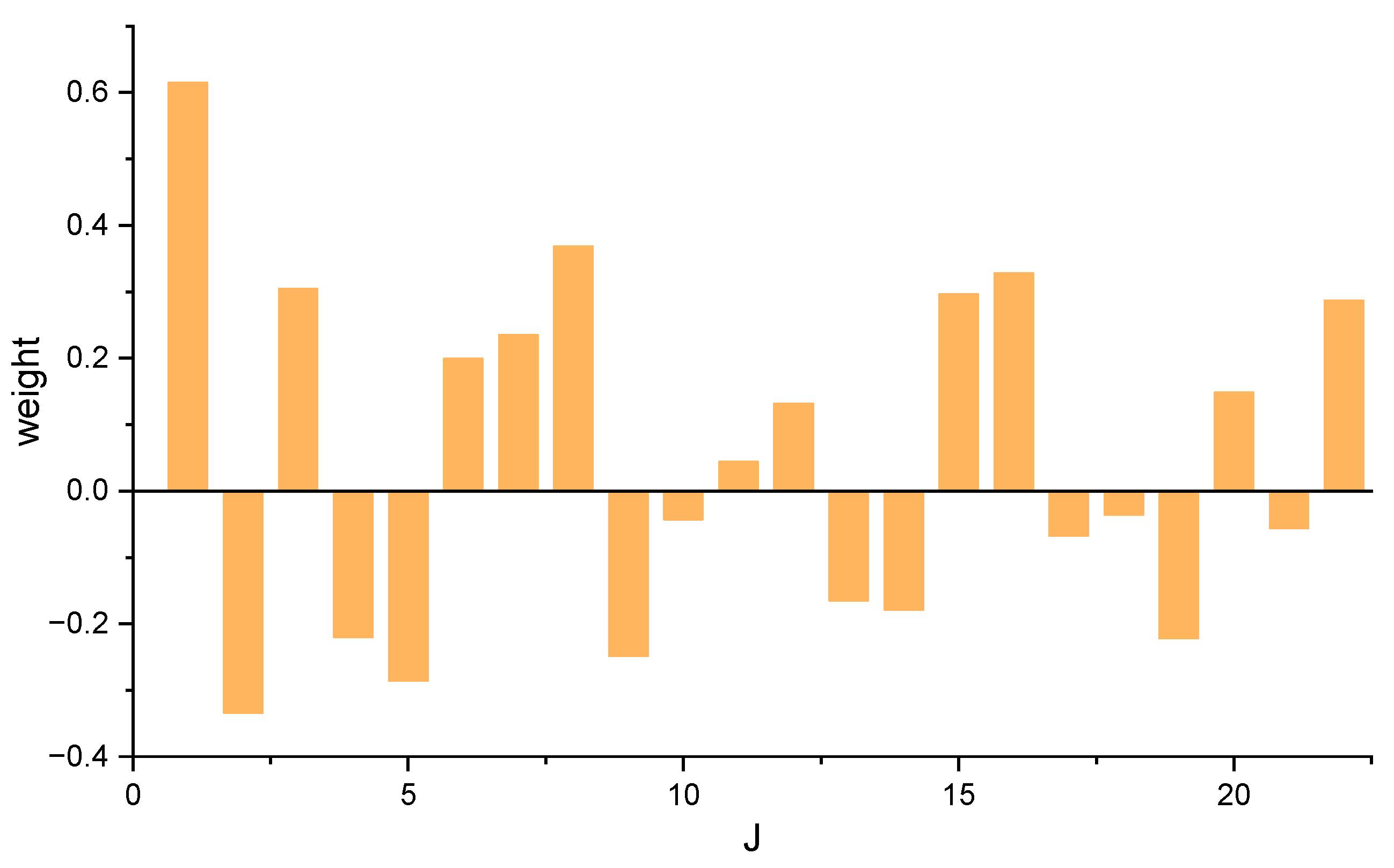
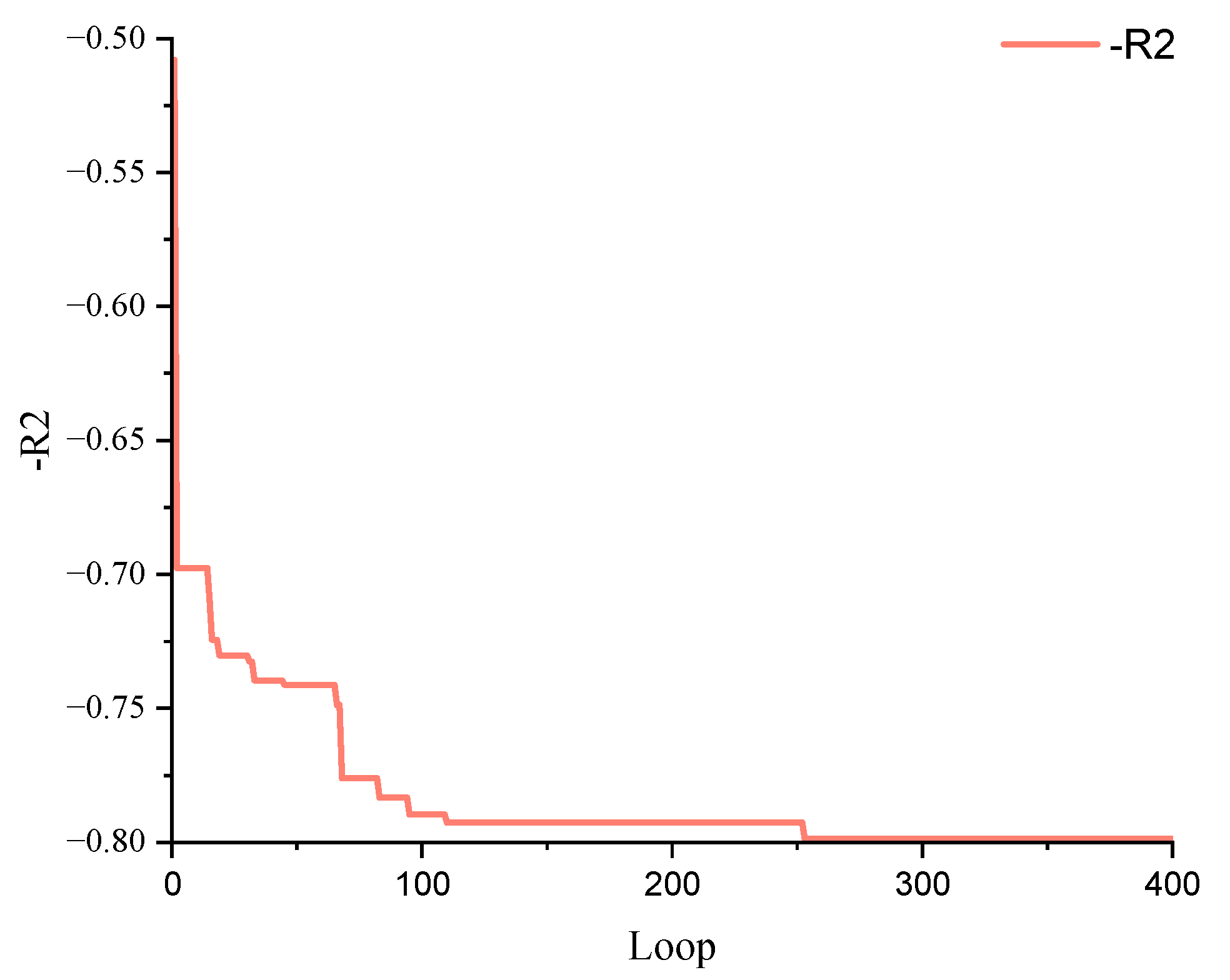
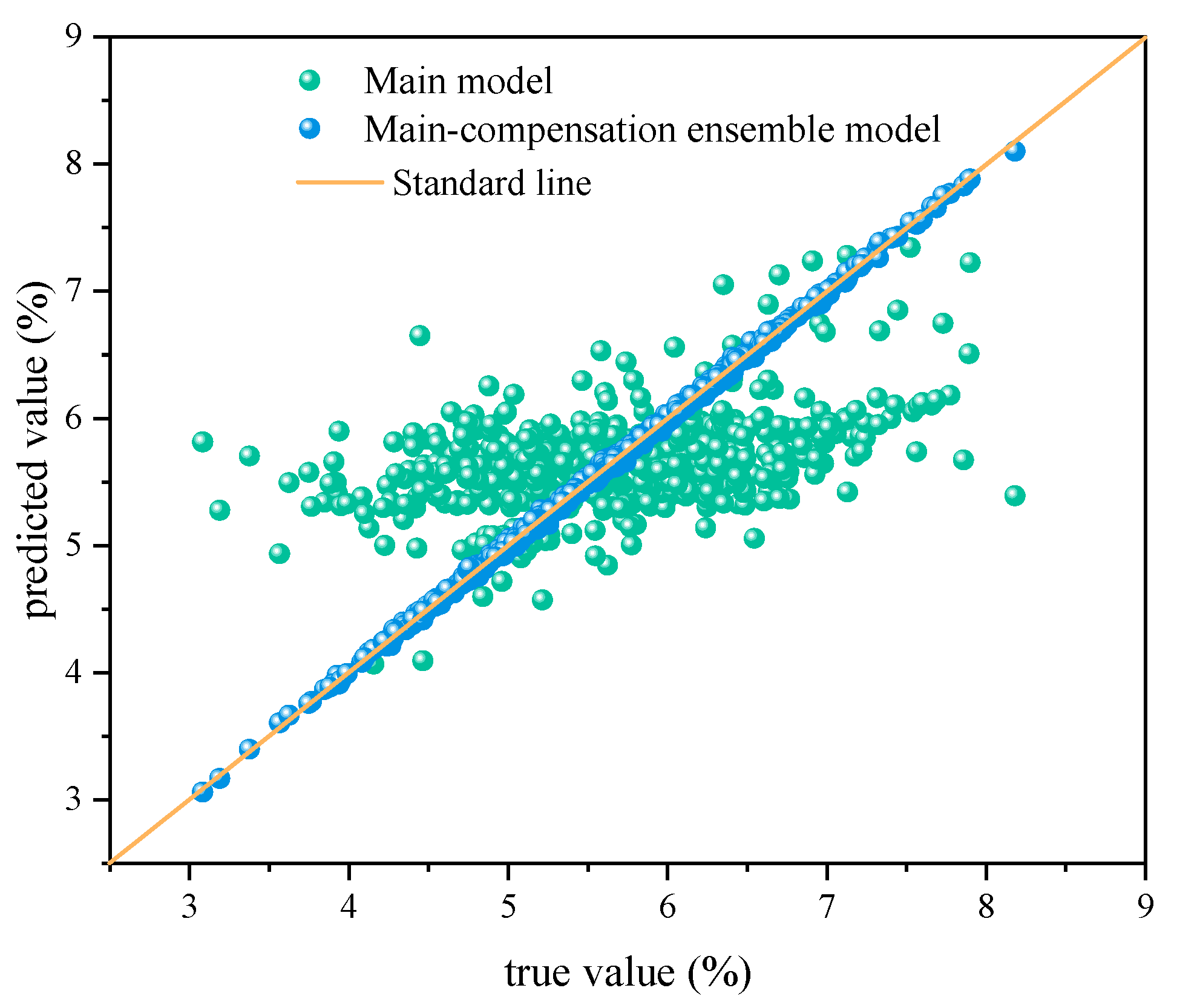
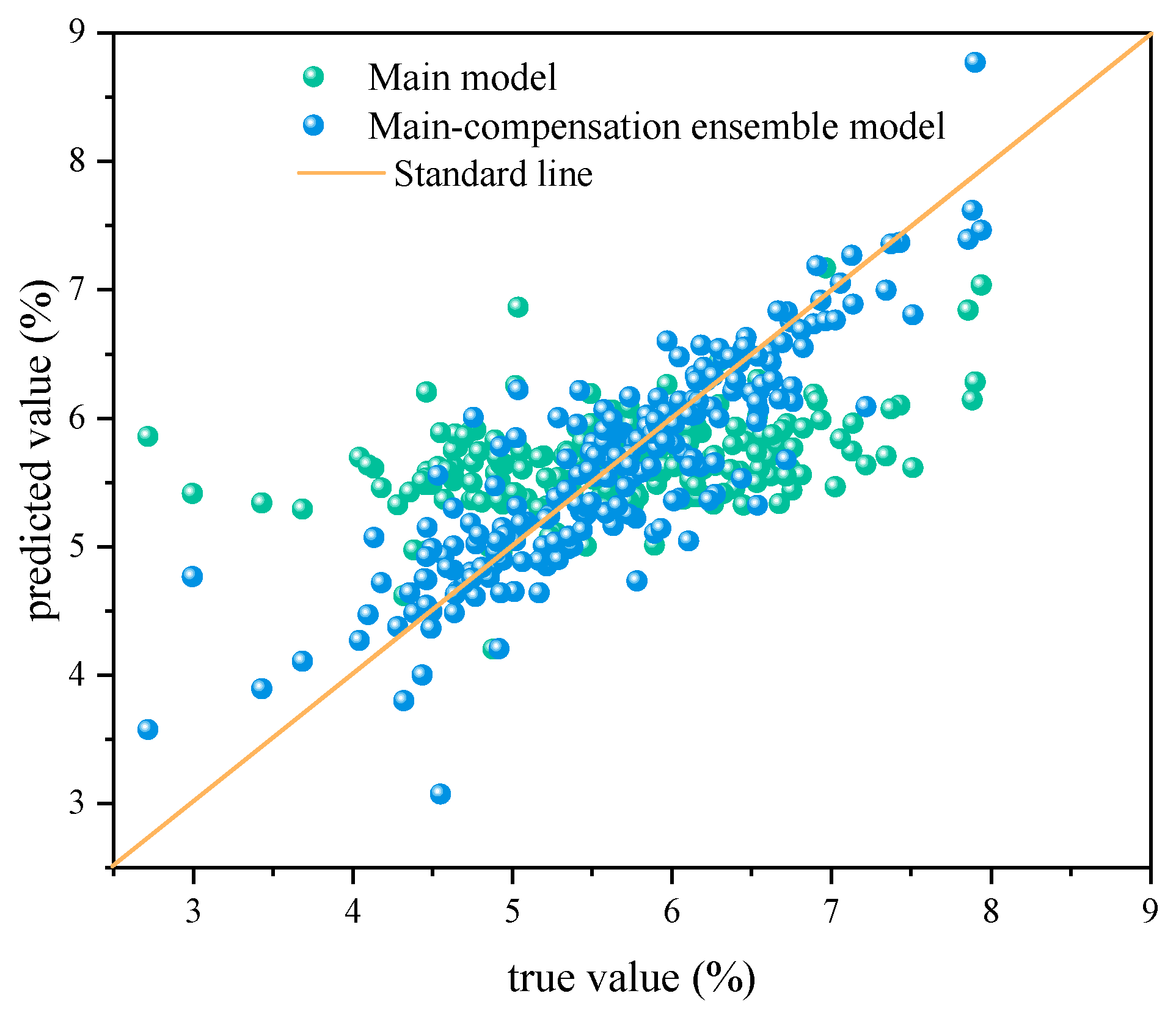
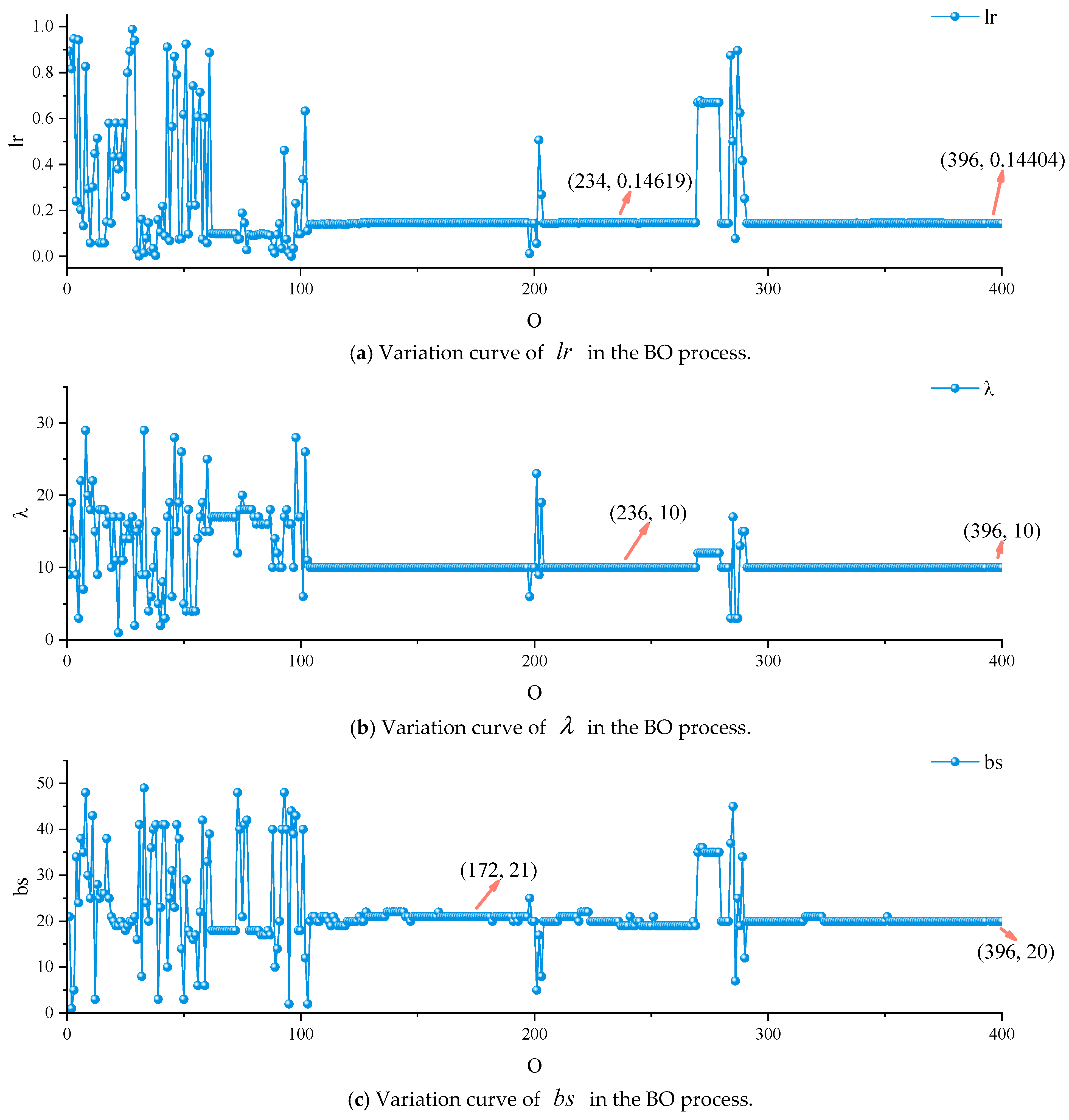
| Data Set | Method | RMSE | MAE | R2 |
|---|---|---|---|---|
| Training set | Main model | 9.0385 × 10−1 | 7.2671 × 10−1 | 1.8305 × 10−1 |
| Main–compensation ensemble model | 2.4573 × 10−2 | 1.9215 × 10−2 | 9.9912 × 10−1 | |
| Testing set | Main model | 9.8680 × 10−1 | 7.8328 × 10−1 | 1.5956 × 10−1 |
| Main–compensation ensemble model | 4.3497 × 10−1 | 3.1282 × 10−1 | 7.6216 × 10−1 |
| Data Set | Method | RMSE | MAE | R2 |
|---|---|---|---|---|
| Training set | XGBoost | 4.9222 × 10−1 ± 1.1614 × 10−6 | 3.6090 × 10−1 ± 2.4410 × 10−6 | 6.4713 × 10−1 ± 2.3640 × 10−6 |
| RF | 8.6432 × 10−1 ± 1.1677 × 10−31 | 6.4993 × 10−1 ± 1.2975 × 10−32 | −8.8061 × 10−2 ± 8.1092 × 10−34 | |
| LRDT | 5.2664 × 10−1 ± 5.1899 × 10−32 | 4.0872 × 10−1 ± 1.2975 × 10−32 | 5.9604 × 10−1 ± 1.2975 × 10−32 | |
| EnTSFRT-LRDT | 4.4932 × 10−1 ± 1.1640 × 10−4 | 3.5266 × 10−1 ± 8.4882 × 10−5 | 7.0088 × 10−1 ± 2.0645 × 10−4 | |
| EnTSFRT-LSTM | 4.5666 × 10−2 ± 4.1522 × 10−4 | 3.3945 × 10−2 ± 1.6713 × 10−4 | 9.9639 × 10−1 ± 1.7202 × 10−5 | |
| BO-EnTSFRT | 6.4563 × 10−1 ± 9.0752 × 10−5 | 5.1347 × 10−1 ± 6.8136 × 10−5 | 5.8308 × 10−1 ± 1.5481 × 10−4 | |
| BO-EnTSFRT-LRDT | 4.3465 × 10−1 ± 2.9193 × 10−32 | 3.4153 × 10−1 ± 1.2975 × 10−32 | 7.2484 × 10−1 ± 5.1899 × 10−32 | |
| BO-EnTSFRT-LSTM | 2.6610 × 10−2 ± 5.8122 × 10−6 | 2.0684 × 10−2 ± 3.3649 × 10−6 | 9.9896 × 10−1 ± 3.8281 × 10−8 | |
| Testing set | XGBoost | 7.4611 × 10−1 ± 5.7058 × 10−5 | 5.6974 × 10−1 ± 9.2326 × 10−6 | 3.0015 × 10−1 ± 1.9958 × 10−4 |
| RF | 9.7815 × 10−1 ± 5.1899 × 10−32 | 7.4468 × 10−1 ± 5.1899 × 10−32 | −2.0272 × 10−1 ± 1.2975 × 10−32 | |
| LRDT | 7.6825 × 10−1 ± 0.0000 | 5.9607 × 10−1 ± 5.1899 × 10−32 | 2.5808 × 10−1 ± 0.0000 | |
| EnTSFRT-LRDT | 7.3435 × 10−1 ± 3.5825 × 10−4 | 5.7583 × 10−1 ± 1.6158 × 10−4 | 2.4216 × 10−1 ± 1.4912 × 10−3 | |
| EnTSFRT-LSTM | 5.7702 × 10−1 ± 1.0583 × 10−3 | 4.2354 × 10−1 ± 6.3545 × 10−4 | 5.8020 × 10−1 ± 2.1789 × 10−3 | |
| BO-EnTSFRT | 8.5004 × 10−1 ± 5.7774 × 10−4 | 6.7746 × 10−1 ± 2.1606 × 10−4 | 3.1419 × 10−1 ± 1.4888 × 10−3 | |
| BO-EnTSFRT-LRDT | 6.4225 × 10−1 ± 1.2975 × 10−32 | 4.9011 × 10−1 ± 5.1899 × 10−32 | 4.8149 × 10−1 ± 2.9193 × 10−32 | |
| BO-EnTSFRT-LSTM | 4.3991 × 10−1 ± 2.0766 × 10−4 | 3.1771 × 10−1 ± 1.1515 × 10−4 | 7.5649 × 10−1 ± 2.4804 × 10−4 |
| Model | Hyperparameter | Range | Step Size |
|---|---|---|---|
| BO | [40, 400] | 40 | |
| / | / | ||
| [0.05, 1] | 0.1 | ||
| Main Model | [0.1, 1] | 0.1 | |
| [3, 30] | 3 | ||
| [5, 50] | 5 | ||
| [0.1, 1] | 0.1 | ||
| [10, 100] | 10 | ||
| [20, 200] | 20 | ||
| Compensation Model | [0.01, 0.1] | 0.01 | |
| [0.05, 1) | 0.05 | ||
| [200, 400] | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W.; Tang, J.; Tian, H.; Wang, T. Flue Gas Oxygen Content Model Based on Bayesian Optimization Main–Compensation Ensemble Algorithm in Municipal Solid Waste Incineration Process. Sustainability 2025, 17, 3048. https://doi.org/10.3390/su17073048
Yang W, Tang J, Tian H, Wang T. Flue Gas Oxygen Content Model Based on Bayesian Optimization Main–Compensation Ensemble Algorithm in Municipal Solid Waste Incineration Process. Sustainability. 2025; 17(7):3048. https://doi.org/10.3390/su17073048
Chicago/Turabian StyleYang, Weiwei, Jian Tang, Hao Tian, and Tianzheng Wang. 2025. "Flue Gas Oxygen Content Model Based on Bayesian Optimization Main–Compensation Ensemble Algorithm in Municipal Solid Waste Incineration Process" Sustainability 17, no. 7: 3048. https://doi.org/10.3390/su17073048
APA StyleYang, W., Tang, J., Tian, H., & Wang, T. (2025). Flue Gas Oxygen Content Model Based on Bayesian Optimization Main–Compensation Ensemble Algorithm in Municipal Solid Waste Incineration Process. Sustainability, 17(7), 3048. https://doi.org/10.3390/su17073048







