Day-to-Day and Within-Day Traffic Assignment Model of Heterogeneous Travelers Within the MaaS Framework
Abstract
1. Introduction
2. Problem Description and Preliminary Model
3. Dual Dynamic Departure Time and Route Choice Adjustment Model for Heterogeneous Users
3.1. Within-Day Traffic Adjustment for Heterogeneous Users
3.1.1. Subscribed User SO Model
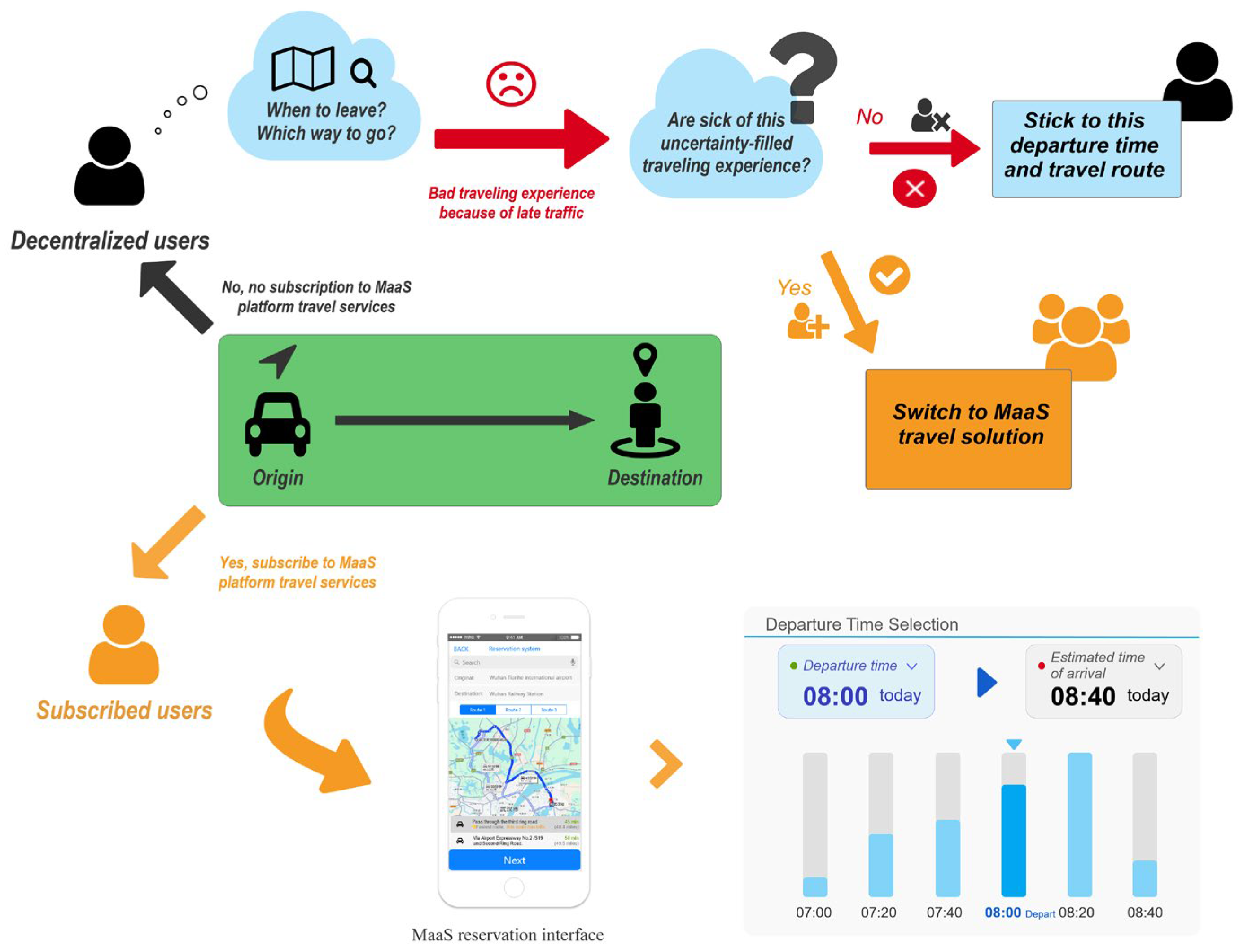
3.1.2. Decentralized Users’ Experience-Based Travel Model
- Departure time adjustment
- 2.
- Travel route adjustment
3.2. The Day-to-Day Flow Adjustment Model Among Heterogeneous Users
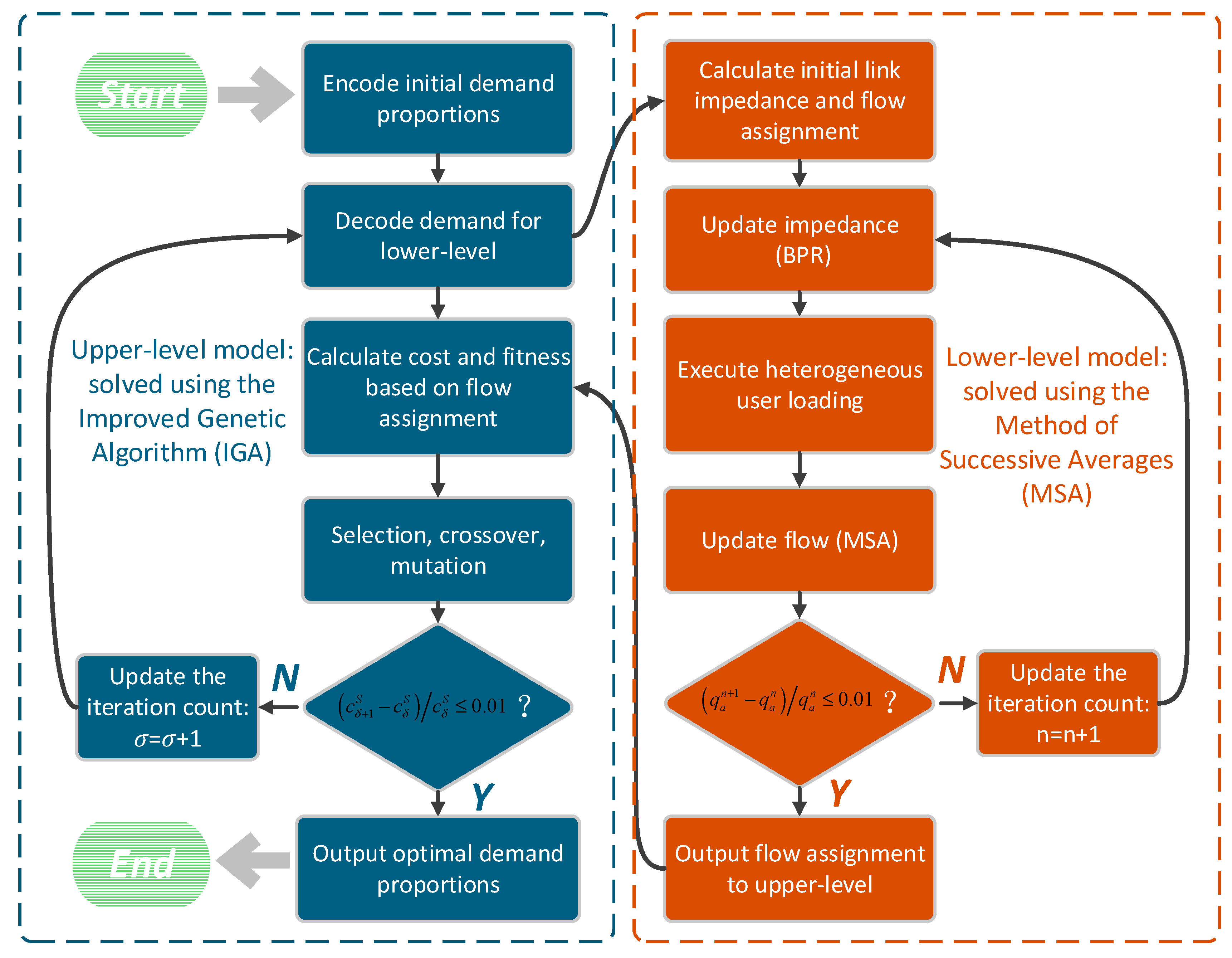
3.3. IGA-MSA Hybrid Algorithm
3.3.1. The Upper-Level Algorithm
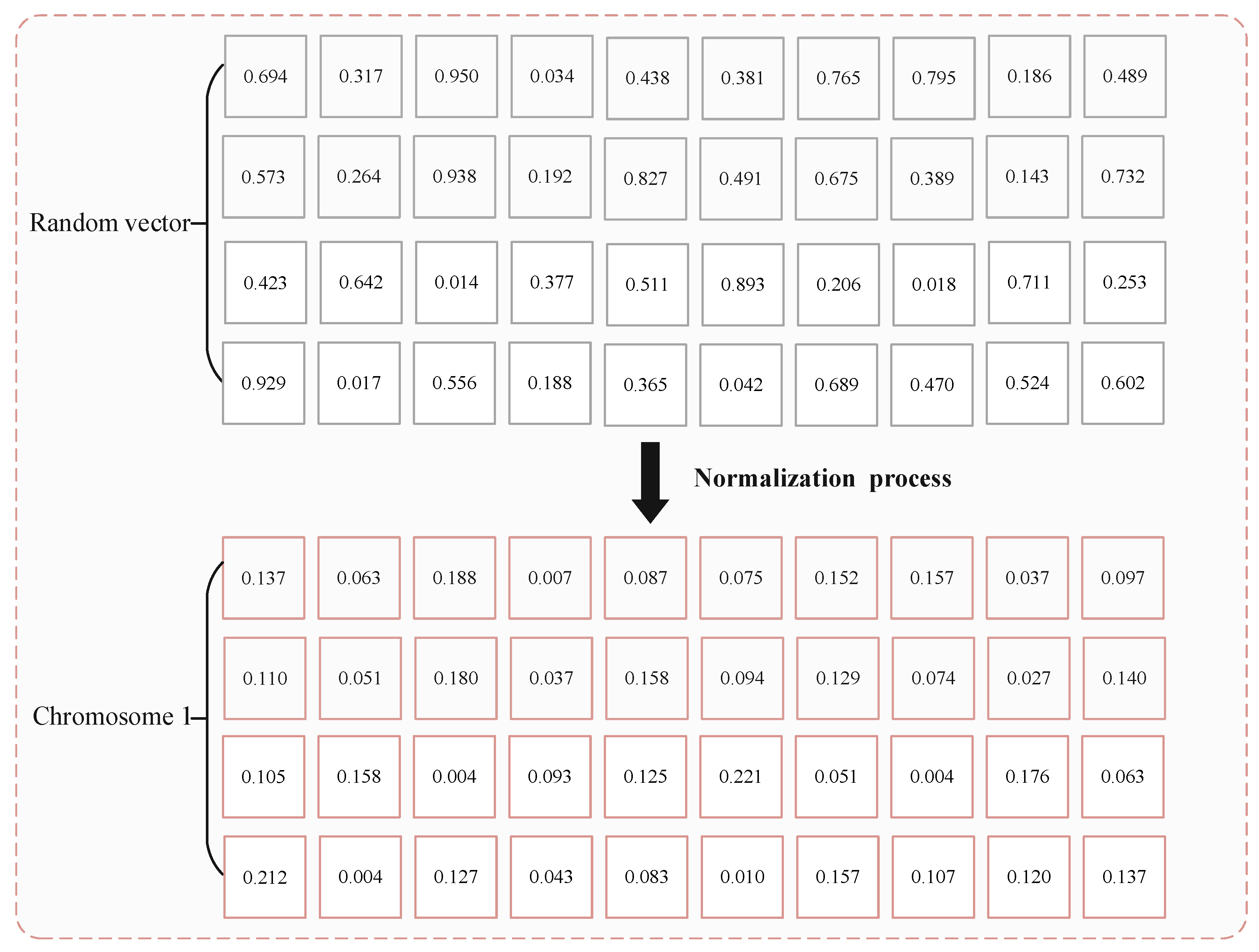
- Chromosome representation and initial population generation
- 2.
- Fitness function
- 3.
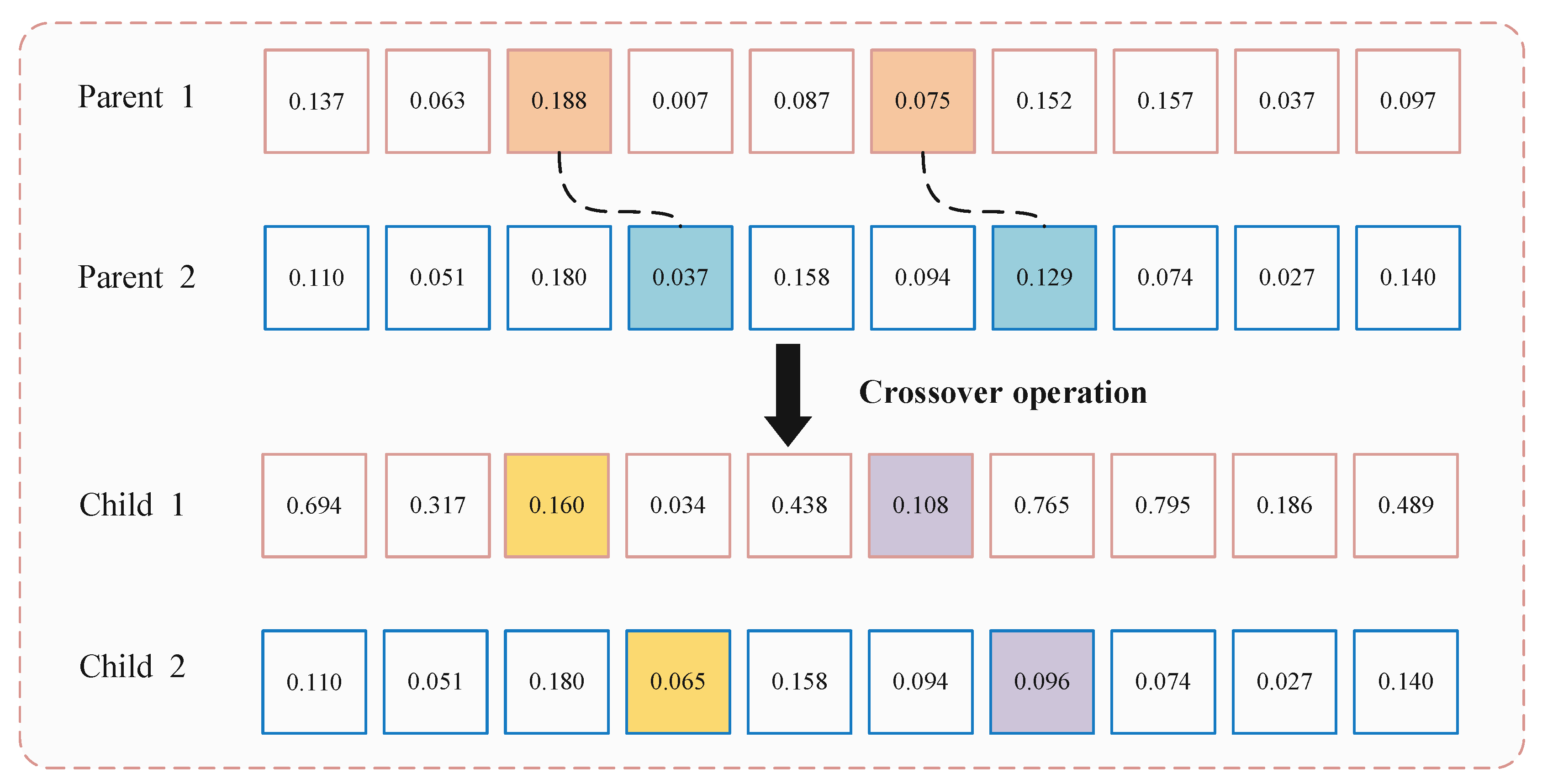
- Crossover operations
- 4.
- Mutation operations
- 5.
- Selection operations
3.3.2. The Lower-Level Algorithm
4. Numerical Examples
4.1. Example Data
4.2. Evolution Results Analysis
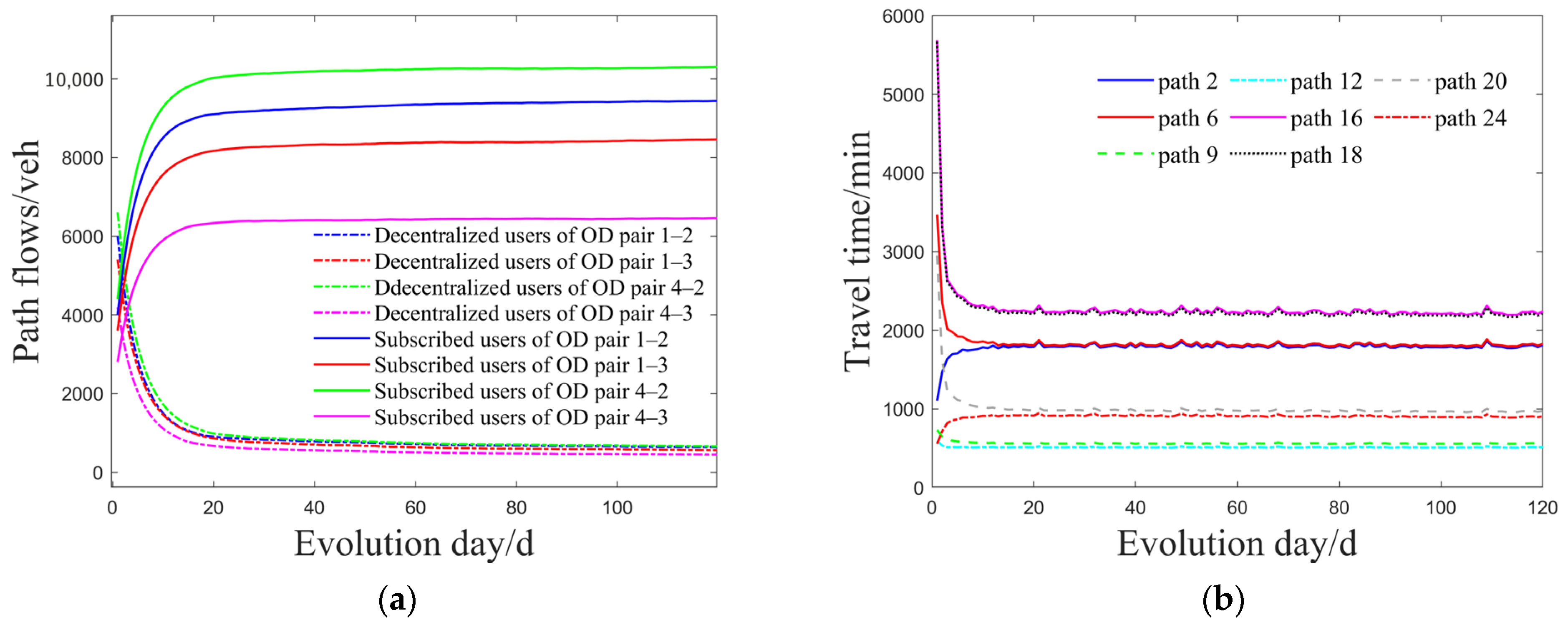
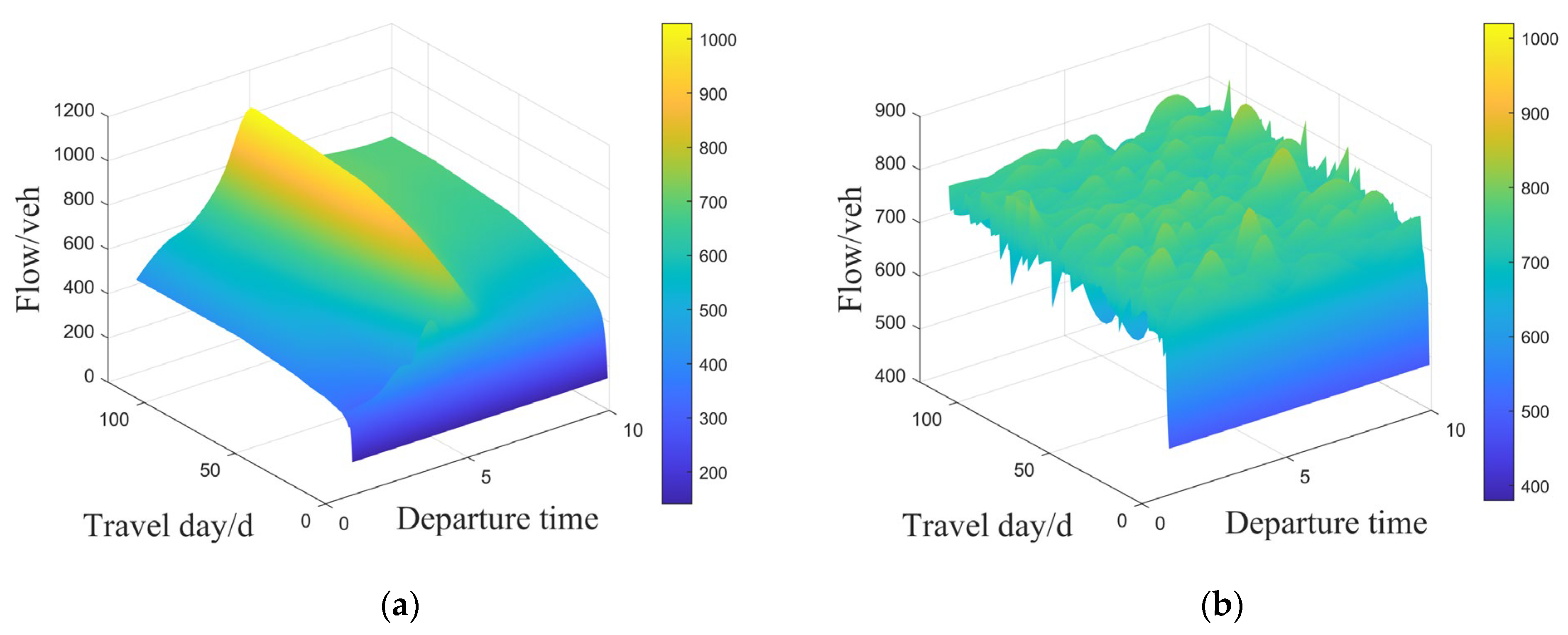
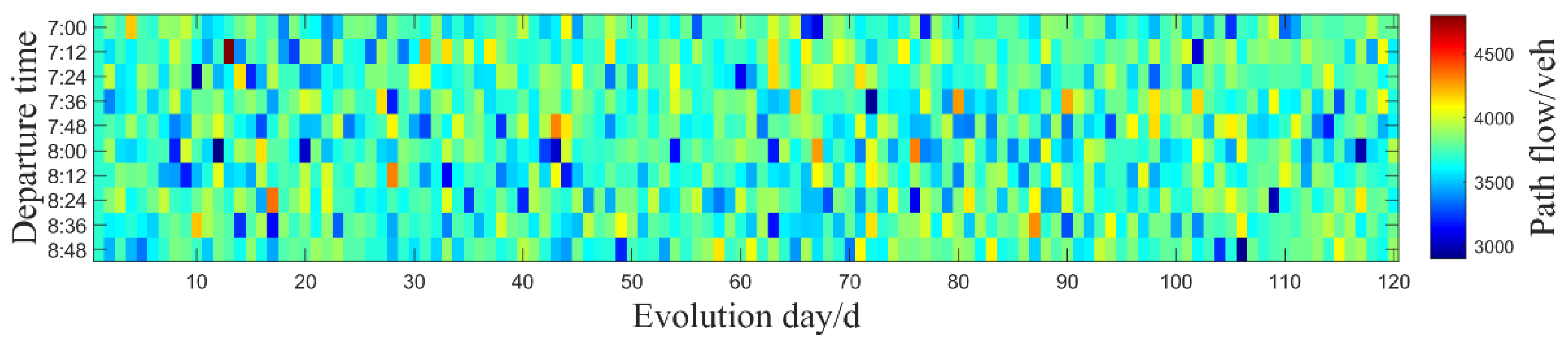
4.2.1. Analysis of Traffic Flow Evolution in the Network
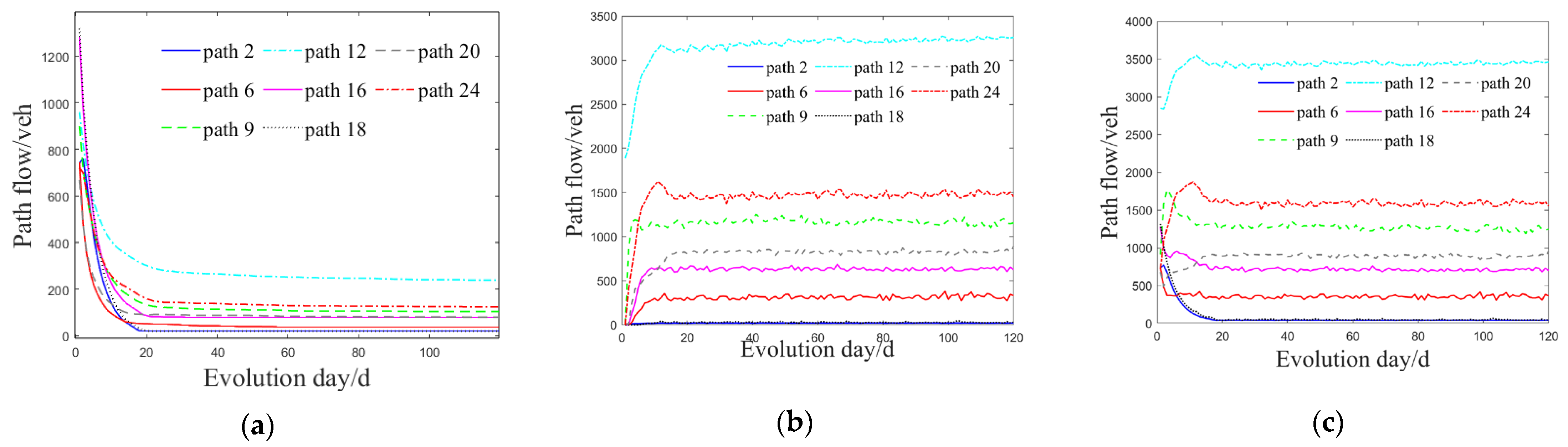
4.2.2. Evaluation of the IGA-MSA Hybrid Algorithm
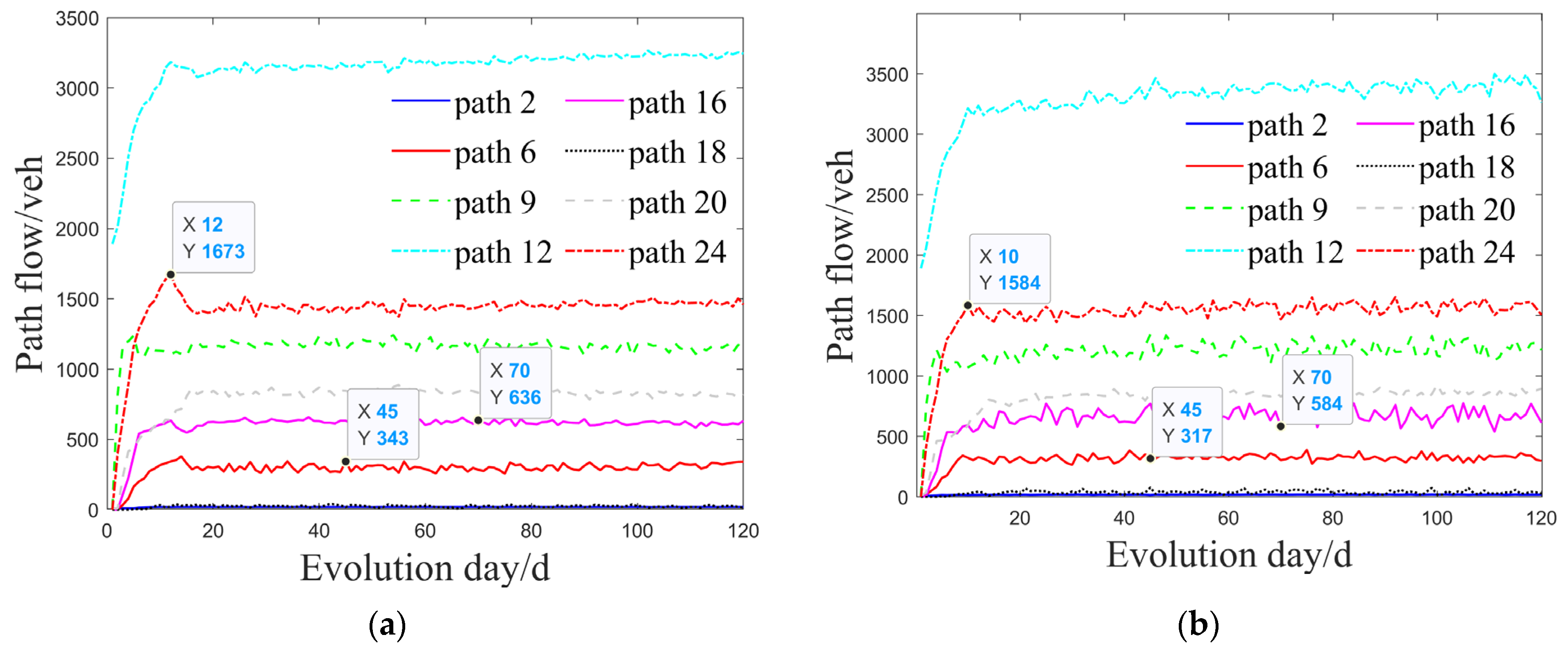
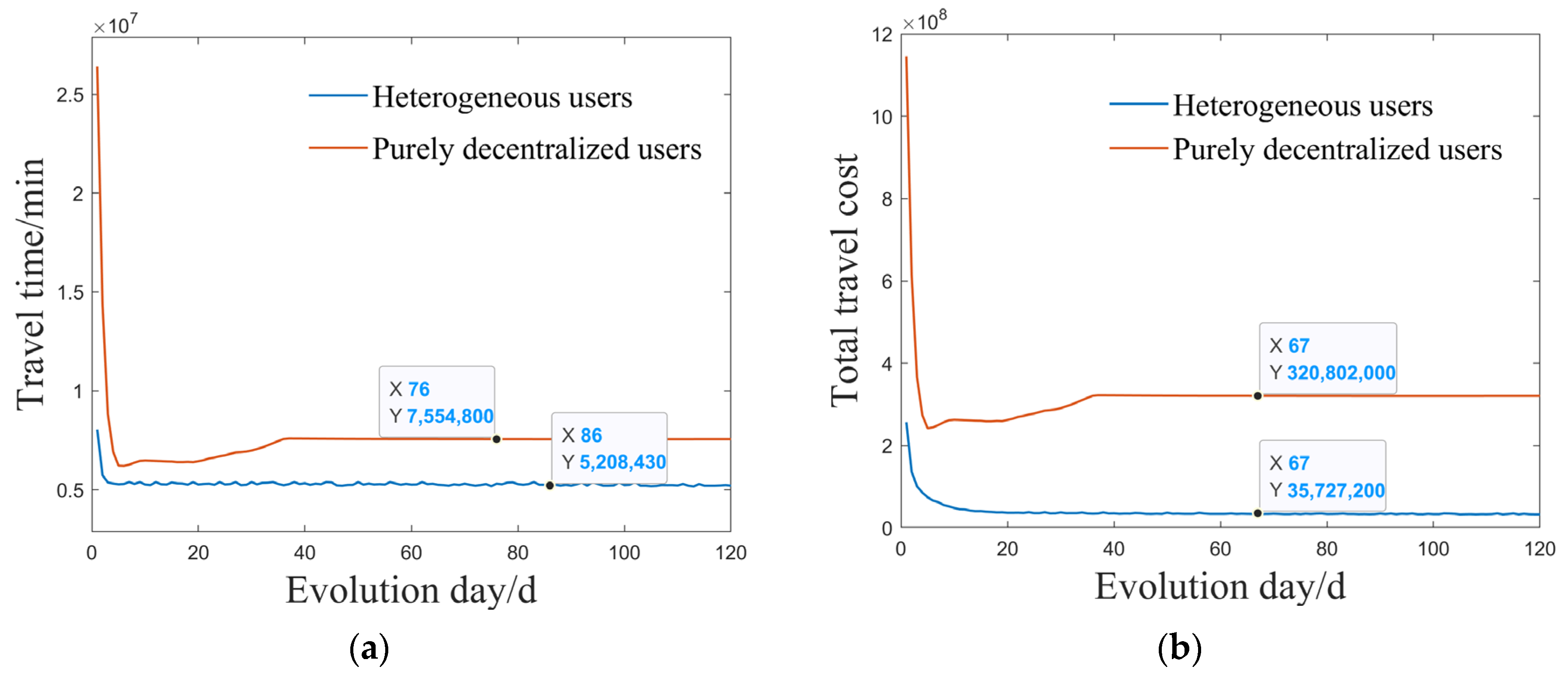
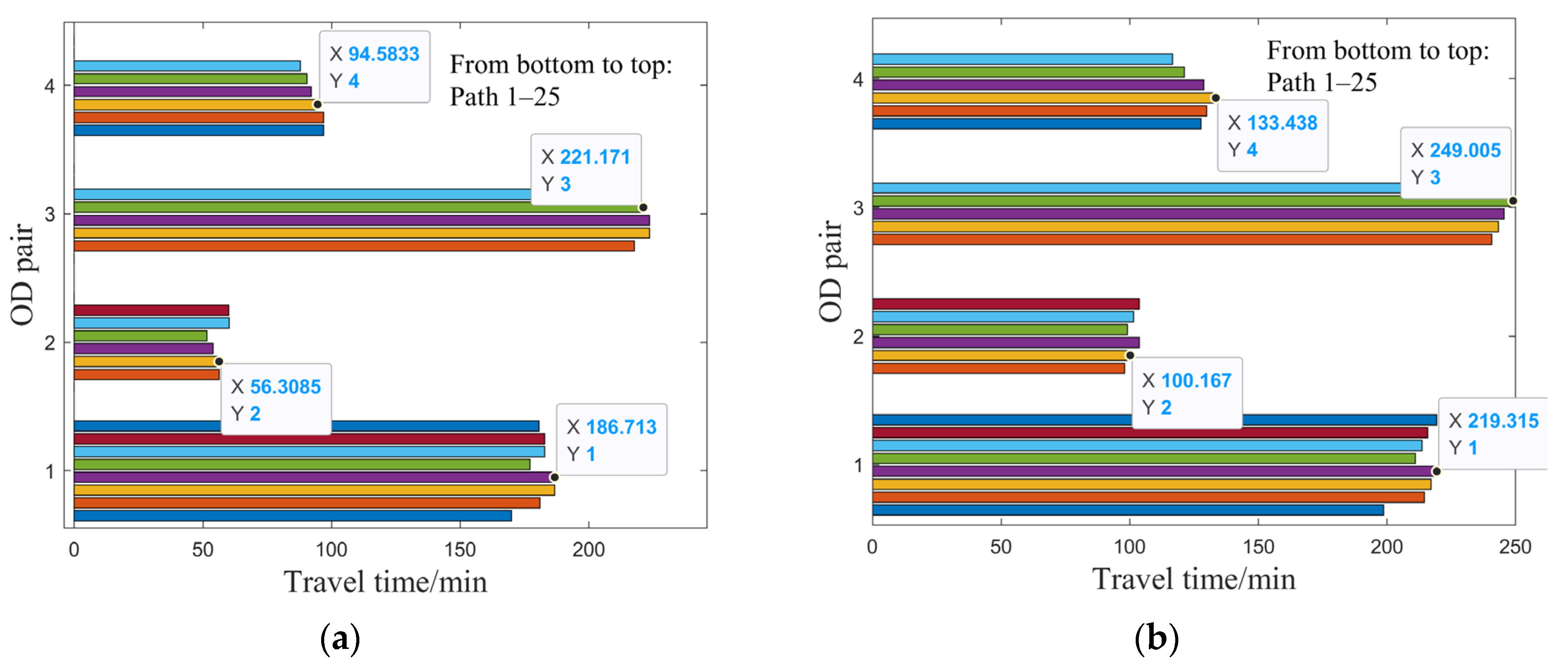
4.2.3. Impact of the MaaS Assignment Model on Traffic Flow Evolution
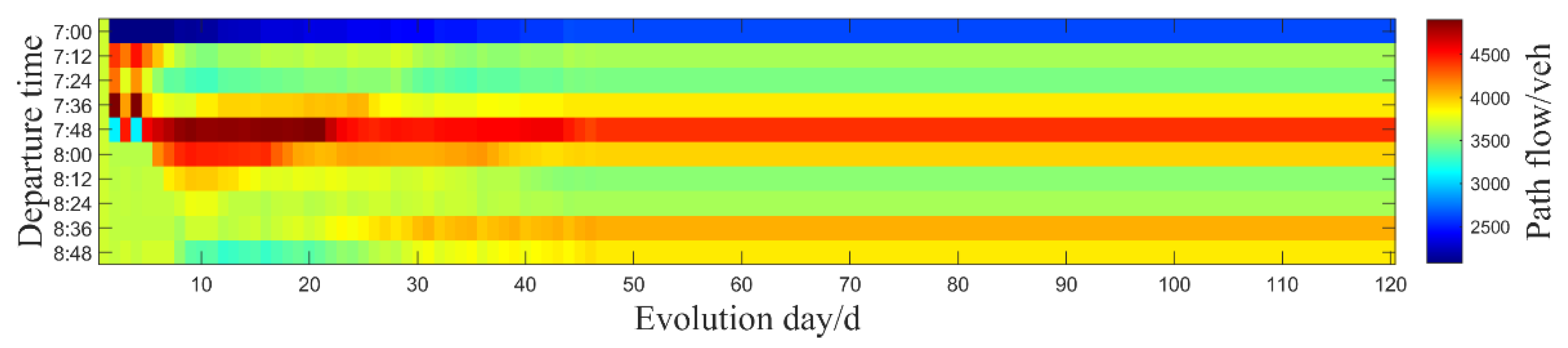
4.2.4. Impact of the MaaS Assignment Model on Departure Times
5. Conclusions
- The MaaS platform significantly attracts private car users by effectively reducing travel costs, prompting many decentralized users to transition to subscribed users gradually. As the system evolves day by day, path and departure-time selection behaviors for both user groups become stable; however, notable differences in path selections across various OD pairs suggest that traffic demand management strategies should be refined based on specific travel demand structures and network capacities;
- Analysis of time-varying traffic demand revealed that decentralized users relying solely on personal experiences tend to concentrate travel within specific time windows, frequently causing peak-hour congestion. Conversely, users guided by the MaaS platform exhibit more evenly distributed departure times, emphasizing the platform’s considerable advantage in managing peak-period traffic flows and reducing congestion risks;
- The proposed IGA-MSA algorithm demonstrated strong performance by effectively reducing total travel costs during the early stages of system evolution and consistently outperforming traditional uniform allocation strategies throughout the evolutionary process. This facilitates more rational and efficient utilization of network capacities.
- The travel behavior model developed in this study assumes all users are fully rational decision-makers, neglecting potential irrational or varied rational decision-making behaviors observed in real-world conditions. Future research could incorporate theories from behavioral economics and psychology to introduce diverse user behavior patterns, enabling more accurate modeling of real-world travel decision processes;
- Although the IGA-MSA algorithm effectively reduces overall travel costs, its current applicability is limited to scenarios with fewer OD pairs and relatively simple, non-overlapping route networks, posing scalability challenges. Future studies could enhance this algorithm by integrating deep learning or advanced heuristic search methods, developing high-performance hybrid dynamic flow allocation algorithms suitable for large-scale, complex networks;
- This research has not addressed the design and evaluation of differentiated incentive mechanisms, which are crucial for enhancing user acceptance of MaaS platforms and accelerating the system’s progression toward optimal conditions. Future studies could explore mixed incentive strategies combining dynamic incentive mechanisms, differentiated pricing, and multi-faceted subsidy models, evaluating their impacts on heterogeneous user travel behaviors. This approach would enable finer management of travel demand, enhancing the practical applicability and adaptability of the MaaS optimization framework proposed herein.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jin, S.T.; Kong, H.; Wu, R.; Sui, D.Z. Ridesourcing, the Sharing Economy, and the Future of Cities. Cities 2018, 76, 96–104. [Google Scholar] [CrossRef]
- Merchant, D.K.; Nemhauser, G.L. A Model and an Algorithm for the Dynamic Traffic Assignment Problems. Transp. Sci. 1978, 12, 183–199. [Google Scholar] [CrossRef]
- Siri, E.; Siri, S.; Sacone, S. A Topology-Based Bounded Rationality Day-to-Day Traffic Assignment Model. Commun. Transp. Res. 2022, 2, 100076. [Google Scholar] [CrossRef]
- Yu, Y.; Han, K.; Ochieng, W. Day-to-Day Dynamic Traffic Assignment with Imperfect Information, Bounded Rationality and Information Sharing. Transp. Res. Part C Emerg. Technol. 2020, 114, 59–83. [Google Scholar] [CrossRef]
- Watling, D. Stability of the Stochastic Equilibrium Assignment Problem: A Dynamical Systems Approach. Transp. Res. Part B Methodol. 1999, 33, 281–312. [Google Scholar] [CrossRef]
- Watling, D.; Hazelton, M.L. The Dynamics and Equilibria of Day-to-Day Assignment Models. Netw. Spat. Econ. 2003, 3, 349–370. [Google Scholar]
- Ye, H.; Xiao, F.; Yang, H. Day-to-Day Dynamics with Advanced Traveler Information. Transp. Res. Part B Methodol. 2021, 144, 23–44. [Google Scholar] [CrossRef]
- Smith, M.J. The Stability of a Dynamic Model of Traffic Assignment—An Application of a Method of Lyapunov. Transp. Sci. 1984, 18, 245–252. [Google Scholar] [CrossRef]
- He, X.; Guo, X.; Liu, H.X. A Link-Based Day-to-Day Traffic Assignment Model. Transp. Res. Part B Methodol. 2010, 44, 597–608. [Google Scholar] [CrossRef]
- Bar-Gera, H. Continuous and Discrete Trajectory Models for Dynamic Traffic Assignment. Netw. Spat. Econ. 2005, 5, 41–70. [Google Scholar]
- Cantarella, G.E. Day-to-Day Dynamic Models for Intelligent Transportation Systems Design and Appraisal. Transp. Res. Part C Emerg. Technol. 2013, 29, 117–130. [Google Scholar] [CrossRef]
- Guo, R.-Y.; Yang, H.; Huang, H.-J.; Tan, Z. Day-to-Day Flow Dynamics and Congestion Control. Transp. Sci. 2016, 50, 982–997. [Google Scholar] [CrossRef]
- Horowitz, J.L. The stability of stochastic equilibrium in a two-link transportation network. Transp. Res. Part B Methodol. 2008, 18, 13–28. [Google Scholar]
- Han, L.; Du, L. On a Link-Based Day-to-Day Traffic Assignment Model. Transp. Res. Part B Methodol. 2012, 46, 72–84. [Google Scholar] [CrossRef]
- Kumar, A.; Peeta, S. A Day-to-Day Dynamical Model for the Evolution of Path Flows Under Disequilibrium of Traffic Networks with Fixed Demand. Transp. Res. Part B Methodol. 2015, 80, 235–256. [Google Scholar] [CrossRef]
- Cantarella, G.E.; Watling, D.P. Modelling Road Traffic Assignment as a Day-to-Day Dynamic, Deterministic Process: A Unified Approach to Discrete- and Continuous-Time Models. EURO J. Transp. Logist. 2016, 5, 69–98. [Google Scholar] [CrossRef]
- Cantarella, G.E.; Watling, D.P. A General Stochastic Process for Day-to-Day Dynamic Traffic Assignment: Formulation, Asymptotic Behaviour, and Stability Analysis. Transp. Res. Part B Methodol. 2016, 92, 3–21. [Google Scholar] [CrossRef]
- Cantarella, G.E.; Cascetta, E. Dynamic Processes and Equilibrium in Transportation Networks: Towards a Unifying Theory. Transp. Sci. 1995, 29, 305–329. [Google Scholar] [CrossRef]
- Bellei, G.; Gentile, G.; Meschini, L.; Papola, N. A Demand Model with Departure Time Choice for Within-Day Dynamic Traffic Assignment. Eur. J. Oper. Res. 2006, 175, 1557–1576. [Google Scholar] [CrossRef]
- De Palma, A.; Ben-Akiva, M.; Lefevre, C.; Litinas, N. Stochastic Equilibrium Model of Peak Period Traffic Congestion. Transp. Sci. 1983, 17, 430–453. [Google Scholar] [CrossRef]
- Arnott, R.; De Palma, A.; Lindsey, R. Departure Time and Route Choice for the Morning Commute. Transp. Res. Part B Methodol. 1990, 24, 209–228. [Google Scholar] [CrossRef]
- Cascetta, E.; Cantarella, C. A day-to-day and within-day dynamic stochastic assignment model. Transp. Res. Part A Gen. 1991, 25, 277–291. [Google Scholar] [CrossRef]
- Bhat, C.R.; Steed, J.L. A Continuous-Time Model of Departure Time Choice for Urban Shopping Trips. Transp. Res. Part B Methodol. 2002, 36, 207–224. [Google Scholar] [CrossRef]
- Srinivasan, K.K.; Guo, Z. Day-to-Day Evolution of Network Flows Under Departure Time Dynamics in Commuter Decisions. Transp. Res. Rec. J. Transp. Res. Board 2003, 1831, 47–56. [Google Scholar] [CrossRef]
- Xiao, Y.; Lo, H.K. Day-to-Day Departure Time Modeling under Social Network Influence. Transp. Res. Part B Methodol. 2016, 92, 54–72. [Google Scholar] [CrossRef]
- Jittrapirom, P.; Caiati, V.; Feneri, A.-M.; Ebrahimigharehbaghi, S.; González, M.J.A.; Narayan, J. Mobility as a Service: A Critical Review of Definitions, Assessments of Schemes, and Key Challenges. Urban Plan. 2017, 2, 13–25. [Google Scholar] [CrossRef]
- Sochor, J.; Arby, H.; Karlsson, I.C.M.; Sarasini, S. A Topological Approach to Mobility as a Service: A Proposed Tool for Understanding Requirements and Effects, and for Aiding the Integration of Societal Goals. Res. Transp. Bus. Manag. 2018, 27, 3–14. [Google Scholar] [CrossRef]
- Matyas, M.; Kamargianni, M. Survey Design for Exploring Demand for Mobility as a Service Plans. Transportation 2019, 46, 1525–1558. [Google Scholar] [CrossRef]
- Polydoropoulou, A.; Tsouros, I.; Pagoni, I.; Tsirimpa, A. Exploring Individual Preferences and Willingness to Pay for Mobility as a Service. Transp. Res. Rec. J. Transp. Res. Board 2020, 2674, 152–164. [Google Scholar] [CrossRef]
- Farahmand, Z.H.; Gkiotsalitis, K.; Geurs, K.T. Mobility-as-a-Service as a Transport Demand Management Tool: A Case Study among Employees in the Netherlands. Case Stud. Transp. Policy 2021, 9, 1615–1629. [Google Scholar] [CrossRef]
- Caiati, V.; Rasouli, S.; Timmermans, H. Bundling, Pricing Schemes and Extra Features Preferences for Mobility as a Service: Sequential Portfolio Choice Experiment. Transp. Res. Part A Policy Pract. 2020, 131, 123–148. [Google Scholar] [CrossRef]
- Butler, L.; Yigitcanlar, T.; Paz, A. Barriers and Risks of Mobility-as-a-Service (MaaS) Adoption in Cities: A Systematic Review of the Literature. Cities 2021, 109, 103036. [Google Scholar] [CrossRef]
- Ben-Elia, E.; Ettema, D. Rewarding Rush-Hour Avoidance: A Study of Commuters’ Travel Behavior. Transp. Res. Part A Policy Pract. 2011, 45, 567–582. [Google Scholar] [CrossRef]
- Karlsson, I.C.M.; Sochor, J.; Strömberg, H. Developing the ‘Service’ in Mobility as a Service: Experiences from a Field Trial of an Innovative Travel Brokerage. Transp. Res. Procedia 2016, 14, 3265–3273. [Google Scholar] [CrossRef]
- Hensher, D.A.; Hietanen, S. Mobility as a Feature (MaaF): Rethinking the Focus of the Second Generation of Mobility as a Service (MaaS). Transp. Rev. 2022, 43, 325–329. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992; ISBN 978-0-262-58111-0. [Google Scholar]
- Kumar, N.; Kumar, T.; Nema, S.; Thakur, T. A Comprehensive Planning Framework for Electric Vehicles Fast Charging Station Assisted by Solar and Battery Based on Queueing Theory and Non-Dominated Sorting Genetic Algorithm-II in a Co-Ordinated Transportation and Power Network. J. Energy Storage 2022, 49, 104180. [Google Scholar] [CrossRef]
- Victer Paul, P.; Ramalingam, A.; Baskaran, R.; Dhavachelvan, P.; Vivekanandan, K.; Subramanian, R. A New Population Seeding Technique for Permutation-Coded Genetic Algorithm: Service Transfer Approach. J. Comput. Sci. 2014, 5, 277–297. [Google Scholar] [CrossRef]
- Hassanat, A.B.; Prasath, V.B.S.; Abbadi, M.A.; Abu-Qdari, S.A.; Faris, H. An Improved Genetic Algorithm with a New Initialization Mechanism Based on Regression Techniques. Information 2018, 9, 167. [Google Scholar] [CrossRef]
- Kaabi, J.; Harrath, Y. Permutation Rules and Genetic Algorithm to Solve the Traveling Salesman Problem. Arab. J. Basic Appl. Sci. 2019, 26, 283–291. [Google Scholar] [CrossRef]
- Masmoudi, M.A.; Braekers, K.; Masmoudi, M.; Dammak, A. A Hybrid Genetic Algorithm for the Heterogeneous Dial-A-Ride Problem. Comput. Oper. Res. 2017, 81, 1–13. [Google Scholar] [CrossRef]
- Zhang, J.; Chung, H.S.H.; Hu, B.J. Adaptive Probabilities of Crossover and Mutation in Genetic Algorithms Based on Clustering Technique. In Proceedings of the Proceedings of the 2004 Congress on Evolutionary Computation (IEEE Cat. No.04TH8753), Portland, OR, USA, 19–23 June 2004; pp. 2280–2287. [Google Scholar]
- Wang, Y. The Hybrid Genetic Algorithm with Two Local Optimization Strategies for Traveling Salesman Problem. Comput. Ind. Eng. 2014, 70, 124–133. [Google Scholar] [CrossRef]
- Aygun, H.; Turan, O. Application of Genetic Algorithm in Exergy and Sustainability: A Case of Aero-Gas Turbine Engine at Cruise Phase. Energy 2022, 238, 121644. [Google Scholar] [CrossRef]
- Zhao, F.; Zeng, X. Optimization of Transit Network Layout and Headway with a Combined Genetic Algorithm and Simulated Annealing Method. Eng. Optim. 2006, 38, 701–722. [Google Scholar] [CrossRef]
- Li, K.-Q.; Yin, Z.-Y.; Zhang, N.; Liu, Y. A Data-Driven Method to Model Stress-Strain Behaviour of Frozen Soil Considering Uncertainty. Cold Reg. Sci. Technol. 2023, 213, 103906. [Google Scholar] [CrossRef]
- Li, K.-Q.; Yin, Z.-Y.; Zhang, N.; Li, J. A PINN-Based Modelling Approach for Hydromechanical Behaviour of Unsaturated Expansive Soils. Comput. Geotech. 2024, 169, 106174. [Google Scholar] [CrossRef]
- Sheffi, Y.; Powell, W.B. An Algorithm for the Equilibrium Assignment Problem with Random Link Times. Networks 1982, 12, 191–207. [Google Scholar] [CrossRef]
- Kato, H.; Sanko, N.; Ishibe, M.; Sakashita, A. Value of Travel Time Savings for Leisure Trip in Autonomous Vehicles: Case Study from the Tokyo Metropolitan Area. Transp. Res. Interdiscip. Perspect. 2024, 24, 101080. [Google Scholar] [CrossRef]


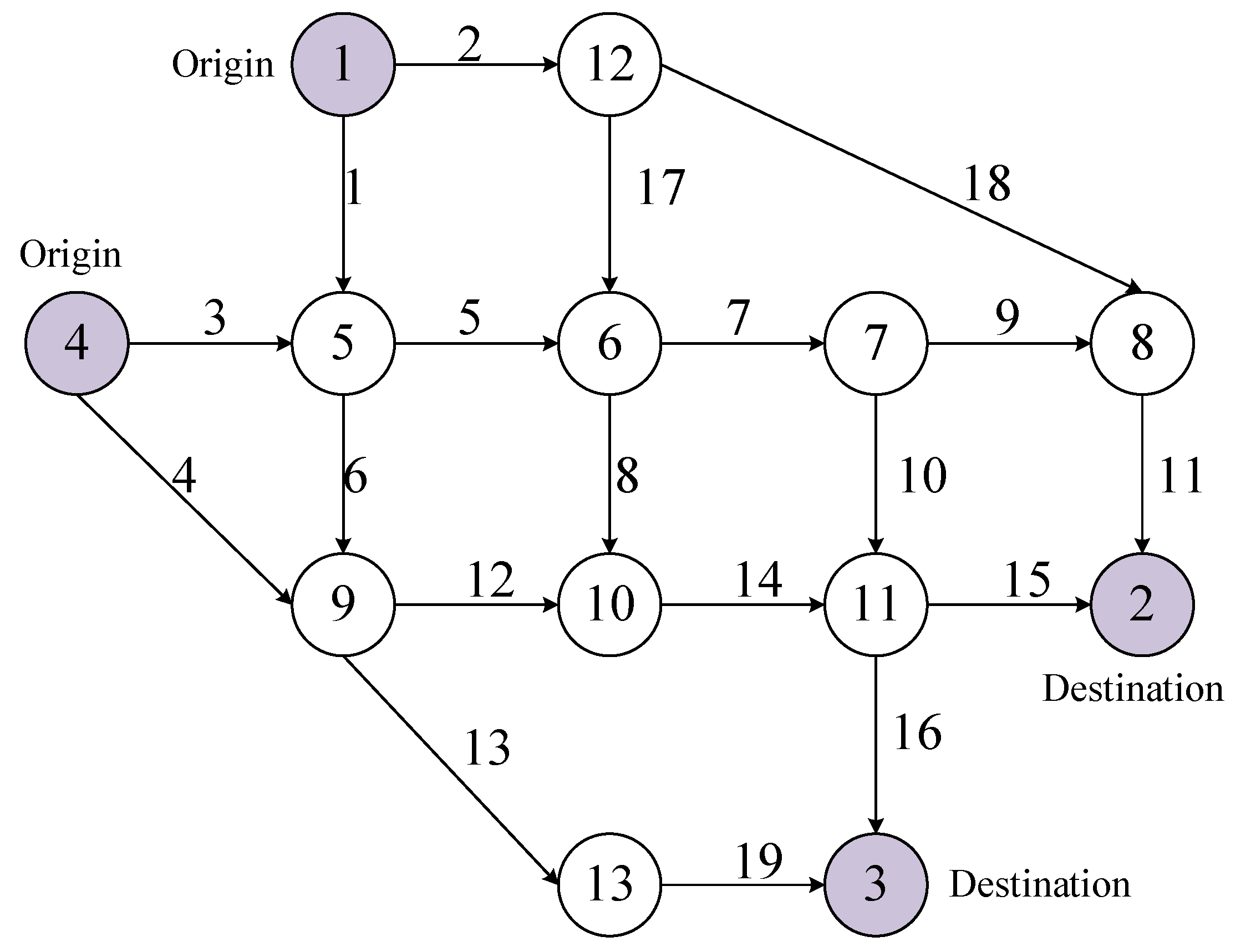



| OD Pair | Path ID | Route | OD Pair | Path ID | Route |
|---|---|---|---|---|---|
| 1–2 | 1 | 2-18-11 | 4–2 | 15 | 3-5-7-9-11 |
| 2 | 2-17-7-9-11 | 16 | 3-5-7-10-15 | ||
| 3 | 2-17-7-10-15 | 17 | 3-5-8-14-15 | ||
| 4 | 2-17-8-14-15 | 18 | 3-6-12-14-15 | ||
| 5 | 1-5-7-9-11 | 19 | 4-12-14-15 | ||
| 6 | 1-5-7-10-15 | 4–3 | 20 | 3-5-7-10-16 | |
| 7 | 1-5-8-14-15 | 21 | 3-5-8-14-16 | ||
| 8 | 1-6-12-14-15 | 22 | 3-6-12-14-16 | ||
| 1–3 | 9 | 1-5-7-10-16 | 23 | 3-6-13-19 | |
| 10 | 1-5-8-14-16 | 24 | 4-12-14-16 | ||
| 11 | 1-6-12-14-16 | 25 | 4-13-19 | ||
| 12 | 1-6-13-19 | ||||
| 13 | 2-17-7-10-16 | ||||
| 14 | 2-17-8-14-16 |
| Link ID | Free-Flow Travel Time (min) | Capacity of the Roadway | Link Length (m) |
|---|---|---|---|
| 1 | 5 | 400 | 4000 |
| 2 | 7 | 600 | 5600 |
| 3 | 3 | 200 | 2400 |
| 4 | 6 | 400 | 4800 |
| 5 | 4 | 700 | 3200 |
| 6 | 7 | 400 | 5600 |
| 7 | 8 | 600 | 6400 |
| 8 | 9 | 300 | 7200 |
| 9 | 4 | 700 | 3200 |
| 10 | 6 | 400 | 4800 |
| 11 | 4 | 300 | 3200 |
| 12 | 3 | 600 | 2400 |
| 13 | 7 | 400 | 5600 |
| 14 | 5 | 700 | 4000 |
| 15 | 8 | 300 | 6400 |
| 16 | 4 | 500 | 3200 |
| 17 | 7 | 700 | 5600 |
| 18 | 6 | 400 | 4800 |
| 19 | 2 | 600 | 1600 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Yang, Y.; Wang, L.; Xie, C.; He, L.; Ma, M. Day-to-Day and Within-Day Traffic Assignment Model of Heterogeneous Travelers Within the MaaS Framework. Sustainability 2025, 17, 2983. https://doi.org/10.3390/su17072983
Chen L, Yang Y, Wang L, Xie C, He L, Ma M. Day-to-Day and Within-Day Traffic Assignment Model of Heterogeneous Travelers Within the MaaS Framework. Sustainability. 2025; 17(7):2983. https://doi.org/10.3390/su17072983
Chicago/Turabian StyleChen, Lingjuan, Yanjing Yang, Lin Wang, Cong Xie, Lin He, and Minghui Ma. 2025. "Day-to-Day and Within-Day Traffic Assignment Model of Heterogeneous Travelers Within the MaaS Framework" Sustainability 17, no. 7: 2983. https://doi.org/10.3390/su17072983
APA StyleChen, L., Yang, Y., Wang, L., Xie, C., He, L., & Ma, M. (2025). Day-to-Day and Within-Day Traffic Assignment Model of Heterogeneous Travelers Within the MaaS Framework. Sustainability, 17(7), 2983. https://doi.org/10.3390/su17072983







