Multi-Objective Optimal Energy Management Strategy for Grid-Interactive Hydrogen Refueling Stations in Rural Areas
Abstract
1. Introduction
1.1. Motivation
1.2. Literature Survey
1.3. Contributions
- A multi-objective optimal energy management model is presented for HRSs located in rural areas with RESs, battery energy storage systems, and hydrogen energy systems, serving various types of EVs such as tractors, combine harvesters, off-road vehicles, cars, and motorcycles. To the best of the authors’ knowledge, this study is the first example in the literature addressing the multi-objective optimal management of grid-interactive, renewable-supported HRSs serving hydrogen-powered vehicles in rural areas.
- One of the objective functions for the operation of the HRS is to maximize the profit, while the other objective is to improve the load factor. The optimum operation can be achieved by selecting one of these two objectives. The proposed structure also calculates the reduction in carbon emissions achieved, contributing to sustainability and a cleaner environment.
- The proposed structure can perform bi-directional trading with both the electrical power grid and the hydrogen gas network. This capability allows for dynamic adjustments to supply and demand, optimizing energy distribution, enhancing grid stability, and supporting the integration of sustainable energy solutions into both sectors.
1.4. Paper Organization
2. Proposed Structure and Mathematical Modeling
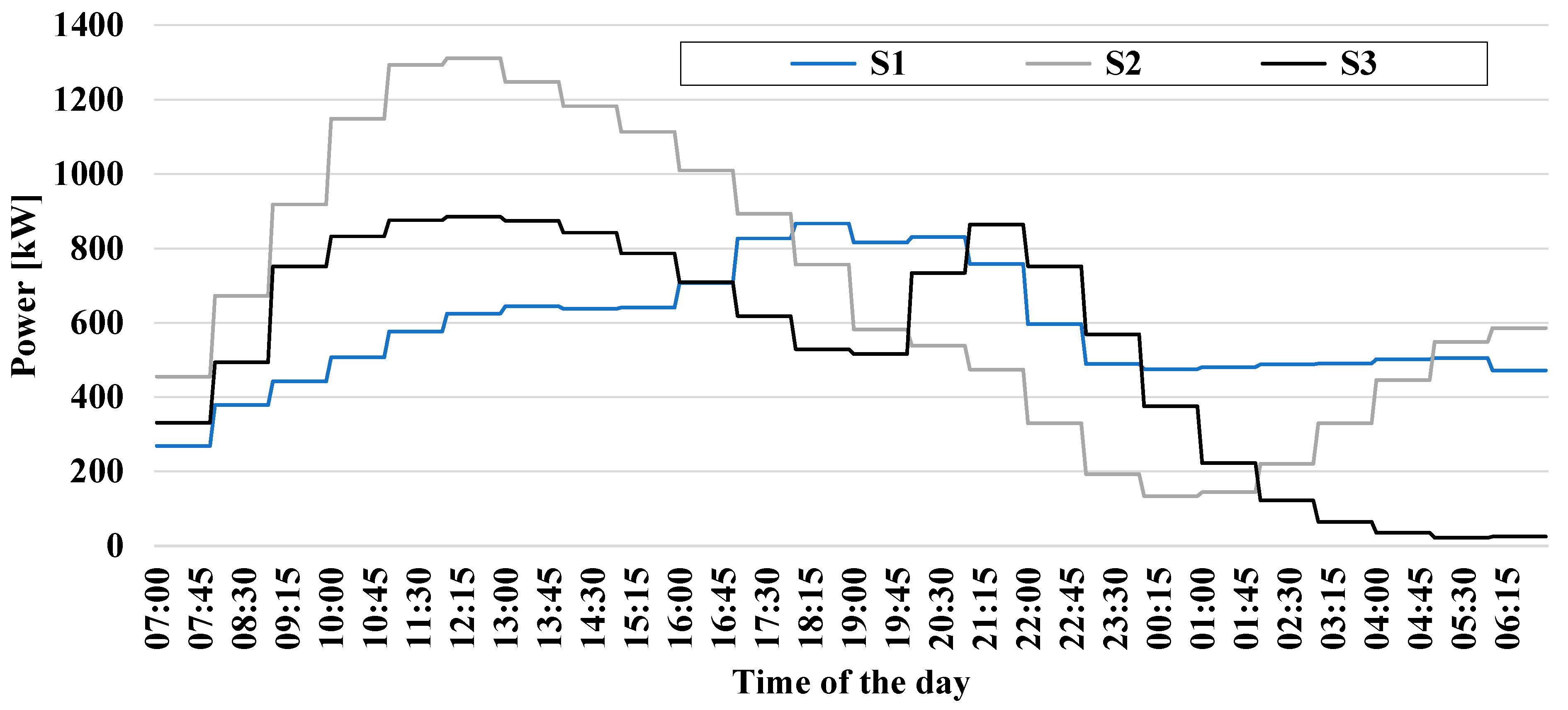
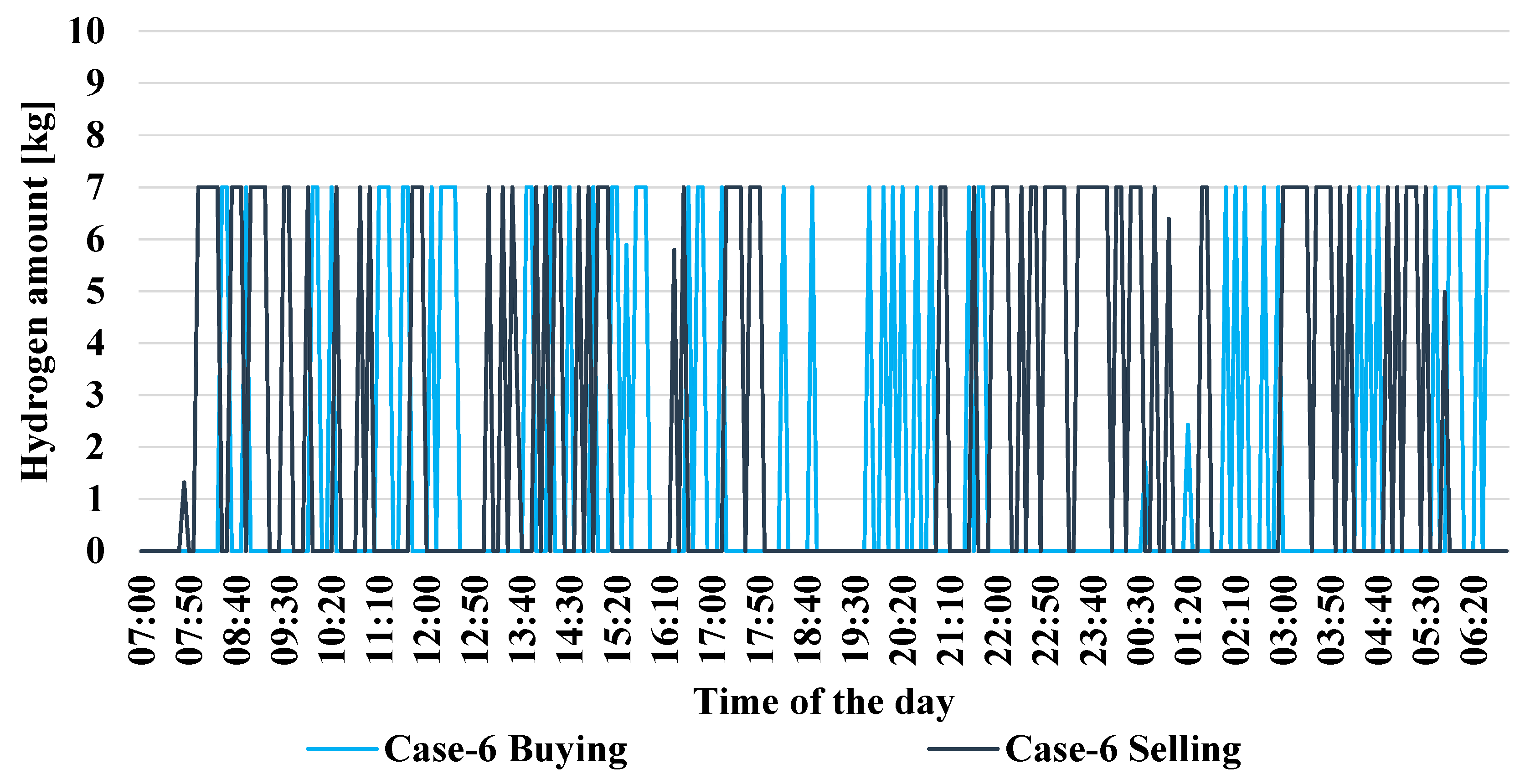
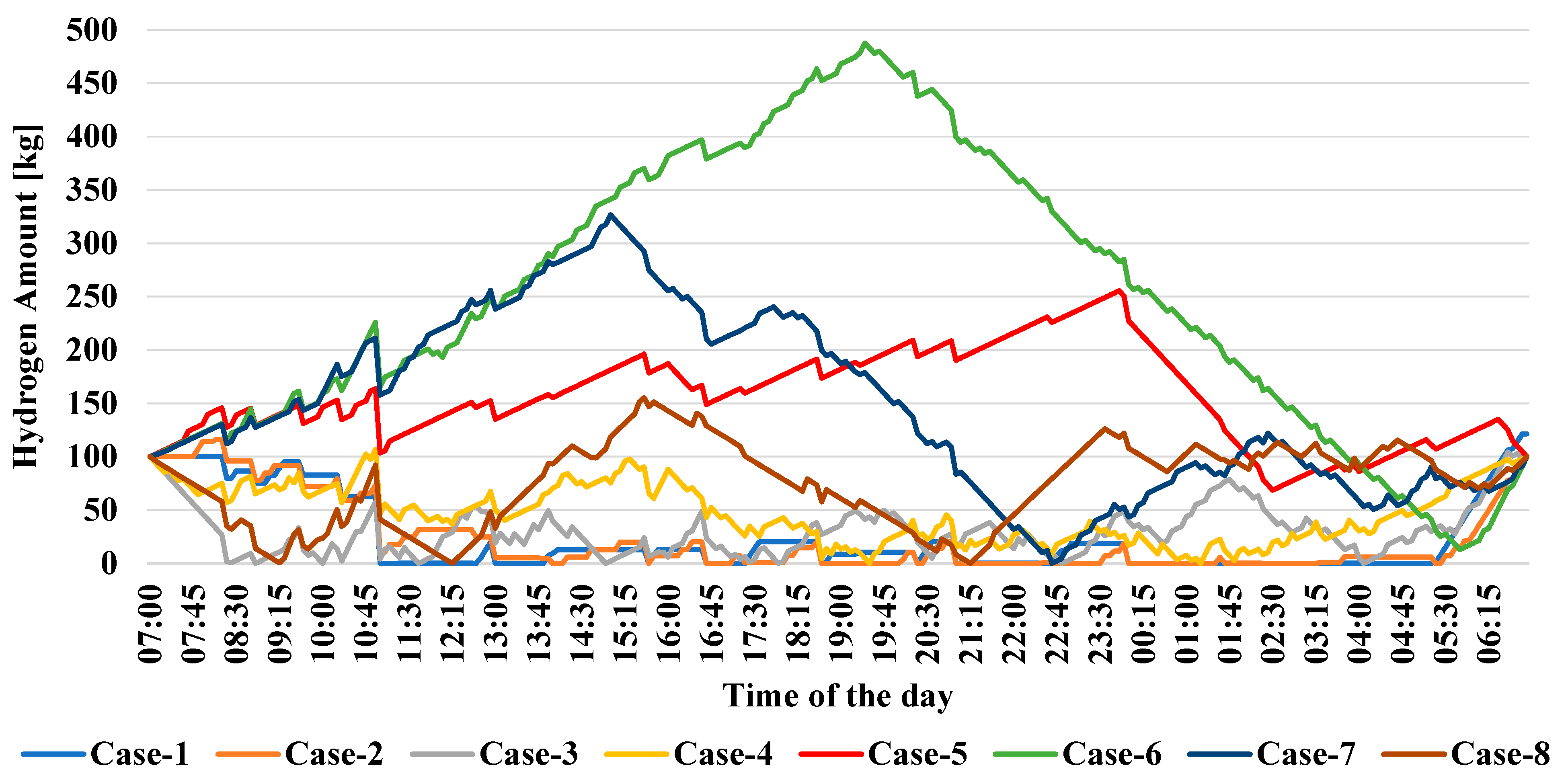
3. Test and Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Saade, R.G.; Zhang, X.; Yu, C.; Yao, J. A Thematic Analysis, Definition, and a Green Aviation Conceptual Model—Putting It All Together. Sustainability 2025, 17, 564. [Google Scholar] [CrossRef]
- Samawi, G.A.; Bwaliez, O.M.; Jreissat, M.; Kandas, A. Advancing Sustainable Development in Jordan: A Business and Economic Analysis of Electric Vehicle Adoption in the Transportation Sector. World Electr. Veh. J. 2025, 16, 45. [Google Scholar] [CrossRef]
- Gibassier, D. Accounting For Social and Environmental Sustainability: A Multi-Capital Approach; Taylor & Francis: London, UK, 2025; pp. 1–238. [Google Scholar] [CrossRef]
- Yıldız, Ö.A.; Sarıçiçek, İ.; Yazıcı, A. A Reinforcement Learning-Based Solution for the Capacitated Electric Vehicle Routing Problem from the Last-Mile Delivery Perspective. Appl. Sci. 2025, 15, 1068. [Google Scholar] [CrossRef]
- Dong, Z.; Tao, Y.; Lai, S.; Wang, T.; Zhang, Z. Powering Future Advancements and Applications of Battery Energy Storage Systems Across Different Scales. Energy Storage Appl. 2025, 2, 1. [Google Scholar] [CrossRef]
- Li, M.; Dai, S.; Shi, Y.; Qin, K.; Brownson, R.C.; Kestens, Y.; Luo, M.; Liu, S.; Su, J.; Liu, G.G.; et al. Heterogeneous impacts of and vulnerabilities to the COVID-19 pandemic. Landsc. Ecol. 2025, 40, 32. [Google Scholar] [CrossRef]
- Martínez, S.H.; Mesman, J.; Sneum, D.M.; Holstenkamp, L.; Harmsen, R.; Menkveld, M.; Akerboom, S.; Faaij, A. From consumers to pioneers: Insights from thermal energy communities in Denmark, Germany and the Netherlands. Energy Sustain. Soc. 2025, 15, 5. [Google Scholar] [CrossRef]
- Çiçek, A.; Erenoğlu, A.K.; Taşcıkaraoglu, A.; Erdinç, O. Energy Management Strategy for a Microgrid Including All-in-One Electric Vehicle Station, Renewable Energy and Demand Response. In Proceedings of the 2023 International Conference on Smart Energy Systems and Technologies (SEST), Mugla, Turkiye, 4–6 September 2023. [Google Scholar] [CrossRef]
- Şafak, B.; Özekinci, D.; Çiçek, A. Üzerinde Fotovoltaik Panele Sahip Olan Elektrikli Araçları Içeren Bir Şarj Otoparkının Çok Amaçlı Optimum Enerji Yönetim Stratejisi. Niğde Ömer Halisdemir Üniversitesi Mühendislik Bilim. Derg. 2023, 13, 1–9. [Google Scholar] [CrossRef]
- Verbruggen, A.; Yermekova, G.; Baigarin, K. Dubious Promises of Hydrogen Energy in a Climate-Constrained World. Energies 2025, 18, 491. [Google Scholar] [CrossRef]
- Tao, Y.; Qiu, J.; Lai, S.; Zhang, X.; Wang, G. Collaborative Planning for Electricity Distribution Network and Transportation System Considering Hydrogen Fuel Cell Vehicles. IEEE Trans. Transp. Electrif. 2020, 6, 1211–1225. [Google Scholar] [CrossRef]
- Woo, H.; Son, Y.; Choi, S. Optimal Scheduling Model for Renewable Energy Source-Assisted Electric and Hydrogen Vehicle Charging Station in HPS Market. In Proceedings of the 2023 IEEE Power & Energy Society General Meeting (PESGM), Orlando, FL, USA, 16–20 July 2023. [Google Scholar] [CrossRef]
- Li, H.; Zhang, X.; Zhong, C.; Wang, Z. Study on the Optimization of Capacity Configuration Strategy for Wind-photovoltaic-hydrogen Energy Storage Stations. In Proceedings of the 2024 3rd International Conference on Energy, Power and Electrical Technology (ICEPET), Chengdu, China, 17–19 May 2024; pp. 108–111. [Google Scholar] [CrossRef]
- Zhu, L.; Xiong, K.; Lei, G.; Luo, Y.; Liu, W. A study on the macro-micro two-stage site selection of electric-hydrogen hybrid refueling stations based on GIS and Fuzzy-TODIM. Int. J. Hydrogen Energy 2024. [Google Scholar] [CrossRef]
- De Padova, A.; Schiera, D.S.; Minuto, F.D.; Lanzini, A. Spatial MILP optimization framework for siting Hydrogen Refueling Stations in heavy-duty freight transport. Int. J. Hydrogen Energy 2024, 94, 669–686. [Google Scholar] [CrossRef]
- Elomiya, A.; Křupka, J.; Simic, V.; Švadlenka, L.; Průša, P.; Jovčić, S. An advanced spatial decision model for strategic placement of off-site hydrogen refueling stations in urban areas. eTransportation 2024, 22, 100375. [Google Scholar] [CrossRef]
- He, Q.; Peng, S.; Zhang, Z.; He, Y.; Fan, L.; Yang, Z.; Wang, X.; Shi, X.; Su, H.; Zhang, J. A systematic framework of resilience assessment based on multi-state transition modeling under two-phase recovery for hydrogen refueling stations. Int. J. Hydrogen Energy 2024, 90, 481–497. [Google Scholar] [CrossRef]
- Hoseyni, S.M.; Mostafa, M.O.M.; Cordiner, J. Mitigating risks in hydrogen-powered transportation: A comprehensive risk assessment for hydrogen refuelling stations, vehicles, and garages. Int. J. Hydrogen Energy 2024, 91, 1025–1044. [Google Scholar] [CrossRef]
- Lu, Z.; Cao, Y.; Zou, Y.; Li, X.; Yang, F.; Khakzad, N.; Chen, C. Dynamic risk analysis of fire and explosion domino accidents at hydrogen refueling stations using Dynamic Bayesian Network. Int. J. Hydrogen Energy 2024, 95, 546–557. [Google Scholar] [CrossRef]
- Tan, H.; Shao, Z.; Wang, Q.; Lin, Z.; Li, Z.; Weng, H.; Mohamed, M.A. A coordinated planning method of hydrogen refueling stations and distribution network considering gas-solid two-phase hydrogen storage mode. Int. J. Hydrogen Energy 2025, 100, 1561–1573. [Google Scholar] [CrossRef]
- Kang, J.; Su, T.; Li, J.; Wang, Z.; Zhang, J. Research on risk evolution, prevention, and control of fire and explosion accidents in hydrogen refueling stations based on the AcciMap-FTA model. Process Saf. Environ. Prot. 2025, 194, 107–118. [Google Scholar] [CrossRef]
- Jordehi, A.R.; Mansouri, S.A.; Tostado-Véliz, M.; Safaraliev, M.; Hakimi, S.M.; Nasir, M. A tri-level stochastic model for operational planning of microgrids with hydrogen refuelling station-integrated energy hubs. Int. J. Hydrogen Energy 2024, 96, 1131–1145. [Google Scholar] [CrossRef]
- Çiçek, A. Yenilenebilir Enerji Destekli Bir Hidrojen Yakıt İkmal İstasyonunun Optimum Enerji Yönetimi. In Proceedings of the 5th International Congress on Engineering Sciences and Multidisciplinary Approaches, İstanbul, Türkiye, 25–26 February 2023; pp. 510–518. [Google Scholar]
- Çiçek, A. Optimal operation of an all-in-one EV station with photovoltaic system including charging, battery swapping and hydrogen refueling. Int. J. Hydrogen Energy 2022, 47, 32405–32424. [Google Scholar] [CrossRef]
- Choi, Y.; Bhakta, S. Hybrid solar photovoltaic-wind turbine system for on-site hydrogen production: A techno-economic feasibility analysis of hydrogen refueling Station in South Korea’s climatic conditions. Int. J. Hydrogen Energy 2024, 93, 736–752. [Google Scholar] [CrossRef]
- Wolf, N.; Neuber, R.; Mädlow, A.; Höck, M. Techno-economic analysis of green hydrogen supply for a hydrogen refueling station in Germany. Int. J. Hydrogen Energy 2025, 106, 318–333. [Google Scholar] [CrossRef]
- Alao, M.A.; Popoola, O.M. Distributed waste-to-hydrogen refuelling station implementation in South Africa: Techno-economic-socio-political and environmental indications. Int. J. Hydrogen Energy 2025, 106, 616–630. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, S.; Decès-Petit, C.; Wang, Y. Holistic Idle Periodic Evaluation method for mass balance monitoring at hydrogen refuelling stations. Int. J. Hydrogen Energy 2025, 97, 66–75. [Google Scholar] [CrossRef]
- Wu, Q.; Bi, Y.; Shi, J.; Wang, S.; Zhang, C.; Huang, S.; Gao, W.; Bi, M. A hydrogen concentration evolution prediction method for hydrogen refueling station leakage based on the Informer model. Int. J. Hydrogen Energy 2025. [Google Scholar] [CrossRef]
- Shoja, Z.M.; Oskouei, A.B.; Nazari-Heris, M. Risk-based optimal management of a multi-energy community integrated with P2X-based vector-bridging systems considering natural gas/hydrogen refueling and electric vehicle charging stations. Renew. Energy Focus 2025, 53, 100680. [Google Scholar] [CrossRef]
- Assunção, R.; Ajeeb, W.; Eckl, F.; Gomes, D.M.; Neto, R.C. Decentralized hydrogen-oxygen co-production via electrolysis for large hospitals with integrated hydrogen refueling station. Int. J. Hydrogen Energy 2025, 103, 87–98. [Google Scholar] [CrossRef]
- Ghaithan, A.M. Multi-objective model for designing hydrogen refueling station powered using on-grid photovoltaic-wind system. Energy 2024, 312, 133464. [Google Scholar] [CrossRef]
- Chu, Y.; Wu, Z.; Yin, Y. Development of a solar-assisted hydrogen-from-power refueling station: A financial incentive model under the Well-to-Wheel and life cycle cost analyses. Int. J. Hydrogen Energy 2025, 103, 288–299. [Google Scholar] [CrossRef]
- Gong, C.; Na, H.; Yun, S.; Kim, Y.J.; Won, W. Liquid hydrogen refueling stations as an alternative to gaseous hydrogen refueling stations: Process development and integrative analyses. eTransportation 2025, 23, 100386. [Google Scholar] [CrossRef]
- Sezer, N.; Bayhan, S. Wind-powered hydrogen refueling station with energy recovery for green mobility in sustainable cities. Energy Convers. Manag. X 2025, 26, 100900. [Google Scholar] [CrossRef]
- SUZUKI-Burgman Fuel-Cell Scooter. Available online: https://www.globalsuzuki.com/Burgman_Fuel-Cell_Scooter/ (accessed on 15 January 2025).
- Toyota Mirai Full Specs. Available online: https://www.toyota.com/mirai/features/mpg_other_price/3002/3003 (accessed on 15 January 2025).
- NEXO: Hyundai’s Hydrogen Fuel-Cell First. Available online: https://www.hyundai.com/au/en/news/vehicles/nexo-hyundai-hydrogen-fuel-cell-first#:~:text=Three-high-pressure-fuel-tanks,a-pressure-of-700-bar (accessed on 15 January 2025).
- Electric Tractors Lead Charge, Hydrogen in the Wind. Available online: https://www.graincentral.com/machinery/electric-tractors-leads-charge-hydrogen-in-the-wind/ (accessed on 15 January 2025).
- XCIENT Fuel Cell Tractor. Available online: https://ecv.hyundai.com/global/en/products/xcient-fuel-cell-tractor-fcev (accessed on 15 January 2025).
- Renewables.ninja—Wind Power and Solar Photovoltaic Power (PV). Available online: https://www.renewables.ninja/ (accessed on 16 November 2023).
- Day-Ahead Market Prices, EPİAŞ—EXIST (Energy Exchange Istanbul). Available online: https://www.epias.com.tr/en/ (accessed on 15 January 2025).
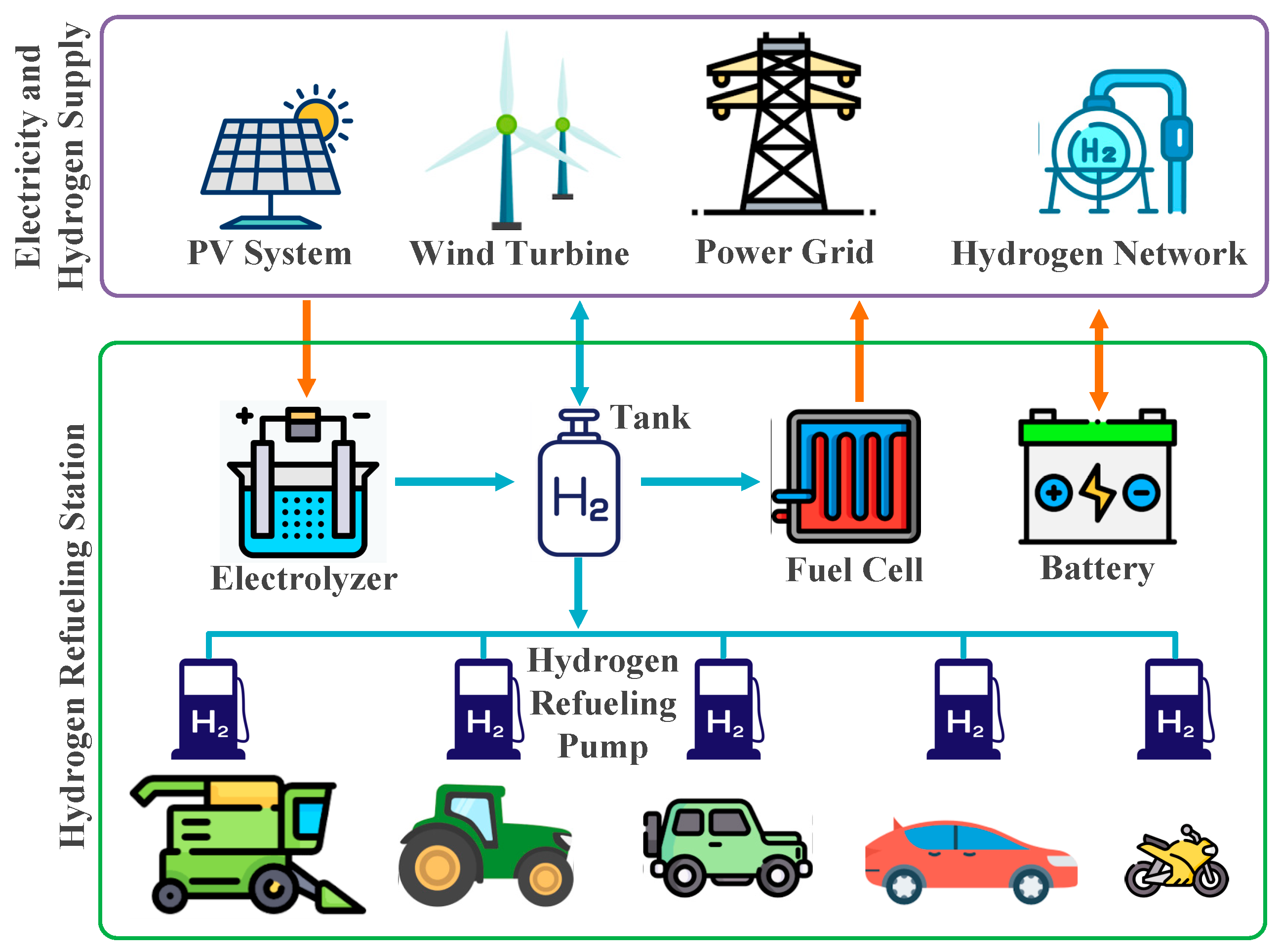




| Definitions of the Proposed Structure | Values |
|---|---|
| Installed capacity of PV system | 0.5 MW |
| Installed capacity of wind power system | 1 MW |
| Minimum capacity of hydrogen tank | 100 kg |
| Capacity of hydrogen tank | 1000 kg |
| Hydrogen pipeline capacity | 7 kg/5 min |
| Unit price of hydrogen energy | $3.03/kg |
| Nominal power of EL | 500 kW |
| Efficiency of EL | 0.7 |
| Nominal power of FC | 500 kW |
| Efficiency of FC | 0.6 |
| DC-AC converter efficiency | 0.95 |
| Battery capacity | 1 MWh |
| Battery charge/discharge power | 250 kW |
| Battery charge/discharge efficiency | 0.9 |
| Time resolution | 5 min |
| A | 33.5 |
| Ramp-up rate and ramp-down rate for FC/EL in a period | 1 |
| Vehicle | Hydrogen Capacity (kg) |
|---|---|
| Suzuki Burgman Fuel-Cell Scooter (Motorcycle) [36] | 0.42 |
| Toyota Mirai (Car) [37] | 5.60 |
| Hyundai Nexo (Car) [38] | 6.33 |
| Van | 8.00 |
| Fendt H2Agrar (Tractor) [39] | 21.00 |
| Combine Harvester | 60.00 |
| Hyundai XCIENT Fuel-Cell Tractor (Truck) [40] | 68.60 |
| Cases | A (Cost) | B (Load Factor) | RESs | Double Capacity of RESs | Double Capacity of the EL |
|---|---|---|---|---|---|
| Case-1 | - | ✓ | - | - | - |
| Case-2 | - | ✓ | ✓ | - | - |
| Case-3 | ✓ | - | - | - | - |
| Case-4 | ✓ | - | ✓ | - | - |
| Case-5 | ✓ | ✓ | - | - | - |
| Case-6 | ✓ | ✓ | ✓ | - | - |
| Case-7 | ✓ | ✓ | ✓ | ✓ | - |
| Case-8 | ✓ | ✓ | ✓ | - | ✓ |
| Cases | Total Cost ($) | |||
|---|---|---|---|---|
| S1 | S2 | S3 | Average | |
| Case-1 | −370.37 | −418.4 | −399.41 | −396.06 |
| Case-2 | 56.49 | 49.34 | −46.99 | 19.61 |
| Case-3 | −219.97 | −265.47 | −268.87 | −251.44 |
| Case-4 | 185.8 | 208.12 | 111.63 | 168.52 |
| Case-5 | −220.58 | −266.79 | −269.79 | −252.39 |
| Case-6 | 184.46 | 207.75 | 111.31 | 167.84 |
| Case-7 | 312.26 | 334.52 | 240.46 | 295.75 |
| Case-8 | 589.97 | 681.69 | 491.83 | 587.83 |
| Cases | Load Factor | |||
|---|---|---|---|---|
| S1 | S2 | S3 | Average | |
| Case-1 | 1 | 1 | 1 | 1 |
| Case-2 | 1 | 1 | 1 | 1 |
| Case-3 | 0.742 | 0.744 | 0.742 | 0.743 |
| Case-4 | 0.222 | 0.332 | 0.248 | 0.267 |
| Case-5 | 0.998 | 0.998 | 0.998 | 0.998 |
| Case-6 | 0.460 | 0.400 | 0.335 | 0.398 |
| Case-7 | 0.809 | 0.646 | 0.635 | 0.697 |
| Case-8 | 0.038 | 0.193 | 0.223 | 0.151 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Şafak, B.; Çiçek, A. Multi-Objective Optimal Energy Management Strategy for Grid-Interactive Hydrogen Refueling Stations in Rural Areas. Sustainability 2025, 17, 2663. https://doi.org/10.3390/su17062663
Şafak B, Çiçek A. Multi-Objective Optimal Energy Management Strategy for Grid-Interactive Hydrogen Refueling Stations in Rural Areas. Sustainability. 2025; 17(6):2663. https://doi.org/10.3390/su17062663
Chicago/Turabian StyleŞafak, Burak, and Alper Çiçek. 2025. "Multi-Objective Optimal Energy Management Strategy for Grid-Interactive Hydrogen Refueling Stations in Rural Areas" Sustainability 17, no. 6: 2663. https://doi.org/10.3390/su17062663
APA StyleŞafak, B., & Çiçek, A. (2025). Multi-Objective Optimal Energy Management Strategy for Grid-Interactive Hydrogen Refueling Stations in Rural Areas. Sustainability, 17(6), 2663. https://doi.org/10.3390/su17062663






